1 Introduction

Fluoride salt-cooled high-temperature reactors (FHRs) [1, 2] are a Gen-IV nuclear energy system that combines the graphite-matrix coated particle fuel (TRISO) adopted in high-temperature gas-cooled reactors and a molten fluoride coolant salt derived from molten salt reactors. This advanced reactor design has several advantages such as intrinsic safety features and potential economic advantages. In 2011, the Chinese Academy of Sciences launched the “thorium molten salt reactor nuclear energy system” (TMSR) project [3, 4], and a 10-MWth solid fuel thorium molten salt reactor (TMSR-SF1) was developed by the Shanghai Institute of Applied Physics, which will be deployed in the next 5–10 years. As a new reactor concept, the radiation damage assessment of the structural materials is crucial to TMSR-SF1 design. Therefore, developing calculation methods to determine the high-resolution neutron flux (especially the fast neutron flux) distribution of the full-scale TMSR-SF1 reactor is necessary.

Currently, Monte Carlo (MC) methods are the main type of computational method applied to model TMSR-SF1 [5, 6]. MC methods are based on a statistical method which simulates individual particles and tracks their histories. These events and information are recorded to obtain their average statistical behaviors as tallies, whereas the possibility of particle transport to different regions varies widely. Therefore, it is very difficult for MC methods to solve global problems that require obtaining tallies over the entire problem space with uniformly low relative uncertainty. However, the fast neutron (E > 0.1 MeV) flux from the core is rapidly attenuated since TMSR-SF1 contains a large amount of neutron moderating material. Therefore, the calculation of the fast neutron flux distribution of TMSR-SF1 is a typical deep penetration global optimization problem which is extremely computationally expensive for a MC simulation. To overcome the inherent statistical limitations in the global problem of MC simulation, numerous global variance reduction (GVR) methods have been proposed to simultaneously increase the computational efficiency and simulation performance for large models [7,8,9,10]. Among these GVR methods, forward-consistent adjoint-driven importance sampling (FW-CADIS) is one of the most efficient and widely used methods.

In 2007, FW-CADIS was proposed by Wagner to improve the performance of MC simulations for global targets [11]. The principle of the FW-CADIS method is to develop an importance function to generate optimal GVR parameters (i.e., source biasing and particle weight window parameters) for MC simulation. The importance function has a negative relevant correlation with the forward flux, which can be beneficial for biasing the MC particles which are evenly distributed over the entire tally region. The FW-CADIS method employs both the forward and the adjoint solutions from deterministic transport calculations to produce the importance function and, thus, to realize variance reduction (VR) for global response problems.

In this study, a two-step subsection approach involving the FW-CADIS technique (Sub-GVR method) was applied to calculate the fast neutron flux distribution of the TMSR-SF1 facility. Firstly, a criticality calculation was performed to generate the space- and energy-dependent fission neutron source. Secondly, a fixed-source GVR calculation employing the FW-CADIS method was carried out to produce the detailed fast neutron flux distribution. A three-dimensional discrete ordinate (SN) code DENOVO [12] was employed to produce the importance function, and a utility code called SN2MCNP was developed to convert the importance function into source biasing and weight window parameters. Compared with other applications of the FW-CADIS method, the fission neutron source region of TMSR-SF1 has a complex geometry which contains a circular truncated cone. For this reason, MCNP5 was employed to implement our application since it provides a user-defined SOURCE subroutine which can be used to flexibly define a source by writing code in this subroutine. A dedicated sampling methodology for TMSR-SF1 was employed in the SOURCE subroutine to implement the source biasing technique.

The remainder of this paper is organized as follows: The methodology including the fission source probability distribution function (PDF), adjoint theory, and FW-CADIS is introduced in Sect. 2. The procedure used to implement the Sub-GVR method is described in Sect. 3. The calculation models are presented in Sect. 4. The simulation results and a detailed discussion are presented in Sect. 5, and conclusions are drawn in Sect. 6.

2 Methodology

2.1 Source probability distribution function

The spatial distribution of the fission neutron source in the core can be expressed as

$$ S(i,j,k) = \bar{R}_{\text{f}} (i,j,k)\sum\limits_{m} {\nu_{m} \frac{{\sigma_{{m{\text{f}}}} (i,j,k)N_{m} (i,j,k)}}{{\sum\nolimits_{m} {\sigma_{{m{\text{f}}}} (i,j,k)N_{m} (i,j,k)} }}} , $$
(1)

where \( m \) is the mth fissionable nuclide, \( i \), j, and \( k \) are the indices used to specify a fuel element, \( \bar{R}_{\text{f}} \) stands for the total fission rate in a fuel element, \( \sigma_{{m{\text{f}}}} \) denotes the effective microscopic fission cross section for nuclide \( m \), \( N_{m} \) refers to the nuclide atomic density of nuclide \( m \) within the fuel, and \( \nu_{m} \) represents the average number of neutrons per fission for nuclide \( m \). If one lets \( \bar{\nu }(i,j,k) = \sum\limits_{m} {\nu_{m} \frac{{\sigma_{{m{\text{f}}}} (i,j,k)N_{m} (i,j,k)}}{{\sum\nolimits_{m} {\sigma_{{m{\text{f}}}} (i,j,k)N_{m} (i,j,k)} }}}, \)then the space PDF of fission neutrons can be given by

$$ S^{\prime}(i,j,k) = \frac{{\bar{R}_{\text{f}} (i,j,k)}}{{\sum\nolimits_{i,j,k} {\bar{R}_{\text{f}} (i,j,k)\sum\nolimits_{m} {\bar{\nu }(i,j,k)} } }} . $$
(2)

In addition, the energy PDF of fission neutrons in a fuel element with indices \( i \), j, and \( k \) is

$$ \chi (i,j,k,E) = \frac{{\sum\nolimits_{m} {\chi_{m} (E)\frac{{\nu_{m} \sigma_{{m{\text{f}}}} (i,j,k)N_{m} (i,j,k)}}{{\sum\nolimits_{m} {\nu_{m} \sigma_{{m{\text{f}}}} (i,j,k)N_{m} (i,j,k)} }}} }}{{\int {\sum\nolimits_{m} {\chi_{m} (E)\frac{{\nu_{m} \sigma_{{m{\text{f}}}} (i,j,k)N_{m} (i,j,k)}}{{\sum\nolimits_{m} {\nu_{m} \sigma_{{m{\text{f}}}} (i,j,k)N_{m} (i,j,k)} }}} } {\text{d}}E}}, $$
(3)

where \( \chi_{m} (E) \) is the fission spectrum corresponding to the mth fissionable nuclide. The fission spectrum of a fissionable nuclide can be characterized by a Watt fission spectrum which can be described as [13]

$$ \chi_{m} (E) = C\exp ( - \,E/a)\sinh (bE)^{1/2} , $$
(4)

where \( a \) and \( b \) are parameters associated with the fissionable nuclide and incident neutron energy, respectively.

2.2 GVR method

2.2.1 Background of GVR

To distinguish between different objectives of MC simulation problems, the terms “source–detector,” “regional,” and “global” are used in this paper to represent problem objectives that are defined as follows: (1) Source–detector: The goal is to calculate the flux or response at a single location. (2) Regional: The goal is to calculate the flux or response over a portion of the problem space. (3) Global: The goal is to calculate the flux or response throughout the entire problem space. For the source–detector and regional problems, one’s interest is in determining a quantity with low statistical uncertainty at a localized region. Numerous VR techniques [14] have been applied successfully, such as the DXTRAN sphere and forced collision techniques, among others. For the global problem, the solution of the whole problem space with uniform low statistical uncertainty is required. Hence, we want to achieve uniform MC particle density over the entire phase space. Many GVR methods have been proposed to solve the global problems, and one of the most successful methods is to employ an adjoint function to speed up convergence.

2.2.2 Adjoint theory

The adjoint function has physical significance as it denotes the importance of a particle to some objective function (e.g., flux, energy deposition, dose, among others) and the main task of most MC simulations is to calculate the objective function at some desired tally regions. Therefore, the adjoint function is well suited for the biasing MC simulations, which leads to the utilization of the adjoint function to generate VR parameters for MC simulations.

The specific response at some location can be written as

$$ R = \int\limits_{4\pi }^{{}} {\int\limits_{E}^{{}} {\int\limits_{V}^{{}} {\phi (r,\hat{\Omega },E)\sigma_{\text{d}} (r,\hat{\Omega },E){\text{d}}r\,{\text{d}}\hat{\Omega }\,{\text{d}}E,} } } $$
(5)

where \( \sigma_{\text{d}} \) denotes some response function and \( \phi \) is the particle flux.

Based on the identity of the adjoint [15] and letting \( \sigma_{\text{d}} = s^{\dag } \), the following equivalent expression can be derived [11]:

$$ R = \int\limits_{4\pi }^{{}} {\int\limits_{E}^{{}} {\int\limits_{V}^{{}} {\phi (r,\hat{\Omega },E)} } } s^{\dag } (r,\hat{\Omega },E){\text{d}}r\,{\text{d}}\hat{\Omega }\,{\text{d}}E = \int\limits_{4\pi }^{{}} {\int\limits_{E}^{{}} {\int\limits_{V}^{{}} {\phi^{\dag } (r,\hat{\Omega },E)} } } s(r,\hat{\Omega },E){\text{d}}r\,{\text{d}}\hat{\Omega }\,\text{d} E, $$
(6)

where \( s \) stands for a fixed source and the superscript \( ^{\dag } \) indicates adjoint quantities.

From Eq. (6), one can conclude that the adjoint function represents the expected contribution (i.e., importance) to the response R from a source particle in some phase space. Therefore, the adjoint function can be used to develop the variance reduction parameters. However, the space-, energy-, and angular-dependent adjoint function may generate a huge amount of variance reduction parameters (tens or hundreds of GB) which would be costly to use in the MC simulation. Consequently, the scalar adjoint function and fixed source are used in the GVR methodology as follows:

$$ \left\{ \begin{array}{ll} &\varphi^{\dag } (r,E) = \int\limits_{4\pi } {\phi^{\dag } (r,\hat{\Omega },E)} \,{\text{d}}\hat{\Omega } \hfill \\ &S(r,E) = \int\limits_{4\pi } {s^{\dag } (r,\hat{\Omega },E)}\, {\text{d}}\hat{\Omega } \hfill \\ \end{array} \right.. $$
(7)

2.2.3 Theoretical model of FW-CADIS

The FW-CADIS method is derived from adjoint theory. In the FW-CADIS methodology, the adjoint source is some response function \( \sigma_{\text{d}} \) weighted with the inverse of the forward flux:

$$ S^{\dag } (r,E) = \frac{{\sigma_{\text{d}} (r,E)}}{{\int\limits_{E} {\varphi (r,E)\sigma_{\text{d}} (r,E)} {\text{d}}E}}. $$
(8)

Intuitively, this is useful for increasing the adjoint importance where the forward flux is low and decreasing the adjoint importance where the forward flux is high.

Using the adjoint source mentioned above, the adjoint function \( \varphi^{\dag } (r,E) \) can be derived [11]. Subsequently, the following equations are used to create GVR parameters:

$$ \hat{S}(r,E) = \frac{{\varphi^{\dag } (r,E)S(r,E)}}{{\int\limits_{E}^{{}} {\int\limits_{V}^{{}} {\varphi^{\dag } (r,E)S(r,E)} } {\text{d}}r{\text{d}}E}} = \frac{{\varphi^{\dag } (r,E)S(r,E)}}{R}, $$
(9)
$$ w_{0} = \frac{S}{{\hat{S}}} = \frac{R}{{\varphi^{\dag } (r,E)}}, $$
(10)
$$ w = \frac{R}{{\varphi^{\dag } (r,E)}} . $$
(11)

The biased source distribution is given by Eq. (9) which is derived from Eq. (6) and the concept of importance sampling [16]. The starting source weight of particles is expressed by Eq. (10). For the transport process, the objective statistical weight of the particles is given by Eq. (11). Notice that Eqs. (10) and (11) have the same form, which means the source particles are created with a weight that is consistent with the objective weight for the position they are born into. This is an important feature of the FW-CADIS method because it eliminates the inconsistency between source biasing and transport biasing, and avoids decreases in the computing efficiency due to the waste of computational resources on unnecessary splitting/rouletting of the starting particles.

3 Implementation of Sub-GVR method

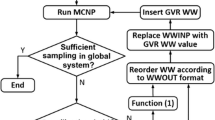
A flowchart of the Sub-GVR method is presented in Fig. 1. In the first step, a criticality calculation is executed with the eigenvalue mode (KCODE) of MCNP5 and an FMESH tally is used to record the effective microscopic fission cross section for each fissionable nuclide and the total fission rate in every mesh cell. After this, a utility python code SN2MCNP is employed to covert the mesh tally (MESHTAL file) to the space- and energy-dependent fission neutron PDF according to Eqs. (2)–(4).

Fig. 1
figure 1

Flowchart of Sub-GVR method implementation

Full size image

The second step is divided into four sub-steps to implement GVR. The first sub-step employs a forward-mode DENOVO calculation using the fission neutron PDF derived from the previous step as a neutron source to generate the forward flux. It should be noted that the forward-mode DENOVO calculation step is intended to acquire an adjoint source to be used for SN adjoint-mode calculation, rather than providing a solution to the problem. Therefore, a relatively coarse mesh is used in the DENOVO model.

For the second sub-step, an adjoint source is produced according to Eq. (8), and subsequently, an adjoint-mode DENOVO calculation is executed, and the scalar adjoint flux is produced.

In sub-step 3, SN2MCNP is used again to read the scalar adjoint function from the DENOVO flux file and then combine these values with the fixed neutron source used in the forward-mode DENOVO calculation to calculate the response according to Eq. (6). SN2MCNP is also applied to convert the scalar adjoint function into the source biasing and weight window parameters. For the source biasing parameters, SN2MCNP outputs a mesh-based biased source distribution file [based on Eq. (9)]. For the weight window parameters, MCNP5 requires lower weight window bounds (WWBs) instead of the center of the weight windows (intervals) as given in Eq. (11). In MCNP5, the width of the window is controlled by the weight window parameter card (WWP card); the parameter \( c \) as the ratio of upper and lower WWBs (\( c = w_{\text{u}} /w_{\text{l}} \)) can be input in the WWP card. Therefore, the space- and energy-dependent lower WWBs for MCNP5 are given by

$$ w_{\text{l}} (r,E) = \frac{R}{{\varphi^{\dag } (r,E)\left( {\frac{c + 1}{2}} \right)}}. $$
(12)

As a consequence, SN2MCNP uses Eq. (12) to generate the standard MCNP5 weight windows file (WWINP file).

In sub-step 4, the user-provided SOURCE subroutine in the MCNP5 source code is employed to apply the source biasing technique to the massive mesh-based source, which cannot be dealt with by the conventional method (using general source specification cards). Besides, the fission neutron source region of TMSR-SF1 has a complex geometry which is inconsistent with the geometry described by a mesh-based source. Therefore, this inconsistency must also be dealt with in the user-provided SOURCE subroutine. The algorithms used to implement the source sampling methodology in the SOURCE subroutine have four steps, as follows: First, a mesh cell is sampled directly from the mesh-based biased source distribution file. Second, the starting positions of particles are sampled uniformly within the mesh cell. The particle source region is described by a regular grid (cylindrical or rectangular grid), and therefore, the area covered by the grid may exceed the actual active core. However, we can resample the starting positions of particles until they are strictly located in the active core or the resampling time exceeds the limit number N (defined by IDUM card). Third, starting energy is sampled according to the biased energy distribution of the chosen mesh cell. In addition, the flight directions of the starting particles are isotropic by default in the SOURCE subroutine. Finally, the statistical weight of the starting particles is modified accordingly based on Eq. (10). The source sampling algorithm is implemented in the Source subroutine. The flowchart of the Source subroutine is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of SOURCE subroutine

Full size image

4 TMSR-SF1 facility model description

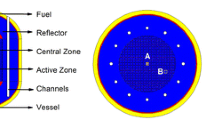
The 10-MWth TMSR-SF1 is a graphite-moderated, salt-cooled thermal reactor. In this design, 6-cm-diameter pebbles fill a cylindrical cavity with upper and lower circular truncated cones. The diameter and height of the cylindrical cavity are 135.0 cm and 180.0 cm, respectively. The minimum diameter of the upper and lower circular truncated cones is 30.0 cm. There are two types of pebbles loaded into the core cavity, namely fuel pebbles containing thousands of TRISO which are located in the top area, and graphite pebbles placed in the bottom area. The pebbles are cooled by the 2LiF–BeF2 mixed salt (FLiBe) that is kept at an operating temperature between 625 and 650 °C. As shown in Fig. 3, the core cavity is surrounded by thick graphite reflectors radially and axially. The other major components of TMSR-SF1 include a Hastelloy pressure vessel, aluminum silicate fiber thermal insulator, concrete biological shield, FLiBe plenum, boronated carbon bricks, stainless steel support plate, and stainless steel thermal shield. Table 1 gives the geometric dimensions of the facility model.

Fig. 3
figure 3

(Color online) Schematic diagram of TMSR-SF1

Full size image
Table 1 Dimensions of TMSR-SF1 facility model
Full size table

5 Results and discussion

To calculate the detailed spatial distribution of the fast neutron flux, a fine rectangular mesh tally was used in this research. All single mesh cells had a uniform size of 4.0 cm × 4.0 cm × 4.0 cm, and the X–Y–Z dimensions of the MCNP5 model of TMSR-SF1 were 820.0 cm × 820.0 cm × 860.0 cm. Therefore, the total number of mesh cells is 9,035,375. In addition, all our calculations were performed on a tower server with an Intel Xeon Processor E7-4830 (12-core, 2.1 GHz).

A one-step eigenvalue mode analog MCNP5 calculation was implemented initially so as to make a comparison. This calculation was performed with 6950 active keff-cycles each with 2 × 105 particles per cycle resulting in a total of 1.39 × 109 histories. The resulting fast neutron flux distribution and associated relative uncertainties are plotted in Fig. 4. As shown in Fig. 4a, most regions have no tally scores, while the nonzero scored mesh cells are mainly concentrated within the pressure vessel because of the existing of large amount neutron moderator material. Low relative uncertainties of the tallies were obtained near the core (source region). The mesh cells far from the core have very few scores or no scores at all.

Fig. 4
figure 4

(Color online) Fast neutron flux distribution computed by one-step analog method. a Fast neutron flux distribution; b relative uncertainty distribution

Full size image

The first step of Sub-GVR method employed a mesh tally including 10,830 orthometric mesh cells and the size of each cell was 7.224 cm × 7.224 cm × 7.224 cm. In this work, only 235U and 238U needed to be considered in the fission neutron source definition, since the calculation was performed at the beginning-of-cycle condition.

TMSR-SF1 is a low-power experimental reactor with a relatively low burn-up level which makes it impossible to use thorium on a large scale. Currently, only trace-level thorium is used as an irradiation material for radiation experimental research and the fuel in the fuel pebbles is UO2 (17.0 wt% 235U enrichment). Therefore, only 235U and 238U need to be accounted for in the neutron source definition, since all other fissionable nuclides make only negligible contributions to the fission in TMSR-SF1.

The data for the fissionable nuclides 235U and 238U, including values for the parameters \( a \) and \( b \) in the Watt fission spectrum function and the number of neutrons per fission, are summarized in Table 2. The parameters \( a \) and \( b \) for 235U correspond to fission reactions caused by thermal neutrons [17], whereas the fission reactions of 238U are almost all caused by fast neutrons. Therefore, the parameters corresponding to fast incident neutrons are used [18]. Figure 5 illustrates the spectral difference for the Watt fission spectra from the two nuclides.

Table 2 Fissionable nuclide properties currently used in this research
Full size table
Fig. 5
figure 5

(Color online) Watt fission neutron spectra for fissionable isotopes 235U and 238U

Full size image

For our application of the Sub-GVR method, the DENOVO SN grid had approximately 1,113,228 cells over the TMSR-SF1 facility model, that is, 102 × 102 × 107 cells in the X–Y–Z directions. A relatively low-order S4 angular quadrature and P3 Legendre scattering cross-section expansion approximation (upscattering was deactivated) were employed to reduce the computational resource requirements. The forward and adjoint DENOVO calculations took 28.17 and 20.34 min of wall-clock time, respectively.

The details of the calculated space PDF of the fission neutron source and the corresponding space PDF of the biased source are shown in Fig. 6. Compared with the PDF of the fission source, the source particles in the external region of the core will be sampled more frequently when using the biased source, which encourages the source particles to have a larger escape probability from the core. In addition, it should be noted that some of the areas in mesh cells are outside the core, which can be ignored by the sampling algorithm in the SOURCE subroutine.

Fig. 6
figure 6

(Color online) Space PDF of neutron source. a Space PDF of fission source; b space PDF of biased source

Full size image

Figure 7 illustrates the energy PDF of the fission neutron source and the biased source in an arbitrarily selected mesh cell in the core. The energy PDF of the fission neutron source derived from Eq. (3) is approximately equal to the Watt fission spectrum of 235U. For the biased source, the sampling probabilities in the high-energy region are increased. Furthermore, the sampling probability for the energy region below 0.1 MeV is set to zero since the source at this region makes no contribution to the fast neutron flux.

Fig. 7
figure 7

(Color online) Energy PDF of neutron source in one arbitrarily selected mesh cell

Full size image

The fixed-source MCNP5 run in the second step utilized 1 × 109 particle histories and required 8114.63 min of calculation time. Plots of the calculated fast neutron flux mesh tally and associated relative uncertainties are shown in Fig. 8. A dramatic improvement in the mesh tally result was obtained by the Sub-GVR method. Extremely uniform and low relative uncertainties were obtained throughout the entire TMSR-SF1 facility model.

Fig. 8
figure 8

(Color online) Fast neutron flux distribution computed by Sub-GVR method. a Fast neutron flux distribution, b relative uncertainty distribution

Full size image

Figure 9 shows the detailed distributions of relative uncertainties for the one-step analog and Sub-GVR approaches. Figure 9a shows the PDF of relative uncertainty, giving the fraction of mesh cells that have relative uncertainties at certain values, and Fig. 9b presents the cumulative distribution functions (CDF) of relative uncertainty, giving the fraction of mesh cells that have relative uncertainties below certain values. As shown in Fig. 9a, the one-step analog calculation yielded relative uncertainties varying uniformly in the range of 0.0–0.98 and rising to 0.98–1.0 radically. For the Sub-GVR scheme, the relative uncertainties were mainly distributed in the range 0.0–0.1, and the fraction of relative uncertainties larger than 10% was almost zero. The CDF graph, presented in Fig. 9b, is particularly useful in illustrating the performance of the two methods. With the one-step analog method, only 2.5, 3.3, and 4.2% of the total mesh cells had relative uncertainty values less than 5, 10, and 20%, respectively, while with the Sub-GVR method, 93.4, 99.7, and 99.9% of the mesh cells had relative uncertainties below these levels. In conclusion, the Sub-GVR method produces a fast flux mesh tally with far more uniform and lower relative uncertainties than the one-step analog method, thus dramatically improving the computational efficiency for this problem.

Fig. 9
figure 9

(Color online) Distribution of relative uncertainties. a PDF of relative uncertainties; b CDF of relative uncertainties

Full size image

To quantitatively compare the computational efficiencies of the two approaches, the mesh tally figure of merit (FOM) is introduced [19], which can be defined as

$$ {\text{FOM}} = \frac{1}{{\bar{r}^{2} T}}, $$
(13)

where \( \bar{r} \) is the mean relative uncertainty of the mesh tally cells and \( T \) is the total execution time. In the Sub-GVR method, \( T \) is the sum of total DENOVO execution time and MCNP5 execution time. The ratio of the FOM from Sub-GVR and the one-step analog calculation can be defined as speedup [20] and is used to quantify the efficiency improvements obtained by using the Sub-GVR method. Table 3 gives detailed information of the two calculation cases. The FOM obtained from applying the Sub-GVR method is 1.11e−1 while that of the analog approach is 1.37e−4, which provides a speedup of 810.2.

Table 3 Comparison of the analog and Sub-GVR approaches
Full size table

The maximum fast flux results of the main components in TMSR-SF1 were also calculated by the Sub-GVR method. Figure 10a gives the maximum fast flux of the main components. From the maximum flux region, which includes the center of the core, to the minimum flux region, which includes the stainless steel thermal shield, the fast flux is attenuated by approximately nine orders of magnitude. Therefore, this is a typical deep penetration problem that is difficult to calculate by analog MC simulation, as demonstrated above. However, by applying the Sub-GVR method, results with uniform and low relative uncertainties were obtained, as shown in Fig. 10b. The relative uncertainties of all maximum fast flux results were less than 5%, which is considered as generally reliable based on years of experience using MCNP5 on a wide variety of problems [21].

Fig. 10
figure 10

Maximum fast flux and associated relative uncertainties of major components. a Maximum fast flux of major components; b relative uncertainties of maximum fast flux

Full size image

6 Conclusion

A two-step subsection approach involving a GVR technique, Sub-GVR, has been implemented and applied in the calculation of a detailed fast neutron distribution throughout a full-scale model of TMSR-SF1. The results obtained using the Sub-GVR method and an analog method were compared, and the former method was demonstrated to be extremely effective in producing the fast neutron flux mesh tally with relatively uniform and low relative uncertainties. The FOM value of the Sub-GVR method was 810.2 times greater than that of the analog method. Furthermore, the maximum fast flux results of the main components in TMSR-SF1 were given, which can be used for the radiation damage assessment of the structural materials. In conclusion, the utilization of the Sub-GVR method has efficiently improved the statistical certainty and considerably reduced the global variance of the tally results through the entire geometry and enabled the calculation of high-fidelity distributions of the fast neutron flux throughout the full-scale TMSR-SF1 facility.