1 Introduction

The properties of hot, dense nuclear matter are usually extracted by comparing the observables in heavy ion collision (HIC) experiments with the corresponding results from transport model simulations. The most popular transport methods for studying HICs at low and intermediate energies are the quantum molecular dynamics (QMD) model [1], the Boltzmann (Vlasov)–Uehling–Uhlenbeck (BUU or VUU) model [2], and their improved versions [3,4,5]. The mean-field potential and nucleon–nucleon cross section (NNCS) are two essential components of these models. The mean-field potential in transport models has been studied extensively [6,7,8]. Regarding the NNCS, it is well known that compared with the free NNCS, the in-medium NNCS is suppressed [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]; however, the degree of suppression is still uncertain and requires further improvement. Thus, the in-medium NNCS has been studied by many groups using different methods [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41].

Recently, a systematic experimental study of nuclear stopping in central collisions at intermediate energies pointed out that the correction factor \({\mathcal{F}}=\sigma _\mathrm{NN}^{\mathrm{in-medium}}/\sigma _\mathrm{NN}^{\mathrm{free}}\) is deduced to be \(0.16\pm 0.04\) at 40 MeV/nucleon and \(0.5\pm 0.06\) at 100 MeV/nucleon [42]. New opportunities emerged to study the in-medium NNCS using transport models based on these stopping data [43,44,45,46]. There are many parameterized in-medium NNCSs adopted by various models. For example, \(\sigma _\mathrm{NN}^{\mathrm{in-medium}}=(1-\eta \rho /\rho _{0})\sigma _\mathrm{NN}^{\mathrm{free}}\) with \(\eta =0.2\) has been adopted in the BUU, relativistic BUU, and improved QMD models [10, 19, 20]. In the pBUU model, the in-medium NNCS is independent of the density, energy, and isospin and reads as \(\sigma _\mathrm{NN}^{\mathrm{in-medium}}=0.85\rho ^{-2/3}/ \tanh \left(\frac{\sigma ^{\mathrm{free}}}{0.85\rho ^{-2/3}}\right)\) [23]. In the isospin-dependent BUU model and the Lanzhou QMD model [47], the NNCS in the nuclear medium is corrected by a factor of \({\mathcal{F}}=\sigma _\mathrm{NN}^{\mathrm{in-medium}}/\sigma _\mathrm{NN}^{\mathrm{free}} =(\mu _\mathrm{NN}^{*}/\mu _\mathrm{NN})^2\). Here, \(\mu _\mathrm{NN}\) and \(\mu _\mathrm{NN}^{*}\) are the k masses of the colliding nucleon partners in free space and in the nuclear medium, respectively [16, 17, 24, 48]. In our previous works, we found that the collective flow and nuclear stopping can be reproduced using the parameterized medium correction factor \({\mathcal{F}}\) (which depends on the density and momentum) for the free NNCS within the ultrarelativistic QMD (UrQMD) model [49,50,51,52,53]. It is desirable to evaluate the differences between the \({\mathcal{F}}\) values extracted from experimental data [42] and the parameterized one adopted currently in the UrQMD model.

This paper is organized as follows. In Sect. 2, we review the UrQMD model with the improved potential. Section 3 presents an investigation of the effects of the in-medium NNCS on the observables of free protons and hydrogen isotopes in HICs in the Fermi energy domain. Finally, a summary is given in Sect. 4.

2 Model description and observables

The UrQMD model is based on the same principles as the QMD model. In the UrQMD model, more than 55 different baryon and 32 different meson species, as well as the corresponding antiparticle and isospin-projected states, are considered. The model has been extensively and successfully used to study the nuclear reactions of p + p, p + A, and A + A systems within a large range of beam energies, from the low-energy regime of the INDRA/GSI experiments up to the highest energies presently available at LHC/CERN. In addition, the other two main features unique to the collision term of the UrQMD model are the unique collision time for each individual collision and the two-step particle production process. More discussions can be found in recent works on the transport model comparison project, i.e., Refs. [3, 4].

At intermediate energies, the potential used in the UrQMD model depends on the momentum and density [1, 49, 54] and reads as

$$\begin{aligned} U=\alpha \cdot \left( \frac{\rho }{\rho _0}\right) +\beta \cdot \left( \frac{\rho }{\rho _0}\right) ^{\gamma } +\; t_\text{md} \ln ^2 \left[ 1+a_\text{md}(\mathbf{p}_{i}-\mathbf{p} _{j})^2 \right] \frac{\rho }{\rho _0}. \end{aligned}$$
(1)

Here, \(\alpha = -393\) MeV, \(\beta = 320\) MeV, \(\gamma = 1.14\), \(t_\text{md} = 1.57\) MeV, and \(a_\text{md}=0.0005\) MeV\(^{-2}\); these values yield an incompressibility \(K_0\) of 200 MeV for isospin-symmetric nuclear matter. In order to better describe the recent experimental data, the surface, surface asymmetry energy, and symmetry energy terms obtained from the Skyrme potential energy density functional have been further introduced into the present version [51,52,53, 55, 56]:

$$\begin{aligned} u_{\text{Skyrme}}= & u_{\text{sur}}+u_{\text{sur,iso}}+u_{\text{sym}}\nonumber \\= & \frac{g_{\text{sur}}}{2\rho _{0}}(\nabla \rho )^{2} +\frac{g_{\text{sur,iso}}}{2\rho _{0}}[\nabla (\rho _{\rm n}-\rho _{\rm p})]^{2}\nonumber \\& +\left( A_{\text{sym}}\frac{\rho ^{2}}{\rho _{0}}+B_{\text{sym}} \frac{\rho ^{\eta +1}}{\rho _{0}^{\eta }}+C_{\text{sym}} \frac{\rho ^{8/3}}{\rho _{0}^{5/3}}\right) \delta ^2. \end{aligned}$$
(2)
$$\begin{aligned} \frac{g_\text{sur}}{2}= & {} \frac{1}{64}(9t_{1}-5t_{2}-4x_{2}t_{2})\rho _{0}, \end{aligned}$$
(3)
$$\begin{aligned} \frac{g_\text{sur,iso}}{2}= & {} -\frac{1}{64}[3t_{1}(2x_{1}+1)+t_{2}(2x_{2}+1)]\rho _{0}, \end{aligned}$$
(4)
$$\begin{aligned} A_\text{sym}= & {} -\frac{t_{0}}{4}(x_{0}+1/2)\rho _{0}, \end{aligned}$$
(5)
$$\begin{aligned} B_\text{sym}= & {} -\frac{t_{3}}{24}(x_{3}+1/2)\rho _{0}^{\eta }, \end{aligned}$$
(6)
$$\begin{aligned} C_\text{sym}= & {} \frac{1}{24}\left(\frac{3\pi ^{2}}{2}\right)^{2/3}\rho _{0}^{5/3}\Theta _\text{sym}, \end{aligned}$$
(7)

where \(\Theta _\text{sym}=3t_{1}x_{1}-t_{2}(4+5x_{2})\) [51,52,53]. In this work, the SV-sym34 force, which gives \(g_{\text{sur}}=18.2\) MeV fm\(^{2}\), \(g_{\text{sur,iso}}=8.9\) MeV fm\(^{2}\), \(A_\text{sym}=20.3\) MeV, \(B_\text{sym}=14.4\) MeV, \(C_\text{sym}=-\,9.2\) MeV, and the slope parameter of the symmetry energy \(L=80.95\) MeV, is chosen.

In the UrQMD model, the in-medium NN elastic cross section is the product of the free cross sections with a medium correction factor \({\mathcal{F}}(\rho ,p)\), which is momentum and density dependent. In the UrQMD model, the free proton-neutron cross sections are larger than the free neutron-neutron (proton-proton) cross sections at low beam energy, which is consistent with experimental data. In our previous work [18, 38,39,40, 50], we found that the medium correction factor F depends on the density, momentum, and isospin. However, the isospin dependence is relatively weak, see, e.g., [57, 58].

$$\begin{aligned} \sigma _\mathrm{NN}^{\mathrm{in-medium}}= {\mathcal{F}} (\rho ,p)*\sigma _\mathrm{NN}^{\mathrm{free}}, \end{aligned}$$
(8)
$$\begin{aligned} {\mathcal{F}}(\rho ,p)= & \frac{\lambda +(1-\lambda )e^{-\rho /\rho _0/\zeta } -f_{0}}{1+(p_\mathrm{NN}/p_{0})^{\kappa }}+f_{0}. \end{aligned}$$
(9)

Here, \(\lambda =1/3\), \(\zeta =1/3\), \(f_{0}=1\), \(p_{0}=0.425\) GeV/c, and \(\kappa =5\), which corresponds to the FU3FP1 parametrization used in Ref. [50]. Moreover, \({\mathcal{F}}(\rho ,p)\) is set to unity when \(p_\mathrm{NN}\) is larger than 1 GeV/c.

Fig. 1
figure 1

(Color online) In-medium correction coefficient \({\mathcal{F}}\) obtained from the parametrization FU3FP1, which is density and momentum dependent

Full size image

The in-medium correction factor \({\mathcal{F}}(\rho ,p)\) obtained from the FU3FP1 parametrization as functions of both the reduced density \(\rho /\rho _{0}\) and momentum \(p=p_\mathrm{NN}\) is shown in Fig. 1. It is seen that the values deduced from the experiment [42] can be covered by the values of the in-medium correction factor \({\mathcal{F}}(\rho ,p)\) obtained from the FU3FP1 parametrization. In order to compare the effect of the in-medium NN cross section on the collective flow and nuclear stopping, three fixed values, \({\mathcal{F}} = 0.2\), 0.3, and 0.5, are further adopted in this work.

Fig. 2
figure 2

(Color online) Charge multiplicity distribution in \(^{197}\text{Au}+^{197}\text{Au}\) central collisions at beam energy of 150 MeV/nucleon. The experimental data are taken from Ref. [69]. The calculations performed with the in-medium correction factors of \({\mathcal{F}}=0.2\) (circles), \({\mathcal{F}}=0.3\) (up-facing triangles), and \({\mathcal{F}}=0.5\) (down-facing triangles) are compared with calculations using the FU3FP1 parametrization of the in-medium NNCS (squares)

Full size image

3 Results and discussion

3.1 Charge distribution

In this work, fragments are recognized by the isospin-dependent minimum spanning tree (iso-MST) method. Nucleons with relative distances smaller than \(R_0^{\rm pp}=2.8\) fm, \(R_0^{\rm nn}=R_0^{\rm np}=3.8\) fm and relative momenta smaller than \(P_0 =0.25\) GeV/c are considered to belong to the same cluster. The charge distribution of Au + Au collisions at a beam energy of 150 MeV/nucleon is displayed in Fig. 2. The distribution of charged fragments decreased exponentially with increasing charge number, and this behavior can be reproduced by both the simulations with FU3FP1 and those with the fixed in-medium correction factors. For large fragments (\(Z \ge 6\)), calculations with \({\mathcal{F}}=0.5\) seem to be closer to the experimental data. However, one cannot conclude that \({\mathcal{F}}=0.5\) is preferable to the others because the charge distribution will also be affected by unconstrained (or less constrained) parameters in the transport model; for example, the chosen coalescence model parameters will strongly influence the charge distribution but not the collective flow and nuclear stopping [51,52,53, 59,60,61,62,63,64,65,66,67,68].

Fig. 3
figure 3

(Color online) Rapidity distribution of the directed flow \(v_{1}\) (upper, \(b =\) 2–5.5 fm) and elliptic flow \(v_{2}\) (lower, b = 5.5–7.5 fm) of free protons from Au + Au collisions at \(E_{\text{{lab}}}\) = 40 (left panels), 100 (middle panels), and 150 MeV/nucleon (right panels)

Full size image

3.2 Collective flow

One can obtain the directed (\(v_{1}\)) and elliptic (\(v_{2}\)) flows from the Fourier expansion of the azimuthal distribution of detected particles [70, 71]; they read as

$$\begin{aligned} v_{1}\equiv \langle \cos (\phi )\rangle= & {} \left\langle \frac{p_{x}}{p_\text{t}}\right\rangle , \end{aligned}$$
(10)
$$\begin{aligned} v_{2}\equiv \langle \cos (2\phi )\rangle= & {} \left\langle \frac{p_{x}^{2}-p_{y}^{2}}{p_\text{t}^{2}}\right\rangle ,~p_\text{t}=\sqrt{p_{x}^{2}+p_{y}^{2}}. \end{aligned}$$
(11)
Fig. 4
figure 4

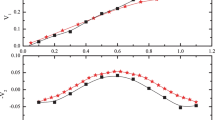
(Color online) Flow excitation functions at mid-rapidity for hydrogen isotopes from \(^{197}\text{Au}+^{197}\text{Au}\) collisions. The results with four in-medium correction factors are represented by different symbols and lines as indicated. The FOPI experimental data (open stars) and INDRA experimental data (solid stars) are taken from Ref. [69]

Full size image

The reduced rapidity (\(y_{z}/y_\text{pro}\)) dependence of the directed (\(v_{1}\)) and elliptic (\(v_{2}\)) flows of free protons from \(^{197}\)Au + \(^{197}\)Au collisions at 40, 100, and 150 MeV/nucleon with different \({\mathcal{F}}\) is shown in Fig. 3. One can see that both \(v_{1}\) and \(v_{2}\) obtained with different \({\mathcal{F}}\) are different, and the differences become more evident with increasing beam energy. The reason is that with increasing beam energy, the collision term plays a more important role. The \(v_1\) and \(v_2\) values obtained with the FU3FP1 and \({\mathcal{F}}=0.3\) are very close to each other. In addition, with a larger \({\mathcal{F}}\), which means a smaller reduction in the cross section, one can obtain a larger slope for \(v_{1}\) and a more negative \(v_{2}\) at mid-rapidity, \(y_{z}/y_{\text{pro}}\) = 0. Nucleons are known to be more likely to undergo a bounce-off (positive \(v_1\) slope) motion and squeeze-out (negative \(v_2\)) pattern because of the increasing collision number.

Figure 4 shows the \(v_1\) slope and \(v_2\) at \(y_{z}/y_{\text{pro}}\) = 0 for hydrogen isotopes calculated with different \({\mathcal{F}}\) values in comparison with the FOPI and INDRA experimental data. The chosen impact parameters are b = 2–5.5 fm and b = 5.5–7.5 fm for \(v_1\) and \(v_2\), respectively. The \(v_1\) slope is obtained assuming \(v_{1}(y_{0})=v_{11}y_{0}+v_{13}y_{0}^{3}+c\) in the range of \(|y_{0}|=|y_{z}/y_{\text{pro}}|<0.4\). With increasing \(E_{\rm lab}\), the value of the \(v_1\) slope increases and the value of \(v_2\) decreases. The results obtained with FU3FP1 and \({\mathcal{F}}=0.3\) are very close to each other. Furthermore, the correction factors \({\mathcal{F}}\) = 0.2 and 0.5 are required to fit the experimental data at beam energies of 40 and 150 MeV/nucleon, respectively. In addition, calculations with the FU3FP1 parametrization can simultaneously reproduce both \(v_1\) and \(v_2\) well.

Fig. 5
figure 5

(Color online) Kinetic energy distribution of free protons from \(^{197}\text{Au}+^{197}\text{Au}\) central collisions at beam energies of 40 (left panels) and 150 (right panels) MeV/nucleon

Full size image

To understand more clearly the influence of the medium correction factor on the NNCS, Fig. 5 shows the proton energy spectra of \(^{197}\text{Au}+^{197}\text{Au}\) collisions at beam energies of 40 and 150 MeV/nucleon. Overall, the energy spectra drop exponentially with energy and can also be affected by changing the medium correction factor. The energy spectrum obtained with \({\mathcal{F}}=\sigma _\mathrm{NN}^{\mathrm{in-medium}}/\sigma _\mathrm{NN}^{\mathrm{free}}=0.2\) has a steeper slope than the others because the number of collisions is smallest in this case.

3.3 Nuclear stopping

The nuclear stopping power is another important observable that characterizes the transparency of colliding nuclei [15, 19,20,21, 50]. In this work, we calculated the two quantities \(R_\mathrm{E}\) and vartl for the same reaction. The former was proposed by the FOPI collaboration [70] and is defined as the ratio of the variances of the transverse and longitudinal rapidity distributions:

$$\begin{aligned} vartl=\frac{\langle y_{x}^{2}\rangle }{\langle y_{z}^{2}\rangle },~~\langle y_{x,z}^{2}\rangle =\frac{\sum (y_{x,z}^{2}N_{y_{x,z}})}{\sum N_{y_{x,z}}}. \end{aligned}$$
(12)

The other quantity, \(R_\mathrm{E}\), was proposed by the INDRA collaboration and is defined as the ratio of the transverse and parallel energies:

$$\begin{aligned} R_\mathrm{E}=\frac{\sum E_{\bot }}{2\sum E_{\Vert }}, \end{aligned}$$
(13)

where \(E_{\bot }\) (\(E_{\Vert }\)) is the transverse (parallel) kinetic energy of particles in the center-of-mass system [72].

Fig. 6
figure 6

(Color online) Comparison of \(R_\text{E}\) (solid symbols) and vartl (open symbols) for free protons from central \(^{197}\text{Au}+^{197}\text{Au}\) (left panels) and \(^{129}\text{Xe}+^{120}\text{Sn}\) (right panels) collisions with four different medium correction factors (dashed lines with different symbols) to the FOPI (open stars) and INDRA (solid stars) experimental data [42, 73]

Full size image

The beam energy dependence of the degree of nuclear stopping for free protons in central HICs is displayed in Fig. 6. Similar to the results shown in Fig. 4, the degree of nuclear stopping can be reproduced well with \({\mathcal{F}}\approx 0.3\) at \(E_{\text{lab}}\) = 40 MeV/nucleon. However, \({\mathcal{F}}\approx 0.5\) is needed at \(E_{\text{lab}}\) = 150 MeV/nucleon. With increasing beam energy, a nuclear medium with higher density and momentum can be created; thus, it is reasonable that the reduction factors at different beam energies are different. With increasing beam energy, the difference in \(R_\text{E}\) between \({\mathcal{F}}=0.3\) and FU3FP1 increases steadily. The experimental data and the trend in stopping power with increasing beam energy can be reproduced reasonably well by the calculations with FU3FP1. In contrast, the other calculations remain almost constant because the reduced factor in the FU3FP1 depends on both the density and momentum. In addition, these conclusions can be confirmed in both \(^{197}\text{Au}+^{197}\text{Au}\) and \(^{129}\text{Xe}+^{120}\text{Sn}\).

4 Summary

The effects of the in-medium nucleon–nucleon cross section on the collective flow and nuclear stopping in the Fermi energy domain are investigated within the UrQMD model, in which medium correction factors of \({\mathcal{F}}=\sigma _\mathrm{NN}^{\mathrm{in-medium}}/ \sigma _\mathrm{NN}^{\mathrm{free}}=0.2,~0.3,~0.5\) and the parametrization factor FU3FP1 (which is density and momentum dependent) are considered. It is demonstrated that to best fit both the collective flow and nuclear stopping data, \({\mathcal{F}}\) \(\approx\) 0.2 and 0.5 are required at beam energies of 40 and 150 MeV/nucleon, respectively. These results are consistent with the results obtained by the INDRA collaboration. The calculations with the FU3FP1 parametrization reproduce both the directed and elliptic flow data reasonably well. The slightly increased stopping power with increasing beam energy can also be found in the calculations with the FU3FP1 parametrization, whereas the calculations with \({\mathcal{F}}\) = 0.2, 0.3, and 0.5 yield roughly flat energy-dependent.