Radar scattering width effects by coating ⁹⁰Sr/⁹⁰Y layers on cylindrical targets

Abstract

In this paper, the ⁹⁰Sr/⁹⁰Y coating effects on scattering width (SW) of cylindrical conductor targets are investigated. The electron density distribution of plasma around cylindrical targets of different radiuses is simulated under different radioactivities in normal or oblique incidence. In normal incidence, the SWs are examined as functions of frequency and scattering angle; while in oblique incidence, the SW is inspected as a function of incident angle at the frequency of 1.5 GHz. The results obtained are compared with those from an ideal perfect electric conductor (PEC) cylinder. It is demonstrated that the SW decreases over a wide frequency range in the back scattering region by coating a ⁹⁰Sr/⁹⁰Y layer on the cylindrical target. Moreover, the reduction in bi-static SW amplitude can reach 3–20 dB, when the incident angle is smaller than 30° at 1.5 GHz. It is a significant improvement in the stealth effect.

1 Introduction

Stealth effect to electromagnetic waves (EMW) is important for the survivability of weapon systems in battlefields and for military defense systems [1,2,3]. Since the bodies of aircraft cabins or missiles can be simplified as cylindrical objects, the study of EMW scattering from a cylindrical target has attracted considerable attention from researchers [4,5,6,7,8,9,10,11], and enhancing the stealth effects by coating new materials has become an attractive area of research [12,13,14,15]. As a type of specific absorbing materials, plasma coating is of significant EMW-absorption effect [16]. The scattering width (SW) of a cylindrical target can be greatly reduced by plasma coating.

Plasma can be induced by charged particles emitted from radioactive sources in the air. ⁹⁰Sr/⁹⁰Y is a perfect β-ray source. It emits no neutrons and ignorable γ-rays but just β-particles in maximum energy of 2.28 MeV and maximum trajectory range of 10 m in air [17,18,19]. In this paper, we investigate the absorption effect of plasma induced by ⁹⁰Sr/⁹⁰Y coating around a cylindrical target. The influences of ⁹⁰Sr/⁹⁰Y layer on mono-static and bi-static SWs of the cylindrical target at normal incidence are analyzed over the frequency range of 0.1–40 GHz, while the influences on bi-static SW at oblique incidence are analyzed at 1.5 GHz.

2 Theoretical background

2.1 Physical behavior of plasma induced by ⁹⁰Sr

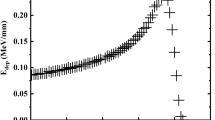
As ⁹⁰Y is the decay product progeny of ⁹⁰Sr, we refer ⁹⁰Sr as ⁹⁰Sr/⁹⁰Y. Figure 1 shows the continuous β spectrum of ⁹⁰Sr [20]. The emitting directions and trajectories of β-particles from ⁹⁰Sr are all random, and the average values are obtained. The average energy losses of β-particles along the radial direction of a cylinder can be calculated. The average ionization energy of air molecules in atmosphere at normal temperature is 36 eV [21]. The average numbers of electron–ion pairs induced by one β-particle are simulated.

Fig. 1

Beta spectroscopy of ⁹⁰Sr

The emitted electrons diffuse in air [22, 23]. The number of electrons, N, passing through a unit area in a unit time is

$$ \left( {\frac{{{\text{d}}N}}{{\text{d} t}}} \right)_{\text{dif}} = - D_{\text{dif}} \nabla n_{\text{e}} , $$

(1)

where n _e is the electron density, and D _dif = 3.7 × 10² cm²/s is the diffusion coefficient in air, as experimentally validated.

The electrons and positive ions are recombined after collision and the n _e changes in the recombination process as

$$ \left( {\frac{{{\text{d}}n_{\text{e}} }}{{\text{d} t}}} \right)_{\text{rec}} \approx - \alpha n_{\text{e}}^{2} , $$

(2)

where α = 1.5 × 10⁻⁶ cm³/s is the recombination coefficient, according to the experiments.

The electrons are absorbed by neutral particles as a result of collision, with the formation of negative ions, which can easily be photodetached by the sunshine. Considering the processes of ionization, diffusion, recombination, absorption and photolysis, the electron density (N _m) distribution in the plasma induced by β-particles from ⁹⁰Sr can be estimated. For un-magnetized plasma (μ _r = 1), the relative dielectric constant ε _r can be derived by

$$ \varepsilon_{\text{r}} = 1 - K_{1} \frac{{\omega_{\text{pe}}^{2} }}{{\omega_{0}^{2} + v_{{{\text{eff}},l}}^{2} }} - jK_{2} \frac{v}{{\omega_{0} }}\frac{{\omega_{\text{pe}}^{2} }}{{\omega_{0}^{2} + v_{{{\text{eff}},l}}^{2} }} , $$

(3)

where v, v _{eff, l} , and ω _pe are

$$ v\sim v_{{{\text{eff, }}l}} \approx 1.5 \times 10^{11} \frac{{N_{\text{m}} }}{{2.7 \times 10^{19} }}\sqrt {\frac{T}{300}} , $$

(4)

$$ \omega_{\text{pe}} = \sqrt {\frac{{n_{\text{e}} e^{2} }}{{m_{\text{e}} \varepsilon_{0} }}} , $$

(5)

and K ₁ and K ₂ are the coefficients related to the ratio of EMW frequency and the effective collision frequency [24].

2.2 Electromagnetic wave scattering from a cylindrical target

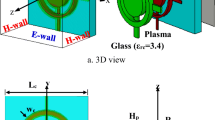
The cylindrical PEC target surrounded by inhomogeneous plasma can be simplified as a multilayered cylinder in the scattering problem. The geometry for an obliquely incident EMW is shown in Fig. 2a. The Z-axis coincides with the axis of the cylinder and X–Z is the incident plane. The tilt angle θ is the angle between the incident direction and the axis of the cylinder in the incident plane. Figure 2b shows cross section of the multilayered cylinder model. The plasma around the cylindrical target (of r ₁ in radius) is divided into J layers, with r _j being the outer radius of the jth layer and m _j being its complex refractive index. The scattering angle φ is defined by the scattering direction and X-axis.

Fig. 2

Multilayered long cylinder model illuminated by EMW. a Geometry of scattering by infinite long inhomogeneous cylinders for oblique incidence; b Cross section of a multilayered cylindrical model

An eigenfunction expansion method is utilized to calculate the scattered filed for its relative simplicity in the situation of thick inhomogeneous layers coated cylinder. Based on Maxwell equations, the field in the jth layer can be written as [6, 9]

$$ E_{j} = \sum\limits_{n} {( - 1)^{n} } \left[ {N_{n,j}^{(1)} - a_{n}^{(j)} N_{n,j}^{(3)} - ib_{n}^{(j)} M_{n,j}^{(3)} } \right], $$

(6)

where M _n and N _n are eigenvectors. For transverse magnetic (TM) incident wave, the coefficients of the scattered field, a _n and b _n , can be expressed as [9]

$$ \begin{aligned} a_{n} & = \frac{{ - ig_{J} \left( {w_{J}^{2} - 1} \right)yn\cos \theta T_{n} \left( y \right)L_{1} }}{{y^{2} L_{2} L_{3} - g_{J} n^{2} \cos^{2} \theta \left( {1 - w_{J}^{2} } \right)}} \\ b_{n} & = T_{n} \left( y \right) \cdot \frac{{y^{2} L_{3} L_{4} - g_{J} n^{2} \cos^{2} \theta \left( {1 - w_{J}^{2} } \right)}}{{y^{2} L_{2} L_{3} - g_{J} n^{2} \cos^{2} \theta \left( {1 - w_{J}^{2} } \right)}}, \\ \end{aligned} $$

(7)

where $y = x_{J} { \sin }\theta ,\eta_{J} = x_{J} \left( {m_{J}^{2} - { \cos }^{ 2} \theta } \right)^{ 1/ 2} ,w_{J} = y/\eta_{J} ,g_{J} = \mu_{J} /m_{J} ,h_{J} = m_{J} y/\eta_{J} ,{\text{and}}\,T_{n} \left( y \right) = J_{n} \left( y \right)/H_{n}^{(1)} \left( y \right) .$ For the jth layer, x _j  = 2πr _j /λ, with λ being wavelength of the incident EMW and μ _j being the plasma permeability in the jth layer. L _1–4 are as follows

$$ L_{ 1} = D_{n}^{( 1)} \left( y \right) - D_{n}^{( 3)} \left( y \right),\quad L_{ 2} = g_{J} D_{n}^{( 3)} \left( y \right){-}h_{J} H_{n}^{b(J)} ,\quad L_{ 3} = D_{n}^{( 3)} \left( y \right){-}g_{J} h_{J} H_{n}^{a(J)} ,\quad L_{ 4} = g_{J} D_{n}^{( 1)} \left( y \right){-}h_{J} H_{n}^{b(J)} , $$

(8)

where $D_{n}^{\left( 1\right)} \left( y \right) = J_{n}^{'} \left( y \right)/J_{n} \left( y \right),D_{n}^{( 2)} \left( y \right) = Y_{n}^{'} \left( y \right)/Y_{n} \left( y \right)\,{\text{and}}\,D_{n}^{( 3)} \left( y \right) = H_{n}^{( 1)'} \left( y \right)/H_{n}^{(1)} \left( y \right)$ are the logarithmic derivatives of the Bessel functions, that are used in computational calculation to overcome the overflow problems for high-order or large-argument cylindrical Bessel functions.

A recursive method is employed to get H ^a(1) _n and H ^b(1) _n [25] and expressed by the following recursive equations

$$ \begin{aligned} A_{n}^{\left( j \right)} & = R_{n}^{\left( j \right)} \cdot \frac{{\left[ {W_{n}^{{a\left( {j - 1} \right)}} - D_{n}^{(1)} (\beta_{j - 1} )} \right]}}{{\left[ {W_{n}^{{a\left( {j - 1} \right)}} - D_{n}^{(2)} (\beta_{j - 1} )} \right]}} \\ B_{n}^{\left( j \right)} & = R_{n}^{\left( j \right)} \cdot \frac{{\left[ {W_{n}^{{b\left( {j - 1} \right)}} - D_{n}^{(1)} (\beta_{j - 1} )} \right]}}{{\left[ {W_{n}^{{b\left( {j - 1} \right)}} - D_{n}^{(1)} (\beta_{j - 1} )} \right]}} \\ H_{n}^{a\left( j \right)} & = \frac{{D_{n}^{(1)} (\eta_{j} ) - A_{n}^{\left( j \right)} D_{n}^{(2)} (\eta_{j} )}}{{1 - A_{n}^{\left( j \right)} }} \\ H_{n}^{b\left( j \right)} & = \frac{{D_{n}^{(1)} (\eta_{j} ) - B_{n}^{\left( j \right)} D_{n}^{(2)} (\eta_{j} )}}{{1 - B_{n}^{\left( j \right)} }} \\ W_{n}^{a\left( j \right)} & = \frac{{\mu_{j} }}{{\mu_{j + 1} }}\left( {\frac{{\beta_{j} }}{{\eta_{j} }} \cdot H_{n}^{a\left( j \right)} + \frac{{n\lambda_{j} }}{{\mu_{j} \eta_{j} }}\frac{{\beta_{j} }}{{\eta_{j} }}} \right) \\ W_{n}^{b\left( j \right)} & = \frac{{m_{j}^{2} }}{{m_{j + 1}^{2} }}\frac{{\mu_{j + 1} }}{{\mu_{j} }}\left( {\frac{{\beta_{j} }}{{\eta_{j} }} \cdot H_{n}^{b\left( j \right)} + \frac{{n\lambda_{j} }}{{m_{j}^{2} }}\frac{{\mu_{j} }}{{\eta_{j} }}\frac{{\beta_{j} }}{{\eta_{j} }}} \right), \\ \end{aligned} $$

(9)

where $A_{n}^{\left( 1\right)} = B_{n}^{( 1)} = 0\,{\text{and}}\,H_{n}^{a(1)} = H_{n}^{b(1)} = J_{n}^{{\prime }} \left( {\eta_{j} } \right)/J_{n} \left( {\eta_{j} } \right)$ are initial values. R ^(j) _n is expressed as

$$ R_{n}^{\left( j \right)} = \left[ {J_{n} \left( {\beta_{j - 1} } \right) \cdot Y_{n} \left( {\eta_{j} } \right)} \right]/\left[ {Y_{n} \left( {\beta_{j - 1} } \right) \cdot J_{n} \left( {\eta_{j} } \right)} \right]. $$

(10)

The D ⁽¹⁾ _n (y), T _n (y), and R _n (y) functions are calculated with the following recursive relations

$$ \begin{aligned} D_{n + 1}^{(l)} (y) = - \frac{n + 1}{\rho } + \frac{1}{{n/\rho - D_{n}^{(l)} (y)}},l = 1,2,3. \hfill \\ T_{n} (y) = T_{n - 1} (y).\frac{{D_{n}^{(3)} (y) + n/\rho }}{{D_{n}^{(1)} (y) + n/\rho }} \hfill \\ R_{n}^{j} (y) = R_{n - 1}^{j} .\frac{{D_{n}^{(2)} (\beta_{j - 1} ) + n/\beta_{j - 1} }}{{D_{n}^{(1)} (\beta_{j - 1} ) + n/\beta_{j - 1} }}.\frac{{D_{n}^{(1)} (\eta_{j} ) + n/\eta_{j} }}{{D_{n}^{(2)} (\eta_{j} ) + n/\eta_{j} }}, \hfill \\ \end{aligned} $$

(11)

where D ⁽¹⁾ _n (y) is evaluated using a downward recurrence formula. The initial value for the downward recurrence formula is generated using the method provided by Lentz [26]. The remaining four functions are computed using the upward recurrence formulas with initial values obtained from Matlab programs.

The electric field can be divided into incident part E _i and scattered part E _s. So, the SW is defined as

$$ \sigma = \mathop {\lim }\limits_{\rho \to \infty } \left[ {2\pi \rho \frac{{\left| {E_{\text{s}} } \right|^{2} }}{{\left| {E_{\text{i}} } \right|^{2} }}} \right]. $$

(12)

The relationship between σ and the scattering coefficients is

$$ \sigma = \mathop {\lim }\limits_{\rho \to \infty } \left[ {2\pi \rho \left( {I_{1} + I_{2} } \right)} \right]. $$

(13)

For TM waves

$$ \begin{aligned} I_{1} & = \frac{2}{{k_{0} \pi r}}\left| {b_{0} + 2\sum\limits_{n = 1}^{\infty } {b_{n} \cos (n\varphi )} } \right|^{2} \\ I_{2} & = \frac{2}{{k_{0} \pi r}}\left| {2\sum\limits_{n = 1}^{\infty } {a_{n} \sin (n\varphi )} } \right|^{2} . \\ \end{aligned} $$

(14)

For transverse electric (TE) waves, the coefficients of the scattered field, a _n and b _n , are [9]

$$ \begin{aligned} a_{n} & = T_{n} \left( y \right) \cdot \frac{{y^{2} L_{5} L_{2} - g_{J} n^{2} \cos^{2} \theta \left( {1 - w_{J}^{2} } \right)}}{{y^{2} L_{2} L_{3} - g_{J} n^{2} \cos^{2} \theta \left( {1 - w_{J}^{2} } \right)}} \\ b_{n} & = \frac{{ - ig_{J} \left( {w_{J}^{2} - 1} \right)yn\cos \theta T_{n} \left( y \right)L_{1} }}{{y^{2} L_{2} L_{3} - g_{J} n^{2} \cos^{2} \theta \left( {1 - w_{J}^{2} } \right)}}, \\ \end{aligned} $$

(15)

where

$$ L_{5} = \frac{{J_{n}^{\prime } \left( y \right)}}{{J_{n} \left( y \right)}} - g_{J} h_{J} H_{n}^{a\left( J \right)} , $$

(16)

and

$$ \begin{aligned} I_{1} & = \frac{2}{{k_{0} \pi r}}\left| {a_{0} + 2\sum\limits_{n = 1}^{\infty } {a_{n} \cos (n\varphi )} } \right|^{2} \\ I_{2} & = \frac{2}{{k_{0} \pi r}}\left| {2\sum\limits_{n = 1}^{\infty } {b_{n} \sin (n\varphi )} } \right|^{2} . \\ \end{aligned} $$

(17)

All the SW values provided in the following sections are represented in normalized form, 10 lg(σ/λ).

2.3 Validation of the algorithm at high frequency

Accuracy of the eigenfunction expansion method used in this work has always been doubted when the size parameter is of high value (x _j  = 2πr _j /λ) [27]. We compare the results of this algorithm with those of an asymptotic solution [28] for SWs of a dielectric layer-coated PEC cylinder in the TM case, as shown in Fig. 3. The cylinder radius is 10 m and the layer is 0.08 m thick. The results of the eigenfunction expansion method and the geometrical optics solution (GO, an asymptotic solution in deep lit region) agree well at 40 GHz and φ > 90°, but are deviating from each other with decreasing frequencies, just because that the GO solution appears to be too simple for the issue. We note that for the TE case the two kinds of results are similar (not shown). Therefore, the calculation results of this work with r _J  = 10 m can be reliable at high frequencies.

Fig. 3

SWs calculated with the eigenfunction expansion method (eigen), and the asymptotic solution (GO). The relative dielectric constants of the coated layer are 0.9994 − 0.16i, 0.9995 − 0.0014i and 0.9998 − 0.00012i at 1, 10 and 40 GHz, respectively, with the relative permeability of 1

The inaccuracy in the eigenfunction expansion results mainly originates from bad convergence of the Bessel functions with large arguments. However, as logarithmic derivatives of the Bessel functions have replaced the Bessel functions, the recursive relations with reliable initial values have enabled us to obtain numerical values with higher orders, thereby the coefficients (a _n and b _n ) can be truncated as tiny as 10⁻¹⁵ in the calculation, so as to ensure accuracy of the results. The truncation order for relatively high frequency is provided in Sect. 3.

Asymptotic solutions have been widely recognized in high frequency EMW scattering problems, but their complicity increases with the number and thickness of the coating layers. Here, the plasma around the cylinder is of 8 m thickness, divided into 100 layers. Thus, eigenfunction expansion is the right method for its unified form in the multilayer situation.

3 Results and discussion

3.1 Electron density distribution of the plasma

Figure 4 shows electron density distribution of the plasma induced by β-particles from the ⁹⁰Sr coating in radioactivity of 1 and 10 Ci/cm², assuming a long cylinder in radiuses of 0.5 and 2 m, respectively. For the cylinder of 0.5 m radius, at 1 Ci/cm², the electron density of the plasma is 1.56 × 10⁹ cm⁻³ adjacent to the ⁹⁰Sr coating, while it is 6.89 × 10⁶ cm⁻³ at 8 m from the coating. As the amount of electron–ion pairs in a unit time increases with the radioactivity, the electron density of the plasma increases accordingly [24]. At 10 Ci/cm², the corresponding electron densities are 4.95 × 10⁹ and 2.18 × 10⁷ cm⁻³, respectively. Compared to the maximum value, the electron densities are reduced by two orders of magnitude at 8 m from the ⁹⁰Sr coating for both radioactivities. The plasma around the cylinder of 2 m radius yields greater electron density at the same radioactivity and distance, while similar density-decreasing behavior with increasing distance up to 8 m. Therefore, the influence of plasma on the EMW propagation at 8 m from the ⁹⁰Sr coating can be ignored and 8 m is set as the thickness of the plasma surrounding the cylinder target in the calculation.

Fig. 4

Electron density distribution of the plasma excited by the ⁹⁰Sr coating

3.2 The mono-static SW

In order to clearly differentiate between the SWs of coated and uncoated cylindrical targets, the reduction of SW is used to display the data

$$ d_{\text{SW}} = {\text{SW}}_{{{\text{with}}\,{}^{90}{\text{Sr}}\,{\text{coating}}}} - {\text{SW}}_{{{\text{without}}\,{}^{90}{\text{Sr}}\,{\text{coating}}}} . $$

(18)

The mono-static d _SWs of the ⁹⁰Sr-coated cylindrical targets (r ₁ = 0.5 and 2 m) verses EMW frequency (0.1–40 GHz) at normal incidence are illustrated in Fig. 5. The insets show the SWs by the corresponding cylinders made with PEC. The mono-static SW by a PEC cylinder increases smoothly with the EMW frequency for TM waves and alternates for TE waves. The oscillations in the TE case arise from the creeping waves of TE polarization. In the backscattering region (from φ = 90° to φ = 180°), the scattered waves are composed of creeping and reflected waves for TE polarization, but mainly reflected waves for TM polarization, and the phase difference between the two waves changes significantly with the EMW frequency [29, 30]. The SW by the ⁹⁰Sr-coated cylindrical target decreases remarkably as the EMW energy is absorbed by the plasma. For the target of 0.5 m radius, the mono-static SW decreases over 0.85 dB at the radioactivity of 1 Ci/cm² in the frequency range of 0.5–7 GHz and more than 2.80 dB at 10 Ci/cm² in 0.8–4 GHz. The full width at half maximum (FWHM) of all d _SW curves can reach 27 GHz. Having the greater plasma density, the mono-static SWs of the ⁹⁰Sr-coated target of 2 m radius decreased more than those in the 0.5 m case, by 1.25 dB at 1 Ci/cm² in 0.6–6 GHz and 3.95 dB at 10 Ci/cm² in 0.6–4 GHz. In addition, the FWHM can also reach 27 GHz.

Fig. 5

Mono-static d _SWs of the cylindrical target with ⁹⁰Sr coating. a TM waves; b TE waves

The truncation orders against the frequency in the TM case are shown in Fig. 6. The orders for different radioactivities are close to each other for cylinders of the same radius, while they increase with the radius, but the increment is not large as the cylinder radius is much smaller than the surrounded plasma thickness. The orders for both radiuses increase linearly with the frequency, reaching 7245 for 0.5 m radius and 8534 for 2.0 m radius. The truncation order is mainly determined by the size parameter x _J [31], and it can be predicted that it shall not exceed 20,000 at 100 GHz for a cylinder of 2 m radius. The truncation orders in the TE case are identical to the TM results.

Fig. 6

Truncation orders in the calculation. I ₁ and I ₂ in Eqs. (14) and (15) are truncated when b _n  ≤ 10⁻¹⁵ and a _n  ≤ 10⁻¹⁵

3.3 The bi-static SW at normal incidence

The bi-static SWs of the cylindrical target (r ₁ = 0.5 m) with and without the ⁹⁰Sr coating for the EMW at normal incidence are calculated in the frequency range of 0.1–40 GHz. The data are displayed in 2D images with scaled colors, as shown in Fig. 7. For TM waves, the bi-static SW by a PEC cylinder increases steadily with the frequency and scattering angle in the back scattering region (Fig. 7a). However, it gets complicated in the forward scattering region (from φ = 0° to φ = 90°). The reason is that several modes of the EMW rays are involved in that scattered filed. Similar phenomenon is observed in the TE case (Fig. 7c). After the PEC cylinder is coated with a 10 Ci/cm^{2 90}Sr layer, SW by the scatter decreases significantly in the back scattering region (Fig. 7b). Comparing Fig. 7b, d, the ⁹⁰Sr reduction effects in the TE and TM cases are similar.

Fig. 7

Bi-static SWs of the cylindrical target at normal incidence. a TM, PEC; b TM, 10 Ci/cm²; c TE, PEC; d TE, 10 Ci/cm²

The bi-static d _SWs of the 10 Ci/cm^{2 90}Sr-coated cylinder are investigated as functions of scattering angle φ at four typical EMW frequencies: 0.2, 1.5, 27, and 40 GHz, as shown in Fig. 8. For TM waves, the d _SWs increase slightly with the scattering angle in the back scattering region. The d _SWs at φ = 90° are −2.87, −3.06, −1.54 and −0.96 dB, for 0.2, 1.5, 27 and 40 GHz, respectively. For TE waves, the d _SWs show a similar trend but with more intense oscillations, especially at low frequencies, which can also be attributed to the phase difference between the creeping and reflected waves.

Fig. 8

Bi-static d _SWs of the cylindrical target coated with ⁹⁰Sr layer at normal incidence. a TM waves; b TE waves

3.4 The bi-static SW at oblique incidence

Bi-static SWs are calculated with obliquely incident EMWs at 1.5 GHz and the cylinder of 0.5 m radius, with and without ⁹⁰Sr coating (10 Ci/cm²), in the back scattering region in incident angles of 0° < θ < 90°, as depicted in Fig. 9. For TM waves, the SW by the PEC cylinder does not change with the incident angle θ, while the SW by the ⁹⁰Sr-coated one decreases remarkably with θ. The reason is that the propagation distance of the EMW in the plasma increases with decreasing incident angles. For TE waves, the SW by the PEC cylinder oscillates with the changes in θ and φ due to the creeping waves, while the SW by the coated one shows a downward trend for small incident angles (θ < 50°), similar to that in the TM case.

Fig. 9

Bi-static SWs at oblique incidence. a TM, PEC; b TM, 10 Ci/cm²; c TE, PEC; d TE, 10 Ci/cm²

The bi-static d _SWs of the 10 Ci/cm^{2 90}Sr-coated cylindrical target are studied as functions of θ at three typical scattering angles: 180°, 135°, and 90°, as shown in Fig. 10. The EMW frequency is 1.5 GHz. For TM waves, the d _SWs of the 10 Ci/cm^{2 90}Sr-coated cylinder decrease with θ and display close values for different scattering angles. The d _SWs reach −5 to −30 dB when θ < 30°. For TE waves, the d _SWs decrease with θ in most of the incident angles but oscillate in the range of 55° < θ < 75°, which can also be attributed to the creeping waves. Moreover, the d _SWs for different scattering angles are no longer close to each other. When θ < 30°, the d _SWs reach −9 to −38, −6 to −31 and − 3 to −20 dB at θ = 180°, 135° and 90°, respectively.

Fig. 10

Bi-static d _SWs of the ⁹⁰Sr-coated cylindrical target at typical incident angles at 10 Ci/cm² for TM waves (a) and TE waves (b)

4 Conclusion

In this paper, influences of ⁹⁰Sr coating on electromagnetic scattering from a cylindrical target are investigated and evaluated. The results demonstrate that the SW of a cylindrical target with ⁹⁰Sr coating decreases effectively. The mono-static SW by the 10 Ci/cm^{2 90}Sr-coated cylindrical target reduces by 2.80 and 3.95 dB for 0.5 and 2 m radiuses, respectively, in the frequency range of 0.4–40 GHz. The bi-static SWs by 10 Ci/cm^{2 90}Sr-coated cylindrical target of 0.5 m radius at normal incidence reduce by 2.87, 3.06, 1.54, and 0.96 dB in the back scattering region, for EMW frequencies of 0.2, 1.5, 27, and 40 GHz, respectively. In addition, the stealth effect can be significantly improved for oblique incidence of EMWs. The bi-static SW by the cylindrical target with 10 Ci/cm^{2 90}Sr coating reduces by 3–20 dB when the incident angle θ is smaller than 30°. The results indicate that ⁹⁰Sr-coated cylindrical objects have significant stealth effect.