Introduction

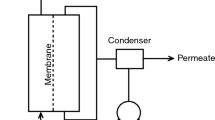
A large proportion of the water on Earth is saline or brackish and must be treated before use. To achieve this, various desalination techniques have been developed to purify saline water. One of these is membrane distillation, which produces a high-purity distillate. Membrane distillation is an evaporation process powered by a difference in vapor pressure between the membrane pores on each side. Various membrane distillation (MD) configurations are available, such as direct-contact MD, air-gap MD, sweeping-gas MD, and vacuum MD. Membrane distillation processes use hydrophobic microporous membranes. Membrane distillation processes use hydrophobic microporous membranes. Because of the porous hydrophobic characteristic of the membrane, only vapor can be transported, while vapor will condense, enabling the collection of clean water (El-Bourawi et al. 2006; Gryta 2010). The most common types of module design in membrane distillation operations are hollow fiber modules, plate and frame modules, tubular modules, and spiral wound modules.

Vacuum membrane distillation (VMD) is based on the evaporation of a solvent through hydrophobic porous membranes by applying a vacuum on the permeate side using a pump (Phattaranawik et al. 2003). VMD is the most efficient of all DM configurations, achieving the highest flux and desalination rate (Huayan et al. 2011). Indeed, compared with other configurations, there is negligible conductive heat loss through the membrane in the VMD process (Safavi and Mohammadi 2009). In addition, the presence of a vacuum on the permeate side leads to a higher partial pressure gradient and imposes an additional driving force for the process (Mohamed et al. 2017). For this reason, we notice an increase in the usage of VMD for different applications.

However, the vacuum level must be carefully monitored because the liquid entry pressure (LEP) can be exceeded to avoid membrane wetting (Hassan et al. 2016). Therefore, the difference between the hydrodynamic pressure of the feed stream and the pressure in the pores should not be greater than the minimum LEP. The LEP is measured by the contact angle and can be applied to characterize the hydrophobicity of the membrane. The water contact angle of a hydrophobic membrane tends to be above 90° to ensure that water droplets do not wet the membrane surface (Yuan and Lee 2013). Membrane properties such as small pore size, low surface energy, high surface roughness, and high surface tension favor high LEP (Fard and Manawi 2014; Rezaei and Sambaber 2016). The operating temperature and feed composition may also influence the LEP indirectly by altering the liquid contact angle and surface tension (Lawson and Lloyd 1997). Various models for estimating the LEP have been proposed in literature, including the Young–Laplace model, Purcell model, and others (Guillen-Burrieza et al. 2015; Servi et al. 2016).

Popular commercial membranes for MD process are prepared using polypropylene (PP), polytetrafluoroethylene (PTFE), polyethylene (PE), and polyvinylidene fluoride (PVDF). PVDF membranes with surface energy of 30.3 × 103 N/m have received the most attention from researchers due to their adequate stability, high solubility, and ease of fabrication and processing (Kang and Cao 2014; Lu et al. 2002). These membranes and their properties when used in plate-and-frame and hollow fiber modules have been studied in literature recently (Eykens et al. 2017; Pangarkar et al. 2016). The membrane is incorporated into a functional package consisting of a housing, the flow channels, the membrane, and its mounting.

The main cost of freshwater production is related to the capital cost of plant construction and its maintenance as well as the annual operating costs. The capital costs include construction, membrane module, auxiliary equipment (such as heat exchangers, pumps), solar collectors, and land and installation costs. The annual operating and maintenance costs include the total annual costs of operation and maintenance of a desalination plant, such as membrane replacement and chemical pretreatment (Al-Obaidani et al. 2008). For this reason, it is very important to reduce the costs of the MD process. One approach to reduce the high energy consumption required to heat the feedwater is to combine VMD with solar collectors (Mericq et al. 2011). Indeed, solar energy is very abundant in the Euro–Mediterranean region. Cabassud and Wirth (2003) reported that the use of a free heating source including solar energy reduces the energy consumption from 100 to 1.3 kWh/m3. The VMD technique offers important advantages with regard to the implementation of solar-driven desalination systems for standalone operation (Saffarinia et al. 2012). Another approach is to use geothermal fluids together with MD. An evaluation of the application of geothermal energy for water desalination was carried out using a VMD configuration (Sarbatly and Chiam 2013). The temperature of the geothermal water, which came from a reservoir located at Ranau, Sabah, Malaysia, was between 56 and 62 °C at the reservoir depth. The authors reported that the water production costs were 0.50 and 1.22 USD/m3 for the VMD desalination plant with and without geothermal energy, respectively. The results of that study revealed that geothermal energy could improve the efficiency of the process by saving around 95% of the total energy consumption. Recent studies (Zhang et al. 2013; Zuo et al. 2014; Lee and Kim 2013; Lovineh et al. 2013; Ben Abdallah et al. 2013) have reported several important approaches for modeling the VMD process. However, these approaches remain global and do not describe what happens on a finer scale, i.e., at the level of a pore of the membrane.

CFD is a powerful tool for predicting the dynamics of the flow within the membrane. To date, little research has been carried out on membrane distillation systems using CFD; For example, Rahimi et al. (2005) carried out CFD simulations and compared the results with experiment to study the fouling of a microfiltration membrane, revealing a good match. Rezakezemi et al. (2011) carried out CFD simulation of water removal by pervaporation from water/ethylene glycol mixtures. Numerical results for different values of the feed flow rate and temperature were compared with experimental data. In this context, we are interested in fine-scale modeling of the flow within a pore using the CFD code Fluent to predict and analyze the hydrodynamic properties of the flow in the VMD process.

Numerical model

Numerical method

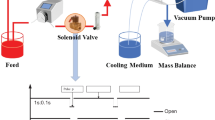
A hydrophobic microporous flat sheet PVDF membrane is considered in this study. The characteristics of the membrane are pore size of 0.22 µm, porosity of 75%, thickness of 200 µm, and thermal conductivity of 0.2 W/m-K.

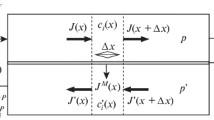
CFD simulations are carried out using the CFD code Fluent in the laminar regime. This code is based on solving the Navier–Stokes equations by the finite-volume discretization model. The pore has a diameter of 0.22 µm. A velocity inlet condition for the water is applied at the entry of the control volume: V = 1.11 m.s−1. A pressure of P = 1 atm is applied at the outlet of the control volume. A vacuum degree of 92 kPa is applied at the pore outlet. The temperature of the feed liquid is 65 °C. A porous medium is applied on the pore. The evaporation model of Lee is employed (Fig. 1).

Fig. 1
figure 1

Boundary conditions

Full size image

The mesh is created using GAMBIT. Figure 2 shows a zoom-in of the meshing of the control volume near the pore entry.

Fig. 2
figure 2

Zoom-in of the meshing near the pore entry

Full size image

Mathematical formulation

VOF model (Ansys Fluent documentation 1)

The volume-of-fluid (VOF) approach can model immiscible fluids by solving a single set of momentum equations and tracking the volume fraction of each fluid. The variables and properties in a cell are representative of one or a mixture of phases, depending on the volume fraction values. Therefore, if αq is the volume fraction of fluid q in the cell, three conditions are possible:

$$ \begin{gathered} \alpha_{q} = 0:{\text{ The cell is empty}}, \hfill \\ \alpha_{q} = {1}:{\text{ The cell is full}}, \hfill \\ 0 \, < \, \alpha_{q} < { 1}:{\text{ The cell contains an interface between the }}q^{{{\text{th}}}} {\text{fluid and one or more other fluids}}. \hfill \\ \end{gathered} $$
(1)
Volume fraction equation (Ansys Fluent documentation 2)

The interfaces between the phases are tracked by solving a continuity equation for the volume fraction of each:

$$\frac{1}{{\rho }_{q}}[\frac{\partial }{\partial \mathrm{t}}\left({\alpha }_{q}{\rho }_{q}\right)+\nabla \cdot \left({\alpha }_{q}{\rho }_{q}\overrightarrow{{v}_{q}}\right)={S}_{\alpha q}+\sum_{p=1}^{n}(\dot{{m}_{pq}}-\dot{{m}_{qp}})],$$
(2)

where \(\dot{{m}_{qp}}\) is the mass transfer from phase q to phase p and \(\dot{{m}_{pq}}\) is the mass transfer from phase p to phase q.

Momentum equation (Ansys Fluent documentation 3)

A single momentum equation is solved, and the resulting velocity field is shared among the phases.

$$\frac{\partial }{\partial \mathrm{t}}\left(\rho \overrightarrow{v}\right)+\nabla \cdot \left(\rho \overrightarrow{v}\overrightarrow{v}\right)=-\nabla p+\nabla \cdot \left[\upmu \left(\nabla \overrightarrow{v}+{\nabla \overrightarrow{v}}^{T}\right)\right]+\rho \overrightarrow{g}+\overrightarrow{F}.$$
(3)
Energy equation (Ansys Fluent documentation 4)

The energy equation is expressed as

$$\frac{\partial }{\partial t}\left(\rho E\right)+\nabla \cdot \left(\overrightarrow{v}(\rho E+p)\right)=\nabla \cdot \left({k}_{\mathrm{eff}}\nabla T\right)+{S}_{h}.$$
(4)

The VOF model treats energy, E, and temperature, T, as mass-averaged variables:

$$E=\frac{\sum_{q=1}^{n}{\alpha }_{q}{\rho }_{q}{E}_{q}}{\sum_{q=1}^{n}{\alpha }_{q}{\rho }_{q}},$$
(5)

where Eq for each phase is based on the specific heat of that phase and the shared temperature.

Surface tension and contact angle (Ansys Fluent documentation 5)

The VOF model can include the surface tension effects along the interface between each pair of phases. The surface tension model used in Fluent is the continuum surface force model proposed by Brackbill et al. (1992). The force at the surface can be expressed as a volume force and added to the momentum equation thus

$${F}_{\mathrm{vol}}=\sum_{ij, i<j}{\upsigma }_{ij}\frac{{\alpha }_{i}{\rho }_{i}{\kappa }_{j}\nabla {\alpha }_{j}+{\alpha }_{j}{\rho }_{j}{\kappa }_{i}\nabla {\alpha }_{i}}{\frac{1}{2}({\rho }_{i}+{\rho }_{j})}.$$
(6)

The surface tension of the water depends on temperature (Weast and Astle 1982). Thus, the value of the surface tension is given in Fig. 3.

Fig. 3
figure 3

Surface tension

Full size image

In conjunction with the surface tension model, the VOF model also offers the possibility to define a wall adhesion angle. The model is derived from work done by Brackbill et al. Instead of applying this boundary condition at the wall itself, the contact angle that the fluid makes with the wall is used to adjust the surface normal in cells close to the wall. The local curvature of the surface is determined by the combination of this contact angle with the normally calculated surface normal one cell away from the wall. This curvature is used to adjust the body force term in the surface tension calculation.

Porous media (Ansys Fluent documentation 6)

The porous medium is modeled by adding a momentum source term to the fluid flow equations. This source term is composed of a viscous loss term and an inertial loss term:

$${S}_{i }=-\left(\sum_{j=1}^{3}{D}_{ij}\upmu {v}_{j}+\sum_{j=1}^{3}{C}_{ij}\frac{1}{2}\rho \left|v\right|{v}_{j}\right),$$
(7)

where \({S}_{i}\) is the source term for the ith (x, y, or z) momentum equation, \(|v|\) is the magnitude of the velocity, and D and C are prescribed matrices. This momentum sink causes a drop in pressure proportional to the velocity of the fluid in the cell.

To recover the case of a simple homogeneous porous medium,

$${S}_{i }=-\left({\frac{\upmu }{\alpha }v}_{i}+{C}_{2}\frac{1}{2}\rho \left|v\right|{v}_{j}\right),$$
(8)

where \(\alpha \) is the permeability and \({C}_{2}\) is the inertial resistance factor.

In laminar flows through porous media, the pressure drop is typically proportional to the velocity and the constant  \({C}_{2}\) can be considered to be zero. The porous media model then reduces to Darcy’s law:

$$\nabla p=-\frac{\upmu }{\alpha }\overrightarrow{v}.$$
(9)

One technique for deriving the related constants is to use the equation of Ergun (1952):

$$\frac{\left|\Delta p\right|}{L}=\frac{150\upmu }{{{D}_{\rm p}}^{2}}\frac{{(1-\upvarepsilon )}^{2}}{{\upvarepsilon }^{3}}{v}_{\infty }+\frac{1.75\rho }{{D}_{\rm p}}\frac{(1-\upvarepsilon )}{{\upvarepsilon }^{3}}{{v}_{\infty }}^{2}.$$
(10)

The second term in this equation can be dropped when modeling laminar flow, resulting in the Blake–Kozeny equation (Ergun 1952):

$$\frac{\left|\Delta p\right|}{L}=\frac{150\upmu }{{{D}_{\rm p}}^{2}}\frac{{(1-\upvarepsilon )}^{2}}{{\upvarepsilon }^{3}}{v}_{\infty }.$$
(11)

Therefore, the coefficient of permeability and the inertial loss can be defined in each direction of the component by

$$\alpha =\frac{{{D}_{\rm p}}^{2}}{150}\frac{{\upvarepsilon }^{3}}{{(1-\upvarepsilon )}^{2}},$$
(12)

where Dp is the pore size and ε is the porosity of the membrane.

The viscous resistance is defined as the inverse absolute permeability. In our case, it is equal to \(\frac{1}{\alpha }=4.59\times {10}^{14} \,{\mathrm{m}}^{-2}\).

Evaporation/condensation model (Ansys Fluent documentation 7)

The evaporation/condensation process is given by the model of Lee. Depending on the temperature regime, the mass transfer can be described as follows:

$$\begin{gathered} {\text{If}}\;T > T_{{{\text{sat}}}} \;{\text{then}}\;\mathop {m^{ \cdot }_{{{\text{ev}}}} }\limits = {\text{coeff}}\times \alpha_{{\text{l}}} \rho_{{\text{l}}} \frac{{\left( {T - T_{{{\text{sat}}}} } \right)}}{{T_{{{\text{sat}}}} }} \hfill \\ {\text{If}}\;T < T_{{{\text{sat}}}} \;{\text{then}}\;\mathop {m^{ \cdot }_{{{\text{ev}}}} }\limits = {\text{coeff}}\times \alpha_{v} \rho_{v} \frac{{\left( {T - T_{{{\text{sat}}}} } \right)}}{{T_{{{\text{sat}}}} }} \hfill \\ \end{gathered} $$
(13)

\(\dot{{m}_{\mathrm{ev}}}\) represents the rate of mass transfer from the liquid phase to the vapor phase, with units of kg/s/m3. The coefficient “coeff” is an empirical coefficient that can be interpreted as a relaxation time. \(\alpha \) and \(\rho \) are the phase volume fraction and the density, respectively.

The saturation temperature depends on the pressure. It can be calculated using the Clausius–Clapeyron equation, which defines the slope of the vapor pressure curve (Kenneth 1988):

$$\frac{\mathrm{DP}}{\mathrm{dT}}=\frac{\Delta {H}_{\mathrm{vap}}}{T({v}_{v}-{v}_{l})}.$$
(14)

Assuming that the vapor phase is an ideal gas and that the specific volume of the liquid \({v}_{l}\) is small compared with the specific volume of the vapor \({v}_{v}\): \({v}_{l}\ll {v}_{v}=\frac{\mathrm{RT}}{P}\).

Then,

$$\begin{aligned}\frac{\mathrm{d}P}{\mathrm{d}T}& =\frac{\Delta {H}_{\mathrm{vap}}.P}{{T}^{2}R}\\ \frac{\mathrm{d}P}{P}& =\frac{\Delta {H}_{\mathrm{vap}}}{R}\frac{\mathrm{d}T}{{T}^{2}}\\ \mathrm{ln}\frac{P}{{P}_{0}}& =-\frac{\Delta {H}_{\mathrm{vap}}}{R}\left(\frac{1}{{T}_{\mathrm{sat}}}-\frac{1}{{T}_{0}}\right).\end{aligned}$$

Thus,

$${T}_{\mathrm{sat}}={(\frac{1}{{T}_{0}}-\frac{R\mathrm{ ln}\frac{P}{{P}_{0}}}{\Delta {H}_{\mathrm{vap}}})}^{-1},$$
(15)

where \({T}_{\mathrm{sat}}\) is the saturation temperature at the pressure of interest, R is the ideal gas constant, P is the vapor pressure of the liquid at the pressure of interest, \({P}_{0}\) is some pressure at which the corresponding \({T}_{0}\) is known (\(373\mathrm{ K}\) at 105 Pa), and \(\Delta {H}_{\mathrm{vap}}\) is the heat of vaporization of the liquid.

Numerical results

Permeate flux calculation

The empirical coefficient “coeff” appearing in the expression of the evaporation model of Lee is usually adjusted according to the experimental data. The default value is 0.1. Alizadehdakhel et al. (2010), Lee (1980), Wu et al. (2007), and De Schepper et al. (2009) used this value in their studies. However, in Yang et al. (2008) and Fang et al. (2010), the coefficient was set to 100. In our work, this coefficient was adjusted to achieve the same permeate flux as obtained by Alanezi et al. (2016), who studied the same configuration.

The permeate flux J is calculated as

$${J=j n}_{\rm p},$$
(16)

where \(j\) is the permeate flux obtained by a single pore and \({n}_{\rm p}\) is the number of pores.

The number of pores contained in a surface of the membrane S = 1 m2 can be calculated as \({n}_{\rm p}=\frac{V}{{V}_{\rm p}}\), where Vp is the volume of one pore and V is the volume of all pores.

So, \({n}_{\rm p}=\frac{V}{{V}_{\rm p}}=\frac{S \cdot \delta \cdot \varepsilon }{\pi {.{r}_{\rm p}}^{2}\cdot \delta \cdot \tau }=\frac{S.\varepsilon }{\pi {\cdot {r}_{\rm p}}^{2}\cdot \tau },\) where \(\delta \) is the membrane thickness, \(\varepsilon \) is the porosity of the membrane, \({r}_{\rm p}\) is the radius of the pore, and \(\tau \) is the tortuosity. The tortuosity is the deviation of the pore structure from a cylindrical shape. The most successful correlation was suggested by Macki–Meares (Srisuricahn et al. 2006) to be

$$\tau =\frac{(2-\varepsilon )^2}{\varepsilon }.$$
(17)

In our study, the tortuosity is equal to \(\tau =\mathrm{2.08}\).

The permeate flux obtained by Alhathal Alanezi et al. was equal to 53.1 kg/m2h. We carry out several simulations while varying the value of the empirical coefficient until arriving at a permeate flux very close to the value of Alhathal Alanezi. The value of the coefficient is equal to 120, and the permeate flux is equal to 53.18 kg/m2h in this case.

Description of the flow within the pore

Figure 4 shows the volume fraction of liquid water in the control volume. The red color indicates pure liquid, while the blue color indicates pure vapor. According to these results, the feed contains only water. The volume fraction of liquid in the pore decreases over time. A mixture formed by liquid and vapor appears at the entry of the pore. Far from the entry of the pore, the liquid disappears and the pore contains only vapor.

Fig. 4
figure 4

Volume fraction of liquid water

Full size image

Temperature polarization

The heat transfer coefficient of the VMD feed-side boundary layer, \({h}_{\rm f}\), is defined as

$$Q={h}_{\rm f} \Delta {T}_{\rm f},$$
(18)

where Q is the rate of heat transfer across the boundary layer and ∆Tf is the temperature drop across the boundary layer.

Experimental values of the heat transfer coefficient are given by Alhathal Alanezi et al. (2016).

Water that evaporates into the pores of the membrane removes the corresponding latent heat evaporation from the liquid feed stream. A non-isothermal boundary layer is formed near the pore, creating a resistance to heat transfer, which reduces the temperature at liquid–vapor interfaces compared with in the liquid feed.

Figure 5 shows the variation of the temperature of the fluid as a function of position in the pore. According to this figure, there is a difference in temperature between the pore entry (0 µm) and the pore outlet (200 µm). Indeed, the heat and mass transfer across the membrane move from the hot feed stream to the cold permeate stream. The temperature gradient causes a difference in temperatures between the liquid–vapor interfaces and the bulk temperatures on both sides of the membrane. This effect is called temperature polarization. Temperature polarization is considered to be one of the main issues raised against MD development because it reduces the permeate flux significantly (Camacho et al. 2013).

Fig. 5
figure 5

Variation of temperature in the pore

Full size image

Figure 6 shows the temperature at the entry of the pore. This figure shows that the temperature decreases gradually near the entry of the pore due to the evaporation of water.

Fig. 6
figure 6

Temperature field near pore entry

Full size image

Effect of contact angle

The contact angle is the angle between the wall and the tangent to the interface at the wall. The wettability of the membrane is a factor that helps to determine the efficiency of the VMD. The hydrophobicity of a membrane is expressed in terms of the contact angle (Fig. 7). In the case of water, a material is considered hydrophobic if the contact angle is greater than 90°. Figure 8 presents the volume fraction of the water for three values of the contact angle. For \(\theta =0^\circ \), the pore is totally wetted, whereas a non-wetting condition is obtained for \(\theta =180^\circ .\) Partial wetting is obtained for a contact angle of \(\theta =90^\circ \).

Fig. 7
figure 7

Porous membrane (Drioli et al. 2011)

Full size image
Fig. 8
figure 8

Effect of contact angle on wetting of the pore

Full size image

Liquid entry pressure

The liquid entry pressure (LEP) is the minimum pressure that must be applied to the feed liquid to overcome the membrane hydrophobic forces and penetrates into the pores.

According to Franken et al. (1987), the LEP can be estimated from the equation

$$\Delta P={P}_{\rm F}-{P}_{\rm P}=-\frac{2B{\gamma }_{\rm L}\mathrm{cos}\theta }{{r}_{\mathrm{max}}},$$
(18)

where PF and PP are the hydraulic pressure on the feed and permeate side, B is a geometric pore coefficient (equal to 1 for cylindrical pores), γL is the liquid surface tension, θ is the contact angle, and rmax is the maximum pore size. Thus,

$${P}_{\rm F}={P}_{\rm P}-\frac{2B{\gamma }_{\rm L}\mathrm{cos}\theta }{{r}_{\mathrm{max}}}.$$
(19)

In this study, the surface tension is equal to 0.065 N/m and the vacuum degree is 92 kPa. Simulations with Fluent are carried out for progressive values of the feed pressure, and the minimum pressure for which the pore is totally wetted is recorded for different values of the contact angle. The results are presented in Fig. 9, showing that good agreement was obtained between the numerical and theoretical values of the wetting pressure.

Fig. 9
figure 9

Comparison between numerical and theoretical wetting pressures

Full size image

Effect of feed temperature

Permeate flux

In this section, the effect of the feed temperature on the permeate flux is studied. To achieve, the temperature of the feed is varied and the permeate flux at the outlet of the pore for different temperature values is presented in Fig. 10a. According to these results, the permeate flux increases with increase of the feed temperature. In fact, increasing the feed temperature from 45 to 85 °C increases the permeate flux by 349%.

Fig. 10
figure 10

Variation of permeate flux and TPC as a function of temperature

Full size image

Temperature polarization coefficient

The temperature polarization coefficient (TPC) is defined as the ratio of the membrane surface temperature at the feed (Tmf) and the bulk feed (Tbf), given by

$$\mathrm{TPC}=\frac{{T}_{\mathrm{mf}}}{{T}_{\mathrm{bf}}}.$$
(20)

Figure 10b presents the evolution of the TPC for a pore as a function of the feed temperature for a vacuum pressure level equal to 92 kPa and a velocity inlet equal to 0.67 m/s. In this case and according to Alhathal Alanezi et al., the heat transfer coefficient is given by \({h}_{\rm f}=23.096 \times {T}_{\rm f}+1381\).

It has been shown that the TPC decreases as the feed temperature increases.

Effect of vacuum pressure

Permeate flux

In this section, the effect of the vacuum pressure on the permeate flux is studied. To achieve this, the vacuum pressure is varied and the permeate flux for the different values of the vacuum pressure is presented for a velocity inlet equal to 1.11 m/s and a feed temperature equal to 65 °C in Fig. 11a. According to these results, the permeate flux increases with increase of the vacuum pressure level. In fact, increasing the vacuum pressure from 90 to 98 kPa increases the permeate flux by 61.05%.

Fig. 11
figure 11

Variation of permeate flux and TPC as a function of vacuum level

Full size image

Temperature polarization coefficient

Figure 11b presents the evolution of the TPC for a pore as a function of the vacuum pressure for a feed temperature equal to 65 °C. This figure shows that the TPC decreases as the vacuum pressure level increases.

Effect of feed velocity

Permeate flux

In this section, the effect of the feed velocity on the permeate flux is studied. To achieve this, the inlet velocity is varied and the permeate flux for different values of the inlet velocity is presented for a vacuum pressure level equal to 92 kPa and a feed temperature equal to 65 °C (Fig. 12a). Based on these results, note that the permeate flux increases with increase of the feed velocity. Indeed, increasing the velocity from 0.32 to 1.25 ms−1 increases the permeate flux by 29.58%.

Fig. 12
figure 12

Permeate flux and TPC variations as a function of feed velocity

Full size image

Temperature polarization coefficient

Figure 12b presents the evolution of the TPC for a pore as a function of the velocity inlet for a feed temperature equal to 65 °C. This figure shows that the TPC increases as the velocity inlet increases.

Shock waves and the Riemann problem

When some fluids pass through porous media, some physical phenomena occur notwithstanding the initial conditions, such as empty area and turbulence caused by the appearance of shock waves. Various approaches to solving Riemann’s problems have been suggested in literature. In numerical analysis, Riemann problems appear naturally in finite volume methods for the solution of conservation law equations due to the discreteness of the grid. To achieve this, the CFD method is widely used. A Riemann problem is a specific initial value problem composed of a conservation equation together with piecewise-constant initial data that contain a single discontinuity in the domain of interest. The Riemann problem is very useful for understanding equations such as the Euler conservation equations because all the properties, such as shocks and rarefaction waves, appear as characteristics in the solution.

To take into account this phenomenon, we modified the momentum equation by adding a viscosity term. We obtain shock waves as follows:

$$\frac{\partial }{\partial t}\left(\rho \overrightarrow{v}\right)+\nabla \cdot \left(\rho \overrightarrow{v}\overrightarrow{v}\right)=-\nabla p+\nabla \cdot \left[\mu \left(\nabla \overrightarrow{v}+{\nabla \overrightarrow{v}}^{T}\right)\right]+\rho \overrightarrow{g}+\overrightarrow{F}+\epsilon\Delta \overrightarrow{v},$$
(21)

where \(\epsilon \) is an artificial viscosity. The physical solution of this problem is also called the entropic solution with a very low value of ε.

Volume fraction evolution

We performed a numerical simulation of the flow using ANSYS Fluent and take a value of \(\epsilon \) equal to \(\epsilon ={10}^{-5}\) Pa-s. The volume fraction of water obtained with and without a source term is shown in Fig. 13. According to this figure, the same evolution of the volume fraction is obtained when a source term is added. Nevertheless, it appears that the volume fraction of water in the pore in the configuration with a source term is lower than that without a source term. As a consequence, when a source term is included in the momentum equation, the pore wetting is reduced.

Fig. 13
figure 13

Time evolution of volume fraction of water obtained with and without source term

Full size image

Liquid entry pressure

Also, we compared the LEP values as a function of the contact angle for the two cases (with and without source term). The results are shown in Fig. 14. Note that the LEP values obtained in the case with a source term are improved and correspond better to the theoretical values.

Fig. 14
figure 14

Comparison between theoretical and numerical wetting pressures obtained with and without source term

Full size image

Conclusions

VMD is based on the evaporation of a solvent through a hydrophobic porous membrane by applying a vacuum on the permeate side. In this paper, numerical modeling of the VMD process using the CFD code Fluent is presented. The proposed model is based on the solution of the Navier–Stokes equations. It takes into account the evaporation of the liquid and the wetting of the pore when the LEP is exceeded. According to this study, CFD provides a powerful tool for modeling and predicting the dynamics of the flow within the membrane at a fine scale.

The temperature polarization effect is also observed. Furthermore, the effect of the feed temperature, vacuum pressure, and feed velocity on the hydrodynamic characteristics of the flow inside the pore is studied. It is observed that the flux increases with increase of the feed temperature, vacuum level, or feed velocity. The effect of the feed temperature, vacuum pressure, and velocity inlet on the temperature polarization coefficient is also examined. It is shown that the TPC decreases with increase of the feed temperature or vacuum level, but increases with increase of the velocity inlet. We also study the effect of adding a source term to the momentum equation to take into account the unusual physical phenomena occurring in the pore, such as the appearance of a shock wave. The results showed that, when a source term is added, the pore wetting is reduced. In addition, better agreement is achieved between the theoretical and numerical values of the liquid entry pressure.