Multicriteria group decision making approach based on an improved distance measure, the SWARA method and the WASPAS method

Abstract

The concept of intuitionistic fuzzy set (IFS) has extensively used to handle the uncertainty of real-life decision making problems. The aim of this study is to propose an integrated multicriteria group decision making (MCGDM) approach with intuitionistic fuzzy information and apply to select the most suitable renewable energy source with respect to multiple aspects of sustainability criteria. For this purpose, we firstly propose an improved distance measure to quantify the degree of difference between IFSs. Some numerical examples are presented to show the effectiveness of the proposed measure over the existing distance measures under the context of IFS. Further, we develop a weighting approach to find the criteria weights, which combines the objective weighting model using improved distance measure and the subjective weighting model using stepwise weighted assessment ratio analysis (SWARA) with intuitionistic fuzzy information. Based on the proposed criteria weighting model, we develop an integrated weighted aggregated sum product assessment (IF-WASPAS) approach for solving MCGDM problems under intuitionistic fuzzy environment. To prove the applicability and efficacy of the developed approach, we implement it on a case study of renewable energy source selection problem with multiple aspects of sustainability including technical, socio-political, environmental, and economic perspectives. Moreover, the sensitivity and comparative analyses are discussed to examine the feasibility and steadiness of introduced approach in order to assess the RES options. In this paper, we present an improved decision making approach, which makes a significant contribution to the renewable energy sources evaluation process with uncertainty.

1 Introduction

Multi-criteria group decision-making (MCGDM) problem is the process of choosing an optimal alternative/option among several alternatives, based on an assessment of how the options are likely to perform with respect to several criteria and considering the judgments of decision experts (DEs). Uncertainty is commonly occurred in the real-life MCGDM problems due to imprecise information and subjectivity of human mind; therefore, the DEs are unable to get an optimal solution for our daily life problems. To deal with uncertain and imprecise information, Zadeh (1965) originated the concept of fuzzy set (FS), which has widely been used by several authors for different purposes. For instance, Chen and Chen (2001) used the idea of geometry to compute the center-of-gravity points of trapezoidal or triangular fuzzy numbers and further proposed an approach to compute the similarity degree between fuzzy numbers. Chen and Fang (2006) studied an interesting approach to build and tune the membership functions for solving the fuzzy classification problems. In a study, Che et al. (2006) proposed a novel approach for generating weighted fuzzy rules from training data to take care of the Iris data classification problem. Based on weighted increment transformation and weighted ratio transformation, Chen et al. (2009) presented an efficient weighted fuzzy interpolative reasoning approach for sparse fuzzy rule-based systems. Based on fuzzy-trend logical relationship groups, Chen and Wang (2010) studied a new fuzzy forecasting approach and used to forecast the Taiwan Stock Exchange Capitalization Weighted Stock Index (TAIEX), the enrollments and the inventory demand. Later, Chen and Niou (2011) presented a new approach to deal with fuzzy multicriteria group decision making (MCGDM) problems based on fuzzy preference relations. With the use of matching theory, Shen et al. (2013) proposed a new reduction method to deal with the state explosion problem in Petri nets. Chen and Jian (2017) developed a new fuzzy forecasting method based on two-factors second-order fuzzy-trend logical relationship groups, similarity measures and particle swarm optimization approaches and applied for forecasting in Taiwan Stock Exchange.

In FS theory, each element has a membership degree (MD), which is a real number between zero and one, and the non-membership degree of an element in a FS is equal to one minus the MD, which may not always be true in real-life problems. To overcome the limitation of FS, Atanassov (1986) introduced the concept of intuitionistic fuzzy set (IFS), which is characterized by the MD, ND and hesitation degree (HD). In IFS, the HD is defined as one minus the sum of membership and non-membership degrees. Due to involvement of MD, ND and HD, the theory of IFS has proven as more useful than FS (Atanassov 1986). In the literature, several authors have focused their study under the contexts of IFS. For instance, Verma (2021) presented generalized intuitionistic fuzzy divergence measure and entropy-based MABAC (multi-attributive border approximation area comparison) model for solving MCGDM problems under intuitionistic fuzzy environment. Using the concept of IFS, Ming et al. (2022) developed an innovative patent infringement early warning model for evaluating and classifying patent infringement risk. Singh and Kumar (2023) developed intuitionistic fuzzy entropy-based knowledge measure and accuracy function, and also examined their utility and validity through numerical examples. In addition, their proposed measure and accuracy function have applied to develop an improved ranking approach under IFS environment. Ejegwa and Ahemen (2023) studied two novel similarity operators of IFSs with their desirable characteristics. To overcome the drawbacks of existing possibility degree measures, Dhankhar and Kumar (2023) introduced an extended IF-possibility degree and applied to develop an algorithm for decision making model. Kumar and Kumar (2023) proposed a modified similarity measure for IFSs and applied for solving pattern recognition, decision making and clustering problems. In addition, they discussed the properties of similarity measure and non-linearity axiom from graphical point of view.

Based on the concept of utility theory, Zavadskas et al. (2012) introduced the idea of weighted aggregated sum product assessment (WASPAS) approach, which can deal with a variety of practical MCGDM problems. It is indeed an integrated model combining the weighted sum model (WSM) and weighted product model (WPM) with a higher level of accuracy compared to WPM and WSM. The classical WASPAS approach has been applied for diverse perspectives. For instance, Stanujkić and Karabašević (2018) proposed a single-valued intuitionistic fuzzy information-based WASPAS approach with its application in website selection problem. Rudnik et al. (2021) extended the classical WASPAS approach using ordered fuzzy numbers and applied to evaluate the improvement projects. With the use of IFS, Xiong et al. (2020) used the WASPAS approach with best worst method for assessing the resilient-green supplier selection problem. Chakraborty and Saha (2022) used a novel fuzzy extension of WASPAS approach for evaluating the healthcare waste treatment technology selection problem. An interval-valued Fermatean fuzzy extension of WASPAS method has provided and applied to evaluate the green suppliers from sustainability points of view (Rani and Mishra 2022). Senapati and Chen (2022) presented an integrated picture fuzzy WASPAS approach for solving multi-criteria air condition system selection problem. Using the picture fuzzy numbers, Hezam et al. (2023) presented an improved WASPAS approach to evaluate the locations for biofuel production plant development by considering the multiple aspects of sustainability. Ebadzadeh et al. (2023) discussed an extended WASPAS approach for evaluating the environmental risks of petrochemical industry under fuzzy environment.

The evaluation of renewable energy source (RES) selection problem depends on numerous conflicting criteria and requires to involve several DEs for making decisions; thus, this problem can be considered as a multi-criteria group decision making (MCGDM) problem. In the literature, Tahri et al. (2015) assessed the photovoltaic solar energy farm locations in Morocco using geographical information system and decision making approach,. In that study, four different criteria, including climate, orography, location, and land use are evaluated and prioritized using analytic hierarchy process (AHP) tool. Mousavi et al. (2017) presented a soft computing based ranking approach using hesitant fuzzy information and presented its application in the assessment of RESs evaluation. An MCGDM model has proposed by Diemuodeke et al. (2019) for the assessment and selection of optimum location for hybrid RES in Nigeria. They evaluated the alternatives with respect to different aspects of sustainability including technical, socio-cultural, environment and economic. Abdel-Basset et al. (2021) gave a single-valued neutrosophic information-based decision making approach for assessing the best site for solar farms in Spain. Sitorus and Brito-Parada (2022) highlighted the shortcomings of existing studies and proposed a hybrid subjective and objective decision making approach for evaluating the RES options. In a study, Kaur et al. (2022) generalized the classical TOPSIS (technique for order of preference by similarity to ideal solution) from fuzzy information perspective and used to evaluate the RES options with respect to multiple criteria. Using spherical fuzzy information, Thanh (2022) proposed a hybrid multicriteria decision making approach to evaluate the RES options for industrial complex project. To select the best RES alternative, Liang et al. (2022) developed a multi-granular linguistic distribution-based MCGDM approach based on linear programming technique for multidimensional analysis of preference. Gupta et al. (2023) presented a MCGDM approach to assess the RES options from trapezoidal intuitionistic fuzzy linguistic perspective.

On the basis of existing works, we identify some key challenges and motivations behind the proposed study, given as.

• Existing intuitionistic fuzzy distance measures proposed by Szmidt and Kacprzyk (1997), Xu (2007a), Wu et al. (2021), Tripathi et al. (2023a) present some counter intuitive cases in order to quantify the degree of difference between IFSs. Thus, there is a need to overcome the drawbacks of existing measures by developing an improved intuitionistic fuzzy distance measure.

• The classical WASPAS approach (Stanujkić and Karabašević, 2018; Xiong et al. 2020; Rudnik et al. 2021; Chakraborty and Saha 2022; Rani and Mishra 2022; Senapati and Chen 2022; Hezam et al. 2023; Ebadzadeh et al. 2023) has been extended from different fuzzy perspectives including fuzzy set, intuitionistic fuzzy set, interval-valued Fermatean fuzzy set, Picture fuzzy set and crisp set. Existing studies avoid the importance of decision experts’ significance values. In addition, these studies consider only objective weights of criteria or subjective weights of criteria or direct assumption of the criteria weights.

• Various authors (Tahri et al. 2015; Mousavi et al. 2017; Diemuodeke et al. 2019; Rani et al. 2020; Abdel-Basset et al. 2021; Sitorus and Brito-Parada 2022; Kaur et al. 2022; Thanh 2022; Liang et al. 2022; Gupta et al. 2023) have proposed different decision making approaches to solve the RES selection problem under different environments. However, there is a lack of intuitionistic fuzzy information-based MCGDM approach to assess the multiple criteria RES options based on a set of decision experts opinions.

Motivated by the concept of IFS and WASPAS, this study develops a MCGDM approach to rank and evaluate the RES options. To the best of author’s knowledge, this is a novel work that develops a MCGDM approach with the combination of the proposed IF-distance measure, the WASPAS method, the SWARA (stepwise weight assessment ratio analysis) method and intuitionistic fuzzy information. The main contributions of this study are presented as.

• To overcome the shortcomings of extant distance measures (Szmidt and Kacprzyk 1997; Xu 2007a; Wu et al. 2021; Tripathi et al. 2023a), an improved intuitionistic fuzzy distance measure is developed and presented some elegant properties. Numerical examples are discussed to show the effectiveness of the proposed distance measure over the existing measures.

• A modified WASPAS approach is introduced to solve the MCGDM problem of renewable energy sources with respect to multiple sustainability criteria.

• To find the criteria weights, an integrated weighted model is presented in which objective weights are computed through distance measure-based formula and the subjective weights are derived using intuitionistic fuzzy SWARA method.

• To verify the practicality and efficacy, the proposed approach is implemented on an empirical study of renewable energy source selection under intuitionistic fuzzy environment.

• Sensitivity and comparative analysis are presented to show the robustness and stability of the obtained results.

Other sections are organized as follows: Sect. 2 presents the preliminaries and proposes an improved distance measure for IFSs. In addition, comparative study is presented to show the drawbacks of existing measures (Szmidt and Kacprzyk 1997; Xu 2007a; Wu et al. 2021; Tripathi et al. 2023a). Section 3 develops an integrated WASPAS method for solving MCGDM problems. Section 4 implements the proposed approach on a study of RES selection problem. Further, sensitivity analysis and comparison with existing studies are also presented in this section. Section 5 concludes the work and giving further research directions.

2 Proposed distance measure for IFSs

This section firstly presents the basic concepts of IFS and further proposes an improved distance measure to quantify the degree of distances between IFSs.

2.1 Preliminaries

Definition 2.1

(Atanassov 1986). An IFS K on $Y = \left\{ {y_{1} ,\,\,y_{2} ,\,\,...,\,\,y_{n} } \right\}$ is defined as

$$K = \left\{ {\left\langle {y_{j} ,\,\,\mu_{K} (y_{j} ),\,\,\nu_{K} (y_{j} )} \right\rangle \,\,:\,\,y_{j} \in Y} \right\},$$

(1)

where $\mu_{K} :Y \to [0,\,\,1]$ and $\nu_{K} :Y \to [0,\,\,1]$ represent the MD and ND, respectively, of y_j to K in Y, with the condition

$$0 \le \mu_{K} \left( {y_{j} } \right) \le 1,\;0 \le \,\nu_{K} \left( {y_{j} } \right) \le 1\;{\text{and}}\;0 \le \,\mu_{K} \left( {y_{j} } \right) + \,\nu_{K} \left( {y_{j} } \right) \le 1,\;\forall \,\,y_{j} \in \,Y.$$

(2)

The hesitation degree of an object $y_{j} \in \,Y$ to K is given by $\pi_{K} \left( {y_{j} } \right) = 1 - \mu_{K} \left( {y_{j} } \right) - \nu_{K} \left( {y_{j} } \right),$ where $0 \le \pi_{K} \left( {y_{j} } \right) \le 1,\,\,\,\forall \,y_{j} \, \in \,Y.$ For convenience, Xu (2007b) characterized the IFN $\varsigma = \,\left( {\mu_{\varsigma } ,\,\nu_{\varsigma } } \right),$ which satisfies $\mu_{\varsigma } ,\,\nu_{\varsigma } \, \in \,\left[ {0,\,1} \right]$ and $0\, \le \,\mu_{\varsigma } + \,\nu_{\varsigma } \le \,1.$

Figure 1 demonstrates the space of an intuitionistic fuzzy (IF) value. It is clear that the IFSs can not only depict uncertain information, but also deal with more inaccurate and ambiguous information. Here, horizontal-axis shows the change of MD, while vertical-axis demonstrates the change of ND.

Fig. 1

The geometrical interpretations of intuitionistic fuzzy number

Definition 2.2

(Xu 2007b). The score and accuracy values of an IFN $\varsigma_{j} = \left( {\mu_{j} ,\,\nu_{j} } \right)$ is defined by

$$S\left( {\varsigma_{j} } \right) = \left( {\mu_{j} - \nu_{j} } \right)$$

(3)

$$A\left( {\varsigma_{j} } \right) = \left( {\mu_{j} + \,\nu_{j} } \right),$$

(4)

respectively. Here, $S\left( {\varsigma_{j} } \right) \in \left[ { - 1,1} \right]$ and $A\left( {\varsigma_{j} } \right) \in \left[ {0,1} \right].$

As $S\left( {\varsigma_{j} } \right) \in \left[ { - 1,1} \right],$ then Xu et al. (2015) discussed a modified score function for IFN, which as.

Definition 2.3

(Xu et al. 2015). Consider $\varsigma_{j} = \left( {\mu_{j} ,\,\nu_{j} } \right)$ be an IFN. Then,

$$S^{*} \left( {\varsigma_{j} } \right) = \frac{1}{2}\left( {S\left( {\varsigma_{j} } \right) + 1} \right),$$

(5)

is defined as normalized score function for IFN $\varsigma_{j} .$ Here, $S^{*} \left( {\varsigma_{j} } \right) \in \left[ {0,1} \right].$

Definition 2.4

(Xu 2007b). Let $\varsigma_{j} = \left( {\mu_{j} ,\,\nu_{j} } \right),$ $j = \,1,\,2,\,...\,,n$ be the collection of IFNs. Then the intuitionistic fuzzy weighted averaging (IFWA) and the intuitionistic fuzzy weighted geometric (IFWG) operators are presented as

$$IFWA_{\psi} \left( {\varsigma_{1} ,\varsigma_{2} ,...,\varsigma_{n} } \right) = \mathop \oplus \limits_{j = 1}^{n} \psi_{j} \,\varsigma_{j} = \left[ {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{j} } \right)^{{\psi_{j} }} } ,\,\prod\limits_{j = 1}^{n} {\nu_{j}^{{\psi_{j} }} } } \right],$$

(6)

$$IFWG_{\psi} \left( {\varsigma_{1} ,\,\varsigma_{2} ,...,\,\varsigma_{n} } \right) = \mathop \otimes \limits_{j = 1}^{n} \,\varsigma_{j}^{{\psi_{j} }} = \left[ {\prod\limits_{j = 1}^{n} {\mu_{j}^{{\psi_{j} }} } ,\,\,1 - \prod\limits_{j = 1}^{n} {\left( {1 - \,\nu_{j} } \right)^{{\psi_{j} }} } } \right].$$

(7)

In Eqs. (6) and (7), $\psi = \left( {\psi_{1} ,\,\psi_{2} ,...,\,\psi_{n} } \right)^{T}$ denotes the weight values of $\varsigma_{j} ,\,\,j\, = 1,\,2,\,...,\,n,$ with $\sum\nolimits_{j = 1}^{n} {\psi_{j} = 1}$ and $\,\psi_{j} \in \left[ {0,\,\,1} \right].$

Definition 2.5

(Xu & Chen 2008). Let $K,\,L,\,M\, \in \,IFSs\left( Y \right).$ An intuitionistic fuzzy distance measure is a real-valued function $d\,:IFSs(Y) \times IFSs(Y) \to [0,\,\,1],$ which fulfils the following axioms:

(r₁). $0 \le d\left( {K,\,L} \right) \le 1,$

(r₂). $d\left( {K,\,L} \right) = 0 \Leftrightarrow \,\,K = \,L,$

(r₃). $d\left( {K,\,K^{c} } \right) = 1$ iff K is a crisp set,

(r₄). $d\left( {K,\,L} \right) = d\left( {L,\,K} \right),$

(r₅). If $K\, \subseteq L \subseteq \,M,$ then $d\left( {K,\,M} \right) \ge d\left( {K,\,L} \right)$ and $d\left( {K,\,M} \right) \ge d\left( {L,\,M} \right),$$\forall \,K,\,L,\,M \in \,IFSs\left( Y \right).$

2.2 Improved distance measure for IFSs

In this section, we propose an improved distance measure for IFSs, which quantifies the degree of distances between IFSs.

Let $K,\,L \in IFSs(Y).$ Then

$$d\left( {K,\,L} \right)\, = \,\,\frac{1}{n}\,\sum\limits_{i\, = 1}^{n} {g\left( {\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|,\,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right|} \right)} ,$$

(8)

where ‘$g$’ is a t-conorm.

Theorem 2.1:

The given function (8) is a valid distance measure for IFSs.

Proof:

To prove this theorem, Eq. (8) needs to satisfy the postulates of Definition 2.5.

(r₁). Since $K,\,L \in IFSs(Y),$ therefore, $0\, \le \,\mu_{K} (y_{i} )\, + \,\nu_{K} (y_{i} )\, \le \,1$ and $0\, \le \,\mu_{L} (y_{i} )\, + \,\nu_{L} (y_{i} )\, \le \,1,$$\forall \,y_{i} \, \in \,Y.$ It implies that $0\, \le \left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|\, \le \,1$ and $0\, \le \left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right| \le \,1.$ Therefore, $0\, \le \,d\left( {K,\,L} \right)\,\, \le \,1.$

(r₂). If $K\, = \,L,$ then it obvious from Eq. (8) that $d\left( {K,\,L} \right)\, = \,0.$ Conversely, if $d\left( {K,\,L} \right)\, = \,0,$ then

$$d\left( {K,\,L} \right)\, = \,\,\frac{1}{n}\,\sum\limits_{i\, = 1}^{n} {g\left( {\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|,\,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right|} \right)} \, = \,0,$$

$$\Leftrightarrow g\left( {\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|,\,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right|} \right)\, = \,0,$$

$$\Leftrightarrow \,\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|\, = \,0\;{\text{and}}\;\,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right|\, = \,0,$$

$$\Leftrightarrow \,\mu_{K} (y_{i} )\, = \,\mu_{L} (y_{i} )\;{\text{and}}\;\nu_{K} (y_{i} )\, = \,\nu_{L} (y_{i} ),$$

$$\Leftrightarrow \,K\, = \,L.$$

(r₃). If K is a crisp set, then $\mu_{K} (y_{i} )\, = \,1,\,\,\nu_{K} (y_{i} )\, = \,0$ or $\mu_{K} (y_{i} )\, = \,0,\,\,\nu_{K} (y_{i} )\, = \,1.$ It implies that $d\left( {K,\,K^{c} } \right)\, = \,\,\frac{1}{n}\,\sum\limits_{i\, = 1}^{n} {g\left( {\left| {1 - \,0} \right|,\,\left| {0 - \,1} \right|} \right)} \, = \,1.$

Conversely, if $d\left( {K,\,K^{c} } \right)\, = \,1,$ then

$$d\left( {K,\,K^{c} } \right)\, = \,\,\frac{1}{n}\,\sum\limits_{i\, = 1}^{n} {g\left( {\left| {\mu_{K} (y_{i} ) - \,\nu_{K} (y_{i} )} \right|,\,\left| {\nu_{K} (y_{i} ) - \,\mu_{K} (y_{i} )} \right|} \right)} \, = \,1,$$

$$\Leftrightarrow g\left( {\left| {\mu_{K} (y_{i} ) - \,\nu_{K} (y_{i} )} \right|,\,\left| {\nu_{K} (y_{i} ) - \,\mu_{K} (y_{i} )} \right|} \right)\, = \,1,\,\,\forall \,i,$$

$$\Leftrightarrow \,\left| {\mu_{K} (y_{i} ) - \,\nu_{K} (y_{i} )} \right|\, = \,1\;{\text{and}}\;\left| {\nu_{K} (y_{i} ) - \,\mu_{K} (y_{i} )} \right|\, = \,1,\,\,\forall \,\,i,$$

$$\Leftrightarrow \,\mu_{K} (y_{i} )\, = \,1\;\text{and}\;\nu_{K} (y_{i} )\, = \,0\; \Leftrightarrow \,K\;{\text{is a crisp set}}.$$

(r₄). The proof is obvious.

Therefore, $\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|\, \le \,\left| {\mu_{K} (y_{i} ) - \,\mu_{M} (y_{i} )} \right|$ and $\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right|\, \le \,\left| {\nu_{K} (y_{i} ) - \,\nu_{M} (y_{i} )} \right|,\,\forall \,y_{i} \, \in \,Y.$

Also, $\left| {\mu_{L} (y_{i} ) - \,\mu_{M} (y_{i} )} \right|\, \le \,\left| {\mu_{K} (y_{i} ) - \,\mu_{M} (y_{i} )} \right|$ and $\left| {\nu_{L} (y_{i} ) - \,\nu_{M} (y_{i} )} \right|\, \le \,\left| {\nu_{K} (y_{i} ) - \,\nu_{M} (y_{i} )} \right|,\,\forall \,y_{i} \, \in \,Y.$

So, $g\left( {\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|,\,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right|} \right) \le \,g\left( {\left| {\mu_{K} (y_{i} ) - \,\mu_{M} (y_{i} )} \right|,\,\left| {\nu_{K} (y_{i} ) - \,\nu_{M} (y_{i} )} \right|} \right)$ and $g\left( {\left| {\mu_{L} (y_{i} ) - \,\mu_{M} (y_{i} )} \right|,\,\left| {\nu_{L} (y_{i} ) - \,\nu_{M} (y_{i} )} \right|} \right) \le \,g\left( {\left| {\mu_{K} (y_{i} ) - \,\mu_{M} (y_{i} )} \right|,\,\left| {\nu_{K} (y_{i} ) - \,\nu_{M} (y_{i} )} \right|} \right),\,\forall \,y_{i} \, \in \,Y.$ It implies that $d\left( {K,\,M} \right) \ge d\left( {K,\,L} \right)$ and $d\left( {K,\,M} \right) \ge d\left( {L,\,M} \right),$$\forall \,K,\,L,\,M \in \,IFSs\left( Y \right).$

Note: (a) If $g\left( {a,\,b} \right)\, = \,\min \left\{ {1,\,a + \,b} \right\},$ then

$$d_{1} \left( {K,\,L } \right)\, = \,\,\frac{1}{n}\,\sum\limits_{i\, = 1}^{n} {\min \left( {1,\,\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right| + \,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right|} \right)} .$$

(b) If $g\left( {a,\,b} \right)\, = \,a\, + \,b\, - \,a.b,$ then

$$d_{2} \left( {K,\,L} \right)\, = \,\,\frac{1}{n}\,\sum\limits_{i\, = 1}^{n} {\left[ \begin{gathered} \left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right| + \,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right| \hfill \\ - \,\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|.\,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right| \hfill \\ \end{gathered} \right]} .$$

(c) If $g\left( {a,\,b} \right)\, = \,\frac{a\, + \,b - 2\,a.b}{{1 - \,a.b}},$ then

$$d_{3} \left( {K,\,L} \right)\, = \,\,\frac{1}{n}\,\sum\limits_{i\, = 1}^{n} {\left[ {\frac{{\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right| + \,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right| - \,2\,\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|.\,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right|}}{{1 - \,\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|.\,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right|\,}}} \right]} .$$

Theorem 2.2

Let $K,\,L\, \in \,IFSs\left( Y \right).$ Then the proposed distance measure (8) satisfies the following properties:

(i) $d\left( {K^{c} ,\,L^{c} } \right)\, = \,d\left( {K,\,L} \right),$

(ii) $d\left( {K,\,L^{c} } \right)\, = \,d\left( {K^{c} ,\,L} \right),$

(iii) $d\left( {K,\,K^{c} } \right)\, = \,0$ iff $\mu_{K} \left( {y_{i} } \right)\, = \,\nu_{K} \left( {y_{i} } \right),\,\,\,i=1,2,...,n,$

(iv) $d\left( {K \cap \,L,\,L} \right)\, \le \,d\left( {K,\,L} \right),$

(v) $d\left( {K \cup \,L,\,L} \right)\, \le \,d\left( {K,\,L} \right).$

2.2.1 Comparison with extant IF-distance measures

In this section, we compare the proposed IF-distance measure with the normalized hamming distance measure (Szmidt and Kacprzyk 1997), normalized Euclidean distance measure (Szmidt and Kacprzyk 1997), generalized distance measure (Xu 2007a), Wasserstein distance measure (Wu et al. 2021) and exponential distance measure (Tripathi et al. 2023a). The results are given in Table 1 on some common data sets.

Table 1 Comparative results obtained by proposed and existing measures 

Normalized Hamming distance measure (Szmidt and Kacprzyk 1997)

$$d_{NH} \left( {K,\,L} \right)\, = \,\,\frac{1}{2n}\,\sum\limits_{i\, = 1}^{n} {\left( {\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right| + \,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right| + \,\left| {\pi_{K} (y_{i} ) - \,\pi_{L} (y_{i} )} \right|} \right)} .$$

(9)

Normalized Hamming distance measure (Szmidt and Kacprzyk 1997)

$$d_{NE} \left( {K,\,L} \right)\, = \,\,\sqrt {\frac{1}{2n}\,\sum\limits_{i\, = 1}^{n} {\left( {\left| {\mu_{K} (y_{i} ) - \,\mu_{L} (y_{i} )} \right|^{2} + \,\left| {\nu_{K} (y_{i} ) - \,\nu_{L} (y_{i} )} \right|^{2} + \,\left| {\pi_{K} (y_{i} ) - \,\pi_{L} (y_{i} )} \right|^{2} } \right)} } .$$

(10)

Generalized distance measure (Xu 2007a)

$$d_{G} \left( {K,\,L} \right) = \frac{1}{2\,n}\left( {\sum\limits_{i = 1}^{n} {\left( {\left| {\mu_{K} (y_{i} )\, - \,\mu_{L} (y_{i} )} \right|^{\alpha } + \left| {\nu_{K} (y_{i} )\, - \,\nu_{L} (y_{i} )} \right|^{\alpha } + \left| {\pi_{K} (y_{i} )\, - \,\pi_{L} (y_{i} )} \right|^{\alpha } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha }}} .$$

(11)

Wasserstein distance measure (Wu et al. 2021)

$$d_{W} \left( {K,\,L} \right) = \sqrt {\left( {\frac{{\mu_{K} (y_{i} )\, - \,\nu_{K} (y_{i} )\,}}{2} - \,\frac{{\mu_{L} (y_{i} )\, - \,\nu_{L} (y_{i} )\,}}{2}} \right)^{2} \, + \,\frac{1}{3}\,\left( {\frac{{\mu_{K} (y_{i} )\, + \,\nu_{K} (y_{i} )\,}}{2} - \,\frac{{\mu_{L} (y_{i} )\, + \,\nu_{L} (y_{i} )\,}}{2}} \right)^{2} } .$$

(12)

Exponential distance measure (Tripathi et al. 2023a)

$$d_{E} \left( {K,\,L} \right) = \frac{{1 - \exp \left[ { - \frac{1}{2}\left( {\sum\limits_{i = 1}^{n} {\left( {\left| {\mu_{K} (y_{i} )\, - \,\mu_{L} (y_{i} )} \right|^{\alpha } + \left| {\nu_{K} (y_{i} )\, - \,\nu_{L} (y_{i} )} \right|^{\alpha } + \left| {\pi_{K} (y_{i} )\, - \,\pi_{L} (y_{i} )} \right|^{\alpha } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha }}} } \right]}}{{1 - \exp \left( { - \left( n \right)^{{{1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha }}} } \right)}},$$

(13)

where $\alpha > 0,\,\,\alpha \ne 1.$

By means of the obtained results in Table 1, we get some interesting outcomes, which as.

• For two different sets of IFSs (Set 1 and Set 2), the distance measures $d_{NH} \left( {K,\,L} \right)\,$ and $d_{1} \left( {K,\,L} \right)\,$ generate counter-intuitive result which are highlighted in Table 1.

• The given sets (Set 3 and Set 5) are different but the distance measure $d_{NE} \left( {K,\,L} \right)\,$ provides the same value. Similar case happens with the measures $d_{G} \left( {K,\,L} \right)$ and $d_{E} \left( {K,\,L} \right).$ Thus, these measures have counter-intuitive results for Set 3 and Set 5.

• Next, when compared the distance measures’ outcomes for all the sets, we obtain that the developed distance measure $d_{2} \left( {K,\,L} \right)$ and $d_{3} \left( {K,\,L} \right)$ have no counter-intuitive cases.

• Finally, it is worth mentioned that the proposed distance measure $d_{2} \left( {K,\,L} \right)$ and $d_{3} \left( {K,\,L} \right)$ provides reasonable results under considered sets, whilst existing measures generate some counter-intuitive cases.

3 Proposed WASPAS approach for solving MCGDM problems

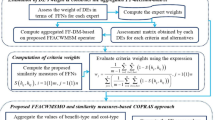
This section develops an integrated WASPAS approach in the context of IFS, where the assessment values of the alternatives over the criteria are characterized by IFNs and the weighs of the criteria and DEs are fully unknown. In the proposed approach, a combined weight-determining model is presented for deriving the objective weights of criteria through intuitionistic fuzzy distance measure-based procedure and the subjective weights through the SWARA method within IFS context. The calculation procedure of developed approach is specified in the following way and graphically presented in Fig. 2:

Fig. 2

Flowchart of developed MCGDM approach for RESs selection

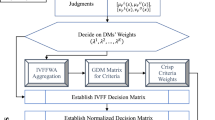
Step 1: Formulate the problem and create the linguistic decision matrix (LDM).

The process of MCGDM aims to evaluate the most suitable option among a set of finite options $S=\left\{{S}_{1},{S}_{2},\dots ,{S}_{p}\right\}$ with respect to a set of criteria $M=\left\{{M}_{1},{M}_{2},\dots ,{M}_{q}\right\}$ based on the group of experts’ opinions. Let $C=\left\{{c}_{1},{c}_{2},\dots ,{c}_{n}\right\}$ be a group of DEs, which present his/her views on each option over a criterion M_j (j = 1,2,…,q) in terms of linguistic variables (LVs). Let $R={\left({\varepsilon }_{ij}^{(k)}\right)}_{p\times q}$ be the corresponding LDM, wherein ${\varepsilon }_{ij}^{(k)}$ denotes the performance value of an option S_i by means of criteria M_j, presented by kth DE, where $i=1, 2,\dots \,,p,\,j=1, 2,\dots , q$.

Step 2: Compute the DEs’ weights.

Firstly, consider the DEs’ weights in terms of LVs and then converted into IFNs corresponding to Table 2. Suppose $c_{k} = \left( {\mu_{k} ,\,\nu_{k} } \right)$ be the intuitionistic fuzzy weight of kth DE, then the numeric weight of kth DE is computed using Eq. (9).

$$\gamma_{k} = \frac{{\left( {\mu_{k} + \pi_{k} \left( {\frac{{\mu_{k} }}{{\mu_{k} + \,\nu_{k} }}} \right)} \right)}}{{\sum\limits_{k = 1}^{n } {\left( {\mu_{k} + \pi_{k} \left( {\frac{{\mu_{k} }}{{\mu_{k} + \nu_{k} }}} \right)} \right)} }},\,\,k = 1,\,2,\,...n.$$

(14)

Table 2 Summary of considered criteria for RESs assessment

Step 3: Construct the aggregated intuitionistic fuzzy decision matrix (A-IFDM).

To construct an A-IFDM, it is essential to combine all the individual DEs’ opinions into the single decision opinion. For this purpose, an IFWA operator is used and created the A-IFDM ${R}_{A}={\left({\delta }_{ij}\right)}_{p\times q},$ where

$$\delta_{ij} = \left( {\mu_{ij} ,\nu_{ij} } \right) = IFWA_{\gamma_{k}}\left( {\varepsilon_{ij}^{(1)} ,\,\varepsilon_{ij}^{(2)} ,...,\,\varepsilon_{ij}^{(n)} } \right) = \,\left( {1 - \prod\limits_{k = \,1}^{n} {\left( {1 - \,\mu_{k} } \right)^{{\gamma_{k} }} } \,,\,\prod\limits_{k = 1}^{n} {\left( {\nu_{k} } \right)^{{\gamma_{k} }} } } \right).$$

(15)

Step 4: Determine the criteria weights by an integrated weighting model.

Suppose $w = \left( {w_{1} ,w_{2} ,...,w_{q} } \right)^{T}$ is the weight vector of criteria set with $\sum\nolimits_{j = 1}^{q} {w_{j} } \, = 1$ and $\,w_{j} \in \left[ {0,\,\,1} \right]$. In the following, we compute the criteria weights by combining objective and subjective weighting procedures:

Case I: Objective weights by the intuitionistic fuzzy distance measure-based formula.

This method unites the degree of difference among the different criteria. The expression of distance measure-based criteria weight-determining procedure is given as

$$w_{j}^{o} = \frac{{\frac{1}{p - 1}\sum\limits_{i = 1}^{p} {\sum\nolimits_{k = 1}^{p} {d\left( {\delta_{ij} ,\,\delta_{kj} } \right)} } }}{{\sum\nolimits_{j = 1}^{q} {\left( {\frac{1}{p - 1}\sum\limits_{i = 1}^{p} {\sum\nolimits_{k = 1}^{p} {d\left( {\delta_{ij} ,\,\delta_{kj} } \right)} } } \right)} }},\,\,\,j = 1,\,2,\,...,q.$$

(16)

Case II: Subjective weights by intuitionistic fuzzy SWARA model.

The SWARA model has been developed to effectively consider the subjective weights of the criteria in the process of solving MCGDM problems. As compared to analytic hierarchy process, the SWARA model does not involve a pairwise comparison and has high reliability, less computational complexity, and simple process of computation. Based on its unique benefits, Bouraima et al. (2023) integrated the SWARA model with combined compromise solution (CoCoSo) method and interval rough set, and applied to evaluate the railway systems with sustainability perspective. Saraç et al. (2023) incorporated the SWARA model with WASPAS method for finding an appropriate sample for vegan cake. Debnath et al. (2023) presented the SWARA-WASPAS methodology for evaluating suppliers in a healthcare testing services. Mardani et al. (2023) developed an intuitionistic fuzzy SWARA tool to evaluate the sustainability criteria for sustainable biomass crop selection problem. In the following steps, we present an integrated intuitionistic fuzzy SWARA (IF-SWARA) model for assessing the criteria weights under IFS context.

Step 4a: Each DE presents their opinion about the considered criteria.

Step4b: Aggregate the individual opinions into a single intuitionistic fuzzy number.

Step 4c: Determine the score value of each intuitionistic fuzzy number using Eq. (3).

Step 4d: Rank the criteria. With the help of the DEs’ choices, the criteria are ranked from the higher priority to the lower priority criteria.

Step 4e: From the second criterion, the relative importance levels are assessed as: the relative importance of criterion (j) in relation to the previous criterion (j − 1). This ratio is called as comparative significance of the mean value and denoted by b_j.

Step 4f: Evaluate the comparative coefficient by using Eq. (17).

$$\phi_{j} = \left\{ \begin{gathered} 1,\,\,\,\,\,\,\,\,\,\,\,j = 1 \hfill \\ b_{j} + 1,\,\,j > 1, \hfill \\ \end{gathered} \right.$$

(17)

Step 4g: Determine the weight of j^th criterion using the formula

$$x_{j} = \left\{ \begin{gathered} 1,\,\,\,\,\,\,\,\,\,\,\,\,j = 1, \hfill \\ \frac{{x_{j - 1} }}{{\phi_{j} }},\,\,\,j > 1. \hfill \\ \end{gathered} \right.$$

(18)

Step 4 h: Find the normalized weight of j^th criterion using Eq. (19).

$$w_{j}^{s} = \frac{{x_{j} }}{{\sum\nolimits_{j = 1}^{q} {x_{j} } }}, j=1,2,...,q.$$

(19)

Case III: Here, we combine the objective weighting model based on the distance measure and subjective weighting model based on the SWARA method. By combining these models, we conquer the drawbacks which arise either in an objective weighting model or a subjective-weighting model. The combined weighting formula is given by Eq. (20).

$$w_{j} = \,\tau w_{j}^{o} + \left( {1 - \,\tau } \right)w_{j}^{s} ,\, \,j\, = 1,\,2,\,...,\,q,$$

(20)

wherein $\tau \in \left[0, 1\right]$ denotes the decision strategy parameter.

Step 5: Normalize the A-IFDM.

If certain benefit and cost types of criteria are presented in the decision matrix, then it is required to normalize the given A-IFDM. For this purpose, convert the A-IFDM into the normalized A-IFDM ${R}_{A}^{N}={\left({\delta }_{ij}^{N}\right)}_{p\times q},$ where

$$\delta_{ij}^{N} = \left( {\mu_{ij}^{N} ,\,\nu_{ij}^{N} } \right) = \left\{ \begin{gathered} \delta_{ij} = \left( {\mu_{ij} ,\,\nu_{ij} } \right),\,\,\,\,\,\,\,\,j \in M_{b} \hfill \\ \left( {\delta_{ij} } \right)^{c} = \left( {\nu_{ij} ,\,\mu_{ij} } \right),\,\,\,\,j \in M_{n} \hfill \\ \end{gathered} \right.,\,i\, = 1,\,2,...,p,$$

(21)

where $M_{b}$ and $M_{n}$ present the sets of benefit and cost types of criteria, respectively.

Step 6: According to the weighted sum model (WSM), the relative importance of each option is computed using Eq. (22). This formula is based on intuitionistic fuzzy weighted averaging operator, given by Eq. (6). Here, $A_{i}^{(1)}$ is an IFN.

$$A_{i}^{(1)} \, = \,\mathop \oplus \limits_{j = 1}^{q} w_{j} \,\delta_{ij}^{N} = \left( {1 - \prod\limits_{j = \,1}^{q} {\left( {1 - \,\mu_{ij}^{N} } \right)^{{w_{j} }} } \,,\,\prod\limits_{j = 1}^{q} {\left( {\nu_{ij}^{N} } \right)^{{w_{j} }} } } \right),\,\,j = 1,\,2,\,...,q.$$

(22)

Step 7: According to the weighted product model (WPM), the relative importance of each option is computed using Eq. (23). This formula is based on intuitionistic fuzzy weighted averaging operator, given by Eq. (7). Here, $A_{i}^{(2)}$ is an IFN.

$$A_{i}^{(2)} \, = \,\mathop \otimes \limits_{j = 1}^{q} \left( {\delta_{ij}^{N} } \right)^{{w_{j} }} = \left( {\prod\limits_{j = 1}^{q} {\left( {\mu_{ij}^{N} } \right)^{{w_{j} }} } ,1 - \prod\limits_{j = \,1}^{q} {\left( {1 - \,\nu_{ij}^{N} } \right)^{{w_{j} }} } \,} \right),\,\,j = 1,\,2,\,...,q.$$

(23)

Step 8: To evaluate the overall significance of each option, we combine the relative importance of each option obtained by the WSM and WPM, presented as

$$A_{i} \, = \,\theta \,A_{i}^{(1)} \, + \,\left( {1 - \,\theta } \right)\,A_{i}^{(2)} \, = \,\theta \,\mathop \oplus \limits_{j = 1}^{q} w_{j} \,\delta_{ij}^{N} \, + \,\left( {1 - \,\theta } \right)\,\mathop \otimes \limits_{j = 1}^{q} \left( {\delta_{ij}^{N} } \right)^{{w_{j} }} ,\,\,i\, = 1,\,2,\,...,\,p.$$

(24)

Here, the parameter ‘$\theta$’ describes the decision precision coefficient that describes the accuracy of WASPAS method.

Step 9: According to the decreasing values of ${A}_{\mathrm{i}}, i=\mathrm{1,2},\dots ,p,$ rank the options and choose the most suitable one.

4 Result and discussion

This section implemented the proposed approach on a case study of RESs assessment in Tamil Nadu, India. Further, sensitivity and comparative analyses are discussed to reveal the robustness and stability of the proposed approach.

4.1 Application of renewable energy source selection

Tamil Nadu, a southern state of India, plays a leading role in the adoption of renewable energy source (RES). This state is known as the oldest power generator in India. Based on reports of June 2017, Tamil Nadu was the third state in India in the production of solar energy (1697 MW). Moreover, with 648 MW, Tamil Nadu holds the second-largest single-site solar farm in the world. Andhra Pradesh, with 2010 MW and Rajasthan with 1961 MW, are the leaders in this sense. Tamil Nadu is capable of taking such a leading role because of three factors: a considerable gap between power demand and supply, the accessibility of rich wind and solar energy resources, and strong policies devised and supported by the Indian government.

Due to the uncertainty of decision making process and the advanced sensitivity of RESs assessment, the precise and appropriate results may not be achieved by a single DE. Therefore, we consider three DEs for determination. The first DE (c₁) has a technical experience and expertise in dealing with numerous technological concerns. The second DE (c₂), from economic and government sector, has a deep understanding of all RESs to improve the performances. Finally, the third DE (c₃) is environmentalists and geologists. Based on the literature review and DEs’ opinions, a survey study has conducted to recognize the main factors that affect the evaluation and selection process of RESs in Tamil Nadu. Thus, a set of 15 criteria are considered to evaluate the RES options. Moreover, these criteria are classified according to four dimensions of sustainability including economic, environmental, socio-political and technical. Table 2 presents the descriptions of considered assessment criteria and shown in Fig. 3. Further, a set of six RES alternatives are considered as Tidal energy (S₁), biomass energy (S₂), Ocean thermal energy (S₃), solar energy (S₅), wind energy (S₅) and hydropower energy (S₆).

Fig. 3

A proposed ranking framework for RES selection

4.2 Implementation of the proposed MCGDM approach

In the subsection we implement the proposed WASPAS approach on a case study of aforesaid RES selection problem under intuitionistic fuzzy environment and present the obtained results.

Step 1: Table 3 shows LVs and corresponding IFNs to determine the significance of the DEs, renewable energy sources and the assessment criteria. Based on Table 3, three DEs present the linguistic performance value of each RES option by means of given criteria, given in Table 4 in the form of the LVs of given DEs as (c₁, c₂, c₃) for RES selection.

Table 3 LRs and corresponding IFNs for RES selection

Table 4 Linguistic decision matrix given by the DEs for RES selection problem

Step 2: Based on Table 3, firstly consider the linguistic significance value of each DE and then converted it into IFN. With the use of Eq. (14), the weight of each of three DE is derived and presented in Table 5.

Table 5 DEs’ weights during the RES selection problem

Step 3: With the use of Eq. (15), an aggregated intuitionistic fuzzy decision matrix is constructed by considering the significance values of DEs and shown in Table 6.

Table 6 A-IF-DM for RES selection

Step 4: To find the criteria weights, this step has divided into three cases.

Case I: Using the proposed intuitionistic fuzzy distance measure-based formula (16), the objective weights of criteria are computed and presented as $w_{j}^{o} =$(0.0568, 0.0473, 0.0727, 0.0678, 0.085, 0.0825, 0.0543, 0.0637, 0.0719, 0.0759, 0.064, 0.0772, 0.0647, 0.06, 0.0563). Figure 4 denotes the graphical structure of obtained objective weights of criteria.

Fig. 4

Objective weight of criteria for the assessment of RESs

Case II: With the use of Table 3, the DEs present the linguistic performance value of each criterion in Table 7. Next, the IFWA operator (6) is used to aggregate the individual performance value of each criterion, given by the DEs. In the last column of Table 7, the score value of each aggregated IFN is computed. Further, with the use of Eqs. (17)– (19), the subjective weight of each criterion is determined through intuitionistic fuzzy SWARA method and required results are presented in Table 8 and Fig. 5. The obtained subjective weights of criteria are $w_{j}^{s}$ = (0.0764, 0.0677, 0.0753, 0.0656, 0.0747, 0.0721, 0.0559, 0.0658, 0.0576, 0.0744, 0.0614, 0.0622, 0.0663, 0.0667, 0.0579)^T.

Table 7 Computation of aggregated IFNs and score values for RES selection

Table 8 Computational outcomes by IF-SWARA model for the evaluation of RESs

Fig. 5

Subjective weights of criteria for the assessment of RESs

Case III: In this case, we combine the results obtained from Case I and Case II to get the benefits of objective and subjective weights of criteria. Using Eq. (20), the combined final weights of criteria are computed (for $\tau =0.5$) as w_j = (0.0666, 0.0575, 0.0740, 0.0667, 0.0799, 0.0773, 0.0551, 0.0647, 0.0648, 0.0752, 0.0627, 0.0697, 0.0655, 0.0634, 0.0571).

Figure 6 demonstrates the weights of various criteria for evaluating RES options. Here, Emissions (M₅) (0.0799) has become the most important criterion in the assessment of RESs. Impact on environment and human (M₆) (0.0773) is the second most important criterion in the assessment of RESs. Job creation (M₁₀) (0.0752) is the third most important criterion, Government support (M₁₂) (0.0697) is the fourth, cost of fuel (M₄) (0.0667) is the fifth most important criteria in the assessment of RESs, and remaining are considered key criteria for evaluating RES options.

Fig. 6

Integrated weight of criteria for the assessment of locations of RESs

Moreover, in Fig. 7, assessment results of different dimensions of sustainability has considered based on the obtained criteria weights and thus, the preference ordering of these dimensions is as follows: Environmental ≻ Socio-political ≻ Economic ≻ Technical. It means environmental dimension with weight 0.277 has highest impact for assessing the RES options. Based on the realistic situations of various areas, it can be suitably changed in combination with different approaches.

Fig. 7

Depiction of weight of diverse dimension of sustainability perspectives

Step 5: Since the criteria M₁-M₇ are cost types and others are benefit types, therefore, there is a need to normalize the A-IFDM using Eq. (21). Thus, the normalized A-IFDM is constructed in Table 9.

Table 9 Normalized A-IFDM for RES selection

Steps 6–7: Using Table 9 and Eq. (22)-Eq. (23), the relative importance of each RES option is computed through WSM and WPM, respectively. The relative importance through WSM is obtained as ${A}_{1}^{(1)}=\left(0.484, 0.414\right),$ ${A}_{2}^{(1)}=\left(0.499, 0.398\right),$ ${A}_{3}^{(1)}=\left(0.472, 0.425\right),$ ${A}_{4}^{(1)}=\left(0.517, 0.380\right),$ ${A}_{5}^{(1)}=(0.536, 0.362)$ and ${A}_{6}^{(1)}=\left(0.499, 0.405\right).$ The relative importance through WPM is obtained as ${A}_{1}^{(2)}=\left(0.450, 0.444\right),$ ${A}_{2}^{(2)}=\left(0.453, 0.444\right),$ ${A}_{3}^{(2)}=\left(0.443, 0.456\right),$ ${A}_{4}^{(2)}=\left(0.454, 0.443\right),$ ${A}_{5}^{(2)}=(0.511, 0.386)$ and ${A}_{6}^{(2)}=\left(0.446, 0.456\right).$

Steps 8–9: From Eq. (24), the overall significance value of each RES option is computed for $\theta =0.5$ and the obtained results is given follows: ${A}_{1}=0.5189,$ ${A}_{2}=0.5277,$ ${A}_{3}=0.5085,$ ${A}_{4}=0.5370,$ ${A}_{5}=0.5748$ and ${A}_{6}=0.5208.$ Based on the obtained significance values, the prioritization of six RES alternatives is $S_{5} \succ S_{4} \succ S_{2} \succ S_{6} \succ S_{1} \succ S_{3}$ and thus, S₅ (wind energy) is the most suitable option for the given data sets.

4.3 Sensitivity analysis

In this section, we analyze the sensitivity of the chosen parameters in the proposed approach. For this purpose, we present two cases.

Case I: In this case, we present the sensitivity analysis with respect to diverse values of parameter $\left( {\theta \in [0,1]} \right)$. In accordance with different values of parameter$\theta$, the overall significance value of each RES option is computed and shown in Fig. 8. When $\theta = 0.0,$ then WASPAS measure reduces to WPM the ranking order of RES options is $S_{5} \succ S_{4} \succ S_{2} \succ S_{6} \succ S_{1} \succ S_{3} ,$ thus, the option S₅ (wind energy) is the optimal alternative. When $\theta = 0.5,$ the ranking of RES options is $S_{5} \succ S_{4} \succ S_{2} \succ S_{6} \succ S_{1} \succ S_{3}$ and S₅ (wind energy) is the optimal alternative, while when $\theta = 1.0,$ then WASPAS measure reduces to WPM and ranking order of RES options is $S_{5} \succ S_{4} \succ S_{2} \succ S_{6} \succ S_{1} \succ S_{3} ,$ thus, the option S₅ (wind energy) is the optimal alternative. This sensitivity analysis of a mathematical structure tells that how the results respond to parameter variations. Hence, we observe that the “IF-distance measure-SWARA-WASPAS” method has good steadiness for diverse parameter values.

Fig. 8

Results of sensitivity analysis of overall significance value over different weight values

Case II: Instead of integrated weights of criteria, we are taking only objective weights through IF-distance measure-based formula, i.e., take $\tau =1$. After computation, the overall significance values of alternatives are A₁ = 0.5205, A₂ = 0.5317, A₃ = 0.5116, A₄ = 0.54, A₅ = 0.5785 and A₆ = 0.5239 and the preference ranking is $S_{5} \succ S_{4} \succ S_{2} \succ S_{6} \succ S_{1} \succ S_{3} .$ Later, with the use of subjective weights through IF-SWARA model, i.e., $\tau =0$, the overall significance values of alternatives are A₁ = 0.5174, A₂ = 0.5238, A₃ = 0.5054, A₄ = 0.534, A₅ = 0.5712 and A₆ = 0.5177 and the preference ranking is $S_{5} \succ S_{4} \succ S_{2} \succ S_{6} \succ S_{1} \succ S_{3} .$ Thus, we can observed that use of different parameter values will improve the stability of the proposed hybrid methodology. Figure 9 shows the different ranking orders of RESs obtained through objective, subjective and integrated criteria weighting models.

Fig. 9

Sensitivity analysis of RESs using objective, subjective and integrated weighting models

4.4 Comparison with existing approaches

In the current section, the proposed WASPAS approach is compared with some of the existing approaches used for RES selection problem under different environments. These approaches are HF-ELECTRE (Mousavi et al. 2017), TFN-TOPSIS (Rani et al. 2020), IF-CoCoSo (Tripathi et al. 2023b), TrIFLN-VIKOR (Gupta et al. 2023) and IF-SWARA-COPRAS (Mardani et al. 2023). From HF-ELECTRE approach (Mousavi et al. 2017), the ranking order of the RES options is $S_{5} \, \succ \,S_{4} \, \succ \,S_{6} \, \succ S_{2} \, \succ \,S_{3} \,\, \succ \,S_{1} \,,$ and the most suitable RES option is wind energy (S₅). From TFN-TOPSIS (Rani et al. 2020) model, the ranking order of the RES options is $S_{5} \, \succ \,S_{4} \, \succ \,S_{2} \, \succ \,S_{6} \, \succ \,S_{3} \, \succ \,S_{1} ,\,$ and the most suitable choice is wind energy (S₅). From IF-CoCoSo (Tripathi et al. 2023b) model, the priority order of RES option is $S_{5} \, \succ \,S_{4} \, \succ \,S_{2} \, \succ \,S_{6} \, \succ \,S_{1} \, \succ \,S_{3} ,\,$ and the most suitable option is wind energy (S₅). From TrIFLN-VIKOR (Gupta et al. 2023) model, the ranking order of the RES options is $S_{5} \, \succ \,S_{4} \, \succ \,S_{2} \, \succ \,S_{1} \, \succ \,S_{6} \, \succ \,S_{3} ,\,$ and the most suitable RES alternative is wind energy (S₅). From IF-SWARA-COPRAS (Mardani et al. 2023) model, the ranking order of the RES options is $S_{5} \, \succ \,S_{4} \, \succ \,S_{2} \, \succ \,S_{6} \, \succ \,S_{1} \, \succ \,S_{3} ,\,$ and the most suitable RES alternative is wind energy (S₅).

Further, we compute the Spearman rank correlation degrees (SRCD) of HF-ELECTRE, TFN-TOPSIS, IF-CoCoSo, TrIFLN-VIKOR and IF-SWARA-COPRAS models with the proposed approach are as 1.0, 0.71, 0.94, 1.0, 0.94, 1.0). The SRCD quantifies the degree and direction of association between two approaches. From Fig. 10, the SRCDs are greater than 0.7 for each existing approach. Further, we have used the Wojciech Salabun (WS) coefficients (Salabun and Urbaniak, 2020) to measure the similarity of rankings, which is sensitive to the significant changes in the ranking. Here, we observed that the WS coefficients are greater than 0.94 for each existing approach. Figure 10 presents the correlation and similarity between the proposed and existing MCGDM approaches. The advantage of WS-coefficient specifies the homogeneity of preferences of options, which shows the homogeneity of prioritizations of considered RESs, is high. Consequently, it can be concluded that there is very resilient association between preference outcomes.

Fig. 10

Correlation plot of the developed MCGDM approach with the existing approaches

Different approaches provide the ranks of six RES options. From the aforesaid discussions, it can easily be noted that the all the approaches have obtained the same optimal choice, which is wind energy (S₅). In the following, we present the main benefits of the proposed MCGDM approach.

• In the decision making approaches given by Rani et al. (2020) and Gupta et al. (2023), the decision experts’ weights are considered randomly. However, the proposed approach provides a formula to derive the weights of decision experts from intuitionistic fuzzy information perspective.

• In the literature, Mousavi et al. (2017), Tripathi et al. (2023b) and Gupta et al. (2023) have computed only the objective weights of sustainability criteria. While the proposed MCGDM approach has computed the combined weights of criteria using the proposed distance measure-based model for objective weights and intuitionistic fuzzy SWARA model for subjective weights of criteria. Due to integration of objective and subjective weights, the proposed MCGDM approach provides the more reasonable and accurate decision outcomes.

• In the proposed MCGDM approach, the overall significance of each RES option is calculated with the integration of relative importance values obtained by WPM and WSM, while existing approaches are based on the compromising solution and outranking solution, which choose closest to an ideal solution. Thus, this method presents more accurate decision in the presence of a group of decision experts.

5 Conclusions

This paper aims to introduce an integrated MCGDM tool to assess and choose the optimal RESs in Tamil Nadu (India). In view of that, first, new intuitionistic fuzzy distance measure is developed and presented some elegant properties to overcome the shortcomings of extant IF-distance measures (Szmidt and Kacprzyk 1997; Xu 2007a, b; Wu et al. 2021; Tripathi et al. 2023a). Second, new IF-distance measure-SWARA tool is discussed to estimate the integrated weight of criteria and dealt with the uncertainty that is generally accompanying with the preferences/opinions of DEs. Next, a hybrid WASPAS approach has developed based on the proposed distance measure and the SWARA models under intuitionistic fuzzy environment. Further, the proposed MCGDM approach has applied to rank the RES options from intuitionistic fuzzy information perspective. The obtained solution by WASPAS method integrates the relative importance values by weighted sum model and weighted product model and then determines the ranks of the options based on the overall significance values, which is one of the main advantages of the proposed work. Next, sensitivity analysis has carried out to examine the influence of different parameters values, which also confirmed that the proposed approach is both stable and feasible. Finally, comparative analysis is discussed to reveal the stability and usefulness of the proposed approach. As per the comparative study, it can be observed that the proposed WASPAS approach is very useful and appropriate for the MCGDM problems with imprecise information about the criteria and DEs’ weights. Some limitations of the proposed MCGDM approach are i) the overall significance values are computed based on the comparison of IFNs using score and accuracy values. This process does not involve the “hesitancy degree (HD)”, which causes information loss; and ii) the proposed MCGDM approach does not consider the dominance of one option over the others. In the further direction, these limitations are planned to be addressed and new approaches are planned to develop for solving large scale MCGDM problems. In addition, the presented methodology can be combined with other decision making approaches, such as ELECTRE, CoCoSo, CODAS, and ARAS to develop the more suitable approaches under different fuzzy environments.