1 Introduction

Significance testing is increasingly used in machine learning and data science, particularly in the context of comparative classification studies [9]. For example, the Friedman test has been widely used for comparing multiple classifiers over multiple data sets [18]. Suppose that we wish to compare a new classifier with three other classifiers. Let us assume that we compare their performance over 50 benchmark data sets. We use the Friedman test to test the global null hypothesis of equal performance between the four classifiers. Suppose that we obtain a p value of 0.001. How should we interpret this result? We would like to invite the reader to briefly ponder over this question.

The question might seem silly, as the answer seems all too obvious: “Reject the null hypothesis of equal performance.” But is this the correct interpretation? As we will discuss, the answer to this question is far more complicated than it seems. Paradoxically, the p value can be close to 0, yet the posterior probability in favor of the null hypothesis can be close to 1. In other words, it is possible to obtain a very small p value, but the evidence after the experiment can convince us that the null hypothesis is almost certainly true. This phenomenon was first observed by Jeffreys [32]. Lindley described the conundrum in his seminal paper as a paradox [36, p.187], and it has since become widely known as the Lindley’s paradox or Jeffreys–Lindley paradox.

The statistical literature contains many papers on the paradox; however, there is no consensus on its relevance for scientific communication [15]. We recently discussed the problem in the context of comparative classification studies [11]. Here, we report the results of our extended study. The goal of the present study is to investigate the relevance of the paradox for machine learning, specifically, for the statistical evaluation of learning algorithms. Our basic research question concerns the interpretability of a significant p value as an evidential weight against the null hypothesis.

Null hypothesis significance testing (NHST) is often portrayed as one coherent theory of statistical testing [9]. However, NHST is an amalgamation of incompatible ideas from two different schools of thought, one going back to Ronald A. Fisher, the other one going back to Jerzy Neyman and Egon Pearson. We will refer to the Fisherian school as significance testing and to the Neyman–Pearsonian school as hypothesis testing. The central ideas underlying their philosophies are fundamentally different, and mixing up these incompatible ideas has been the root of many problems [28,29,30]. The Jeffreys–Lindley paradox arises from a conflict between the Bayesian and frequentist interpretation and can manifest itself in both significance testing and hypothesis testing. Here, we will investigate the paradox from the Fisherian perspective and focus on the p value.

Our novel contributions are twofold. First, we demonstrate that (i) the paradox can manifest itself easily in common benchmark studies, and that (ii) it has severe repercussions for the current research practice in machine learning and data science. Although significance testing is widely believed to lend scientific rigor to the analysis of empirical data [9] and a significant p value is a de facto gatekeeper for publication [39], our results suggest that p values are, at best, highly overrated as evidential measures, and at worst, can be downright misleading. As an over-reliance on p values might have contributed to the current reproducibility crisis in biomedical and psychological research, we are concerned that a similar crisis might be imminent for the machine learning community. Therefore, we argue that a reform of the current research practice is needed.

This paper is organized as follows. First, we briefly review the p value and some of its misconceptions. We then revisit the Jeffreys–Lindley paradox and describe the rationale for our experiments. We conclude the paper with a discussion of the implications for the current research practice in machine learning and offer for debate possible avenues to alleviate the looming crisis.

2 The p value, revisited

Loosely speaking, the p value is the probability of observing data as extreme as, or more extreme than, the actually obtained data, given that the null hypothesis is true. Formally, the null hypothesis, H0, can be stated as follows [3]:

$$\begin{aligned} \mathrm {H0}: \mathbf{X } \sim f(\mathbf{x },\theta ), \end{aligned}$$
(1)

where X denotes data, and \(f(\mathbf{x },\theta )\) is a probability density with parameter \(\theta \). The p value can now be stated as

$$\begin{aligned} p\, {\text {value}} = P(t(\mathbf{X }) \ge t(\mathbf{x _{\mathrm{obs}}})~|~\mathrm {H0}), \end{aligned}$$
(2)

where our observed data is \(\mathbf{x _{\mathrm{obs}}}\), and \(T = t(\mathbf{X })\) is a statistic that we calculate from our data by using the statistical function \(t(\cdot )\), for example, the arithmetic mean. We use the statistic T to assess the compatibility of the null hypothesis with the observed data, where large values of T indicate less compatibility. Hence, the p value can be interpreted as a measure of compatibility between the null hypothesis and the observed data.

The p value is also a random variable that is uniformly distributed over the unit interval [0, 1] when the null hypothesis is true [50]. For example, if the null hypothesis is true, then values between 0.04 and 0.05 are as likely to be observed as values between 0.54 and 0.55, or between 0.72 and 0.73, or any other interval of the same width. This property will be important later when we interpret the results of our computational experiments.

Although the p value is arguably one of the most commonly reported values in the scientific literature to underpin the interpretation of experimental results, it is also one of the most recondite values [26]. A pervasive misconception is that the p value is the probability of the null hypothesis being true [24]. Interpreting the conditional probability in Eq. 2 as the probability of the null hypothesis being true is such a common fallacy that it has been given a name: the fallacy of the transposed conditional, sometimes also referred to as the prosecutor’s fallacy.

A small p value may invite the following interpretation: “As the p value is smaller than 0.05, the null hypothesis can be rejected.” However, this interpretation leads us into semantic quicksand, as the idea of rejecting or accepting a null hypothesis is firmly embedded in the Neyman–Pearsonian paradigm where the p value does not exist. In the Neyman–Pearsonian school of thought, we are interested in a null hypothesis and an alternative hypothesis and in the associated Type I and Type II error rates that we make when we decide for or against the null hypothesis. These error rates are frequentist errors that we make in the long run. By contrast, the p value does not have any valid interpretation as long run, repetitive error rate [8, 28]. Also, note that there is no alternative hypothesis in the Fisherian paradigm.

An often chosen arbitrary cutoff for the p value is 0.05. When the p value is smaller than 0.05, it is considered significant. There seems to be nothing wrong with statements such as “p value \(< \alpha \).” However, the \(\alpha \) level (commonly set to 0.05) belongs to the Neyman–Pearsonian testing where it denotes the Type I error. Juxtapositions of “p value” with “Type I/II errors” or “rejection region” conflate incompatible ideas and should therefore be avoided. This mixing of incompatible ideas in NHST was denoted as “inconsistent hybrid” [22, p.587].

The Fisherian school considers the p value an evidential weight for or against the null hypothesis [25]: the smaller the p value, the smaller the evidence in favor of the null hypothesis, i.e., the less compatible is the null hypothesis with the observed data. The evidential property of the p value, however, has been questioned [8, 23, 47]. The reason is that an evidential measure requires two competing hypotheses—but in the Fisherian paradigm, there is only one hypothesis, the null hypothesis, while a formal alternative hypothesis does not exist.

Let’s return to the introductory example—what is the correct interpretation of a p value of 0.001, then? A formally correct answer to this question is the following: “Given that the null hypothesis of no difference in performance is true, the probability of observing a difference (in performance) as large as the observed one (or even larger) is 0.001.” As Fisher reminded us, a small p value might also be an indication of problems with the study design or data collection [19]. If we assume that there are no such problems, then we might interpret the small p value as an indication that “something surprising is going on” [8, p.329]. Therefore, we might not wish to entertain the null hypothesis that there is no difference in performance. Another common reasoning goes like this: “Either the null hypothesis is true and a rare event has happened, or the null hypothesis is false.” Yet there is a logical flaw in this reasoning because “the rare event” does not refer to the actual result that we obtained, but it also includes the “more extreme results” (cf. the inequality sign in Eq. 2)—which we actually did not observe.

Note that neither the Fisherian nor the Neyman–Pearsonian school of testing provides posterior probabilities of H0 (or H1) being true. In contrast to Bayesian testing, there is also no concept of prior probability.

3 The Jeffreys–Lindley paradox, revisited

We will describe the paradox by largely adopting Lindley’s notation and Bartlett’s correction of Lindley’s original equation [2]. Let \(x = (x_1, x_2, \ldots , x_n)\) be a random sample from a normal distribution with mean \(\theta \) and known variance \(\sigma ^2\). The null hypothesis is H0: \(\theta = \theta _0\) and the alternative hypothesis is H1: \(\theta \ne \theta _0\). Let the prior probability of H0 being true be c and let the remainder of the prior probability be uniformly distributed over some interval of width I, containing \(\theta _0\) as its midpoint. The probability density function under the alternative hypothesis is therefore \(f_{\mathrm {H}1}(\theta ) = \frac{1}{I}\). We consider the arithmetic mean, \(\bar{x}\), of the data, which is well within the interval. The posterior probability of H0 given the sample, P(H0|x), is then calculated according to Bayes’ theorem,

$$\begin{aligned} P(\mathrm {H0}|x) = \frac{c \cdot \exp \left( -\frac{n}{2} \frac{(\bar{x} - \theta _0)^2}{\sigma ^2} \right) }{c \cdot \exp \left( -\frac{n}{2} \frac{(\bar{x} - \theta _0)^2}{\sigma ^2} \right) + (1 -c) \int \exp \left( -\frac{n}{2} \frac{(\bar{x} - \theta )^2}{\sigma ^2} \right) \frac{1}{I} \mathrm{d}\theta }, \end{aligned}$$
(3)

where the integral is taken over the domain of \(\theta \), i.e., the interval of width I. If we change the limits of the integral to \(-\,\infty \) to \(+\,\infty \), then the equal sign changes to \(\ge \), since the denominator becomes larger. But the resulting integral over the new limits can now be evaluated as \(\int _{-\infty }^{+\infty } \exp \left( -\frac{n}{2} \frac{(\bar{x} - \theta )^2}{\sigma ^2} \right) \mathrm{d}\theta = \sigma \sqrt{2\pi n^{-1}}\).

Let us assume that \(\bar{x}\) is significant at the \(\alpha \) level. This means that \(\bar{x} = \theta _0 \pm z_{\alpha /2} \cdot \frac{\sigma }{\sqrt{n}}\), where \(z_{\alpha /2}\) is the quantile of the standard normal distribution for probability \(\alpha /2\). Plugging this expression into Eq. 3, we obtain

$$\begin{aligned} P(\mathrm {H0}|x) \ge \frac{c \cdot \exp \left( {-\frac{1}{2} z^2_{\alpha /2}}\right) }{c \cdot \exp \left( {-\frac{1}{2} z^2_{\alpha /2}}\right) + \frac{(1 - c)}{I} \sigma \sqrt{\frac{2\pi }{n}}}. \end{aligned}$$
(4)

From Eq. 4, we see that \( P(\mathrm {H0}|x) \rightarrow 1\) for \(n \rightarrow +\infty \). This means that for any value c and \(\alpha \in (0, 1)\), a value n can be found, dependent on c and \(\alpha \), such that

  1. 1.

    The sample mean \(\bar{x}\) is significantly different from \(\theta _0\) at the \(\alpha \) level.

  2. 2.

    The posterior probability P(H0|x), i.e., the probability that \(\theta = \theta _0\), is \(1 - \alpha \).

In the words of Lindley, “[t]he usual interpretation of the first result is that there is good reason to believe \(\theta \ne \theta _0\); and of the second, that there is good reason to believe \(\theta = \theta _0\).” [36, p.187]. Both conclusions are in conflict, which is the paradox.

Lindley uses a Gaussian model with known variance as example, but the paradox can be generalized. The paradox can also be stated in terms of the p value:

  1. 1.

    A statistical test for H0 reveals that a result, x, is significant with a p value of p.

  2. 2.

    There exists a sample size n so that the posterior probability of H0 given x, \(P(\mathrm {H0}|x)\), is \(1 - p\).

This means that a p value can be very small, hence providing overwhelming evidence against the null hypothesis, while at the same time, the posterior probability of the null hypothesis being true can be close to 1. Thus, our conclusion based on significance testing is diametrically opposed to our conclusion based on the Bayesian paradigm.

The factor \(\frac{1}{I}\) in Eqs. 3 and 4, which was missing in Lindley’s seminal paper, adds an important caveat to Lindley’s argument [15, 51]. The crucial point is the assumption that the prior distribution of \(\theta \) under the alternative hypothesis is uniform over an interval I. This means that the prior probability density function of \(\theta \) under the alternative hypothesis is \(\frac{1}{I}\) in the interval. At first, this factor does not seem to matter much, as the posterior probability still approaches 1 for \(n \rightarrow \infty \). And indeed, the factor does not invalidate the paradox. But the posterior probability of the null hypothesis now depends not only on the prior, c (and of course on \(\alpha \)), but also on the probability density over I. This means that two Bayesians, although they agree on the prior probability of H0, can arrive at a different posterior probability of H0 once they have seen the data because they might assume a different density under the alternative hypothesis.

4 Theoretical considerations

This study is concerned with the relevance of the paradox for machine learning research, specifically, the comparison of classifiers. How can the paradox manifest itself in this common type of analysis? Let us assume that a comparative study involves m classifiers that are benchmarked on n data sets. The global null hypothesis is that there is no performance difference between the classifiers. Formally, the null hypothesis is \(\mathrm {H0}:\theta _1 = \theta _2 = \ldots \theta _m\), where \(\theta _i\) is the test statistic for the ith classifier.

There are now two possibilities, either there is no real difference (H0 is true) or there is (H0 is false), i.e., at least one \(\theta \) is different from the others. We refer to the second possibility as H1.

We investigate the Jeffreys–Lindley paradox by focusing on the p value. We are not interested in calculating the posterior probability of H0 and H1. Instead, we are interested in the following question: under which hypothesis is it more likely to observe a significant p value from an interval [a, b], \(0< a< b < 0.05\), depending on the sample size, n? Hence, we are interested in the likelihood ratio

$$\begin{aligned} \mathrm {LR} = \frac{P(p\,\mathrm {value} \in [a,b]~|~\mathrm {H0}, n)}{P(p\,\mathrm {value} \in [a,b]~|~\mathrm {H1}, n)}, \end{aligned}$$
(5)

where the probabilities are estimated by relative frequencies.

Equation 5 is motivated by our basic research question about the interpretability of a significant p value as an evidential weight against the null hypothesis.

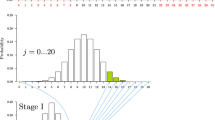
Consider Fig. 1, which shows three different hypothetical densities of p values. If H0 is true, then the p values are uniformly distributed over [0, 1], irrespective of the sample size. This means that no matter how many data sets we include, the p value can assume any value from [0, 1] with equal probability (red line in Fig. 1).

If, on the other hand, at least one of the classifiers performs differently from the others (H0 is false), then the number of data sets matters because it determines the sample size for the global test. If H0 is indeed false, then the p value should decrease with larger sample sizes. This is immediately obvious when the statistic of interest is the sample mean, as in Lindley’s example. The larger the sample size, the smaller the standard error, everything else being equal. In other words, we are chasing smaller and smaller differences by increasing the sample size.

In comparative classification studies, a researcher has usually full control over how many (and which) benchmark data sets to include. By including more data sets (i.e., increasing n), the researcher is therefore “pushing” the p value toward zero, provided that a difference does exist. Consequently, for a larger number of data sets, \(n_1\), we expect to see a distribution of p values as shown in the blue curve in Fig. 1, in contrast to the green curve that we expect to see for a comparatively smaller number of data sets, \(n_2 < n_1\).

Fig. 1
figure 1

Schematic illustration of the effect of the number of data sets on the distribution of p values when the null hypothesis is true and when it is false (color figure online)

Full size image

Consider now an interval containing p values that are commonly considered significant, for example, [0.02, 0.03]. Note that this is not a rejection region from the Neyman–Pearsonian paradigm. It is simply an interval that contains a number of significant p values, for example, \(p = 0.027\). If we obtain such a small p value in a real experiment, we might say that there is evidence against the null hypothesis of no difference. But consider now Fig. 1 again: in which scenario is this p value more likely, H0 being false (blue distribution) or H0 being true (red distribution)? In Fig. 1, the density of p values in the interval is much higher when H0 is true. Therefore, it is more likely that the p value of 0.027 came from the red distribution, which means that H0 is more, not less, likely to be true.

In our experiments, we need to compare a number of classifiers on a number of data sets. We need to consider two scenarios, (i) the null hypothesis is true, and (ii) the null hypothesis is not true. These are the only two conditions that matter—the concrete significance test (as long as it is appropriate), the concrete data sets, or learning algorithms are irrelevant.

5 Materials and methods

We used random forest as the learning algorithm to induce classifiers [13]. Briefly, random forest is an ensemble learning technique that combines several simple classification trees into one model. Random forest is one of the state-of-the-art learning algorithms for classification tasks. For our experiments, we used the R [42] implementation randomForest [35].

We used the Friedman test, which is nowadays widely applied to compare the performance of multiple classifiers over multiple data sets [18]. Briefly, the Friedman test is an omnibus test for the global null hypothesis of no difference. The Friedman test requires that for each data set, the classifiers are assigned a rank score, reflecting best classifier, second best, and so on based on a performance measure of choice. The p value of the Friedman test is the probability of observing sums of ranks at least as far apart as the observed ones, given that the null hypothesis of no difference is true. We used the R implementation friedman.test of the package stats [42].

We designed two different experiments. In the first experiment (Fig. 2), the null hypothesis is true, i.e., there is no real difference in performance between the classifiers. Each training set contains 1000 cases of two classes. There are 500 cases of the positive class, \(\mathbf x _{+}\), and 500 cases of the negative class, \(\mathbf x _{-}\). Each positive training case is described by 10 real values from a normal distribution with mean 0 and variance 1, \(\mathcal {N}(0,1)\), while each negative training case is described by ten real values from \(\mathcal {N}(0.5,1)\). Each test set also consists of 1000 cases (500 positives and 500 negatives). Like the training cases, each positive test case is described by 10 real values from a normal distribution \(\mathcal {N}(0,1)\); each negative test case is described by ten real values from \(\mathcal {N}(0.5,1)\).

We built four random forest classifiers. Each random forest consists of ten trees, and each tree was trained with the default settings on the training set and then applied to the corresponding test set. The performance was evaluated based on classification accuracy. We then applied the Friedman test to obtain the p value. This procedure was repeated \(i = 1\ldots 1000\) times for each \(n = 5\ldots 50\), where n indicates the number of data sets. For example, \(n = 10\) means that we consider 10 different pairs of training and test sets. We built four random forest models using the 10 training sets and applied them to the corresponding 10 test sets. We then used the Friedman test and obtained the p value \(P_i\). We repeated this procedure \(i = 1\ldots 1000\) times to obtain 1000 p values for \(n = 10\). Then we inspected their frequency distribution (Fig. 2). Since the number of data sets ranges from 5 to 50, we obtained 46 such histograms.

Fig. 2
figure 2

Experiment #1: the null hypothesis of equal performance is true. Here, n training sets are generated by randomly sampling 500 positive cases \(\mathbf x _{+}\) from \(\mathcal {N}(0,1)\) and 500 negative cases \(\mathbf x _{-}\) from \(\mathcal {N}(0.5,1)\). Four random forest classifiers are trained on the training sets and then applied to the corresponding test sets. The p value \(P_i\) is calculated with the Friedman test. This process (yellow background) is repeated \(i = 1\ldots 1000\) times, leading to 1000 p values. The entire experiment is repeated 46 times, for \(n = 5\ldots 50.\) The resulting 46 histograms are available at https://osf.io/snxwj/ (color figure online)

Full size image
Fig. 3
figure 3

Experiment #2: the null hypothesis of equal performance is false. Here, n training sets are generated by randomly sampling 500 positive cases \(\mathbf x _{+}\) from \(\mathcal {N}(0,1)\) and 500 negative cases \(\mathbf x _{-}\) from \(\mathcal {N}(0.5,1)\). Four random forest classifiers are trained on the training sets and then applied to the corresponding test sets. Before the p value \(P_i\) is calculated with the Friedman test, the predictions of three classifiers are deliberately corrupted. This process (highlighted yellow background) is repeated \(i = 1\ldots 1000\) times, leading to 1000 p values. The entire experiment is repeated 46 times, for \(n = 5\ldots 50.\) The resulting 46 histograms are available at https://osf.io/snxwj/ (color figure online)

Full size image

The second experiment (Fig. 3) was almost identical to the first one, except that this time, before applying the Friedman test, we deliberately corrupted the predictions of all but the first classifier as follows:

  1. 1.

    We randomly selected 15 test cases that had been predicted as positive and changed the predictions to negative;

  2. 2.

    We randomly selected 15 test cases that were predicted as negative and changed the predictions to positive.

Thereby, we made sure that the predictions of classifiers #2, #3, and #4 are worse than those of the uncorrupted classifier #1. Thus, in this experiment, the null hypothesis of equal performance is false. Classifier #1 is clearly better than its competitors. Supplementary materials, including R code, are provided at the project website at https://osf.io/snxwj/.

6 Results

The project website contains an animation showing how the histograms of p values change with increasing n, the number of data sets [10]. As an example, Fig. 4a shows the histograms for \(n = 10\) when the null hypothesis is true and when it is false. Figure 4b shows the histograms for \(n = 50\) when the null hypothesis is true and when it is false.

Fig. 4
figure 4

a H0 is true: 10 data sets are used to compare the performance of 4 good random forest (RF) classifiers (all trained with the same parameter settings). The histogram shows the frequency of p values for 1000 repetitions (average p value, 0.49). H0 is false: 10 data sets are used to compare the performance of 1 good RF classifier and 3 corrupted RFs. The histogram shows the frequency of p values for 1000 repetitions (average p value, 0.09). b H0 is true: 50 data sets are used to compare the performance of 4 good random forest (RF) classifiers (all trained with the same parameter settings). The histogram shows the frequency of p values for 1000 repetitions (average p value, 0.48). H0 is false: 10 data sets are used to compare the performance of 1 good RF classifier and 3 corrupted RFs. The histogram shows the frequency of p values for 1000 repetitions (average p value, \(2.08\times 10^{-5}\))

Full size image

As stated before, the p value is a random variable that is uniformly distributed over the unit interval [0, 1] when the null hypothesis is true. Importantly, this uniform distribution is independent of the sample size n—it does not matter whether we use 10, 50, or any number of data sets. This is exactly what we observe in our experiments (Fig. 4). Irrespective of n, the distribution of p values is uniform. Note that the average p value is about the same for \(n = 10\) and \(n = 50\) (0.49 vs. 0.48).

By contrast, the number of data sets does have an influence when the null hypothesis is false. When we use only \(n = 10\) data sets (Fig. 4a), we rarely see any p values above 0.2. For \(n = 50\), the p values become even smaller (Fig. 4b). Note that the average p value is now drastically different for \(n = 10\) and \(n = 50\) (0.09 vs. \(2.08\times 10^{-5}\)). As we discussed in Sect. 4, when the null hypothesis is false, we are “pushing” the p values toward 0 by using a larger number of data sets, whereas the number of data sets has no influence on the p values when H0 is true.

We consider now [0.003, 0.030] as an interval of significant p values. How many p values is this interval expected to contain when the null hypothesis is true? As the p values are uniformly distributed over [0, 1], and since there are 1000 p values in each histogram, we expect 28 p values in this interval. For \(n = 5\ldots 50\), the experimentally obtained average is 24.5 (with \(\hbox {sd} = 5.0\), \(\hbox {min} = 16\), \(\hbox {max} = 36\)).

Fig. 5
figure 5

Number of p values in [0.003, 0.03] as a function of n, the number of data sets, when the null hypothesis is false (i.e., there is a real difference). The horizontal red line indicates the expected number of p values in the interval when the null hypothesis is true (i.e., there is no difference). For \(n = 40\), the likelihood ratio is LR = 1.27 in favor of the null hypothesis being true (color figure online)

Full size image

Figure 5 shows the number of p values in the interval [0.003, 0.030] as a function of n when the null hypothesis is false. As we can see, the number of p values increases with a larger number of data sets, reaching its peak with 402 p values for \(n = 12\). However, by further increasing n, we are decreasing the number of p values in the interval. For \(n = 37\), there are 29 p values in the interval, which is close to the expected number of 28 when the null hypothesis is true. For \(n > 37\), the number of p values drops below 28. For \(n = 40\), we see 22 p values in the interval. Hence, the estimated likelihood ratio (LR) in favor of the null hypothesis being true is \(\mathrm {LR} = \frac{28}{22} = 1.27\). The experimental value of the number of p values in the interval under the null hypothesis is 35, so the empirical likelihood ratio is even higher, with \(\mathrm {LR} = \frac{35}{22} = 1.59\). The paradox is even more pronounced when we consider \(n = 50\) data sets. Here, we obtain \(\mathrm {LR} = \frac{28}{3} = 9.33\) as the estimated likelihood ratio in favor of the null hypothesis being true. In our experiments, when we use 50 data sets and observe a p value somewhere between 0.003 and 0.03, it is almost ten times more likely that the null hypothesis is true than false!

Not convinced? Let’s imagine the following thought experiment. Suppose that Alice carries out a new experiment using 50 data sets (with the same characteristics as before) and four random forest classifiers. Alice does not tell Bob whether she intentionally corrupted the predictions of three classifiers as described above. All what Alice reveals is that she obtained a p value of, say, 0.007. Imagine the following dialogue:

Alice::

“I compared four classifiers on 50 data sets and obtained a p value of 0.007. Do you believe that this result constitutes compelling evidence to conclude that the null hypothesis of no difference is implausible?”

Bob::

“Given that your p value is much smaller than the conventional 0.05, yes, I think that there is compelling evidence against the null hypothesis.”

Alice::

“However, I used four classifiers that really perform the same, so the null hypothesis is in fact true.”

Bob::

“Well, then a very rare event must have happened. Let’s play this game again. I’m confident that I’ll get it right this time.”

Alice carries out further experiments. In half of these experiments, she intentionally corrupts three classifiers, while in the other half, she does not. Hence, in half of these experiments, the null hypothesis is false, whereas in the other half, it is true. She then groups her experiments based on the observed p values, so that all experiments with a p value in [0.003, 0.030] represent one group. She then randomly selects one experiment from this group and tells Bob:

Alice::

“I compared again four classifiers on 50 data sets. This time, I obtained a p value of 0.01. What is your interpretation now?”

Bob::

“My interpretation is the same as before: the small p value is sufficient evidence for me to conclude that the null hypothesis is false.”

For every game that Bob wins, he loses about nine. The reason is that, in the described series of iterated games, p values in [0.003, 0.030] are about nine times more likely when the null hypothesis is true.

7 Discussion

In this study, we presented computational experiments that illustrate the relevance of the Jeffreys–Lindley paradox for machine learning research, specifically for the comparison of multiple classifiers over multiple data sets. The upshot of these experiments is that a significant p value is far more difficult to interpret than is commonly assumed. Even when the p value is very small, say between 0.003 and 0.03, the result can be in better agreement with the null hypothesis of no difference in performance. And the more data sets we include in our study, the more likely we are to encounter the paradox, since larger and larger sample sizes lead to smaller and smaller p values when the null hypothesis is false. Comparative classification studies that involve many data sets are nowadays very common in machine learning; for example, 64 data sets in [55] and 54 data sets in [6].

This problem is a deep one. It has severe implications for the current research practice in machine learning. The results of our study suggest that the p value should not be used for the comparison of learning algorithms. There are of course several possible objections to this conclusion and to our experiments, including the following:

Objection 1 The paradox pivots on the distinction between the Bayesian posterior probability and the p value, which indeed are two different things. Consequently, there is no reason why they should be numerically the same (compare [15]).

Response to objection 1 This objection is justified, but it cannot resolve the conflict between the two radically different conclusions that we might arrive at: the small p value convinces us that the null hypothesis is false, whereas the posterior probability convinces us of the exact opposite.

Objection 2 Despite the paradox, NHST has been widely and successfully used in a wide array of studies and scientific fields. Does this not indicate that the impact of the paradox is overstated?

Response to objection 2 Lindley argues that the posterior probability of H0 in Eq. 4 tends to 1 very slowly, so that for moderate sample sizes n, the posterior probability may be less than the prior probability of H0 at a given significance level [36, p.190]. This means that the frequentist and Bayesian concepts are usually in reasonable agreement. In the age of big data, however, large sample sizes are the norm, not the exception. Typical benchmark studies in machine learning nowadays often include dozens of data sets [6, 55]. This means that chasing ever smaller p values becomes increasingly easy, and with larger n, we are bound to encounter (unknowingly) the paradox more often. Also, it is by no means uncontroversial whether science has really benefited from NHST testing [31, 38].

Objection 3 The computational experiments include no real-world benchmark data sets, which are commonly used when learning algorithms are compared with each other. The experiments involve only synthetic data sets with particular properties. Hence, the interpretation hinges on one particular example, and it is unclear whether it can be generalized.

Response to objection 3 We have recently shown that the Friedman test is not suitable when the data sets represent diverse entities that cannot be thought of as random samples from one superpopulation [9]. In the present study, however, the synthetic data sets are random samples from known distributions and therefore describe a best-case scenario, in the sense that the applied statistical test is appropriate. If the paradox can manifest itself easily in a best-case scenario, in how many studies with real-world data sets may it go unnoticed?

Objection 4 The interval [0.003, 0.030] is not a valid rejection region for p values. A proper interval needs to include 0, for example, [0, 0.030]. This is also the reason why p values are usually stated as “\(P < \alpha \).” If we consider an interval that includes zero, then there is no problem with the likelihood ratio as described in Sect. 4.

Response to objection 4 This objection confuses two different ideas. First, as we discussed in Sect. 2, a p value is not the same as a rejection region. It is true that p values are often stated as inequalities, but this practice is actually discouraged. A p value is a probability, and it should be communicated exactly (i.e., with an equal sign). One can of course argue that the \(\alpha \) in “\(P < \alpha \)” is just the name of a variable (commonly representing 0.05), but it is then easily confused with the Type I error rate and causes unnecessary confusion. Second, and more importantly, the interval [0.003, 0.030] is just that—an interval that contains real numbers between 0.003 and 0.030. When we repeat an experiment 1000 times, we obtain 1000 p values, and some of them fall in this interval (Fig. 1). The fact that we focus on one particular interval is irrelevant; what matters is that we consider a range of p values that would usually be considered significant.

We speculate that the use of significance tests in machine learning and data science is motivated by a genuine desire for rigorous analyses. Somehow, a significance test seems to provide a certain reassurance in the validity of the results [18], and it also seems to have a role to play in “telling the story” of an empirical investigation [34]. However, the problems of the p value have been known for decades. Some researchers [48, 49] and journal editors [44, 53] have called for an abandonment of the p value altogether. But it seems that the p value has become so deeply engrained in many fields (e.g., biomedical sciences, epidemiology, social sciences, psychology, machine learning) that it might be “too familiar to ditch” [38, p.41].

In 1996, the American Psychological Association (APA) addressed the problem, but the established task force did not recommend the abandonment of p values; instead, APA suggested that p values be supplemented and improved by other methods [34]. In 2016, the American Statistical Association (ASA) released a statement on the use of p values, with the aim to stop the misuse of significance testing [54]. However, there was a disagreement between leading statisticians on exactly what the statement should recommend. One year later, it still had little effect on research practice, although the statement suggested that “[...] the method was damaging science, harming people—and even causing avoidable deaths.” [38, p.38]. But despite the recent authoritative statements and several decades of criticisms, significance testing has been largely unperturbed, enjoying an unbroken popularity in many sciences [40] and an even rising popularity in machine learning [9].

Many scientists believe that there is currently a reproducibility crisis: more than 70% of researchers from various fields were unable to reproduce another scientist’s experiments, and more than 50% were even unable to reproduce their own experiments [1]. Clearly, there is no single solution to the reproducibility crisis [4]. It is well possible that, at least to some extent, significance testing has to bear some of the blame for the current situation [40] and “why most published research findings are false” [31], but this is controversial [46]. We believe that improper use of significance testing, misconceptions about the p value, and the resulting misinterpretation of research findings contributed to the current situation. We are concerned that a similar reproducibility crisis might be imminent for the machine learning community. What could be done to alleviate this problem? We would like to offer the following four points for debate.

First, a change of the current research practice would need to be accompanied by a reform of university curricula; otherwise, the circularity of “We teach it because it’s what we do; we do it because it’s what we teach” [54, p.129] cannot be overcome. Instead of significance testing, alternative statistical tools should be given more emphasis, such as Bayesian methods. Importantly, the role of statistics in science should be made clearer. The proper role of statistics is estimation, not decision making [16, 41, 45]. We need to teach the next generation of data scientists that thinking in the significant/nonsignificant dichotomy is generally not a good idea because “[i]t is essentially consideration of intellectual economy that makes a pure significance test of interest.” [16, p.81].

Second, critical voices like those expressed in the recent ASA statement need to be echoed well beyond the statistical community. More journal editors, reviewers, and funding agencies need to be made aware of the valuable lessons that can be learned from the ongoing p value controversy.

Third, as Cohen reminded us, there is no “objective mechanical ritual to replace [null hypothesis significance testing]” [14, p.1001]. Nonetheless, there are better alternatives. For example, a confidence interval disentangles the effect size and the precision and is therefore the better inferential tool [14, 17, 41, 48]. Still, a very large sample size may lead to a very narrow confidence interval, which might exclude the null value. It is then tempting to interpret the confidence interval as a mere statistical test and report a significant finding. However, both boundaries of the interval might be so close to the null value that, despite the significance, the effect size can be considered negligible. For an illustrative example, see [12]. A second alternative is confidence curves, which depict an infinite number of p values by nesting confidence intervals at all levels. With confidence curves, we can assess how compatible the data are with an infinite number of possible null hypotheses. Thereby, the curves do not give undue emphasis to the single null hypothesis of no difference and its single p value. Also, confidence curves shift our focus on the effect size, that is, the magnitude of the difference in performance, and not on the dichotomous outcome “significant” versus “nonsignificant.” A further alternative is Bayesian hypothesis testing [5]. Bayesian tests have many advantages. First and foremost, they can tell us what we actually want to know, that is, the probability of the null hypothesis being true, given the observed data. Another task for which p values are often used is variable selection. In the context of regression models, the variable importance (VIMP) index was recently proposed as a more interpretable alternative to the p value for a regression coefficient [37]. Using a bootstrapping approach, VIMP measures the predictive effect size of a variable, i.e., how much a variable contributes to the prediction error of a regression model. Developing alternatives to the p value is an interesting scope for research in data science.

Fourth, research publications could be routinely accompanied by open source program code that makes the retraceability of all analytical steps (including data preprocessing) possible. A similar idea was recently expressed in [33]. This code should be extremely well commented; in fact, comments should represent the major part of such scripts. Instead of just describing what the code does, the script could also describe which assumptions were being made, which other approaches could have been possible, how intermediate results were interpreted, etc. Also, references to relevant literature could be included. We refer to such scripts as retraceability scripts. In essence, retraceability scripts would describe not only what and why something was done, but also how the researcher thought about the problem. The latter aspect is in fact crucial when a statistical test was implemented. The reason is that statistical tests are far less objective than is commonly believed [7]. For example, a researcher’s intentions have an influence on how the p value is calculated, and it does not even matter whether these intentions were actually realized or not (for illustrative examples, see [7, 9]). A retraceability script could be published alongside the main paper or hosted at a project website. The Open Science Framework (OSF) [20] by the Open Science Foundation is a free, public repository for archiving all project-related materials. In our view, two aspects make OSF particularly interesting for hosting such materials. First, OSF can assign a permanent document object identifier to each project, thereby making them citable resources. Second, studies can be registered before they are conducted. Each action within OSF is archived with a time stamp. Experimental plans and ideas can be described in detail and deposited as supplementary materials. Even negative results could become publishable, which would alleviate the file drawer problem [43], i.e., the selective publishing of only positive or confirmatory findings, which do not necessarily paint a true picture of reality and lead to a publication bias.

We believe that there can be a time and place for significance tests, but not for comparing the performance of classifiers over multiple data sets. With the advent of big data and the ever-increasing computing power, it becomes easier and easier to chase smaller and smaller effects and eventually obtain a significant result. Large data sets can be analyzed in many different ways, which was described as the “researcher degrees of freedom” [52] and “garden of forking paths” [21]. As Hays reminded us, “[v]irtually any study can be made to show significant results if one uses enough subjects regardless of how nonsensical the content may be.” [27, p.415].

8 Conclusions

The Jeffreys–Lindley paradox is one of many arguments against significance testing. Unfortunately, too much importance is often given to the p value. This recondite value is far more difficult to interpret than is commonly believed. Our conclusion, therefore, is that significance tests should be avoided in comparative classification studies in machine learning. Specifically, we caution against the use of the Friedman test, a view which is also shared by Benavoli et al. [6].

It is possible that the current research practice might entail a reproducibility crisis, similar to the current situation in other fields of science. We offered for debate four avenues that might contribute to alleviating this looming crisis. As a first step, what is needed is that we raise the awareness of the many problems of the p value.