1 Introduction

Many railroad and highway projects have been established in cold regions, which account for a large proportion of the Earth’s land surface. In China, permafrost areas represent approximately 22.93% of all land area [1]. The construction of large-scale transport infrastructure, represented by the Sichuan–Tibet Railway, is fully underway, and thus an increasing number of tunnels is expected to be built in cold regions. The rocks surrounding tunnels in cold regions are prone to freezing, resulting in the generation of frost heaving forces in tunnels that severely threaten their structural integrity and operational security. The direct relationship between frost heaving forces and surrounding rock parameters must be quantitatively studied to assess the frost heaving behaviors of surrounding rock in practical engineering [2,3,4]. Thus, in the construction of modern tunnels in cold regions worldwide, the calculation and prediction of frost heaving forces have emerged as key problems that must be solved to realize the anti-freezing design.

The generation of frost heaving forces in rocks involves constraints imposed by and interactions between temperature, water, and stress fields, and thus represents a complex thermal–hydro-mechanical (THM) multi-physical field coupling problem [5,6,7,8]. THM coupling processes at low and normal temperatures differ in terms of the occurrence of phase transitions, which are complex state transition processes in the pore space of rocks. Such coupling problems have been research hotspots in various fields. Studies of frost heave started in 1920s, when Taber observed the formation of ice lenses in a one-side freezing test of saturated soil [9]. This research generated interest in studying frost heaving mechanisms; however, initial studies on THM coupling in porous media focused mainly on water and heat migration in frozen soils [10]. Later, capillary theory was developed to explain the presence of migration-driving forces in porous media [11]. Nevertheless, theoretical simulations considerably underestimated these driving forces, and the mechanism of ice lens formation remained unclear. In the 1970s, scholars noticed that water migration caused by segregation potential at the freezing front of rocks led to freezing damage [12, 13]. Areas with low water content, low water conductivity, and no frost heave were observed at the freezing front, and these areas were characterized by their separation temperature, unfrozen water content, pore pressure, and hydraulic conductivity [12, 14, 15]. Later studies highlighted that the temperature gradient considerably influences the migration of water and heat [16]. Based on these concepts, scholars derived segregation potential theory, which holds that water flux is proportional to the temperature gradient at a freezing front. However, this theory cannot reflect the pressure of water or clarify the relationship between the suction of the freezing front and frost heaving rate [14, 17].

Advancements in computational methods and experimental equipment have accelerated the development of THM coupling and heat transfer models [18,19,20,21,22,23,24,25]. In the models developed in the past decade, physical–mechanical parameters, such as the elastic modulus, porosity, and quality, have been used to describe the freezing damage degree of porous rocks [26,27,28,29,30]. In most of the experimental studies, the rock specimens have been frozen in cryogenic boxes, and the effects of the temperature boundary and water content on the rocks were ignored.

During the freezing of tunnels in cold regions, the frost heaving forces and deformation of rock are generated gradually in the direction of the temperature gradient rather than simultaneously in all directions. This has been confirmed by monitoring frost heaving pressures in experiments and practical engineering scenarios [31, 32]. Thus, to address the limitations of the existing techniques, a unidirectional freezing experimental method with a controlled boundary temperature gradient was designed in this study.

Specifically, a novel frost heaving model was developed based on coupled THM, considering the influence of the water migration and ice–water phase change in surrounding rocks. The model was validated by the results of the unidirectional freezing experiment in which the boundary temperature gradient was controlled. The characteristics of various physical fields, including the ice–water phase transition, water migration, and frost heave deformation, were studied. Moreover, the influence of temperature and water content on rocks was explored, and the relationship between the maximum frost heaving stress and water content was clarified.

The process flow of this research is illustrated in Fig. 1.

Fig. 1
figure 1

Process flow of this research

Full size image

2 Methodology

2.1 Frost Heaving Model

According to Fourier’s law, the latent heat of a phase change can be treated as a heat source. Water migrates only in liquid form and obeys Darcy’s law, and the movement of ice crystals is ignored. Only the migration of unfrozen water during freezing is considered, and the phase change induced by evaporation is neglected. The elastic deformation of the solid governs the stress field.

2.1.1 Governing Equations

  1. (1)

    Heat transport equation

In rock and soil environments, convective heat transfer is considerably smaller than heat conduction and can be neglected [33,34,35]. Thus, the heat transfer during a freezing–thawing process can be described as

$$\rho C\left(\theta \right)\frac{\partial T}{\partial t}=\lambda \left(\theta \right){\nabla }^{2}T+L\cdot {\rho }_{i}\frac{\partial {\theta }_{i}}{\partial t}$$
(1)

where \(T\) is the soil temperature in \(^\circ{\rm C}\); \(t\) is the time; \(\rho\) is the soil density in kg·m−3; \(C\left(\theta \right)\) is the thermal capacity of soil in kJ/(kg·\(^\circ{\rm C}\)); \(\lambda \left(\theta \right)\) is the thermal conductivity of soil in W/(m·\(^\circ{\rm C}\)); \(L\) is the latent heat of phase change, equal to 334.5 kJ/kg; \({\rho }_{i}\) is the ice density in kg·m−3; \({\theta }_{i}\) is the volumetric ice content in %.

  1. (2)

    Water migration equation

Based on water diffusion theory, the water migration equation can be written as follows, when the ice–water phase change is considered [35, 36]:

$$\frac{\partial {\theta }_{u}}{\partial t}+\frac{{\rho }_{i}}{{\rho }_{w}}\frac{\partial {\theta }_{i}}{\partial t}=\nabla \left[\mathrm{D}\left({\theta }_{u}\right)\nabla {\theta }_{u}+k\left({\theta }_{u}\right)\right]$$
(2)

where k(θu) is the permeability coefficient in the direction of gravitational acceleration in m/s; and \({\theta }_{u}\) and \({\rho }_{w}\) are volumetric unfrozen water content and density, respectively. \({\theta }_{u}\) changes with the soil temperature T. D(θu)is the water diffusion coefficient of soil in m/s and can be expressed as [37, 38]

$$D\left( {\theta_{u} } \right) = \frac{{k\left( {\theta_{u} } \right)}}{{c\left( {\theta_{u} } \right)}} \cdot I$$
(3)

where c(θu) is the specific water capacity in 1/m; and I is the impedance factor, which indicates the hindering effect of pore ice on unfrozen water migration [37, 39]. The expressions for k(θu) and c(θu) and are as follows:

$$I={10}^{-10{\theta }_{i}}$$
(4)
$$k\left( {\theta_{u} } \right) = k_{s} \cdot S^{l} \left( {1 - \left( {1 - S^{1/m} } \right)^{m} } \right)^{2}$$
(5)
$$c\left( {\theta_{u} } \right) = a_{0} m/\left( {1 - m} \right) \cdot S^{1/m} \left( {1 - S^{1/m} } \right)^{m}$$
(6)

where \({k}_{s}\) is the permeability coefficient of saturated soil in m/s; a0, m, and l are constitutive parameters determined by the subject nature, \({a}_{0}\) is related to mass in 1/m, m and l are fitting parameters in 1; and \(S\) refers to the degree of saturation with respect to the total volume of the liquid water and ice in the pore space. Using the VG model and Gardner permeability coefficient mode [39,40,41], S of frozen soil is defined as a variable, as follows [38]:

$$S=\frac{{\theta }_{u}-{\theta }_{r}}{{\theta }_{s}-{\theta }_{r}}$$
(7)

where \({\theta }_{s}\) is the saturated water content, and \({\theta }_{r}\) is the remain water content.

A coupling term between the heat conduction and water transfer equations is introduced to connect the model with the hydrothermal equation. This term, i.e., the solid–liquid ratio Bi, is the volume ratio of ice and unfrozen water in the soil [37], and is defined as follows:

$$B_{i} = \frac{{\theta_{i} }}{{\theta_{u} }}\left\{ {\begin{array}{*{20}c} {1.1\frac{{T^{B} }}{{T_{f} }} - 1 T < T_{f} } \\ {0 T \ge T_{f} } \\ \end{array} } \right.$$
(8)

where Tf is the freezing temperature of the surrounding rock in \(^\circ{\rm C}\), and B is the characteristic parameter of soils, which is a fitting parameter determined by experiment or empirical correction.

Moreover, the water content of permafrost is defined as \(\theta ={\theta }_{u}+\frac{{\rho }_{i}}{{\rho }_{w}}\cdot {\theta }_{i}\), which is used to calculate the thermal conductivity and thermal capacity [42]. Thus

$$\frac{\partial {\theta }_{u}}{\partial t}=\frac{\partial {\theta }_{u}}{\partial T}\frac{\partial T}{\partial t}$$
(9)
$$\frac{\partial {\theta }_{i}}{\partial t}=\frac{\partial \left({B}_{i}\cdot {\theta }_{u}\right)}{\partial t}={\theta }_{u}\cdot \frac{\partial {B}_{i}}{\partial t}+{B}_{I}\cdot \frac{\partial {\theta }_{u}}{\partial t}$$
(10)
  1. (3)

    Frost heaving deformation

The freeze–thaw deformation of the specimens is small-scale. Thus, the plastic strain of the saturated sandstone samples during freezing was neglected. The strain generated by phase changes and water migration must be considered when calculating frost heaving stress. Given that the density ratio of water to ice is equal to the reciprocal of the volume ratio of ice to water, the volumetric strain generated in the freezing process can be defined as

$$\varepsilon =\left(\frac{{\rho }_{w}}{{\rho }_{i}}-1\right)\left({S}_{0}{\theta }_{s}-S{\theta }_{s}\right)$$
(11)

where S0 refers to the initial value of S, and \(\varepsilon\) is the volume strain increment.

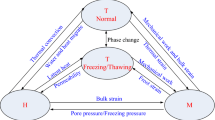
Equations (1), (2), (3), (8), and (11) describe the THM coupling process, which can accurately represent the relationship between the temperature, unfrozen water content, ice content, and strain. The THM coupling relationship is illustrated in Fig. 2.

Fig. 2
figure 2

Schematic of cross-couplings between multi-physical processes

Full size image

2.1.2 Finite-Element Simulation

The calculating model with the size of 100 × 50 × 50 mm3 was established using COMSOL 6.0, as shown in Fig. 3. The upper boundary of the model had no displacement constraint, and its temperature was set as −10 \(^\circ{\rm C}\). The side boundaries constrained normal displacement and were set as adiabatic boundaries. Moreover, normal displacement was restrained at the bottom, and its temperature was set as 10 \(^\circ{\rm C}\). The model had 8959 computational units. The parameters of the calculation model are listed in Table 1.

Fig. 3
figure 3

Numerical calculation model and its boundary conditions

Full size image
Table 1 Initial parameter selection for the calculation model
Full size table

2.2 Verification Experiment

2.2.1 Sample Preparation

To verify the accuracy of the frost heaving model, a frost heaving experiment was conducted using sandstone samples with different porosities, as shown in Fig. 4. The samples were 100 × 50 × 50 mm3, and the initial physical and mechanical parameters are summarized in Table 2.

Fig. 4
figure 4

Sandstone samples and drying equipment

Full size image
Table 2 Initial physical and mechanical parameters of the sandstone samples
Full size table

2.2.2 Experimental Scheme

Figure 5 shows the setup of the unidirectional freezing experiment for sandstone, which was conducted to verify the devised model. The temperature boundaries for the specimens were the same as those of the finite-element model. Figure 6 shows the monitoring system for the verification experiment: (1) T-thermocouples were connected to the JK-8UC multi-channel temperature collector. The surface temperature data of the specimen were monitored by the T-thermocouples and collected by the JK-8UC multi-channel temperature collector. The monitoring deviation of the T-thermocouples was within 1 \(^\circ{\rm C}\). (2) The frost heaving displacement results were recorded using a displacement meter and SP-10B displacement digital display instrument.

Fig. 5
figure 5

Unidirectional freezing experiment of saturated sandstone

Full size image
Fig. 6
figure 6

Primary monitoring devices

Full size image

3 Results and Discussion

3.1 Comparison of the Model Experiment and Simulation Results

Because the temperature curves of different samples were similar, only the results for XH-2 are presented. Figure 7a shows the time-dependent temperature variations in XH-2 during the freezing test and numerical calculations. Although the temperature law was similar at each point, the values varied. The temperature decreased rapidly in the initial stage of freezing (0–5 h) and then stabilized after 5 h. For example, during the second hour, the temperatures at points 1 and 4 were − 7 \(^\circ{\rm C}\) and 3 \(^\circ{\rm C}\), respectively, whereas the corresponding temperatures were − 9 \(^\circ{\rm C}\) and 2.5 \(^\circ{\rm C}\) during the fifth hour. Figure 7b shows the vertical displacement–time curves of different sandstone specimens. The frost heaving displacements varied with the water contents but the variation trends were similar for all specimens: the displacement increased rapidly in the initial stage and then stabilized. For example, the displacements of the specimens with water contents of 1.32% (0.05 mm) and 15.07% (0.62 mm) stabilized after 3 h and 8 h, respectively.

Fig. 7
figure 7

Comparison of temperature and frost heaving displacement results obtained through the experiment and simulation

Full size image

As shown in Fig. 7a, the experimental and numerical calculation results are in good agreement with an accuracy of more than 95%, which indicates that the coupling model can effectively predict the temperature values. Figure 7b shows that the model slightly underestimated the displacement values compared with the test results. For example, for specimens with water contents of 1.32%, 8.58%, and 15.07%, the measured displacements were 0.06 mm, 0.32 mm, and 0.62 mm, respectively, whereas the numerical results were 0.05 mm, 0.28 mm, and 0.56 mm, respectively. The accuracy of displacement field was more than 80%. The differences in the test and simulation values are attributable to the following aspects. (1) The frost heaving model is an isotropic continuous-medium model that reflects the linear-elastic strain in only the vertical direction. Thus, the numerical displacements are smaller than the measured values. (2) In the coupling model, the effect of the impedance factor I [the parameter that limits the volume change owing to the ice–water phase change, see Eq. (4)] is considered in the temperature and water fields. Hence, the measured displacements take longer to stabilize than the simulated values. Despite these differences, the results of the devised frost heaving model and numerical calculations can be considered reliable.

3.2 Analysis of Ice–Water Phase Change and Water Migration

3.2.1 Ice–Water Phase Change

Coarse red sandstone specimens with a water content of 15.07% were used to illustrate the variation law of the ice–water phase change during freezing. The distributions of the volumetric water content and ice content at different time instants during the freezing process are shown in Fig. 8.

Fig. 8
figure 8

Distributions of water and ice contents after different freezing periods (Unit: 1)

Full size image

A phase change interface between ice and water was observed in the rock during unidirectional freezing, the height of which changed over time. For example, at 3 h, 5 h, and 40 h, the interface heights were 0.075 m, 0.055 m, and 0.05 m, respectively. In the first 3 h, the average freezing rate was approximately 0.009 m/h, and this decreased to approximately 1.43 × 10–4 m/h in the period from 5 to 40 h. In the later stage of freezing, the ice–water phase change was stable and in dynamic equilibrium. The change in the freezing rate is attributable to the following aspects: (1) The presence of ice hinders the phase change of water (effect of the impedance factor I). (2) The thermophysical parameters of sandstone, such as the thermal conductivity and specific heat capacity, changed during the freezing process. Moreover, the maximum ice and water contents were approximately 0.1651 and 0.1507, respectively, which indicates that the volume increased after the water transformed to ice. The expansion rate was approximately 1.0956. Furthermore, although the changes in the water and ice contents over time were similar, they exhibited opposing variation trends. At 40 h, the water and ice contents at the top were 0.001 and 0.1651, respectively, and the corresponding values at the phase change interfaces were 0.15 and 0, respectively. This phenomenon occurred because part of the water froze at the low temperatures, and the degree of phase change was proportional to the temperature gradient.

3.2.2 Water Migration

Figure 9 shows the time-dependent variation curves of the volumetric water and ice contents for different height (H) in the vertical direction.

Fig. 9
figure 9

Distribution curves of the volumetric water and ice contents

Full size image

The distribution laws of the volumetric ice and water contents exhibit correspondence, i.e., in the upper part of the sandstone specimen, the volumetric ice and water contents increased and decreased rapidly, respectively. As shown in Fig. 9a, the distribution of the volumetric ice content fluctuated during freezing, which indicates that ice was always present in layers in the sandstone specimen (as shown in Fig. 8). The volumetric ice content was zero when H was 0.05 m, and thus this height corresponded to the interface between ice and water. As shown in Fig. 9b, when H was 0.04–0.05 m, the water content was lower than 15.07%, and the ice content remained zero. This finding indicates that a freeze–pump effect occurred after the pores of the rock froze, resulting in water migration. That is, a water transport process occurred during freezing, causing part of the unfrozen water at H = 0.04–0.05 m to migrate to the frozen zone.

As shown in Fig. 9c, d, the water content, degree of phase change, and rate of decrease in the water content were inversely proportional to the distance from the upper boundary (cold source). This relationship became more apparent as the depth increased. Owing to the presence of a temperature gradient during freezing, the ice content decreased at increasing depths. The values stabilized in the upper part of the specimen (H > 0.05 m, Fig. 9d) after 5 h. In contrast, after 5 h, the water content decreased in the lower part (H ≤ 0.05 m, Fig. 9c). Moreover, no ice–water phase change occurred at the bottom, indicating the migration of water to the upper part of the specimen (Fig. 8). This phenomenon persisted after freezing for 40 h.

3.3 Analysis of Frost Heaving Mechanisms

Figure 10 shows the distributions of the vertical frost heaving stress and strain. Figure 11 shows the variations in the frost heaving stress and strain over time.

Fig. 10
figure 10

Distributions of the frost heaving strain and stress

Full size image
Fig. 11
figure 11

Frost heaving stress and the strain during freezing

Full size image

As shown in Fig. 10, the changes in the frost heaving strain and stress were similar to the water field distributions. The maximum frost heaving strain (1.23 × 10–2) was observed at the top (H = 0.1 m), and the value gradually decreased in the vertical direction. At 40 h, the frost heaving strain at the phase change interface is 6.4 × 10–4, not 0. This indicated that there was a transition zone between the frozen zone and the unfrozen zone in which ice–water phase change and water migration occurred (Figs. 8f and 9b). Moreover, as shown in Fig. 11, the frost heaving stress and strain first appeared at the top and gradually decreased downward in the vertical direction. For example, at H = 0.1 m, 0.07 m, and 0.06 m, the maximum frost heaving strain values were 1.23 × 10–2, 1.15 × 10–2, and 1.07 × 10–2, respectively, and the maximum frost heaving stress values were 0.02 MPa, 0.014 MPa, and 0.0083 MPa, respectively. In contrast, at H = 0.05 m, the maximum frost heaving stress was approximately 0.183 MPa, and then the stress gradually decreased. The maximum frost heaving stress at 40 h was 0.158 MPa. Furthermore, the maximum frost heaving stress always appeared near the phase transition interface.

According to Fig. 11b, the frost heaving stress first appeared at H = 0.1 m and then appears at each point in the vertical direction. That is, the frost heaving stress exhibited a downward transfer phenomenon and accumulated near the phase transition interface. Interestingly, the frost heaving stress also exhibited a stratified distribution, similar to the ice content (Fig. 8), potentially because of the change in the direction vector of the frost heaving stress over time. Specifically, in the process of downward transmission, the frost heaving stresses at different points offset or supplemented one another.

3.4 Analysis of Maximum Frost Heaving Stress and Temperature

3.4.1 Maximum Frost Heaving Stress

To examine the effect of the initial volumetric water content of the specimen on the maximum frost heaving stress during unidirectional freezing, the validated simulation model was used to perform simulations in which the initial water content was varied from 0 to 20%, and the other operating conditions (e.g., the temperature boundary and thermal conductivity) were kept constant. Next, a scatter plot of the maximum frost heaving stress with different initial water contents was obtained and fitted. Figure 12 shows the data fitting results for the maximum frost heaving stress.

Fig. 12
figure 12

Maximum frost heaving stress with different volumetric water content

Full size image

A good fit for the numerical calculations was obtained. The maximum frost heaving stress exhibited an exponential relationship with the volumetric water content, which can be expressed as \(y=Ax{e}^{Bx}\), where A and B are 0.00466 and 0.07063, respectively. The coefficient of determination is 0.99292. In particularly, when the volumetric water content was lower and higher than 10%, respectively, the maximum frost heaving stress increased slowly and rapidly with increasing volumetric water content, respectively. Overall, the maximum frost heaving stress of rock specimens can be accurately predicted based on their initial volumetric water contents. This framework can provide parametric guidance and facilitate the establishment of design standards for anti-freezing measures for tunnels in cold regions.

3.4.2 Effect of Temperature

The above discussion indicates that the frost heaving stress accumulated at the ice–water phase change interface, which is thus a critical location for sandstone subjected to freezing. In general, the temperature affected the location of the phase–change interface. Therefore, a series of simulations were performed to study the effect of the temperature on the ice–water phase change:

  1. (1)

    The cold source temperature was maintained at − 10 \(^\circ{\rm C}\), and the heat source temperature was set to 6 \(^\circ{\rm C}\), 8 \(^\circ{\rm C}\), 10 \(^\circ{\rm C}\), 12 \(^\circ{\rm C}\), and 14 \(^\circ{\rm C}\), corresponding to temperature differences of 16 \(^\circ{\rm C}\), 18 \(^\circ{\rm C}\), 20 \(^\circ{\rm C}\), 22 \(^\circ{\rm C}\), and 24 \(^\circ{\rm C}\), respectively.

  2. (2)

    The heat source temperature was maintained at 10 \(^\circ{\rm C}\), and the cold source temperature was set to − 5 \(^\circ{\rm C}\), − 10 \(^\circ{\rm C}\), and − 15 \(^\circ{\rm C}\), corresponding to temperature differences of 15 \(^\circ{\rm C}\), 20 \(^\circ{\rm C}\), and 25 \(^\circ{\rm C}\), respectively. Figure 13 shows the variations in ice–water phase change interface height with temperature.

Fig. 13
figure 13

Variation curves of the ice–water phase change interface height with temperature

Full size image

The following observations can be made: (1) The interface height was linearly related to the temperature difference and average temperature between two boundaries. (2) When the heat source temperature was constant (10 \(^\circ{\rm C}\)), the interface height was inversely proportional to the temperature difference and proportional to the average temperature. For example, when the cold source temperatures were − 5 \(^\circ{\rm C}\), − 10 \(^\circ{\rm C}\), and − 15 \(^\circ{\rm C}\), the interface heights were 0.065 m, 0.05 m, and 0.035 m, respectively, and the average temperatures were 2.5 \(^\circ{\rm C}\), 0, and − 2.5 \(^\circ{\rm C}\), respectively. (3) When the cold source temperature was constant (− 10 \(^\circ{\rm C}\)), the interface height was proportional to the temperature difference and average temperature. For example, when the heat source temperatures were 6 \(^\circ{\rm C}\), 8 \(^\circ{\rm C}\), and 10 \(^\circ{\rm C}\), the interface heights were 0.038 m, 0.044 m, and 0.05 m, respectively, and the average temperatures were − 2 \(^\circ{\rm C}\), − 1 \(^\circ{\rm C}\), and 0, respectively. (4) By adjusting the temperature source (e.g., cold sources can be controlled by anti-freezing and insulation measures, and heat sources can be controlled using geothermal energy), the temperature difference between the tunnel interior and surrounding rocks could be altered to raise the average temperature. These changes would decrease the freezing depth and enable effective prevention and control of freezing damage.

4 Conclusions

The freezing of rocks is accompanied by complex THM coupling. This paper devises a frost heaving model based on THM coupling to analyze the thermal–hydro-variations and frost heaving mechanisms in rocks subjected to unidirectional freezing. The following conclusions are derived from the test and simulation results.

  1. (1)

    The frost heaving model takes into account water migration and ice–water phase change, and can accurately reflect the frost heaving mechanism. The calculation method and results can provide parametric guidance and a theoretical basis for subsequent engineering-scale calculations.

  2. (2)

    The rate of ice–water phase change was high in the first 3 h, with an average rate of approximately 0.009 m/h, and the rate decreased to approximately 1.43 × 10–4 m/h from 5 to 40 h. In the later stage of freezing, the phase change was in dynamic equilibrium. A transition zone with a width of 0.004 m was observed between the frozen and unfrozen zones after 40 h.

  3. (3)

    The directional vector of the frost heaving stress changed over time. The stress distribution was stratified. The maximum frost heaving stress occurred near the phase transition interface, the location of which depended on the temperature gradient. H was 0.05 m with an average temperature of 0 \(^\circ{\rm C}\).

  4. (4)

    A novel contribution of this study is the derivation of the relationship between the maximum frost heaving stress (y) and volumetric water content (x): \(y=Ax{e}^{Bx}\), where A and B are 0.00466 and 0.07063, respectively. This function can provide engineers with parametric guidance for the design of anti-freezing measures for geotechnical engineering projects in cold regions.