1 Introduction

An efficient numerical model is necessary for performance-based seismic design and seismic analysis of reinforced concrete (RC) structures. Fiber section beam element has been widely used in the field of seismic nonlinear analysis of RC structures over the years [1,2,3]. However, it is still not sufficiently accurate, which may be mainly due to the neglect of considering the bond-slip effect [4]. Experimental results have reported that the additional deformation caused by reinforcement slip contributes approximately 30–40% of the total lateral deformation [5, 6]. Therefore, it is important to consider the bond-slip effect in the numerical model to evaluate the seismic failure process and seismic performance for structures. Some researchers have tried to consider the slip effect of the reinforcement in fiber section model. Monti et al. [7] considered the effect on the elements of steel bar using the finite element method, which was difficult to adopt because of a large amount of calculation required for the slip at integral points. Zhao et al. [8] constructed a zero-length section element implemented in OpenSees software to model the strain penetration. However, the assumption of the plane-section resulted in a super high strain imposed on the extreme concrete fibers. Pan et al. [9] derived the slip of anchorage reinforcement at the macro level to modify the stress–strain skeleton curve and the hysteretic curve, and Wang et al. [10] also used a similar method to develop a constitutive model of steel bar considering slip and verified its accuracy. However, equivalent bond stress in these two studies totally relied on the results of Sezen [11], which was inadequate in powerful evidence. It is hence important to develop a reliable and practical analysis methodology to assess the bond-slip effect.

In addition, corrosion is generally acknowledged as the main cause of deterioration of RC structures in marine and offshore environment. Corrosion directly reduces the strength and ductility of steel bar [12,13,14], and corrosion products could expand 2–6 times volume of the initial steel bar [15]. Furthermore, internal pressure induced at the bar/concrete interface splits the concrete cover and weakens the bond performance between the reinforcement and concrete [16, 17], which increases the risk of the degradation of seismic capacity and durability of RC structure [18, 19]. At present, large amounts of researches on the corrosion effect on mechanical properties of steel bars have been carried out [20,21,22,23,24], with different test methods and strength indexes to detect various kinds of bars specimens under different degrees of corrosion. This also brings controversy and even paradox, which requires appropriate screening and statistical analysis to comprehensively conduct model construction and verification research. It is simultaneously noted that corrosion may have a significant influence on bond-slip properties of reinforcing steel. Most researchers paid attention to the influence of corrosion on bond strength [25, 26], while only a few concerned the whole bond-slip curve. At present, the bond-slip curve of corroded steel bars is obtained via two methods. One is to maintain the whole form of that for uncorroded reinforcement, and just replace the parameter of bond strength with that under corrosion [27, 28]. The other is to establish empirical formula through statistical analysis of the experimental results [29]. There is no consensus on the results and methods for evaluating the effect of corrosion on the slippage of reinforcement [30], and it is meaningful to propose a method to simplify the modeling procedure but fit the experimental data well.

The study of corrosion effect on reinforcement properties has advanced in recent years. Kashani et al. conducted a comprehensive experimental and computational study on the inelastic behavior of corroded reinforcement, especially inelastic buckling and low cycle fatigue degradation [31,32,33,34]. On this basis, Afsar Dizaj et al. developed a modeling technique to simulate the nonlinear behavior of RC rectangular columns using nonlinear fiber beam-column elements [35], and further provided modeling guidelines for nonlinear analysis and vulnerability assessment of corroded RC structures [36]; Salami et al. used an advanced material model considering bar buckling, low-cycle fatigue and bond-slippage to simulate failure modes of RC columns under multiple seismic excitation [37]. The practical engineering showed that the reinforcement in the tensile area was more likely to reinforcement slip because of the reduction of restraint effect and bond strength caused by stirrup corrosion, and of the mechanical properties degradation of the corroded longitudinal reinforcement, while the corresponding compression zone was more prone to buckling. However, the researches on occurrent sequences of tensile slip and compression buckling are lacking. To simplify the complexity of the problem, this paper focuses on the sliding of corroded reinforcement under tension, ignoring the impact of compression buckling and fatigue.

The researches about the corrosion effect on the performance of RC members are mainly focused on the nonlinear behavior of beams and plates under monotonous and cyclic loads, while the studies on the structural response of columns are rather limited. Moreover, most of the existing literature has reported the deterioration effect of corrosion on the overall performance (such as bearing capacity, stiffness, ductility, etc.), but the specific reason has not been analyzed in detail. It is really difficult to determine whether it is caused by the material properties degradation of steel and/or concrete, or the bond properties degradation between them because there is a strong interaction between the main influence variables. For RC beams, Cairns et al. showed that, compared with those without bond damage, the ultimate bearing capacity of beams with large bond loss at the end of bars may decrease slightly, if the end was well anchored [38]; Castel et al. found that the residual flexural strength of corroded RC beams was mainly a function of the mass loss, but not significantly affected by the bond strength loss [39]; similarly, Kallias et al. also pointed out that the bond damage could be ignored for the reinforcement with well-anchored end [40]. In their experimental testing with pure flexural loading, Azad et al. found that, as the mass loss exceeded 10%, the residual flexural strength of corroded RC beams was influenced by the bond strength loss and damage in concrete significantly [41]. For RC columns, Afsar Dizaj et al. believed that the reinforcement in the column base was unlikely to be corroded, so the corrosion effect could be neglected when considering the bond-slip [42]; Aquino et al. indicated that the bond degradation caused by corrosion determined the ductility and bearing capacity loss of corroded columns [43]. These studies showed that, due to the lack of test data and the inconsistency of current results, the influence of bond deterioration induced by corrosion on the performance of RC members had not been fully recognized. The author considers that the reinforcement in pier under the marine environment, whether in the foundation or at the "splash zone" of the lower end, tends to be seriously rusted. The bond degradation and reinforcement slip are aggravated by both the cracking and splitting of the concrete cover caused by corrosion, and the insufficient constraint caused by stirrups corrosion or lack of stirrups in the pier. Therefore, in this paper, the adverse effect of corrosion is considered in the calculation formula derivation for steel bar slip. See Sect. 3.3 for details.

From the above discussion, it can be seen that corrosion and reinforcement slip are two essential factors in the analysis of seismic performance of structures in a chloride environment. Yet, no appropriate model has considered both factors. In this paper, the degradation equations of corroded reinforcement mechanical properties are obtained by regression analysis of the available experimental data. The bond-slip curve of the corroded reinforcement is from shifting that of uncorroded rebar and approximately described by a stepped function. Based on the non-uniform distribution of bond stress and tensile stress along the length of anchorage, the theoretical formulas of the equivalent strain considering the slip effect are established. Furthermore, equivalent strain is used to modify the elastic modulus and hardening modulus of corroded reinforcement under perfect bond condition. To consider the effect of corrosion, the parameters of the constitutive model of cover and core concrete, such as strength, are modified directly. The response of corroded RC columns under cyclic loading is simulated by the fiber section beam element model. The model results show excellent agreement with the experimental tests, which verifies the ability of the model to simulate the seismic nonlinear response of corroded RC structures. A flowchart of the main contents of this research is shown in Fig. 1.

Fig. 1
figure 1

Flowchart of main contents

Full size image

2 Mechanical Properties of the Corroded Reinforcement

It is well known that corrosion can be divided into uniform corrosion and pitting corrosion [20, 21], which are associated with different degradation mechanisms and processes. Under chloride attack, pitting corrosion is the main morphology, and is characterized by a higher dispersion of the steel bars mechanical properties. To define an appropriate degradation equation for mechanical properties of corroded steel bars, 171 test records are collected and statistically regressed through accurate literature review [44,45,46,47,48,49,50,51]. The steel bar embedded in concrete becomes the main screening condition for the test information, to better approximate the actual corrosion. Due to fewer researches on naturally corroded steel rebar available, the test data of artificially accelerated corrosion are also included. The test data of strength and stress are converted into non-dimensional form and regressed into a function of corrosion degree. To satisfy the requirement of consistency in context and model construction, the corrosion degree is expressed in terms of mass loss percentage. Since some experiments have found that degradation of the elastic modulus due to corrosion is not obvious [24], and also for the convenience of formula derivation in the following part of this paper, it is assumed that the elastic modulus is not affected. In this paper, only the nominal mechanical properties (based on the nominal cross-sectional area of the reinforcement) are considered, to modify the constitutive laws of the corroded reinforcement without reducing the steel diameter. The test results and corresponding literature are shown in Fig. 2.

Fig. 2
figure 2

Mechanical properties degradation: a yield strength, b ultimate strength, c ultimate strain

Full size image

Degradation equations for the mechanical parameters are obtained by regression:

$$ f_{{{\text{ycorr}}}} = \left( {1 - 1.33\eta_{{\text{m}}} } \right)f_{{\text{y}}} , $$
(1)
$$ f_{{{\text{ucorr}}}} = \left( {1 - 1.36\eta_{{\text{m}}} } \right)f_{{\text{u}}} , $$
(2)
$$ \varepsilon_{{{\text{ucorr}}}} = e^{{ - 5.3\eta_{{\text{m}}} }} \varepsilon_{{\text{u}}} , $$
(3)

where \(f_{{{\text{ycorr}}}}\), \(f_{{{\text{ucorr}}}}\) and \(\varepsilon_{{{\text{ucorr}}}}\) are the yield strength, ultimate strength and ultimate strain for corroded reinforcement, respectively, \(f_{{\text{y}}}\), \(f_{{\text{u}}}\) and \(\varepsilon_{{\text{u}}}\) are for uncorroded reinforcement respectively, and \(\eta_{{\text{m}}}\) is the average mass loss percentage.

Obviously, the mechanical parameters decrease with the increase of the average mass loss percentage. The most significant effect of corrosion is on the deformation capacity, because of the localization of tensile deformation due to the reduction of cross section of corroded reinforcement. There is no significant difference between the degradation of yield strength and ultimate strength. As shown in Fig. 2a, b, the yield strength and ultimate strength disperse slightly as the average mass loss percentage remains less than 10%; otherwise, the dispersion becomes larger. The ultimate strain for corroded reinforcement also shows a similar law. As shown in Fig. 2c, when the corrosion rate is less than 7.5%, the dispersion of test data is relatively small.

In terms of the degradation model of yield strength, ultimate strength and ultimate strain of corroded reinforcement, through the accelerated test of bars embedded in concrete, Du et al. [14] regressed its calculation formulas, which have been widely accepted by the industry. In the formulas, yield strength and ultimate strength are the true strengths derived from the actual cross section, and the strength reduction factors are both 0.5. However, if the nominal strength is considered (calculated according to the initial cross area of the reinforcement), the strength degradation factor will be 1.4. In Eqs. (1) and (2), the degradation factors are 1.33 and 1.36, respectively, which are very close to the results of [14]. For the calculation formula of ultimate strain, this paper uses exponential fitting, while Du et al. used linear fitting. The two fitting results are shown in Fig. 3. It can be seen that the difference is very small when the corrosion rate is less than 5% and becomes larger as the rate increases beyond 10%. In addition, according to the formula of Du et al., when the corrosion rate is 20%, the ultimate strain will degenerate to zero, inconsistent with the existing test results shown in Fig. 2c. This indicates the limitation of the formula in reference [14]. However, the formula proposed in this paper can also be applied in the case of severe corrosion.

Fig. 3
figure 3

Comparison of degradation models of ultimate strain for corroded steel bars

Full size image

3 Calculation of Slip for Corroded Reinforcement

3.1 Bond-Slip Curves for Corroded Steel Bar

To deduce the formula for calculating the slip of corroded reinforcement, the whole bond-slip curve must be provided. In the existing researches, the bond-slip model of uncorroded reinforcement has been basically established, and the model provided by CEB-FIP 2010 [52] is acknowledged mostly. However, there are few experimental data about the corrosion effect, let alone the inconsistent results. The theoretical and experimental studies found that the concrete cracking or splitting induced by corrosion reduced the confinement resistance and promoted steel bar to slide [53, 54]. This phenomenon is shown in the bond-slip curve as the decrease of bond strength and reinforcement slip during bond failure. Therefore, it is reasonable to propose that bond-slip curve for corroded reinforcement could be obtained by shifting that for uncorroded reinforcement along the slip axis, which has been realized and tested by [53, 54].

In general, the modes of bond failure between uncorroded steel bar and concrete, splitting of the cover concrete or pull-out, depend on the confinement level; once corroded, splitting will be the main mode due to the reduction of confinement. Thus, in this paper, the local bond-slip curve corresponding to splitting failure for uncorroded bars given in CEB-FIP model code is defined as the initial curve (the fine solid line in Fig. 4).

Fig. 4
figure 4

Schematic of obtaining the bond stress-slip curve for corroded rebar

Full size image

The range of the curve left shift, equivalent slip seq is determined by the degree of corrosion, following a linear relationship with penetration depth x in Eq. (4):

$$ s_{{{\text{eq}}}} = \gamma x, $$
(4)

where the proportional constant γ equals 8.1 in [55].

Bond-slip can be considered as an average behavior of the interaction between steel and concrete [56]. Thus, the average corrosion depth x could be calculated by Eq. (5):

$$ x = {{d_{0} \left( {1 - \sqrt {1 - \eta_{{\text{m}}} } } \right)} \mathord{\left/ {\vphantom {{d_{0} \left( {1 - \sqrt {1 - \eta_{{\text{m}}} } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}, $$
(5)

where d0 is the diameter of uncorroded steel bar, and \(\eta_{{\text{m}}}\) is mass loss percentage.

The average critical corrosion depth xcr is obtained by substituting Eq. (5) with an empirical threshold of mass loss percentage 1.5% suggested in [29] and [57], that is 0.003764d0.

As shown in Fig. 4, τucorr is the bond strength of corroded reinforcement, which is obtained as:

$$ \tau_{{{\text{ucorr}}}} = \tau_{u} \left( {{{s_{{1{\text{c}}}} } \mathord{\left/ {\vphantom {{s_{{1{\text{c}}}} } {s_{1} }}} \right. \kern-\nulldelimiterspace} {s_{1} }}} \right)^{\alpha } , $$
(6)

where \(s_{{1{\text{c}}}}\) is the slip corresponding to the peak bond stress of corroded reinforcement, which is the solution of Eq. (7):

$$ \tau_{{\text{u}}} \left( {{s \mathord{\left/ {\vphantom {s {s_{1} }}} \right. \kern-\nulldelimiterspace} {s_{1} }}} \right)^{\alpha } = {{\left[ {\left( {\tau_{{\text{u}}} - \tau_{{\text{f}}} } \right)\left( {s + s_{{{\text{eq}}}} } \right) + \tau_{{\text{f}}} s_{1} - \tau_{{\text{u}}} s_{3} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {\tau_{{\text{u}}} - \tau_{{\text{f}}} } \right)\left( {s + s_{{{\text{eq}}}} } \right) + \tau_{{\text{f}}} s_{1} - \tau_{{\text{u}}} s_{3} } \right]} {\left( {s_{1} - s_{3} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {s_{1} - s_{3} } \right)}}, $$
(7)

where \(\tau_{{\text{u}}}\), \(\tau_{{\text{f}}}\), \(s_{1}\) and \(s_{3}\) are the parameters of bond-slip model for uncorroded steel bars, with the specific values in [52], and the model parameter \(\alpha\) is taken as 0.4.

A number of investigations have shown that the bond strength increases slightly with corrosion initially, and then decreases obviously [26, 27], in which the stirrups effect is not considered. Through the pull-out test of deformed steel bars with stirrups, Fang et al. found that the influence of mild corrosion on bond strength is not obvious [58]. Therefore, in the process of shifting the bond-slip curve, the relationship of the normalized bond strength \(\kappa_{{\text{u}}}\) (\({{\tau_{{{\text{ucorr}}}} } \mathord{\left/ {\vphantom {{\tau_{{{\text{ucorr}}}} } {\tau_{{\text{u}}} }}} \right. \kern-\nulldelimiterspace} {\tau_{{\text{u}}} }}\)) with the degree of corrosion (average corrosion depth x) is proposed in Fig. 5, where the bond strength remains unchanged at the beginning, and then decreases to the final constant residual strength with corrosion after it exceeds the limit level, reflecting the three stages of bond-slip curve for uncorroded steel bar (closing translation, activating translation and stabilization).

Fig. 5
figure 5

Normalized bond strength-average corrosion depth

Full size image

Almusallam reported that residual bond strength \(\tau_{{{\text{fcorr}}}}\) still existed (10%) even though the mass loss percentage was 80% [59], which suggested that it should not be ignored. This paper defines \(\tau_{{{\text{fcorr}}}}\) proportionally to bond strength in Eq. (8):

$$ \tau_{{{\text{fcorr}}}} = \xi \tau_{{{\text{ucorr}}}} , $$
(8)

where \(\xi\) is the residual coefficient of bond strength in Fig. 5. When the reinforcement yields in the distributed length, the bond stress reduces, and the residual bond stress is suggested 0.4 times the bond strength [52], with the results in [60] for reference, consequently, \(\xi\) is defined as follows:

$$ \xi = \left\{ {\begin{array}{*{20}l} {0.4} & {x \le x_{{{\text{cr}}}} } \\ {0.1 \le 0.023d_{0} - 0.165 < 0.4} & {x > x_{{{\text{cr}}}} } \\ \end{array} } \right.. $$
(9)

In addition, \(s_{{3{\text{c}}}}\) shown in Fig. 4 is the solution of Eq. (10):

$$ {{\left[ {\left( {\tau_{{\text{u}}} - \tau_{{\text{f}}} } \right)\left( {s + s_{{{\text{eq}}}} } \right) + \tau_{{\text{f}}} s_{1} - \tau_{{\text{u}}} s_{3} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {\tau_{{\text{u}}} - \tau_{{\text{f}}} } \right)\left( {s + s_{{{\text{eq}}}} } \right) + \tau_{{\text{f}}} s_{1} - \tau_{{\text{u}}} s_{3} } \right]} {\left( {s_{1} - s_{3} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {s_{1} - s_{3} } \right)}} = \xi \tau_{{{\text{ucorr}}}} . $$
(10)

3.2 Distribution of Bond Stress and Tensile Stress Along Anchorage Length

Some research results show that the distribution of bond stress along the corroded anchorage bar is uneven in different stress states [61]. In this study, the bond stress of any segment along the anchorage reinforcement follows the same bond-slip curve on the assumption that bond-slip stick to an average behavior. It has been observed that [8], the slip at yielding may be smaller or larger than s1, but generally it may not exceed s3. On the assumption that the uncorroded steel bar is linear elastic material and the bond stress is uniformly distributed along the development length, the slip of the steel bar at yield is estimated around 0.6 mm in [11], which is larger than s1 (0.3 mm) given by CEB-FIP 2010 [41] in Fig. 6. However, the assumption of uniform distribution for the bond stress [9, 11] before yielding, represented by the horizontal line from point A to point B in Fig. 6, may not be appropriate. Similarly, from the yield strength to the ultimate strength (the curve from point B to point C in Fig. 6), su may be 30–50 times sy, which indicates unreasonable for the bond stress to remain uniformly distributed after yielding.

Fig. 6
figure 6

Equivalent description of bond-slip curve

Full size image

Thus, to solve the problem of non-uniform distribution, and to simplify the integral calculation, a stepped function is introduced to approximate the bond stress distribution in Fig. 6. Symbols \(\tau_{1}\) and \(\tau_{2}\) correspond to the equivalent bond stress of the ascending and descending branch of the bond stress-slip curve of corroded reinforcement, respectively. In previous studies, the assumed equivalent bond stress was calculated according to the characteristic slip value (such as yield slip), whereas in this paper, equivalent bond stress is defined firstly, and the characteristic slip is satisfied by adjusting the corresponding development length. The approach in this paper bears the advantage that the non-uniformity of bond stress is fully considered.

According to the principle of equal area, the equivalent bond stress can be calculated by:

$$ \tau_{1} = {{\tau_{{{\text{ucorr}}}} \int_{0}^{{s_{{1{\text{c}}}} }} {\left( {{\kappa \mathord{\left/ {\vphantom {\kappa {s_{{1{\text{c}}}} }}} \right. \kern-\nulldelimiterspace} {s_{{1{\text{c}}}} }}} \right)^{0.4} {\text{d}}\kappa } } \mathord{\left/ {\vphantom {{\tau_{{{\text{ucorr}}}} \int_{0}^{{s_{{1{\text{c}}}} }} {\left( {{\kappa \mathord{\left/ {\vphantom {\kappa {s_{{1{\text{c}}}} }}} \right. \kern-\nulldelimiterspace} {s_{{1{\text{c}}}} }}} \right)^{0.4} {\text{d}}\kappa } } {s_{{1{\text{c}}}} }}} \right. \kern-\nulldelimiterspace} {s_{{1{\text{c}}}} }}, $$
(11)
$$ \tau_{2} = {{\left( {\tau_{{{\text{ucorr}}}} + \tau_{{{\text{fcorr}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\tau_{{{\text{ucorr}}}} + \tau_{{{\text{fcorr}}}} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}. $$
(12)

3.3 Calculation Strategy for Slip of Corroded Anchorage Reinforcement

The differential equation [11] for bond stress of longitudinal reinforcement is Eq. (13):

$$ \tau \left( z \right) = \frac{{d_{0} }}{4}\frac{{{\text{d}}\sigma_{{\text{s}}} }}{{{\text{d}}z}}, $$
(13)

where \(\tau\) and \(\sigma_{{\text{s}}}\) represent the bond stress and nominal stress of corroded rebar at the z, respectively.

Since the yield platform could be shortened or even lost due to corrosion [12, 22, 24], the bilinear model is used in Eq. (14):

$$ \sigma_{{\text{s}}} = \left\{ {\begin{array}{*{20}l} {E_{{\text{s}}} \varepsilon_{{\text{s}}} } & {\varepsilon_{{\text{s}}} \le \varepsilon_{{{\text{ycorr}}}} } \\ {f_{{{\text{ycorr}}}} + E_{{{\text{sh}}}} \left( {\varepsilon_{{\text{s}}} - \varepsilon_{{{\text{ycorr}}}} } \right)} & {\varepsilon_{{\text{s}}} > \varepsilon_{{{\text{ycorr}}}} } \\ \end{array} ,} \right. $$
(14)

where \(\varepsilon_{{\text{s}}}\) is the strain, \(f_{{{\text{ycorr}}}}\) is the yield stress in Eq. (1), \(E_{{\text{s}}}\) and \(E_{{{\text{sh}}}}\) are the elastic and hardening modulus of uncorroded reinforcing bar, respectively, \(f_{{{\text{ucorr}}}}\) is the ultimate strength in Eq. (2), \(\varepsilon_{{{\text{ycorr}}}}\) is the yield strain, and calculated by \({{f_{{{\text{ycorr}}}} } \mathord{\left/ {\vphantom {{f_{{{\text{ycorr}}}} } {E_{0} }}} \right. \kern-\nulldelimiterspace} {E_{0} }}\).

There is a variant relationship between \(s_{{{\text{ycorr}}}}\) and \(s_{{1{\text{c}}}}\), analyzed in Sect. 3.1, which is expressed as different positions between the yield length of the steel bar and the distribution length of equivalent bond stress in Fig. 6. The theoretical slip is derived in two cases.

\(s_{{{\text{ycorr}}}} \le s_{{1{\text{c}}}}\), for case 1.

By integrating Eq. (11), the stress of corroded reinforcement is written as:

$$ \sigma_{{\text{s}}} \left( z \right) = \left\{ {\begin{array}{*{20}l} {{{4\tau_{1} z} \mathord{\left/ {\vphantom {{4\tau_{1} z} {d_{0} }}} \right. \kern-\nulldelimiterspace} {d_{0} }}} \hfill & {0 \le z \le l_{E} } \hfill \\ {{{4\tau_{1} z} \mathord{\left/ {\vphantom {{4\tau_{1} z} {d_{0} }}} \right. \kern-\nulldelimiterspace} {d_{0} }}} \hfill & {l_{{\text{y}}} < z \le l_{1} } \hfill \\ {{{\left[ {4\tau_{1} l_{1} + 4\tau_{2} \left( {z - l_{1} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {4\tau_{1} l_{1} + 4\tau_{2} \left( {z - l_{1} } \right)} \right]} {d_{0} }}} \right. \kern-\nulldelimiterspace} {d_{0} }}} \hfill & {l_{1} < z \le l_{3} } \hfill \\ {{{\left[ {4\tau_{1} l_{1} + 4\tau_{2} \left( {l_{3} - l_{1} } \right) + 4\tau_{{{\text{fcorr}}}} \left( {z - l_{3} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {4\tau_{1} l_{1} + 4\tau_{2} \left( {l_{3} - l_{1} } \right) + 4\tau_{{{\text{fcorr}}}} \left( {z - l_{3} } \right)} \right]} {d_{0} }}} \right. \kern-\nulldelimiterspace} {d_{0} }}} \hfill & {l_{3} < z \le l_{{\text{u}}} } \hfill \\ \end{array} } \right. $$
(15)

where \(l_{1}\) and \(l_{3}\) correspond to development length related to \(\tau_{1}\) and \(\tau_{2}\), respectively. Symbol \(l_{{\text{y}}}\) and \(l_{{\text{u}}}\) denote the distribution length of nominal yield stress and ultimate stress, respectively, in Fig. 7, with Eq. (19) for a detailed calculation.

Fig. 7
figure 7

Distribution of stress and equivalent bond stress

Full size image

Combining Eqs. (14) and (15), the nominal strain of corroded steel bars are obtained, such that:

$$ \varepsilon_{{\text{s}}} \left( z \right) = \left\{ {\begin{array}{*{20}l} {{{4\tau_{1} z} \mathord{\left/ {\vphantom {{4\tau_{1} z} {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}}} \hfill & {0 \le z \le l_{{\text{y}}} } \hfill \\ {{{4\tau_{1} l_{{\text{y}}} } \mathord{\left/ {\vphantom {{4\tau_{1} l_{{\text{y}}} } {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}} + {{4\tau_{1} \left( {z - l_{{\text{y}}} } \right)} \mathord{\left/ {\vphantom {{4\tau_{1} \left( {z - l_{{\text{y}}} } \right)} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \hfill & {l_{{\text{y}}} < z \le l_{1} } \hfill \\ {{{4\tau_{1} l_{{\text{y}}} } \mathord{\left/ {\vphantom {{4\tau_{1} l_{{\text{y}}} } {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}} + 4{{\left[ {\tau_{1} \left( {l_{1} - l_{{\text{y}}} } \right) + \tau_{2} \left( {z - l_{1} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\tau_{1} \left( {l_{1} - l_{{\text{y}}} } \right) + \tau_{2} \left( {z - l_{1} } \right)} \right]} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \hfill & {l_{1} < z \le l_{3} } \hfill \\ {{{4\tau_{1} l_{{\text{y}}} } \mathord{\left/ {\vphantom {{4\tau_{1} l_{{\text{y}}} } {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}} + {{4\left[ {\tau_{1} \left( {l_{1} - l_{{\text{y}}} } \right) + \tau_{2} \left( {l_{3} - l_{1} } \right) + \tau_{{{\text{fcorr}}}} \left( {z - l_{3} } \right)} \right]} \mathord{\left/ {\vphantom {{4\left[ {\tau_{1} \left( {l_{1} - l_{{\text{y}}} } \right) + \tau_{2} \left( {l_{3} - l_{1} } \right) + \tau_{{{\text{fcorr}}}} \left( {z - l_{3} } \right)} \right]} {\left[ {d_{0} E_{{{\text{sh}}}} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {d_{0} E_{{{\text{sh}}}} } \right]}}} \hfill & {l_{3} < z \le l_{{\text{u}}} } \hfill \\ \end{array} } \right.. $$
(16)

At any point z in the longitudinal direction of the rebar, the slip can be expressed as:

$$ s\left( z \right) = \int_{0}^{z} {\varepsilon_{{\text{s}}} \left( \kappa \right){\text{d}}} \kappa . $$
(17)

By substituting Eq. (16) into (17), the theoretical slip is obtained, such that:

$$ s\left( z \right) = \left\{ {\begin{array}{*{20}l} {{{2\tau_{1} z^{2} } \mathord{\left/ {\vphantom {{2\tau_{1} z^{2} } {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}}} \hfill & {0 \le z \le l_{{\text{y}}} } \hfill \\ {{{2\tau_{1} l_{{\text{y}}} \left( {2z - l_{{\text{y}}} } \right)} \mathord{\left/ {\vphantom {{2\tau_{1} l_{{\text{y}}} \left( {2z - l_{{\text{y}}} } \right)} {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}} + {{2\tau_{1} \left( {z - l_{{\text{y}}} } \right)^{2} } \mathord{\left/ {\vphantom {{2\tau_{1} \left( {z - l_{{\text{y}}} } \right)^{2} } {d_{0} E_{{{\text{sh}}}} }}} \right. \kern-\nulldelimiterspace} {d_{0} E_{{{\text{sh}}}} }}} \hfill & {l_{{\text{y}}} < z \le l_{1} } \hfill \\ {{{2\tau_{1} l_{{\text{y}}} \left( {2z - l_{{\text{y}}} } \right)} \mathord{\left/ {\vphantom {{2\tau_{1} l_{{\text{y}}} \left( {2z - l_{{\text{y}}} } \right)} {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}} + {{\left[ {2\tau_{1} \left( {l_{1} - l_{{\text{y}}} } \right)\left( {2z - l_{1} - l_{{\text{y}}} } \right) + 2\tau_{2} \left( {z - l_{1} } \right)^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {2\tau_{1} \left( {l_{1} - l_{{\text{y}}} } \right)\left( {2z - l_{1} - l_{{\text{y}}} } \right) + 2\tau_{2} \left( {z - l_{1} } \right)^{2} } \right]} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \hfill & {l_{1} < z \le l_{3} } \hfill \\ \begin{gathered} {{2\tau_{1} l_{{\text{y}}} \left( {2z - l_{{\text{y}}} } \right)} \mathord{\left/ {\vphantom {{2\tau_{1} l_{{\text{y}}} \left( {2z - l_{{\text{y}}} } \right)} {\left( {{\text{d}}_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{\text{d}}_{0} E_{{\text{s}}} } \right)}} + {{2\tau_{1} \left( {l_{{\text{y}}} - l_{1} } \right)\left( {l_{{\text{y}}} + l_{1} - 2z} \right)} \mathord{\left/ {\vphantom {{2\tau_{1} \left( {l_{{\text{y}}} - l_{1} } \right)\left( {l_{{\text{y}}} + l_{1} - 2z} \right)} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}} \hfill \\ + {{\left[ {2\tau_{2} \left( {l_{1} - l_{3} } \right)\left( {l_{1} + l_{3} - 2z} \right) + 2\left( {z - l_{3} } \right)^{2} \tau_{{{\text{fcorr}}}} } \right]} \mathord{\left/ {\vphantom {{\left[ {2\tau_{2} \left( {l_{1} - l_{3} } \right)\left( {l_{1} + l_{3} - 2z} \right) + 2\left( {z - l_{3} } \right)^{2} \tau_{{{\text{fcorr}}}} } \right]} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}} \hfill \\ \end{gathered} \hfill & {l_{3} < z \le l_{{\text{u}}} } \hfill \\ \end{array} } \right.. $$
(18)

According to Eq. (18), the approximate development length of bond stress can be obtained by omitting the lower order term as follows:

$$ \left\{ {\begin{array}{*{20}l} {l_{{\text{y}}} = {{f_{{{\text{ycorr}}}} d_{0} } \mathord{\left/ {\vphantom {{f_{{{\text{ycorr}}}} d_{0} } {\left( {4\tau_{1} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {4\tau_{1} } \right)}}} \hfill \\ {l_{1} = l_{{\text{y}}} + \sqrt {{{E_{{{\text{sh}}}} d_{0} s_{{1{\text{c}}}} } \mathord{\left/ {\vphantom {{E_{{{\text{sh}}}} d_{0} s_{{1{\text{c}}}} } {\left( {2\tau_{1} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2\tau_{1} } \right)}}} } \hfill \\ {l_{3} = l_{1} - \left( {l_{1} - l_{y} } \right){{\tau_{1} } \mathord{\left/ {\vphantom {{\tau_{1} } {\tau_{2} }}} \right. \kern-\nulldelimiterspace} {\tau_{2} }} + \sqrt {\left( {l_{1} - l_{y} } \right)^{2} \left[ {\left( {{{\tau_{1} } \mathord{\left/ {\vphantom {{\tau_{1} } {\tau_{2} }}} \right. \kern-\nulldelimiterspace} {\tau_{2} }}} \right)^{2} - \left( {{{\tau_{1} } \mathord{\left/ {\vphantom {{\tau_{1} } {\tau_{2} }}} \right. \kern-\nulldelimiterspace} {\tau_{2} }}} \right)} \right] + {{d_{0} E_{{{\text{sh}}}} s_{3} } \mathord{\left/ {\vphantom {{d_{0} E_{{{\text{sh}}}} s_{3} } {\left( {2\tau_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2\tau_{2} } \right)}}} } \hfill \\ {l_{{\text{u}}} = l_{3} + {{\left[ {{{d_{0} f_{{{\text{ucorr}}}} } \mathord{\left/ {\vphantom {{d_{0} f_{{{\text{ucorr}}}} } 4}} \right. \kern-\nulldelimiterspace} 4} + l_{1} \left( {\tau_{2} - \tau_{1} } \right) - l_{3} \tau_{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {{{d_{0} f_{{{\text{ucorr}}}} } \mathord{\left/ {\vphantom {{d_{0} f_{{{\text{ucorr}}}} } 4}} \right. \kern-\nulldelimiterspace} 4} + l_{1} \left( {\tau_{2} - \tau_{1} } \right) - l_{3} \tau_{2} } \right]} {\tau_{{{\text{fcorr}}}} }}} \right. \kern-\nulldelimiterspace} {\tau_{{{\text{fcorr}}}} }}} \hfill \\ \end{array} } \right.. $$
(19)

According to a similar derivation, the equations of case 2 (\(s_{{1{\text{c}}}} < s_{{{\text{ycorr}}}} \le s_{{3{\text{c}}}}\)) are given as:

$$ s\left( z \right) = \left\{ {\begin{array}{*{20}l} {{{2\tau_{1} z^{2} } \mathord{\left/ {\vphantom {{2\tau_{1} z^{2} } {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}}} \hfill & {0 \le z \le l_{1} } \hfill \\ {{{2\left[ {l_{1} \left( {\tau_{1} - \tau_{2} } \right)\left( {2z - l_{1} } \right) + \tau_{2} z^{2} } \right]} \mathord{\left/ {\vphantom {{2\left[ {l_{1} \left( {\tau_{1} - \tau_{2} } \right)\left( {2z - l_{1} } \right) + \tau_{2} z^{2} } \right]} {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}}} \hfill & {l_{1} < z \le l_{{\text{y}}} } \hfill \\ {{{\left[ {2\tau_{1} l_{1} \left( {2z - l_{1} } \right) + 2\tau_{2} \left( {l_{{\text{y}}} - l_{1} } \right)\left( {2z - l_{1} - l_{y} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {2\tau_{1} l_{1} \left( {2z - l_{1} } \right) + 2\tau_{2} \left( {l_{{\text{y}}} - l_{1} } \right)\left( {2z - l_{1} - l_{y} } \right)} \right]} {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}} + {{2\tau_{2} \left( {z - l_{{\text{y}}} } \right)^{2} } \mathord{\left/ {\vphantom {{2\tau_{2} \left( {z - l_{{\text{y}}} } \right)^{2} } {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \hfill & {l_{{\text{y}}} < z \le l_{3} } \hfill \\ \begin{gathered} {{2\left[ {l_{1} \left( {\tau_{1} - \tau_{2} } \right)\left( {2z - l_{1} } \right) + l_{{\text{y}}} \tau_{2} \left( {2z - l_{{\text{y}}} } \right)} \right]} \mathord{\left/ {\vphantom {{2\left[ {l_{1} \left( {\tau_{1} - \tau_{2} } \right)\left( {2z - l_{1} } \right) + l_{{\text{y}}} \tau_{2} \left( {2z - l_{{\text{y}}} } \right)} \right]} {\left( {d_{0} E_{{\text{s}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{\text{s}}} } \right)}} \hfill \\ {{ + 2\left[ {\tau_{2} \left( {l_{3} - l_{{\text{y}}} } \right)\left( {2z - l_{3} - l_{{\text{y}}} } \right) + \tau_{{{\text{fcorr}}}} \left( {z - l_{3} } \right)^{2} } \right]} \mathord{\left/ {\vphantom {{ + 2\left[ {\tau_{2} \left( {l_{3} - l_{{\text{y}}} } \right)\left( {2z - l_{3} - l_{{\text{y}}} } \right) + \tau_{{{\text{fcorr}}}} \left( {z - l_{3} } \right)^{2} } \right]} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{0} E_{{{\text{sh}}}} } \right)}} \hfill \\ \end{gathered} \hfill & {l_{3} < z \le l_{{\text{u}}} } \hfill \\ \end{array} } \right., $$
(20)
$$ \left\{ {\begin{array}{*{20}l} {l_{1} = \sqrt {{{E_{0} d_{0} s_{{1{\text{c}}}} } \mathord{\left/ {\vphantom {{E_{0} d_{0} s_{{1{\text{c}}}} } {\left( {2\tau_{1} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2\tau_{1} } \right)}}} } \hfill \\ {l_{{\text{y}}} = l_{1} + {{\left( {{{d_{0} f_{{{\text{ycorr}}}} } \mathord{\left/ {\vphantom {{d_{0} f_{{{\text{ycorr}}}} } 4}} \right. \kern-\nulldelimiterspace} 4} - l_{1} \tau_{1} } \right)} \mathord{\left/ {\vphantom {{\left( {{{d_{0} f_{{{\text{ycorr}}}} } \mathord{\left/ {\vphantom {{d_{0} f_{{{\text{ycorr}}}} } 4}} \right. \kern-\nulldelimiterspace} 4} - l_{1} \tau_{1} } \right)} {\tau_{2} }}} \right. \kern-\nulldelimiterspace} {\tau_{2} }}} \hfill \\ {l_{3} = l_{y} + \sqrt {{{E_{{{\text{sh}}}} d_{0} s_{3} } \mathord{\left/ {\vphantom {{E_{{{\text{sh}}}} d_{0} s_{3} } {\left( {2\tau_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2\tau_{2} } \right)}}} } \hfill \\ {l_{{\text{u}}} = l_{3} + {{\left[ {{{d_{0} f_{{{\text{ucorr}}}} } \mathord{\left/ {\vphantom {{d_{0} f_{{{\text{ucorr}}}} } 4}} \right. \kern-\nulldelimiterspace} 4} + l_{1} \left( {\tau_{2} - \tau_{1} } \right) - l_{3} \tau_{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {{{d_{0} f_{{{\text{ucorr}}}} } \mathord{\left/ {\vphantom {{d_{0} f_{{{\text{ucorr}}}} } 4}} \right. \kern-\nulldelimiterspace} 4} + l_{1} \left( {\tau_{2} - \tau_{1} } \right) - l_{3} \tau_{2} } \right]} {\tau_{{{\text{fcorr}}}} }}} \right. \kern-\nulldelimiterspace} {\tau_{{{\text{fcorr}}}} }}} \hfill \\ \end{array} } \right.. $$
(21)

It should be noted that in the above derivation, the bond stress development length is the theoretical length. In fact, the reinforcement may be pulled out before the stress reaches the ultimate strength after yielding, which is not included in this study.

Equations (18) and (20) provide the formulas to compute the theoretical average slip (sycorr and sucorr) of corroded steel bars corresponding to yield strength and ultimate strength.

4 Modified Constitutive Model of Corroded Reinforcement

4.1 Skeleton Curve of Uniaxial Stress–Strain Relationship

Axial deformation of the element with a characteristic length \(L_{{\text{d}}}\) near the column base is analyzed in Fig. 8, which clearly shows the deformation of different fibers with perfect bond and slip. Symbol \(\varepsilon_{{\text{s}}}\) is the mechanical strain of steel bar fiber; \(\varepsilon_{{\text{c}}}\) is the strain of the concrete fiber in the same position as the reinforcement; \(\overline{\varepsilon }\) is the average strain of the element in the same position as the reinforcement; \(s_{{{\text{tot}}}}\) is the total slip of steel bar fiber.

Fig. 8
figure 8

The deformation of different fibers in the element with perfect bond and slip

Full size image

These paper models the slip effect by combining the influence of reinforcement slip into the material model of reinforcement. The advantage is that the sum contributions of rebar deformation and anchorage slip can be expressed by a single equivalent strain \(\varepsilon^{\prime}_{{\text{s}}}\), without the additional need of interface elements or springs, etc. in the fiber element. Therefore, the traditional fiber model can be used directly to simulate the element with reinforcement slip. According to the condition of deformation coordination, \(\varepsilon^{\prime}_{{\text{s}}}\) is specified to equal the average strain \(\overline{\varepsilon }\) of the element in the same position as the steel bar fiber, as shown in Fig. 8, that is:

$$ \varepsilon^{\prime}_{{\text{s}}} = \overline{\varepsilon } = \varepsilon_{{\text{s}}} + {{s_{{{\text{tot}}}} } \mathord{\left/ {\vphantom {{s_{{{\text{tot}}}} } {L_{{\text{d}}} }}} \right. \kern-\nulldelimiterspace} {L_{{\text{d}}} }}. $$
(22)

In the model, the steel bar fiber accounts not only for the tensile response of the rebar inside the component but also for its anchorage outside the element, in either footing. This simulation strategy is also shown in references [7, 61].

The entire relative slip of a longitudinal bar that occurs within a concrete crack, at the interface of beam-column joint panels or at the footing of columns, may be calculated by combining the slip-on both sides of the crack. When an adequate anchorage length is available, the relative slip on both sides of the crack can be considered approximately equal [62]. Therefore, the total slip can be written as \(s_{{{\text{tot}}}} = 2s\), and s is calculated by Eqs. (18) or (20). It has been demonstrated that the simulation accuracy of structural displacement and overall stiffness can be greatly improved just by the bond-slip model in the local cracking element [9], and Ld could take the length of some elements near the column footing. Since the local cracking of reinforced concrete columns under earthquake usually occurs in the plastic hinge region, Ld could take the plastic hinge length.

The total strain of corroded reinforcement defined by Eq. (22) needs an iterative calculation in finite element simulation, which is difficult to adapt to complex structures. To consist with the basic framework of the constitutive model of perfectly bonded corroded reinforcement with variable ideal bond, the stress–strain relationship is assumed to be a bilinear model. The elastic modulus and hardening modulus of corroded steel bars under perfect bond condition are modified by the average slip strain corresponding to its yield strength and ultimate strength, respectively. In this way, a simplified bilinear stress–strain model is established.

According to Eq. (22), the equivalent strain corresponding to yield strength and ultimate strength can be obtained directly in Eqs. (23) and (24):

$$ \varepsilon^{\prime}_{{{\text{ycorr}}}} = \varepsilon_{{{\text{ycorr}}}} + {{s_{{{\text{ycorr}}}} } \mathord{\left/ {\vphantom {{s_{{{\text{ycorr}}}} } L}} \right. \kern-\nulldelimiterspace} L}_{{\text{d}}} , $$
(23)
$$ \varepsilon^{\prime}_{{{\text{ucorr}}}} = \varepsilon_{{{\text{ucorr}}}} + {{s_{{{\text{ucorr}}}} } \mathord{\left/ {\vphantom {{s_{{{\text{ucorr}}}} } L}} \right. \kern-\nulldelimiterspace} L}_{{\text{d}}} . $$
(24)

Based on the assumption that the bond-slip effect is not related to the yield strength and ultimate strength, the equivalent elastic and the hardening modulus of corroded steel bars can be expressed as:

$$ E^{\prime}_{{\text{s}}} = {{f_{{{\text{ycorr}}}} } \mathord{\left/ {\vphantom {{f_{{{\text{ycorr}}}} } {\left( {\varepsilon_{{{\text{ycorr}}}} + {{s_{{{\text{ycorr}}}} } \mathord{\left/ {\vphantom {{s_{{{\text{ycorr}}}} } {L_{{\text{d}}} }}} \right. \kern-\nulldelimiterspace} {L_{{\text{d}}} }}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\varepsilon_{{{\text{ycorr}}}} + {{s_{{{\text{ycorr}}}} } \mathord{\left/ {\vphantom {{s_{{{\text{ycorr}}}} } {L_{{\text{d}}} }}} \right. \kern-\nulldelimiterspace} {L_{{\text{d}}} }}} \right)}} = \beta E_{{\text{s}}} , $$
(25a)
$$ \beta = {{\varepsilon_{{{\text{ycorr}}}} } \mathord{\left/ {\vphantom {{\varepsilon_{{{\text{ycorr}}}} } {\left( {\varepsilon_{{{\text{ycorr}}}} + {{s_{{{\text{ycorr}}}} } \mathord{\left/ {\vphantom {{s_{{{\text{ycorr}}}} } {L_{{\text{d}}} }}} \right. \kern-\nulldelimiterspace} {L_{{\text{d}}} }}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\varepsilon_{{{\text{ycorr}}}} + {{s_{{{\text{ycorr}}}} } \mathord{\left/ {\vphantom {{s_{{{\text{ycorr}}}} } {L_{{\text{d}}} }}} \right. \kern-\nulldelimiterspace} {L_{{\text{d}}} }}} \right)}}, $$
(25b)
$$ E^{\prime}_{{{\text{sh}}}} = {{\left( {f_{{{\text{ucorr}}}} - f_{{{\text{ycorr}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {f_{{{\text{ucorr}}}} - f_{{{\text{ycorr}}}} } \right)} {\left[ {\varepsilon_{{{\text{ucorr}}}} - \varepsilon_{{{\text{ycorr}}}} + {{\left( {s_{{{\text{ucorr}}}} - s_{{{\text{ycorr}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {s_{{{\text{ucorr}}}} - s_{{{\text{ycorr}}}} } \right)} {L_{{\text{d}}} }}} \right. \kern-\nulldelimiterspace} {L_{{\text{d}}} }}} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\varepsilon_{{{\text{ucorr}}}} - \varepsilon_{{{\text{ycorr}}}} + {{\left( {s_{{{\text{ucorr}}}} - s_{{{\text{ycorr}}}} } \right)} \mathord{\left/ {\vphantom {{\left( {s_{{{\text{ucorr}}}} - s_{{{\text{ycorr}}}} } \right)} {L_{{\text{d}}} }}} \right. \kern-\nulldelimiterspace} {L_{{\text{d}}} }}} \right]}} = b^{\prime}E^{\prime}_{{\text{s}}} , $$
(26a)
$$ b^{\prime} = {{E_{{{\text{sh}}}} \left( {\varepsilon_{{{\text{ucorr}}}} - \varepsilon_{{{\text{ycorr}}}} } \right)} \mathord{\left/ {\vphantom {{E_{{{\text{sh}}}} \left( {\varepsilon_{{{\text{ucorr}}}} - \varepsilon_{{{\text{ycorr}}}} } \right)} {\left\{ {E_{{\text{s}}} \left[ {\beta \left( {\varepsilon_{{{\text{ucorr}}}} + {{s_{{{\text{ucorr}}}} } \mathord{\left/ {\vphantom {{s_{{{\text{ucorr}}}} } L}} \right. \kern-\nulldelimiterspace} L}_{{\text{d}}} } \right) - \varepsilon_{{{\text{ycorr}}}} } \right]} \right\}}}} \right. \kern-\nulldelimiterspace} {\left\{ {E_{{\text{s}}} \left[ {\beta \left( {\varepsilon_{{{\text{ucorr}}}} + {{s_{{{\text{ucorr}}}} } \mathord{\left/ {\vphantom {{s_{{{\text{ucorr}}}} } L}} \right. \kern-\nulldelimiterspace} L}_{{\text{d}}} } \right) - \varepsilon_{{{\text{ycorr}}}} } \right]} \right\}}}, $$
(26b)

where β and \(b^{\prime}\) are the elastic and hardening modulus correction factors, respectively.

The simplified stress–strain relationship considering the effects of corrosion and reinforcement slip is shown in Fig. 9. Since the degradation of deformation modulus under compression is regarded as the result of compression buckling of longitudinal reinforcement, the model can be derived on the tensile loading conditions, and also can be adopted to compressive loading. In addition, under cyclic loading, the repeated opening and closing of cracks may lead to the sliding of compression bars. The curve described by the thick solid line in Fig. 9 could also be used as the skeleton curve of the hysteretic model of the steel bars.

Fig. 9
figure 9

Modified stress–strain relationship

Full size image

4.2 Hysteretic Model

Menegotto-Pinto model [63] is used to describe the hysteretic rule of corroded longitudinal reinforcement in Fig. 10. The formulation of the hysteresis rule is as follows:

$$ \tilde{\sigma }_{{\text{s}}} = b^{\prime}\tilde{\varepsilon }_{{\text{s}}} + {{\left( {1 - b^{\prime}} \right)\tilde{\varepsilon }_{{\text{s}}} } \mathord{\left/ {\vphantom {{\left( {1 - b^{\prime}} \right)\tilde{\varepsilon }_{{\text{s}}} } {\left( {1 + \tilde{\varepsilon }_{{\text{s}}}^{{R_{i} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {R_{i} }}} \right. \kern-\nulldelimiterspace} {R_{i} }}}} }}} \right. \kern-\nulldelimiterspace} {\left( {1 + \tilde{\varepsilon }_{{\text{s}}}^{{R_{i} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {R_{i} }}} \right. \kern-\nulldelimiterspace} {R_{i} }}}} }}, $$
(27)
$$ \tilde{\sigma }_{{\text{s}}} = {{\left( {\sigma_{{\text{s}}} - \sigma_{{{\text{sr}}}}^{i} } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{{\text{s}}} - \sigma_{{{\text{sr}}}}^{i} } \right)} {\left( {\sigma_{{{\text{so}}}}^{i} - \sigma_{{{\text{sr}}}}^{i} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sigma_{{{\text{so}}}}^{i} - \sigma_{{{\text{sr}}}}^{i} } \right)}}, $$
(28)
$$ \tilde{\varepsilon }_{{\text{s}}} = {{\left( {\varepsilon_{{\text{s}}} - \varepsilon_{{{\text{sr}}}}^{i} } \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon_{{\text{s}}} - \varepsilon_{{{\text{sr}}}}^{i} } \right)} {\left( {\varepsilon_{{{\text{so}}}}^{i} - \varepsilon_{{{\text{sr}}}}^{i} } \right),}}} \right. \kern-\nulldelimiterspace} {\left( {\varepsilon_{{{\text{so}}}}^{i} - \varepsilon_{{{\text{sr}}}}^{i} } \right),}} $$
(29)
Fig. 10
figure 10

Hysteresis model for corroded reinforcement

Full size image

where \(\sigma_{{\text{s}}}\) and \(\varepsilon_{{\text{s}}}\) are the nominal stress and strain of corroded steel bar, \(\sigma_{{{\text{sr}}}}^{i}\) and \(\varepsilon_{{{\text{sr}}}}^{i}\) are the stress and strain at the strain reversal point on the curve, \(\sigma_{{{\text{so}}}}^{i}\) and \(\varepsilon_{{{\text{so}}}}^{i}\) are the stress and strain at the corner of a quadrilateral enclosing the hysteretic curve, \(b^{\prime}\) is defined in Eq. (26b).

\(R_{i}\) is the curve parameter describing Bauschinger effect, estimating the transition degree from elasticity to plasticity by Eqs. (30) and (31):

$$ R_{i} = R_{0} - {{\alpha_{1} \xi^{i} } \mathord{\left/ {\vphantom {{\alpha_{1} \xi^{i} } {\left( {\alpha_{2} + \xi^{i} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\alpha_{2} + \xi^{i} } \right)}}, $$
(30)
$$ \xi^{i} = \frac{{\left| {\varepsilon_{{{\text{so}}}}^{i} - \varepsilon_{{{\text{sr}}}}^{i - 1} } \right|}}{{\varepsilon_{{{\text{ycorr}}}} }}, $$
(31a)
$$ \varepsilon_{{{\text{sr}}}}^{0} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{{{\text{ycorr}}}} } & {\dot{\varepsilon }_{{\text{s}}} \ge 0} \\ { - \varepsilon_{{{\text{ycorr}}}} } & {\dot{\varepsilon }_{{\text{s}}} < 0} \\ \end{array} } \right., $$
(31b)

where \(R_{0}\), \(\alpha_{1}\) and \(\alpha_{2}\) are experimentally determined parameters. In this paper, according to Filippou et al. [5], it is assumed that \(R_{0} = 20\), \(\alpha_{1} = 18.5\), and \(\alpha_{2} = 0.15\).

The cyclic loading tests on steel bars with different corrosion degrees have been carried out in [64]. R0 is obtained by regression based on constant R1 and R2. The variation of R0 with the degree of corrosion is not obvious. When the slip effect is considered, \(R_{0}\) is modified as \(\beta R_{0}\), and \(\beta\) is defined in Eq. (25b).

5 Effects of Corrosion on Unconfined and Confined Concrete

In the numerical modeling in Sect. 6, the skeleton curves for the compressive constitutive relation of cover and core concrete use the constitutive models of unconfined and confined concrete proposed by Hoshikuma [65] respectively, as shown in Fig. 11. The law of hysteresis is based on Yassin model [66]. The mathematical expression of the uniaxial constitutive model of confined concrete is as follows:

$$ \sigma = \left\{ {\begin{array}{*{20}l} {E_{0} \varepsilon \left\{ {1 - \frac{1}{n}\left( {\frac{\varepsilon }{{\varepsilon_{{{\text{cc}}0}} }}} \right)^{n - 1} } \right\}} \hfill & {0 \le \varepsilon \le \varepsilon_{{{\text{cc}}0}} } \hfill \\ {f_{{{\text{cc}}0}} - E_{{{\text{des}}}} \left( {\varepsilon - \varepsilon_{{{\text{cc}}0}} } \right)} \hfill & {\varepsilon_{{{\text{cc}}0}} < \varepsilon \le \varepsilon_{{{\text{ccu}}}} } \hfill \\ {0.2f_{{{\text{cc}}0}} } \hfill & {\varepsilon_{{{\text{ccu}}}} < \varepsilon } \hfill \\ \end{array} } \right., $$
(32)
Fig. 11
figure 11

Uniaxial constitutive laws for a cover concrete and b confined concrete

Full size image

where, the physical meaning of all model parameters is shown in Fig. 11, and the specific calculation process is referred to [65].

For the cover unconfined concrete, volumetric expansion caused by steel rust will develop splitting stresses to reduce concrete strength. According to [67], the reduction of compressive strength is assumed as follows:

$$ f^{\prime}_{{{\text{c}}0}} = \frac{{f_{{{\text{c}}0}} }}{{1 + \kappa \left( {{{\varepsilon_{1} } \mathord{\left/ {\vphantom {{\varepsilon_{1} } {\varepsilon_{{{\text{c}}0}} }}} \right. \kern-\nulldelimiterspace} {\varepsilon_{{{\text{c}}0}} }}} \right)}}, $$
(33)

where \(f_{{{\text{c}}0}}\) and \(\varepsilon_{{{\text{c}}0}}\) are the compressive strength and peak strain of uncorroded cover concrete, respectively. Parameter \(\kappa\) depends on the diameter and roughness of the reinforcement, which can be taken as 0.1. The tensile strain caused by corrosion cracking is denoted by \(\varepsilon_{1}\), whose calculation process is expressed in [67].

Due to the corrosion of stirrups, the confined effect of core concrete will decrease. In this study, the compressive strength, peak strain, degradation rate and ultimate strain in Hoshikuma model [65] are modified as:

$$ f^{\prime}_{{{\text{cc}}0}} = f_{{{\text{c}}0}} + 3.8\alpha \rho_{{{\text{sh}}}} f_{{{\text{yhcorr}}}} , $$
(34)
$$ \varepsilon^{\prime}_{{{\text{cc}}0}} = 0.002 + {{0.033\beta \rho_{{{\text{sh}}}} f_{{{\text{yhcorr}}}} } \mathord{\left/ {\vphantom {{0.033\beta \rho_{{{\text{sh}}}} f_{{{\text{yhcorr}}}} } {f_{{{\text{c}}0}} ,}}} \right. \kern-\nulldelimiterspace} {f_{{{\text{c}}0}} ,}} $$
(35)
$$ E^{\prime}_{{{\text{des}}}} = 11.2{{f_{{{\text{c}}0}}^{2} } \mathord{\left/ {\vphantom {{f_{{{\text{c}}0}}^{2} } {\left( {\rho_{{{\text{sh}}}} f_{{{\text{yhcorr}}}} } \right),}}} \right. \kern-\nulldelimiterspace} {\left( {\rho_{{{\text{sh}}}} f_{{{\text{yhcorr}}}} } \right),}} $$
(36)
$$ \varepsilon_{{{\text{ccu}}}} = \varepsilon_{{{\text{c}}0}} + {{0.8f^{\prime}_{{{\text{cc}}0}} } \mathord{\left/ {\vphantom {{0.8f^{\prime}_{{{\text{cc}}0}} } {E^{\prime}_{{{\text{des}}}} ,}}} \right. \kern-\nulldelimiterspace} {E^{\prime}_{{{\text{des}}}} ,}} $$
(37)

where \(\rho_{{{\text{sh}}}}\) is the volumetric ratio of corroded transverse steel bars. Since the influence of corrosion on the geometric configuration of reinforcement is not considered in the modeling process, and the effect is only reflected in the performance degradation, the corrosion effect can be ignored for \(\rho_{{{\text{sh}}}}\), the same as in reference [68]. \(f_{{{\text{yhcorr}}}}\) is the yield strength of corroded stirrup. The degradation of mechanical properties is calculated by Eq. (1). The corrosion percentage \(\eta_{{\text{m}}}\) should be replaced by that of stirrups \(\eta_{{{\text{sm}}}}\). Feng et al. [69] established the regression equation of the corrosion percentage relationship between stirrup and longitudinal reinforcement, which is used in this paper:

$$ \eta_{{{\text{sm}}}} = 6.0263\eta_{{\text{m}}} + 1.2479. $$
(38)

6 Seismic Analysis of RC Columns Based on the Proposed Material Model

The experimental results related to the influence of corrosion on RC column specimens in [70], are used to verify the basis of the proposed reinforcement model.

6.1 Test Descriptions

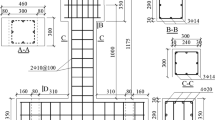
The geometric dimensions and reinforcement layout of the specimen are in Fig. 12. C30 grade concrete is used for the column, with an average 28d compressive strength of 30 MPa. The thickness of the concrete cover is 30 mm. HRB335 and HPB235 are used for the longitudinal main reinforcements and the stirrups, respectively. The measured yield strength of stirrups is 230.68 MPa, and the volumetric ratio is 0.87%. Specimens are corroded to theoretical target between 5 and 10%, with the actual measured mass loss percentage 3.83–8.41%. The axial compression ratio of all the tested specimens is set to 0.2, and equivalent to a vertical compression load of 314KN on the top of the columns. A small displacement of 2 mm is applying at the preloading stage. Subsequent displacements increase to 4 and 6 mm. Details of other tests are available in [70].

Fig. 12
figure 12

Details of the specimens (mm)

Full size image

6.2 Modeling Strategy of Fiber Beam Element

To simulate the seismic performance of RC structures, the non-linear seismic analysis platform (NSAP) has been developed by the author's group, and here several experiments are simulated to validate it.

The element type of the platform is force-based three-dimensional Timoshenko beam element. The modified reinforcement constitutive model and the concrete material constitutive model considering corrosion are introduced into the beam element. The column footing is constrained to fixed-end simplified as a cantilever, without the base. The localization phenomenon caused by strain softening is mainly concentrated in the plastic hinge region for practical engineering. To capture it accurately, the finite element mesh size becomes the key problem in modeling, and the plastic hinge length is usually used as the element length [71]. For the consistency of the element length with the plastic hinge length (about 200 mm, according to the calculation scheme proposed in [72]), 12 nodes are evenly arranged in the longitudinal direction of the whole column, and discretized into 11 elements (100 mm in length) with 2 integral points in each, as shown in Fig. 13.

Fig. 13
figure 13

Finite element model

Full size image

For computational efficiency and accuracy, the cross section of integration point adopts 64 concrete section fibers composing of 16 circumferential and 4 radial divisions, with the location and area determined by the details of each section, as shown in Fig. 13. In the only obvious area for slip effect in the actual engineering earthquake damage, such as the column footing (in this paper, two elements near the column base, the sum of the lengths is 200 mm), this paper uses a modified stress-strain model assuming the slip evenly distributed in the element steel fibers. While, in other parts, the Original stress–strain model is still adopted. To be consistent with the test, the corrosion effect is only accounted for within 500 mm of the column base. The cover and core concrete fibers of the integral point section use the Hoshikuma model introduced in Sect. 5, and the parameters are listed in Table 1. All the parameters related to the reinforcement model are calculated according to Sects. 2 and 3, and listed in Table 2.

Table 1 Model parameters of confined and unconfined concrete
Full size table
Table 2 Parameters of the reinforcement model
Full size table

6.3 Discussion on Simulation Results

As to column responses in terms of load and displacement, Fig. 14 compares numerical results obtained from the model proposed by this paper with experimental results. Figure 14a is the cyclic load–displacement curve without corrosion, which shows agreement with the experimental results in the following aspects, such as the shape of the hysteretic curve, the degree of pinching, the development trend of the overall response, the bearing capacity, as well as initial and unloading stiffness of reinforced concrete columns. Figure 14b, c show the curves corresponding to mass loss percentage of 3.83 and 8.0%, respectively. The numerical and experimental results are in agreement in only one loading direction, while they differ greatly in the opposite direction. This is due to the loading sequence and the non-uniform corrosion on the surface of column, resulting in the obvious asymmetry of the curves in the two opposite loading directions during the repeated loading process, which is not considered in the modeling. The numerical results also indicate that with the corrosion penetration, the shrinkage of the hysteresis loop increases, the fullness degree decreases, and the area of the hysteresis loop shrinks. It can be seen from Fig. 14 that the initial stiffness of corroded column obtained by numerical simulation is slightly greater than that of test results, which may be due to the consideration of the rigid connection between column and foundation in finite element modeling, without the foundation. In addition, some errors may result from assuming the same distribution length of equivalent strain caused by reinforcement slip and of the whole plastic hinge. Numerical results reflecting slip effects by this reinforcement model are expressed in Fig. 15, in which the column stiffness and bearing capacity with reinforcement slip are substantially distinct from those without reinforcement slip. It can be seen that considering slip effects in reinforcement model gives reasonable prediction for stiffness (both initial and unloading) and bearing capacity of column, while ignorance of reinforcement slip results in overestimation of 28.3% larger than the measured value for column stiffness and 13.5% larger for capacity. It indicates that the effect of bone-slip on the seismic performance of RC columns should be taken into account. The lateral force versus displacement skeleton curves corresponding to different corrosion degrees is illustrated in Fig. 16, showing a good display of this model for all the skeleton curves representing elastic, elastic–plastic and destruction stages. Except for the elastic stage, corrosion significantly affects the skeleton curves. The yield load and peak load of specimens decrease with corrosion penetration depth in longitudinal reinforcement gradually, by 1.3 and 3.5% for mass loss percentage 3.83%, and by 33.8 and 16.3% for mass loss percentage 8.0%, respectively, as shown in Fig. 16. The lateral displacement corresponding to the peak bearing capacity also decreases with the increase of mass loss percentage, 42.2 and 56.6% respectively, which testifies the brittleness of the structure increases, and the obvious deterioration effect of corrosion on the seismic ductility of RC columns and the increased risk of brittle failure.

Fig. 14
figure 14

Hysteretic curves with different corrosion rates: a 0%, b 3.83%, c 8.0%

Full size image
Fig. 15
figure 15

Comparison of numerical results with and without slip

Full size image
Fig. 16
figure 16

Simulated skeleton curves

Full size image

In the same test described in Sect. 6.1, the energy dissipation characteristics of corroded columns are introduced in reference [73]. With a certain displacement amplitude, the energy dissipation of RC pier under cyclic loading is confined in the area surrounded by the hysteretic loop. Figure 17 shows the experimental results (data point) and numerical simulation curves (line) of the hysteretic energy dissipation with different corrosion rates, which rise with the increase of the loading displacement. The curves corresponding to 0 and 3.84% are close, coinciding with the experimental results. However, the significantly lower energy consumption with 8.0% corrosion rate than that with 3.84%, indicates that more serious corrosion will significantly reduce the energy consumption capacity of the structure. Additionally, as for the corrosion rate 8.0%, the symmetrical numerical simulation results are quite different from the experimental results with obvious asymmetry, which maybe caused by the non-uniformity of corrosion, and could lead to the larger lateral deformation and earlier yield of one side of the column than the other side. Other material models for the longitudinal bars at different positions in the pier are needed for asymmetry prediction to minimize the difference, which is not studied in this paper. In the initial loading stage, during the displacement less than 10 mm, the energy consumption corresponding to various corrosion rates is basically the same due to the small area enclosed by the hysteresis loop. While for the displacement more than 20 mm, the corrosion shows a significant impact. However, with the increase of corrosion rate, it becomes easier for the reinforcement to fracture and the concrete cover to fall off, and the energy consumption increases slowly. In general, Fig. 17 indicates that the numerical results basically represent the influence law of steel corrosion on structural energy consumption.

Fig. 17
figure 17

Hysteretic energy dissipation-displacement relationships

Full size image

7 Conclusions

A simplified reinforcement model considering corrosion and bond-slip effect is proposed in this paper and used in fiber beam element to simulate the hysteretic response of RC columns with different corrosion degrees. The following conclusions are obtained:

  • The degradation of mechanical parameters from regression analysis shows that the corrosion has a significant impact on the mechanical properties of steel bars, especially on the ultimate strain. The numerical results show that the stiffness, bearing capacity and hysteretic energy consumption decrease with the increase of corrosion rate, which further proves the importance of corrosion effects.

  • The average yield strain and ultimate slip strain are used to modify the elastic and hardening modulus of reinforcement, respectively, and then the effects of corrosion and reinforcement slip are considered on the material model level. Although the theoretical derivation process is complex, its formulation is simple, convenient for complex simulation. By retaining the model framework of perfectly bonded reinforcement, it can well estimate the influence of corrosion and bond-slip on seismic analysis of RC columns.

  • Stepped equivalent bond stress is used to simplify the integral calculation of theoretical slip, and the non-uniformity of bond stress distribution along the development length is fully considered.

  • When the steel bar is slightly corroded (less than 7.5–10% mass loss percentage), the slip effect of the steel bar is the main factor affecting the calculation accuracy; otherwise the simulation accuracy is determined by both the corrosion damage and the slip effect.