1 Introduction

The metamaterials which are synthetic materials with interesting features that are not found in the nature receive significant attentions. Metamaterials generally include a periodic arrangement of small metal or dielectric–magnetic scatterers and have different applications in antennas, filters, photonic band gap (PBG) structures, etc. (Caloz and Itoh 2005; Zouhdi et al. 2002; Capolino 2009; Engheta and Ziolkowski 2006). In many applications, a one-layer implementation of metamaterials is more preferable because of its advantages such as lightness, low space occupancy and low losses. A surface periodic arrangement of isolated electrically small scatterers is called metafilm or metasurface. As depicted in Fig. 1, the scatterers can be of any shapes and dimensions, and the only necessary condition is that they are electrically small, in comparison with the wavelength, in the surrounding material (Kuester et al. 2003). Surface periodic arrays have applications such as superstrate in reconfigurable antennas (Majumder et al. 2016; Pramodh Kumar et al. 2017), reactive impedance surfaces (Mosallaei and Sarabandi 2004; Chatterjee et al. 2018), frequency selective surfaces (Ramezani et al. 2018) and controllable surfaces (Holloway et al. 2005) from microwave to terahertz frequency ranges.

Fig. 1
figure 1

Metafilm structure

Full size image

The plane wave interaction with periodic surfaces has been studied by many researchers. According to the Floquet periodic nature of the plane wave, the problem space decreases to one cell (Harms et al. 1994); then, the problem is solved by means of a numerical method such as method of moments (MoM), finite element method (FEM) or finite difference time domain (FDTD). However, in many practical applications, there is a need to calculate the fields due to finite sources which are located in the vicinity of the structure. One of the efficient full-wave methods to analyze the fields in such situation is the array scanning method (ASM) (Lovat et al. 2011; Bakhtafrouz and Borji 2015a, b), but this method is numerically demanding.

If the structural components and the periodicity of the periodic surface are much smaller than the wavelength, the surface can be homogenized. Unlike bulk metamaterials, the effective permittivity or permeability cannot be uniquely defined for metasurfaces; however, it has been shown that the surface polarization can properly explain electromagnetic properties of metafilms (Holloway et al. 2009). After characterizing the metasurface with its surface polarizations, the discrete distribution of scatterers could be replaced by a plane with continuous electric and magnetic surface polarization densities. In Kuester et al. (2003), the generalized sheet transition conditions (GSTC) were derived to determine field discontinuities at the plane of a metasurface which is replaced by its surface polarization densities. In Holloway et al. (2005), the reflection and transmission coefficients due to transverse electric (TE) and transverse magnetic (TM) incident plane waves on a metafilm were calculated. The surface polarization parameters can be obtained by means of the analytical formulae presented in Kuester et al. (2003) if the polarizabilities of each individual scatterers are known. The polarizabilities of simple structures such as magneto-dielectric spheres (Holloway et al. 2005), square PEC patches (Holloway et al. 2008) circular PEC patches and PEC spheres (Collin 1991) are known analytically. However, there have been presented retrieval formulae to obtain surface polarization densities of metafilms which include complex shape scatterers with unknown polarizabilities in Holloway et al. (2009). This is the strength of this homogenization method that it can be used for any arbitrary shape structures.

In an electromagnetic problem, the fields in the presence of a metasurface can be calculated using the electric field integral equation (EFIE) method if the electric field Green’s function is known. In Liang et al. (2016), the dyadic electric filed Green’s function was calculated by means of the TE and TM reflection coefficients for a metafilm which is located in free space. However, the EFIE is not suitable to solve an electromagnetic problem of arbitrary shape elements, because of the higher-order singularity of the kernel of the integral, especially when the observation point stays on the integration interval. Another presented integral equation form is the mixed potential integral equation (MPIE) which employs vector and scalar potential Green’s functions with the advantage of weaker singularity behavior (Michalski and Zheng 1990). Therefore, the purpose of this paper is calculation of magnetic vector and the electric scalar potentials related to the dipoles which excite the homogenized metasurface. Also it can be generalized to metasurfaces which are located in a multilayer medium.

In this paper, the GSTC conditions and the analytical and retrieval methods to obtain the surface polarization dyads of a metafilm, are reviewed. Then the Hertzian magnetic vector potential Green’s function for a dipole-excited metafilm which is located in free space is derived and the electric fields which are calculated by means of these potentials are verified with numerical results. Also the transverse and longitudinal electric scalar potential Green’s function corresponding to the problem are achieved. Finally, some remarks are explained in the conclusion.

2 Formulation and Theory

2.1 Generalized Sheet Transition Conditions (GSTC)

A surface periodic arrangement of arbitrary shape non-touching scatterers with size and periodicity much less than the wavelength in the surrounding medium can be replaced by a thin surface with effective surface polarization densities. This surface polarization leads to discontinuity in the fields around. This discontinuity carried out by generalized sheet transition conditions (GSTC) which was derived by Kuester et al. (2003)

$$\begin{aligned} \hat{z} \times \left. {\vec{H}} \right|_{{z = 0^{ - } }}^{{0^{ + } }} & = j\omega \varepsilon \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\alpha }_{ES} \cdot \left. {\vec{E}_{t,av} } \right|_{z = 0} \\ & \quad + \hat{z} \times \nabla_{t} \left[ {\alpha_{MS}^{zz} H_{z,av} } \right]_{z = 0} \\ \end{aligned}$$
(1)
$$\begin{aligned} \left. {\vec{E}} \right|_{{z = 0^{ - } }}^{{0^{ + } }} \times \hat{z} & = - j\omega \mu \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\alpha }_{\text{MS}} \cdot \left. {\vec{H}_{{t,{\text{av}}}} } \right|_{z = 0} \\ & \quad - \nabla_{t} \left[ {\alpha_{\text{ES}}^{zz} E_{{z,{\text{av}}}} } \right]_{z = 0} \times \hat{z} \\ \end{aligned}$$
(2)
$$\left. {D_{z} } \right|_{{z = 0^{ - } }}^{{0^{ + } }} = - \nabla \cdot \left( {\varepsilon \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\alpha }_{\text{ES}} \cdot \left. {\vec{E}_{{t,{\text{av}}}} } \right|_{z = 0} } \right)$$
(3)
$$\left. {B_{z} } \right|_{{z = 0^{ - } }}^{{0^{ + } }} = \nabla \cdot \left( {\mu \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\alpha }_{\text{MS}} \cdot \left. {\vec{H}_{t,av} } \right|_{z = 0} } \right)$$
(4)

where \(\hat{z}\) is the unit normal vector to the periodic surface, t denotes the tangential component, \(\vec{E}\) and \(\vec{H}\) are electric and magnetic fields, respectively, Dz is the normal component of the electric displacement density, Bz is the normal component of magnetic flux density, \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\alpha }_{\text{ES}}^{{}} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\alpha }_{\text{MS}}^{{}}\) are the electric and magnetic polarization density dyads, respectively, ω is the angular frequency, ε is the permittivity and μ is the permeability of the surrounding medium. The term j denotes the imaginary unit.

It is assumed that the scatterers are arranged in such way that the electric and magnetic surface polarization dyads are diagonal

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\alpha }_{\text{ES}} = \alpha_{\text{ES}}^{xx} \hat{x}\hat{x} + \alpha_{\text{ES}}^{yy} \hat{y}\hat{y} + \alpha_{\text{ES}}^{zz} \hat{z}\hat{z}$$
(5)
$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\alpha }_{\text{MS}} = \alpha_{\text{MS}}^{xx} \hat{x}\hat{x} + \alpha_{\text{MS}}^{yy} \hat{y}\hat{y} + \alpha_{\text{MS}}^{zz} \hat{z}\hat{z}.$$
(6)

If the polarizabilities of any individual scatterer are known, the dyads elements can be calculated with dipole interaction assumption between elements as (Kuester et al. 2003):

$$\alpha_{\text{ES}}^{tt} = \frac{{N\left\langle {\alpha_{E,tt} } \right\rangle }}{{1 - {{N\left\langle {\alpha_{E,tt} } \right\rangle } \mathord{\left/ {\vphantom {{N\left\langle {\alpha_{E,tt} } \right\rangle } {\left( {4R} \right)}}} \right. \kern-0pt} {\left( {4R} \right)}}}}$$
(7)
$$\alpha_{\text{ES}}^{zz} = \frac{{N\left\langle {\alpha_{E,zz} } \right\rangle }}{{1 + {{N\left\langle {\alpha_{E,zz} } \right\rangle } \mathord{\left/ {\vphantom {{N\left\langle {\alpha_{E,zz} } \right\rangle } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}}}}$$
(8)
$$\alpha_{\text{MS}}^{tt} = \frac{{N\left\langle {\alpha_{M,tt} } \right\rangle }}{{1 + {{N\left\langle {\alpha_{M,tt} } \right\rangle } \mathord{\left/ {\vphantom {{N\left\langle {\alpha_{M,tt} } \right\rangle } {\left( {4R} \right)}}} \right. \kern-0pt} {\left( {4R} \right)}}}}$$
(9)
$$\alpha_{\text{MS}}^{zz} = \frac{{N\left\langle {\alpha_{M,zz} } \right\rangle }}{{1 - {{N\left\langle {\alpha_{M,zz} } \right\rangle } \mathord{\left/ {\vphantom {{N\left\langle {\alpha_{M,zz} } \right\rangle } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}}}}.$$
(10)

In (7)–(10) \(t = \left\{ {x\,{\text{or}}\,y} \right\}\), N is the number of scatterers per unit area \(\left( {N = {1 \mathord{\left/ {\vphantom {1 {p_{x} p_{y} }}} \right. \kern-0pt} {p_{x} p_{y} }}} \right)\), \(\alpha_{{{\text{E}},{\text{ss}}}} ,\alpha_{{{\text{M}},{\text{ss}}}} \,\left\{ {s = x,y,z} \right\}\) are the electric and magnetic polarizabilities of each scatterer, respectively, and have closed-form formulae for simple shapes. Symbol <> denotes an average over the scatterer. R is a constant that was calculated in (Maslovski and Tretyakov 1999) for a square array of scatterers with period d as:

$$R \simeq 0.6956\;d.$$
(11)

Also if the metafilm is constructed by arbitrary shape elements with unknown polarizabilities, the surface polarization densities can be retrieved from scattering parameters. It needs only to know the reflection and transmission coefficients due to TE and TM plane wave incident on metafilm at two different incident angles. These parameters can be achieved from simulation or measurement (Holloway et al. 2009).

Using TE reflection and transmission at normal and arbitrary θ incident angles, the surface polarizations obtained as:

$$\alpha_{MS}^{xx} = - \frac{2j}{{k_{0} }}\frac{R\left( 0 \right) - T\left( 0 \right) + 1}{R\left( 0 \right) - T\left( 0 \right) - 1}$$
(12)
$$\alpha_{ES}^{yy} = \frac{2j}{{k_{0} }}\frac{R\left( 0 \right) + T\left( 0 \right) - 1}{R\left( 0 \right) + T\left( 0 \right) + 1}$$
(13)
$$\alpha_{MS}^{zz} = \frac{{\alpha_{ES}^{yy} }}{{\sin^{2} \theta }} - \frac{2j\cos \theta }{{k_{0} \sin^{2} \theta }}\frac{R\left( \theta \right) + T\left( \theta \right) - 1}{R\left( \theta \right) + T\left( \theta \right) + 1}.$$
(14)

And the remained parameters can be obtained by TM incident as:

$$\alpha_{ES}^{xx} = \frac{2j}{{k_{0} }}\frac{R\left( 0 \right) + T\left( 0 \right) - 1}{R\left( 0 \right) + T\left( 0 \right) + 1}$$
(15)
$$\alpha_{MS}^{yy} = - \frac{2j}{{k_{0} }}\frac{R\left( 0 \right) - T\left( 0 \right) + 1}{R\left( 0 \right) - T\left( 0 \right) - 1}$$
(16)
$$\alpha_{ES}^{zz} = \frac{{\alpha_{MS}^{yy} }}{{\sin^{2} \theta }} + \frac{2j\cos \theta }{{k_{0} \sin^{2} \theta }}\frac{R\left( \theta \right) - T\left( \theta \right) + 1}{R\left( \theta \right) - T\left( \theta \right) - 1}.$$
(17)

In (12)–(17), R(0) and T(0) are reflection and transmission coefficients at normal incident and R(θ) and T(θ) are reflection and transmission coefficients due to plane wave incidence at angle of θ with respect to z-axis. Also k0 is the wave vector in free space.

2.2 Dyadic Hertzian Vector Potential Green’s Function

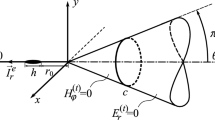
The reflection and transmission coefficients due to TE and TM incident waves which illuminate a surface with electric and magnetic surface polarizations in spectral domain were calculated in Liang et al. (2016), and then, the electric field dyadic Green’s function for a dipole-excited metafilm was obtained. Furthermore, the analytical formulae for the probable excited surface wave poles were presented. As mentioned before, since the electric field Green’s function shows highly singular behavior, the EFIE formulation of MoM in an electromagnetic problem that uses the electric field Green’s function is not suitable enough. Therefore, it is preferable to use the other form of integral equation, namely MPIE which utilizes the both magnetic vector and electric scalar potential Green’s functions (Michalski and Zheng 1990). In the following, the Hertzian magnetic vector potential Green’s function is derived using the method discussed in Bagby and Nyquist (1987) for vertical and horizontal Hertzian dipoles which are located above the metafilm.

The Hertzian vector potentials \(\left( {\vec{\varPi }_{\ell } } \right)\) at the top and bottom of the metafilm satisfy the Helmholtz equation (Bagby and Nyquist 1987):

$$\left( {\nabla^{2} + k_{0}^{2} } \right)\vec{\varPi }_{\ell } = \left\{ {\begin{array}{*{20}c} { - \frac{{\hat{J}}}{{j\omega \varepsilon_{0} }}\delta \left( {\vec{r} - \vec{r^{\prime}}} \right)} & {\ell = 1} \\ 0 & {\ell = 2} \\ \end{array} } \right.$$
(18)

where ℓ = 1 and 2 point to the top and bottom of the metafilm, respectively. \(\vec{r}\) and \(\vec{r}^{\prime }\) denote the observation and the source points, respectively, and \(\hat{J}\) is the vector of the unit impressed current element.

After determining the vector potential, the fields are obtained from the following expressions (Bagby and Nyquist 1987)

$$\vec{E} = \left( {k_{0}^{2} + \nabla \nabla .} \right)\vec{\varPi }$$
(19)
$$\vec{H} = j\omega \varepsilon_{0} \nabla \times \vec{\varPi }.$$
(20)

The Helmholtz equation (18) is usually calculated in the spectral domain with the help of the Fourier transform

$$\tilde{f}(k_{x} ,k_{y} ,z) = \frac{1}{{\left( {2\pi } \right)^{2} }}\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {e^{{ - jk_{x} x - jk_{y} y}} F(x,y,z){\text{d}}x{\text{d}}y} }$$
(21)
$$F(x,y,z) = \int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {e^{{jk_{x} x + jk_{y} y}} \tilde{f}(k_{x} ,k_{y} ,z)\;{\text{d}}k_{x} {\text{d}}k_{y} } }. \,$$
(22)

In this work, the metasurface with periodic planar PEC elements is considered. Because of the thin thickness of the scatterers, magnetic flux passing through the lateral faces as well as induced dipole moment in z-direction is zero, i.e., \(\alpha_{MS}^{xx} = \alpha_{MS}^{yy} = \alpha_{ES}^{zz} = 0\). It is assumed that the array is so symmetric that the surface polarization dyads are diagonal and \(\alpha_{ES}^{xx} = \alpha_{ES}^{yy}\).

By applying the jump boundary conditions (1) and (2) to the fields calculated by (19), the boundary conditions for Hertzian magnetic vector potentials corresponding to the vertical electric dipole (VED) source illuminating the metafilm, in the spectral domain, are obtained as:

$$\frac{\partial }{\partial z}\tilde{\pi }_{{z_{1} }} = \frac{\partial }{\partial z}\tilde{\pi }_{{z_{2} }}$$
(23)
$$\tilde{\pi }_{{z_{1} }} - \tilde{\pi }_{{z_{2} }} = \chi_{ES}^{yy} \frac{\partial }{\partial z}\tilde{\pi }_{{z_{1} }}.$$
(24)

In the same way, for a x-directed horizontal electric dipole (HED), we have:

$$\frac{\partial }{\partial z}\tilde{\pi }_{{z_{1} }} = \frac{\partial }{\partial z}\tilde{\pi }_{{z_{2} }}$$
(25)
$$\tilde{\pi }_{{z_{1} }} - \tilde{\pi }_{{z_{2} }} = \chi_{ES}^{yy} \left[ { - jk_{x} \tilde{\pi }_{x} + \frac{\partial }{\partial z}\tilde{\pi }_{{z_{1} }} } \right] - jk_{x} \chi_{MS}^{zz} \tilde{\pi }_{x}$$
(26)
$$\begin{aligned} - jk_{x} \left( {\tilde{\pi }_{{z_{1} }} - \tilde{\pi }_{{z_{2} }} } \right) = \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\chi_{ES}^{xx} \left[ { - k_{x}^{2} \tilde{\pi }_{x} - jk_{x} \frac{\partial }{\partial z}\tilde{\pi }_{{z_{1} }} + k_{0}^{2} \tilde{\pi }_{x} } \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + k_{y}^{2} \chi_{MS}^{zz} \tilde{\pi }_{x}. \hfill \\ \end{aligned}$$
(27)

By solving the Helmholtz equation (18) with the aid of the Fourier transform (21) and enforcing the boundary conditions (23) and (24) for a VED excitation, the Hertzian magnetic vector potential in the spectral domain is obtained as:

$$\tilde{\pi } = \left\{ {\begin{array}{*{20}c} {\left( {\frac{{e^{{ - jk_{z} \left| {z - z^{\prime}} \right|}} }}{{2jk_{z} \left( {j\omega \varepsilon_{0} } \right)}} + A_{zz} e^{{ - jk_{z} z}} } \right)\hat{a}_{z} } & {z > 0} \\ {B_{zz} e^{{jk_{z} z}} \hat{a}_{z} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {z < 0} \\ \end{array} } \right.$$
(28)

with unknown coefficients as:

$$A_{zz} = \frac{{k_{z} \alpha_{ES}^{xx} }}{{k_{z} \alpha_{ES}^{xx} - 2j}}v_{z}$$
(29)
$$B_{zz} = \frac{ - 2j}{{k_{z} \alpha_{ES}^{xx} - 2j}}v_{z}.$$
(30)

Also for x-directed HED located above the metafilm, the symmetric and asymmetric vector potentials are derived as:

$$\tilde{\pi } = \left\{ {\begin{array}{*{20}c} {\left( {\frac{{e^{{ - jk_{z} \left| {z - z^{\prime}} \right|}} }}{{2jk_{z} \left( {j\omega \varepsilon_{0} } \right)}} + A_{xx} e^{{ - jk_{z} z}} } \right)\hat{a}_{x} + A_{zx} e^{{ - jk_{z} z}} \hat{a}_{z} } & {z > 0} \\ {B_{xx} e^{{jk_{z} z}} \hat{a}_{x} + B_{zx} e^{{jk_{z} z}} \hat{a}_{z} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {z < 0} \\ \end{array} } \right.$$
(31)

with coefficients which are obtained by enforcing the boundary conditions (25)–(27) as:

$$A_{xx} = - \frac{{\alpha_{ES}^{xx} k_{0}^{2} - \alpha_{MS}^{zz} k_{\rho }^{2} }}{{\alpha_{ES}^{xx} k_{0}^{2} - \alpha_{MS}^{zz} k_{\rho }^{2} - 2jk_{z} }}v_{x}$$
(32)
$$\begin{aligned} A_{zx} & = - B_{zx} \\ & = \frac{{ - 2jk_{x} k_{z} \left( {\alpha_{ES}^{xx} - \alpha_{MS}^{zz} } \right)}}{{\left( {\alpha_{ES}^{xx} k_{0}^{2} - \alpha_{MS}^{zz} k_{\rho }^{2} - 2jk_{z} } \right)\left( {2j - k_{z} \alpha_{ES}^{xx} } \right)}}v_{x} \\ \end{aligned}$$
(33)
$$B_{xx} = - \frac{{2jk_{z} }}{{\alpha_{ES}^{xx} k_{0}^{2} - \alpha_{MS}^{zz} k_{\rho }^{2} - 2jk_{z} }}v_{x}$$
(34)
$$v_{s} = \frac{{e^{{ - jk_{z} z^{\prime}}} }}{{2jk_{z} \left( {j\omega \varepsilon_{0} } \right)}}\,,\,\,\,\,\,\,s = x,y,z.$$
(35)

Equations (31)–(35) are valid for y-directed HED if \(k_{x}\) and \(v_{x}\) are replaced by \(k_{y}\) and \(v_{y}\), respectively.

As expected, the surface wave poles have the same closed-form formulae as the electric field Green’s function (Liang et al. 2016)

$$k_{zp,TM} = \frac{2j}{{\alpha_{ES}^{xx} }}$$
(36)
$$k_{zp,TE} = \frac{{j\left( {1 \pm \sqrt {1 + k_{0}^{2} \alpha_{MS}^{zz} \left( {\alpha_{ES}^{xx} - \alpha_{MS}^{zz} } \right)} } \right)}}{{\alpha_{MS}^{zz} }}.$$
(37)

Notice that in (Liang et al. 2016) the magnetic surface susceptibility dyad \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\chi }_{MS}\) was employed instead of magnetic polarization dyad \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\alpha }_{MS}\). Actually, the magnetic surface susceptibility and magnetic surface polarization differ only in a minus sign, i.e., \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\chi }_{MS} = - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\alpha }_{MS}\).

2.3 Electric Field Green’s Function

After determining the dyadic magnetic vector potential, electric field dyad due to electric current element can be obtained by means of (19) in the spectral domain as:

$$\tilde{G}_{EJ}^{xx} = \left\{ {\begin{array}{*{20}c} {\left( {k_{0}^{2} - k_{x}^{2} } \right)\left[ {\frac{{e^{{ - jk_{z} \left| {z - z^{\prime}} \right|}} }}{{2jk_{z} \left( {j\omega \varepsilon_{0} } \right)}} + A_{xx} e^{{ - jk_{z} z}} } \right] + k_{z} k_{x} A_{zx} e^{{ - jk_{z} z}} } & {z > 0} \\ {\left( {k_{0}^{2} - k_{x}^{2} } \right)B_{xx} e^{{jk_{z} z}} \, - k_{z} k_{x} B_{zx} e^{{jk_{z} z}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {z < 0} \\ \end{array} } \right.$$
(38)
$$\tilde{G}_{EJ}^{yx} = \left\{ {\begin{array}{*{20}c} { - k_{x} k_{y} \left[ {\frac{{e^{{ - jk_{z} \left| {z - z^{\prime}} \right|}} }}{{2jk_{z} \left( {j\omega \varepsilon_{0} } \right)}} + A_{xx} e^{{ - jk_{z} z}} } \right] + k_{z} k_{y} A_{zx} e^{{ - jk_{z} z}} } & {z > 0} \\ { - k_{x} k_{y} B_{xx} e^{{jk_{z} z}} \, - k_{z} k_{y} B_{zx} e^{{jk_{z} z}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {z < 0} \\ \end{array} } \right.$$
(39)
$$\tilde{G}_{EJ}^{zx} = \left\{ {\begin{array}{*{20}c} {k_{z} k_{x} \left[ {\frac{{ \pm e^{{ - jk_{z} \left| {z - z^{\prime}} \right|}} }}{{2jk_{z} \left( {j\omega \varepsilon_{0} } \right)}} + A_{xx} e^{{ - jk_{z} z}} } \right] - k_{z}^{2} A_{zx} e^{{ - jk_{z} z}} } & {z > 0} \\ { - k_{z} k_{x} B_{xx} e^{{jk_{z} z}} \, - k_{z}^{2} B_{zx} e^{{jk_{z} z}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {z < 0} \\ \end{array} } \right.$$
(40)
$$\tilde{G}_{EJ}^{xz} = \left\{ {\begin{array}{*{20}c} {k_{z} k_{x} \left[ {\frac{{ \pm e^{{ - jk_{z} \left| {z - z^{\prime}} \right|}} }}{{2jk_{z} \left( {j\omega \varepsilon_{0} } \right)}} + A_{zz} e^{{ - jk_{z} z}} } \right]} & {z > 0} \\ { - k_{z} k_{x} B_{zz} e^{{jk_{z} z}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {z < 0} \\ \end{array} } \right.$$
(41)
$$\tilde{G}_{EJ}^{zz} = \left\{ {\begin{array}{*{20}c} {k_{\rho }^{2} \left[ {\frac{{e^{{ - jk_{z} \left| {z - z^{\prime}} \right|}} }}{{2jk_{z} \left( {j\omega \varepsilon_{0} } \right)}} + A_{zz} e^{{ - jk_{z} z}} } \right]} & {z > 0} \\ {k_{\rho }^{2} \left[ {B_{zz} e^{{jk_{z} z}} } \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {z < 0} \\ \end{array} } \right.$$
(42)

Subsequently,\(\tilde{G}_{EJ}^{yy}\),\(\tilde{G}_{EJ}^{xy}\), \(\tilde{G}_{EJ}^{zy}\) and \(\tilde{G}_{EJ}^{yz}\) can be obtained using (38)–(41) by replacing kx with ky and vice versa. Also \(v_{x}\) must be replaced by \(v_{y}\).

2.4 Scalar Potential Green’s Function

Using the Lorentz gauge (43) which relates the potentials of an \(\hat{u}\)-directed dipole to each other, the electric field (19) can be rewritten by means of magnetic vector potential and electric scalar potential as (44).

$$\nabla \cdot \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\varPi } \cdot \hat{u}} \right) + \mu_{0} \left( {\frac{1}{j\omega }\frac{\partial V}{{\partial u^{\prime } }}} \right) = 0$$
(43)
$$\vec{E} = k_{0}^{2} \vec{\varPi } - \nabla V$$
(44)

where V is the electric scalar potential due to one point charge (Gay-Balmaz et al. 1997). By expanding (43), the longitudinal and transverse scalar potentials in the spectral domain are obtained, respectively, as:

$${\tilde{\text{v}}}^{\text{n}} = \frac{\omega }{{\mu_{0} k_{z} }}\left\{ {\begin{array}{*{20}c} {\frac{{e^{{ - jk_{z} \left| {z - z^{\prime}} \right|}} }}{{2jk_{z} \left( {j\omega \varepsilon_{0} } \right)}} + A_{zz} e^{{ - jk_{z} z}} } & {z > 0} \\ {B_{zz} e^{{jk_{z} z}} } & {z < 0} \\ \end{array} } \right.$$
(45)
$${\tilde{\text{v}}}^{\text{t}} = \frac{j\omega }{{\mu_{0} }}\left\{ {\begin{array}{*{20}c} {\frac{{e^{{ - jk_{z} \left| {z - z^{\prime}} \right|}} }}{{2jk_{z} \left( {j\omega \varepsilon_{0} } \right)}} + \left( {A_{xx} - \frac{{k_{z} }}{{k_{x} }}A_{zx} } \right)e^{{ - jk_{z} z}} } & {z > 0} \\ {\left( {B_{xx} + \frac{{k_{z} }}{{k_{x} }}B_{zx} } \right)e^{{jk_{z} z}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {z < 0}. \\ \end{array} } \right.$$
(46)

The unknown coefficients in (45) and (46) have already been given in (29)–(30) and (32)–(35), respectively.

3 Numerical Results

In this section, two metasurfaces are considered and the electric fields arising from VED \(\left( {\vec{J}_{z} } \right)\) and y-directed HED \(\left( {\vec{J}_{y} } \right)\) illuminating them are calculated. First, a PEC square patch array is considered. The electric and magnetic polarizabilities of a PEC square patch are known analytically. Therefore, the analytical formulae (7)–(10) can be used to calculate the surface polarization densities. The second intended metasurface is a Jerusalem cross array. Since the polarizabilities of a Jerusalem cross are not known, The retrieval relations (12)–(17) should be used to obtain the surface polarization densities.

As the surface polarization densities are determined, the electric fields can be calculated using (38)–(42). The Sommerfeld integrals arising due to the inverse Fourier transform (22) are calculated on real \(k_{\rho }\) axis (Mosig and Sarkar 1986). The results are compared with commercial numerical software FEKO and also the array scanning method (ASM). Because of the non-periodic nature of the dipole element, it was necessary to import the full structure in FEKO software. However, computational resources are limited and the periodic structure must be truncated. Results show excellent agreement with numerical full-wave methods.

The relative error diagrams of the calculated electric fields in the presence of the considered metasurfaces are calculated using Eq. (47).

$${\text{RE}} = \left| {\frac{{E_{\text{proposed}} - E_{\text{Full - wave}} }}{{E_{\text{Full - wave}} }}} \right|.$$
(47)

3.1 A PEC Square Patch Array

First, the array includes squares with dimensions: width \(\ell\) = 1.8 mm, gap g = 0.2 mm and periodicity \(p = \ell + g\left( {{p \mathord{\left/ {\vphantom {p {\lambda = 0.1}}} \right. \kern-0pt} {\lambda = 0.1}}} \right)\) is considered. The source element has been located at (x′, y′, z′) = (0,0,3 mm) above the metafilm.

Two heights for the observation points are considered, (x, y = 0, z = 5) mm which is a quarter of the wavelength in the surrounding medium, i.e., free space and (x, y = 0, z = 2) mm which is same as the lattice period. The surface polarization density of a PEC square patch array can be calculated analytically as (Holloway et al. 2008)

$$\alpha_{ES,xx} = \alpha_{ES,yy} = p\,f_{e}$$
(48)

where

$$f_{e} = \frac{{1.02x^{3} }}{{1 - 0.367x^{3} }},\,\,\,\,x = \frac{\ell }{p}$$
(49)
$$\alpha_{M,zz} { = 0} . 4 5 4 8\ell^{3}.$$
(50)

The electric fields due to a VED and a y-directed HED which illuminate the metafilm and the corresponding relative errors are shown in Figs. 2 and 3, respectively. As it can be seen, the fields show good agreement with full-wave methods when the observation points are larger than the lattice constant. As expected, approaching the surface the evanescent higher-order Floquet modes become obvious. These modes are considerable when the observation point becomes closer to the surface.

Fig. 2
figure 2

a The z-component of electric field due to a 1-Amp VED located at (x′, y′, z′) = (0, 0, 3 mm), over a square PEC patch array with dimensions: l = 1.8 mm, g = 0.2 mm, p = l + g = 2 mm (λ/10 at 15 GHz), the observation points are along the x-axis, i.e., y = 0 and two different heights (x, y = 0, z = 2, 5) mm, b the relative error of the fields calculated in part a. c The fields at observation points near the surface (x, y = 0, z = 1, 0.1) mm (along the x-axis with heights smaller than the lattice constant)

Full size image
Fig. 3
figure 3

a The y-component of electric field due to a 1-Amp y-directed HED located at (x′, y′, z′) = (0,0,3 mm), over a square PEC patch array with dimensions: l = 1.8 mm, g = 0.2 mm, p = l + g = 2 mm (λ/10 at 15 GHz), the observation points are along the x-axis, i.e., y = 0 and two different heights (x, y = 0, z = 2,5) mm, b the relative error of the fields calculated in part a. c The fields at observation points near the surface (x, y = 0, z = 1,0.5) mm (along the x-axis with heights smaller than the lattice constant)

Full size image

As mentioned, it is necessary to import a truncated array in the full-wave commercial software. In this work, a 4λ × 4λ surface (at 15 GHz) located in free space has been simulated in numerical software FEKO.

3.2 A Jerusalem Cross Array

The second metafilm which is considered in this paper is a Jerusalem cross array with parameters: p = 4.3 mm, g = 0.1 mm, d = 2.8 mm and w = t=0.2 mm.

The dipole source is placed above the metafilm at position (0,0,10 mm). The reflection and transmission coefficients due to TE and TM plane waves which illuminate the surface at two incident angles, normal incidence and θ = 30° obtained by commercial numerical software Ansys HFSS employing Floquet boundary conditions and Floquet ports. After that, the surface polarization densities are calculated by retrieval relations at frequency f = 6.9 GHz. While the surface polarization dyads are calculated, the fields due to electric dipole which excites the metasurface turn out employing (38)–(42).

The z components of electric fields due to the VED and corresponding relative errors are depicted in Fig. 4. The observation points are at x-axis (y = 0) and different heights, i.e., (x, y = 0, z = 8) mm which is larger than the lattice periodicity, (x, y = 0, z = 4.3) mm which is equal to the lattice constant and (x, y = 0, z = 2) mm which is smaller than the lattice constant.

Fig. 4
figure 4

a the z-component of electric field due to a 1-Amp VED located at (x′, y′, z′) = (0,0,10 mm), over a Jerusalem cross array with dimensions: g = 0.1 mm, d = 2.8 mm and w = t = 0.2 mm, p = 4.3 mm (λ/10 at 6.9 GHz), the observation points are along the x-axis, i.e., y = 0 and three different heights (x, y = 0, z = 2, 4.3, 8) mm, b the relative error of the fields calculated in part a. c The fields at an observation point near the surface (x, y = 0, z = 0.5) mm (along the x-axis with height smaller than the lattice constant)

Full size image

Also, an observation point close to the surface (at a distance about λ/100) is considered to investigate the effect of the evanescent higher-order Floquet modes in the vicinity of the surface. The relative error diagram shows that when the observation height becomes smaller than the lattice constant the higher-order Floquet modes appear. And when the height becomes closer to the surface, this effect will increase.

Subsequently, the y components of the fields due to y-directed HED are presented in Fig. 5.

Fig. 5
figure 5

a the y-component of electric field due to a 1-Amp y-directed HED located at (x′, y′, z′) = (0,0,10 mm), over a Jerusalem cross array with dimensions: g = 0.1 mm, d = 2.8 mm and w = t=0.2 mm, p = 4.3 mm (λ/10 at 6.9 GHz), the observation points are along the x-axis, i.e., y = 0 and three different heights (x, y = 0, z = 8,4.3) mm, b the relative error of the fields calculated in part a. c The fields at an observation point near the surface (x, y = 0, z = 0.5) mm (along the x-axis with height smaller than the lattice constant)

Full size image

One of the sources of error can be the numerical error caused by numerical analysis in the calculation of scattering parameters and polarization density dyads. In this section, a 3λ × 3λ surface has been implemented in commercial numerical software FEKO to validate the results.

4 Conclusion

In this paper, the magnetic Hertzian vector potential Green’s functions are derived for vertical and horizontal dipole that excite the metafilm located in free space. The metasurface was assumed to consist of separated planar periodic elements, which can be replaced by a surface with its equivalent surface polarization densities. The discontinuity of the fields arising from the surface polarizations was characterized by generalized sheet transition conditions. Then the electric field Green’s function is calculated using the obtained magnetic vector potentials.

Two types of metasurfaces are considered to validate the results, A PEC square patch array whose surface electric and magnetic polarization dyads can be obtained analytically and a Jerusalem cross array whose polarization densities must be retrieved from plane wave reflection and transmission coefficients. Both arrays have λ/10 periodicity at the operation frequency and results show good agreement with the fields calculated by commercial numerical software FEKO and ASM-MoM method. However, it is shown that when the height of the observation point from the metasurface becomes smaller than the lattice constant, the effect of the evanescent higher-order Floquet modes becomes obvious. This effect is increased with approaching the metasurface.

Also the electric scalar potential Green’s function due to one point charge is calculated by means of corresponding magnetic vector potential linked by the Lorentz gauge. These vector and scalar potentials can be used together in the mixed potential integral equation (MPIE) for the method of moment (MoM) in an electromagnetic problem with the advantage of weaker singularity behavior of the kernel of the integrals.