1 Introduction

In recent years, due to a quick decrease in fossil fuels and an increasing demand for high-quality and reliable electrical power, new generating sources in electrical power systems have emerged. Centralized power generation units are giving way to smaller and more distributed production units named DGs (Kantamneni et al. 2015; Breckling 1989; Hawkes and Leach 2009). The term DG refers to the power produced near the consumer, not a centralized generation. DGs include a wide range of generating systems such as DEG, MT, FC, WTG, PV, BESS, FESS. RESs like PV and WTG decrease greenhouse gases and consequently improve the problem of global warming. Furthermore, the distributed generating network considerably reduces the power loss occurring in a centralized system, but the fluctuating nature of RESs leads to new problems and may endanger the power system stability which means innovating methods for managing DG units are necessary (Yunwei and Nejabatkhah 2014). The solution is to put these units together with storage systems and loads to construct a small local power system called microgrid. This system organizes and manages DGs in a better way and brings higher capacity and more flexibility in comparison with a single DG.

From a power system point of view, MG is a relatively new notion different from common energy systems in which electricity is usually produced in large power plants and then passed through the transmission and distribution networks. Actually, MG as a part of the distribution network consists of DG units, local loads, a connection for importing and exporting electricity from and/or the main power system, and an energy management system. It supplies loads in its local area and can disconnect from the main power system in either emergency or pre-arranged situations, and exhibits itself as an entity relative to the main power system. In some cases, the islanded performance of MG is the only operational mode, e.g., in off-grids for distant areas (Al-Saedi et al. 2012; Dekker et al. 2012). In an islanded MG, frequency control is a more complicated task, whereas, in a grid-connected MG, frequency regulation is dictated by the main power system.

In an islanded MG, there are some challenges like load changes, the intermittent nature of RESs (PV and WTG), uncertainties, and modeling errors (Shayeghi et al. 2009). RESs outputs depend on the environmental conditions. For example, the output power of a WTG is proportional to the cube of the wind speed. In other words, RESs cannot supply loads consistently which in turn results in an imbalance between the load and the produced power (Haoran et al. 2015). Thus, a frequency deviation from the nominal value occurs. This imbalance seriously degrades the performance of the islanded MG (Bevrani 2009).

To keep frequency deflection small in the islanded MGs, the conventional control strategies are not appropriate any more and more complex control algorithms are necessary for approaching better performance despite undesirable disturbances and model uncertainties (Bevrani et al. 2015). The control signals are applied to some dispatchable DGs to reduce the imbalance between the produced power and the demanded load. The RES units are not contributed in the frequency control since they are not controllable. Therefore, the DEG output power is preferred to be used for compensating the mismatch between the demand side and the produced energy. However, we cannot completely overcome the sudden load changes by controlling DEGs. Since BESS provides faster time response, it is used for handling high-frequency load transients and immediate diminishing of the frequency deviations.

To reduce the frequency deviations in the islanded MGs, some control strategies have been proposed (Bevrani et al. 2015; Sundaram and Jayabarathi 2011; Dong et al. 2011; Annamraju and Nandiraju 2018; Han et al. 2015; Kumar et al. 2017; Lam et al. 2016; Hua et al. 2017; Malek and Khodabakhshian 2017; Sedghi and Fakharian 2017). PID control is studied by many researchers (Sundaram and Jayabarathi 2011; Dong et al. 2011). In Annamraju and Nandiraju (2018), a novel two-stage adaptive fuzzy logic-based PI controller for the frequency control of a MG consisting of the RES units along with some parametric uncertainties and load perturbations is presented. PI control methods are understood very well but have limited ability in balancing among some specifications like overshoot, rise time, and damping oscillations. In Han et al. (2015), using µ synthesis, a robust control strategy is obtained to decline the frequency deviations. Bevrani et al. (2015) use H∞ and µ synthesis robust control techniques to reduce the effects of the wind power and solar power fluctuations, load changes, and the dynamical perturbations on the frequency of an islanded MG. A H∞ control structure against some parametric uncertainties and load disturbances is obtained in Kumar et al. (2017).

Also, a robust H∞ controller for the frequency regulation problem is proposed for an isolated MG consisting of DEG, PV, and BESS units (Lam et al. 2016). In Lam et al. (2016), the LMI method is adopted to design a multi-variable H∞ controller. The frequency regulation issue is formulated as a H∞ control problem against the wind power and solar radiation variations in Hua et al. (2017).

In Malek and Khodabakhshian (2017), a multi-objective LMI-based approach is used to regulate the islanded MG frequency deviations despite several uncertainties and disturbances such as the RES power and load demand variations. In Sedghi and Fakharian (2017), the droop frequency control of an islanded MG against the load perturbations and emergency conditions such as a DG unit disconnection is discussed.

Besides, the stabilization of a MG system frequency with many plugs in electrical vehicles (PHEVs) on the consumer side is investigated (Vachirasricirikul and Ngamroo 2012). In Vachirasricirikul and Ngamroo (2012), the controller parameters are optimized based on a specified-structure mixed H2/H∞ control. In Sedhom et al. (2019), a multi-stage H∞ controller based on harmony search algorithm is investigated for an islanded MG. The proposed method is based on applying the H∞ robust control as a secondary controller with the droop control method to improve its performance.

In some works, coordinated control strategies are discussed for the MG frequency control (Pahasa and Ngamroo 2018; Yunhao et al. 2018). In Pahasa and Ngamroo (2018), the authors propose a coordinated control of PHEVs, PVs, and ESSs for the MG frequency control using a centralized model predictive control (CMPC) considering the variation of PHEV numbers. In Yunhao et al. (2018), an islanded MG including PV, DEG, and BESS units is considered in which frequency can be affected by the renewable energy fluctuation and the load variations. A robust coordinated control for the PV, DEG, and BESS units is proposed. Furthermore, the sliding mode load frequency control (LFC) is designed to improve the dynamic characteristics of the coordinated strategy and restrain the randomness and volatility of the source and load. In Zhao et al. (2019), a novel primary control strategy based on the output regulation theory for the voltage and frequency regulations in a MG system with fast-response BESS, in the presence of some disturbance signals, is presented.

All the mentioned designed controllers are of integer order. Most physical systems are realized by fractional-order differential equations, and their integer description may cause specific differences between the mathematical model and the real system (Ahuja et al. 2014; Ahuja and Aggarwal 2014; Yeroglu and Tan 2011; Cao et al. 2005; Petras et al. 1998). For these types of systems, fractional-order controllers ensure better performance relative to corresponding integer-order controllers. Generally, it is shown that fractional-order controllers result in more flexibility in control design than integer-order controllers (Meng and Xue 2009; Liang and Wang 2012; Cao and Cao 2006; Zhang and Li 2011).

A few works have been done about applying fractional-order controllers to the power systems. In Zhang and Li (2011), to reduce frequency deviations, a FOPID controller is designed using optimization based on Kriging. According to the obtained results, in the nominal operational mode, the FOPID controller acts better than the PID controller in both performance and robustness.

In this work, we aim to reduce the frequency deviations in an islanded MG despite the load changes, the PV and WTG output variations, and some model uncertainties. A fractional-order controller is chosen because it has more tuning parameters and flexibility compared to the classic integer-order PID controller. Five design specifications including robust stability condition, minimizing the control effort, and the effect of disturbances (the load variations and the RESs output power fluctuations) are involved to design the robust FOPID controller. By comparison, we apply H∞ and classic PID controllers in our islanded MG. We will show that the robust FOPID controller leads to a faster and less oscillatory response.

The rest of the article is organized as follows: The model of the islanded MG is illustrated in Sect. 2. Designing the robust FOPID controller is discussed in Sect. 3. In the next section, another robust control strategy, a H∞ controller, is proposed. The time-domain simulation results are shown in Sect. 5, and finally, a conclusion is presented in Sect. 6.

2 MG Modeling

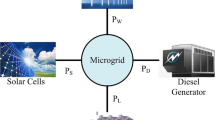
MGs have two operational modes, connected to main network and islanded mode. When a MG is connected to main network, the entire performance of the MG is dictated by main power system, while in the islanded mode, the MG works as an independent system and is responsible for regulating frequency and voltage itself. This article focuses on frequency regulation of MGs in the islanded mode. The islanded MG consists of DGs such as PV, WTG, DEG, BESS and a consumer considered as a variable load. The simplified construction of this MG is shown in Fig. 1.

Fig. 1
figure 1

Structure of the islanded MG (https://goo.gl/images/QB64y6)

Full size image

Output power of PV and WTG units depends on environmental conditions (solar radiation and wind speed) and is not controllable. Therefore, RESs are not considered as a permanent source to supply loads, resulting in an imbalance between produced power and demanded load. In other words, not only can these DGs cooperate in frequency regulation, but their fluctuating nature also can cause frequency deviation from its nominal value. The DEG unit is used to compensate electrical energy shortage in the islanded MG. Based on frequency change sensed, the speed governor in DEG provides the primary frequency control function. Indeed, in this control loop, the governor positions the main valve in order to bring enough fuel into the diesel engine to control the output mechanical power. By approaching the mechanical power to the demanded power, the frequency deviation can be reduced. But the primary frequency control is not enough to restore the MG frequency. Thus, a secondary frequency controller is employed for restoring the frequency deviation at zero. In this work, a robust FOPID controller is considered as the secondary control. In the case that the demanded load and the produced power change rapidly, DEG cannot compensate these changes immediately. To eliminate this drawback, the BESS unit is used because of its faster time response.

In the islanded MG, total power is supplied by PV, WTG, DEG, and BESS units. It should be noted that BESS can act either as a power generator or as a load when it is charging. Therefore, the total generated power \((P_{\text{t}} )\) can be written as:

$$P_{\text{t}} = P_{\text{DEG}} + P_{\text{WTG}} + P_{\text{PV}} \pm P_{\text{BESS}}$$
(1)

where \(P_{\text{DEG}} , P_{\text{WTG}} ,P_{\text{PV}}\) and \(P_{\text{BESS}}\) are produced power by DEG, WTG, PV, and BESS units, respectively. Imbalances between the load power \((P_{\text{L}} )\) and total generated power affect the frequency deviation \(\left( {\Delta f} \right)\) as follows:

$$\Delta P_{\text{t}} - \Delta P_{\text{L}} = 2H\frac{{{\text{d}}\Delta f\left( t \right)}}{{{\text{d}}t}} + D\Delta f\left( t \right)$$
(2)

in which the constant parameters H and D are inertia constant and load damping coefficient, respectively. The damping coefficient is expressed as a percent change in load for a 1% change in frequency.

By considering the simplified transfer functions for RESs, DEG, and BESS, a model for the islanded MG is illustrated in Fig. 2 where \(T_{\text{WTG}} , T_{\text{PV}}\) and \(T_{\text{BESS}}\) are time constants of WTG, PV, and BESS, respectively (Bevrani et al. 2012, 2015; Han et al. 2015; Marinescu and Serban 2009; Habibi et al. 2013). In this islanded MG, variations of the wind power \(\left( {\Delta P_{\text{wind}} } \right)\), the solar radiation power \(\left( {\Delta P_{\varphi } } \right)\), and the demanded load are considered as disturbance signals. In DEG system, R is the droop factor and implies the speed regulation due to governor action. The governor and turbine constants are shown by \(T_{\text{g}}\) and \(T_{\text{t}}\), respectively. The typical value for \(R, T_{\text{g}} , T_{\text{t}} , T_{\text{WTG}} , T_{\text{PV}} , T_{\text{BESS}}\) and nominal values for constants H and D are given in Table 1.

Fig. 2
figure 2

Simplified transfer function model of the islanded MG

Full size image
Table 1 Parameters of the MG system
Full size table

The aim of this paper is tuning FOPID controller to ensure robust stability and robust performance specifications against parametric uncertainties, PV and WTG power fluctuations, and load variation.

3 Robust FOPID Control Design

3.1 Uncertainty Modeling

There are two sources of uncertainty, namely parametric uncertainty and unmodeled dynamics uncertainty (Skogestad and Postlethwaite 2007). Any uncertain parameter is limited within an interval of \(\left[ {\alpha_{\hbox{min} } , \alpha_{\hbox{max} } } \right]\) and can be defined by the following set:

$$\alpha_{P} = \bar{\alpha }\left( {1 + r_{\alpha } \Delta } \right)$$
(3)

where \(\bar{\alpha }\) is the average of all possible values of the uncertain parameter. \(r_{\alpha } = \left( {\alpha_{\hbox{min} } - \alpha_{\hbox{max} } } \right)/\left( {\alpha_{\hbox{min} } + \alpha_{\hbox{max} } } \right)\) is relative uncertainty, and \(\Delta\) is any real scalar satisfying \(\left\| \Delta \right\| \le 1\).

There is also a third kind of perturbation which is actually a combination of parametric and unmodeled uncertainties, namely, lumped perturbation. In this type, one or many sources of parametric uncertainties and/or unmodeled uncertainties are combined into a lumped perturbation. Frequency domain is suitable for lumped uncertainty description (Skogestad and Postlethwaite 2007). Also, it is more usual to represent parametric uncertainties by complex perturbations. For example, we can simply replace the real perturbation, \(- \,1 \le \Delta \le 1\), by a complex perturbation \(\left| {\Delta \left( {j\omega } \right)} \right| \le 1\). This is, of course, conservative as it introduces possible plants that are not present in the original set. However, if there are multiple real perturbations, then conservatism may be reduced by lumping these perturbations into a single complex perturbation (at least for the SISO case). Moreover, there are different ways to describe complex perturbations such as additive perturbation, inverse additive perturbation, input/output multiplicative perturbation, and inverse input/output multiplicative perturbation.

In this paper, we assume a 50% variation for H and D parameters which, according to (2), directly affect the MG frequency. The perturbed islanded MG is presented using output multiplicative configurations depicted in Fig. 3. Thus, the set of possible perturbed plant models \((\varPi )\) is defined as:

$$\varPi : G_{\text{P}} \left( s \right) = G\left( s \right)\left( {1 + w_{0} \left( s \right)\Delta_{0} \left( s \right)} \right)$$
(4)

where \(G\left( s \right)\) is the nominal transfer function of the MG system, presented in Fig. 4.

$$G\left( s \right) = \frac{{R\left( {T_{\text{BESS}} s + 1} \right)}}{{\begin{array}{*{20}l} {\left\{ {R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right) \times \left[ {\left( {D + 2Hs} \right)\left( {T_{\text{BESS}} s + 1} \right) + 1} \right]} \right\}} \hfill \\ {\quad + \,\left( {T_{\text{BESS}} s + 1} \right)} \hfill \\ \end{array} }}$$
(5)
Fig. 3
figure 3

Closed-loop system of the islanded MG with the output multiplicative uncertainty

Full size image
Fig. 4
figure 4

\(G\left( s \right)\), the nominal transfer function model of the MG open-loop system

Full size image

In (4), \(\Delta_{0} \left( s \right)\) is any stable transfer function which at each frequency is less than or equal to one in magnitude (Skogestad and Postlethwaite 2007) and \(w_{0} \left( s \right)\) is a normalizing coefficient for the uncertainty block in Fig. 3. \(w_{0} \left( s \right)\) can be obtained so that inequality in (6) is satisfied.

$$\left| {w_{0} \left( {j\omega } \right)} \right| \ge l_{0} \left( \omega \right), \forall \omega$$
(6)

where

$$l_{0} \left( \omega \right) = \mathop {\hbox{max} }\limits_{{G_{\text{P}} \in \varPi }} \left| {\frac{{G_{\text{P}} \left( {j\omega } \right) - G\left( {j\omega } \right)}}{{G\left( {j\omega } \right)}}} \right|$$
(7)

\(\left| {G_{\text{p}} \left( {j\omega } \right) - G\left( {j\omega } \right)/G\left( {j\omega } \right)} \right|\) is plotted in Fig. 5, for a 50% changes in H and D. The upper bound in Fig. 5 is chosen as \(l_{0} \left( s \right)\). According to (6), we chose \(w_{0} \left( s \right)\) as follows:

$$w_{0} = 1.0662l_{0} \left( s \right) = \left| {\frac{{s^{4} + 25.06s^{3} + 182.8s^{2} + 323.4s + 18.75}}{{s^{4} + 2506s^{3} + 282.8s^{2} + 1928s + 4185}}} \right|$$
(8)
Fig. 5
figure 5

\(\left| {G_{\text{p}} \left( {j\omega } \right) - G\left( {j\omega } \right)/G\left( {j\omega } \right)} \right|\) for different values of \(H\) and \(D\)

Full size image

3.2 FOPID Control Design

As mentioned before, here DEG is used to compensate electrical power shortage. DEG output power is regulated using the FOPID controller. FOPID is a generalized form of PID controller, in which integral and derivative operators are of non-integer orders \(\lambda\) and \(\mu\), respectively (\(0 < \lambda ,\mu < 2\)) (Pan and Das 2015; Podlubny 1999a). Transfer function of the FOPID controller is defined as follows:

$$G_{\text{c}} \left( s \right) = k_{\text{p}} + k_{\text{d}} s^{\mu } + \frac{{k_{i} }}{{s^{\lambda } }}$$
(9)

where \(\lambda\), \(\mu\), \(k_{\text{p}}\), \(k_{\text{i}}\), and \(k_{\text{d}}\) are integral order, derivative order, proportional coefficient, integral coefficient, and derivative coefficient, respectively (Podlubny 1999b; Saidi et al. 2013, 2015a, b; Monje et al. 2004, 2006; Majid et al. 2009).

The FOPID controller should be able to reduce effects of uncertainties and disturbances on the MG frequency. In Fig. 6, the islanded MG with uncertainty block, disturbance signals, and controlled outputs \(\left( {z_{1} ,z_{2} } \right)\) is shown. The design specifications are determined as robust stability, minimization of the control effort, and effects of the disturbances on the MG frequency. These specifications are formulated as the following constraints:

$$\left| {w_{ 0} T_{{y_{\text{d}} y}} } \right| < 1$$
(10a)
$$\left| {w_{0} T_{{y_{\text{d}} z_{2} }} } \right| = \left| {W_{\text{u}} KS} \right| < 1$$
(10b)
$$\left| {T_{{w_{1} z_{1} }} } \right| < 1$$
(10c)
$$\left| {T_{{w_{2} z_{1} }} } \right| < 1$$
(10d)
$$\left| {T_{{w_{3} z_{1} }} } \right| < 1$$
(10e)

where

$$w = \left[ {\begin{array}{*{20}c} {w_{1} } & {w_{2} } & {w_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\Delta P_{\text{wind}} } & {\Delta P_{\varphi } } & {\Delta P_{\text{L}} } \\ \end{array} } \right]$$
(11)
$$y = \Delta f$$
(12)
Fig. 6
figure 6

Closed-loop structure of the islanded MG with the output multiplicative uncertainty, disturbance signals, and controlled outputs

Full size image

In (10a), \(T_{{y_{\text{d}} y}}\) is the transfer function of the closed-loop system in Fig. 6. This constraint ensures robust stability against the parametric uncertainties. \(T_{{y_{\text{d}} z_{2} }}\) is the transfer function from the reference input \(\left( {y_{\text{d}} } \right)\) to the controlled output \(z_{2}\). Thus, constraint (10b) leads to minimizing the control effort. To reduce the effects of the disturbances on the MG frequency, in (10c), (10d), and (10e), the norm of the transfer functions from the disturbance inputs \(w_{1} , w_{2}\), and \(w_{3}\) to the controlled output \(z_{1}\) are minimized, respectively. Based on the block diagram given in Fig. 6, we have:

$$T_{{y_{\text{d}} y}} \left( s \right) = \frac{{R\left( {T_{\text{BESS}} s + 1} \right)\left( {k_{\text{d}} s^{\lambda + \mu } + k_{\text{p}} s^{\lambda } + k_{\text{i}} } \right)}}{{\begin{array}{*{20}c} {s^{\lambda } \left\{ {R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right) \times \left[ {\left( {{\text{D}} + 2Hs} \right)\left( {T_{\text{BESS}} s + 1} \right) + 1} \right]} \right.} \\ {\left. { + \left( {T_{\text{BESS}} s + 1} \right)} \right\} + R\left( {T_{\text{BESS}} s + 1} \right)\left( {k_{\text{d}} s^{\lambda + \mu } + k_{\text{p}} s^{\lambda } + k_{\text{i}} } \right)} \\ \end{array} }}$$
(13a)
$$T_{{y_{\text{d}} z_{2} }} \left( s \right) = W_{\text{u}} \frac{{\begin{array}{*{20}c} {\left\{ {R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right) \times \left[ {\left( {{\text{D}} + 2Hs} \right)\left( {T_{\text{BESS}} s + 1} \right) + 1} \right]} \right.} \\ {\left. { + \left( {T_{\text{BESS}} s + 1} \right)} \right\}\left( {k_{\text{d}} s^{\lambda + \mu } + k_{\text{p}} s^{\lambda } + k_{\text{i}} } \right)} \\ \end{array} }}{{\begin{array}{*{20}c} {s^{\lambda } \{ R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right) \times \left[ {\left( {{\text{D}} + 2Hs} \right)\left( {T_{\text{BESS}} s + 1} \right) + 1} \right]} \\ { + \left( {T_{\text{BESS}} s + 1} \right)\} + R\left( {T_{\text{BESS}} s + 1} \right)\left( {k_{\text{d}} s^{\lambda + \mu } + k_{\text{p}} s^{\lambda } + k_{\text{i}} } \right)} \\ \end{array} }}$$
(13b)
$$T_{{w_{1} z_{1} }} \left( s \right) = - W_{\text{e}} s^{\lambda } \frac{{R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right)\left( {T_{\text{BESS}} s + 1} \right)}}{{\begin{array}{*{20}c} {\left( {T_{\text{WTG}} s + 1} \right)\left\{ {s^{\lambda } R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right)\left( {{\text{D}} + 2Hs} \right)} \right.} \\ {\left( {T_{\text{BESS}} s + 1} \right) + s^{\lambda } R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right) + s^{\lambda } } \\ {\left. {\left( {T_{\text{BESS}} s + 1} \right) + R\left( {T_{\text{BESS}} s + 1} \right)\left( {k_{\text{d}} s^{\lambda + \mu } + k_{\text{p}} s^{\lambda } + k_{i} } \right)} \right\}} \\ \end{array} }}$$
(13c)
$$T_{{w_{2} z_{1} }} \left( s \right) = - W_{\text{e}} s^{\lambda } \frac{{R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right)\left( {T_{\text{BESS}} s + 1} \right)}}{{\begin{array}{*{20}c} {\left( {T_{\text{PV}} s + 1} \right)\left\{ {s^{\lambda } R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right)\left( {{\text{D}} + 2Hs} \right)} \right.} \\ {\left( {T_{\text{BESS}} s + 1} \right) + s^{\lambda } R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right) + s^{\lambda } } \\ {\left. {\left( {T_{\text{BESS}} s + 1} \right) + R\left( {T_{\text{BESS}} s + 1} \right)\left( {k_{\text{d}} s^{\lambda + \mu } + k_{\text{p}} s^{\lambda } + k_{\text{i}} } \right)} \right\}} \\ \end{array} }}$$
(13d)
$$T_{{w_{3} z_{1} }} \left( s \right) = - W_{\text{e}} s^{\lambda } \frac{{R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right)\left( {T_{\text{BESS}} s + 1} \right)}}{{\begin{array}{ll} {\left\{ {s^{\lambda } R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right)\left( {{\text{D}} + 2Hs} \right)\left( {T_{\text{BESS}} s + 1} \right)} \right.} \\ \quad+\, { s^{\lambda } R\left( {T_{\text{g}} s + 1} \right)\left( {T_{\text{t}} s + 1} \right) + s^{\lambda } \left( {T_{\text{BESS}} s + 1} \right)} \\\quad+\, {\left. { R\left( {T_{\text{BESS}} s + 1} \right)\left( {k_{\text{d}} s^{\lambda + \mu } + k_{\text{p}} s^{\lambda } + k_{\text{i}} } \right)} \right\}} \\ \end{array} }}$$
(13e)

where \(W_{\text{e}} ,W_{\text{u}}\) are weighting functions for minimizing error and control signals in the desired frequency range.

To minimize the error signal, a frequency response with larger amplitude in low frequencies is assigned for \(W_{\text{e}}\) as follows:

$$W_{\text{e}} = 0.01\frac{{s^{3} + 5s^{2} + 10s + 60}}{{s^{3} + 100s^{2} + 15s + 3}}$$
(14)

Due to physical limitations, the fuel valve in DEG operated by the control signal cannot be regulated fast. Thus, minimizing the control effort in the higher frequency range is more critical. The weighting function \(W_{\text{u}}\) is chosen so that a larger amplitude in higher frequencies is obtained.

$$W_{\text{u}} = 0.25\frac{s + 1}{0.01s + 9}$$
(15)

The amplitudes of \(W_{\text{e}}\), \(W_{\text{u}}\) versus frequency are plotted in Fig. 7.

Fig. 7
figure 7

Magnitude of the weighting functions \(W_{\text{e}} ,W_{\text{u}}\)

Full size image

We use optimization toolbox in MATLAB to minimize specifications in (10). Finally, the FOPID controller parameters are designed as follows: (Table 2).

Table 2 FOPID controller parameters
Full size table

To verify that the constraints in (10) are satisfied by the designed FOPID controller, frequency response of \(w_{0} T_{{y_{\text{d}} y}} , T_{{y_{\text{d}} z_{2} }} , T_{{w_{1} z_{1} }} , T_{{w_{2} z_{1} }} , T_{{w_{3} z_{1} }}\) transfer functions is plotted in the frequency range of \(0.01\)–\(100\, \left( {{\text{rad}}/{\text{s}}} \right)\) in Figs. 8, 9, 10, 11, and 12, respectively.

Fig. 8
figure 8

Frequency response of \(w_{0} T_{{y_{\text{d}} y}}\)

Full size image
Fig. 9
figure 9

Frequency response of \(T_{{y_{\text{d}} z_{2} }}\)

Full size image
Fig. 10
figure 10

Frequency response of \(T_{{w_{1} z_{1} }}\)

Full size image
Fig. 11
figure 11

Frequency response of \(T_{{w_{2} z_{1} }}\)

Full size image
Fig. 12
figure 12

Frequency response of \(T_{{w_{3} z_{1} }}\)

Full size image

According to Figs. 8, 9, 10, 11, and 12, constraints (10a)–(10e) are satisfied for the designed FOPID controller, in the given frequency range.

4 H∞ Control Design

In H∞ control strategy, controller is synthesized so that the following inequality is satisfied:

$$\left\| {\begin{array}{*{20}c} {W_{1} S} \\ {W_{2} U} \\ {W_{3} T} \\ \end{array}_{\infty } } \right\| < 1$$
(16)

where S denotes the transfer function from the reference input \(y_{\text{d}}\) to the output \(e\) in Fig. 6 and is introduced as the sensitivity function as follows:

$$S = T_{{y_{\text{d}} e}} = \frac{1}{1 + C\left( s \right)G\left( s \right)}$$
(17)

where \(G\left( s \right)\) is the nominal transfer function of the uncontrolled MG system shown in Fig. 4 and \(C\left( s \right)\) is the controller transfer function. Also, in (16), \(T_{{y_{\text{d}} u}}\) is the transfer function from the input \(y_{\text{d}}\) to the control signal \(u\) used to minimize the following control effort:

$$U = T_{{y_{\text{d}} u}} = \frac{C\left( s \right)}{{1 + C\left( s \right){\text{G}}\left( {\text{s}} \right)}} = C\left( s \right)S\left( s \right)$$
(18)

Finally, we minimize the complement sensitivity function \(T\) to achieve robust stability. \(T\) is the closed-loop transfer function from the input \(y_{\text{d}}\) to the output \(y\), obtained as follows:

$$T = T_{{y_{\text{d}} y}} = \frac{C\left( s \right)G\left( s \right)}{1 + C\left( s \right)G\left( s \right)}$$
(19)

In (16), \(W_{1} , W_{2} , W_{3}\) are weighting functions that involve information about tracking error, the control signal, and uncertainties, respectively. Applying \(W_{1}\) results in small tracking error in lower frequencies and is given as follows:

$$W_{1} = 0.01\frac{1}{0.08s + 0.01}\frac{{s^{3} + 5s^{2} + 10s + 60}}{{s^{3} + 100s^{2} + 15s + 3}}$$
(20)

Also, the weighting function \(W_{2}\) is chosen in the same way as \(W_{u}\) in (15). Also, \(W_{3}\) is the multiplicative coefficient that sets similar to \(w_{0}\) in (8).

To get the H∞ controller, we use hinfsyn in Robust Control Toolbox in MATLAB. The controller is gained by solving the following optimization problem:

$$\mathop { \hbox{min} }\limits_{C\left( s \right)} \left\| {\begin{array}{*{20}c} {W_{1} S} \\ {W_{2} C\left( s \right)S} \\ {W_{3} T} \\ \end{array} } \right\|_{\infty }$$
(21)

The H∞ controller is obtained as follows:

$$C\left( s \right) = \frac{\begin{aligned} & 0.3976s^{23} + 441.8s^{22} + 8.23 \times 10^{4} s^{21} + 6.385 \times 10^{6} s^{20} \\ & \quad + \,2.891 \times 10^{8} s^{19} + 8.852 \times 10^{9} s^{18} + 1.985 \times 10^{11} s^{17} \\ & \quad + \,3.418 \times 10^{12} s^{16} + 4.653 \times 10^{13} s^{15} + 5.101 \times 10^{14} s^{14} \\ & \quad + \,4.55 \times 10^{15} s^{13} + 3.317 \times 10^{16} s^{12} + 1.976 \times 10^{17} s^{11} \\ & \quad + \,9.568 \times 10^{17} s^{10} + 3.724 \times 10^{18} s^{9} + 1.146 \times 10^{19} s^{8} \\ & \quad + \,2.715 \times 10^{19} s^{7} + 4.774 \times 10^{19} s^{6} + 5.907 \times 10^{19} s^{5} \\ & \quad + \,4.769 \times 10^{19} s^{4} + 2.282 \times 10^{19} s^{3} + 5.912 \times 10^{18} s^{2} \\ & \quad + \,5.268 \times 10^{17} s + 1.474 \times 10^{16} \\ \end{aligned} }{\begin{aligned} & s^{24} + 270.6s^{23} + 2.986 \times 10^{4} s^{22} + 1.86 \times 10^{6} s^{21} \\ & \quad + \,7.629 \times 10^{7} s^{20} + 2.246 \times 10^{9} s^{19} + 5.014 \times 10^{10} s^{18} \\ & \quad + \,8.78 \times 10^{11} s^{17} + 1.233 \times 10^{13} s^{16} + 1.409 \times 10^{14} s^{15} \\ & \quad + \,1.318 \times 10^{15} s^{14} + 1.011 \times 10^{16} s^{13} + 6.344 \times 10^{16} s^{12} \\ & \quad + \,3.229 \times 10^{17} s^{11} + 1.314 \times 10^{18} s^{10} + 4.186 \times 10^{18} s^{9} \\ & \quad + \,1.009 \times 10^{19} s^{8} + 1.747 \times 10^{19} s^{7} + 2.002 \times 10^{19} s^{6} \\ & \quad + \,1.317 \times 10^{19} s^{5} + 3.931 \times 10^{18} s^{4} + 7.241 \times 10^{17} s^{3} \\ & \quad + \,8.081 \times 10^{16} s^{2} + 4.602 \times 10^{15} s^{1} + 1.002 \times 10^{14} \\ \end{aligned} }$$
(22)

5 Time-Domain Simulation Results

In this section, the MG performance is investigated using the designed FOPID controller in the presence of the disturbance signals \(\left( {\Delta P_{\text{wind}} ,\Delta P_{\varphi } ,\Delta P_{\text{L}} } \right)\) and the parametric uncertainties in H and D. The disturbances are considered as random signals whose magnitude changes every 20 s as depicted in Figs. 13a, 14a, and 15a. Also, a 50% uncertainty for H and D is regarded. In other words, these parameters vary in the following ranges:

$$\begin{aligned} & 0.006 < {\text{D}} < 0.018 \\ & 0.1 < 2H < 0.3 \\ \end{aligned}$$
(23)
Fig. 13
figure 13

a Pattern of the wind power variation. b The MG frequency deviation against the wind power variation using the designed FOPID, H∞, and PID controllers

Full size image
Fig. 14
figure 14

a Pattern of the solar power variation. b The MG frequency deviation against the solar power variation using the designed FOPID, H∞, and PID controllers

Full size image
Fig. 15
figure 15

a Pattern of the load variation. b The MG frequency deviation against the load variations using the designed FOPID, H∞, and PID controllers

Full size image

Moreover, the results obtained by applying the classic PID and H∞ controllers to the islanded MG are compared with those obtained by the designed FOPID controller. The PID controller is synthesized based on the constraints in (10). We use the MATLAB optimization toolbox to design the PID controller parameters based on the constraints in (10). The obtained PID parameters are given in Table 3.

Table 3 PID controller parameters
Full size table

For comparison purposes, first, the impact of each disturbance signal on the islanded MG frequency is considered one by one. In another test, the system response is investigated in the presence of all three disturbance signals and parametric uncertainties simultaneously. In each case, all proposed controllers are applied and compared:

  1. (a)

    Variation of the wind power \(\left( {\Delta P_{\text{wind}} } \right)\): Fig. 13a shows the pattern of the wind power. The islanded MG frequency deviation is plotted in Fig. 13b.

  2. (b)

    Variation of the solar radiation power \(\left( {\Delta P_{\varphi } } \right)\): Due to Fig. 14a, an ascendant step-change is considered for the solar power fluctuation. The changes occur every 20 s. In Fig. 14b, the MG frequency is represented.

  3. (c)

    Load fluctuation \(\left( {\Delta P_{\text{L}} } \right)\): Like \(\Delta P_{\text{wind}}\) and \(\Delta P_{\varphi }\), a step-change is applied in the demanded load every 20 s. Figure 15a, b represents the load variations and the MG system output, respectively.

  4. (d)

    Applying \(\Delta P_{\text{wind}}\), \(\Delta P_{\varphi }\), \(\Delta P_{\text{L}}\): All disturbance signals are plotted in Fig. 16a. The MG frequency deviation in the presence of all disturbances is shown in Fig. 16b.

    Fig. 16
    figure 16

    a Pattern of all disturbance signals. b Frequency deviation of the MG system against all disturbance signals using the designed FOPID, H∞, and PID controllers

    Full size image
  5. (e)

    Applying \(\Delta P_{\text{wind}}\), \(\Delta P_{\varphi }\), \(\Delta P_{\text{L}}\), and uncertainty: In this case, the MG frequency against all disturbance signals and a 50% increment in Hand D parameters are investigated. The MG frequency deviation is presented in Fig. 17.

    Fig. 17
    figure 17

    Frequency deviation of the MG system against all disturbance signals and uncertainty using the designed FOPID, H∞, and PID controllers

    Full size image

Figure 13b shows the MG frequency deviation in the presence of the wind power variation. Time response specifications in \(t = 60\,{\text{s}}\) are depicted in Table 4. In comparison with the designed FOPID controller, the designed PID controller results in a frequency deviation with a little smaller overshoot and settling time, but the FOPID controller still brings a less oscillatory response. Also, the frequency deviation converges to zero in a shorter time using the FOPID controller. For example, for a step-change in \(t = 60\,{\text{s}}\), the frequency deviation decreases to zero after 2 s using the FOPID controller, while it takes 4 and 15 s using the PID and \(H_{\infty }\) controllers, respectively. The designed H∞ controller gives the largest overshoot, steady-state error, and settling time among the other designed controllers.

Table 4 Time response specifications in the presence of the wind power variation
Full size table

Figure 14b depicts the MG performance in the presence of the solar power variation. According to Fig. 14b and Table 5, in \(t = 60\,{\text{s}}\), the PID controller results in a frequency deviation with a little smaller overshoot than the FOPID controller. However, the frequency deviation is reduced to zero with the least oscillations and during the shortest time using the FOPID controller compared to the other designed controllers. Both the PID and FOPID controllers bring zero steady-state error and zero settling time.

Table 5 Time response specifications in the presence of the solar power variation
Full size table

Consider the MG system with the load variations. As shown in Fig. 15b and Table 6, the MG system with the designed FOPID controller has a smoother response and a smaller settling time compared to the designed PID and \(H_{\infty }\) controllers. For a load change in \(t = 40\,{\text{s}}\), the frequency deviation reduces to zero after 2 s using the FOPID controller, while it takes 5 and 8 s using the PID and \(H_{\infty }\) controllers, respectively. The largest overshoot, steady-state error, and settling time are obtained using the H∞ controller.

Table 6 Time response specifications in the presence of the load variation
Full size table

All three disturbance signals are shown in Fig. 16a. There is a step-change every 20 s. The MG performance in the presence of all three disturbance signals is depicted in Fig. 16b. For a step-change in \(t = 60\,{\text{s}}\), time response specifications are depicted in Table 7. The designed FOPID controller gives the smallest overshoot and settling time among the other designed controllers. In addition, using the FOPID controller, the MG frequency deviation decreases to zero faster with fewer oscillations. For instance, in \(t = 60\,{\text{s}}\), the frequency deviation converges to zero after 2 s using the FOPID controller, whereas it takes 4 and 10 s using the designed PID and \(H_{\infty }\) controllers, respectively. Unlike the \(H_{\infty }\) controller, the PID and FOPID controllers result in zero frequency deviation before the next step-change, in t = 80 s, occurs.

Table 7 Time response specifications in the presence of all three disturbance signals
Full size table

The frequency deviation of the MG system with all three disturbance signals and a 50% increment in H and D parameters is presented in Fig. 17. Time response specifications in t = 60 s are shown in Table 8. The smallest overshoot and settling time are obtained using the FOPID controller. It also has a faster and smoother response than the designed PID and \(H_{\infty }\) controllers. Only PID and FOPID controllers give zero frequency deviation before the next step-change, in \(t = 80\,{\text{s}}\), occurs.

Table 8 Time response specifications in the presence of all three disturbance signals and a 50% increment in H and D parameters
Full size table

For more investigation, the bode diagram of the nominal MG system with the FOPID, PID, and \(H_{\infty }\) controllers is shown in Fig. 18. For each controller, the gain margins (GM) and phase margin (PM) are obtained in Table 9. The FOPID controller results in a larger GM and PM which provides the MG system with more robustness. The negative value of GM for the MG system with H∞ controller still gives stability because the open-loop transfer function is non-minimum phase.

Fig. 18
figure 18

Bode diagram of the nominal MG system using the designed FOPID, PID, and \(H_{\infty }\) controllers

Full size image
Table 9 Gain margin and phase margin of the MG system using the FOPID, PID, and \(H_{\infty }\) controllers
Full size table

As a comparison, the performance of the designed FOPID controller in the MG system is compared to the \(H_{\infty }\) and PI controllers applied in Bevrani et al. (2015) and Sedhom et al. (2019). The \(H_{\infty }\) controller for the islanded MG system is the same as the designed controller in (22), and the PI controller parameters are tuned based on the constraints in (10). The obtained PI parameters are given in Table 10. Figure 19 shows the frequency deviation of the MG system with the designed FOPID, PI, and \(H_{\infty }\) controllers in the presence of the disturbance signals and a 50% increment in H and D parameters. As a result, the FOPID controller gives a smoother response and a smaller settling time than the PI and \(H_{\infty }\) controllers.

Table 10 PI controller parameters
Full size table
Fig. 19
figure 19

Frequency deviation of the MG system against all disturbance signals and uncertainty using the designed FOPID, H∞, and PI controllers

Full size image

6 Conclusion

In this paper, FOPID controller is tuned based on the robust stability and robust performance specifications to reduce the effects of the PV and WTG output power fluctuations, load variations, and the parametric uncertainties on the islanded MG frequency. The FOPID controller has more tuning parameters than the PI and PID controllers; thus, a more complicated design method is needed. However, it is shown the FOPID controller results in a better performance for the MG system than the other integer-order controllers.

In the MG system with the wind power variation as the disturbance signal, the designed FOPID controller leads to a frequency deviation with a little larger overshoot and settling time compared to the designed PID controller, but gives a smoother response and a shorter time for which the frequency deviation converges to zero. In the presence of the variation of solar radiation power, both the FOPID and PID controllers nearly result in a small frequency deviation. Although a little smaller overshoot is obtained using the PID controller, the FOPID controller causes less oscillatory response and makes it possible to reduce the frequency deviation to zero in a shorter time. In the MG system with the load variation, a smaller settling time, a smoother response, and a shorter time to achieve zero frequency deviation are attained using the FOPID controller. In the presence of all disturbance signals and a 50% increment in H and D parameters, the FOPID controller results in a smaller overshoot, a shorter settling time, a less oscillatory response, and a shorter time to decrease the frequency deviation to zero in comparison with the PI, PID, and \(H_{\infty }\) controllers. In all the experiments, the FOPID controller reduces the frequency deviation to zero during half the time that the PID controller does. Also the designed H∞ controller gives the largest overshoot and settling time among the other designed controllers, and it does not completely eliminate the frequency deviation.

As another consequence, the FOPID controller gives a larger value of GM and PM compared to the designed PID and H∞ controllers. In other words, this fractional-order controller provides more robustness against the parametric uncertainties and the less oscillatory response against the disturbance signals. As a further study in the future, the application of the FOPID controller in the islanded MG system with challenges such as time delays will be investigated.