Hybrid Coarse and Fine Controller Tuning Strategy for Magnetic Levitation System

Abstract

The magnetic levitation system requires a finely tuned controller to suspend a ball in the air. Any imbalance in the force balance condition might result in high fluctuations causing the ball to fall out of levitation. A hybrid tuning strategy based on successful levitation and minimization of vibrations has been designed and tested in real time. The proportional–integral–derivative controller has been tuned in two stages. The parameters of the controller have been calculated by the traditional pole placement technique for coarse tuning and evaluation of bounds. Nature-based non-traditional optimization techniques have been used to minimize the integral of the absolute error within this threshold limit for finer tuning. This novel strategy has been employed to find the best combination of the controller parameters such that levitation is ensured by coarse tuning and error is minimized by fine tuning. Real-time robustness analysis has also been done by means of rejection of external disturbance induced manually in the levitated stage.

1 Introduction

Levitation is the phenomenon of suspension of an object in air without any physical support, done solely by balancing forces. It occurs when the gravitational force exerted on the object is counterbalanced by an equal and opposite magnetic attractive force caused by the current in the electromagnet. The suspended object is free from physical contact with any other object, so frictional losses due to contacting surfaces are negligible and the efficiency is fairly high. The phenomenon is being successfully applied in numerous fields like transportation through high-speed maglev trains (Lu and Dang 2019), launching of vehicles in the outer space, turbines, magnetic bearings and in the biomedical world.

The magnetic levitation system, developed by Feedback Instruments Limited, UK, is a very helpful academic test bed to understand and analyse the phenomenon, controller tuning, configuration and design. The system is unstable in open-loop configuration but can be made to obtain a desirable response by a suitably tuned controller in feedback configuration. The current entering the electromagnetic coil has to be continuously measured and manipulated by a controller as it is directly proportional to the attractive force required to keep the object in the levitated state. The challenge is to find the best combination of the values of the controller parameters such that the object does not fall down or get attracted to the electromagnet but remains suspended for the stipulated duration with minimum oscillations which may be caused due to quantization and computational truncation errors.

1.1 Literature Survey

The literature survey was done under different subheads starting with the historical development of the PID controllers, maglev system, pole placement and optimization techniques. In 1942, Ziegler–Nichols formulated a fast and simple rule-based chart to tune a controller in order to eliminate present, past and future errors (Ziegler and Nichols 1942). Astrom and Hagglund compiled a comprehensive book on the PID Controllers in 1995 (Astrom and Hagglund 1995). Bennett presented the important role played by PID controllers in the industrial growth of USA (Bennett 2000). In 2000, Li et al. discussed the problems faced in using PID controllers along with their remedies in their research article in 2006 (Li et al. 2005). Atherton and Majhi analysed the derivative kick problem and proposed a modified PI–PD controller in (1999). Tan et al. (2006) proposed a criterion based on the system robustness and disturbance rejection to make comparative evaluation of the performance of different tuning algorithms. Wu et al. (2014) presented a compilation of different tuning algorithms and their suitability for different systems.

Traditional tuning strategies were investigated for coarse tuning. Pole placement technique has been found to be suitable as it takes the system dynamics into account (Ogata 1997). In 1995, Valasek and Olgac (1995) proposed an efficient pole placement technique based on eigenvalues of the desired system for feedback stabilization of the linear systems. Hwang and Fang (1994) developed an algorithm to derive the controller parameters based on the dominant pole placement to minimize the integral of the absolute errors. In 2008, Wang et al. (2008) proposed two simple methods based on root locus and Nyquist plot to ensure guaranteed dominance of the two poles of a PID controller. Sujitjorn applied pole placement with state PID feedback on various applications including magnetic ball suspension (Sujitjorn and Wiboonjaroen 2011). Gao et al. (2012) applied pole placement to evaluate the parameters of PID controller to achieve matched dynamics and stability. Nicolau (2013) designed a PID controller by combining pole placement and symmetrical optimum criterion in 2013.

Optimization methods and their applications in the engineering field were elaborated in a 2014 editorial article by Tsai et al. (Rao 2009; Tsai et al. 2012). In order to minimize vibrations caused due to error, the integral of the absolute error has been chosen as the objective function to be minimized. Lopez et al. developed quality performance indices in 1976 (Lopez et al. 1967). Duarte-Mermoud and Prieto (2004) established in 2004 that the quality of response of a dynamical system can be judged by these indices.

For fine tuning, non-traditional nature inspired stochastic techniques have been chosen as they have the ability to make parallel search for any random combination of the controller parameters to attain minimization of the error. Kristinsson and Dumont (1992) applied genetic algorithm in 1992 for identification of a system in both continuous and discrete time. Hassanzadeh and Mobayen (2008) applied genetic algorithm to design an optimum controller for maglev system with integral of the absolute error and other parameters as objective function and a random range of lower and upper bounds for controller parameters. Mirjalili and Mirjalili (2014) proposed a metaheuristic optimization algorithm in 2014.

Mathematical modelling of the maglev system is necessary to understand its working. Wong built up an experimental laboratory educational project to demonstrate magnetic levitation (Wong 1986; Magnetic Levitation: Control Experiments 2011). Hajjaji and Ouladsine (2001) improvised on this set-up and devised a nonlinear model and a control law.

Ghosh and Krishnan (2014) proposed a feedforward control configuration to achieve a better response. Pati and Negi (2019) applied internal model control and particle swarm optimization to tune a controller for the magnetic levitation system. Starbino and Sathiyavathi (2019) used sliding mode controller for magnetic levitation system in a real-time environment. Swain and Sain (2017) applied fractional order PID in real-time implementation of the magnetic levitation system with the characteristic equation as the objective function and bounds based on initial guesses. Sain and Swain (2016) tuned a tilted proportional–integral–derivative controller using genetic algorithm and random experimental bounds. Maji et al. applied PID and fractional order PID tuned by particle swarm optimization and other algorithms with integral square error minimization and random boundary values (Maji and Roy 2015; Roy et al. 2015). Oliveira et al. (2016) applied grey wolf algorithm to tune a PID controller for different systems in control applications with integral of the absolute error and integral time weighted absolute error as the objective function and random experimental bounds. Yadav and Verma (2016) applied this algorithm to the maglev system to minimize integral time weighted absolute error and integral time squared error with random guess values as boundary limits. Naumovic and Veselic (2008) discussed hardware details of the maglev system and also tried remote monitoring of the experimental set-up.

1.2 Problem Identification

The purpose of the above survey was to investigate the existing literature and the following observations have been made:

• There has been a lack of proper mathematical modelling, block diagrams and hardware descriptions of the maglev system.

• Upper and lower bounds have been taken randomly without incorporating dynamics specific to the model.

• In some cases, results have been tested in simulated model but have not verified in the actual real-time set-up.

1.3 Contribution

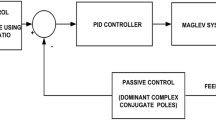
This paper aims at designing a novel hybrid tuning strategy which combines the traditional and non-traditional techniques to tackle two major problems, that is, successful levitation and the minimization of the error. In stage I, which is also equivalent to coarse tuning, the parameters have been explored for successful levitation range using the traditional pole placement (PP) technique. The best case from this technique has been chosen as a good solution and the controller parameters thus obtained can be considered in situations where approximate coarse tuning is required.

In stage II, for fine tuning, the results obtained in the first stage are utilized as threshold boundary limits and further exploited to find the best combination of the controller parameters. It has been done by using non-traditional optimization techniques like genetic algorithm (GA), particle swarm optimization (PSO) and grey wolf optimization (GWO) such that the integral of the absolute error (IAE) is minimized as shown in Fig. 1.

Fig. 1

Hybrid tuning strategy

The rest of the paper is organized as follows: Sect. 2 deals with the basics of the proportional–integral–derivative (PID) controller, tuning and the pole placement technique. Various non-traditional optimization techniques have been discussed in Sect. 3. Section 4 deals with the working and mathematical modelling of the magnetic levitation system. The new tuning strategy and the responses have been discussed in Sect. 5. Results, disturbance rejection and actual hardware implementations, have been analysed in Sect. 6, and the conclusions have been discussed in Sect. 7.

2 PID Controller

The modern day proportional–integral–derivative (PID) controllers are ubiquitous in the optimal automatic control applications (Ziegler and Nichols 1942; Astrom and Hagglund 1995; Bennett 2000). The proportional term reduces offset errors up to a certain limit but high values of gain can increase oscillations. The integral action can eliminate offset errors and increase the speed of the response, but high values can cause instability, oscillations or windup errors (Li et al. 2005). The derivative action acts on the transients and minimizes overshoots but makes the system susceptible to noise (Atherton and Majhi 1999).

The three components can be expressed as

$$\text{Proportional term} = K_{\text{P}}*e(t)$$

(1)

$${\text{Integral}}\;{\text{term}} = K_{\text{I}} \mathop \int \limits_{0}^{t} e\left( t \right)$$

(2)

$${\text{Derivative}}\;{\text{term}} = K_{\text{D}} \frac{{{\text{d}}e\left( t \right)}}{{{\text{d}}t}}.$$

(3)

The unstable maglev system can be stabilized by using a properly tuned controller in the feedback configuration.

2.1 Controller Tuning

Judicious choice of these three error terms is called tuning, and it helps in tracking a trajectory with minimum deviations. The transfer function of a mutually independent parallel form of a PID controller can be written as

$${\text{G}}_{\text{c}} \left( s \right) = K_{\text{P}} + \, K_{\text{I}} /s + sK_{\text{D}} = \frac{{sK_{\text{P}} + K_{\text{I}} + K_{\text{D}} s^{2} }}{s}.$$

(4)

It can be concluded from the transfer function that the job of a PID controller is to insert two zeroes and a pole at the origin and the tuning involves adjusting the location of their placement such that the performance of the overall set-up is altered. Conventional tuning rules are formula based and work well in most stable industrial process control set-ups where coarse tuning is sufficient. They do not give optimal results in sensitive and unstable systems as they are inherently oscillatory in nature (Tan et al. 2006; Wu et al. 2014).

2.2 Pole Placement (PP) Technique

This traditional design approach allows the poles to be placed at any arbitrary predetermined location by a control law, provided the system is completely controllable (Ogata 1997; Valasek and Olgac 1995). The farthest distances at which the poles can be placed are limited by the control constraints. The values of the controller parameters required to place the pole at a suitable location can be found by using time domain specifications (Hwang and Fang 1994; Wang et al. 2008). The actual closed-loop response of the controller and the plant in the cascade is compared to the desired response and the coefficients of the similar powers on both the sides are equated (Sujitjorn and Wiboonjaroen 2011; Gao et al. 2012). This relation has been used to calculate the parameters of the PID controller (K_P, K_I, K_D) for various locations of pole assignments for a successful levitation range (Nicolau 2013).

The purpose of selection of pole placement technique was to incorporate the system dynamics in the closed-loop transfer function in determining the values of the parameters of the controller. Once levitation is ensured by this technique, the best combination of these three parameters required for minimizing the error is searched using non-traditional optimization techniques.

3 Optimization

Optimization process aims at finding the extremum value of a function from amongst a set of multiple options available. Traditional gradient-based methods like Newton’s method, calculus of variations and dynamic programming, etc., have been used to obtain maxima or minima for continuous differential functions. They are deterministic and direct search methods with simple calculations.

If the system is discontinuous, unstable or complex combinatorial in nature that seeks to optimize multiple and conflicting objectives, then these methods cannot be applied satisfactorily. Also they are more likely to get trapped at saddle points and give suboptimal results. Due to these inherent drawbacks and limitations, non-traditional stochastic optimization search techniques were developed, some of which are inspired by naturally occurring phenomena like genetic evolution of man, swarm behaviour and the food searching abilities of many species.

The basic steps required in the formulation of an optimization problem are as follows (Rao 2009; Tsai et al. 2012):

• a. Formulation of an objective function depending on the system dynamics.

• b. Choosing a set of variables that can cause an impact on the objective function.

• c. Incorporating a set of constrains or limitations that cannot be trespassed.

• d. Applying a suitable optimization technique which searches the extremum value of the objective function without violating the constraints.

3.1 Objective Function

In this work, the objective function is the minimization of the absolute error or any deviation between the desired response and the actual response. Since the model under consideration is unstable, it is desirable to eliminate all the overshoots and undershoots and quarter decay ratio for the whole chosen duration of levitation. Adhering to our objective in the design requirement, the integral of the absolute error (IAE) has been chosen as the function that has to be minimized. The formula is given by

$$IAE = \int\limits_{0}^{\infty } {\left| {e(t)} \right|\;{\text{d}}t} .$$

(5)

It integrates the total error and gives fewer oscillations without penalizing large errors or errors that occur after some time lapse. Other performance indices penalize either the magnitude or the instance of occurrence of the error, and hence, they have not been chosen in this case (Lopez et al. 1967; Duarte-Mermoud and Prieto 2004).

It is pictorially represented by the shaded area under the overshoots and undershoots as shown in Fig. 2.

Fig. 2

Absolute error shown by the shaded portion

3.2 Variables

In the present system, the variables that can cause modification in the current and subsequently in the objective function are the controller parameters, i.e. K_P, K_I and K_D.

3.3 Constraints

The constraints imposed on the system are related to the system dynamics which determine the upper and lower bounds, linearization constraints, the voltage level, the current in the electromagnetic coil, the distance at which the ball levitates and the operating range of the sensors. The constraints have been incorporated in the objective function by numerical modelling and also by actual experimentation in the present work.

3.4 Nature Inspired Non-Traditional Optimization Techniques

Nature inspired population-based techniques introduce some amount of randomness in order to explore a wide range of possible solutions and choose the best value from amongst them in a number of search stages/iterations. They utilize guided search or heuristic information to speed up the convergence rate. The candidate solutions or search agents combine individual and collective performance to locate a better solution. As these are stochastic methods, the result of two iterations might be different, so a number of simulations are required to reach a decisive conclusion.

Magnetic levitation is a highly sensitive application so even minor changes in the combination of the controller parameters might result in high oscillations and large absolute errors. Therefore, it is desirable that optimum combination is found by parallel search techniques employed by these algorithms after successful levitation range is determined by pole placement technique. Since there is no single technique which works well for all the problems, three different techniques have been applied to find the parameters.

3.4.1 Genetic Algorithm (GA)

This evolutionary optimization technique inspired by the evolution of species was a pioneering work in non-traditional optimization field by John Holland in 1960 (Kristinsson and Dumont 1992). In this algorithm, the candidate solutions combine randomly by selection, crossover and mutation processes to give a new candidate solution and its fitness is evaluated. Better candidates subsequently lead to optimum solutions mimicking Darwin’s theory of survival of the fittest. The central theme of this algorithm is robustness or survival in a new environment where parameters change or are subjected to external variations. Numerically, the candidate solution is a binary coded string in a set of arrays, which after initialization, combines with another fitter string to produce a new candidate solution in a number of iterative stages (Hassanzadeh and Mobayen 2008). This algorithm might converge towards local optimum values and has a slower rate of convergence as compared to other modern algorithms.

3.4.2 Particle Swarm Optimization (PSO)

This technique, based on food searching ability of a flock of birds, was developed by Eberhart and Kennedy in 1995. It has some similarities with genetic algorithm in the sense that a population of candidate solutions is required for each iterative stage. However, the means of locating the optimal solution is different as the individual properties of each candidate/bird and of the collective group/flock are utilized as the heuristic information. The flock members do extensive search to locate a food source, and once it is located, other members are communicated about the direction of the location so that they all can reach the source. Numerically, the exploration and exploitation of optimal solution is done in two steps. The direction of each candidate is evaluated by determining its position and velocity and the information is stored as personal best value for that individual. The direction of the best flock member is stored as the global best value. Artificial intelligence is used to determine and communicate the modifications required to be done by other candidate solutions based on these two best values. This method of search prevents premature and local convergence with lesser number of parameters.

3.4.3 Grey Wolf Optimization (GWO)

This recent algorithm developed by Mirjalili and Mirjalili (2014) is inspired by the hunting capabilities of a pack of grey wolves found in colder regions of the arctic. This species is highly organized in its functioning and has a social hierarchy of specialized wolves to carry out different activities of the pack. The peculiar hunting operations are carried out in stages which involve as follows:

• Searching—extensive search in the snow covered areas by means of the scent of the prey.

• Encircling—after the prey is located, other wolves are directed towards the destination to encircle the prey and closely observe it from concealed hideouts.

• Attacking—after careful estimation of the size and nature of the prey, it is chased down and attacked.

Each pack has a social hierarchy with the most powerful and strong alpha male or female at the apex. They are responsible for making the decisions and are the primary predators for the pack. The second level, beta, consists of the managers and advisors whose primary task is to give suggestions to the alpha and manage the pack if the alpha dies. The third category is the delta which consists of the welfare managers and old alpha and beta wolves. The omega category is the least significant category, commanded by the rest three and is given the leftover portion of the food.

This well-organized strategy is simulated into a numerical algorithm to achieve faster convergence towards the global optimum value after extensive explorative search. It is different from other techniques in the sense that it utilizes leadership advantage of the top three best solutions to decide the vector direction of the movement of the other candidates. The main advantage of this technique is faster convergence due to the use of a leadership heuristic vector found by using the best three solutions. It has fewer decision variables to be adjusted and lesser storage requirements.

4 Magnetic Levitation System

4.1 Working of the Model

The test bed for this case study is a working model of the magnetic levitation system designed by the Feedback Instruments, UK. It consists of a mechanical–electrical hardware unit and a software part. The structural framework, 33-210, consists of an electromagnet protruding downwards from the top portion, a pair of infrared (IR) transmitter–receiver supported by the parallel frame at the opposite ends in the middle portion and the bottom part consists of signal conditioning elements. The steel ball is supposed to be levitated at an equilibrium position obtained by the linearization of the transfer function (Wong 1986). The effect of the gravitational force due to the weight of the ball has to be nullified by varying the attractive force depending on the current in the electromagnet.

The voltage output of the controller is fed to a resistance-inductance (RL) component which converts it into a current to be supplied to the electromagnet. This current creates an electromagnetic force which controls the position of the ball. The force has to be reduced if the ball moves closer to the magnet so that it does not get attracted to the electromagnet and has to be increased if the ball moves far away so that it remains levitated with as little vibrations as possible. The infrared transmitter–receiver pair is used to sense the position of the ball and it is converted into an equivalent voltage by a potentiometer. This voltage is compared with a set reference voltage to estimate the error or deviation of the actual signal. The measured signals are transferred to a computer by means of an analogue–digital interface card 33-301, to allow designing, configuration and tuning of controller parameters by the software support.

Thus, the amount of regulation required is manoeuvered by the controller as the voltage across the controller indirectly controls the position of the ball.

The block diagram to show the working of the set-up is shown in Fig. 3.

Fig. 3

Working of the maglev system

The parameters used for the model are shown in Table 1 (Magnetic Levitation: Control Experiments 2011):

Table 1 Physical parameters of maglev system

4.2 Mathematical Modelling

The ball can levitate only if the upward electromagnetic force of attraction is counterbalanced by a downward gravitational force. The attractive force, f_e, depends directly on the square of the current flowing in the coil and inversely on the square of the distance of the ball from the magnet (Hajjaji and Ouladsine 2001). It follows inverse-square law, i.e. the current has to be increased if the ball moves away from the coil and tends to fall and vice versa.

$$f_{\text{e}} = k\frac{{i^{2} }}{{x^{2} }}$$

(6)

The ball experiences a downward force due to gravitational pull and is given by

$$f_{\text{g}} = mg.$$

(7)

Newton’s second law states that the net force acting on the ball is an algebraic sum of all the forces acting on it.

$$m\ddot{x} = f_{\text{g}} {-} \, f_{\text{e}}$$

(8)

Substituting the value of f_e and f_g, we get,

$$m\ddot{x} = mg{-}k \frac{{{{i}}^{2} }}{{{{x}}^{2} }}$$

(9)

$$\ddot{x} = g = \frac{k }{m}\frac{{i^{2} }}{{x^{2} }}$$

(10)

If both these forces, f_e and f_g, are equal in magnitude and opposite in direction then the ball levitates. This equation is linearized around an equilibrium point (i₀, x₀), in order to assess its local stability and to apply the tools of linear control. As the deviation is minimum at the equilibrium point, we take $\ddot{x} = 0$ which gives,

$$g - \frac{k }{m}\frac{{i^{2} }}{{x^{2} }} = 0$$

(11)

$$\frac{k }{m} = g\frac{{x_{0}^{2} }}{{i_{0}^{2} }}$$

(12)

The parameters obtained after substituting the values from Table 2 are current i₀ is 0.8 A, position x₀ is 0.009 m and the corresponding voltage is − 1.5 V.

Table 2 Controller parameters obtained by pp technique

Let there be small deviations ∆i, ∆x from the equilibrium point then x = x₀ + ∆x and i = i₀ + ∆i

Applying Taylor’s expansion formula, we get

$$\Delta \ddot{x} = - \left( {\frac{{\partial f\left( {i,x} \right)}}{\partial i}\left| {i_{0} ,x_{0}\Delta i + \frac{{\partial f\left( {i,x} \right)}}{\partial x}} \right|i_{0} ,x_{0}\Delta x} \right)$$

(13)

$$\Delta \ddot{x} = - \frac{k}{m}\left( {\frac{2i}{{x^{2} }}\left| {i_{0} ,x_{0}\Delta i + \frac{{ - 2i^{2} }}{{x^{3} }}} \right|i_{0} ,x_{0}\Delta x} \right)$$

(14)

Substituting the value of $\frac{k }{m}$, Eq. (14) becomes,

$$\Delta \ddot{x} = - \frac{2g}{{i_{0} }}\Delta i + \frac{2g}{{x_{0} }}\Delta x\;{\text{or}}$$

(15)

$$\Delta \ddot{x} = \, - K_{i}\Delta i + \, K_{x}\Delta x$$

(16)

where K_I = $\frac{2g}{{i_{0} }}$ and K_x = $\frac{2g}{{x_{0} }}$

Taking Laplace transform,

$$s^{2}\Delta x = - K_{i}\Delta i + \, K_{x}\Delta x$$

(17)

The transfer function of the maglev system is given by Ghosh and Krishnan (2014),

$$M\left( s \right) = \frac{{\Delta x}}{{\Delta i}} = \frac{{ - K_{i} }}{{\left( {s^{2} - K_{\text{x}} } \right)}}$$

(18)

Substituting the values of K_I and K_x, we get the value of M(s) as

$$M(s) = \frac{ - 24.525}{{\left( {s^{2} - 2180} \right)}}.$$

(19)

In order to find the overall transfer function of the set-up, the electrical resistance–inductance circuit, maglev system and the infrared sensor gain blocks have to be taken in cascade as shown in the block diagram of Fig. 4.

Fig. 4

Modelling of the maglev system

The voltage output from the controller is converted to the required current by an internal resistance–inductance (RL) circuit which given by the equation,

$$i = 1.05\;{\text{v}}$$

(20)

The position of the ball is converted into equivalent voltage by an infrared (IR) photo sensor and potentiometer and is given by

$$x_{v} = 143.48 \, x_{o} - \, 2.8$$

(21)

where x_o is the distance from the electromagnet where the ball levitates.

The overall transfer system can be found as

$$G(s) = \frac{{\Delta x_{v} }}{{\Delta u}} = K1.\;M(s) K2 = \frac{ - 3653.3575}{{s^{2} - 2180}} .$$

(22)

The inferences drawn from the derivation of the transfer function are as follows:

• The system has a negative gain,

• Nonlinear by virtue of a quadratic term and

• Unstable as one of the two poles lies at + 46.69 on the right hand side of the s plane (Pati and Negi 2019; Starbino and Sathiyavathi 2019).

5 Novel Tuning Strategy

In spite of the accurate mathematical modelling and derivation of the transfer function, there are some uncertain dynamic factors, nonlinearities and errors that are bound to occur when applied in the real systems. Any tuning algorithm merely based on the mathematical model of the closed-loop transfer function might perform well in a simulated environment but can differ in the real runs. The novel strategy adopted in this paper eliminates the need of taking any random initial guess of boundary limits required to fix the search area for exploration by non-traditional algorithms.

This hybrid strategy combines coarse and fine tuning strategies for suspension at the equilibrium position with minimum oscillations. For coarse tuning, pole placement technique has been used as it takes system dynamics into account and for fine tuning nature inspired stochastic techniques have been used.

In stage I, controller parameters for different pole assignments have been calculated. There is a limit to the distance at which the poles can be assigned as it is constrained by higher control effort requirements and system dynamics. The assignment for which the ball levitated for stipulated duration has been determined by conducting actual experimentations. Once the broad boundary zone of successful levitation was determined, the controller parameters were fine-tuned around the best value in stage II to find the best combination of K_P, K_I and K_D in that zone for minimum error in the second stage. As random parallel processing of all the three parameters was required to search for the best combination, population-based evolutionary and swarm optimizations have been employed for the purpose.

The steps followed for this strategy were as follows:

• a. Modelling of the system.

• b. Choosing a suitable input signal to get a clear picture of the system robustness.

• c. Applying pole placement technique for coarse tuning.

• d. Determining the range of values of the parameters of the controller for successful levitation by real-time experimentation.

• e. Using these values as boundary conditions for different population-based algorithms to fine tune the response and minimize absolute error.

• f. Testing the robustness under live runs by manually disturbing the ball under levitated state at 20 s and 30 s instants approximately.

5.1 Modelling of the System

Modelling involves formulating a sequence of flow of signals from input to output and relating each block by a mathematical relation such that overall transfer function of the system can be derived as done in Sect. 6 in detail.

5.2 Choice of Input Signal

Analysing the performance of a feedback system based on the parameters of a step input response is convenient but it does not indicate robustness to frequent changes in the input. As the system under present consideration is highly sensitive, an uneven square wave with mean amplitude of − 1.5 V for 50 s duration has been chosen as the input signal. The first step change of a small magnitude of − 0.5 V has been applied after 15 s in order to allow initial transients to settle down. These transients in the first 5 s are caused due to unintentional force applied by the hands while allowing the ball freeway to levitate. The next step change has been applied after 10 s with a rise of 1 V. The current has to be proportionately decreased otherwise the ball gets attracted. The third step change is the most critical one and is applied at 35 s instant with a drop of 1 V. The current in the electromagnet has to immediately change in the opposite direction very accurately at this instant otherwise the ball falls down. Most run time failures occurred at this step change due to predominance of gravitational pull and survival at this juncture can be considered as the measure of the robustness of the tuning parameters.

The experiments have been conducted in the real-time set-up after conducting simulations in Simulink platform of MATLAB.

5.3 Coarse Tuning by Pole Placement Technique (Stage I)

In order to apply this technique for coarse tuning, the location of the pole is varied randomly along the negative s plane and the response is analysed at each location. The transfer function of the closed-loop system with the actual plant gain and the PID controller in cascade is given by

$$T(s) = \frac{y\left( s \right)}{r\left( s \right)} = \frac{{{\text{Gc}}\left( s \right){\text{Gp}}\left( s \right)}}{{1 + {\text{Gc}}\left( s \right){\text{Gp}}\left( s \right)}}.$$

(23)

Substituting the values of ${\text{Gc}}\left( {\text{s}} \right)$ and ${\text{Gp}}\left( {\text{s}} \right)$ from Eqs. (4) and (22), respectively, we get the actual closed-loop response as

$$T(s) = \frac{{(sK_{\text{P}} + K_{\text{D}} s^{2} + K_{{{\text{I}} }} )\left( { - 3653.3575} \right)}}{{s\left( {s^{2} - 2180} \right) + (sK_{\text{P}} + K_{\text{D}} s^{2} + K_{{{\text{I}} }} )\left( { - 3653.3575} \right)}}.$$

(24)

The dominant poles are calculated first to find the desired response. The parameters chosen are as follows (Swain and Sain 2017):

$${\text{Damping}}\;{\text{ratio}},\;\xi \, = 0.8$$

$${\text{Settling}}\;{\text{time}}, t_{\text{s}}= 2\;\text{s}$$

Natural frequency of the system can be calculated as

$$\omega_{\text{n}} = \, 4/\xi t_{\text{s}} = \, 2.5.$$

Using these parameters, the desired system transfer function can be calculated as

$$\begin{aligned} R(s) & = \frac{{\omega_{\text{n}}^{2} }}{{\left( {s^{2} + 2\xi \omega_{\text{n}} s + \omega_{\text{n}}^{2} } \right) }} \\ & = \frac{6.25}{{\left( {{\text{s}}^{2} + 4 {\text{s}} + 6.25 } \right) }}. \\ \end{aligned}$$

(25)

The dominant closed-loop poles are calculated by the formula,

$$s = - \xi \omega_{\text{n}} \pm \omega_{\text{n}} \sqrt {\xi^{2} - 1} = \, - 2 \, \pm {\text{ j }}1.5.$$

(26)

Compatibility in the order of the equations is necessary to compare the actual response with the desired response. The actual response T(s) is of the third order and the desired response R(s) is of the second order. An additional pole is inserted in the desired response to obtain the degree balance requirement. The location of this additional pole is suitably adjusted to get the desired response. In order to vary the location, the new pole assignment is chosen as a multiple of the real part of the dominant pole. In this case, the real part of the pole $\xi \omega_{\text{n}}$ is − 2. The new assignment of pole p can be at any multiple of $\xi \omega_{\text{n}}$ in the negative half of s plane.

Applying this method and equating characteristic equations of the actual and the desired response, we get,

$$\begin{aligned} & (s + p)(s^{2} + 2\xi \omega_{\text{n}} s + \omega_{\text{n}}^{2} ) \\ & \quad = s \left( {s^{2} - 2180} \right) + (sK_{\text{P}} + K_{\text{D}} s^{2} + K_{{{\text{I}} }} )\left( { - 3653.3575} \right) \\ \end{aligned}$$

(27)

K_P, K_I and K_D can be calculated by using this equation.

$$K_{\text{P}} = - \frac{{\left( {2\xi \omega_{\text{n}} p + \omega_{\text{n}}^{2} } \right) + 2180 }}{3653.3575}$$

(28)

$$K_{{{\text{I}} }} = - \frac{{p\omega_{\text{n}}^{2} }}{3653.3575}$$

(29)

$$K_{{{\text{D}} }} = - \frac{{2\xi \omega_{\text{n}} + p }}{3653.3575}$$

(30)

5.4 Determination of Range of Successful Levitation

The range of values for successful levitation for various pole assignments is tabulated in Table 2.

The responses for these locations were first run in the simulated model and the comparative plots are presented in Fig. 5.

Fig. 5

Comparative simulated response for PP

The simulated response shows a reduction in the peak overshoots as the location of the pole is moved away from the origin. This environment is good for preliminary analysis but in order to reach to a concrete conclusion, real-time experiments have to be conducted.

When the real-time experiments were conducted, it was observed that the ball did not levitate for the full duration for low values of pole assignment. It levitated for around 35 s when the pole assignment was at − 600 $\xi \omega_{\text{n}}$. So this location can be considered as the lower boundary limit as shown in Fig. 6.

Fig. 6

Real-time response for PP at 600 $\xi \omega_{\text{n}}$

Figure 7 shows that the ball levitates for the full duration of 50 s for the pole assignment at − 900 $\xi \omega_{\text{n}}$ so this can be taken as the best value of the controller parameters by pole placement technique.

Fig. 7

Real-time response for PP at 900 $\xi \omega_{\text{n}}$

As the location is shifted more towards the negative axis, the response tends to get distorted. This observation is in contrast to the one shown in simulated environment. The distortion occurs as higher control efforts are required for force balance conditions at this assignment as shown in Fig. 8.

Fig. 8

Real-time response for PP at 1200 $\xi \omega_{\text{n}}$

The controller parameters at this pole assignment can be taken as the upper boundary limit. Figure 9 shows the comparative responses for the real-time runs for the controller parameters at these pole assignments.

Fig. 9

Comparative real-time response for PP

Therefore, the upper and lower bounds for K_P, K_I and K_D can be tabulated in Table 3.

Table 3 Boundary values from coarse tuning

These are the threshold limits for the controller parameters for successful levitation. By applying this strategy to determine boundary limits, successful levitation is ensured for the controller settings within this range. The value of parameters at − 900 $\xi \omega_{\text{n}}$ can be taken as the controller settings of K_P, K_I and K_D if coarse tuning is required. The optimum value lies in this vicinity. We can further fine tune the parameters for reduction in error or any deviation from desired response by applying optimization algorithms and by narrowing the bounds.

5.5 Fine Tuning by Non-traditional Techniques (Stage II)

The levitation of the ball is very sensitive to any fluctuations in the current and accurate choice of controller parameters is necessary to allow optimum current in the electromagnetic coil. The application of non-traditional optimization technique is necessary to search for the best combination of the controller parameters by parallel search technique within this boundary. The search criterion is based on the minimization of a fitness function which is integral of the absolute error in this case. MATLAB toolboxes have been used for the application of population-based algorithms GA, PSO and GWO.

5.5.1 Tuning by Genetic Algorithm (GA)

The parameters chosen for this algorithm are as follows: population size = 50, crossover probability rate = 0.8, mutation rate = 0.05 and maximum generation = 100.

The algorithm (Sain and Swain 2016) was run a number of times and the parameters corresponding to the lowest value of IAE have been taken as shown in Table 4. The occurrence of this low value IAE was only once amongst a number of twenty sample runs.

Table 4 Controller parameters obtained by ga

The simulated response and the real-time responses are shown in Figs. 10 and Fig. 11, respectively.

Fig. 10

Simulated response for GA

Fig. 11

Real-time response for GA

5.5.2 Tuning by Particle Swarm Optimization (PSO)

The values of parameters chosen were as follows: C1 = factor responsible for personal best value = 1.2, C2 = factor responsible for global best value = 1.2, W = weighting factor that combines with random numbers in the range (0,1) to give best exploitation and exploration = 0.9, number of swarm = 50, number of iterations = 125

The controller parameters obtained by PSO algorithm (Maji and Roy 2015; Roy et al. 2015) are enumerated in Table 5 and the response in the real time is shown in Fig. 12. The frequency of obtaining the value of IAE in this range was higher than that of GA.

Table 5 Controller parameters obtained by PSO

Fig. 12

Real-time response for PSO

5.5.3 Tuning by Grey Wolf Optimization (GWO)

The parameters chosen were as follows: number of wolves = 30, number of iterations = 125

This algorithm was also run a number of times, and the values of the controller corresponding to lowest values of IAE are tabulated in Table 6.

Table 6 Controller parameters for different iterations by GWO

The real-time response is shown in Fig. 13.

Fig. 13

Real-time response for GWO

The real-time controller output for GWO is shown in Fig. 14.

Fig. 14

Real-time output of the controller for GWO

5.6 Testing of Robustness

The analysis of results obtained and their robustness has been discussed in detail in Sect. 6 separately when the ball was subjected to manual disturbance.

6 Result Analysis and Hardware Implementation

As the boundary limits were determined by pole placement technique and the system dynamics were taken into account, the parameters obtained by the optimization techniques did result in successful levitation for all the algorithms. The advantage of using the boundary threshold limits is that there is no question of failure of levitation in this range. The comparative real-time responses for both coarse and fine tuning algorithms are shown in Fig. 15.

Fig. 15

Comparative real-time response for PP, GA, PSO and GWO

Two critical cases have been encircled in the figure and zoomed for better view and analysis.

7 Critical Tuning Condition at 25 and 35 Sec Step Change

In the first case, there is a voltage rise of 1 V and the system has maximum peak overshoot. The zoomed response of encircle 1 is shown in Fig. 16.

Fig. 16

Zoomed response of encircle 1-peak overshoot

It clearly indicates that the response by the coarse tuning technique, pole placement (PP) has the maximum peak followed by genetic algorithm (GA) response, particle swarm (PSO) response and the least peak overshoot by fine tuning technique, grey wolf optimization (GWO) response.

The second case of encircle 2 is zoomed in Fig. 17.

Fig. 17

Zoomed response of encircle 2-critical peak undershoot

It is the most critical case for levitation under consideration. There is a sharp transition of 1 V at 35 s instant. If the attractive force by electromagnet is even slightly less, the peak value would increase and the ball would start oscillating vigorously leading to dropping out of the levitation. At this instant too, the best response with minimum undershoots was observed for GWO. The comparative performance results of both the coarse and fine tuning techniques are tabulated in Table 7.

Table 7 Comparative performance parameters for PP, GA, PSO AND GWO

The values of absolute error show the sensitivity of the system to variations in the parameters. The numerical variations in individual parameters are very less and yet the combination of these parameters results in large errors.

The above results clearly indicate the advantage of this tuning strategy. The coarse tuning technique does give a satisfactory response as it takes system specific dynamics into account and the fine tuning technique improves the response. If this strategy had not been followed, then there would be chances of failure of levitation of the ball or higher oscillations.

7.1 Comparison of Convergence Curves

The convergence curves for the worst and the best optimization techniques in this case are illustrated in Figs. 18 and 19, respectively.

Fig. 18

Convergence curve for GA

Fig. 19

Convergence curve for GWO

The objective of using these optimization techniques was to minimize absolute error and both the curves indicate the degree of reduction in error. The convergence curve by GA shows persistence of some error, whereas that for GWO shows negligible error.

7.2 Disturbance Rejection and Robustness Analysis

In order to further check for robustness of these values, the suspended ball was subjected to external disturbance. The ball was touched by hand with slight thrust to check whether it fell out of levitation or if the transients wax or wane due to disturbance. If the ball continues to levitate and transients settle down, then the system can be considered to be robust under such settings of the controller. The ball was touched around 20 s and 30 s instants which accentuates the oscillations due the intentional disturbance. The real-time responses, when the ball was subjected to manual disturbance, for GA, PSO and GWO are represented in Figs. 20, 21, 22, respectively.

Fig. 20

Real-time response for GA with disturbance

Fig. 21

Real-time response for PSO with disturbance

Fig. 22

Real-time response for GWO with disturbance

In this case too, the least oscillations were observed for GWO technique (Oliveira et al. 2016; Yadav and Verma 2016). The fluctuations were of lower amplitude and it died out faster as compared to the responses by the other two algorithms.

Numerically, also the sensitivity and complimentary sensitivity functions are used to determine the robustness. The open-loop gain, L(s) = G_c(s)G_p(s), is a function used in determining both sensitivity, S(s), and complimentary sensitivity C(s),

$$S(s) = \frac{1}{1 + L\left( s \right)}$$

(31)

$$C(s) = \frac{L\left( s \right)}{1 + L\left( s \right)} = 1 - S(s)$$

(32)

All the values of complementary sensitivity values obtained by different techniques are less than two which is the required condition. It is the least for GWO as shown in Table 8.

Table 8 Comparative complimentary sensitivity and sensitivity values

7.3 Hardware Implementation

The actual layout consists of three segments, the plant unit 33-210, the computer unit and the interface unit between the two provided by 33-301. The software part of the computer unit has been used to adjust the customized controller gains for fine and coarse tuning settings. The actual photograph of layout is shown in Fig. 23.

Fig. 23

Actual photograph of the set-up during a live run

The actual response of the ball and the controller output can also be seen on the screen. The plant unit shows an electromagnet at the top, the ball in the levitated state during an actual experimental run and the infrared sensor to detect the position of the ball. It also has built in power supply and can work in standalone mode with convenient sockets for changing control input, set point and gain in the main unit (Naumovic and Veselic 2008). The interface with the plant unit, 33-210, and the computer unit has been provided by a hardware circuit 33-301, which modifies the signals and matches the impedances of both the units. The zoomed analogue–digital interface can be seen in Fig. 24.

Fig. 24

Actual photograph of the analogue control interface

The interface circuit scales down the error and provides an offset voltage of − 2.8 V. A voltage follower is used to match the impedance between the control signal and the plant so that the voltage and current levels are sufficiently high to drive the maglev system. The interface card clearly shows A/D, D/A converters and the use of four low power LM348 N op-amps with high gain and internal compensation. Only one has been used to generate the square waveform. The advantage of input characteristic of this op-amp is that it allows a differential input voltage much higher than its supply voltages. The resistances and capacitances can be chosen to set the frequency of the feedback pole. A 64 W/50 K variable potentiometer with 25 turns and having a resistance range of 10 Ω to 2 MΩ has been used to convert ball position into equivalent voltage. The power supply requirement is + 15 V and the layout is such that inter amplifier capacitive coupling is minimized.

8 Conclusion

This paper has successfully addressed the problems encountered at the commencement of this research work with the compilation of several missing links. The working and modelling of the maglev system has been done with suitable illustrations. Traditional pole placement technique has been applied to find successful zone of levitation and also as a means of coarse tuning. The values of the controller parameters thus obtained have been used as the boundary constraint for various nature-based optimization techniques. This hybrid tuning strategy resulted in successful levitation in all the runs for different non-traditional algorithms. It serves the dual purpose of obtaining successful levitation for the full stipulated duration of 50 s and of minimization of fluctuations. If only one strategy had been used, there could have been a probability of the ball falling out of levitation or the response could have been highly oscillatory. If the boundary threshold limits had been taken randomly without considering system dynamics then the actual experimental run might have resulted in unsuccessful levitation. The results clearly indicate the superiority of the hybrid tuning strategy which is a combination of the traditional and non-traditional techniques.

8.1 Future Scope

Other traditional and non-traditional techniques can be applied with a better choice of variable parameters and with different controller configurations to further improve levitation technology.