1 Introduction

An ad hoc network is a collection of distributed nodes with wireless connections (Yang 2014; Thakkar and Kotecha 2015). The nodes in such networks are connected via the source or target nodes that form a single leap connection. This type of connection is common in all wireless networks with router mediator (Palmieri 2017). In each wireless information transmission passage, two nodes in the beginning and end of the path are called the host and the router. Thus, each node not only can work independently, but also can work as a router or a host and mediate between two other nodes at the same time if necessary (Kuila and Jana 2014; Haque et al. 2015). Due to the nodes mobility, the network structure changes continuously that forces an appropriate mechanism for determining its structure at every moment (Nguyen et al. 2015). Indeed, an ad hoc network is a momentary connection established with a specific structure based on the source location, target and mediator nodes. If there is no need for making connection, each node works independently (Joe and Ramakrishnan 2015). In this connection, each node can be as the router or mediator to information transmission between other nodes; thus, the connection between two nodes out of the signaling area would be possible. Obviously, in such structure each node needs to be equipped with a transceiver module. This specific mechanism of connection between the network nodes requires a specific hardware and software structures, and it also makes unique features for the network that completely distinguishes it from other wireless networks. Figure 1 shows an ad hoc network (Akkaya and Younis 2012; Iwanicki 2016; Gara et al. 2015). Nowadays, there are different functions for these networks due to their wide growth in the commercial, industrial and urban environments. Therefore, performance improvement in such networks is concerned with routing and security fields, that can be divided into three major groups, namely wireless mesh networks (WMN), wireless sensor networks (WSN) and mobile ad hoc networks (MANET). The fundamental mechanisms of these groups have the same principles and features. However, there are major distinctions in the functional features, such as volume of information processed in the nodes, and existence of limitations, such as battery lifespan. For example, the main limitation of WSN is its power supply. Thus, the best option in designing of WSN is a network with low energy consumption for increasing the lifespan of the nodes. It is worth mentioning that mobile ad hoc networks have rechargeable batteries and there is no any limitation in power supply, but it should be considered (Farooq 2015; Wang et al. 2014; Luiz et al. 2014). In all rate control algorithms, we are looking for the methods that can run end-to-end operation. The basic question raised is the existence of a rate control algorithm to achieve a fair straightforward assignment without the help of network nodes. In such methods, the destination nodes only rely on the received implicit feedbacks from the network, such as transmission delays, and do not receive direct feedbacks from the network nodes.

Fig. 1
figure 1

A sample of ad hoc networks

Full size image

The main reason for research on this type of methods is their simple implementation in large networks without needing for changes on switches and network routers. Accordingly, the complexity of the calculation relies on the end nodes. In the wireless networks, bandwidth limitation is generally a bottleneck in transmitting network information. In the most methods of routing and controlling the transmission of information, all nodes are assigned with similar bandwidth, resulting in traffic in some of the data transmission paths. If the allocation of bandwidth to the nodes in the routing algorithm is considered as one of the target function for routing, it can lead to reducing the traffic and the nodes overhead. Therefore, the quality of data transfer can be improved and the network can be easily developed. The fixed bandwidth rate allocation for all wireless network nodes can make increasing the probability of high traffic for a particular route and staying out some other paths. Scalability, low convergence speed and high overhead cause the traffic and bandwidth problems in such networks. Motivated by the above discussions, in order to overcome these limitations, the contribution of this paper is to propose a fuzzy-hierarchical algorithm for achieving high-speed rate allocation. The fuzzy logic is adopted due to its simplicity in calculation, leading to speed improvement.

The reminder of this paper is structured as follows. An overview of the MANET is introduced in Sect. 2. The proposed algorithm for optimal allocation rates between different nodes of the network is presented in Sect. 3. Stability analysis is derived in Sect. 4. Simulations are provided in Sect. 5. Finally, the main conclusions are drawn in Sect. 6.

2 MANET

As shown in Fig. 1, a sample of ad hoc networks is an independent collection of mobile users who can make connection with others through wireless passages using limited bandwidth and without any infrastructure and central control. This network can work independently without any fixed node, and has an access point to one or more fixed networks. Existence of wireless connection passages limits the connection capacity of these networks in comparison with hardwired networks. Nevertheless, noise and interference decrease the efficiency of such networks to less than the maximum possible efficiency for radio networks. However, due to high efficiency and simple implementation, there is no requirement for transmission of massive volume of information (Palmieri 2017). If the unpredictable node connection loss occurs, then these networks are not efficient and reliable. Therefore, the MANET is an appropriate solution. In addition, in the absence of connection setup or when the setup is too expensive and cannot be directly used, the mobile wireless users can make connection using the MANET. The nodes in MANET are equipped with wireless transmitters and receivers and may apply broadcast or peer-to-peer antennas (Haque et al. 2015). The MANET is a programmed and configured multilevel wireless network that makes a collection of mobile groups. Due to the nodal mobility, battery availability and wireless intervention, the protocol path maintains connection when the connection fails in this path (Vassilaras et al. 2013; Kumar and Mehfuz 2016). Since there are limitations in the transmitter and receiver, the mobile nodes cannot make direct connection with all nodes.

Therefore, if there is no possibility to make direct connections, then wireless information can be transferred by other nodes that act as the routers (Kumar and Mehfuz 2016). The requirements of service include the bandwidth, service acceptable power, delay and its variations. In a network with a collection of quality of service (QoS) mechanisms, there is a tradeoff between efficiency and quality as shown in Fig. 2. Networks may be used in different points of this curve. For instance, most of the LANs in the Microsoft networks are able to provide a good quality for IP telephony service, and therefore, they can be applied in point P1. On the contrary, most of the international WANs are efficient due to reasons related to the cost, but they could not provide an appropriate quality for IP telephony service. Accordingly, they can be adopted in point P2 (Sathiamoorthy and Ramakrishnan 2016; Yu et al. 2014; Grassi et al. 2014; Kumar and Sachin 2016). As mentioned above, most of the LANs used in P1 with a lot of arrangement efforts have inappropriate efficiency. The general goal for providing different QoS mechanisms is to increase the efficiency of a specific network. When complexity of QoS mechanisms is high, performance of the network is outstanding. Figure 3 illustrates this fact. Nowadays, some works were reported to design high mobility speed services with trivial delays and enable terminal users to conform their rates to the network condition with minimum information about congestion of the network. With their potential ability, these networks can provide the terminal users (Jiang et al. 2015; Das and Tripathi 2015). These networks do not need complex mechanisms for controlling the permission of focused connection, timing and prior saving of sources.

Fig. 2
figure 2

Relationship between the quality and efficiency (Bernet 2001)

Full size image
Fig. 3
figure 3

Effect of the complexity of QoS mechanism on the network function (Bernet 2001)

Full size image

3 Methodology

Two important topics in the MANET are providing routing algorithm and selection of an appropriate route for data transmission. The path is usually selected in terms of the nodes’ energy in the path, empty path and node overhead. In this paper, we study the bandwidth allocation of the nodes as a desirable criterion for choosing the route to send the data. The available bandwidth for each node in the methods reported in the literature was set to a constant value or based on the node load. But, in the current research work, a novel algorithm is proposed to select the bandwidth (assignment rate) for each node. Besides, in the core of the proposed algorithm, a fuzzy logic algorithm is embedded to improve the allocation rates and convergence speed. Nowadays, the main form of the internet rate control is the end-to-end control in the transmission layer, presented in TCP algorithm. This rate control is based on the users’ observations from their congestion status. The TCP’s effectiveness in many fields has been reported; however, it is not very efficient in real-time traffic and multi-destination service support (Benamar et al. 2014; Tahir et al. 2017). Here, we consider the network including a limited number of sources with capacity \(C_{j} ,j \in J\), where the path Rr is a nonempty subset of J. Denoting the network confluence matrix by A, if the source (link) j is on the path r, then Ajr = 1; else Ajr = 0. Rr is related to the traffic of user P, and the function Ur(xr) is supposed to be increasing, strictly convex, and continuously differentiable with respect to xr ≥ 0. The following relationship is used to maximize the cost function of the overall system:

$$\begin{aligned} & {\text{SYSTEM}}\,\left( {U,A,C} \right) \\ & {\text{Max}}\quad \sum\limits_{r \in \Re } {U_{r} (x_{r} )} \\ & {\text{Subject}}\,{\text{to}} \\ & A^{\text{T}} X \le C \\ & X \ge 0 \\ \end{aligned}$$
(1)

In the above equation, C = (cj, j ∈ J) is the capacity vector of the links, U = (Ur (.), r ∈ ℜ) is the cost function vector, X = (xr, r ∈ ℜ) denotes the users’ rate vector and matrix A = (Ajr, j ∈ J, r ∈ ℜ) shows the relationship between the links and paths. From complete convexity of the cost function and compactness of the bound area, it has a unique solution. Since the income function of each user for the network is unknown, the equation is divided into the following two subequations, which are solved by the users and the network independently.

  • User P equation:

    $$\begin{aligned} & {\text{USER}}_{r} (U_{r} ;l_{r}){:} \\ & {\text{Max}}\;U_{r} (w_{r} /l_{r} ) - w_{r,} w_{r} \ge 0 \\ \end{aligned}$$
    (2)

  • Network equation:

    $$\begin{aligned} & {\text{NETWORK}}\, \, (A,C;\varOmega){:} \\ & {\text{Max}}\quad \sum\limits_{r \in \Re } {\omega_{r} \log (x_{r} )} \\ & {\text{Subject}}\,{\text{to}} \\ & A^{T} X \le C,X \ge 0, \\ \end{aligned}$$
    (3)

where λr is the cost per rate unit for user P and ωr is a cost that should be paid in the time unit by user P.

In Eqs. (2) and (3), the wireless data are represented by Ω = (ωr, r ∈ ℜ), Λ = (λr, r ∈ ℜ) and X = (xr, r ∈ ℜ), which are applied in ωr = λr. xr and r ∈ ℜ. Also, X is the unique solution of the SYSTEM (U, A, C). If for a specific group of users with desired parameters, Ω = (ωr, r ∈ ℜ) solves the NETWORK (A, C; Ω), then the result vector X = (xr, r ∈ ℜ) can solve the weighted mode of SYSTEM (U, A, C). The cost function can be rewritten as

$$\sum\nolimits_{r} {\alpha_{r} U_{r} (x_{r} )} ,\quad \alpha_{r} = {{\omega_{r} } \mathord{\left/ {\vphantom {{\omega_{r} } {\left( {x_{r} U_{r}^{{\prime }} (x_{r} )} \right)}}} \right. \kern-0pt} {\left( {x_{r} U_{r}^{{\prime }} (x_{r} )} \right)}}$$
(4)

Thus, selection of the vector Ω by the network (instead of selection by the users) leads to implicit weighting of the cost functions of different users by the network. By dividing the main SYSTEM equation into two subequations, there is no need for the network to know the users’ cost function. The Lagrange function for the NETWORK equation is as

$$L(X,z;\mu ) = \sum\limits_{r \in \Re } {\omega_{r} \cdot \log x_{r} + \mu^{\text{T}} \left( {C - A^{\text{T}} X - z} \right)}$$
(5)

where \(z \ge 0\) is the slack variables vector and \(\mu\) is the Lagrange ratio vector (or cost vector).

$$\frac{\partial L}{{\partial x_{r} }} = \frac{{\omega_{r} }}{{x_{r} }} - \sum\limits_{{j \in R_{r} }} {\mu_{j} }$$
(6)

Therefore, the fixed point of the primary equation is in the form:

$$x_{r} = \frac{{\omega_{r} }}{{\sum\nolimits_{{j \in R_{r} }} {\mu_{j} } }}$$
(7)

where \(\left( {\mu_{j} ,j\, \in\,J} \right)\) and \(\left( {x_{r} ,r \in \Re } \right)\) satisfying

$$A^{\text{T}} X \le C \, , \, \mu^{\text{T}} \left( {C - A^{\text{T}} X} \right) = 0, \, \mu \ge 0 \,$$
(8)

In the presence of background network traffic, the capacity of the links is a continuous time function. The hierarchical algorithm is introduced primarily by a simple example. The assumed network given in Fig. 4 has five subnetworks, namely A, B, C, D and E. In this figure, the data can be exchanged by a backbone network, where the border of the backbone network is shown by dashed line. Some users in subnetwork A in Fig. 4 desire to connect to some of the terminal nodes in subnetwork C. Continuous lines in the backbone network represent the cumulative rate of the users in subnetwork A passing toward subnetwork C. Notice that the optimal passages for different users are preselected by the routing algorithms based on an appropriate criterion, and thus, the goal is only to allocate fair rates to the users. The number of users in subnetwork p who want to make connection with subnetwork q in time t is denoted by ntpq. It is supposed that the random behavior of ntpq is ignored in the current discussion. Hence, the main purpose is to allocate an appropriate rate to these users based on the proposed algorithms.

Fig. 4
figure 4

The hierarchical topology

Full size image

Generally, each subnetwork consists of a limited number of groups of users who pass a common traffic path through backbone network and the proposed hierarchical algorithms can apply on these groups of users. Indeed, each group of users can be considered as a virtual user. Figure 5 displays the circulated growth of rate allocation in hierarchical algorithms. As the high-level algorithm gets closer to convergence and virtual user rate gets closer to terminal magnitude, low-level algorithm takes the responsibility of the rate allocation to the terminal users in the network.

Fig. 5
figure 5

Circulated growth of rate allocation in hierarchical algorithms

Full size image

From Eq. (4), the optimal rate in proportional balance criterion (Ω, α) can be applied in the following equation:

$$x_{r}^{*} = \left( {\omega_{r} /\lambda_{r}^{*} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} ,\quad r \in \Re$$
(9)

In other words,

$$\omega_{r} = \left( {x_{r}^{*} } \right)^{\alpha } \cdot \sum\limits_{{j \in R_{r} }} {p_{j} \left( {\sum\limits_{{s:j \in R_{s} }} {x^{ * }_{s} } } \right)} ,\quad r \in \Re$$
(10)
$$\lambda_{r}^{*} = \sum\limits_{{j \in R_{r} }} {p_{j} \left( {\sum\limits_{u \in j} {x_{u}^{*} } } \right)}$$
(11)

It is assumed that most of the links at the level of the virtual users have high congestion. Therefore, a great amount of λ*r is related to the backbone network that can be estimated as

$$\lambda_{r}^{*} \cong \sum\limits_{\begin{subarray}{l} \, j \in R_{r} \\ \& j \in {\text{Backbone}} \end{subarray} } {p_{j} \left( {\sum\limits_{u \in j} {x_{u}^{*} } } \right)}$$
(12)

For example, for users s1 and s2, we have

$$x_{2}^{*} = \left( {\frac{{\omega_{2} }}{{\lambda_{2}^{*} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} ,\quad x_{1}^{*} = \left( {\frac{{\omega_{1} }}{{\lambda_{1}^{*} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}}$$
(13)
$$\lambda_{1} \approx \lambda_{2} \approx \varLambda_{1}^{*} \mathop = \limits^{\vartriangle } p_{6} \left( {\sum\limits_{{u:L_{6} \in R_{u} }} {x_{u}^{*} } } \right)$$
(14)

where \(\varLambda_{1}^{*}\) is a part of the cumulative penalty function corresponding to the users 1 and 2 and \((\lambda_{1} \, , \, \lambda_{2} )\) are in the common traffic path in the backbone network.

In the fixed point, the cumulative rate of data transfer for the first subnetwork is

$$x_{1}^{*} + x_{2}^{*} = \left( {\frac{{\omega_{1} }}{{\lambda_{1}^{*} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} + \left( {\frac{{\omega_{2} }}{{\lambda_{2}^{*} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} \cong \frac{{\left( {\omega_{1} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} + \left( {\omega_{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} }}{{\left( {\varLambda_{1}^{*} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} }}$$
(15)

It can be assumed that the first subnetwork is a virtual user with

$$\varOmega_{1} = \left( {\omega_{1}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} + \omega_{2}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} } \right)^{\alpha }$$
(16)

In the fixed point, the cumulative rate of user 1 denoted by \(\chi_{1}\) is as

$$\chi_{1}^{*} = \frac{{\left( {\omega_{1} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} + \left( {\omega_{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} }}{{\left( {\varLambda_{1}^{*} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} }}$$
(17)

Using Eqs. (16) and (17), we get

$$x_{1}^{*} \cong \left( {\frac{{\omega_{1} }}{{\varOmega_{1} \,}}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} \cdot \chi_{1}^{*}$$
(18)

In general, it is assumed that \(S\,\mathop = \limits^{\vartriangle}\, \{S_{i} |i = 1,2, \ldots,Q\}\) and \({\mathcal{R}}\,\mathop = \limits^{\vartriangle}\, \{{\mathcal{R}}_{i} |i = 1,2, \ldots,Q\}\) are corresponded to the source and target virtual users, respectively. Furthermore, Q shows the number of input (or output) virtual users.

3.1 User Rate Allocation Algorithm in Boundary Router

The proposed hierarchical algorithm in the place of backbone boundary router for determining the rate of user su is given in Eqs. (19)–(22).

$$x{}_{u}[n + 1] = \left\{ {a_{i}^{n} .\chi_{i} [n].\left( {\frac{{\omega_{u} }}{{\varOmega_{i} }}} \right)^{{\frac{1}{\alpha }}} + (1 - a_{i}^{n} ).\left[ {x_{u} [n] + k_{u} .(\omega_{u} - x_{u}^{\alpha } [n] \cdot \lambda_{u} [n])} \right]} \right\}^{ + } \quad i = 1,2, \ldots ,Q,\;u \in i$$
(19)
$$\varOmega_{i}\, \mathop = \limits^{\Delta }\, \left( {\sum\limits_{u \in i} {\omega_{u}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} } } \right)^{\alpha }$$
$$a_{i}^{n}\, \mathop = \limits^{\Delta }\, \tanh [M.\left| {\chi_{i} [n] - \chi_{i} [n - 1]} \right|/(\chi_{i} [n] + \varepsilon )]\quad \varepsilon ,M > 0$$
(20)

where ε is a very small value and M controls the sensitivity of \(a_{i}^{n}\) with respect to variation in χi [n].

3.2 Virtual User Rate Allocation Algorithm in the Backbone in Boundary Router

In fact, we use the Jacob algorithm and the allocation rate for virtual users passing through backbone in the place of boundary router.

$$\chi_{i} [n + 1] = \left\{ {\chi_{i} [n] + K_{i} \, \cdot \frac{{\varOmega_{i} - \chi_{i}^{\alpha } [n] \cdot \varLambda_{i} [n]}}{{\alpha \cdot \chi_{i}^{\alpha - 1} [n] \cdot \varLambda_{i} [n] \, + \chi_{i}^{\alpha } [n]\, \cdot \left. {\frac{\partial }{{\partial \chi_{i} (t)}}\varLambda_{i}^{{}} (t)} \right|_{t = n} }}} \right\}^{ + }$$
(21)
$$\varLambda {}_{i}[n] = \sum\limits_{\begin{subarray}{l} \, j \in R_{{S_{i} }} \\ \& j \in {\text{Backbone}} \end{subarray} } {p_{j} \left( {\sum\limits_{{u:j \in R_{u} }} {\chi_{u} [n]} } \right)}$$
(22)

Equations (19)–(22) are a combination of Golestani’s and Kelly’s algorithms with a high-level algorithm. The high-level algorithm is applied on the part of the network that forms the backbone network. As the topological structure of this part lacks the complexities of the main network, it is possible to apply the high-speed algorithms, such as the Jacob algorithm in this level of hierarchy (Wang et al. 2014). It is also possible to use larger amount of k in high-level hierarchy since, as the network becomes larger, the users due to unawareness of the topology of the network have to use smaller amount of k in order to make sure about the convergence. Because of fewer terminal nodes in the high-level hierarchy (in fact, the subnetwork in this level acts as virtual users), bigger amount of k can be selected, leading to faster rate allocation algorithm. ani tends to zero as the rate of \(\chi_{i} [n]\) converges. From Eqs. (20) and (21), first high-level algorithm is used to get faster desired rate. As the rates get closer to the desired amount, the algorithm gradually behaves similar to the Golestani’s algorithm vague. But in this condition, the algorithm uses primary conditions similar to the final amount.

4 Stability Analysis

In practical implementation purposes, the rate allocation algorithms in Eqs. (10) and (11) must be used. It is assumed that the size of receivers’ congestion window is equal to one and the sender congestion window size in (W, a)-fair and MANET models are updated using Eqs. (9)–(11). From there, we have

$$\begin{aligned} & cwnd_{r} [n + 1] = \left\{ cwnd_{r} [n] + k_{r} .T_{r} [n].(w_{r} - \left( {\frac{{cwnd_{r} [n]}}{{T_{r} [n]}}} \right)^{\alpha } .d_{r} [n])\right\} \\ & CWND_{r} [n + 1] = CWND_{r} [n] + \frac{{m_{r} }}{{T_{r} [n]}} - \left( {\frac{{m_{r} }}{{T_{r} [n]}} + \frac{{(CWND_{r} [n]^{2} )}}{{2m_{r} T_{r} [n]}}} \right).d_{r} [n] \\ \end{aligned}$$
(23)

where

$$d_{r} [n] = T_{r} [n] - \overline{d}_{r}$$
(24)

In Tahir et al. (2017) and references therein, it was shown that the stability analysis of Eq. (23) can be derived using the following Lyapunov function.

$$V(x) = \sum\limits_{r} {\sqrt {\frac{{2m_{r} }}{{T_{r} }}} \arctan \left( {\frac{{x_{r} T_{r} }}{{\sqrt {2m_{r} } }}} \right)\sum\limits_{j \in J} {\int\limits_{0}^{j \in S} {\sum {x_{S} } p_{j} (y){\text{d}}y} } }$$
(25)

The stability properties of the window-based (Ω, α) fair model can be demonstrated after defining some preliminary terms. The following two definitions are assumed.

$$X_{r} = \frac{{w_{r} }}{{T_{r} }},\;\;s_{r} = X_{r}^{\alpha - 1} (w_{r} - X_{r} \overline{d}_{r} ) - w_{r}$$
(26)

where wr is the congestion window of flow r.

Theorem

Consider Eq. (10) with Lyapunov function\(V\left( w \right) = \frac{1}{2a}\mathop \sum \nolimits_{r} s_{r}^{2\alpha } .\)If there exists a unique value w*, which can minimize V(.), then w* is a stable point of the system.

Proof

The window-based Eqs. (21) and (22) can be transformed to the following continuous-time representation as

$$\frac{{dw_{r} }}{dt} = k_{r} T_{r} \left( {\omega_{r} - \left( {\frac{{w_{r} }}{{T_{r} }}} \right)^{\alpha } (T_{r} - \overline{d}_{r} )} \right)$$
(27)

where kr is a nonnegative constant coefficient.

Based on the definitions mentioned above, Eq. (27) can be simplified as

$$\frac{{{\text{d}}w_{r} }}{{{\text{d}}t}} = k_{r} T_{r} s_{r}$$
(28)

By differentiating V(.) with respect to time, it yields

$$\frac{{{\text{d}}V(w)}}{{{\text{d}}t}} = \sum\limits_{r} {s_{r}^{2\alpha - 1} \frac{{{\text{d}}s_{r} }}{{{\text{d}}t}}}$$
(29)

Based on the definition sr and some mathematical computations, it can be easily shown that

$$\frac{{{\text{d}}s_{r} }}{{{\text{d}}t}} = X_{r}^{\alpha - 2} \left\{ {[(\alpha - 1)w_{r} - \alpha X_{r} \overline{d}_{r} ]} \right\}\frac{{{\text{d}}X}}{{{\text{d}}t}}$$
(30)

Also, from definitions Xr and sr, we obtain

$$\frac{{{\text{d}}X_{r} }}{{{\text{d}}t}} = - k_{r} s_{r}$$
(31)

Finally, using Eqs. (18)–(22), it can be concluded that

$$\frac{{{\text{d}}V(w)}}{{{\text{d}}t}} = \sum\limits_{r} {k_{{}} s_{r}^{2\alpha } X_{r}^{\alpha - 2} \frac{\alpha }{T}(T_{r} - \overline{d}_{r} )}$$
(32)

Thus, V(w) is a Lyapunov function and the vector w* = (wr*), r = 1, …, M (M is the number (Ω, α) fair flows) is a stable point of the system. Notice that the overall system given in Eqs. (28) and (29) is also locally stable if \(k_{r} D_{r} \le 0\), where Dr is sum of the direct and return delays, and kr is defined in Eq. (27) (Johari and Tan 2001; Basagni et al. 2013).

5 Simulation

The network used in this paper is selected based on IEEE 802.11 standard, which is simulated in a 200 m * 200 m room with a variable number of nodes. Other parameters are listed in Table 1. In the network links, some bottlenecks are defined with minimum bandwidth. Table 2 demonstrates the bottleneck links and their packet capacity to the transmission.

Table 1 Parameters used in the simulation
Full size table
Table 2 Bottleneck link capacity
Full size table

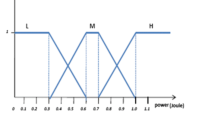
Here, a fuzzy logic algorithm is embedded to improve calculation overhead in low-level rate allocation algorithm. This algorithm gets all network nodes xr and estimated \(\lambda_{r}^{*}\) based on the membership function shown in Table 3. The inputs are the error (xr) and error difference \((\lambda_{r}^{*} )\) denoted by e and Δe, respectively, and they are normalized using appropriate scaling factors (xr for e and \(\lambda_{r}^{*}\) for Δe). The inputs e and Δe are defined as follows:

$$e(k) = \frac{Ppv(K) - Ppv(K - 1)}{Vpv(K) - Vpv(K - 1)}$$
(33)
$$\Delta e(k) = e(k) - e(k - 1)$$
(34)

The so-called variable fuzzy-hierarchical algorithm is adopted to select the appropriate variable universe stretching factor. The membership functions and its definition are summarized in Table 3. To assess the efficiency of the proposed fuzzy-hierarchical algorithm, its performance is compared with other algorithms, namely Kelly (Sathiamoorthy and Ramakrishnan 2016), hierarchical I (Tahir et al. 2017), hierarchical II (Weixia et al. 2017) and fuzzy (Goudarzi and Hassanzadeh 2006). An output linguistic variable is utilized to represent the route. Figure 6 displays the flowchart of the proposed algorithm. Figure 7 describes the user (user number = 3) bandwidth rate in different algorithms. As can be seen, the proposed fuzzy-hierarchical algorithm presents a better behavior in comparison with other algorithm. In fuzzy and hierarchical algorithms, the user bandwidth rate increases slower than others. Although, this occurs for users 9 and 38 as displayed in Figs. 8 and 9, respectively. Referring to these figures, it can be concluded that the fuzzy-hierarchical hybrid algorithm is superior in terms of convergence speed than others. Subsequently, hierarchical algorithms I and II have the highest convergence rate. The normal fuzzy algorithms and the Kelly’s algorithm are fast, but they have less convergence than the hierarchical methods. The fractures in Figs. 10 and 11 are due to user 4 passage from two bottleneck links 17 and 48. The cumulative rate on the 48th link has lower slope increasing. Besides, in some cases the bottleneck capacity varies with time, when the slope of the capacity curve is negative, the capacity decreases rapidly. Since, the fuzzy-hierarchical algorithm is faster than the bottleneck capacity, thus it is able to track the capacity of the link. The proposed algorithm has a superior convergence rate in comparison with the Kelly’s method.

Table 3 Fuzzy membership functions
Full size table
Fig. 6
figure 6

Flowchart of the proposed algorithm

Full size image
Fig. 7
figure 7

User bandwidth rate for number 3 in different algorithms

Full size image
Fig. 8
figure 8

User bandwidth rate for number 9 in different algorithms

Full size image
Fig. 9
figure 9

User bandwidth rate for number 38 in different algorithms

Full size image
Fig. 10
figure 10

Transfer cumulative rate in 17 bottleneck link

Full size image
Fig. 11
figure 11

Transfer cumulative rate in 48 bottleneck link

Full size image

6 Conclusion

An efficient routing algorithm plays an important role to achieve better performance in the MANET networks. The purpose of this paper is to design an optimum allocation algorithm, namely fuzzy-hierarchical algorithm. We improve the expanding property of the existing rate allocation algorithms by reducing the amount of exchanged information that should be rewritten. It is discussed that the algorithm had an outstanding performance in terms of convergence rate in such networks. Simulation results illustrate the effectiveness of the proposed algorithm.