1 Introduction

Natural convective heat transfer is one of the most fundamental heat transfer mechanisms that plays a significant role in diverse industrial and engineering applications such as heat exchangers, energy storage systems, solar collectors, and electronics cooling (Xiong et al. 2021a, 2021b). Therefore, the improvement of heat transfer performance in such devices is of great significance. The term ‘nanofluid’ was first introduced by Choi in 1995 (Choi and Eastman 1995). Nanofluids are thought to be useful in enhancing the heat transfer performance of fluids and have gained much attention in recent years (Izadi et al. 2020, 2014, 2013, 2015). Many researchers have focused on the effectiveness of nanofluids on natural convective heat transfer (Izadi 2020; Sajjadi et al. 2021).

Putra et al. (Putra et al. 2003) undertook an experimental investigation on the natural convection of \(Al_{2} O_{3}\) and CuO–water nanofluids in a horizontal cylinder. They showed that, unlike the forced convection, natural convection heat transfer of nanofluids systematically deteriorates with adding nanoparticles. They suggested that fluid/particle slip and sedimentation are two mechanisms possibly responsible for that behavior. In a similar study with the same finding, Koloulias et al. (Kouloulias et al. 2016) experimented with the γ-\(Al_{2} O_{3}\)-deionized \({H}_{2}O\) nanofluid in the classical Rayleigh–Benard configuration. They speculated that the sedimentation layer of nanoparticles, caused by poor nanofluid stability, imposes additional thermal insulation in the system, which is the main reason for the reported heat transfer degradation. Pakravan and Yaghoubi (Pakravan and Yaghoubi 2011) theoretically investigated the natural convection of nanofluids employing Brownian motion, thermophoresis, and Dufour effects. They also developed a theoretical correlation for estimation of Nusselt number, in which the trend of decreasing Nusselt number with volume fraction is visible.

There are also several experimental results published in the literature that focused on the natural convective behavior of other nanofluids such as \(TiO_{2}\)–water (Hu et al. 2014a; Moradi et al. 2015), ZnO-EG/W (Li et al. 2015), and \(SiO_{2} {-}\) water (Haddad et al. 2016). Likewise, the outcomes of these studies reveal the adverse effect of nanoparticles on the natural convective heat transfer of nanofluids. Li et al. (Li et al. 2015) maintained that the decrease in the wall temperature gradient caused by the addition of nanoparticles is more dominant than the increase in thermal conductivity, so the heat transfer deterioration would occur.

On the other hand, there are some experimental studies on alumina–water nanofluid that could observe the enhancement of natural convective heat transfer of the nanofluid in some ranges of nanoparticle concentration (Moradi et al. 2015; Nnanna 2007; Hu et al. 2014b; Ghodsinezhad et al. 2016; Ho et al. 2010). In other words, nanofluids show heat transfer improvement with nanoparticle addition up to an optimum level of volume fraction at which the maximum value of heat transfer can be obtained. Further increase in the volume fraction would adversely diminish the heat transfer performance of nanofluids. Nnanna (Nnanna 2007) explained that heat transfer deterioration at higher volume fractions is due to kinematic viscosity increment and its resulting reduction in Rayleigh number. Hu et al. (Hu et al. 2014b) argued that this is because the heat transfer of nanofluid is more sensitive to viscosity than to thermal conductivity at high concentrations. The research of Ghodsinezhad et al. (Ghodsinezhad et al. 2016) supports the idea that claims “for nanofluids with thermal conductivity more than the base fluid, there may exist an optimum concentration which maximizes the heat transfer in natural convection”. Ho et al. (Ho et al. 2010) evaluated the free convection heat transfer of alumina–water nanofluid in vertical square enclosures of three different sizes that were differentially heated across two vertical walls. They found that, for volume fractions of higher than 2%, the heat transfer of nanofluid is less than that of the base fluid. In contrast, nanofluid with a concentration of 0.1% in the largest enclosure with high Rayleigh numbers shows significant enhancement in heat transfer rate. They concluded that the considerable rise in heat transfer at small volume fractions of nanoparticles is caused by not only the alteration in thermophysical properties but also particle/fluid interactions such as thermophoresis and Brownian diffusion. There are some other experimental studies (Giwa et al. 2020a, 2020b) on other aspects of nanofluids, for example the effect of magnetic fields on flow and heat transfer behaviors of ferro-fluids. Recently, Murshed et al. (Murshed et al. 2020) reviewed the experimental studies on natural convection of nanofluids.

Regarding numerical investigations, Khanafer et al. (Khanafer et al. 2003) were the first to carry out a numerical study on the natural convection of nanofluids. In 2003, they analyzed the effect of suspended copper nanoparticles on fluid flow and heat transfer processes within the two-dimension enclosure. They assumed nanofluid to be a homogeneous mixture and utilized the single-phase model for the simulation. Their results showed that by increasing the volume fraction of nanoparticles, the heat transfer of nanofluid would continuously increase. Likewise, Ravnik and Ŝkerget (Ravnik and Škerget 2015) got the same results in their single-phase study on the natural convection of nanofluids. By comparing the experimental observations and the last two mentioned studies, it appears that there are considerable controversies between these two types of findings, and these numerical studies failed to observe the heat transfer deterioration in high volume fractions of nanoparticles, which was seen in experiments. It seems that assuming nanofluid as a uniform fluid and applying the single-phase method for its simulation can lead to controversial results since the slip velocity mechanisms would not be considered in the single-phase model. This controversy is also attributed to the uncertainties in different correlations which predict thermal conductivity and viscosity of nanofluids. Inconsistencies in such correlations, use of which is unavoidable in single phase simulations, would lead to contradictory results. Different definitions of Nusselt number can also be a reason for that (Choi et al. 2014).

On the other hand, there exist some numerical single phase works (Haddad et al. 2016; Mahian et al. 2016; Abu-Nada 2009) which have employed experimental correlations to calculate thermophysical properties of nanofluids, and could gain similar results to experiment. Nevertheless, with various and even controversial correlations developed for nanofluids’ thermophysical properties, these studies are unlikely to give a generalized solution to the prediction of nanofluid natural convection behavior. In addition, these studies are usually unable to give a good insight into interphase interaction effects. Accordingly, new attempts have been made to gain a better understanding of the characteristics of nanofluids, using two-phase approaches. Some of these studies are discussed in the following:

Buongiorno (Buongiorno 2006) tried to explain the increase of forced convection heat transfer in nanofluids. For this purpose, he considered seven slip mechanisms that can produce a relative velocity between nanoparticles and base fluid namely, inertia, Brownian diffusion, thermophoresis, diffusiophoresis, Magnus effect, fluid drainage, and gravity. He concluded that only Brownian diffusion and thermophoresis are two important slip mechanisms in nanofluids flow. He also developed a two-phase model which is known as the Buongiorno model.

Following the introduction of Buongiorno’s model (Buongiorno 2006), many researchers have attempted to study the nanofluid behavior using this method. Pakravan and Yaghoubi (Pakravan and Yaghoubi 2013) applied the mixture model for studying the natural convection of nanofluids in a square cavity and incorporated the effects of thermophoresis and Brownian diffusion. They found a decreasing trend in Nusselt numbers as the thermophoresis parameter and nanoparticle volume fraction increased. Their results indicated that nanoparticle migration has a strong impact on the thermo-hydrodynamics of nanofluids in natural convection. Hence, they concluded that disregarding the distribution of nanoparticles in nanofluids and assuming a uniform mixture in the single-phase methods may lead to unreliable results. Garoosi et al. (Garoosi et al. 2014) studied natural and mixed convection of alumina–water nanofluid in the square cavity using the Buongiorno model. Their results indicated that there is an optimal volume fraction for each Rayleigh and Richardson number where the maximum heat transfer is obtained. Mixed convection of nanofluid in an inclined enclosure was investigated by Esfandiary et al. (Esfandiary et al. 2016). They considered the Brownian motion and thermophoresis as two important slip mechanisms and compared the results of the two-phase mixture model with the single-phase method. They found that the two-phase mixture model was more accurate and showed better agreement with experimental measurements. A study of the relationship between natural convection of nanofluid and nanoparticles sedimentation was carried out by Meng et al. (Meng et al. 2016) using single-phase and two-phase mixture models. They concluded that particle sediment had a considerable effect on the natural convection of nanofluids since the sedimentation layer causes the heat to transfer through the conduction mechanism rather than convection. Yekani Motlagh and Soltanipour (Motlagh and Soltanipour 2017) examined the natural convection of alumina–water nanofluid in inclined enclosures with the Buongiorno method. They argued that in low Rayleigh numbers, where the dominant heat transfer mechanism is conduction, heat transfer continuously improves with volume fraction increment. However, for high Rayleigh numbers, the maximum heat transfer happens in an optimal volume fraction. The same results have been also found by Wang et al. (Wang et al. 2019) in a partially heated enclosure. Quintino et al. (Quintino et al. 2017) carried out similar research on metallic nanofluids and found that nanoparticle dispersion and nanofluid circulation result in forming two stationary layers of nanofluid in the top and bottom of the cavity that leads to heat transfer deterioration.

Several studies have also focused on the natural convection of \(CuO\)-water nanofluid by using the two-phase mixture model and found that the presence of \(CuO\) nanoparticles impedes heat transfer (Choi et al. 2014; Astanina et al. 2018). Choi et al. (Choi et al. 2014) explained that the reason for heat transfer deterioration with increasing the nanoparticle volume fraction is the increase in viscosity as well as the decrease in thermal expansion coefficient and specific heat. As mentioned in the literature, the performance of the two-phase Buongiorno model in simulation of nanofluids natural convection proves better than the single-phase model. However, this model has the drawback of requiring empirical correlations to calculate the nanofluid’s thermophysical properties which are subject to uncertainties. Another two-phase method, introduced to study two-phase fluid flows, is called the two-fluid model. There are some investigations, which employed the two-fluid model (also called the Eulerian model) to simulate forced or mixed convection of nanofluids (Kalteh et al. 2011; Ebrahimnia-Bajestan et al. 2016; Akbari et al. 2011, 2012; Göktepe et al. 2014; Ambreen and Kim 2017; Abhijith and Venkatasubbaiah 2020; Ghasemi et al. 2017; Rezaei Gorjaei and Rahmani 2021). Like previous studies, these investigations have found that two-phase models give more precise results in predicting convective heat transfer and friction factor. Kalteh et al. (Kalteh et al. 2011) considered the Eulerian method to simulate the forced convection heat transfer of copper–water nanofluid. They mentioned that one of the most significant advantages of this model, which solves two sets of conservation equations (mass-momentum-energy) for each phase, is that there is no need for correlations to model the thermophysical properties of nanofluids.

As can be seen in the literature, there is little or no work done on the natural convective heat transfer of nanofluids by using the Eulerian two-phase method. Accordingly, this paper aims to simulate the laminar natural convection of nanofluid with the assist of the Eulerian two-fluid model and show the superiority of this method. The results of the present study can assist design engineers to choose the most appropriate two-phase model for nanofluid simulations.

2 Methods

2.1 Problem Description

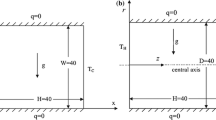
The present study aims to evaluate the performance of the two-fluid model in comparison with other models for predicting the experimental data (Ho et al. 2010). The computational geometry corresponds to the experimental study of Ho et al. (Ho et al. 2010). It is a two-dimensional vertical square cavity filled with alumina–water nanofluid, where the left and right sidewalls are at constant hot (\(T_{H}\)) and cold temperatures (\(T_{C}\)), respectively, with horizontal insulated walls. The height of enclosure (L) is 25 mm and the average temperature \(\left( {T_{avg} } \right)\) of nanofluids is 299 K. A schematic of the cavity and imposed boundary conditions is shown in Fig. 1. The simulations were performed for four different volume fractions, i.e. \(\varphi\)=0.1%, 0.3%, 1%, and 2%. Rayleigh numbers are varying between \(5 \times 10^{5}\) and \(3.5 \times 10^{6}\), in which the regime of flow is laminar (Fusegi and Hyun 1994). Since the flow in this particular problem is intrinsically transient, the unsteady forms of conservation equations were solved.

Fig. 1
figure 1

Schematic of the cavity

Full size image

2.2 Mathematical Formulation

2.2.1 Single-Phase Model

In the single-phase model, nanoparticles are assumed to be uniformly dispersed in the base fluid, so in this method, nanofluids are treated as homogenous mixtures. Moreover, there is no slip velocity and temperature difference between base fluid and nanoparticles. In other words, nanoparticle and base fluid are assumed to flow with the same velocity and temperature.

For single-phase method with Newtonian fluid and incompressible flow assumptions, three conservation equations i.e. mass, momentum, and energy equations are solved:

Mass:

$$\nabla \cdot v = 0$$
(1)

Momentum:

$$\rho_{nf} \frac{\partial v}{{\partial t}} + \rho_{nf} v \cdot \nabla v = - \nabla P + \mu_{nf} \nabla^{2} v - \rho_{0,nf} g\beta_{nf} \left( {T - T_{0} } \right)$$
(2)

where subscript \(nf\) stands for nanofluid. \(v\), \(g\), \(P\), \(\rho\), \(\beta\) and \(\mu\) are mixture velocity and gravity vectors, pressure, density, thermal expansion coefficient, and viscosity, respectively. The last term on the right-hand side of Eq. (2) represents the buoyancy term that comes into play in natural convection flows. \(T_{0}\) is the reference temperature (299 K) and \(\rho_{0,nf}\) denotes the nanofluid density at the reference temperature.

Energy:

$$\left( {\rho C_{P} } \right)_{nf} \frac{\partial T}{{\partial t}} + \left( {\rho C_{P} } \right)_{nf} v \cdot \nabla T = k_{nf} \nabla^{2} T$$
(3)

\(C_{P}\) and k represent the specific heat and thermal conductivity, respectively.

By considering no-slip condition at the walls, the boundary conditions would be adjusted as follows:

$$\left\{ {\begin{array}{*{20}c} {u = v = 0,\quad \frac{\partial T}{{\partial y}} = 0 \quad \quad \quad \quad {\text{on horizontal walls of the cavity}}} \\ {u = v = 0, \quad T = T_{H} \quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{on the left sidewall}}} \\ {u = v = 0, \quad T = T_{C} \quad \quad \quad \quad \quad \quad \quad \quad {\text{on the right sidewall}}} \\ \end{array} } \right.$$
(4)

Several experimental studies have measured the effective thermophysical properties of nanofluids. For single-phase modeling, the proposed correlations of Ho et al. (Ho et al. 2010) have been used to calculate the nanofluids thermal conductivity (\(k_{nf}\)) and viscosity (\(\mu_{nf}\)), which are as follows:

$$k_{nf} = k_{f} \left( {1 + 2.944\varphi_{p} + 19.672\varphi_{p}^{2} } \right)$$
(5)
$$\mu_{nf} = \mu_{f} \left( {1 + 4.93\varphi_{p} + 222.4\varphi_{p}^{2} } \right)$$
(6)

Subscripts f and p stand for base fluid and nanoparticles, respectively, and \(\varphi_{p}\) demonstrates the volume fraction of nanoparticles.

Nanofluids density, specific heat, and thermal expansion coefficient are calculated as below (Ho et al. 2010)

$$\rho_{nf} = \left( {1 - \varphi_{p} } \right)\rho_{f} + \varphi_{p} \rho_{p}$$
(7)
$$\left( {\rho C_{p} } \right)_{nf} = \left( {1 - \varphi_{p} } \right)\left( {\rho C_{p} } \right)_{f} + \varphi_{p} \left( {\rho C_{p} } \right)_{p}$$
(8)
$$\left( {\rho \beta } \right)_{nf} = \left( {1 - \varphi_{p} } \right)\left( {\rho \beta } \right)_{f} + \varphi_{p} \left( {\rho \beta } \right)_{p}$$
(9)

The quantities of thermophysical properties of water and alumina nanoparticles in average temperature are tabulated in Table 1 which are used in both single-phase and two-phase models. Since the temperature differences between the two vertical walls are relatively small, the variation of thermophysical properties such as thermal conductivity and viscosity are also small. Therefore, we can neglect these small variations and consider constant properties at the average temperature.

Table 1 Thermophysical properties of water and alumina nanoparticle at average temperature (299 K) (Ho et al. 2010; Wang et al. 1999)
Full size table

2.2.2 Two-Fluid Model

The two-fluid model is one of the Eulerian-Eulerian methods that solves two sets of conservation equations for each phase and employs the effect of interphase interactions. In this method, pressure is also shared by two phases (Vanaki et al. 2016). The governing equations of this model are two sets of mass, momentum, and energy equations.

Mass equations for fluid and nanoparticle phases are as follows (Fluent 2006):

$$\frac{\partial }{{\partial t}}\left( {\varphi _{f} \rho _{f} } \right) + \nabla \cdot \left( {\varphi _{f} \rho _{f} v_{f} } \right) = 0$$
(10a)
$$\frac{\partial }{\partial t}\left( {\varphi_{p} \rho_{p} } \right) + \nabla \cdot \left( {\varphi_{p} \rho_{p} v_{p} } \right) = 0$$
(10b)

Momentum equations for each of two phases are (Fluent 2006):

$$\frac{\partial }{{\partial t}}\left( {\varphi _{f} \rho _{f} v_{f} } \right) + \nabla \cdot \left( {\varphi _{f} \rho _{f} v_{f} v_{f} } \right) = - \varphi _{f} \nabla p + \nabla \cdot \tau _{f} - \rho _{{0,f}} g\beta _{f} \left( {T - T_{0} } \right){\text{ }} - F_{{lift,p}} - F_{{drag,p}} - F_{{TH}} - F_{B}$$
(11a)
$$\begin{aligned} \frac{\partial }{\partial t}\left( {\varphi_{p} \rho_{p} v_{p} } \right) + \nabla \cdot \left( {\varphi_{p} \rho_{p} v_{p} v_{p} } \right) = & - \varphi_{p} \nabla p + \nabla \cdot \tau_{p} - \rho_{0,p} g\beta_{p} \left( {T - T_{0} } \right) + F_{lift,p} \\ & \, + F_{drag,p} + F_{TH} + F_{B} \\ \end{aligned}$$
(11b)

where \(\tau_{f}\) and \(\tau_{p}\) are base fluid and nanoparticles stress tensors, and \(F_{lift,p}\), \(F_{drag,p}\), \(F_{TH}\), and \(F_{B}\) represent the lift, drag, thermophoresis, and Brownian force, respectively, that base fluid exerts on the nanoparticle phase. The stress tensors are defined as (Fluent 2006):

$${\varvec{\tau}}_{f} = \varphi_{f} \mu_{f} \left( {\nabla {\mathbf{v}}_{f} + \nabla {\mathbf{v}}_{f}^{T} } \right)$$
(12a)
$${\varvec{\tau}}_{p} = \varphi_{p} \mu_{p} \left( {\nabla {\mathbf{v}}_{p} + \nabla {\mathbf{v}}_{p}^{T} } \right)$$
(12b)

Energy equations for fluid and nanoparticles are as follows (Fluent 2006):

$$\frac{\partial }{{\partial t}}\left( {\varphi _{f} \rho _{f} C_{{p,f}} T_{f} } \right) + v_{f} \cdot \nabla \left( {\varphi _{f} \rho _{f} C_{{p,f}} T_{f} } \right) = {\text{ }}\tau _{f} :\nabla v_{f} - \varphi _{f} \nabla \cdot q_{f} {\text{ }} + \varphi _{f} T_{f} \beta _{f} \left( {\frac{{\partial p}}{{\partial t}} + v_{f} \cdot \nabla p} \right) + Q_{{pf}} {\text{ }}$$
(13a)
$$\frac{\partial }{{\partial t}}\left( {\varphi _{p} \rho _{p} C_{{p,p}} T_{p} } \right) + v_{p} \cdot \nabla \left( {\varphi _{p} \rho _{p} C_{{p,p}} T_{p} } \right) = \tau _{p} :\nabla v_{p} - \varphi _{p} \nabla \cdot q_{p} {\text{ }} + \varphi _{p} T_{p} \beta _{p} \left( {\frac{{\partial p}}{{\partial t}} + v_{p} \cdot \nabla p} \right) - Q_{{pf}}$$
(13b)

where \(q_{f}\) and \(q_{p}\) are base fluid and nanoparticle phase conduction heat fluxes:

$$q_{f} = - k_{f} \nabla T_{f}$$
(14a)
$$q_{p} = - k_{p} \nabla T_{p}$$
(14b)

\(Q_{pq}\) denotes the heat transfer rate between two phases (Fluent 2006):

$$Q_{pf} = h_{pf} \left( {T_{p} - T_{f} } \right)$$
(15)
$$h_{pf} = \frac{{6k_{f} \varphi_{p} \varphi_{f} Nu_{p} }}{{d_{p}^{2} }}$$
(16)

\(Nu_{p}\) is the Nusselt number of nanoparticle phase and can be calculated from Ranz and Marshall correlation (Ranz and Marshall 1952):

$$Nu_{p} = 2 + 0.6Re_{p}^{0.5} Pr^{0.333}$$
(17)

where \(Re_{p}\) denotes the relative Reynolds number based on nanoparticle diameter and \(Pr\) is the Prandtl number of base fluid:

$${\text{Re}}_{p} = \frac{{\rho_{f} \left| {v_{p} - v_{f} } \right|d_{p} }}{{\mu_{f} }}$$
(18)
$$\Pr = \frac{{C_{p,f} \mu_{f} }}{{k_{f} }}$$
(19)

In this study, the normal fluxes of nanoparticles at the walls are considered zero (\(J_{p} \cdot n = 0\)) corresponding to impermeable walls condition. \(J_{p}\) is the total flux of nanoparticles and is the summation of Brownian diffusion and thermophoresis fluxes (Esfandiary et al. 2016):

$$J_{p} = J_{p,B} + J_{p,T}$$
(20)
$$J_{p,B} = - \rho_{p} D_{B} \nabla \varphi , D_{B} = \frac{{k_{B} T}}{{3\pi \mu_{f} d_{p} }}$$
(21)
$$J_{p,T} = - \rho_{p} D_{T} \nabla T,\quad \quad D_{T} = K_{TH} \frac{{\nu_{q} }}{T}\varphi ,$$
(22)

At the walls, there is no normal mass flux of nanoparticles. Therefore, the following boundary conditions for mass flux can be obtained:

$$\frac{\partial \varphi }{{\partial y}} = 0\quad \quad {\text{on horizontal walls of the cavity}}$$
$$\frac{\partial \varphi }{{\partial x}} = - \frac{{D_{T} }}{{D_{B} }}\frac{\partial T}{{\partial x}}\quad \quad {\text{on sidewalls of the cavity}}$$
(23)

The other boundary conditions would be the same as that of the single-phase method (Eq. 4).

Thermophysical Properties At the nanoscale, materials start exhibiting new features. For example, the thermal conductivity of nanoparticle becomes lower than that of bulk one (Beck et al. 2009). The thermal conductivity of bulk alumina is around 36 \(\mathrm{W}/\mathrm{m}\bullet \mathrm{K}\) (Wang et al. 1999), while for alumina nanoparticle, it is much lower than that. Wang et al. (Wang et al. 1999) has proposed the quantity of 2.5 \(W/m \cdot K\) for thermal conductivity of alumina nanoparticle, which was used in this study.

In the two-fluid model, the nanoparticle phase is considered as a fluid. Therefore, it is essential to assign a measure of viscosity for it. For this purpose, Eqs. (6) and (24) were combined to get the Eq. (25).

$$\mu_{nf} = \mu_{p} \varphi_{p} + \mu_{f} \left( {1 - \varphi_{f} } \right)$$
(24)
$$\mu_{p} = \mu_{f} \left( {5.93 + 222.4\varphi_{p} } \right)$$
(25)

Interaction Forces In this study, four interphase forces namely, lift, drag, thermophoresis, and Brownian diffusion have been taken into accounst to investigate the behavior of nanofluids. It should be noted that since these forces are interactions, they are equal in magnitude and opposite in directions for the other phase. Below are formulations of the forces that base fluid exerts on the nanoparticle phase:

Lift force (Ekambara et al. 2008):

$$F_{lift,p} = - 0.5\rho_{f} \varphi_{p} \left( {v_{f} - v_{p} } \right) \times \left( {\nabla \times v_{f} } \right)$$
(26)

Drag force (Fluent 2006):

$$F_{drag,p} = K_{drag} \left( {v_{f} - v_{p} } \right)$$
$$K_{drag} = \frac{{\varphi_{f} \varphi_{p} \rho_{p} f}}{{\tau_{p} }}$$
$$\varphi_{f} = 1 - \varphi_{p}$$
$$\tau_{p} = \frac{{\rho_{p} d_{p}^{2} }}{{18\mu_{f} }}$$
$$f = \frac{{C_{D} {\text{Re}}_{p} }}{24}$$
(27)

where \(d_{p}\) is the diameter of nanoparticles.

\(C_{D}\) can be calculated from Schiller and Naumann correlation (Schiller and Naumann 1935):

$$C_{D} = \left\{ {\begin{array}{*{20}l} {{{24\left( {1 + 0.15\text{Re} _{p}^{{0.687}} } \right)} \mathord{\left/ {\vphantom {{24\left( {1 + 0.15\text{Re} _{p}^{{0.687}} } \right)} {\text{Re} _{p} }}} \right. \kern-\nulldelimiterspace} {\text{Re} _{p} }}} & {\text{Re} _{p} \le 1000} \\ {0.44\text{Re} _{p} {\text{ }}} & {\text{Re} _{p} \ge 1000} \\ \end{array} } \right.$$
(28)

Thermophoresis force (Yoa et al. 1990):

$$F_{TH} = \frac{{18\varphi_{p} \mu_{f} }}{{d_{p}^{2} }}v_{TH}$$
$$v_{TH} = - k_{TH} \frac{{\nu_{f} }}{T}\nabla T$$
(29)

where \(v_{TH}\) represents the thermophoretic velocity and \(\nu_{f}\) denotes the kinematic viscosity of the base fluid. \(k_{TH}\) is the thermophoresis parameter, whose quantity depends on the type of base fluid, particle, and fluid flow.

The thermophoresis parameter (\(k_{TH}\)) was calculated using Michaelides (Michaelides 2015) relation, which has been recently developed for nanofluids:

$$K_{TH} = A\left( {\frac{\alpha }{{\alpha_{0} }}} \right)^{ - B}$$
(30)

where \(\alpha\) is the nanoparticle radius, and \(\alpha_{0}\) is a constant which equals 1 nm (Michaelides 2015). For alumina–water nanofluid, the coefficients \(A\) and \(B\) are 1227 and 1.434, respectively (Michaelides 2015).

Brownian diffusion force could be obtained from its slip flux (Buongiorno 2006) as:

$$F_{B} = - \frac{{6k_{B} T}}{{\pi d_{p}^{3} }}\nabla \varphi_{p}$$
(31)

where \(k_{B}\) is the Boltzmann constant.

Another important parameter that should be considered is the nanoparticle diameter. Since nanoparticles agglomerate when dispersed in a fluid, the effective diameter of nanoparticles in nanofluid is usually more than their nominal size in powder form. An increase in nanoparticle volume fraction and decrease in mixture stability would lead to a larger nanoparticle size. Ho et al. (Ho et al. 2010) measured the effective diameter of the nanofluid at \(\varphi = 0.1\%\) and \(\varphi = 4\%\) and found \(d_{p}\) to be 129 nm and 167 nm, respectively. The effective nanoparticle diameter for other volume fractions have been gained by linear interpolation of these two values.

2.3 Numerical Procedure

The simulation of the present problem has been done by an in-house Fortran code, and the governing equations were solved using the finite volume approach. The linear momentum equations in each direction are discretized by the second-order approximate factorization method (Pletcher et al. 2012). The pressure and velocity components are coupled by the SIMPLE algorithm.

2.4 Grid Independence Study

A grid independence study has been performed to ensure that meshing is fine enough. Accordingly, grid study has been undertaken for both single-phase and two-phase models:

2.4.1 Single-Phase Modeling

For the grid study of the single-phase model, simulations were performed for pure water (\(\varphi = 0\)) with Ra = 7.4 × 105. Four grid structures with 100, 130, 171, and 200 nodes on each side of the cavity were tested, which were stretched near the walls, and the given Nusselt numbers were 8.75, 8.70, 8.65, and 8.63, respectively. The difference between the last two Nusselt numbers is about 0.2%. Therefore, the 171 \(\times\) 171 grid would be adequate for single-phase simulation. Comparison of temperature and velocity profiles for various mesh sizes in the midsection of the cavity can be seen in Fig. 2. This mesh grid is shown in Fig. 3.

Fig. 2
figure 2

Grid independence study results for single-phase modeling, a Temperature, b x-component of velocity, c y-component of velocity

Full size image
Fig. 3
figure 3

The generated 171 \(\times\) 171 mesh grid inside computational domain

Full size image

2.4.2 Two-Phase Modeling

For grid study of the two-phase model, simulations were performed for nanofluid with a volume fraction of 0.1% and Ra = 2.1 × 106. Three mesh sizes with 130, 171, and 200 nodes on each side were evaluated, and the obtained averaged Nusselt numbers were 10.28, 10.21, and 10.24, respectively. The difference between the two latter is less than 0.3%, so the 171 \(\times\) 171 grid was also chosen for two-phase studies. Figure 4 shows the temperature and velocity profiles of the primary phase with various mesh sizes in the midsection of the cavity, performed by two-phase simulations.

Fig. 4
figure 4

Grid independence study results for two-phase modeling, a Temperature, b x-component of velocity, c y-component of velocity

Full size image

3 Results and Discussion

The present study aims to evaluate the performance of the Eulerian Two-fluid model in simulation of nanofluids natural convection. Hence, the obtained results of this method have been compared with experimental measurements of Ho et al. (Ho et al. 2010) and other numerical methods, namely single-phase and mixture models.

Figure 5 shows the comparison between single-phase model, mixture model (Pakravan and Yaghoubi 2013), and two-fluid modeling of the present study for the prediction of experimental measurements of Ho et al. (Ho et al. 2010). This figure indicates that the present two-fluid modeling is more accurate than other modeling approaches.

Fig. 5
figure 5

Comparison of different numerical methods in simulation of heat transfer coefficients at φ = 2%

Full size image

Figure 6 illustrates the variation of Nusselt number with Rayleigh number at different volume fractions, obtained by present numerical simulations as well as experimental measurement. The two dimensionless parameters i.e. Nusselt and Rayleigh numbers were calculated as below:

$$Nu = hL/k_{nf}$$
(32)
$$Ra = \rho_{nf}^{2} C_{p,nf} \beta_{nf} g \cdot TL^{3} /\mu_{nf} k_{nf}$$
(33)

where L is 25 mm. Also, \(k_{nf}\) and \(\mu_{nf}\) are measured using Eqs. (5) and (6), respectively.

Fig. 6
figure 6

Variations of Nusselt number with Rayleigh number at a φ = 0.1%, b 0.3%, c 1%, d 2%

Full size image

Figure 7 depicts the variation of Nusselt number with volume fraction at Ra = 2.5 × 106 for single-phase and two-phase methods and experimental data. Since, the results at this Rayleigh number are not exactly available for all cases of single-phase model, two-fluid model, and experiment, the depicted points on Fig. 7 are interpolated values at Ra = 2.5 × 106. From Figs. 6 and 7 it can be seen that single-phase modelling overestimates the Nusselt number of both pure water and nanofluid (The values on Fig. 7 with \(\phi = 0\) is corresponding to base fluids). This overestimation has been observed in other studies (Pakravan and Yaghoubi 2013; Esfandiary et al. 2016) with different correlations for thermophysical properties. The reason for the lower heat transfer of a nanofluid in the two-fluid model can be attributed to the Brownian diffusion and thermophoresis interactions. As mentioned by Li and Peterson (Li and Peterson 2010) in their experimental study, the movement of nanoparticles in nanofluid, caused by Brownian diffusion and thermophoresis, can delay and impede the natural convective flow and consequently lead to heat transfer deterioration. Figure 7 also indicates that by increasing volume fraction the deviations between experimental measurements and numerical data become larger for both single-phase and two-fluid models.

Fig. 7
figure 7

Variation of Nusselt number with volume fraction at Ra = 2.5 × 106 for single-phase, two-phase and experimental data

Full size image

On the other hand, both the single-phase and two-fluid models predicted a similar trend in heat transfer variation of nanofluid with volume fraction, as shown in Fig. 8. This is due to using the same thermophysical properties for both models. Generally, the competing effects of increase in viscosity and increase in thermal conductivity with volume fraction governs the variation of Nusselt number with volume fraction. It is worth noting that, although single phase model predicts the trend of Nusselt number with volume fraction truly the value of Nusselt number resulted from single-phase model is far from that of two-fluid model. This figure shows the variation of Nusselt number with volume fraction at different Rayleigh numbers in single-phase and Eulerian two-fluid models. Moreover, it can be seen that the difference of Nusselt numbers obtained by the single-phase and Eulerian models are nearly the same and is around 1 for most of the studied cases. In both models and for all Rayleigh numbers, the concentration of 0.3% gives the maximum value of the Nusselt number and a marginal improvement in heat transfer relative to the base fluid. Further increase in volume fraction would worsen the heat transfer rate and lead to heat transfer deterioration. This trend is in agreement with experimental observations (Moradi et al. 2015; Ghodsinezhad et al. 2016), which observed an optimum level of heat transfer at a specific concentration, followed by heat transfer reduction at higher volume fractions. Recently, the experiments conducted by Sharifpur et al. (Sharifpur et al. 2021) showed that for zinc oxide–water nanofluid, the maximum heat transfer enhancement occurs at 0.1% volume fraction. At this optimum volume fraction for maximum Nusselt number, it seems that the effect of enhanced thermal conductivity of nanofluid is stronger than the negative effects of viscosity increase due to nanoparticles addition (Moradi et al. 2015). Moreover, Fig. 8 demonstrates that, with the same amount of increase in Rayleigh numbers, heat transfer improvement in low Rayleigh number flows is more than that of high Rayleigh flows. According to the relation \(Nu \propto Ra^{\frac{1}{4}}\) this observation is similar to natural convection of pure fluids (Bejan 2013). The results of Fig. 8 also shows that predicted Nusselt numbers using simulations are always higher than experimental ones. Comparing the experimental measurements of Ho et al. (Ho et al. 2010) for pure water with available correlations for pure fluids such as Berkovsky and Polevikov which is available at (Bejan 2013) shows that the Nusselt number of water measured by Ho et al. is smaller than the values obtained by correlations. We speculate that there are some heat losses in the experiment which lead to deterioration of Nusselt number which is not considered in the simulations.

Fig. 8
figure 8

Variation of Nusselt number with volume fraction at different Rayleigh numbers in single-phase and two-fluid models

Full size image

It should be noted that heat transfer of nanofluid is influenced by combined effects of viscosity and thermal conductivity of nanofluid. Higher viscosity leads to heat transfer degradation due to weaker natural convection circulation, while thermal conductivity growth would enhance it. By comparing the numerical data of base fluid and nanoparticle in the two-phase simulation, it was found that both phases flow with nearly the same temperature and velocity. Hence, temperature and velocity distribution for both phases are almost the same, and the related curves and contours obtained for each phase can be considered as the whole nanofluid characterizations.

Figure 9 shows the temperature and velocity distribution of nanofluid at the midsection of the cavity at different volume fractions, obtained by two-fluid model simulation, where the temperature difference is equal to 7.9 K. As it is evident in the diagram, nanoparticle addition to the base fluid has little effect on temperature distribution, and it is approximately the same for all the volume fractions under consideration, while it causes the magnitude of maximum x and y-velocity of nanofluid to decline. Therefore, near the walls, nanofluid with higher concentration circulates with lower speed, which is a negative effect on natural convection heat transfer. The velocity decline can be explained by the increase of viscosity and density of nanofluid with volume fraction increment.

Fig. 9
figure 9

a Temperature, b x-component of velocity and c y-component of velocity profiles of nanofluid at different concentrations by two-fluid simulation (∆T = 7.9 K)

Full size image

Figures 10 and 11 show the nanoparticle distributions for 2% and 0.3% alumina–water nanofluid. From the figures, it can be found that nanoparticle distribution is not uniform, although the differences of volume fraction within the cavity are small. The interaction forces between nanoparticles and base fluid (i.e., drag force, lift force, thermophoresis force, and Brownian diffusion) are responsible for nanoparticles migration and non-uniform distribution (Buongiorno 2006). Moreover, nanoparticles are more accumulated near the center of the cavity. This distribution has been also observed by Khalili et al. (Khalili et al. 2017) in their experimental investigation. Nevertheless, the previous studies with two-phase mixture models (Pakravan and Yaghoubi 2013) have failed to get similar results for nanoparticle distribution. Therefore, it indicates that the Eulerian two-fluid model is more accurate than the mixture model, in the prediction of both Nusselt number and nanoparticle distribution. In addition, as Figs. 10 and 11 indicates, the non-uniformity in nanoparticles is very small, and changing Rayleigh number from 6.5 × 105 to 2 × 106 does not show any significant changes.

Fig. 10
figure 10

Nanoparticle distribution for 2% nanofluid at a Ra = 6.3 × 105, b Ra = 1.1 × 106, c Ra = 1.7 × 106

Full size image
Fig. 11
figure 11

Nanoparticle distribution for 0.3% nanofluid at a Ra = 6.5 × 105, b Ra = 1.3 × 106, c Ra = 2 × 106

Full size image

Furthermore, the lower nanoparticle concentration near the walls would cause the effective thermal conductivity of nanofluids to decrease in these regions. Consequently, the natural convection flow cannot fully benefit from the nanoparticle's heat transfer characteristics. Figs. 10 and 11 can also be used to describe the reason for difference between single-phase model and two-fluid model. As can be seen in Fig. 8, the single-phase model always overestimates the Nusselt number compared to two-fluid model. In single-phase model the mechanisms for nanoparticles migration (i.e., thermophoresis and Brownian diffusion) are not considered. Therefore, the single-phase model assumes that nanoparticles are uniformly distributed. As Figs. 10 and 11 show, two-fluid model results in non-uniform nanoparticle distribution with lower volume fraction near walls. Lower volume fraction near walls causes lower effective thermal conductivity near walls which lead to lower heat transfer rates with respect to single-phase modelling.

4 Conclusions

The natural convective flow of alumina water nanofluid in a square cavity is investigated, using the Eulerian two-fluid model. The following conclusions are obtained:

The results are in good agreement with experimental measurements, and they indicate that the Eulerian two-fluid model can better predict the Nusselt number of nanofluid in natural convection, compared with mixture model and single-phase simulation. Our results indicate that the error in prediction of Nusselt number with two-fluid model is the half of the single-phase model. The maximum difference between single-phase model and experimental values is about 27%, while the corresponding value from two-fluid model is 13%. In addition, the nanoparticles distribution predicted by the Eulerian two-fluid model is consistent with experimental observations, which is not the case for the mixture model. Therefore, it could be concluded that, in the case of nanofluids natural convection, the two-phase models are more accurate than single-phase models, and among two-phase models, the two-fluid model is superior to the mixture model. Moreover, Nanoparticle distributions form similar shapes to streamlines, where higher magnitude of velocity results in lower nanoparticle concentration and vice versa.

It is also revealed that alumina nanoparticles would enhance the natural convective heat transfer of nanofluid, up to a concentration of 0.3%. At higher volume fractions, heat transfer of nanofluid deteriorates, compared to that of the base fluid. In addition, the results indicate that, with the same amount of increase in Rayleigh numbers, heat transfer enhancement at low Rayleigh flows would be more than that of high Rayleigh flows. Nusselt number at 0.3% volume fraction is 1.5–4.5% more than base fluid. The value of this enhancement in Nusselt number decreases with Rayleigh number. The lower limit is for Rayleigh number 2.5 × 106 and the upper limit is for 7.5 × 105. Adding more nanoparticle to the base fluid reduces the Nusselt number. At 2% volume fraction Nusselt number is up to 5% lower than base fluid.