1 Introduction

Reducing the resistance and increasing the speed of high-speed craft have always been one of the primary aims of designers in developing new hull forms for this type of vessels. Therefore, they have taken an essential step toward increasing the stability and decreasing the drag of the vessel by introducing different novel hulls. Planning hulls are one of the most common types of high-speed crafts used for variety of military and recreational purposes. The development of various types of longitudinal discontinuities such as spray rails as well as transverse discontinuities such as transverse steps can have a significant effect on reducing the drag and increasing the stability of planing hulls (Niazmand Bilandi et al. 2018). Among the most essential advantages of stepped hulls are the low ratio of drag to lift at high speeds and the decrease in wetted surface area due to the flow separation from the step(s). In fact, the two important dimensions of the step, which are the height of the step and the longitudinal distance of the step from the aft of the vessel, play an important role in the hydrodynamics of the stepped hulls. Transverse steps have so far been designed in various types such as flat, dinaplan, and sweepback. The presence of steps on the bottom of the planing hull leads to the formation of air cavities in the bottom and significantly reduces the frictional resistance. Several experimental, analytical, and numerical research have been performed on transverse steps. Makasyeyev (2009) proposed a mathematical method to predict the air cavity formed behind the step, based on the dimensionless numbers of Froude and Cavitation and other effective features. Matveev (2012) used a sink and source method to simulate a two-dimensional planing hull. He stated that the most important factors influencing the shape of the cavity are the number, height, and position of the steps. Brizzolara and Federici (2010) have also examined the effect of the presence of air cavities in hydrodynamic behavior of stepped planing hulls by comparing stepped and non-stepped models. In 2009, Savitsky (2010) conducted some extensive experiments on several types of single-step mono-hulls to provide empirical formulas for prediction of wake profiles in different deadrise angles. The results of this research are semi-empirical formulas based on the results of conducted tests. These relations facilitate the design conditions of stepped hulls. They can be used for specific ranges of parameters such as trim angle, velocity coefficient, and load factor of these type of vessels.

Numerical simulation is a conventional method of predicting the hydrodynamic behavior of a vessel. In this method, by eliminating human errors and the cost of testing, or the complex process of solving equations in the mathematical methods, an accurate solution is obtained in a shorter time and at a lower cost. Also, many hydrodynamic details that cannot be obtained using experiments or mathematical methods can be easily presented using numerical simulation. Therefore, many researchers have used a variety of numerical methods to study the hydrodynamics of planing hulls (Shademani and Ghadimi 2017a, b, c, d; Sajedi et al. 2019; Doustdar and Kazemi 2019; Lotfi et al. 2015). In 2012, Garland and Maki (Garland and Maki 2012) conducted a study on two-dimensional stepped planing hulls that examined the optimal height of step for maximum possible lift. Numerical studies on the hydrodynamics of single-step planing hulls were also followed by some other researchers (Brizzolara and Federici 2013; Fu et al. 2014). Hay et al. (2006) conducted a study in which they simulated a two-phase flow around moving objects using dynamic mesh method. This numerical method was used to calculate the unstable flow around a prismatic body that collided with the water surface, symmetrically, and asymmetrically. The very high validity of the results determined the applicability of the mentioned method for accurate free surface modeling. Ghadimi et al. (2014) presented a parametric study by providing a computer program. They examined the position and three-dimensional profile of the spray. Taunton et al. (2010) studied a new series of hard chine planing hulls in an experimental study in calm water and the presence of waves. In these experiments, three models of a same vessel were studied in stepless, single-step, and double-step modes. Vitiello et al. (2012), Lee et al. (2014), and Svahn (2009) are researchers who have worked experimentally and numerically on one and double-step vessels. Cucinotta et al. (2017) investigated the effect of bubble injection on hydrodynamic performance and drag of single-step high-speed mono-hulls. De Marco et al. (2017) examined the flow pattern around the vessel and examined the effect of step on hydrodynamic behavior of a vessel. On the other hand, some research has been done on the stability of stepped planing hulls. If the left and right sides of the step are not ventilated in the same way, a yaw motion could be applied to the vessel by the fluid, which can eliminate the stability (Timmins 2014; Ghadimi and Panahi 2018, 2019). Another valuable study that has been done on stepped planing hulls is the study of the effect of loading and deadrise angle on the vessel. The performance of a stepped planing hull could reduce by an incorrect selection of the center of gravity and weight distribution (Kazemi and Salari 2017; Konstantin et al. 2015). Afriantoni et al. (2020) studied the stability of high-speed craft with hull angle variations.

According to the presented literature review, providing step(s) in a planing hull usually reduces resistance. However, no comprehensive study has been performed on the effect of different shapes of steps on stepped planing hulls. So far, the effect of the angle of the various steps on the performance of the planing hull has not been studied and compared. Therefore, in the current paper, four planing models with different forms of step are investigated experimentally and numerically. The numerical simulation is conducted in two degrees of freedom, namely the motions of heave and pitch using Star CCM + software. Among these four models, the first model is a non-step model, and the other three models are equipped with transverse step, pointed aft step, and re-entrant Vee step, respectively. The aim of this study is to investigate the effect of step shape and angle on mono-hull planing-hull performance. This paper compares hydrodynamic parameters such as drag, trim, and rise-up. In numerical simulation, the pressure contours, wave pattern, and wake of different models are compared with each other.

2 Problem Definition

Three types of step forms are used in high-speed vessels. The first type of step is flat and is known as the transverse step. The second and third forms of the steps are angled, which are called pointed aft and re-entrant Vee step. Figure 1 shows these three forms of steps, along with a view of the bottom of the non-step model.

Fig. 1
figure 1

Model A: non-step—model B: transverse step—model C: pointed aft step—model D: re-entrant Vee step

Full size image

Until recently, the stepped vessels used mostly flat steps. However, nowadays, the use of angled steps is more common. The primary reason for this increase is proper ventilation of these types of steps while the vessel is moving. In this paper, the performances of these three types of steps are compared.

3 Introducing Test Models

In the present paper, four planing hull models are studied, experimentally. All models are similar and differ only in the shape of steps. These models are made based on a hard-chine planing-hull prototype and are shown in Fig. 1. The length, width, and weight of these models are 2640 mm, 551 mm, and 86 kg, respectively. The distance from the center of gravity of the models to their aft is 791 mm. The weight factor (CD) is equal to 0.5. Table 1 shows the full specifications of these models.

Table 1 Principal characteristic of the investigated models
Full size table

Figure 2 shows a body plan view of model A. The models are based on a Cougar vessel prototype and are modeled on a 1: 5 scale. The deadrise angle of these models in the aft is 24°. The height of the steps of these models is 25 mm, which is about 4% of their width. This percentage is in the range of height-to-width ratio of the investigated models in some experimental and numerical research done in different papers. Table 2 provides a comparison between this ratio in some well-known studies.

Fig. 2
figure 2

Body lines of model A

Full size image
Table 2 Height-to-width ratio of step in some well-known experimental studies
Full size table

3.1 Description of Experiments

The experiments are conducted in the towing tank of the National Persian Gulf Marine Laboratory. The main specifications of this laboratory are given in Table 3. All tests are performed according to ITTC recommendations. All experiments conducted performed in calm water with a temperature of 293 K, a density of 1002 kg/m3, and a viscosity of 1.9E−6 m2/s. The maximum speed of the carriage is 19 m/s, and it has two different speed modes. Low-speed mode covers speeds from 0 to 5 m/s, and the high-speed mode ranges from 5 to 19 m/s. Three sensors are installed on the models to determine the resistance, trim, and rise-up.

Table 3 Dimensions and features of towing tank
Full size table

Figure 3 shows a view of the installation of the sensors on the model. The models are attached to the carriage and towed at the intersection of the shaft direction with the center of gravity. The angle of the shaft direction with the horizon is 6°, and the distance of the center of gravity from the aft of the model is 791 mm. Figure 3 shows two potentiometers and one dynamometer.

Fig. 3
figure 3

Location of sensors on the models

Full size image

Potentiometers 1 and 2 measure the value of rise-up in two different positions, and the value of the center of gravity is calculated using simple mathematical calculations as in

$$\tau {\text{ = tan}}^{ - 1} \left(\frac{{Z_{10} - Z_{1} }}{{L_{10 - 1} }}\right)$$
(1)

Table 4 also shows the error associated with the sensors and laboratory meters.

Table 4 Error values in laboratory sensors
Full size table

The uncertainty condition for resistance and trim is calculated according to Eqs. 2 and 3.

$${{U}_{\rm CT}}^{2}={\left({{U}_{{\varvec{B}}}}_{\rm CT}^{\rm Tw}\right)}^{2}+{\left({K.U}_{{P}_{\rm CT}}\right)}^{2}$$
(2)
$${\left({U}_{\tau }\right)}^{2}={\left({B}_{\tau }\right)}^{2}+{\left({P}_{\tau }\right)}^{2}$$
(3)

Equations 2 and 3 represent uncertainties of total drag and total trim, respectively. These two quantities are calculated based on the total drag coefficient and trim of the models, respectively. The results of calculations performed for model A (without step) are given in Table 5.

Table 5 The uncertainty for model A
Full size table

3.2 Experimental test results

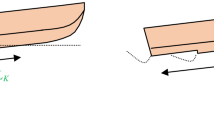
Table 6 shows the measured trim and drag from the experiments of models A, B, C, and D in the towing tank. Figure 4 shows images taken by a video camera connected to the carriage.

Table 6 Measured parameters for models A, B, C, and D
Full size table
Fig. 4
figure 4

Dry surface area below the stepped models at the speed of 9 m/s, a model B, b model C, c model D

Full size image

The results of test model A show that at speeds above 8 m/s, the porpoising phenomenon occurs. However, the results of other test models show that they are stable with the help of steps. The reason for this stability is the proper pressure distribution at the bottom of the stepped models. Model C has the lowest resistance and the highest dry surface area due to proper ventilation. On the other hand, model D has the highest resistance among the tested models due to lack of proper ventilation. Of course, all stepped models are stable and porpoising is avoided at any speed. Figure 4 shows a view of models B, C, and D.

Subsequently, numerical simulations are performed in Star CCM + software. With the help of experimental data, the numerical results are validated and finally the pointed aft and re-entrant steps are modeled with different angles to extract the optimal angle.

4 Numerical Simulation

4.1 Governing Equations of Turbulent Flow

First, equations are written for instantaneous quantities, that is, time-averaged quantities along with oscillating quantities. Then, each side of the equation is averaged over time. It should be noted that if there is an equation for instantaneous quantities, this equation will also be established for its time average (for a specific range of time). Finally, equations can be simplified to the point where time-averaged quantities appear. As a result, the following statement is obtained for compressible flow:

$$\frac{\partial }{{\partial x}_{i}}\left(\overline{\rho {u}_{i}}\right)+\frac{\partial }{\partial {x}_{i}}(\overline{p{^{\prime}}{{u}^{^{\prime}}}_{i}})=0$$
(4)

Since ρ' = 0, the above equation for the incompressible flow is as follows:

$$\frac{\partial \overline{{u}_{i}}}{\partial {x}_{i}}=0$$
(5)
$$\rho \left[\frac{\partial \overline{{u}_{i}}}{\partial t}+\overline{{u}_{j}}\frac{\partial \overline{{u}_{i}}}{\partial {x}_{j}}\right]=\overline{{B }_{l}}-\frac{\partial \overline{\rho }}{\partial {x}_{i}}+\frac{\partial }{\partial {x}_{j}}\left[\mu \frac{\partial \overline{{u}_{i}}}{\partial t}-\rho \overline{{u{^{\prime}}}_{i}{u{^{\prime}}}_{j}}\right]$$
(6)

The only difference between the above momentum equation and the momentum equation with instantaneous quantities is the addition of the last term, \(\rho \overline{{u{^{\prime}}}_{i}{u{^{\prime}}}_{j}}\), on the right side of the equation. This term is called turbulent tension or Reynolds tension. The only difference between laminar flow and turbulent flow equations is the presence of this term. In general, this term is not a physical tension, but an effect of inertia (momentum) exchange. It should be noted that this term has been moved to the right from the left side of the momentum equation, where there are inertial expressions.

On the other hand, Reynolds stress tensor, \((\overline{{u{^{\prime}}}_{i}{u{^{\prime}}}_{j}})\), is based on Boussinesq’s hypothesis:

$$\overline{{u{^{\prime}}}_{i}{u{^{\prime}}}_{j}}={v}_{t}\left(\frac{\partial {U}_{i}}{\partial {x}_{j}}+\frac{\partial {U}_{j}}{\partial {x}_{i}}\right)+\frac{2}{3}{\delta }_{ij}k$$
(7)

In the above relation, \({v}_{t}\) represents the vortex viscosity used in the standard \(k-\epsilon\) turbulence model. This parameter is obtained using the relation \({v}_{t}={C}_{\mu }\frac{{k}^{2}}{\varepsilon }\), where \({C}_{\mu }\) is an empirical constant and is assumed 0.99. The parameters of \(k\) and \(\epsilon\) also represent the kinematic energy of the turbulence and the scattering rate of \(k\), respectively. These two parameters are obtained using the standard \(k-\epsilon\) turbulence model. Standard \(k-\epsilon\) is a two-equation model that uses the following transfer equations to express the turbulent properties of the flow.

$$\frac{\partial k}{\partial t}+\frac{\partial }{\partial {x}_{i}}\left(k\overline{{U }_{i}}\right)=\frac{\partial }{\partial {x}_{i}}\left[\left(v+\frac{{v}_{t}}{{\sigma }_{k}}\right)\frac{\partial k}{\partial {x}_{i}}\right]+{P}_{k}-\varepsilon$$
(8)
$$\frac{\partial \varepsilon }{\partial t}+\frac{\partial }{\partial {x}_{i}}\left(\varepsilon \overline{{U }_{i}}\right)=\frac{\partial }{\partial {x}_{j}}\left[\left(v+\frac{{v}_{t}}{{\sigma }_{\varepsilon }}\right)\frac{\partial \varepsilon }{\partial {x}_{j}}\right]+\frac{\varepsilon }{k}\left({{C}_{\varepsilon 1}P}_{k}-{C}_{\varepsilon 2}\varepsilon \right)$$
(9)

These two equations consist of four adjustable constants of \({C}_{\varepsilon 1}=0.44\), \({C}_{\varepsilon 2}=1.92\) and turbulent Prandtl numbers of \(k\) and \(\epsilon\), that is \({\sigma }_{k}=1\) and \({\sigma }_{\varepsilon }=1.3\).

4.2 Volume of Fluid (VOF) Model

Volume of Fluid model is used to simulate free surface. This model uses a concept called equivalent fluid. Here, it is assumed that the (two) phases of the fluid share the same velocity and pressure. This ultimately allows them to be solved as a single-phase flow with the same set of governing equations of momentum and mass described in the previous section. Volumetric fraction, \({\alpha }_{i}\), of phase i describes which cell surface is filled with the corresponding fluid (Afriantoni et al. 2020).

$${\alpha }_{i}=\frac{{V}_{i}}{V}$$
(10)

The fluid volume method is appropriate when the provided grid is dense enough to resolve the connection between the two non-mixed fluids, and this model is a simple multiphase model. As observed in Fig. 5, where the volume fraction value is 0.5, the free surface is defined as a boundary. It should be noted that this location is not at the center of the control volume, but the geometric values (Mancini 2015).

Fig. 5
figure 5

The basis of the fluid volume fraction method (CD-Adapco 2017)

Full size image

An additional equation called volume fraction convention equation is added to the mass and momentum equations to simulate the dynamics of the waves. Assuming that the flow is incompressible, this equation is defined as follows (Mancini 2015):

$$\frac{\partial }{\partial t}\underset{V}{\overset{}{\int }}{\alpha }_{i}\mathrm{d}V+\underset{V}{\overset{}{\int }}{\alpha }_{i}\left(V-{V}_{b}\right)n\mathrm{d}S=0$$
(11)

The physical properties of the equivalent fluid inside a control volume are calculated as functions of the physical properties (density and viscosity) of the phases and their volumetric fractions (Mancini 2015).

$$\left\{\begin{array}{l}\rho =\sum_{i}{\rho }_{i}{\alpha }_{i}\\ \mu =\sum_{i}{\mu }_{i}{\alpha }_{i}\\ 1=\sum_{i}{\alpha }_{i}\end{array}\right.$$
(12)

4.3 Methods in CFD Simulation

To achieve high accuracy in software simulations, it is necessary to perform precise geometry modeling, to properly select the computational domain, meshing, determination of boundary and initial conditions, selection of appropriate solver and time step. In the present paper, the simulation is based on the parameters presented in Table 7.

Table 7 Specifications of CFD simulation
Full size table

To properly estimate all the unknown hydrodynamic parameters at each time step, the RANS equations are solved in implicit unsteady and iterative manner. The coupled pressure–velocity and the whole solution process are based on the SIMPLE method. The selected turbulence model is \(k-\epsilon\). The simulation is done in two degrees of freedom, namely the heave and pitch motions. These degrees of freedom are simulated using the dynamic fluid-body interaction (DFBI) model of the software. The RANS solver computes the forces and moments exerted on the models. This model also solves the motion equations and computes the displacements, velocities, and linear as well as angular accelerations relative to the coordinate system connected to the vessel. On the other hand, due to the transitional and rotational motions of the models, a moving domain, connected to the model inside a stationary domain, is required. The mesh changing in the overset dynamic mesh method is more suitable for monitoring the severe heave and pitch motions than the morphing method. The two-phase flow, which includes water and air, is solved using the VOF model and is based on tracking the free surface boundary.

Studies show that the size of computational domain and the distance of the model from its boundaries greatly affect the accuracy of the results. In fact, the domain boundaries should be far enough away from the model so that the effects of the model geometry on the flow do not affect the domain boundaries. According to ITTC recommendation of 2011 (ITTC 2008a), the distance from the back boundary to the hull should be between 3 and 5 times the length of the model, and the distance between the upstream, top, bottom and sides to the hull should be between one and two times the length of the model. Also, to increase the accuracy of results and Kelvin wave pattern around the model, a control volume in the shape of a cone with an angle of 19.28° has been created. The center of this control volume is the free surface, and smaller cells are used in this region. Figure 6 shows one of the options proposed by Sheingart (2014) to create a computational domain. In this figure, \({L}_{P}\) is the length of the vessel, and λ is calculated using Eq. (13). The U parameter also indicates the horizontal component of the flow velocity.

Fig. 6
figure 6

Selection pattern of computational domain (Failed 2014)

Full size image
$$\lambda \approx 2\pi \frac{{U}^{2}}{g}$$
(13)

The general computational domain, as shown in Fig. 6, is a rectangular cube whose length depends on the model velocity. Based on Eq. 17, with increasing speed, the domain length must also increase. Therefore, in the present paper, all simulations are performed in a computational domain with dimensions proportional to the highest speed examined. Figure 7 shows a view of this computational domain. The length overall (LOA) of the model is assumed to be 2.64 m. The next important step in simulation process is to apply the boundary conditions of the problem. In the simulation process, due to the high computational cost, half of the model is modeled, and the symmetry condition is applied. As observed in Fig. 7, the upstream and downstream boundaries are velocity inlet and pressure outlet, respectively. The model is considered a no-slip wall, and the conditions of the upper and bottom sides are velocity inlet.

Fig. 7
figure 7

Computational domain

Full size image

The discretization of the computational domain is performed using a structured mesh with quadrilateral (hexagonal) cells. This type of mesh is the most suitable and high-quality option to model complex two-phase problems and is used for external flows. The process of selecting the size of the mesh is done in relation to a base value, and then, the required corrections are made around the model, step, moving domain, and free surface. The top, front, and side views of the mesh, as well as the boundary layer around the stepped model, are shown in Fig. 8.

Fig. 8
figure 8

The top, front, and side views of the mesh and the boundary layer around the stepped model

Full size image

An important criterion that should be considered in the production of the grid within the boundary layer is \({y}^{+}\), which refers to the dimensionless distance of the first node of the mesh from the surface. Using the standard turbulence model of \(k-\epsilon\), which consists of two equations, a series of additional wall functions are required to obtain the relations of the variables between the wall and the totally turbulent region. The velocity in this region changes logarithmically relative to \({y}^{+}\) (Eq. 14). Under the Stanford Convention, the von Karman constant is defined as K = 0.41 and B = 5 (ITTC 2008a).

$${U}^{+}=\frac{1}{\kappa }\mathrm{ln}\left({y}^{+}\right)+B$$
(14)

\({U}^{+}\) is the dimensionless velocity of flow and a function of the frictional velocity, \({u}_{t}\). Another point to note is the choice of time step (\(\Delta t\)) according to Eq. 19, which is expressed as a function of length (\(l\)) and velocity (\(V\)) based on the ITTC recommendation of 2008 (ITTC 2011). Here, this length is assumed to be equal to the wetted length of the keel (\({L}_{k}\)) of the model.

$$\Delta t=0.01\sim 0.005\frac{l}{V}$$
(15)

It should also be noted that the Courant number (CFL) remains below 1 as a function of the time step, speed, and minimum element length in the direction of fluid flow. Equation 16 defines the Courant number.

$$C=\frac{V_{i}\cdot \Delta t}{\Delta x_{i}}\le C_{\rm max}$$
(16)

\(\Delta x\) is the distance of the first cell, the smallest cell, from the body surface. Of course, the Courant number changes as the Froud number changes.

4.4 Validation

Validation of drag, trim, and rise-up calculations of model B for three different types of structured trimmer hexahedral dynamic mesh is performed at a Froude number of 1.97 (speed of 9 m/s). Table 8 shows the calculated resistance of model B for different mesh at 9 m/s speed. It is observed that by increasing the number of cells to more than \(1.7\times {10}^{6}\), there are no significant changes in the resistance force, and therefore, this number of cells is suitable for this simulation.

Table 8 Accuracy of the computed resistance using different numbers of cells
Full size table

Uncertainty of numerical simulation at this speed can be determined based on the method provided by Wilson et al. (2001). Recommendation of ITTC in 2008 (2008b) explains that the \({U}_{{\rm SN}}\) numerical simulation uncertainty consists of three different uncertainties: repetition, \({U}_{{\rm I}}\), grid, \({U}_{{\rm G}}\), and time stack, \({U}_{{\rm TS}}\). Equation 17 calculates the overall uncertainty of the simulation:

$${U}_{{\rm SN}}^{2}={U}_{{\rm I}}^{2}+{U}_{{\rm G}}^{2}+{U}_{{\rm TS}}^{2}$$
(17)

According to Wilson et al. (2001), the most critical source of numerical simulation uncertainty is grid uncertainty. Therefore, as presented in Table 8, the grid convergence Index (GCI) of three different grids has been calculated using the reliability factor of 1.25 proposed by Roache (2002). Studies show that the convergence coefficient, \({R}_{K}={\varepsilon }_{{21}_{K}}/{\varepsilon }_{{32}_{K}}\), is in the range of \(0<{R}_{K}<1\), so it satisfies the monotonic convergence. In this method, the average value of apparent order is calculated using Eq. 22.

$${P}_{{\rm avg}}=\frac{1}{\mathrm{ln}({r}_{21})}\left|\mathrm{ln}\left|{\varepsilon }_{32}/{\varepsilon }_{21}\right|+q({P}_{{\rm avg}})\right|$$
(18)

where

$$q\left({P}_{{\rm avg}}\right)={\rm ln}\left(\frac{{r}_{21}^{{P}_{{\rm avg}}}-s}{{r}_{32}^{{P}_{{\rm avg}}}-s}\right)$$
(19)

In the present study, mesh correction factors are \({r}_{21}=\sqrt{2}\) and \({r}_{32}=\sqrt{2}\). Besides, for the calculated parameters such as trim, drag, and rise-up, which are denoted by φ, there are two relations of ε21 = φ2 − φ and ε32 = φ3 − φ2, which are given in Eq. 18. Subsequently, four parameters of extrapolated value, defined approximated relative error, extrapolated relative error, and fine-grid convergence index, are defined in Eqs. 20–23, respectively. These parameters are all used in the calculation of the ultimate value of GCI. Defined parameters are obtained for intended hydrodynamics resistance in Table 9.

Table 9 CGI method for hydrodynamics resistance
Full size table
$${\varphi }_{\rm ext}^{32}=\left({r}_{32}^{{P}_{{\rm avg}}}{\varphi }_{2}-{\varphi }_{3}\right)/\left({r}_{32}^{{P}_{{\rm avg}}}-1\right)$$
(20)
$${e}_{\rm a}^{32}=\left|\frac{{\varphi }_{2}-{\varphi }_{3}}{{\varphi }_{2}}\right|$$
(21)
$${e}_{\rm ext}^{32}=\left|\frac{{\varphi }_{\rm ext}^{23}-{\varphi }_{2}}{{\varphi }_{\rm ext}^{23}}\right|$$
(22)
$${\rm GCI}_{\rm fine}^{32}=\frac{1.25{e}_{\rm a}^{32}}{{r}_{32}^{{P}_{{\rm avg}}}-1}$$
(23)

Table 10 compares the results of the simulation of stepped models at two speeds of 8 and 9 m/s with the corresponding experimental measurements.

Table 10 Comparison of experimental and numerical results at the speeds of 8 and 9 m/s
Full size table

Figure 9 displays the \({y}^{+}\) value at the bottom of the models. These values are for models B and C at speeds of 8, 9 and 10 m/s. As evident in Fig. 9, these values of \({y}^{+}\) are all less than 100, which is acceptable according to the selected turbulence model.

Fig. 9
figure 9

The value of \({y}^{+}\) for model B at the speeds of a 9 m/s, and b 10 m/s, and for model C at the speeds of c 9 m/s, and d 10 m/s

Full size image

4.5 Simulation and Numerical Results

4.5.1 Trim, Rise-Up, and Drag

In addition to the steps used in the experimental study, other types of steps have been modeled to examine the effect of step shape on the performance of models. Table 11 shows the main specifications of all types of steps studied in the present paper. The three steps, which were first tested, are given the same name in this table and are marked in dark color. Figure 10 is presented to provide a proper understanding of the values given in Table 11.

Table 11 Numerical models
Full size table
Fig. 10
figure 10

Identifying the parameters used in Table 11

Full size image

Simulations are conducted at three speeds of 8, 9, and 10 m/s. The results of rise-up, trim and drag are given separately in Tables 12, 13, 15 and 16. In three angles of 156°, 134° and 114°, the performance of stepped vessels has been investigated.

Table 12 Computed resistance, trim, and rise-up of the models equipped with a transverse step
Full size table
Table 13 Computed resistance, trim, and rise-up of the models equipped with a pointed aft step at a speed of 8 m/s
Full size table

Among the three models of B0, B, and B1, the drag of model B is the lowest. This is because the trim and rise-up of this model are more than those of other models. Model B, on the other hand, has the highest drag and the lowest rise-up. Figure 11 shows the trim, drag, and rise-up at three speeds for the three models equipped with a transverse step.

Fig. 11
figure 11

Comparison of drag, trim, and rise-up of models equipped with a transverse step at 9 m/s speed

Full size image

In general, by decreasing the angle in three positions of B0, B, and B1, the drag is reduced. As the angle decreases, the trim and rise-up also decrease. The model equipped with a pointed aft step has less drag than the model equipped with a transverse step. One of the reasons for this reduction is the proper ventilation of the pointed aft step. All models equipped with pointed aft steps with different angles, at three speeds of 8, 9, and 10 m/s, exhibit less drag than the models equipped with transverse steps. Tables 14 and 15 show the numerical results of the resistance, trim, and rise-up of the models equipped with pointed aft steps at speeds of 9 and 10 m/s.

Table 14 Computed resistance of resistance, trim and rise-up of the models equipped with pointed aft step at a speed of 9 m/s
Full size table
Table 15 Computed resistance of resistance, trim and rise-up of the models equipped with pointed aft at a speed of 10 m/s
Full size table

As observed in Tables 13, 14, and 15, drag decreases as the trim angle and rise-up decrease.

Figures 12, 13, and 14 show the effect of step length on drag, trim, and rise-up. If the step is as much as 27% of the vessel length away from the aft of the vessel, the best performance is achieved. In model B, which has the lowest drag, step is at such a distance from the aft of the model. The lowest and highest values of trim and rise-up are also provided in B1 and B0 models, respectively.

Fig. 12
figure 12

Effect of the position of pointed aft step at an angle of 156° on a drag, b trim, and c rise-up of the models

Full size image
Fig. 13
figure 13

Effect of the position of pointed aft step at an angle of 134° on a drag b trim c rise-up

Full size image
Fig. 14
figure 14

Effect of the position of pointed aft step at an angle of 114° on a drag b trim c rise-up

Full size image

The performance of models equipped with pointed aft steps is shown in two ways in Figs. 12, 13, 14 and 15. Figures 12, 13 and 14 show the trim, drag, and rise-up values of these models. By comparing these diagrams, the effect of the location of this type of step on the performance of the model can be predicted. The three positions on which the pointed aft steps are mounted, B0, B, and B1 are 25, 27, and 29% of the model’s length to the aft of the models, respectively. Also, the pointed aft step in each of the positions of B0, B, and B1 is studied at three angles of 156, 134, and 114, respectively.

Fig. 15
figure 15

Effect of angle on pointed aft steps in the positions of a B0, b B, and c B1

Full size image

The diagrams in Figs. 12, 13 and 14 show that a location must be specified according to the specific gravity center to select the appropriate step. This optimal location will definitely provide the best ventilation for the steps. Of course, this optimal location may not be the same as the optimal transverse step location. In general, the efficiency of angled steps is higher than the transverse steps. Figure 15 shows the effect of the step angle on the performance of the vessel. Figure 15a–c represents the performance of models whose steps are in positions B0, B, and B1, respectively.

As shown in Fig. 15, as the angle decreases, the drag of all three models equipped with pointed aft steps decreases, too. By reducing the angle, better ventilation is achieved at the bottom of the model. In fact, the lower the angle, the better the ventilation at the bottom of the model.

Figure 15a shows the results for models equipped with pointed aft steps, whose steps are provided in 25% of the model’s length to the aft of the models at angles of 156, 134, and 114. The lowest and highest drag correspond to 114° and 156°, respectively.

The results of the models equipped with re-entrant Vee steps are presented in Table 16. The study is conducted at two locations with an angle of 156° for three speeds of 8, 9, and 10 m/s. The performance of this type of step is investigated for three speeds of 8, 9, and 10 m/s by creating it at different locations with an angle of 156°. The values of trim, rise-up and drag of these models show that due to the inability of re-entrant Vee steps to provide proper ventilation, drag of the models equipped with these steps is higher than other stepped models studied in this article. The results of simulating these models are given in Table 16.

Table 16 Resistance, trim, and rise-up of models equipped with re-entrant Vee steps at a speed of 9 m/s and 10
Full size table

In general, it can be concluded that models equipped with pointed aft steps have a lower drag on the corresponding speeds than other stepped models. Meanwhile, the models equipped with transverse step and re-entrant Vee steps have less drag, respectively.

4.6 Pressure and Wetted Surface Area of the Bottom of Models

Figures 16 and 17 show the pressure contours and the wetted surface area of the bottom of the models, respectively. Figure 16 shows the pressure contour of models equipped with pointed aft step, for the placement of steps in three longitudinal locations of B0, B and B1 with an angle of 156° at speeds of 8 and 9 m/s. As the speed of the models increases, the momentum of water flow under the model, increases. As a result of this increase in speed and momentum, flow separation occurs. By increasing the flow separation, the stagnation line moves toward the aft of the model. As a result, the pressure moves backward, and the aft of the model pulls more out of the water, resulting in less trim angle. The lowest trim angle is related to the model equipped with pointed aft step in position B1.

Fig. 16
figure 16

Pressure contours on the bottom of the models equipped with pointed aft steps in three longitudinal positions of B0, B, and B1 and the angle of 156° in two speeds of 8, and 9 m/s

Full size image
Fig. 17
figure 17

Volume fraction contour on the bottom of the models equipped with pointed aft steps for three longitudinal locations of B0, B, and B1, and at an angle of 156° at the speeds of 8 and 9 m/s

Full size image

The wetted surface area of the models equipped with pointed aft steps with three longitudinal locations of B0, B, and B1 has been shown in two speeds of 8 and 9 m/s in Fig. 17. As the speed of the model increases, the wetted surface area of its aft body decreases.

4.7 Wave Pattern and Positions of the Models

Wave pattern and rooster tail behind the models equipped with pointed aft step are illustrated in Fig. 18 at the speed of 9 m/s for positioning the steps at three different angles of 156, 134, and 114 and the best location, i.e., location B.

Fig. 18
figure 18

Wave pattern and rooster tail behind the models equipped with pointed aft step at the speed of 9 m/s and at three different angles of 156, 134, and 114

Full size image

It is observed in Fig. 18 that, as the angle of the steps decreases, the rooster tail increases.

5 Conclusions

In this paper, four models of high-speed craft with different step shapes are studied experimentally and numerically. The effects of three types of steps, namely transverse step, pointed aft step, and re-entrant Vee step are examined. Hydrodynamic performance of these types of stepped models is compared with each other and with the non-step model. Numerical simulations are conducted in two degrees of freedom. Accordingly, the heave and pitch motions of these models are predicted by Star CCM + software. Comparison of the performance of these models are done through the computed drag, trim, and rise-up. Also, the pressure contours, wave pattern, and the wake formation behind the models are obtained using the numerical simulation. Based on the acquired results, one may conclude the followings:

  1. 1-

    The non-step model is unstable longitudinally at the speed of 8 m/s and beyond, but all the stepped models are stable at all speeds.

  2. 2-

    The lowest resistance of the stepped models is obtained by using the pointed aft step. This reduction in drag is caused by two reasons: a decrease in wetted surface area and proper ventilation.

  3. 3-

    The highest drag is related to the non-step model and then to the model equipped with re-entrant vee step. The reason for this increase in drag is the lack of proper ventilation.

  4. 4-

    The effect of pointed aft step on the performance of the models is further studied numerically at three angles of 156°, 134°, and 114°. The results showed that at all speeds, the resistance decreases with decreasing angle.

  5. 5-

    Based on the obtained results from the experimental and numerical tests, the optimum case is the stepped hull equipped with the pointed aft step, which has the lowest step angle among all investigated models, i.e., 114°, and is located at 27% of the vessel length to the vessel aft.

  6. 6-

    By reducing the angle of the pointed aft step, the trim and rise-up are reduced.