1 Introduction

The increasing use of CF-reinforced polymer composites in leading industries such as aerospace, automotive, and marine confirms the need for high-strength yet lightweight materials; these features will increase the productivity of the designed structure. On the other hand, these composites have high strength in the fiber direction and have a strength equal to the strength of the polymer matrix in the transverse direction (perpendicular to the fiber direction), which is too small. CNTs can be used to improve the transverse strength of these composites. By adding a percentage of CNTs to the polymer matrix, its mechanical properties will be significantly increased. These composites, which are composed of more than two components, are called hybrid composites. There are different methods to study the behavior and performance of these types of composites. Experimental testing is an expensive method that requires precise equipment. An alternative method is a numerical simulation, which allows the examination of all the relevant parameters in addition to reducing costs.

The study of hybrid nano-composites by simulation using the multi-scale method is very efficient. As mentioned, CNTs can be used in CF-reinforced polymer composites to improve the transverse mechanical properties. Due to the use of materials at the nano-scale, it is necessary to study the behavior of composites at this scale carefully. One of the most important methods of simulating materials at the nano-scale is the use of the MD method.

In recent years, many researchers have studied the behavior of nano-composites by using MD simulations. Soleimany et al. (2021a) investigated the mechanical and thermal properties of CNT as well as polymeric nano-composites reinforced with different percentages of CNTs. Han and Elliott (2007) and Alian et al. (2015) estimated the elastic modulus of a CNT-reinforced polymer composite using MD simulation. Al-Ostaz et al. (2008), Zheng et al. (2017), as well as Dikshit and Engle (2018), studied the mechanical properties of nano-composites with different polymer substrates reinforced with CNTs using MD simulation. Al-Ostaz et al. (2008) found that SWCNT behaves as a linear elastic material. Dikshit and Engle (2018) also found that CNT reinforced epoxy composite is five times stiffer than the pure epoxy matrix.

So far, much research has been accomplished on the multidimensional study of nano-composites. There are two concurrent and sequential approaches for multi-scale analysis. In the concurrent multi-scale approaches, several computational methods are related in a hybrid model in which different scales of material behavior are considered concurrently (Nakano et al. 2001). In the sequential approaches, hierarchical computational methods are related in such a way that the calculated values of a computational simulation on a scale are used to define the simulation parameters at a larger scale (Kremer and Muller-Plathe 2001; Raabe 2002).

Al Mahmud et al. (2019) studied the mechanical properties of a three-phase hybrid nano-composite consisting of graphene laminates, CF, and epoxy polymer based on a sequential multi-scale approach. Their calculations were performed at the nano-scale and micro-scale to estimate the mechanical properties. Alian et al. (2017) extracted the mechanical properties of CNT reinforced polymer composites by nano-scale and micro-scale simulations. Radue et al. (2018) investigated the mechanical properties of three-phase nano-composites consisting of CFs, CNTs, and epoxy polymers and examined the effect of different polymers on the mechanical properties of nano-composites. The result of their research shows a significant increase in the elastic modulus of polymer nano-composite by increasing the percentage of carbon nanotubes. Zeng et al. (2008) also investigated the simulation of multi-scale polymer nano-composite. They introduced some computational methods that have been applied to polymer nano-composites, covering from molecular scale to micro-scale to meso-scale and macro-scale. Izadi et al. (2021) developed a multi-scale method for predicting Young's modulus of fullerene-reinforced polymer nano-composites. In their research, MD simulations were conducted to calculate Young's modulus of nano-composite unit cell, and then a micromechanics model was developed for a composite with multi-inclusion reinforcements.

The FE method has also been used to study the multi-scale behavior of composite materials. Rafiee and Firouzbakht (2018) investigated the simulation of multi-scale CNT-reinforced polymer composite on the micro-scale. In a multi-scale study using an FE method, Han et al. (2015) investigated the damage of a CF-reinforced composite at the micro and macro-scales. They investigated the effect of the middle layer. The study was conducted on the microscopic computational model of a single fiber composite with thermal residual stress and damage initiation of unidirectional composite using ABAQUS FEM software. Guo et al. (2018) in a multi-scale study estimated the mechanical properties of a graphene-reinforced polymeric nano-composite at both micro and macro-scales by three-dimensional simulation using the FE method. Their simulation results show that Young's modulus and shear modulus of the graphene-reinforced composites will increase significantly with increasing graphene volume fraction. In another study, Rai and Chattopadhyay (2018) investigated damage in a CNT-reinforced polymer composite in a periodic unit cell. In their research, the placement of CNTs has been investigated randomly and along the axis. Giannopoulos (2019) linked MD and FEM for predicting the mechanical behavior of fullerene reinforced nylon-12. For this purpose, a numerical study was conducted in two stages. The first is an MD approach and the second is a classical continuum mechanics (CM) method, grounded on the FEM and requires the utilization of some MD data regarding the RVE of a nano-composite. The results show that the performance of the MD-only is as well as the FEM-MD combined method.

Montazeri and Naghdabadi (2009) investigated the compressive properties of CNT-reinforced polymeric nano-composites by a multi-scale method using the FE method. In their study, CNTs were investigated on a nano-scale and polymeric nano-composites were investigated on a micro-scale. In the research process, the multi-scale method has been used concurrently. In another study, Soleimany et al. (2021b) investigated residual mechanical stresses by modeling a CNT at the nano-scale and applying it concurrently at the micro-scale to model the polymeric nano-composite using the FE method. They found that choosing SWCNTs with a larger diameter causes the SWCNT alone and polymer matrix reinforced with SWCNTs to sustain larger mechanical loading. Ayatollahi et al. (2011), as in the previous study, extracted the mechanical properties of polymeric nano-composites for different loadings on nano-composites by modeling CNTs at the nano-scale and polymeric nano-composites at the micro-scale.

Numerous studies have been employed at the micro-scale to estimate mechanical properties, residual stress and investigate damage and failure (Maligno et al. 2008; Chen and Zhang 2018; Naderi and Iyyer 2020). For example, Chen and Zhang (2018) investigated residual stresses in fiber-reinforced composites from a micromechanical method. Micromechanical equations and FE methods have been used in their research. Using a micromechanical model, Naderi and Iyyer (2020) investigated the effect of composite lamina thickness on the initiation of damage in CF-reinforced composites by the uniaxial tensile strength test. They found that with decreasing 90° lamina thickness damage progression mechanism will change and the incidence of cracks in matrix loading will reduce. Maligno et al. (2008) also investigated the effect of residual stresses due to the curing process on the initiation of damage to CF-reinforced polymer composites by longitudinal and transverse tension. Their study is based on different failure criteria and a stiffness degradation technique for damage analysis of the RVE subjected to mechanical loading after curing.

Lapczyk and Hurtado (2007) studied an anisotropic progressive damage model for predicting failure and post-failure behavior in fiber-reinforced materials. They predicted damage using Hashin 2D failure damage criteria and verified their result with experimental studies. Molavizadeh and Rezaei (2019) employed progressive damage analysis (PDA) in order to optimize the geometry and winding angle of a composite pressure vessel. They optimized the strength and buckling stability of elliptical composite deep-submerged pressure shells using two different filament winding patterns, namely geodesic and planar. In the research, numerical modeling was performed using ABAQUS software and User MATerial (UMAT) subroutine, and the Puck failure criterion was selected for PDA. Leonetti et al. (2018) investigated a multi-scale damage analysis of periodic composites with a computational strategy, whose purpose is to reduce the computational cost associated with a classical FE micro-modeling approach.

The present study aims to numerically investigate the initiation and propagation of damage on a standard sample of CNT-CF-reinforced polymeric nano-composite laminate by uniaxial tensile application. In this regard, the mechanical properties of laminate have been extracted using the sequential multi-scale method, and then the PDA has been modeled. In order to estimate the mechanical properties of a three-component nano-composite, it is first necessary to extract the mechanical properties of CNT-reinforced polymeric nano-composites as equivalent resin. In the present study, the properties of the equivalent resin have been adapted from the results of a study conducted by the authors of the same paper, which was extracted by MD simulation at a nano-scale with the assistance of Material Studio software (Soleimany et al. 2021a). Then, including the mechanical properties of the equivalent resin, the mechanical properties of the three-component nano-composite at the micro-scale have been extracted by considering it as a periodic unit cell using the FE method in ABAQUS software. In the following, the strength properties of CNT-CF-reinforced polymeric nano-composites have been calculated analytically. Finally, with the mechanical and strength properties of the three-component nano-composite, the damage process of nano-composite laminate with \({[0/90]}_{s}\) stacking sequence on a macro-scale using the uniaxial FE method and Hashin-type 3D failure criterion has been simulated using USDFLD subroutine.

2 Description of Problem

The present study simulates the PDA of a three-component nano-composite consisting of a polymer matrix, nano-reinforcement, and unidirectional fibers using ABAQUS FE software and Hashin-type 3D failure criterion. Multi-scale modeling has been utilized to predict the mechanical properties of a three-component nano-composite as input to the numerical solution of the simulation process. The polymer used in this research is Epon-828 resin with the scientific name Diglycidyl-Ether-Bisphenol-A (DGEBA) and hardener EPI-CURE-Curing-Agent-3234 with the scientific name of Triethylenetetramine- (TETA) which has a ratio of three to one and a polymerization percentage of 65%. The nanotube used is a single-walled CNT (3,3). The fibers used are produced from unidirectional CF type T300 and their mechanical properties have been presented in Table 1.

Table 1 Mechanical properties of CF T300 (Miyagawa et al. 2005)
Full size table

Figure 1 indicates the multi-scale simulation process of the present study. As observed in the first step, the properties of the CNT-reinforced polymeric nano-composite are calculated using MD simulation on the nano-scale. In the second step, the mechanical properties of the three-component nano-composite consisting of polymer and CNT (equivalent resin), and CF are calculated using the FE software ABAQUS and the periodic boundary condition method. Furthermore, in this scale, the strength properties of nano-composites are determined using micromechanical equations. The strength properties may be computed using the MD method for higher accuracy, or the mechanical properties may be calculated analytically using micromechanical relationships. In this study, the multi-scale solution process at nano, micro, and macro-scales is assumed, which expresses the relationship between the results of MD, FEM and analytical solution methods. For this reason, the calculation of mechanical properties has been accomplished by the MD method, and the calculation of strength properties has been conducted by the analytical method.

Fig. 1
figure 1

Multi-scale study of CNT-CF-reinforced polymeric nano-composites

Full size image

Considering the fact that the periodic boundary condition method has been used to perform the analysis in the second step, the results calculated in the second step can be employed in the third step. In other words, a representative volume element (RVE) in the second step will have the same properties as a lamina in the third step, or meso-scale. In the fourth step or macro-scale, a nano-composite laminate is examined. Having the mechanical and strength properties of a polymeric nano-composite reinforced with CNT and CF in the second and third steps, a standard tensile test specimen with \({[0/90]}_{s}\) lay-up is analyzed using the FEM. This standard sample has been subjected to uniaxial tension so that in addition to analyzing the applied stress on the laminate by displacement control method, using the USDFLD subroutine, the initiation and propagation of laminate damage have been examined using Hashin-type 3D equations.

In the present study, the mechanical properties of CNT, polymer and two-component nano-composites (first step) have been adapted from the results of the study of the authors of this study, which was extracted using the MD simulation method (Soleimany et al. 2021a). The mechanical properties of the polymer matrix were calculated in different percentages of crosslinking from 10 to 65%. The effect of the crosslinking percentage on the mechanical properties was investigated and then crosslinking percentage of 65% has been selected due to its more desirable properties. As mentioned, a two-component polymer nano-composite is reinforced with CNTs. CNTs with different structures that have been randomly placed inside the cell were investigated. In this study, CNT (3,3) has been selected as the reinforcing phase. The mechanical properties of polymer nano-composites reinforced with CNT (3,3) were calculated and the effect of the weight percentage of CNTs on the nano-composite was investigated (Soleimany et al. 2021a).

The mechanical properties of CNT and the mechanical properties of CNT-reinforced composite cells with weight fractions of 0.5, 1, and 2% of CNT have been presented in Tables 2 and 3, respectively (Soleimany et al. 2021a). Then, the properties of CNT-reinforced nano-composites are used as input information in micro-scale calculations, which is called equivalent resin.

Table 2 Mechanical properties of single-walled CNTs (3,3) (Soleimany et al. 2021a)
Full size table
Table 3 Mechanical properties of nano-composite cell reinforced with single-walled CNTs (3,3) (Soleimany et al. 2021a)
Full size table

2.1 Mechanical Properties of CNT-CF-Reinforced Polymeric Nano-Composites

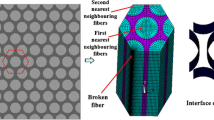
In this section, the mechanical properties of CNT-CF-reinforced polymeric nano-composite are extracted using micromechanical and FE methods. The three-phase nano-composite studied results from the combination of equivalent resin with CF at a volume fraction of 45%. The results of the mechanical properties of the equivalent resin (CNT-reinforced polymeric nano-composite) have been presented in Table 2. In order to extract the mechanical properties on a micro-scale, a simulation of a CNT-CF-reinforced polymeric nano-composite cell has been performed using ABAQUS FE software. The mechanical properties of nano-composite include elastic modulus, Poisson's ratio, and shear modulus will use on a larger scale. For modeling, one fiber has been embedded in the middle of the polymer matrix and the other is embedded in the corners of a polymer cube cell in the form of four quarters of a circle of fibers. In this regard, a cell with dimensions of 13 μm with CF with a diameter of 7 μm in the middle and around the cell has been modeled (Fig. 2). The cell's total volume equals \({V}_{total}={a}^{3}=2197\) μm3, and the volume of each structural component is equal to \({V}_{fiber}=2\pi {r}^{2}h=2\pi \times {3.5}^{2}\times 13=1000.5\) μm3, and \({V}_{\mathrm{resin}}={V}_{\mathrm{total}}-{V}_{\mathrm{fiber}}=1196.5\) μm3, respectively.

Fig. 2
figure 2

Polymeric nano-composite cell model consisting of equivalent resin and reinforcing CF

Full size image

In the simulation process of an RVE, a small element of a larger object has been considered and assumed to be repeated in all directions. Periodic boundary conditions should be applied to the cell in such a way that, after meshing the piece, all the nodes on the facing laminates are placed precisely on top of each other and constrained. The finer mesh leads to more additional elements and nodes and applying periodic boundary conditions will take more time. Figure 3 shows a random volumetric element of a fiber-randomly-reinforced composite in which the periodic boundary conditions are observed (Al-Ostaz et al. 2007). For all surfaces and edges, it is necessary to observe Eqs. (1) to (3) in order to make a correct definition to solve the problem in the simulation.

$$U\left(x+L\right)=U\left(x\right)+{\varepsilon }^{^\circ }x\ \ \ \forall x\in {\beta }_{\delta }^{2}$$
(1)
$$U\left(x+L\right)=U\left(x\right)\ \ \ \forall x\in {\beta }_{\delta }^{1}$$
(2)
$$t\left(x+L\right)=-t\left(x\right)\ \ \ \forall x\in {\beta }_{\delta }^{1}$$
(3)

where \(U\) is the displacement at the point \(x\), \({\varepsilon }^{^\circ }\) represents the applied strain and t is the surface traction. Also \(L=Le\) (\(e\) is a unit vector).

Fig. 3
figure 3

Application of the periodic boundary condition and loading in a composite unit cell

Full size image

According to Figs. 3 and 4, the cell periodic boundary conditions assume to have been derived from a larger volume element with aligned fiber distribution in each direction. In FEM simulation, it is necessary to apply periodic boundary conditions to the RVE in order to consider the properties of the calculated RVE materials to be equivalent to the properties of the composite material at the macro-scale. An RVE can be assumed to be regular or irregular (composite with randomly distributed inclusion or aligned distributed inclusions). In both cases, the PBC must be defined for the RVE to show that it is a very small part of a large material that contains repetition in all dimensions, and by removing the PBC for calculating the mechanical properties, the computational error will increase. Many studies have been done in this regard that used PBC, such as Han et al. (2015) and Taheri-Behrooz and Pourahmadi (2019). The model has been meshed using the wedge C3D6 element with six nodes and includes 42,042 nodes and 77,248 elements in total. By applying periodic boundary conditions on the model and applying loading by the displacement control method at the value of 2.6 μm (strain value of \(\varepsilon =\Delta L/L=0.2\)) along the \(x\)-axis, the elastic modulus (\({E}_{1}\)) and stress values in the \(x\)-direction are extracted. The stress contour (\({S}_{11}\)) in the \(x\)-direction has been shown in Fig. 4. As observed, the stress in the CF is very high and the stress in the matrix is lower. The elastic modulus in the \(x\)-direction is obtained by dividing the average of all applied stresses to the nodes by the applied strain value. Also, the shear modulus after applying the shear force (tangentially on two surfaces) is calculated by dividing the average applied stresses (to the desired laminate) by the total shear strains.

Fig. 4
figure 4

Stress contour (N/cm2) under different loading conditions

Full size image
$$E= \frac{\mathrm{Stress}}{\mathrm{Axial\ strain}} ; \left\{\begin{array}{c}{\mathrm{E}}_{11}= \frac{\frac{\sum \mathrm{forces\ in\ direction\ }1\mathrm{\ for\ all\ nodes}}{\mathrm{Surface\ area\ in\ direction }\ 1}}{\frac{\Delta \mathrm{L}}{\mathrm{L}}}\\ {\mathrm{E}}_{22}= \frac{\frac{\sum \mathrm{ forces\ in\ direction\ }2\mathrm{\ for\ all\ nodes}}{\mathrm{Surface\ area\ in\ direction\ }2}}{\frac{\Delta \mathrm{L}}{\mathrm{L}}}\\ {\mathrm{E}}_{33}= \frac{\frac{\sum \mathrm{forces\ in\ direction\ }3\mathrm{\ for\ all\ nodes}}{\mathrm{Surface\ area\ in\ direction\ }3}}{\frac{\Delta \mathrm{L}}{\mathrm{L}}}\end{array}\right.$$
(4)
$$\mathrm{G}= \frac{\mathrm{Shear\ stress}}{\mathrm{Shear\ strain}} ; \left\{\begin{array}{c}{\mathrm{G}}_{12}= \frac{\frac{\sum \mathrm{forces\ in\ direction\ }12\mathrm{\ for\ all\ nodes}}{\mathrm{Surface\ area\ in\ direction\ }12}}{\frac{{\Delta \mathrm{L}}_{1}}{{\mathrm{L}}_{1}}+\frac{{\Delta \mathrm{L}}_{2}}{{\mathrm{L}}_{2}}}\\ {\mathrm{G}}_{13}= \frac{\frac{\sum \mathrm{forces\ in\ direction\ }13\mathrm{\ for\ all\ nodes}}{\mathrm{Surface\ area\ in\ direction\ }13}}{\frac{{\Delta \mathrm{L}}_{1}}{{\mathrm{L}}_{1}}+\frac{{\Delta \mathrm{L}}_{3}}{{\mathrm{L}}_{3}}}\\ {\mathrm{G}}_{23}= \frac{\frac{\sum \mathrm{forces\ in\ direction\ }23\mathrm{\ for\ all\ nodes}}{\mathrm{Surface\ area\ in\ direction\ }23}}{\frac{{\Delta \mathrm{L}}_{2}}{{\mathrm{L}}_{2}}+\frac{{\Delta \mathrm{L}}_{3}}{{\mathrm{L}}_{3}}}\end{array}\right.$$
(5)

Poisson's ratio can also be calculated using Eq. (6).

$$\nu = \frac{-\mathrm{ Transverse\ strain}}{\mathrm{Axial\ strain}} ; \left\{\begin{array}{c}{\nu }_{12}= \frac{\frac{{\Delta L}_{2}}{{L}_{2}}}{\frac{{\Delta L}_{1}}{{L}_{1}}}\\ {\nu }_{13}= \frac{\frac{{\Delta L}_{3}}{{L}_{3}}}{\frac{{\Delta L}_{1}}{{L}_{1}}}\\ {\nu }_{23}= \frac{\frac{{\Delta L}_{3}}{{L}_{3}}}{\frac{{\Delta L}_{2}}{{L}_{2}}}\end{array}\right.$$
(6)

The stress contour in 6 different solution steps for loading in different directions has been shown in Fig. 4. Based on the results of numerical analysis and Eqs. (4) to (6), the mechanical properties of the three-phase nano-composite have been extracted as described in Table 4.

Table 4 Mechanical properties of CNT-CF-reinforced nano-composite
Full size table

2.2 Strength Properties of CNT-CF-Reinforced Polymeric Nano-Composite

There are various theories to study the failure analysis process in composite materials, and most of them have been developed based on the strength properties of composite materials. In this regard, in the present study, having the strength properties of all three components of nano-composite, including polymer, CNT, and CF, and with the help of micromechanical equations, the strength properties have been calculated. The strength properties of each nano-composite component have been listed in Table 5.

Table 5 Strength properties of polymer, CNT and CF
Full size table

Strength properties including tensile and compressive strength in the direction of the fiber (longitudinal), tensile and compressive strength in the direction perpendicular to the fiber (transverse), and shear strength can be calculated using Eqs. (7–13). To calculate the strength properties of a three-phase nano-composite, it is necessary first to extract the strength properties of equivalent resin and then estimate the strength properties of nano-composite consisting of equivalent resin and CF (Barbero 2018).

$${F}_{1t}= \left[{V}_{f}+ \frac{{E}_{m}}{{E}_{f}} \left(1- {V}_{f}\right)\right]{F}_{ft}$$
(7)
$${F}_{1c}= {G}_{12} {\left(1+4.76 \chi \right)}^{-0.69};\ \ \chi = \frac{{G}_{12} {S}_{\alpha }}{{F}_{6}};$$
$${G}_{12}= {G}_{m}\left[\frac{\left(1+{V}_{f}\right)+ \left(1-{V}_{f}\right){G}_{m}/{G}_{f}}{\left(1-{V}_{f}\right)+ \left(1+{V}_{f}\right){G}_{m}/{G}_{f}}\right]$$
(8)

where \({F}_{1t}\) and \({F}_{1c}\) represent the longitudinal tensile and compressive strengths, \({V}_{f}\) and \({V}_{m}\) are the volumetric percentages of the fiber and the matrix, respectively, \({G}_{f}\) and \({G}_{m}\) are the shear modulus of the fiber and the matrix, respectively, \({F}_{ft}\) is the tensile strength of the fiber and, \({E}_{m}\) and \({E}_{f}\) are respectively the matrix elastic modulus and fiber elastic modulus in the direction of the fiber. Furthermore, \({G}_{12}\) represents the shear modulus, χ is the computational coefficient, \({F}_{6}\) is the shear strength and \({S}_{\alpha }\) is the non-axial standard deviation of fibers. \({S}_{\alpha }\) is a parameter calculated using laboratory tests, and the lower the value, the higher the quality of the fiber. According to the research results conducted in this field, a value of 1 degree is considered for \({S}_{\alpha }\) in this study (Barbero 2018; Ahmadian et al. 2019).

$${F}_{2t}= {F}_{\mathrm{mt}}{C}_{v} \left[1+ \left({V}_{f}- \sqrt{{V}_{f}}\right)\left(1- \frac{{E}_{m}}{{E}_{T}}\right)\right]$$
(9)
$${F}_{2c}= {F}_{mc}{C}_{v} \left[1+ \left({V}_{f}- \sqrt{{V}_{f}}\right)\left(1- \frac{{E}_{m}}{{E}_{T}}\right)\right]$$
(10)

where \({F}_{2t}\) and \({F}_{2c}\) are the transverse tensile and compressive strengths, respectively, \({F}_{mt}\) and \({F}_{mc}\) are the tensile and compressive strengths of the matrix and \({E}_{T}\) are the transverse elastic modulus of the fiber, respectively. \({C}_{v}\) is an experimental factor for calculating void spaces, the value of which in this study is equal to 1 (Barbero 2018).

$${F}_{4}= {F}_{2c}\mathrm{cos}{\alpha }_{0}\left(\mathrm{sin}{\alpha }_{0}+ \mathrm{cos}{\alpha }_{0}\mathrm{cot}2{\alpha }_{0}\right)$$
(11)
$${F}_{6}= {F}_{ms}{C}_{v} \left[1+ \left({V}_{f}- \sqrt{{V}_{f}}\right)\left(1- \frac{{G}_{m}}{{G}_{f}}\right)\right]$$
(12)

where \({F}_{4}\) is intralaminar shear strength in plane 2–3 and \({F}_{6}\) is in-plane shear strength in plane1–2, \({F}_{ms}\) represents the shear strength of the matrix and \({\alpha }_{0}\) denotes the Angle of the fracture plane. The value of \({\alpha }_{0}\) in this study is assumed to be 54 degrees. Also in this study, the values of \({F}_{6}\) and \({F}_{5}\) are assumed to be equal (\({F}_{5}\) is the shear strength on plane 3–1). It should be noted that the strength properties of the unidirectional composite can be calculated using Eqs. (7) to (12) and, the Eqs. (13) to (15) are used for composites with random placement of fibers (Barbero 2018):

$${F}_{csm-t}= \left\{\begin{array}{c}\frac{4}{\pi }{F}_{6}\left(1+ \mathrm{ln}\alpha \right)\ for\ \alpha >1\\ \frac{4}{\pi }{F}_{6}\alpha\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ for\ \alpha \le 1\end{array}\right.;\ \ \alpha = \sqrt{\frac{{F}_{1t}{F}_{2t}}{{{F}_{6}}^{2}}}$$
(13)
$${F}_{csm-4} = {F}_{4}$$
(14)
$${F}_{csm-6} = \frac{1}{2}{F}_{csm-t}$$
(15)

where \({F}_{csm-t}\) is the tensile strength equal to the value of compressive strength. Also, \({F}_{csm-4}\) is the intralaminar shear strength and \({F}_{csm-6}\) is the in-plane shear strength. Because interlaminar shear in equivalent resin has no meaning, Eq. (14) is not applicable in this study and Eq. (15) has been used as the shear strength of equivalent resin.

Using Eqs. (7) to (15) and the mechanical and strength properties of each component of nano-composite, the strength properties of the equivalent resin to different weight percentages of CNT as well as the nano-composite consisting of equivalent resin and CF with a volume fraction of 45% have been calculated and listed in Tables 6 and 7.

Table 6 Strength properties of equivalent resin consisting of epoxy polymer and CNT
Full size table
Table 7 Strength properties of polymeric nano-composites consisting of equivalent resin and CF
Full size table

2.3 Investigation of Degradation in CNT-CF-Reinforced Polymeric Nano-Composites

In this section, after extracting the mechanical and strength properties of a three-component polymeric nano-composite, the numerical analysis of the initiation and propagation of damage on a standard macro-scale sample has been discussed. In order to simulate PDA, a Hashin-type 3D criterion has been used, which expresses different failure modes for fibers and matrices in terms of stress. Two methods of gradual degradation in mechanical properties have also been assumed. This gradual property degradation occurs based on the damage corresponding to the fiber and matrix failure modes. Failure criteria and material degradation rules corresponding to each degradation mode have been coded as USDFLD subroutine and are attached to the ABAQUS software as PDA simulation tools.

A Hashin-type 3D criterion has been developed for transverse unidirectional isotropic composite laminates in which quadratic polynomials are the failure criteria. Due to the presence of two dissimilar phases in composites, failure occurs in different modes. Considering the impossibility of expressing these modes with a simple function, Hashin has presented a different failure criterion for damage to the matrix and fibers including Eqs. (16) to (22) (Tserpes et al. 2002):

$${\left(\frac{{\sigma }_{11}}{{F}_{1t}}\right)}^{2}+{\left(\frac{{\sigma }_{12}}{{F}_{6}^{2}}\right)}^{2}+{\left(\frac{{\sigma }_{13}}{{F}_{5}^{2}}\right)}^{2}=1,\ \left({\sigma }_{1}>0\right); \, \mathrm{ Fibre\ tensile\ failure}$$
(16)
$$\frac{{\sigma }_{11}}{{F}_{1c}}=1,\ \left({\sigma }_{1}<0\right); \, \mathrm{ Fibre\ compressive\ failure}$$
(17)
$${\left(\frac{{\sigma }_{22}}{{F}_{2t}}\right)}^{2}+ {\left(\frac{{\sigma }_{12}}{{F}_{6}}\right)}^{2}+ {\left(\frac{{\sigma }_{23}}{{F}_{4}}\right)}^{2}=1,\ \left({\sigma }_{2}>0\right); \, \mathrm{ Matrix\ tensile\ cracking}$$
(18)
$${\left(\frac{{\sigma }_{22}}{{F}_{2c}}\right)}^{2}+ {\left(\frac{{\sigma }_{12}}{{F}_{6}}\right)}^{2}+ {\left(\frac{{\sigma }_{23}}{{F}_{4}}\right)}^{2}=1,\ \left({\sigma }_{2}<0\right); \, \mathrm{ Matrix\ compressive\ cracking}$$
(19)
$${\left(\frac{{\sigma }_{11}}{{F}_{1c}}\right)}^{2}+{\left(\frac{{\sigma }_{13}}{{F}_{5}}\right)}^{2}+{\left(\frac{{\sigma }_{12}}{{F}_{6}}\right)}^{2}=1,\ \left({\sigma }_{1}<0\right); \, \mathrm{ Fiber-matrix\ shear-out}$$
(20)
$${\left(\frac{{\sigma }_{33}}{{F}_{3t}}\right)}^{2}+ {\left(\frac{{\sigma }_{13}}{{F}_{5}}\right)}^{2}+ {\left(\frac{{\sigma }_{23}}{{F}_{4}}\right)}^{2}=1,\ \left({\sigma }_{3}>0\right); \, \mathrm{ Delamination\ in\ tension}$$
(21)
$${\left(\frac{{\sigma }_{33}}{{F}_{3c}}\right)}^{2}+ {\left(\frac{{\sigma }_{13}}{{F}_{5}}\right)}^{2}+ {\left(\frac{{\sigma }_{23}}{{F}_{4}}\right)}^{2}=1,\ \left({\sigma }_{3}<0\right); \, \mathrm{ Delamination\ in\ compression}$$
(22)

As observed, the Hashin-type 3D failure criterion can predict separate damage modes for composite laminate. Two methods have been employed in order to investigate the effect of degrading the mechanical properties of materials. In the first method, when an element is damaged according to Eqs. (16–22), the properties of that element will completely be zero. In the second method, as one of the damage equations in the element in each element reaches a value of one, the properties of that element degrade according to Table 8. In this research, it is assumed that the element's damage occurs instantaneously and, while the criteria number reaches one, the mechanical properties degrade. This process continues until all the elements are damaged. The coefficients of material properties degradation for the initiation of damage to the matrix due to tension and pressure and the failure of fiber due to tension and pressure were proposed by Tan (1991), which was developed by Camanho and Matthews (1999). Chang and Chang (1987) have proposed the zero value of the coefficients in shear and delamination, Tserpes et al. (2002) have presented the set of these coefficients in the form of Table 8. It is important to note that to avoid convergence problems in the FE method, the properties of the materials zeroed in this table will have very small numerical values. Figure 5 shows the flowchart of numerical calculations.

Table 8 Degradation coefficients of mechanical properties of materials (Tserpes et al. 2002)
Full size table
Fig. 5
figure 5

Flowchart of numerical calculations using USDFLD subroutine

Full size image

To apply the material properties degradation, a stiffness matrix is used in which the material properties degradation coefficients will be multiplied. The stiffness matrix of the linear orthotropic material usable in the ABAQUS FE software for the 3D element is defined in Eq. (23). In a three-dimensional solution, the composite layers are modeled in the thickness direction by three-dimensional solid elements to calculate the strain state and the resulting stresses.

$$\left\{\begin{array}{c}\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{33}\end{array}\\ \begin{array}{c}{\sigma }_{12}\\ {\sigma }_{13}\\ {\sigma }_{23}\end{array}\end{array}\right\}= \left[\begin{array}{cc}\begin{array}{ccc}{C}_{11}^{0}& {C}_{12}^{0}& {C}_{13}^{0}\\ {C}_{21}^{0}& {C}_{22}^{0}& {C}_{23}^{0}\\ {C}_{31}^{0}& {C}_{32}^{0}& {C}_{33}^{0}\end{array}& \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}& \begin{array}{ccc}{C}_{44}^{0}& 0& 0\\ 0& {C}_{55}^{0}& 0\\ 0& 0& {C}_{66}^{0}\end{array}\end{array}\right]\left\{\begin{array}{c}\begin{array}{c}{\varepsilon }_{11}\\ {\varepsilon }_{22}\\ {\varepsilon }_{33}\end{array}\\ \begin{array}{c}{\gamma }_{12}\\ {\gamma }_{13}\\ {\gamma }_{23}\end{array}\end{array}\right\}$$
(23)

where the stiffness coefficients of the matrix \({C}_{ij}^{0}\) in Eq. (23) using elastic material constants are:

$$\begin{aligned} C_{{11}}^{0} & = \frac{{\left( {1 - \nu _{{23}} \nu _{{32}} } \right)E_{{11}} }}{\Delta };\;C_{{22}}^{0} = \frac{{\left( {1 - \nu _{{13}} \nu _{{31}} } \right)E_{{22}} }}{\Delta }; \hfill \\ \;C_{{33}}^{0} &= \frac{{\left( {1 - \nu _{{12}} \nu _{{21}} } \right)E_{{33}} }}{\Delta };C_{{12}}^{0} = C_{{21}}^{0} = \frac{{\left( {\nu _{{12}} + \nu _{{13}} \nu _{{32}} } \right)E_{{22}} }}{\Delta } = \frac{{\left( {\nu _{{21}} + \nu _{{31}} \nu _{{23}} } \right)E_{{11}} }}{\Delta }; \hfill \\ C_{{13}}^{0} &= C_{{31}}^{0} = \frac{{\left( {\nu _{{13}} + \nu _{{12}} \nu _{{32}} } \right)E_{{33}} }}{\Delta } = \frac{{\left( {\nu _{{31}} + \nu _{{21}} \nu _{{23}} } \right)E_{{11}} }}{\Delta }; \hfill \\ C_{{23}}^{0} &= C_{{32}}^{0} = \frac{{\left( {\nu _{{23}} + \nu _{{13}} \nu _{{21}} } \right)E_{{33}} }}{\Delta } = \frac{{\left( {\nu _{{32}} + \nu _{{31}} \nu _{{12}} } \right)E_{{22}} }}{\Delta }; \hfill \\ C_{{44}}^{0} &= G_{{12}} ;\;C_{{55}}^{0} = G_{{13}} ;\;C_{{66}}^{0} = G_{{23}} ; \hfill \\ \Delta &= 1 - \nu _{{12}} \nu _{{21}} - \nu _{{23}} \nu _{{32}} - \nu _{{13}} \nu _{{31}} - 2\nu _{{21}} \nu _{{32}} \nu _{{13}} \hfill \\ \end{aligned}$$
(24)

According to Fig. 6, the polymer composite laminate is taken from ASTM-D3039 (ASTM D 3039/D 3039 M-08 2002a) and ASTM-D5766 (ASTM D 5766/D 5766 M-02a 2002b). Composite laminate has a cross-ply lay-up and placement angle of \(\left[ {0/90} \right]_{S}\) with a thickness of 2.5 mm with a central open-hole with dimensions \(w/D = 6\). The specimen is fixed on one side and subjected to tension on the other side.

Fig. 6
figure 6

Standard sample of composite laminate tensile test (Unit: mm)

Full size image

Open-hole composite laminate has meshed with a three-dimensional, hexagonal, eight-node linear brick and reduced integration elements with hourglass control (C3D8R). In order to have high accuracy in the FE analysis, the results must be independent of the element size. Consequently, a convergence study has been accomplished to evaluate the accuracy. According to Fig. 7, the results of force analysis are not affected by changing the size of the mesh. In other words, refinement of the mesh (adding more elements) has little to no effect on the solution. The maximum force results converge to a repeatable solution considering about 76,264 elements. Figure 8 shows the composite laminate meshing and the lay-up of the composite laminate as well as how to apply the boundary conditions for PDA have been also shown in Fig. 9. As can be seen, smaller elements have been used in areas close to the hole to increase sensitivity.

Fig. 7
figure 7

Mesh convergence study for 2% wt. CNT-CF-reinforced polymeric nano-composite laminate under tension

Full size image
Fig. 8
figure 8

Meshing display of composite laminate

Full size image
Fig. 9
figure 9

Display of lay-up of the open-hole composite laminate and applying boundary conditions for PDA

Full size image

3 Verification of PDA of Nano-Composite Laminate

In recent years, several studies have been performed to investigate the degradation of composite laminates by experimental methods as well as simulations. Chang et al. (1991) investigated the failure of open-hole composite laminates with different lay-ups in two dimensions. In this study, the performance of the developed subroutine based on the Hashin-type 3D failure criterion has been evaluated using the available experimental and numerical results. Simulations have been performed with both methods of degrading material properties, degrade to zero and degrade by applying a reduction coefficient. The material system used by Chang et al. is T300/976 with \(E_{11} =\) 139.75 GPa, \(E_{22} =\) 12.82 GPa, \(\nu_{12} =\) 0.23, \(G_{12} =\) 6.96 GPa, \(F_{1t} =\) 1516 MPa, \(F_{2t} =\) 44.5 MPa, \(F_{1c} =\) 1592 MPa, \(F_{2c} =\) 253 MPa, \(F_{6} =\) 107 MPa (Chang et al. 1991). In order to simulate 3D, other required properties of the material are considered as \(E_{33} =\) 12.82 GPa, \(\nu_{13} = \nu_{23} =\) 0.23, \(G_{13} = G_{23} =\) 6.96 GPa, \(F_{4} = F_{5} =\) 107 MPa. The composite laminates \(\left[ {\left( { + 45/ - 45} \right)_{4} } \right]_{S}\) containing the central through-hole with a diameter of 6.35 mm, and thickness of 2.28 mm and width of 25.4 mm under uniform axial tension are considered. The maximum calculated tolerable force for the laminate is shown in Table 9. As can be seen, the performed simulation presents similar results as the experimental test of the study by Chang et al. (1991).

Table 9 The maximum calculated tolerable force for the T300/976 composite laminate
Full size table

The results of Table 9 show a slight difference in this study's experimental test and simulation. Figure 10 shows how to apply force from the moment of the start of tension to the moment of failure. Figure 11 also shows the onset of damage up to the moment of failure for composite laminate with a \(\left[ {\left( { + 45/ - 45} \right)_{4} } \right]_{S}\) stacking sequence step by step in layers (+ 45) and (− 45) for the case where the material properties degrade by a coefficient.

Fig. 10
figure 10

Maximum tolerable force in \(\left[ {\left( {45/ - 45} \right)_{4} } \right]_{S}\) laminates with two methods of degradation

Full size image
Fig. 11
figure 11

Damage formation in T300/976 composite laminates \(\left[ {\left( {45/ - 45} \right)_{4} } \right]_{{\text{S}}}\) due to gradual degradation of the material properties with coefficient: a (+ 45) degree layer; and b (− 45) degree layer

Full size image

4 The results of PDA in CNT-CF-Reinforced Polymeric Nano-Composites

In the simulation process, the displacement control method has been used and the displacement value of 5 mm has been considered for the free end of the specimen. The process of damage formation for 2% wt. CNT-CF-reinforced polymeric nano-composite laminates, assuming the material properties will be zero after damage, has been shown in Fig. 12. Also, Fig. 13 shows the process of damage formation, assuming a degradation in the mechanical properties occurs with the degradation coefficient of the material after damage.

Fig. 12
figure 12

Damage formation for 2% wt. CNT-CF-reinforced polymeric nano-composite laminate assuming zero properties of materials after damage: a layers 1 and 4; and b layers 2 and 3

Full size image
Fig. 13
figure 13

Damage formation for 2% wt. CNT-CF-reinforced polymeric nano-composite laminate assuming material properties degradation with degradation coefficient after damage: a layers 1 and 4; and b layers 2 and 3

Full size image

When the properties of the material reach zero, the force at the moment of damage is 7643 N and the maximum tolerable force of the laminate is 14437 N. The first layer of the laminate has been failed by the displacement of the free end of the laminate by 0.9 mm, which is the same layer of zero degrees, and the laminate is completely degraded by the displacement of one millimeter. In the case of material properties degradation by a factor, the force at the moment of damage is 7655 N and the maximum tolerable force of the laminate is 21331 N. The first layer of the laminate is damaged by the displacement of the free end of the laminate by 1.3 mm, which is the same layer of zero degrees, and the laminate is completely degraded by the displacement of 1.4 mm. The force changes due to the displacement of the free end of the laminate have been shown in Fig. 14.

Fig. 14
figure 14

Diagram of force variation in terms of displacement of 2% wt. CNT-CF-reinforced polymeric nano-composite laminate

Full size image

As explained, the mechanical properties of the elements in the developed USDFLD subroutine are degraded after damage and with the increase of the applied load, this process continues progressively until the structure failed from total degradation. In this study, the largest contribution of degradation is due to the mode of fiber failure.

In Tables 10 and 11, the tensile analysis results of nano-composite for different percentages of CNTs have been developed using the subroutine with the help of solution-dependent variables (SDV) and field variables (FV). Also in Fig. 15 and 16, the force diagram based on the displacement of the free end of the laminate has been shown for the conditions of degrading the material's mechanical properties to zero and degrading the mechanical properties of the material by applying a coefficient.

Table 10 Tensile analysis results of CNT-CF-reinforced polymeric nano-composite laminate under the conditions of material properties degrade to zero
Full size table
Table 11 Tensile analysis results of CNT-CF-reinforced polymeric nano-composite laminate under the conditions of material properties degradation by applying a coefficient
Full size table
Fig. 15
figure 15

Diagram of force variation in terms of displacement of CNT-CF-reinforced polymeric nano-composite laminates under tension and the conditions of material properties degrade to zero

Full size image
Fig. 16
figure 16

Diagram of force variation in terms of displacement of CNT-CF-reinforced polymeric nano-composite laminates under tension and the conditions of material properties degradation by applying a coefficient

Full size image

According to Table 10 and Fig. 15, in conditions where the material's mechanical properties tend to zero after the initiation of damage, with increasing CNTs, the maximum tolerable stress on the laminate increases, and also the displacement of the laminate free end increases. The same trend is true when the degradation in material properties occurs by applying a coefficient after the initiation of damage, as shown in Table 11 and Fig. 16. The obvious difference between Figs. 15 and 16 is in the maximum force, which indicates that if the applying degradation coefficient progressively accompanies the material's mechanical properties, the maximum bearing force of the laminate increases significantly. The results also show that the damage initiation force and the tolerable displacement of the laminate in both cases increase with the increasing content of CNTs. The displacement of the free end of the laminate at the time of failure of the first composite layer increased with the presence of a nanotube.

5 Discussion and Conclusion

In this research, using the multi-scale method, the mechanical and strength properties of CNT-CF-reinforced polymeric composite have been extracted, and then the initiation and propagation of progressive damage in a composite laminate have been investigated. The mechanical properties of the polymer matrix consisting of Epon-828 epoxy and TETA hardener with different percentages of CNT are taken from the results of the authors of the same research, which have been extracted at the nano-scale using MD (Soleimany et al. 2021a). The results of the mechanical properties of the resulting nano-composite have been used as an equivalent resin in the present study in order to obtain a three-component nano-composite by adding CF. In this case, on a micro-scale, the mechanical properties of the three-component nano-composite have been estimated. Micro-scale mechanical properties have been estimated using the FE method with the help of ABAQUS FE software and the application of periodic boundary conditions. Then, the strength properties of the equivalent resin and the strength properties of the nano-composite lamina have been extracted analytically. After that, including the mechanical and strength properties of the three-component nano-composite, the initiation and propagation of progressive damage on the nano-composite laminate with a central open-hole under tensile loading has been investigated. Damage simulation has been accomplished using the Hashin-type 3D criterion with the material degradation rules, developing a numerical code and attaching it to ABAQUS FE software. Degradation of material properties after the damage has been investigated based on the two methods, zero material properties after damage and degradation of materials with degradation coefficient after damage.

The general results of this research can be mentioned as follows:

  • By increasing the CNT content in the composite, the elastic modulus and shear modulus and the strength properties of the composite will increase, which leads to an increase in the force tolerance to the laminate due to uniaxial tensile strength. Of course, the adding CNT to the composite has no effect on the strength of the composite in the fiber direction, but it has a significant effect in the direction perpendicular to the fiber.

  • The initiation and evolution of damage and maximum tolerable force on the open-hole composite laminate were estimated using a Hashin-type 3D damage criterion. Using the written USDFLD code and the proposed method, it is also possible to investigate and analyze damage in large and complex composite structures.

  • As the CNT weight fraction in the nano-composite increases, the force required to initiate damage to the open-hole composite laminate increases.

  • By increasing the displacement of the composite laminate free end with \(\left[ {0/90} \right]_{s}\) stacking sequence, the force increases and with the initiation of damage to the element, the properties of that element decrease and the damaged element is analyzed with new properties until the end of the tensile analysis.

  • If the mechanical properties become zero after damage, the composite laminate tolerates less force compared to the conditions where its mechanical properties are degraded by a degradation coefficient after damage.