1 Introduction

Hydraulic jumps are extensively used in hydraulic engineering applications as the energy dissipator below chutes, weirs, gates, and spillways to protect the tailwater from severe scour and possible destruction. The optimum state for designing the dimensions of the stilling basin from an economy and safety viewpoint and increasing the efficiency of the hydraulic jump is considered by hydraulic engineers (Palermo and Pagliara 2017).

A hydraulic jump in a horizontal, rectangular, smooth, and prismatic channel is referred to as classical. The classical hydraulic jump has been extensively studied by Rajaratnam (1965), Leutheusser and Kartha (1972), Herbrand (1973), Peterka (1978), McCorquodale and Khalifa (1983), Hager and Bremen (1989), Wu and Rajaratnam (1995), Hager (2013), Carollo et al. (2009) and Mnassri and Triki (2020) (Hager 2013; Hager and Bremen 1989; Herbrand 1973; Leutheusser and Kartha 1972; Peterka 1978; Rajaratnam 1965; Wu and Rajaratnam 1995; Mnassri and Triki 2022; McCorquodale and Khalifa 1983; Carollo et al. 2009).

The combination of the stilling basin with the transition to the tailwater channel has been a long-standing challenge. A hydraulic jump in abrupt expansions can be found where the width of the approaching supercritical flow is smaller in comparison to that of the downstream channel (Zare and Doering 2011). In an abruptly expanding, rectangular and horizontal channel, depending on the tailwater depth, three jumps can be formed. In the lower tailwater, the toe of the jump is lower than the point at which the cross-wave hits the channel’s wall (point A in Fig. 1) and an R-jump will be formed. By increasing the tailwater depth, the jump occurs between the expansion section and point (A), as shown in Fig. 1; the result is an S-jump. This jump is more like an asymmetrical and oscillating jet, forming without surface rollers. By increasing the tailwater, the toe of the jump is higher than the junction section, leading to the formation of a T-jump. This jump can be symmetric or asymmetric, depending on how far the toe of the jump can be formed from the junction (Rajaratnam and Subramanya 1968).

Fig. 1
figure 1

Classification of hydraulic jumps in a prismatic channel with sudden expansion

Full size image

Hager (1985) studied the characteristics of the hydraulic jump in a gradually and abruptly expanding channel width in non-prismatic rectangular channels. The results showed that the hydraulic jump in an expanding channel needs a lower tailwater depth under identical inflow conditions. Also, the relative energy loss of the non-prismatic version was the weakest for the usual hydraulic jump and the best for an abrupt enlargement; length characteristics were nearly independent of the width ratio and had the same order of magnitude as in prismatic channels (Hager 1985).

Alhamid (2004) also studied the S-jump on sloping basins. He found that S-jumps had a smaller sequent depth ratio and a similar jump length at high expansion ratios, relative to the classical jump. He also showed that the S-jump was more efficient than the classical in prismatic channels and that efficiency increases with decreasing approach channel width (Alhamid 2004).

Further, Bremen and Hager (1993) studied jumps in the expanding channel, finding that the efficiency of the T-jump was always larger and needed less tailwater in comparison to classical jumps (Bremen and Hager 1993). Pagliara et al. 2009 also indicated that the energy loss was larger for the hydraulic jump in expanding channels than in the classical jump (Pagliara et al. 2009). In addition, Hassanpour et al. (2017) studied the characteristics of the hydraulic jump in a gradually expanding rectangular stilling basin. They showed that the sequent depth ratio and the relative length of the jump were decreased by reducing the divergence ratio (Hassanpour et al. 2017).

Torkamanzad et al. (2019) showed that the sudden asymmetric expanding basin with discrete roughness elements over the bed not only increased the efficiency in dissipating additional energy and reduced the sequent depth, as well as the basin length, but also had a significant effect on the formation of the flow symmetry downstream of the basin (Torkamanzad et al. 2019).

Daneshfaraz et al. (2020) investigated the characteristics of hydraulic jump in an abrupt expanding stilling basin with rough bed. The results demonstrated that sequent depth and the length of the S-jump on the rough bed were reduced to 20 and 16%, respectively. Also, S-jump with rough beds reduces the secondary depth by about 58.5% compared to classical hydraulic jump (Daneshfaraz et al. 2020).

The stability of the hydraulic jump has to be controlled under all possible flow conditions. Sometimes, an abrupt drop (negative step) is applied to the stilling basin to stabilize the hydraulic jump location and prevent the potential downstream erosion. The occurrence of the hydraulic jump at an abrupt drop can alter the design of stilling basins (Moore and Morgan 1957; Kawagoshi and Hager 1990; Ohtsu and Yasuda 1991; Chanson and Toombes 1998). Hager and Bretz (1986) also classified the hydraulic jumps in the vicinity of a negative step into six flow patterns, depending upon the inflow and tailwater flow conditions (Fig. 2). When the tailwater depth is lowered from the A-jump condition (Fig. 2a), at a certain stage, the A-jump is changed into a stationary standing wave; this is called the maximum wave (Fig. 2b), characterized by the formation of a large standing eddy downstream of the jet; the more the tailwater depth is lowered from the condition of the maximum wave, the more it passes from the upward curved jet through the downward curved jet (Fig. 2c) to change into a B-jump (Fig. 2d). Formations of upward and downward curved jets are not desirable because of the violent undulations propagating far downstream (Hager and Bretz 1986).

Fig. 2
figure 2

Flow conditions (from Ohtsu and Yasuda, 1991): a A-jump, b wave jump, c wave train, d B-jump (maximum plunging condition), and e minimum B-jump (limited jump)

Full size image

The present work was motivated by the lack of information about the effects of the abrupt expansion and a negative step, on hydraulic jump characteristics properties at a range of Froude number, and the absence of comparative analysis of the sequent depths in the same experiments. Few attempts have been made to study the effects of abrupt expanding channel in the presence of a negative step on the hydraulic jump characteristics. In this study, therefore, based on a large experimental program, the effects of the channel expansion ratio and the negative step, separately and simultaneously, and the inflow Froude number on various aspects of the hydraulic jump have been discussed. In the following, we focus on the S-jump as well as on the B-jump; therefore, the toe of jump is between the point at which the cross-wave hits the channel’s wall (point A in Fig. 1) and the expansion section close to it. The S-jumps and B-jumps are of practical importance because of their stability and efficiency with a comparatively small tailwater depth (Rajaratnam and Subramanya 1968).

2 Materials and Methods

2.1 Experimental Setup

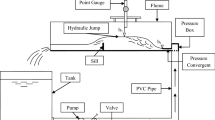
The experiments were conducted in a flume with Plexiglas bed and walls, which was 8.0 m in length, 0.40 m in width, and 0.60 m in depth. It was connected to a hydraulic circuit allowing for the circulation of discharge. The supply pipe was provided with a valve to regulate the water supplied into the flume. The supercritical depth of the flow was controlled by the upstream sluice gate while the tail water depth was controlled by the downstream sluice gate. The discharge in the flume was obtained from an overhead tank. It was measured by a calibrated magnetic flow meter located in the supply line with \(\pm 5\mathrm{\%}\) accuracy. Depths of flow, \({d}_{1}\) and \({d}_{2}\) were measured with a point gauge of ± 1 mm accuracy. The jump length \(\left({L}_{j}\right)\) was measured by a graduated rule as the distance between the toe of the jump and the location where the gradually varied flow started (Hager 2013). The jump roller was measured by a gradual rule as the distance between the toe of the jump and the end section of the roller (stagnation point). The total run number was 108 using Q, which ranged from 30 to 50 \(L/s\); the upstream Froude number \(\left({\mathrm{Fr}}_{1}\right)\) was from 4.9 to 9.5. Four Plexiglas physical models were built with the expanding ratio \(\left(B={b}_{2}/{b}_{1}\right)\) of 1, 1.33, 1.6, and 2 (where \({b}_{1}\) and \({b}_{2}\) are the widths of the stilling basin upstream and downstream of the hydraulic jump, respectively). The experiment’s sudden drop heights \(\left(s=0.03 and 0.06 m\right)\) extended to the location of the width change. In all of these experiments, an attempt was made to place the jump toe at the location of the channel width change (S-jump), as well as the channel drop (B-jump). The flow channel section of the experiments is illustrated in Fig. 3.

Fig. 3
figure 3

Definition sketch for S-jump on the negative step

Full size image

2.2 Dimensional Analysis

The sequent depth \(\left({d}_{2}\right)\) in a horizontal and abruptly expanding channel with a suddenly negative step depends on the following variables:

$${f}_{1}\left(g,s,{d}_{1},{d}_{2},{{b}_{1},{b}_{2},V}_{1},\rho ,\mu \right)=0$$
(1)

Here \({\mathrm{f}}_{1}\) is the functional symbol, \(\rho\) is water density, \(\mathrm{g}\) is the gravity acceleration, \({d}_{1}\mathrm{ and }{d}_{2}\) are the approach flow and sequent depths of the hydraulic jump, respectively,\({V}_{1}\) is the upstream mean incident velocity, and \(\upmu\) is water viscosity. According to the \(\uppi\)-theorem of dimensional analysis (Barenblatt 1987), a dimensionless functional relation is obtained using only six dimensionless groups:

$${f}_{1}\left({\pi }_{1},{\pi }_{2},{\pi }_{3},{\pi }_{4},{\pi }_{5},{\pi }_{6}\right)=0$$
(2)

Choosing \({V}_{1}, {d}_{1}, \rho\) as the repeating variables and rearranging the dimensionless groups results in:

$${f}_{1}\left(\frac{{\mathrm{d}}_{2}}{{\mathrm{d}}_{1}},\frac{{V}_{1}^{2}}{{\mathrm{d}}_{1}g},\frac{{V}_{1}{\mathrm{d}}_{1}}{\vartheta },\frac{{b}_{2}}{{\mathrm{d}}_{1}},\frac{{b}_{1}}{{\mathrm{d}}_{1}},\frac{s}{{\mathrm{d}}_{1}}\right)=0$$
(3)

\({V}_{1}{d}_{1}/\vartheta\) is the Reynolds number \(\left({Re}_{1}\right)\) based on \({y}_{1}\). The values of the Reynolds number were in the range of 75,000–250,000 and viscous effects could be neglected (Hager and Bremen 1989; Rajaratnam and Subramanya 1968). Therefore, \({\mathrm{d}}_{2}/{\mathrm{d}}_{1}\), \({L}_{j}/{\mathrm{d}}_{1}\) and \(\Delta E/{E}_{1}\) depend on the Froude number \(\left({Fr}_{1}{=V}_{1}/\sqrt{{\mathrm{d}}_{1}g}\right)\), expansion ratio \(\left(B={b}_{2}/{b}_{1}\right)\) and step height \(\left(S=s/{\mathrm{d}}_{1}\right)\), So the sequent depth ratio is as follows:

$${\frac{{\mathrm{d}}_{2}}{{\mathrm{d}}_{1}}=f}_{1}\left(\frac{{V}_{1}^{2}}{{d}_{1}g},\frac{{b}_{2}}{{b}_{1}},\frac{s}{{d}_{1}}\right)$$
(4)

Similarly, for the jump length and energy loss, the results are as follows:

$${\frac{{L}_{\mathrm{j}}}{{d}_{2}}=f}_{2}\left(\frac{{V}_{1}^{2}}{{d}_{1}g},\frac{{b}_{2}}{{b}_{1}},\frac{s}{{d}_{1}}\right)$$
(5)
$$\frac{\Delta E}{{E_{1} }} = f_{3} \left( {\frac{{V_{1}^{2} }}{{d_{1} g}},\frac{{b_{2} }}{{b_{1} }},\frac{s}{{d_{1} }}} \right)$$
(6)

2.3 Theoretical Considerations

2.3.1 Sequent Depth Ratio

Applying the momentum equation for Sects. 1 and 2 (Fig. 3), after neglecting the bed shear stress, gives (Bremen and Hager 1993; Ohtsu et al. 1999):

$${F}_{1}-{F}_{2}+{\mathrm{F}}_{s}+{F}_{\mathrm{e}}=\frac{\gamma }{g}\mathrm{Q}\left({{\beta }_{2}V}_{2}-{\beta }_{1}{V}_{1}\right)$$
(7)

where \({F}_{1}=\frac{1}{2}\gamma {b}_{1}{d}_{1}^{2}\) and \({F}_{2}=\frac{1}{2}\gamma {b}_{2}{d}_{2}^{2}\) are the hydrostatic pressure forces, Q is discharge, β1 and β2 denote the momentum correction factors in Sects. 1 and 2, and V1 and V2 indicate the average flow velocities in Sects. 1 and 2, respectively (V1 = q1/d1 and V2 = q2/d2). On the other hand, q is the discharge per unit width (m3/s/m), γ is the specific weight of water (N/m3), and \({F}_{\mathrm{s}}\) is the pressure force enacted from the face of the negative step. In view of streamlines of the flow passing above the negative step, \({F}_{\mathrm{s}}\) can be written as follows (USBR 1955):

$${F}_{s}=k\gamma s{\mathrm{b}}_{1}\left({d}_{1}+s/2\right)$$
(8)

Here, s is the height of negative step, k is the ratio of the actual pressure force on the face of the negative step to the hydrostatic pressure force, and \({F}_{\mathrm{e}}\) is the pressure force from the expansion side walls (Bremen and Hager 1993). For the present spatial B-jump, it was observed during the experiments that the flow depth in front of the expansion side walls was of the order d1 + s. Therefore, \({F}_{\mathrm{e}}\) could be defined as:

$${F}_{\mathrm{e}}=\frac{1}{2}\gamma \left({b}_{2}-{b}_{1}\right){\left({d}_{1}+s\right)}^{2}$$
(9)

Substituting F1, F2, Fs and Fe into Eq. (7), introducing the parameters D = d2/d1 and B = b2/b1, and because of the turbulent flow in the hydraulic jump, the values of β1 and β2 are considered to be 1. So Eq. (7) yields:

$$\frac{1}{2}\gamma b_{1} d_{1}^{2} - \frac{1}{2}\gamma b_{2} d_{2}^{2} + k\gamma sb_{1} \left( {d_{1} + \frac{s}{2}} \right) + \frac{1}{2}\gamma \left( {b_{2} - b_{1} } \right)\left( {d_{1} + s} \right)^{2} = \frac{\gamma }{g}Q\left( {\beta_{2} V_{2} - \beta_{1} V_{1} } \right)$$
(10)

After performing mathematical manipulations and introducing parameters \(\mathrm{D}={d}_{2}/{d}_{1}\) and \(B={b}_{2}/{b}_{1}\), Eq. (11) yields:

$$1 - {\text{BD}}^{2} + \frac{ks}{{d_{1} }}\left( {2 + \frac{s}{{d_{1} }}} \right) + \left( {{\text{B}} - 1} \right)\left( {1 + \frac{s}{{d_{1} }} + \frac{{s^{2} }}{{{\text{d}}_{1}^{2} }}} \right) = 2Fr_{1}^{2} \left( {\frac{1}{{{\text{BD}}}} - 1} \right)$$
(11)

2.3.2 The Energy Dissipation

An analytical equation for estimating the energy loss was developed based on Rajaratnam’s (1967) studies, according to the conditions of the present study, for the relative energy dissipation in the free hydraulic jump (Rajaratnam 1967):

$$\frac{\Delta E}{{E_{1} }} = \frac{{E_{1} - E_{2} }}{{E_{1} }}$$
(12)

Here, \({E}_{1}\) is the upstream and \({E}_{2}\) is the downstream energy head of the hydraulic jump. \({E}_{1}\) and \({E}_{2}\) can be calculated using the equations (Pourabdollah et al. 2022; Rajaratnam and Hurtig 2000):

$${E}_{1}={d}_{1}+\frac{{V}_{1}^{2}}{2g}+{\mathrm{Z}}_{1}={d}_{1}+\frac{{Fr}_{1}^{2}{d}_{1}}{2}+s$$
(13)
$${E}_{2}={d}_{2}+\frac{{V}_{2}^{2}}{2g}+{\mathrm{Z}}_{2}={d}_{2}+\frac{{Fr}_{2}^{2}{d}_{2}}{2}$$
(14)

By substituting \({E}_{1}\) and \({E}_{2}\) in Eq. (12) and performing mathematical simplification, the relative energy loss becomes:

$$\frac{\Delta E}{{E_{1} }} = \frac{{E_{1} - E_{2} }}{{E_{1} }} = \frac{{\left( {1 + \frac{{Fr_{1}^{2} }}{2} + \frac{s}{{d_{1} }}} \right) - \left( {{\text{D}} + \frac{{Fr_{1}^{2} }}{{2{\text{B}}^{2} {\text{D}}^{2} }}} \right)}}{{\left( {1 + \frac{{Fr_{1}^{2} }}{2} + \frac{s}{{d_{1} }}} \right)}}$$
(15)

3 Results and Discussion

In this study, in order to investigate the S-jump on the abruptly expanding basin with the negative step, such characteristics as the length of the hydraulic jump, sequent depth, and energy loss were evaluated. The results are discussed in the following sections.

3.1 Sequent depth ratio

The sequent depth ratios \(\left({d}_{2}/{d}_{1}\right)\), considering the Eq. (4), is dependent on the inflow Froude number \(\left({Fr}_{1}\right)\), the relative height of the negative step \(\left(s/{d}_{1}\right)\) and the divergence ratio of walls \(\left(B={b}_{2}/{b}_{1}\right)\). To evaluate the effect of dissipative elements on the sequent depth ratio of the hydraulic jump, the values of \(\left({d}_{2}/{d}_{1}\right)\) were plotted versus the Froude number, as shown in Fig. 4, for different expansion ratios and heights of negative steps.

Fig. 4
figure 4

Comparison between d2/d1 and Fr1 and those obtained in previous research

Full size image

Figure 4 shows the variation of the sequent depth ratio with the approach flow Froude number and different expansion ratios together, along with the results obtained by Herbrand (1973), Alhamid (2004), and Hassanpour et al. (2017). According to Fig. 4, for all expansion ratios, the sequent depth values decrease by increasing the expansion ratio. Also, the sequent depth ratio increases as the height of the step is raised. The results show that the sequent depth ratio for the hydraulic jump on the expanding channel was smaller than that of the corresponding classic hydraulic jump on a rectangular one.

The results also demonstrated that \(k\) is a function of \({B,Fr}_{1},D \mathrm{and} \frac{s}{{d}_{1}}\) in the expanding channel. By using Eq. (11) and the experimental data, the values of \(k\) were calculated as follows:

$$k=-9.8-5.6{Fr}_{1}+9.7\mathrm{B}+4.2\mathrm{D}+0.3\frac{s}{{d}_{1}} , {R}^{2}=0.72$$
(16)

Figure 5a compares the measured d2/d1 and those calculated by Eqs. (11) and (16). According to this figure, the maximum error is \(\pm 15\%\). There is an excellent agreement between the computed and experimental results.

Fig. 5
figure 5

Comparison between the measured and calculated values, a (Eq. 11) and values of d2/d1 and b (Eq. 15) values of ΔE/E1

Full size image

The relation between the sequent depth ratio \(\left({d}_{2}/{d}_{1}\right)\), the Froude number, and different heights of the negative step and expansion ratios of the channel walls described by the following regression-based equation with a coefficient of determination \(\left({R}^{2}\right)\) equal 0.94.

$$\frac{{d}_{2}}{{d}_{1}}=4.78+0.92{Fr}_{1}-2.83B+0.7\frac{s}{{d}_{1}} , {R}^{2}=0.94$$
(17)

Note from Eq. (17) that the sequent depth ratio is increased with raising the inflow Froude number and the step height. Also, the sequent depth ratio is decreased with increasing expansion ratio.

To evaluate the reduction in the tailwater depth, \({d}_{2}\), a jump was required to be formed on the expanding channel and bed roughness in comparison with \({d}_{2}^{*}\), which refers to the classical jump obtained by the Belanger equation (Belanger 1828) with the same upstream conditions. Rajaratnam (1967) defined a dimensionless depth deficit parameter, Y. It could be observed that this parameter was similar to the submergence factor of the submerged hydraulic jumps and is obtained as follows (Rajaratnam 1967):

$$Y=\frac{{d}_{2}^{*}-{d}_{2}}{{d}_{2}^{*}}\times 100$$
(18)

The average dimensionless parameter of the depth and length of jump, and the percentage increase in energy loss for each experiment can be seen in Table 1. As shown, by increasing the height of the step, D values care decreased, which means that the negative steps increased the sequent depth of the hydraulic jump, as compared to the classic jump, while abrupt expanding decreased the sequent depth of the hydraulic jump.

Table 1 Average dimensionless parameter of the depth and length of jump, and the percentage increase in energy loss
Full size table

Hydraulic jumps of the type S in the expanding channels are asymmetric, either oscillatory or stably asymmetric, much analogous to pressurized diffusor flow (Bremen and Hager 1993). The laboratory observations in this study showed that the asymmetric flow in a sudden divergent channel became the symmetrical flow despite a negative step. Therefore, the hydraulic jump length in the sudden expansion channel with the negative step was significantly reduced when compared to the sudden expansion channel without it; also, the sequent depth was increased (Fig. 6).

Fig. 6
figure 6

Hydraulic jump in a sudden expanding channel: a without a sudden negative step and b with a sudden negative step

Full size image

3.2 Relative Length of the Hydraulic Jump

Previous studies of hydraulic jumps on the abrupt expanding channel (basin length for S-jump) have defined and measured the jump length \(\left({L}_{j}\right)\) in different ways. Rajaratnam and Subramanya (1968), for example, defined the end of the basin at the section where the velocity distribution was uniform (Rajaratnam and Subramanya 1968).

Alternatively, Ohtsu et al. (1999) defined the basin length at the end of the top roller (Ohtsu et al. 1999). On the other hand, Bremen and Hager (1993) estimated the length of the hydraulic jump at the end of the section, where only small air bubbles reached the surface of the water. In this study, the suggested definition of Bremen and Hager (1993) was used to measure this length, as it was fast and more conservative (Bremen and Hager 1993).

The main goal in applying a negative step in an abruptly expanding stilling basin is to decrease the jump length, stabilize the jump position, and avoid jump runoffs toward the downstream region. Additionally, observations of this study showed that these negative steps prevented the flow asymmetry. The relation between \({L}_{\mathrm{j}}/{d}_{1}\) and \({Fr}_{1}\) values for different expansion ratios on negative steps is plotted in Fig. 7. As can be seen from this figure, the length of the hydraulic jump was increased by raising the inflow Froude number. According to the experimental observation, by increasing the expansion ratio, because of the asymmetry of the flow in an abruptly expanding channel, the jump length was increased; the installing step elements stabilized the jump on the stilling basin and the jump length was decreased. In the same way, L is the dimensionless deficit, which can be obtained as follows:

$$L = \frac{{L_{j}^{*} - L_{j} }}{{L_{j}^{*} }} \times 100$$
(19)

where \({L}_{j}^{*}\) is the length of a classical hydraulic jump using the USBR (1955) data with the same upstream conditions, \({d}_{1}\), and \({Fr}_{1}\). The values obtained for the parameter L are shown in the Table 1 (USBR 1955).

Fig. 7
figure 7

Variations of Lj/d1 versus Fr1 in this study as compared to the previous research

Full size image

The regression-based relation between the relative length of the hydraulic jump \(\left({L}_{\mathrm{j}}/{d}_{1}\right)\), the inflow Froude number \(\left({Fr}_{1}\right)\), the expanding ratio \(\left(B\right)\) and the relative height of negative step \(\left(s/{d}_{1}\right)\) can be described by the following equation, with a coefficient of determination, \({R}^{2},\) equal to 0.82, as:

$$\frac{{L}_{\mathrm{j}}}{{d}_{1}}=33.35+6.66{Fr}_{1}-21B-3.38\frac{s}{{d}_{1}} , {R}^{2}=0.82$$
(20)

Equation (20) shows that as the Froude number is increased, the relative length of the jump is also raised. Additionally, by increasing the relative height of the negative step and the expansion ratio, the relative energy loss is decreased. Figure 7 represents the results of the present study and those of Hassanpour et al. (2017), together with the data of USBR (1955) (Hassanpour et al. 2017; USBR 1955).

3.3 Energy Dissipation

The loss of energy in the jump \(\left(\Delta E\right)\) is equal to the difference between the specific energy before and after the jump \(\left({E}_{1}-{E}_{2}\right)\) (Abbaspour et al. 2009); as shown in Fig. 8, the relative energy loss \(\left(\Delta E/{E}_{1}\right)\) was plotted versus Froude numbers for different expansion ratios and heights of steps. This figure shows that for similar Froude numbers, the energy loss of a jump in the abruptly expanding channel was raised by increasing the expansion ratio, while the negative steps increased the energy loss of a jump. Figure 8 compares the results of the present study with those of Hassanpour et al. (2017) and Torkamanzad et al. (2019) (Pagliara et al. 2009; Hassanpour et al. 2017).

Fig. 8
figure 8

Variations of ΔE/E1 versus Fr1 in this study in comparison to the previous research

Full size image

Figure 5b shows the comparison between the measured \(\Delta E/{E}_{1}\) and those calculated by Eq. (15). According to this figure, the maximum error was \(\pm 7\%\). The agreement between the computed and experimental results was excellent.

The percent gain energy loss parameter, G, was defined by the following equation (Tokyay 2005):

$$G = \frac{{\Delta E^{*} - \Delta E}}{{\Delta E^{*} }} \times 100$$
(21)

where \({\Delta E}^{*}\) is the energy loss in a classical hydraulic jump for the same upstream conditions \({d}_{1}\), and \({Fr}_{1}\). The values obtained for the parameter G are shown in Table 1. According to this table, the negative values for the G parameter indicate an increase in the energy dissipator in the abrupt expanding channel compared to the classical state, while adding a negative step in hydraulic jump reduces energy loss. The following empirical equation, as obtained by regression with the value of \(\left({R}^{2}=0.91\right),\) could be used to predict the relation between the relative energy loss \(\left( {\Delta E/E_{1} } \right)\), the upstream Froude number,\({Fr}_{1}\), the expansion ratio (B), and the relative height of the negative step\(\left(s/{d}_{1}\right)\)

$$\frac{\Delta E}{{E_{1} }} = 0.17 + 0.052Fr_{1} + 0.11B - 0.03\frac{s}{{d_{1} }}{ },\quad R^{2} = 0.91$$
(22)

Equation (22) shows that with increasing the Froude number and the expansion ratio, the relative energy loss is increased as well. Additionally, with increasing the relative height of the negative step, the relative energy loss is decreased.

4 Sensitivity Analysis

To distinguish the significance of each input variable on sequent depth ratio, relative energy loss, and jump length ratio, sensitivity analysis was performed on the experimental data in this study. In the analysis, one parameter of Eqs. (17), (20), and (22) was eliminated each time to assess its affection the output. In this way, the RMSE values are characterized as common statistical errors. Results of sensitivity analysis are presented in Table 2.

Table 2 Sensitivity analysis for parameters in the different experiments
Full size table

5 Conclusions

To reduce the construction costs of a stilling basin, a change in the plan and profile sections of the basins appears useful. To design a stilling basin economically, a change in its dimensions can be applied. In this research, the main characteristics of a hydraulic jump under both the effect of the height of negative steps and abruptly expansion channel conditions were investigated. Experimental observations showed that the hydraulic jump at the abrupt expanding channel was asymmetric, which decreased in the sequent depth and the length jump 45.03 and 14.75%, respectively, while the energy loss 28.84% increased. It should be noted that with negative steps, the hydraulic jump was changed to a symmetrical one. Also, the length of the hydraulic jump in the abrupt expansion channel with a negative step was significantly reduced and reached 41.48% compared to the abrupt expansion channel without negative step. In contrast, the negative step had the opposite effect on the amount of secondary depth reduction and the increase of energy loss. Eventually, the secondary depth reduction in the hydraulic jump in the sudden expansion channel with a negative step reached 26.42% and the increase in energy loss also reached 13.64%.