1 Introduction

As a future-oriented cement-based material, ultra-high-performance concrete (UHPC) offers ultra-high strength, high toughness and favorable durability (Zohrevand and Mirmiran 2011; Hassan et al. 2012; Hannawi et al. 2016; Xu et al. 2019a). However, UHPC without confinement exhibits high brittleness under compression, limiting its wide application in engineering construction. To overcome this drawback, UHPC is poured into steel tubes (or fiber reinforce plastic tube) to improve ductility (Xu et al. 2019b; Cai et al. 2021). Along with superior mechanical behaviors, the formed UHPC-filled steel tube members (UHPCFSTs) show several advantages over concrete-filled steel tube members (CFSTs) in reducing self-weight, amount of cement and carbon emissions. As a new type of high-performance composite structure, UHPCFSTs have a broad application prospect in modern structures including super high-rise buildings, long-span bridges and heavy haul railway. Currently, many experimental studies have focused on the nonlinear responses of rectangular UHPCFST members such as axial compression behavior (Chen et al. 2018; Yan et al. 2019), eccentric compression behavior (Zhang et al. 2020; Yan et al. 2021a, b) and flexure behavior (Guler et al. 2012; Huang et al. 2020; Li et al 2021). These achievements lay the foundation for the applications of UHPCFSTs.

Several numerical methods have been put forward to predict nonlinear responses of CFSTs such as three dimensional (3D) finite element method and fiber beam element (FBE) model (Han 2016). In addition, differential quadrature and Bezier methods (Kabir and Aghdam 2019; Yan et al. 2021a) were also alternatively used to predict nonlinear behaviors of CFST beam-column under axial compression due to their high stability and accuracy. FBE model exhibits higher efficiency than 3D finite element model in computing nonlinear behaviors of complex structures. At present, the FBE model is widely used to compute static (Vrcelj and Uy 2002; Ahmed et al. 2012, 2020), seismic (Valipour and Foster 2010; Jiang et al. 2019), fire resistance (Kamila et al. 2019) and impact-resistance behaviors of CFSTs. The accuracy of FBE model is largely dependent on the input materials and interactions between the steel tube and concrete such as confinement effect, local buckling of steel tubes and bond-slip in the interface.

Studies have shown that steel tubes under compression, especially those with square and rectangular steel shape with large width-to-thickness ratios, are liable to be locally buckled due to the initial defect (as shown in Fig. 1). This is attributed to the unequal stress distribution in rectangular steel tubes and smaller critical buckling stress due to the larger width-to-thickness ratio. Local buckling significantly affects the static and cyclic behaviors of thin-walled CFSTs (Valipour and Foster 2010; Liang et al. 2007; Cai et al. 2022). Generally, two methods are adopted when considering the local buckling in FBE model. The first one is using effective distribution width (Uy 2000; Vrcelj and Uy 2002; Ahmed et al. 2012, 2020), whereby steel tubes in ineffective distribution width are out of work due to local buckling and the longitudinal stress is zero. However, it is difficult to determine the critical buckling stress and effective distribution width is difficult because the regression analysis for different types of steel shows a significant deviation, resulting in computational problem.

Fig. 1
figure 1

Local buckling of steel tubes

Full size image

Similar to this work, several studies also considered local buckling by modifying envelopes of steel. However, such studies focused on the static behaviors of CFSTs under monotonic loading (Lai and Varma 2016; Lai et al. 2016; Tao et al. 2021) with concrete strength no more than 90 MPa. Because of the lack of rectangular steel tube-confined UHPC model, few studies have investigated nonlinear behaviors of UHPCFSTs using the FBE model. Besides, the current code provisions were mainly formulated based on results on CFSTs. Considering the difference in mechanical properties between UHPC and ordinary concrete, whether these code provisions are suitable for UHPCFTSTs needs to be further researched.

In this paper, the effective compressive envelopes of steel and confined UHPC model were successfully incorporated into the FBE model to consider the local buckling and passive confinement effect on the UHPC. Meanwhile, an experimental database of UHPCFST members was established, which covered a wide range of material and geometric parameters. Using this database, the nonlinear static and cyclic behaviors of UHPCFTs were computed to verify the validity of the FBE model, the effects of local buckling on the performance of UHPCFSTs were evaluated, and the suitability of current code provisions were comprehensively evaluated. Finally, a novel and simplified N–M interaction curve was established to predict the ultimate bending strength of UHPCFSTs.

2 Modeling Technology

The FBE model (Han 2016) was performed on MATLAB, as shown in Fig. 2, the element was meshed as 0.5 mm for each fiber. The bond-slip in the interface was neglected.

Fig. 2
figure 2

The FBE model of UHPCFSTs

Full size image

2.1 Stress–Strain Model of UHPC and Steel

2.1.1 UHPC

As discussed previously, the accuracy of FBE model is largely dependent on the input materials and interaction between the steel tubes and concrete. The strength and ductility of concrete can be improved through confinement by steel tubes. Therefore, passive confinement effect should be considered in FBE model. The current stress–strain models of confined UHPC (Le and Fehling 2017; Le et al. 2018; Ren et al. 2017) are mainly focused on circle steel tubes.

For rectangular steel tubes, the confined stress is non-uniform. A stress–strain model of rectangular steel tube-confined UHPC based on equivalent method was proposed in our previous work (Cai et al. 2022), which included two branches:

The ascending branch

$$\sigma_{{\text{c}}} = f_{{{\text{cc}}}} [\frac{{r(\varepsilon /\varepsilon_{{{\text{cc}}}} )}}{{r - 1 + (\varepsilon /\varepsilon_{{{\text{cc}}}} )^{r} }}],r = \frac{{E_{{\text{c}}} }}{{E_{{\text{c}}} - f_{{{\text{cc}}}} /\varepsilon_{{{\text{cc}}}} }},\;\varepsilon \le \varepsilon_{{{\text{cc}}}}$$
(1)

The descending and horizontal branches

$$\sigma_{{\text{c}}} = f_{{{\text{cy}}}} + (f_{{{\text{cc}}}} - f_{{{\text{cy}}}} )\exp \left[ { - \left( {\frac{{\varepsilon - \varepsilon_{{{\text{cc}}}} }}{\alpha }} \right)^{\varsigma } } \right],\;f_{{{\text{cy}}}} { = }0.81f_{{{\text{cc}}}} - 48,\;\varepsilon > \varepsilon_{{{\text{cc}}}}$$
(2)

where Ec is the elastic modulus of UHPC which is taken as \(3840\sqrt {f_{{\text{c}}} }\)(Graybeal 2007);\(f_{{{\text{cy}}}}\)(Unit: MPa) denotes plateau stress; α and \(\zeta\) are the parameters determining the shape of the descending branches,\(\zeta\) is the constant,\(\zeta = 4.0\)(Cai et al. 2022),\(\alpha = 0.005 + 0.0075\xi\),\(\xi\) denotes confinement index which is taken as \(A_{s} f_{{\text{y}}} /(A_{{\text{c}}} f_{{\text{c}}} )\), As, Ac are the areas of steel tube and UHPC, fy is the yield strength of steel, fc is the peak strength of UHPC without confinement; εcc (Unit: ε) and fcc (Unit: MPa) denote the peak stress and strain considering passive confinement effect, which are given by:

$$\varepsilon_{{{\text{cc}}}} /\varepsilon_{{\text{c}}} = 4.67\exp [ - 24(f_{{{\text{cc}}}} /f_{{\text{c}}} - 1)] + 1.57,f_{{{\text{cc}}}} /f_{{\text{c}}} = 1 + 0.051\exp (38.3f_{{{\text{el}}}} /f_{{\text{c}}} )$$
(3)

where \(f_{{{\text{el}}}}\) denotes the effective confined pressure (Cai et al. 2022),\(\varepsilon_{{\text{c}}}\) denotes peak strain without confinement, which is given as (Le and Fehling 2017):

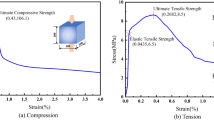
$$\varepsilon_{{\text{c}}} = 0.00083f_{{\text{c}}}^{0.276}$$
(4)

The constitutive model of UHPC under uniaxial tension (Hu et al. 2018) was adopted in this work, as shown in Fig. 2. The residual plastic strain (εpl) (Mander et al. 1988) was calculated when unloading from compressive envelope curve, whilst the unloading branch pointed to the origin when unloading from tensile envelope curve.

2.1.2 Steel

In this work, a bilinear model with a hardening stiffness of 0.01 Es (Es = 205 GPa) was adopted for steel under tension, and local buckling was taken into account for compressive envelope curve. Sakino et al. (2004) put forward an effective compressive stress–strain model, in which local buckling was considered by reducing the strength and creating descending branches. The model is divided into three categories according to width-to-thickness ratio, as shown in Fig. 3. The parameters of key points are shown in Table 1.

Fig. 3
figure 3

The compressive envelopes of steel

Full size image
Table 1 The parameters of effective envelopes of steel (Sakino et al. 2004)
Full size table

In this model, stiffness is no longer Es when unloading from compressive and tensile envelopes. To consider the reduction of stiffness caused by local buckling, the unloading stiffness in compressive envelope curve (Euc) by Dhakal and Maekawa (2002) was adopted, as given in Eq. (5):

$$E_{{{\text{uc}}}} /E_{{\text{s}}} = (f_{{{\text{s}},\min }} /f_{{{\text{t}},\min }} )^{2}$$
(5)

where \(f_{{{\text{s}},\min }}\) and \(f_{{{\text{t}},\min }}\) denote the stresses at the minimum strain point on the compressive skeleton curve with and without considering local buckling, respectively. Using the method by Dodd and Restrepo-Posada (1995), unloading stiffness (Eut) in tensile envelope curve was calculated, as shown in Eq. (6):

$$E_{{{\text{ut}}}} /E_{{\text{s}}} = 0.82{ + }\frac{1}{{5.55{ + }1000\varepsilon_{{{\text{s,}}\max }} }}$$
(6)

where εs, max is the maximum plastic tensile strain.

2.2 Computation procedure of FBE Model

The computation steps for the FBE model were as follows:

  1. 1.

    Geometric and physical parameters were inputted into the model.

  2. 2.

    Section was discretized into fibers and the coordinates were obtained.

  3. 3.

    An curvature increment φ and lateral displacement Δ were computed.

  4. 4.

    Assuming the strain at the neutral axis (ε0), fiber stress σci and σsi was calculated according to strains and loading history.

  5. 5.

    Axial force Nin and ultimate bending strength Min. were computed.

  6. 6.

    Two loading paths were evaluated to determine whether the equilibrium conditions were satisfied: |Nin-N|< 10–2, |Min- Nin(e0 + Δi)|/ Min < 10–2. If not, steps 4–6 were repeated until the equilibrium condition was satisfied. Then, the lateral force Pi was computed. In this step, the ε0 was determined by dichotomy.

  7. 7.

    Steps 3–7 were repeated and the data was recorded until the maximum curvature was reached.

  8. 8.

    N–Δ and P–Δ curves were plotted.

A flow diagram of the computation process is shown in Fig. 4.

Fig. 4
figure 4

A flow diagram of the computation process

Full size image

3 Model Validation

To validate the universality and reliability of the FBE model, experimental results on UHPCFST members in published literature were collected for validation.

3.1 UHPCFST Short Columns Under Axial Compression

The axial compression behavior of UHPCFST short columns with both ends hinged was tested by Chen et al. (2018) and Xiong et al. (2017a) using the axial displacement loading pattern. The material parameters of partial specimens are summarized in Table 2. The axial load-axial strain (N–ε) curves were computed with and without local buckling considered using FBE model, as shown in Figs. 5 and 6.

Table 2 Details of specimen for computation (Chen et al. 2018; Xiong et al. 2017a)
Full size table
Fig. 5
figure 5

The computation of N–ε curves (Chen et al. 2018)

Full size image
Fig. 6
figure 6

The computation of N–ε curves (Xiong et al. 2017a)

Full size image

In Figs. 5 and 6, the axial force exactly reached its peak when the axial stress of UHPC reached fcc. In addition, due to the bond-slip in the interface, certain deviations were observed in the ascending branch between the computation and test results. The failure modes of UHPCFSTs under axial compression were governed by the confinement indexes ξ. For specimens SS1-2 and SS1-3 with small ξ of 0.466 and 0.398, respectively, compression failure occurred on the principal shear plane with crack (Chen et al. 2018). At a higher b/t value, neglecting local buckling for this series overestimated the peak loads and residual strengths. For specimens S2 and S3 with relatively large ξ of 1.25 and 1.34, respectively, the failure with multiple bulges occurred. At lower b/t value, the effect of local buckling was negligible.

Besides, the errors of peak strains and peak loads between the computed results and tested values were within the range of 8%, indicating the correctness and reliability of the FBE model. To further analyze the effect of confinement index on the behavior of UHPCFSTs, a parametric analysis was conducted. As can be seen in the analysis result in Fig. 7, the peak load and residual strength increased concomitantly with increasing confinement index, and the specimen exhibited greater stiffness in the ascending branch.

Fig. 7
figure 7

The effect of confinement index on the N–ε curves

Full size image

3.2 UHPCFSTs Subjected to Eccentric Compression

The eccentric behavior of square UHPCFST short columns with both ends hinged was tested by Zhang et al. (2020) using the displacement loading pattern. The material parameters of partial specimens are summarized in Table 3. The axial force-lateral displacement (N–Δ) curves were computed with and without local buckling considered using FBE model, as shown in Fig. 8.

Table 3 Details of specimen for computation (Zhang et al. 2020)
Full size table
Fig. 8
figure 8

The computation of N–Δ curves (Zhang et al. 2020)

Full size image

Notably, the compressive yield occurred at relatively low load levels because of the small value of strength ratio fy/fc, the axial load reached its peak at the point where peak stress (fcc) was slightly exceeded. The in-plane bending failure was observed for this series (Zhang et al. 2020). Similarly, local buckling had little effects on the peak load and post-peak ductility because of the small width-to-thickness ratio (b/t = 30), which were negligible.

The errors of peak loads between the computed results and tested values were within the range of 7%, which further demonstrated the correctness of the FBE model. To further analyze the effect of eccentric distance on the behavior of UHPCFSTs, a parametric analysis was conducted. As can be seen in the analysis result shown in Fig. 9, the peak load and negative stiffness (descending branch) decreased with the increase in eccentric distance.

Fig. 9
figure 9

The effects of eccentric distance on N–Δ curves

Full size image

3.3 Flexural Behavior of UHPCFSTs

The performance of UHPCFST beams with both ends hinged under flexure was tested by Huang et al. (2020) and Guler et al. (2012) using the displacement loading pattern, with section sizes of 120 mm × 120 mm × 5 mm and 80 mm × 80 mm × 2.5 mm, respectively. In this work, the vertical load–deflection (F–Δ) curve at mid-span and moment–curvature (M–φ) curve were computed and the results are shown in Figs. 10 and 11.

Fig. 10
figure 10

Computation of F–Δ curves(Huang et al. 2020)

Full size image
Fig. 11
figure 11

Computation of M–φ curves (Guler et al. 2012)

Full size image

As can be seen in Fig. 10, local buckling occurred at high displacement due to the small b/t (24) and had little effects on the performance of UHPCFST beam under flexure. Further, as shown in Fig. 11, for the hollow steel tube with a small b/t of 32, neglecting local buckling overvalued post-peak ductility. This is mainly because the hollow steel tubes are susceptible to be locally buckled subjected to flexure.

3.4 Cyclic Behavior of UHPCFSTs

The performance of UHPCFST cantilever columns under cyclic loading was tested by Cai (2022) using the displacement loading pattern. Details of partial specimens are summarized in Table 4. The lateral load–displacement (P–Δ) hysteretic curves were computed, and results are as shown in Fig. 12.

Table 4 Details of specimen for computation (Cai 2022)
Full size table
Fig. 12
figure 12

The computation of P–Δ hysteretic curves (Cai 2022)

Full size image

The failure modes of UHPCFST columns under cyclic loading were governed by the axial compression ratio (Cai 2022). When the axial compression ratios were 0 and 0.15 (Fig. 12a, b), flexure failure was observed, but the effect of local buckling was insignificant. However, as the axial compression ratio increased to 0.45 (Fig. 12c), the failure modes of UHPCFSTs changed from the flexure failure to compression-flexure. In this case, ignoring local buckling greatly overvalued the peak load and post-peak ductility, with peak load overestimated by 16.4% (the computed and test values were 113.4 kN and 97.4 kN, respectively).

Similarly, for the specimens under small stress levels in Fig. 12d–f, the influence of local buckling tended to increase gradually as b/t increased from 30 to 60.

The errors of peak loads for this series were approximately within the range of 9%.

4 Proposed N–M Interaction Curve

In this work, 36 rectangular UHPCFST columns subjected to combined axial compression and bending were collected to assess the applicability of current code provisions. Details of the specimens are summarized in Table 5.

Table 5 Experimental database of rectangular UHPCFSTs under combined axial compression and bending
Full size table

4.1 Assessment of Current Design Codes

Although the load-deformation curve can reveal the working mechanism and describe mechanical properties of UHPCFSTs, it is not convenient for engineering applications. Therefore, a practical calculation method is needed.

At present, there are several code provisions for predicting ultimate strength of composite structures, such as AISC 360-10 (2010), EC4 (2004), GB50936 (2014) and AIJ (2001). However, these code provisions are focused on normal concrete. Considering the significant differences in mechanical properties between UHPC and normal concrete, these codes may be not appropriate for UHPCFSTs. In this work, the experimental database in Table 5 was used to assess the applicability of these code provisions. Mean values (MVs) and standard deviations (SDs) of the bending strengths of the specimens were computed by design codes AISC 360-10, EC4, GB50936 and AIJ. As can be seen in the computed results shown in Fig. 13, MVs were 0.833, 0.863, 0.799 and 0.869, respectively, which suggests that all these code provisions undervalue the ultimate bending strengths of UHPCFSTs. The maximum error between computed and tested value reached 74.5% in Fig. 13c.

Fig. 13
figure 13

The comparison of ultimate bending strength between codes and test results

Full size image

4.2 Proposed Practical Method

In this work, a novel and simplified N–M interaction curve of UHPCFSTs was developed, as shown in Fig. 14, and the expression is given by Eq. (7):

$$\frac{M}{{M_{{\text{u}}} }} = \left( {1 - \frac{N}{{N_{{{\text{uc}}}} }}} \right)\left( {1 - \frac{N}{{N_{{{\text{ut}}}} }}} \right)$$
(7)

where \(M_{{\text{u}}}\) denotes the pure bending strength,\(N_{{{\text{uc}}}}\) and \(N_{{{\text{ut}}}}\) denote the axial compression and tensile strengths. It can be inferred that the parabola always goes through these three points:\((0,N_{{{\text{uc}}}} )\),\((0,N_{{{\text{ut}}}} )\),\((M_{{\text{u}}} ,0)\).

Fig. 14
figure 14

A typical N–M interaction curve

Full size image
  1. 1.

    Axial compression strength Nuc

In this work, the experimental database of square UHPCFSTs under axial compression was established which covers a wide range of geometrical and material parameters, as shown in Table 6.

Table 6 The experimental database of square UHPCFSTs under axial compression
Full size table

Based on the superposition theory and considering the passive confinement to the UHPC,\(N_{{{\text{uc}}}}\) was obtained by regression analysis (Fig. 15) as shown in Eq. (8):

$$N_{{{\text{u}}c}} = f_{{\text{c}}} A_{{\text{c}}} (1 + 1.11\xi )$$
(8)
Fig. 15
figure 15

The regression analysis of Nuc

Full size image

Previous experimental research indicated that, the coefficient in Eq. (8) was about 1.5 for circle steel tube-confined ordinary concrete columns and about 1.25 for circle steel tube-confined UHPC columns. This is mainly because the dilatability of UHPC is not as prominent as that for ordinary concrete. In this work, the coefficient was smaller than 1.25 because of weaker confinement effect of rectangular steel tubes compared with that of circle steel tubes.

  1. 2.

    Pure bending strength Mu

An experimental database of square UHPCFST beams subjected to flexure was established, as shown in Table 7.

Table 7 The experimental database of square UHPCFSTs under pure bending
Full size table

Based on the unified theory of CFSTs (Yu et al. 2013), Mu was calculated using the following formula:

$$M_{{\text{u}}} = \gamma_{{\text{m}}} f_{{{\text{sc}}}} W_{{{\text{sc}}}}$$
(9)

where \(f_{{{\text{sc}}}}\)(\(f_{{{\text{sc}}}} = N_{{{\text{uc}}}} /A_{{{\text{sc}}}}\)) denotes the composite strength,\(A_{{{\text{sc}}}}\) denotes the area of whole section.\(W_{{{\text{sc}}}}\) denotes flexural modulus and γm denotes the plastic coefficient. Referring to the research by Han (2016), γm was obtained by regression analysis (Fig. 16) and the expression is shown as Eq. (10):

$$\gamma_{{\text{m}}} = 1.2 + 0.45\ln (\xi + 0.1)$$
(10)
Fig. 16
figure 16

The regression analysis of γm

Full size image
  1. 3.

    Axial tensile strength Nut

\(N_{{{\text{ut}}}}\) was calculated using the following formula (Lai et al. 2020):

$$N_{{{\text{ut}}}} = (1.1{ + }0.4\alpha_{{\text{s}}} )A_{{\text{s}}} f_{{\text{y}}} + 0.9A_{{\text{c}}} f_{{\text{t}}}$$
(11)

where \(a_{{\text{s}}}\) denotes the steel content which is taken as \(a_{{\text{s}}} = A_{{\text{s}}} /A_{{{\text{sc}}}}\), ft is the tensile strength of UHPC.

In this work, the experimental database in Table 5 was used to evaluate the validity of the proposed practical method. As can be seen in Figs. 17, 18 and Table 5, the computed results using Eq. (7) show a reasonably good agreement with the tested values. The MV of Mc/Mt is 1.04.

Fig. 17
figure 17

The comparisons of proposed N–M interaction curves with test values

Full size image
Fig. 18
figure 18

The comparison of ultimate bending strengths between computed and test results

Full size image

The discrepancy between the practical method and experimental results is related to the uncertainty of UHPC strength.

5 Conclusions

In this paper, a FBE model considering local buckling and passive confinement effect was developed to compute the nonlinear responses of UHPCFSTs. Meanwhile, an experimental database of UHPCFSTs was established and used to comprehensively evaluate the effects of local buckling and the suitability of current code provisions. Finally, a novel and simplified N–M interaction curve was put forward. The following conclusions can be drawn from the analysis in this work:

  1. 1.

    The established FBE model can accurately simulate the axial compression, eccentric compression, pure bending and cyclic behaviors of UHPCFST members.

  2. 2.

    Neglecting local buckling of thin-walled steel tubes would result in overestimation of the peak loads and residual strengths (post-peak ductility) of UHPCFSTs by up to 16.4%. To provide sufficient confinement to the core UHPC and reduce the effect of local buckling, the width-to-thickness ratios of rectangular steel tubes must be less than 30 in engineering design.

  3. 3.

    Because of significant differences in mechanical properties between UHPC and normal concrete, the current code provisions markedly undervalue the ultimate bending strength of UHPCFSTs, with a maximum error of 74.5%.

  4. 4.

    Based on the collected experimental database, a novel and simplified N–M interaction curve was established for predicting the ultimate bending strengths of UHPCFSTs with a high MV accuracy of 1.04.

The nonlinear responses of UHPCFSTs were computed by numerical simulation and the UHPCFST members are the main research objects. To promote the application of UHPCFSTs in engineering, the established FBE model will be used to compute nonlinear behaviors of the UHPCFST framework in future.