Numerical Investigation of Reinforced Concrete and Steel Fiber-Reinforced Concrete Exterior Beam-Column Joints under Cyclic Loading

Abstract

This study presented the influence of steel fiber-reinforced concrete in reducing the transverse reinforcements in the beam-column joint panel zone to solve the reinforcement congestion problem using numerical simulation. A nonlinear finite element approach in ABAQUS/Standard is implemented to simulate the specimens under cyclic loading. The model accuracy is verified by using existing experimental studies available in the published literature. To investigate the influence of steel fiber by reducing the number of transverse reinforcements in the joint panel zone, an adequate shear-reinforced concrete joint is selected as a control specimen from the validated specimens. Totally eight specimens including the control specimen are investigated, of which one reinforced concrete specimen was modeled without any transverse reinforcement in joint and the remaining specimens are modeled by the addition of volume fraction of steel fiber of 1%, 1.5%, and 2% in concrete by the reduction of transverse reinforcements in joint from the control specimen. The result revealed that the addition of 1.5% and 2% volume fractions of steel fiber to concrete could effectively accommodate up to 67% reduction of transverse reinforcement in joint, and addition of 1% volume fraction of steel fiber with the reduction of 33% transverse reinforcement in the beam-to-column joint could effectively comparable to the adequate shear-reinforced concrete joint.

1 Introduction

In the past five decades, numerous researchers have devoted significant efforts to investigate, review and develop design guides to ensure proper and adequate joints performance in reinforced concrete structures under large deformations (Ehsani and Wight 1982; Durrani and Wight 1982; Gustavo et al. 2005).

The current design codes regarding reinforced concrete structures, such as (Eurocode 82004; ACI Committee 318 2014) requires a high amount of transverse reinforcements in the beam-column joint panel zone in order to achieve adequate stiffness, ductility and improve energy dissipation capacity. However, the use of closely spaced transverse reinforcements in joints with simultaneous use of longitudinal reinforcements in the beam and column to avoid premature failure of the beam-column joint regions and adjacent members leads to high congestion of reinforcing bars (Ibarra and Bishaw 2016). This accumulation of reinforcing bars in the joint area causes construction difficulties, pouring and consolidation of concrete, lack of bond areas between steel and concrete, space voids within the joint core leading to abrupt, and unpreventable concrete crushing failure especially in the most vulnerable joints, such as exterior joints (Li and Leong 2014; Ibarra and Bishaw 2016; Saghafi and Shariatmadar 2018). It affects the stiffness, ductility, tension stiffening, strength, and cracking behavior of reinforced concrete structural members (ACI Committee 408 R-03 2003).

Experimental studies by (Jiuru et al. 1992; Canbolat et al. 2005; Parra-Montesinos 2006; Gustavo et al. 2005; Kheni et al. 2015; Saghafi and Shariatmadar 2018) have demonstrated that SFRC is capable of improving the seismic performance of reinforced concrete structural members. Various researchers have highlighted that the addition of steel fiber in normal concrete can considerably improve the flexural strength and ductility (Song and Hwang 2004; Thomas and Ramaswamy 2007; Choi and Bae 2019) and energy absorption capacity and fracture toughness (Bischoff 2003) of the reinforced concrete (RC) members and thus changing the failure modes from brittle into more ductile failures.

The use of SFRC as a minimum shear reinforcement for beams has been permitted in (ACI Committee 318 2008) following the research study by (Parra-Montesinos 2006). Also, (ACI Committee 544 1988) provides design guides for SFRC; however, it does not contain any provisions for beam-column joints. Moreover, (ACI Committee 544.1R-96 2002) indicated that there is a shortage of sufficient research studies on SFRC beam to column joints and also recommended that a continuous study is required for the application of SFRC. Therefore, the addition of steel fiber in normal concrete has been a significant effect to increase its tensile response and to promote ductility compared to conventional concrete. Besides, the use of SFRC can be a feasible solution to solve the problem of reinforcement congestion in the beam-column joint region and prevent brittle damage. Experimental study of such joint behavior is not feasible to evaluate the effect of several parameters involved in joint behavior specially in countries which do not have advanced structural laboratories. However, nonlinear finite element analysis can be a convenient and reliable solution to investigate such effects.

In this study, nonlinear finite element analysis of RC and SFRC beam to column joints is carried out using the finite element software ABAQUS. The finite element model is validated against existing RC and SFRC beam-column joints tested by (Choi and Bae 2019). After validation of the model, the performance of SFRC joints under reverse cyclic loading was investigated by varying the contents of steel fiber added in concrete with the reduction of the number of transverse reinforcement in the joint area.

2 Research Significance

This study provides a nonlinear finite element investigation on the response of RC and SFRC beam-to-column joints under cyclic loading. The use of steel fibers in reducing the number of transverse reinforcements in beam-column joints and its influence on joints seismic performance can not be fully understood through a limited number of experimental tests and single steel fiber volume fractions. There is also a relative lack of research on the applications of SFRC in beam-column joint subassemblies. Most of the available studies used SFRC only in the critical regions. In this study, the whole member of the beam-column joint assemblage was made with steel fiber-reinforced concrete for SFRC specimens and normal concrete for RC specimens to explore its seismically important structural responses under cyclic load, mainly including the hysteretic response, failure modes, energy dissipation, ductility, and stiffness degradation.

Furthermore, due to the high expenses and restrictions of specimen fabrication, experimental tests for reinforced concrete structures are needs spending a great amount of time and money. Hence, nonlinear finite element analysis has been one of the well-known convenient and reliable solution to investigate the behavior of reinforced concrete structures. However, finite element investigations on the utilization of SFRC in structural elements, particularly the reduction of transverse reinforcement in beam-column joint subassemblies by using SFRC have not been comprehensively examined. Moreover, numerical studies using the concrete damaged plasticity (CDP) model on the cyclic behavior of SFRC beam-column joints have still been limited. An extensive numerical study has been carried out to explore the influence of the steel fiber volume fraction content added to concrete coupling with the reduction of transverse reinforcements in the beam-column joint panel zone on the response of SFRC beam-column joints under reverse cyclic loading using the CDP model implemented in ABAQUS.

3 Finite Element Model

A three-dimensional nonlinear finite element model has been developed in ABAQUS (Simulia 2017) to investigate the seismic behavior of RC and SFRC beam-column joints. The considered geometry of the exterior joint was similar to that of the cross-section adopted by (Choi and Bae 2019) (presented in the next section). There are numerous types of elements available in ABAQUS. An eight-node hexahedral (brick) element has higher capabilities of converging due to its increased node count, resulting in a more accurate analysis (Puso and Solberg 2006). Due to this, a three-dimensional eight-node brick element (C3D8R) with reduced integration and hourglass control was used for modeling of normal concrete, steel fiber-reinforced concrete and steel plate. The reinforcement bars can be modeled using truss, solid and beam elements. The adoption of solid elements in the finite element model is computationally difficult. Truss elements are selected because the reinforcement bars does not provide high bending stiffness. So, a 2-node three-dimensional linear truss element (T3D2) is adopted to model all steel reinforcements. Each node has three degrees of freedom in T3D2, which makes this element compatible with the three-dimensional eight-node brick element (C3D8R) used to model the concrete materials.

The interaction of steel rebar and concrete is utilized by using the embedded (perfect bond) approach. After conducting mesh sensitivity analysis, a uniform mesh size of 40 mm is chosen for the whole geometry for all elements. To replicate the boundary conditions of the experimental setup, the lower end of the column was defined to be a pin support (displacement constrained in the x-, y-, and z-direction) and the upper end was set as roller support (displacement constrained in x and z-direction) as displayed in Fig. 1. Surface-based tie constraint is used for modeling the interactions between concrete materials and loading steel plate at the tip of the beam; it was constrained in y-direction for cyclic loading application. The developed finite element model details are shown in Figs. 1, 2 and 3.

Fig. 1

Boundary conditions and loading

Fig. 2

Meshing of FE model

Fig. 3

Reinforcement model (specimen JTR-0-BTR)

3.1 Material Model Utilized for Normal Concrete and Steel Fiber-Reinforced Concrete

The plasticity theory is mostly used in modeling of quasi-brittle nature of concrete materials. But, the use of plasticity theory is appropriate only in compression zones (Bahraq et al. 2019). A number of models based on fracture mechanics such as crack-band theory, fictitious crack model and smeared crack model are used in tension zones (Lee and Fenves 1998). Therefore, an approach is required that could consider the nonlinear behavior of quasi-brittle concrete materials in a single constitutive model.

To simulate the quasi-brittle nature of concrete materials different constitutive models supported by ABAQUS such as concrete smeared cracking model, brittle cracking model and concrete damaged plasticity (CDP) model (Jankowiak and Lodygowski 2015). Among the material models existed in ABAQUS for the modeling of normal concrete and SFRC in compression and cracking in tension, concrete damaged plasticity (CDP) model is adopted in this paper. The CDP model provides a general capability for modeling and adequately capturing the nonlinear behavior of quasi-brittle materials both in tension and compression appropriately (Najafgholipour et al. 2017; Behnam et al. 2018; Bahraq et al. 2019). Moreover, the CDP model is effective for the analysis of concrete structures under monotonic, cyclic, and dynamic loading (Najafgholipour et al. 2017; Behnam et al. 2018).

The CDP model employed in ABAQUS has delivered the stable regime with better accuracy for modeling the nonlinear and post-peak behavior of normal concrete and other quasi-brittle materials when compared to the experimental test results (Abdelatif et al. 2015; Genikomsou and Polak 2015; Wosatko et al. 2015; Luk and Kuang 2017). The typical damaged plasticity model uses the concepts of tensile cracking and compressive crushing to represent the inelastic behavior of concrete. Under uniaxial compressive loading, the CDP model behaves linearly until the value of the initial yield is reached, followed by a stress hardening and strain softening beyond the ultimate stress. For complete descriptions of the CDP model and its parameters identification can be found in references (Abdelatif et al. 2015; Simulia 2017; Genikomsou and Polak 2015; Wosatko et al. 2015; Lubliner et al. 1989; Lee and Fenves 1998).

After the calibration of CDP model parameters on the specimen JNR-2-BTR experimentally tested by (Choi and Bae 2019), the values of CDP model parameters presented in Table 1 are adopted. According to (ACI Committee 544, 1988) report, SFRC with a fiber content up to 2% by volume has a density in the same range as normal concrete of 2306–2403 kg/m³. Also, according to the (ACI 544.1R-96, 2002) report, the density and Poisson’s ratio of SFRC are in the same range as the normal concrete when the volume percentage of steel fiber is up to 2%. As a result, the Poisson's ratio and density are taken as 0.2 and 2400 kg/m³, respectively, for both normal concrete and steel fiber-reinforced concrete.

Table 1 Adopted input parameters of the CDP model

3.1.1 Compressive Behavior

The uniaxial stress–strain compressive behavior of normal concrete is determined in accordance with the model proposed by (Carreira and Chu 1985). The behavior of concrete was assumed as elastic and linear up to $0.4f_{{\text{c}}}^{^{\prime}}$ and the plastic behavior was defined using Eqs. (1) and (2).

$$f_{{\text{c}}} = f_{{\text{c}}}^{^{\prime}} *\frac{{\beta \left( {\frac{{ \varepsilon_{{\text{c}}}^{^{\prime}} }}{{\varepsilon_{{\text{c}}} }}} \right)}}{{\beta - 1 + \left( {\frac{{\varepsilon_{{\text{c}}}^{ } }}{{ \varepsilon_{{\text{c}}}^{^{\prime}} }}} \right)^{\beta } }}$$

(1)

$$\beta = \frac{1}{{1 - f_{{\text{c}}}^{^{\prime}} /\varepsilon_{{\text{c}}}^{^{\prime}} E_{{\text{c}}} }}\,{\text{and}}\,\varepsilon_{{\text{c}}}^{^{\prime}} = 0.0022$$

(2)

where $f_{{\text{c}}}$ is the uniaxial compressive stress (MPa), $f_{{\text{c}}}^{^{\prime}}$ is cylinder compressive strength of normal concrete (MPa), $E_{{\text{c}}}$ is the initial modulus of elasticity, $\varepsilon_{{\text{c}}}^{ }$ is the uniaxial compressive strain of concrete, $\varepsilon_{{\text{c}}}^{^{\prime}}$ is the strain at the peak value of stress, and $\beta$ is a material parameter that depends on the stress–strain diagram. The values of compressive strength of normal concrete ($f_{{\text{c}}}^{^{\prime}}$) and its modulus of elasticity are 54.8 MPa and 32,209 MPa, respectively, are used from the test result reported by (Choi and Bae 2019). The concrete ultimate strain $\varepsilon_{u}$ was assumed to a value of $4\varepsilon_{{\text{c}}}^{^{\prime}}$ according to (Wang and Hsu 2001). Several investigators have proposed models for the characterization of the stress–strain behavior SFRC in compression (Ezeldin and Balagurur 1992; Barros and Figueiras 1999; Nataraja et al. 1999; Bencardino et al. 2008; Lee et al. 2015). All have relatively similar approximations of the SFRC behavior subjected to uniaxial compression. In this study, the stress–strain model recommended by (Lee et al. 2015) was adopted to represent the SFRC behavior in compression. Based on this constitutive model, the behavior of the SFRC was assumed to be elastic linear up to reaching $0.4f_{{{\text{cs}}}}^{^{\prime}}$ and the plastic behavior was defined using Eqs. (3)–(8).

$$f_{{{\text{cs}}}} = f_{{{\text{cs}}}}^{^{\prime}} \left[ {\frac{{A\left( {\varepsilon_{{{\text{cs}}}}^{ } /\varepsilon_{0}^{ } } \right)}}{{A - 1 + \left( {\varepsilon_{{{\text{cs}}}}^{ } /\varepsilon_{0}^{ } } \right)^{B} }}} \right]$$

(3)

where; for pre-peak:

$$A = B = \frac{1}{{1 - \left( {\frac{{f_{{{\text{cs}}}}^{^{\prime}} }}{{\varepsilon_{0}^{ } E_{{{\text{cs}}}}^{ } }}_{ }^{ } } \right)^{ } }}\quad {\text{for}}\; \varepsilon_{{{\text{cs}}}}^{ } /\varepsilon_{0}^{ } \le 1.0$$

(4)

For post-peak:

$$B = \left( {\frac{{f_{{{\text{cs}}}}^{^{\prime}} }}{{\varepsilon_{0}^{ } E_{{{\text{cs}}}}^{ } }}_{ }^{ } } \right)^{0.064} \left[ {1 + 0.882\left( {V_{{\text{f}}} \frac{{l_{{\text{f}}} }}{{d_{{\text{f}}} }}_{ }^{ } } \right)^{ - 0.882} } \right] \ge A$$

(5)

$$A = 1 + 0.723\left( {V_{{\text{f}}} \frac{{l_{{\text{f}}} }}{{d_{{\text{f}}} }}} \right)^{ - 0.957} \quad {\text{for}}\, \varepsilon_{{{\text{cs}}}}^{ } /\varepsilon_{0}^{ } > 1.0$$

(6)

where;

$$\varepsilon_{0}^{ } = \left( {0.0003V_{{\text{f}}} \frac{{l_{{\text{f}}} }}{{d_{{\text{f}}} }}_{ }^{ } + 0.0018} \right)f_{{{\text{cs}}}}^{ 0.12}$$

(7)

$$E_{{{\text{cs}}}} = \left( { - 367V_{{\text{f}}} \frac{{l_{{\text{f}}} }}{{d_{{\text{f}}} }}_{ }^{ } + 5520} \right)f_{{{\text{cs}}}}^{^{\prime} 0.41}$$

(8)

where $f_{{\text{cs }}}$ is uniaxial compressive stress of SFRC, $f_{{{\text{cs}}}}^{^{\prime}}$ is the compressive strength of SFRC, $E_{{{\text{cs}}}}$ is the initial elastic modulus of SFRC, $\varepsilon_{{{\text{cs}}}}^{ }$ is uniaxial compressive strain of SFRC, $\varepsilon_{0}^{ }$ is the strain of SFRC at peak stress, $V_{{\text{f}}}^{ }$ is the steel fiber volume fraction, $l_{{{\text{f}} }}^{ }$ is length steel fiber and $d_{{\text{f}}}^{ }$ is the diameter of steel fiber. Hooked steel fiber with a length of 30 mm and a diameter of 0.5 mm was used for consistency with the experimental study by (Choi and Bae 2019). Equation (9) which is proposed by (Ou et al. 2012) was used to estimate the compressive strength of SFRC because it gives an approximately equal value with the experimental test data reported by (Choi and Bae 2019).

$$f_{{{\text{cs}}}}^{^{\prime}} = f_{{\text{c}}}^{^{\prime}} + 2.35{\text{RI}}$$

(9)

where, $f_{{\text{c}}}^{^{\prime}}$ is the normal concrete compressive strength; $f_{{{\text{cs}}}}^{^{\prime}}$ is the compressive strength of SFRC and ${\text{RI}}$ is the fiber reinforcing index which expressed in Eq. (10):

$${\text{RI}} = V_{{\text{f}}} \frac{{l_{{\text{f}}} }}{{d_{{\text{f}}} }}_{ }^{ }$$

(10)

The ultimate strain for SFRC was set to the value $\varepsilon_{u} = 0.02$ according to the work reported by (Wang 2006) for $V_{{\text{f}}}^{ } > 0.5\%$.

3.1.2 Tensile Behavior

The uniaxial tensile stress–strain relationship of normal concrete was estimated by using Eqs. (11), (12), and (13) proposed by (Wang and Hsu 2001):

$$\sigma_{t}^{\left( 1 \right)} = E_{{\text{c}}} *{ }\varepsilon_{t}^{ } \quad {\text{for }}\,\varepsilon_{t}^{ } \le \varepsilon_{{{\text{cr}}}}^{ }$$

(11)

$$\sigma_{t}^{\left( 2 \right)} = f_{t}^{\prime } \left( {\frac{{\varepsilon_{{{\text{cr}}}}^{ } }}{{\varepsilon_{t}^{ } }}} \right)^{0.4} \quad {\text{for}}\,\varepsilon_{t} > \varepsilon_{{{\text{cr}}}}$$

(12)

$$\varepsilon_{{{\text{cr}}}}^{ } = f_{t}^{^{\prime}} /E_{{\text{c}}}$$

(13)

where $\sigma_{t}$ is the tensile strength of concrete,${ }E_{{\text{c}}}$ is the modulus of elasticity of concrete, $\varepsilon_{t}^{ }$ is the concrete tensile strain, $\varepsilon_{{{\text{cr}}}}^{ }$ is cracking strain and $f_{t}^{^{\prime}}$ is cracking stress of the concrete (peak tensile stress). Equation (14), which is proposed by (Genikomsou and Polak 2015), is used to evaluate the concrete tensile strength:

$$f_{t}^{^{\prime}} = 0.33\sqrt {f_{{\text{c}}}^{^{\prime}} }$$

(14)

There are a number of different constitutive models developed by researchers to represent the tensile behavior of SFRC (Barros and Figueiras 1999, 2001; Lok and Xiao 1999). In this study, the equation proposed by (Lok and Xiao 1999) was adopted to represent the tensile behavior of SFRC based on the following reasons: (i) The model is applicable for fiber volume fractions in the range of 0.5–3.0%, which includes the range considered in the present study. (ii) The model is adaptable as it allows for different values of aspect ratio ($l_{{{\text{f}} }}^{ } / d_{{{\text{f}} }}^{ }$) and bond stress $({\uptau }_{d }^{ }$). The uniaxial tensile stress–strain relationships of SFRC by (Lok and Xiao 1999) model are expressed by Eqs. (15), (16), and (17):

$$\sigma = f_{t}^{ } \left[ {2\left( {\frac{{\varepsilon_{ }^{ } }}{{\varepsilon_{t0}^{ } }}} \right)^{ } - \left( {\frac{{\varepsilon_{ }^{ } }}{{\varepsilon_{t0}^{ } }}} \right)_{ }^{ 2} } \right]\quad {\text{for}}\,0 \le \varepsilon \le \varepsilon_{t0}^{ }$$

(15)

$$\sigma = f_{t}^{ } \left[ {1 - \left( {1 - \frac{{f_{tu}^{ } }}{{f_{t}^{ } }}} \right)\left( {\frac{{\varepsilon_{ }^{ } - \varepsilon_{t0}^{ } }}{{\varepsilon_{t1}^{ } - \varepsilon_{t0}^{ } }}} \right)} \right]\quad {\text{for}}\,\varepsilon_{t0}^{ } \le \varepsilon \le \varepsilon_{t1}^{ }$$

(16)

$$\sigma = f_{tu}^{ } \quad {\text{for}}\,\varepsilon_{t0}^{ } \le \varepsilon \le \varepsilon_{tu}^{ }$$

(17)

where $f_{t }$ is the ultimate uniaxial tensile strength of SFRC,${ }\varepsilon_{t0}^{ }$ is the corresponding ultimate tensile strain, $f_{tu}^{ }$ is residual strength from the strain$, \varepsilon_{t1}^{ }$, as presented in Fig. 4. These values are defined in Eqs. (18) and (19) by (Lok and Xiao 1998) as follows:

$$f_{tu}^{ } = \eta v_{{f^{ } }} \tau_{{d^{ } }} \frac{{l_{{{\text{f}}^{ } }} }}{{d_{{{\text{f}}^{ } }} }} { }$$

(18)

$$\varepsilon_{t1}^{ } = \tau_{{d^{ } }} \frac{{l_{{{\text{f}}^{ } }} }}{{d_{{{\text{f}}^{ } }} }}\frac{1}{{E_{{sf^{ } }} }}$$

(19)

where $\eta$ is the fiber orientation factor in a three-dimensional (3D) case. (Lok and Xiao 1999) taken as 0.50 for slabs and 0.405 for beams. In the present work, $\eta$ is taken as 0.50. The value of modulus elasticity of steel fiber ($E_{sf } )$ 200 GPa used for study based (Amin and Gilbert 2019) recommendation. According to (Lok and Xiao 1998), ultimate tensile strain ($\varepsilon_{t0}^{ } )$ of SFRC corresponding to $f_{t}^{ }$ expressed in Eq. (20).

$$\varepsilon_{t0}^{ } = \frac{{2f_{t}^{ } }}{{E_{t0 } }}$$

(20)

where, $E_{t0}$ is the initial tangent modulus of SFRC.

Fig. 4

Tensile stress–strain behavior of SFRC used in FE model by (Lok and Xiao 1999)

For hooked-type steel fibers, the value of bond stress $\left( {\tau_{{d^{ } }} } \right)$ 6.8 MPa is used in this study as proposed by (Lim et al. 1987). Equation (21), which is the correlation between splitting tensile strength ($f_{{{\text{spt}}}}$) and compressive strength $\left( {f_{{{\text{cs}}}} } \right)$ of SFRC proposed by (Xu and Shi 2009), is used to evaluate the splitting tensile strength ($f_{{{\text{spt}}}}$) of SFRC.

$$f_{{{\text{spt}}}} = 0.21\left( {f_{{{\text{cs}}}} } \right)^{0.83}$$

(21)

However, the CDP model requires uniaxial tensile strength as an input. Thus, Eq. (22) given by (Eurocode 22004) is used to convert the splitting tensile strength into a uniaxial one.

$$f_{{{\text{ct}}}} = 0.9f_{{{\text{spt}}}}$$

(22)

3.2 Steel Reinforcement and Steel Plate Modelling

The stress–strain behavior of steel bars was modeled as a bilinear elasto-plastic material using a strain hardening ratio of 0.01 recommended by (Kachlakev and Miller 2001). The mathematical expression expressed by Eqs. (23), (24), and (25).

$$\sigma_{{{\text{s}} }} = E_{{\text{s}}} \varepsilon_{{\text{s}}} \quad {\text{for}}\,\varepsilon_{{\text{s}}} \le \varepsilon_{{\text{y}}}$$

(23)

$$\sigma_{{\text{s}}} = f_{{\text{y}}} + E^{\prime}_{{\text{s}}} \left( {\varepsilon_{{\text{s}}} - \varepsilon_{{\text{y}}} } \right)\quad {\text{for}}\,\varepsilon_{{\text{y}}} < \varepsilon_{{\text{s}}} \le \varepsilon_{{\text{u}}}$$

(24)

$${ }E^{\prime}_{{\text{s}}} = 0.01\,E_{{\text{s}}} = \frac{{f_{{\text{u}}} - f_{{\text{y}}} }}{{\varepsilon_{{\text{u}}} - \varepsilon_{{\text{y}}} }}$$

(25)

where $\sigma_{{\text{s}}}$ is stress at strain $\varepsilon_{{\text{s}}}$, $f_{y}$ is yield stress at yield strain $\varepsilon_{{\text{y}}} , f_{{\text{y}}}$ ultimate stress at the ultimate strain $\varepsilon_{{\text{u}}}$, Es is Young’s modulus of reinforcement bar;${ }E^{\prime}_{{\text{s}}}$ is the slope of the hardening branch. To avoid the premature failure of concrete materials at the cyclic loading point a 20-mm-thick steel plate is modeled with the elastic modulus ($E_{{\text{s}}} )$ of 200 GPa and Poisson’s ratio of 0.3.

4 Loading

The (ACI Committee 374 2013) recommendation for reverse cyclic loading protocol is used with the same loading history as reported in the experimental study, as displayed in Fig. 5. In order to incorporate both the axial load and cyclic load in the finite element simulation, two loading steps are defined in modeling by following the experimental study loading protocol. In the first step, the axial load is applied at the column top surface as a pressure load (10% of column axial load capacity) in a load-controlled mode and kept constant in the second step. Then, the reverse cyclic loading is applied in the second step on the tip of the beam in terms of displacement-controlled mode, where the displacement is determined from the drift ratio (%) based on the expression given in Eq. (26).

$${\text{Drift}}\,{\text{ratio}} \left( \% \right) = \frac{\Delta l}{{l_{{\text{b}}} }} \times 100$$

(26)

where $\Delta l$ and $l_{{\text{b}}}$ are the applied cyclic displacement at the beam end and the beam length from column face to the cyclic displacement point, respectively.

Fig. 5

Schematic representation of the loading history based on ACI 374 (Choi and Bae 2019)

5 Analysis Approach

The nonlinear finite element analysis (NLFEA) is performed in ABAQUS/standard (Simulia 2017) by considering both geometric and nonlinearities with viscose regularization. A full Newton iterative solver with the default matrix storage is employed to solve the numerical simulation. Newton–Raphson equilibrium iteration provides convergence at the end of each load increment within tolerance limits for all degrees of freedom in the model (Najafgholipour et al. 2017; Behnam et al. 2018). Automatic increments with a large value for the maximum number of increments and very small step time are used to increase the rate of convergence.

6 Validation of the Finite Element Model

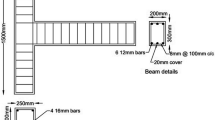
One RC and one SFRC beam-column joint specimens, namely JTR-0-BTR and JNR-2-BTR, which were experimentally tested by (Choi and Bae 2019) are selected to validate the finite element model. The dimensions, material properties, boundary conditions, loading application, etc., were the same as the experimental model. The reinforcement details and geometry of these two specimens are displayed in Fig. 6. The properties of reinforcing bars reported by (Choi and Bae 2019) as presented in Table 2 with Poisson’s ratio of 0.3 are used. Furthermore, the geometry, details and variables of the two tested beam-column joint specimens are reported in Table 3. The JTR-0-BTR is an adequate shear-reinforced concrete beam-column joint designed based on (ACI-ASCE Committee 352 2002) hoop spacing recommendation and made with normal concrete (NC). Specimen JNR-2-BTR is modeled with a 2% volume fraction of steel fiber and without transverse reinforcement in the joint.

Fig. 6

Details of the two selected specimens tested by (Choi and Bae 2019) (units: MPa & mm)

Table 2 Mechanical properties of reinforcing bars (Choi and Bae 2019)

Table 3 Cross-sections, variables and details of specimens tested by (Choi and Bae 2019)

Table 4 presents the compressive and indirect tensile splitting strength of NC and SFRC which were reported in the experimental study and used for the present study. A constant column axial load which is 10% of the column axial compressive strength is applied on the top end of the column and the cyclic loading is applied at the end of the beam similar to the experimental study by (Choi and Bae 2019). To replicate the experimental study, hooked steel fiber with a length of 30 mm and diameter of 0.5 mm is used.

Table 4 Mechanical properties of concrete tested by (Choi and Bae 2019)

6.1 Comparison of Experimental Results With Numerical Results

6.1.1 Load–Displacement Response

Figures 7 and 8 show the comparison of hysteretic and envelope curves obtained from NLFEA compared with the experimental results of JTR-0-BTR and JNR-2-BTR, respectively. The load–displacement results obtained by the NLFEA are in good agreement with that of the experimental results. It is obvious that more micro-cracks are present in the test, while finite element models do not include these micro-cracks (Mohamed et al. 2014). The ABAQUS models show the envelope curve precisely as compared to the test results; however, the hysteretic loops of the ABAQUS models exhibit a fat-pinching distance as expected from the modeling due to the adoption of the embedded method to simulate the interaction between concrete and reinforcements. In order to express the overall model accuracy and associated average overestimation or underestimation of the NLFEA, the error (%) and mean model accuracy [M (%)] are evaluated based on the relation given in (Behnam et al. 2018) and they are defined in Eqs. (27) and (28).

$${\text{Error}}\left( \% \right) = \left| {\frac{{{\text{NLFEA}}\,{\text{ result}} - {\text{Test}}\,{\text{ result}}}}{{{\text{Test}}\,{\text{ result}}}}} \right| \times 100$$

(27)

$${\text{Mean model accuracy}},\,M\left( \% \right) = \frac{{{\text{NLFEA }}\,{\text{result}}}}{{{\text{Test}}\,{\text{ result}}}} \times 100$$

(28)

Fig. 7

Load–displacement hysteretic and envelope curves of JTR-0-BTR (Choi and Bae 2019) (Note: 1 mm = 0.0394 in.)

Fig. 8

Load–displacement hysteretic and envelope curves of JNR-2-BTR (Choi and Bae 2019) (Note: 1 mm = 0.0394 in.)

The average maximum load obtained from the NLFEA of specimens JTR-0-BTR and JNR-2-BTR is lower than that reported from the experimental study by 11.98% and 3.35%, respectively, as presented in Table 5. The model prediction of the joint diagonal cracking load and maximum load leads to an error below 5% and 12%, respectively, which once again shows that the numerical results are in good agreement compared to the results reported from the experimental study.

Table 5 Diagonal cracking load and maximum load comparisons of NLFEA prediction with the experimental results of the two specimens

6.1.2 Failure Patterns

Figures 9 and 10 illustrate the comparison of crack patterns obtained by NLFEA and reported from the experimental study of JTR-0-BTR and JNR-2-BTR at the maximum load stage, respectively. It is depicted that the finite element result of the SFRC specimen also sufficiently exhibits the cracking distribution similar to the experimental test. Based on the comparisons, it can be concluded that the developed nonlinear finite element model can successfully predict the seismic behavior of both RC and SFRC beam-column joints.

Fig. 9

Comparison of crack patterns at maximum load stage of JTR-0-BTR (Choi and Bae 2019)

Fig. 10

Comparison of crack patterns at maximum load stage of JNR-2-BTR (Choi and Bae 2019)

7 Details of Models for Parametric Study

From the two experimentally tested beam-column joint specimens by (Choi and Bae 2019) namely JTR-0-BTR and JNR-2-BTR, which are numerically modeled and validated against experimental results in the validation section, the adequate shear-reinforced concrete specimen JTR-0-BTR is selected as a control specimen for the present study. The other specimens are developed by varying the steel fiber volume fraction and the number of stirrups in the joint panel zone reproduced from the control specimen. Three different volume fraction of steel fiber ($V_{{\text{f}}}$) of 1%, 1.5% and 2% are considered by coupling with a different number of shear reinforcements in the joint panel zone.

Similar to the experimental study conducted by (Choi and Bae 2019), hooked steel fiber with a length of 30 mm and a diameter of 0.5 mm was used in this study. For a better understanding of the beam-column joint seismic behavior, one normal concrete specimen without reinforcement in the joint area is also investigated. The control specimen (JTR-0-BTR) is one of the validated normal concrete specimen, which had six transverse rebars in the joint panel zone designed according to ACI 352-02 Type 2 detailing method (ACI 352 2002). The reinforcement details (i.e., except for the number of stirrups in joint panel zone) and dimensions of beam and columns used in the experimental specimens JTR-0-BTR (Choi and Bae 2019) were kept identical for the numerical modeling of all specimens. The reinforcement details of the joint panel zone of the control specimen and the other seven specimens which originated from the control specimen are illustrated in Figs. 11 and 12, respectively. For the properties of longitudinal reinforcement bars and stirrups, similar to the experimental study by (Choi and Bae 2019), the values presented in Table 2 are used. The description of specimens with modeling parameters are recorded in Table 6.

Fig. 11

Joint reinforcement details of the control specimen JTR-0-BTR (reproduced from (Choi and Bae 2019)

Fig. 12

Modified from the control specimen). (Note: Dimensions in mm, 1 MPa = 145 psi, 1 mm = 0.039 in.)

Joint reinforcement details of specimens for numerical study (

Table 6 Variables and details of all specimens considered in the numerical study

The naming of the specimens is based on the number of transverse reinforcements in the joint panel zone, the content of steel fiber and the axial load ratio. The first part, “JS” and the one-digit number represent the number of stirrups in the joint panel zone. In the second part, “NC” indicates that the specimen is made of normal concrete and “SFRC” indicates that the specimen is made of steel fiber-reinforced concrete, and the following number represents the amount of volume fraction of steel fiber in percent. The letter “A” and the following 2-digit number in the last part represents the applied axial load ratio in percent. This is while the name of the JTR-0-BTR in the experimental study by (Choi and Bae 2019) described as “JTR” indicates that the joint panel zone was reinforced with stirrup spacing recommended by the ACI 352 Type 2 detailing method (ACI 352, 2002). “JNR” indicates that no stirrup was installed in the joint panel zone. “BTR” indicates that the beams reinforced by hoops have (ACI 352 2002) recommended hoop spacing.

8 Results and Discussions of the Parametric Study

8.1 General Behavior and Failure Patterns

According to the CDP model, the crack distribution in the specimen can be approximately described by the development of tensile damage (Liu et al. 2020). The maximum principal plastic strain is the main indicator of cracking initiation and propagations in the CDP model (Najafgholipour et al. 2017; Behnam et al. 2018). The crack distribution and failure patterns of each specimen during the simulation are illustrated in Figs. 13, 14 and 15 at three loading stages.

Fig. 13

Crack patterns of the simulated specimens corresponding to 0.35% drift ratio

Fig. 14

Crack patterns of the simulated specimens corresponding to 0.75% drift ratio

Fig. 15

Crack patterns of the simulated specimens corresponding to the failure stage

The initial flexural cracks in the control specimen were observed at the bottom of the beam near the beam-column junction at a drift ratio of 0.2%. At a drift ratio of 0.35% minor diagonal cracks initiated to the joint panel zone (See Fig. 13a). These diagonal cracks expanded and established an X-pattern at a drift ratio of 0.5%. Thereafter, major diagonal cracks expanded and significant dense cracks forming in the joint region at a drift ratio of 0.75% as depicted in Fig. 14a. With the increase of loading cycles, the propagation of cracks significantly increased in the joint and beam plastic hinge region. After 3.5% drift ratio, significant crushing of concrete occurred and the specimen lost more of its maximum load-carrying capacity. The failure of the control specimen (JTR-0-BTR) was a beam-joint failure (B-J failure) mode (See Fig. 15a).

The initial flexural cracks in specimen JS0-NC-A10 were observed similar to those in the control specimen at 0.2% drift ratio. However, specimen JS0-NC-A10 suffered significant diagonal cracks at a drift ratio of 0.35%, as shown in Fig. 13b, which confirms that the probability of joint failure is more than that of the control specimen. With an increase of loading, specimen JS0-NC-A10 reached its maximum load stage in both push and pull direction at 0.50% drift ratio. At a drift ratio of 0.75% diagonal cracks extended further into the joint panel zone (See Fig. 14b). Due to extensive damage of the joint core, the specimen had lost more of its maximum strength at 1% drift ratio. The failure of JS0-NC-A10 was joint shear failure (J failure) mode (See Fig. 15b).

In specimen JS0-SFRC1-A10, a few flexural cracks initiated in the beams at a drift of 0.2%. However, no significant joint cracking was observed in the joint panel zone up to a drift ratio of 0.35% in the specimen JS0-SFRC1-A10 (See Fig. 13c). This is due to the bridging action of 1% volume fraction of steel fiber. The initiation of few diagonal cracks were observed at the last cycle of 0.50% drift ratio. At a drift ratio of 0.75%, the cracking was mainly concentrated in the joint panel zone and forming an X-pattern as displayed in Fig. 14c. In subsequent loading cycles, crushing of concrete in the joint panel zone occurred. At 2.0% drift ratio, the cracks significantly concentrated in the joint region and the specimen significantly reduced its load-carrying capacity. The failure of JS0-SFRC1-A10 was a joint shear failure (J failure) mode (see Fig. 15c).

Specimen JS0-SFRC1.5-A10 showed a behavior almost similar to that of JS0-SFRC1-A10 until diagonal cracks appeared in the joint at 0.75% drift ratio. However, flexural cracks appeared in the beam were fewer than flexural cracks observed in specimen JS0-SFRC1-A10 (see Fig. 13d). The initial diagonal cracks in JS0-SFRC1.5-A10 initiated into the joint at the first loading cycle of 0.75% drift ratio, which shows JS0-SFRC1.5-A10 experienced significant delayed diagonal cracks compared to the control specimen and JS0-SFRC1-A10 due to the presence of 1.5% volume fraction of steel fiber. The X-shaped diagonal cracks are developed at the last cycle of 0.75% drift ratio, as shown in Fig. 14d, which confirms that the probability of joint failure is less than that of the control specimen. After 5% drift ratio, the specimen significantly lost its strength and reached its failure load stage. As observed from the failure stage, the inclusion of 1.5% volume of steel fiber fraction in concrete changed the failure mode from brittle to moderate ductile failure. The failure of JS0-SFRC1.5-A10 was a beam-joint failure (B-J failure) mode, as shown in Fig. 15d.

Compared to the control specimen, specimen JS0-SFRC2-A10 experienced delayed initial crack and no significant rack was observed up to the last cycle of 0.25% drift ratio. At a drift ratio of 0.35%, some flexural cracks developed on the beam, as shown in Fig. 13e. Similar to JS0-SFRC1.5-A10, major diagonal cracks in the joint are induced at a drift ratio of 0.75% in JS0-SFRC2-A10. However, the intensity of diagonal cracks developed in JS0-SFRC2-A10 were less than the diagonal cracks observed in JS0-SFRC1.5-A10, as depicted in Fig. 14e. This improvement of joint performance was due to the consequence of excellent bridging capability provided by the 2% volume fraction of steel fiber than 1.5% volume fraction of steel fiber. Beyond the drift ratio of 5%, the cracks extended in the joint panel zone and beam plastic hinge region. The failure of JS0-SFRC2-A10 was a combination of beam and joint failure (B-J failure) mode, as shown in Fig. 15e.

In specimen JS2-SFRC1-A10, the initial flexural cracks were observed at the bottom of the beam near the column face at a drift ratio of 0.2%. At a drift ratio of 0.35%, flexural cracks developed and propagated on the beam surface as shown in Fig. 13f. Compared to the control specimens, specimen JS2-SFRC1-A10 experienced a delay of cracks. During the first cycle of 0.75% drift ratio, minor diagonal cracks initiated in the joint region. Subsequently, X-shaped diagonal cracks formed in the joint panel zone, as displayed in Fig. 14f. With continuing loading, more cracks started to concentrate on the beam plastic hinge region. At 5.0% drift ratio, the magnitude of crack becomes significant both in the joint and beam plastic hinge region. As observed from the damages, the failure of JS2-SFRC1-A10 was decided as a beam-joint failure (B-J failure) mode (see Fig. 15f).

The flexural cracks in JS2-SFRC1.5-A10 are insignificant up to the last loading cycle of 0.25% drift ratio compared to the control specimen. However, flexural cracks developed and propagated on the beam surface at a drift ratio of 0.35%, as depicted in Fig. 13g. At a drift ratio of 0.75% drift ratio, diagonal cracks initiated in the joint region (see Fig. 14g). A dense type pattern of cracks concentrates in the beam plastic hinge zone at 1.5% drift ratio. When the loading continued, more cracks developed at the joint and beam plastic hinge region. The failure of JS2-SFRC1.5-A10 was a beam-joint failure (B-J failure) mode (see Fig. 15g).

In specimen JS2-SFRC2-A10, the propagation amount of cracks were much less compared to the normal concrete specimens and the other SFRC specimens which were modeled without joint transverse reinforcements. At a drift ratio of 0.35%, a few flexural cracks appeared and propagated slowly in the beam (see Fig. 13h). At a drift ratio of 0.50%, multiple flexural cracks were observed in the beam. The cross diagonal cracks initiated in the joint region at a drift ratio of 0.75% as depicted in Fig. 14h and further developed with the increase of the drift ratio. With increasing loading cycles, significant dense cracks developed and propagated on the joint panel zone. After the last cycle of 5% drift ratio, the beam-column junction was extremely damaged an excessive deformation occurred in the beam plastic hinge region. The failure of JS2-SFRC2-A10 was a beam-joint failure (B-J failure) mode (see Fig. 15h).

8.2 Load–Displacement Response and Load-Carrying Capacities

The load–displacement response is one of the fundamental characteristics that allows to indicate the seismic performance of the structures under cyclic loading (Park and Paulay 1975). The load–displacement hysteretic loops obtained from eight specimens are presented in Figs. 16a–h and the comparison of their peak loads are recorded in Table 7. The cyclic loading simulations were done according to the (ACI Committee 374 2013) cyclic loading protocol, which applied exactly the same cyclic loading history as the validated experimental study by (Choi and Bae 2019). The hysteretic loops obtained from the analyses exhibit a fat-pinching distance. The fat-pinching behavior of the hysteretic loops may occur due to the complexity in the constitutive modeling of the reinforcement and concrete, and the adoption of the embedded (perfect bond) method to simulate the bond between reinforcement and concrete.

Fig. 16

Load–displacement hysteretic responses of the specimens. (Note: 1 mm = 0.0394 in.)

Table 7 Peak loads and their comparison of all simulated specimens

The maximum load in the control specimen was recorded to be 84.33 kN and 83.40 kN, in the push and pull load directions, respectively, at the drift level of ± 1.25%. Once the concrete was highly crushed at the first cycle of 7.5% drift ratio, its strength decreased to an average value of 71.29 kN. This is while, the normal concrete specimen JS0-NC-A10 exhibited the maximum load of 52.65 kN and 54.21 kN, in the push and pull load directions, respectively, at the drift ratio of 0.50%. These results show that specimen JS0-NC-A10 exhibited a decrease of its average maximum load-carrying capacity by 36.29% compared to that of the control specimen. This strength reduction was due to the lack of shear reinforcement in the joint region of JS0-NC-A10. Likewise, JS0-SFRC1-A10 exhibited a reduction of its average maximum load-carrying capacity by 7.4% compared to the control specimen.

The maximum load of 91.31 kN and 90.22 kN in the push and pull directions, respectively, were recorded at ± 2.5% drift level in the specimen JS0-SFRC1.5-A10. This specimen exhibited 8.23% higher than the control specimen in its average maximum load-carrying capacity. While, JS0-SFRC2-A10 exhibited a maximum load of 100.73 kN and 98.72 kN in the push and pull directions at ± 2.5% drift ratio, respectively. This clearly shows that specimen JS0-SFRC2-A10 exhibited an increase of its average peak load-carrying capacity compared to that of the control specimen by 18.91%. These results confirmed that there was a remarkable improvement of maximum load-carrying capacity, especially when using a 2% volume fraction of steel fiber in concrete compared to 1% and 1.5% volume fraction of steel fibers.

The maximum load of 89.05 kN and 90.13 kN were recorded in the specimen JS2-SFRC1-A10 at ± 1.5% drift ratio in the push and pull directions, respectively. This showed that the specimen JS2-SFRC1-A10 exhibited a 6.83% higher average peak load than the control specimen, but it presented a decrease of 5.65% and 12.77% compared with JS2-SFRC1.5-A10 and JS2-SFRC2-A10, respectively. Furthermore, the specimen JS2-SFRC1.5-A10 experienced an average maximum load of 93.38 kN and 95.29 kN in the push and pull directions, respectively, at a drift ratio of $\pm$ 1.5%. This shows an improvement of 12.48% in average maximum load-carrying capacity relative to the control specimen. Thus, the analysis results indicated that effective usage of steel fiber-reinforced concrete can be used as an alternative solution to the reduction of transverse reinforcements along with enhancement of load-carrying capacity.

8.3 Load–Displacement Envelop Curve and Ductility Factor

The envelop curve was built by joining the peak point of the first cycle of the load–displacement hysteresis curve as shown in Fig. 17. Ductile structural components contribute to energy dissipation by resisting seismic behavior during an earthquake (Paulay and Priestley 1992; Mostofinejad and Akhlaghi 2017b). Using the envelop curves the ultimate displacement, yield displacement and ductility factors are calculated for all specimens in the directions of push and pull reported in Table 8. The ductility is investigated using the concept of displacement ductility factor presented in terms of displacement ductility factor ($\mu_{\Delta }$), which is computed as the ratio of ultimate displacement ($\Delta_{u}$) to yielding displacement ($\Delta_{y}$), as stated in the Eq. (29) (Mostofinejad and Akhlaghi 2017b):

$$\mu_{\Delta } = \frac{{\Delta_{u} }}{{\Delta_{y} }}$$

(29)

Fig. 17

Comparison of load–displacement envelope curves. (Note: 1 mm = 0.0394 in.)

Table 8 Ductility factors of all simulated specimens (Note: 1 mm = 0.0394 in.)

An idealized bilinear force–displacement curve has been a general practice to define the ductility parameters of reinforced concrete components. In this study, reduced stiffness equivalent elasto-plastic theory defined by (Sheikih and Khoury 1993) and (Li et al. 2019) is adopted according to the shape of the envelope curves.

Various alternative definitions have been proposed for the estimation of the yield displacement (Park and Priestley 1987; Paulay and Priestley 1992). In this study, the determination of yield displacement is based on (Park and Priestley 1987) idealized bilinear force–displacement curve with reduced stiffness found on the secant stiffness at 75% of the peak load. The point of the two branches was adopted to determine the yielding point ($P_{u} , \,\Delta_{y}$) based on 75% of the peak load of the specimens, where the ascending branch connecting the coordinate origin and the point ($0.75P_{u} , \,\Delta_{y1}$) on the envelope curve. According to (Mostofinejad and Akhlaghi 2017a; Hu and Kundu 2018); ultimate displacement is defined as the one corresponding to a 15% decrease in maximum load during the reversal loading, which includes the damage executed on the specimen during loading, or the buckling or fracturing of the reinforcement bars. Thus, the points on the post-peak branch ($P = 0.85P_{u} )$ was expressed as the failure load stage of the specimens, corresponding to ultimate displacement ($\Delta_{u}$).

As expressed in Table 8, the application of the steel fiber in concrete improved the ductility of the SFRC specimens significantly. The lowest ductility factor of the specimens JS0-NC-A10, JS0-SFRC1-A10 and JS2-SFRC1-A10 is decreased by 63.69%, 56.61% and 4.10%, respectively, with respect to the control specimen, while the lowest ductility factor of the specimens JS0-SFRC1.5-A10, JS0-SFRC2-A10, JS2-SFRC1.5-A10 and JS2-SFRC2-A10 is increased by 7.26%, 15.08%, 13.41%, and 33.15%, respectively, with respect to the control specimen. This indicated that 1.5% and 2% volume fraction of steel fiber in concrete greatly enhance the ductility compared to 1% volume fraction of steel fibers even without stirrups in the joint. This is one of the main desired characteristics in the present research since it would confirm the investigation of the effectiveness of the steel fiber content used.

8.4 Energy Dissipation

A reinforced concrete structural member dissipates greater plastic energy by undergoing inelastic behavior during seismic loading. In this study, the plastic energy dissipation by all specimens was obtained from ABAQUS simulation output at each drift ratio. Figure 18 shows the plastic dissipated energy at each drift ratio of all specimens. It is observed that the specimens JS0-NC-A10 and JS0-SFRC1-A10 dissipated considerably very lower amounts of energy than the control specimen did due to the joint shear failure occurred at the lower drift cycles. While, the plastic dissipated energy exhibited by SFRC specimens containing 1.5% and 2% volume fraction of steel fiber are much higher than the control specimen did especially after 2.0% drift ratio. The plastic energy dissipated by JS0-SFRC1.5-A10, JS0-SFRC2-A10, JS2-SFRC1-A10, JS2-SFRC1.5-A10, and JS2-SFRC2-A10-A10 at 3.5% drift ratio representing increases of 29.22%, 43.56%, 14.73%, 37.92%, and 49.43%, respectively, over the corresponding value depicted in the control specimen. This indicated that the appropriate use of volume fraction of steel fiber in concrete can be improved the plastic energy dissipation capacity of the beam-column joint, even when stirrups not installed in the joint.

Fig. 18

Comparison of plastic energy dissipation of the specimens

8.5 Stiffness Degradation

In the present study, the beam-column joint cyclic stiffness was evaluated by using the slope of peak-to-peak points of each first cycle out of three cycles at each drift ratio. Then, the cyclic secant stiffness at different cycles was calculated using the Eqs. (30) (Mostofinejad and Akhlaghi, 2017a).

$$K_{i}^{ } = \frac{{P_{i}^{ + } - P_{i}^{ - } }}{{D_{i}^{ + } - D_{i}^{ - } }}$$

(30)

where $K_{i}$ is the cyclic secant stiffness in each first cycle out of three reversal cycles at each drift ratio, $P_{i}^{ + }$ and $P_{i}^{ - }$ are the peak loads in each first cycle out of three reversal cycles at each drift ratio at the positive and negative loading directions, whereas $D_{i}^{ + }$ and $D_{i}^{ - }$ are the displacements corresponding to the peak loads $P_{i}^{ + }$ and $P_{i}^{ - }$, respectively.

Figure 19 illustrates the cyclic stiffness degradation of all specimens in each series at an increasing drift ratio. In general, an increase of steel fiber content leads to an increase of peak-to-peak stiffness. For example, at a drift ratio of 3.5%, the peak-to-peak secant stiffness of the specimens JS0-SFRC1.5-A10, JS0-SFRC2-A10, JS2-SFRC1-A10, JS2-SFRC1.5-A10 and JS2-SFRC2-A10 were + 8.05%, + 23.63%, -3.12%, + 17.65%, and + 31.09% relative to the control specimen. Compared to the control specimen, however, the specimens JS0-NC-A10 and JS0-SFRC1-A10 exhibited much higher stiffness degradation after 0.5% drift ratio. While the specimen JS2-SFRC1-A10 exhibited a comparable stiffness degradation with the control specimen after 2.0% drift ratio.

Fig. 19

Comparison of peak-to-peak secant stiffness values of the specimens

9 Conclusions

Based on the nonlinear finite element simulation results of the present study the following conclusions can be drawn:

• 1. The comparison of the finite element and experimental results indicated that the nonlinear finite element modeling confirms the capability of the model to predict the behaviors of both the conventional reinforced concrete and steel fiber-reinforced concrete beam-column joints.

• 2. The effective use of steel fiber volume fractions in concrete with the appropriate reduction of transverse reinforcements within beam-column joints significantly improved the global seismic behavior of the joints. The load-carrying capacity, ductility, stiffness and energy dissipation capacity of the SFRC beam-column joint using 1.5% and 2% steel fiber volume fraction in concrete significantly improved even without transverse reinforcement in joint panel zone compared to the control specimen (i.e., adequately reinforced specimen according to ACI318-14 requirements and ACI 352 recommendations) and SFRC joint with 1% steel fiber volume fraction.

• 3. In the view of damages and crack patterns, the bridging action of steel fiber, which contributed to delaying the initiation of visible cracks, can efficiently restrain the widening of cracks and reduce the damages initiated by the concrete spalling. Also, it can be used to prevent joint shear failure and change the failure mode from joint shear failure to beam flexural failure and preserving the integrity of the joint concrete core.

• 4. The analysis results revealed that the addition of 1.5% volume fractions of steel fiber in concrete could effectively accommodate up to 67% reduction of transverse reinforcement in the joint panel zone, whereas the use of 2% volume fraction of steel fiber in concrete with approximately up to 100% reduction of transverse reinforcement in joint panel zone provides better seismic performance without significant shear cracks than the control specimen (i.e., adequately reinforced specimen according to ACI318-14 requirements and ACI 352 recommendations). Moreover, the addition of a 1% volume fraction of steel fiber could allow up to 33% reduction of transverse reinforcements in the beam-column joint panel zone.