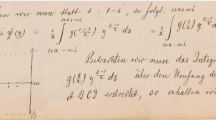Ramanujan identities of higher degree

Abstract

We use techniques regarding generalized Dirichlet series developed in Franke (Ramanujan J 46(1):91–102, 2018) to obtain formulas for a wide class of L-functions at rational arguments. It is shown that these values are related to special functions on the upper half plane which possess similar properties as modular forms. Several formulas of Ramanujan involving values of L-functions at integer arguments turn out to be special cases of the main theorem.

1 Introduction

This paper continues the study of L-functions at rational points which was done in the case of Dirichlet L-functions in [6]. In that paper the author generalized some classical identities for Dirichlet L-functions by Ramanujan, for example the following formula involving values of the Riemann zeta function at integers

$$\begin{aligned}&\alpha ^{-N} \left( \frac{1}{2} \zeta (2N+1) + \sum _{k=1}^\infty \frac{1}{k^{2N+1} (e^{2\alpha k} - 1)}\right) \nonumber \\&\qquad \quad = (-\beta )^{-N} \left( \frac{1}{2} \zeta (2N+1) + \sum _{k=1}^\infty \frac{1}{k^{2N+1} (e^{2\beta k } - 1)}\right) \nonumber \\&\qquad \quad - 2^{2N} \sum _{k=0}^{N+1} (-1)^k \frac{B_{2k}}{(2k)!} \frac{B_{2N + 2 - 2k}}{(2N + 2 - 2k)!} \alpha ^{N+1 - k} \beta ^k, \end{aligned}$$

(1.1)

where $N > 0$ is an integer and $\alpha , \beta$ are positive real numbers such that $\alpha \beta = \pi ^2$. A proof for this relation is also given in [2]. One notes that the terms $\frac{1}{2}\zeta (2N+1)$ on both sides and the finite sum over the Bernoulli numbers come from the residues of the completion $\Lambda (s) := (2\pi )^{-s}\Gamma (s)\zeta (s)\zeta (s + 2N + 1)$ at the points $s=0$ and $s = -2N$ (note that $\zeta (0) = - \frac{1}{2}$), and $s = -2N-1, -2N+1, \ldots , -1, 1$, respectively. The infinite sums are of Lambert type but can be rearranged to power series in $z = e^{-2\alpha }$ (and $z = e^{-2\beta }$) with coefficients identical to those of the Dirichlet series $\zeta (s)\zeta (s + 2N + 1)$.

The formula (1.1) is associated to the number field $K = \mathbb {Q}$, but for example the following new formula corresponds to the case where $K = \mathbb {Q}(\sqrt{D})$ is a real quadratic number field: let $N \in \mathbb {N}$, $d_K$ and $\chi _D(d)$ be the discriminant and character associated to K. Let

$$\begin{aligned} {c(n) := 2\sum _{d|n} \chi _D(d)\sigma _{-2N-1}(d)\sigma _{-2N-1}\left( \frac{n}{d}\right) } \end{aligned}$$

be the coefficients of the Dirichlet series $2\zeta _K(s)\zeta _K(s + 2N + 1)$, where $\zeta _K(s)$ is the Dedekind zeta function associated to K. Then we have for all $\alpha , \beta > 0$ with $\alpha \beta = 4\pi ^2 d_K^{-1}$:

$$\begin{aligned} \begin{aligned}&\alpha ^{-2N} \left( - \zeta '_{K}(0)\zeta _{K}(2N+1) + \sum _{n=1}^\infty c(n)K_0(2\alpha \sqrt{n})\right) \\&\quad =\,\beta ^{-2N} \left( - \zeta '_{K}(0)\zeta _{K}(2N+1) + \sum _{n=1}^\infty c(n) K_0(2\beta \sqrt{n})\right) \\&\qquad +\,\sum _{\begin{array}{c} \ell = 0 \\ \ell \ \text {even} \end{array}}^{2N-2} \alpha ^{2N-2\ell -2} \left( \frac{\zeta '_{K}(\ell - 2N + 1)\zeta _{K}(\ell + 2) + \zeta _{K}(\ell - 2N + 1) \zeta '_{K}(\ell + 2)}{(2N-\ell -1)!^2}\right. \\&\qquad \left. +\,\frac{- 2\zeta _{K}(\ell - 2N + 1)\zeta _{K}(\ell + 2)\log (\alpha )}{(2N - \ell - 1)!^2}\right. \\&\qquad \left. +\,2 \frac{H_{2N-\ell -1} - \gamma }{(2N-\ell -1)!^2} \zeta _{K}(\ell - 2N + 1)\zeta _{K}(\ell + 2) \right) \\&\qquad + R_K \zeta _{K}(2N+2) (\alpha ^{-2N-2} - \beta ^{-2N-2}), \end{aligned}\nonumber \\ \end{aligned}$$

(1.2)

where $K_0$ is the bessel function, $H_n := \sum _{j=1}^n \frac{1}{j}$ is the nth harmonic number, $\gamma = 0,57721\ldots$ is the Euler–Mascheroni constant and $R_K$ is given by

$$\begin{aligned} {R_K = \frac{2\log (\varepsilon ) h_K}{\sqrt{|d_K|}},} \end{aligned}$$

where $h_K$ is the class number and $\log (\varepsilon )$ the regulator of K. This new result is analogous to (1.1) in the following sense: the infinite sums now involve functions of higher degree, the terms $- \zeta (0)\zeta (2N+1)$ in (1.1) are replaced by $-\zeta '_K(0)\zeta _K(2N+1)$ and the finite sum now also involves values of $\zeta _K'$ at integer arguments and a logarithmic term since the degree of K is not $n = 1$ but $n = 2$ and the completion ${\hat{D}}(s) = \left( \frac{4\pi ^2}{d_K} \right) ^{-s} \Gamma (s)^2 \zeta _K(s) \zeta _K(s + 2N+ 1)$ has also poles of order 2 in the critical strip. At this point the reader shall be hinted to a connection to Maass Eisenstein series. Indeed, the coefficients $a(n) := \chi _D(n)\sigma _0(n)$ generate the Dirichlet series $\zeta _{\mathbb {Q}(\sqrt{D})}(s)^2$ and

$$\begin{aligned} {u_D(z) := y^{\frac{1}{2}} \sum _{n=1}^\infty a(n)K_0\left( \frac{2\pi n y}{|D|}\right) \sin \left( \frac{2\pi n x}{|D|}\right) , \qquad z = x+iy,} \end{aligned}$$

is a corresponding Maass Eisenstein series on $\Gamma _D := \Gamma _0(D) \cup S\Gamma _0(D)$ with eigenvalue $\frac{1}{4}$ with respect to the hyperbolic Laplacian operator. Here $S := \begin{pmatrix}0 &{} -1 \\ 1 &{} 0\end{pmatrix}$ is the inversion and

$$\begin{aligned} {\Gamma _0(N) := \left\{ \begin{pmatrix}a &{} b \\ c &{} d\end{pmatrix} \in \mathrm {SL}_2(\mathbb {Z}) \Big | \begin{pmatrix}a &{} b \\ c &{} d\end{pmatrix} \equiv \begin{pmatrix}* &{} * \\ 0 &{} *\end{pmatrix} \mod N\right\} } \end{aligned}$$

the usual congruence subgroup with level N. In this paper we consider the situation that $K_0(*ny) \sin (*nx)$ is replaced by $K_0(*\sqrt{-ni\tau })$, which is (when looking at the corresponding gamma factor) is a function of degree 2. Note that in [11] Lewis and Zagier study the exchange by $e^{-*in\tau }$, which is a function of degree 1.

The theory behind the curious formula (1.1) can be explained by the fact that the values $\zeta (2N+1)$ appear as coefficients of certain period polynomials (or rational functions more generally speaking) of Eichler integrals

$$\begin{aligned} {\mathcal {E}_f(\tau ) := c_k \int \limits _{\tau }^{i\infty } (f(z) - a(0))(z - \tau )^{k-2} \mathrm {d}z, \qquad \tau \in \mathbb {H}\ (= \text {upper half plane}),} \end{aligned}$$

where f is a modular form of weight k with Fourier expansion $f(z) = \sum _{n=0}^\infty a(n)q^n$ (where as usual $q := e^{2\pi i z}$) and $c_k$ is some normalizing constant. An example of the situation looks as follows. Let $\chi$ be a primitive character with conductor $m > 1$ and Gauß sum $\mathcal {G}(\chi )$. We denote the weight k slash operator for $\begin{pmatrix}a &{} b \\ c &{} d\end{pmatrix} \in \mathrm {GL}_2(\mathbb {R})^+$ as usual by

$$\begin{aligned} f|_k\begin{pmatrix}a &{} b \\ c &{} d\end{pmatrix}(z) := (ad - bc)^{k/2} (c\tau + d)^{-k} f\left( \frac{az+b}{cz+d}\right) . \end{aligned}$$

We now find that if

$$\begin{aligned} {F_k(\tau , \chi ) := \frac{\mathcal {G}(\chi )}{m} \sum _{n=1}^\infty \sum _{\ell = 1}^m \frac{\overline{\chi }(\ell n)q^{n/m}}{n^k(e^{2\pi i \ell /m} - q^{n/m})},} \end{aligned}$$

we have

$$\begin{aligned} \left( F_k - C F_k|_{1-k}S\right) (\tau ) = P(\tau ), \end{aligned}$$

(1.3)

where $C = \chi (-1)$ and P is a polynomial which degree is at most k. The coefficients of P are related to values of L-functions at integer arguments. In particular, one can compute

$$\begin{aligned} {P(\tau ) = \sum _{\ell =0}^k \frac{(-1)^\ell }{\ell !} L(-\ell , \chi )L(k-\ell , \overline{\chi }) \left( - \frac{2\pi i \tau }{m}\right) ^\ell .} \end{aligned}$$

As easy corollaries we obtain identities in the spirit of Ramanujan, e.g.

Here, $\zeta _5 = \exp (2\pi i /5)$. To receive this formula one chooses $\chi$ to be the Legendre symbol modulo 5 and substitutes $\tau = i$ into (1.3). For more about the general theory of Eichler integrals and period polynomials the reader is referred to [5]. In [7] transcendental values of Eichler integrals are investigated.

In [6] this author generalized the above identities to the case of not only integer but rational arguments. We proved the following: let $\chi \not = \chi _0$ be a primitive character modulo m, k and b be positive integers and $k \equiv 1 \mod 2$. We define $M_{k,b}(\tau , \chi )$ as a holomorphic function on the upper half plane given by a generalized Fourier series

$$\begin{aligned} M_{k,b}(\tau , \chi ) = \sum _{n=1}^\infty \lambda _{k,b}(n, \chi )q^{bn^{1/b}/m}, \qquad q := e^{2\pi i \tau }, \end{aligned}$$

(1.4)

where the coefficients $\lambda _{k,b}(n, \chi )$ are defined by the identity

$$\begin{aligned} {\sum _{n=1}^\infty \lambda _{k,b}(n, \chi )n^{-s} = \prod _{j=1}^b L\left( s + \frac{j-1}{b}, \chi \right) L\left( s + \frac{j-1}{b} + k, \overline{\chi }\right) .} \end{aligned}$$

Then we have

Theorem 1.1

(see [6], p. 94) Let

$$\begin{aligned} {\gamma _\ell = \left( \frac{2\pi b}{m}\right) ^{-\ell } \frac{(-1)^{\ell }}{(-\ell )!} \prod _{j=1}^b L\left( \frac{\ell + j - 1}{b} ,\chi \right) L\left( \frac{\ell + j - 1}{b} + k ,\overline{\chi }\right) } \end{aligned}$$

if $1 - bk - b \leqslant \ell \leqslant 0$ and $\gamma _\ell = 0$ otherwise. Then we have the modular identity

$$\begin{aligned} {M_{k,b}(\tau , \chi ) - (-1)^B(- i\tau )^{bk - 1} M_{k,b}(-1/\tau , \chi ) = \sum _{\ell = 1 - bk - b}^b \gamma _\ell (-i\tau )^{-\ell },} \end{aligned}$$

where $B = b(k - \chi (-1))/2$.

As a result, products of values of Dirichlet L-functions at rational arguments are linked with objects which have similar properties like classical modular forms.

The purpose now is to generalize this concept to a much wider class of L-functions. The main problem here is that the gamma factor $\gamma (s)$ of L-functions in the completion $\Lambda (s, L) := \gamma (s)L(s)$ (which continues to a meromorphic function on the complex plane and satisfies a functional equation of the standard type) is not of he form $\gamma (s) = A^s \Gamma (s)$ in general. Consequently, the exponential terms in (1.4) are replaced by functions which arise as special cases of the Meijer G-function

$$\begin{aligned} G_{p,q}^{\,m,n} \!\left( \left. \begin{matrix} a_1, \dots , a_p \\ b_1, \dots , b_q \end{matrix} \; \right| \, z \right) = \frac{1}{2 \pi i} \int _{\mathcal {L}} \frac{\prod _{j=1}^m \Gamma (b_j - s) \prod _{j=1}^n \Gamma (1 - a_j +s)}{\prod _{j=m+1}^q \Gamma (1 - b_j + s) \prod _{j=n+1}^p \Gamma (a_j - s)} \,z^s \mathrm {d}s, \end{aligned}$$

where $0 \leqslant n < p$, $0 \leqslant m < q$ are integers and $\mathcal {L}$ describes a suitable path of integration in the sense of an inverse Mellin transformation. For any further details the reader may wish to consult [1, p. 374].

To arrive at this point, we consider generalized Dirichlet series $\sum _{n=1}^\infty a(n)n^{-s/b}$, collected in the vector space $\mathcal {D}((\gamma , \gamma ^*), \sigma , k)$, with absolute abscissa $\sigma$ and properties described in Definition 2.5 in detail, such as a functional equation under $s \mapsto k - s$. They are completed by gamma factors of the form

$$\begin{aligned} {\gamma (s) = ab^s \prod _{j=1}^n \Gamma (a_j + s)^{c_j} \Gamma (b_j - s)^{d_j}} \end{aligned}$$

specified in Definition 2.1 with exponential decay in vertical strips. This is a very general situation and many important Dirichlet series do fit into this family. The main formalism of this paper now is the following theorem.

Theorem 1.2

(cf. Theorem 2.8) Let $\mu \in \mathbb {N}$ and ${\tilde{\gamma }} = (\gamma _j)_{1 \leqslant j \leqslant \mu }$ and ${\tilde{\gamma }}^* = (\gamma ^*_j)_{1 \leqslant j \leqslant \mu }$ be collections of gamma factors in $\mathfrak {W}_{\varvec{\mathrm {a}}, \varvec{\mathrm {b}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}$. We then have a map

The maps $G^\mu$ come from a generalized Gauß formula for gamma factors explained in Proposition 2.3.

The Dirichlet series in the image of the $\mathcal {T}_\mu$ may contain information about L-series at rational arguments. Indeed, with the help of a converse theorem Theorem 2.7 presented in Sect. 2 we obtain curious holomorphic objects on the upper half plane with certain transformation properties tied to constants of interest.

We shall be especially interested in the case that $\gamma (s)$ is of the form $\gamma (s) = A^s \Gamma (s)^n$ for some integer $n \geqslant 1$. Explicitly, we can then write this functions for each $n \in \mathbb {N}$ and $c>0$ as

$$\begin{aligned} {W_n(\tau ) := \frac{1}{2\pi i} \int \limits _{c - i\infty }^{c + i\infty } \Gamma (s)^n (-i\tau )^{-s} \mathrm {d}s, \qquad \tau \in \mathbb {H}.} \end{aligned}$$

We say that the function $W_n$ has degree n (this denotation seems natural by the application to number fields). In the case $n=2$, for example, when studying L-functions of quadratic number fields, the expressions $W_2$ are $K_0$-Bessel functions. An example looks as follows.

Theorem 1.3

(cf. Theorem 3.4) Let $w > 1$ and $b > 0$ be integers with $w \equiv 1 \mod 2$. Let ${\tilde{K}} = (K_1, K_1', \ldots , K_b, K_b')$ be a collection of real quadratic number fields as above. For all $\tau \in \mathbb {H}$ we define the (holomorphic) function

$$\begin{aligned} {E_{w,b}(\tau ; {\tilde{K}}) = 2\Delta b\sum _{\nu =1}^\infty c_{w,b}(\nu ; {\tilde{K}})K_0\left( 4\pi b \root 2b \of {\frac{\nu }{D}} \sqrt{- i \tau } \right) ,} \end{aligned}$$

where $D = \sqrt{|d_{K_1} \cdot d_{K_1'} \cdots d_{K_b} \cdot d_{K_b'}|}$ and $\Delta$ is some constant depending on the collection ${\tilde{K}}$. Then, for all $\tau \in \mathbb {H}$, we have an identity

$$\begin{aligned} {E_{w,b}(\tau ; {\tilde{K}}) - (-i\tau )^{bw - 1} E_{w,b}(-1/\tau ; {\tilde{K}}_\mathrm {inv}) = \sum _{\alpha = 0}^{w+1} P_\alpha (\tau ) + \log (-i\tau )Q_\alpha (\tau ),} \end{aligned}$$

where the $P_i$ and $Q_j$ are rational functions with $P_\alpha \equiv Q_\alpha \equiv 0$ whenever $1 < \alpha$ and $\alpha \equiv 0 \mod 2$.

The coefficients $c_{w,b}(\nu ; {\tilde{K}})$ arise from products of Dedekind zeta functions corresponding to the fields $K_1, K_1', \ldots , K_b, K_b'$, the explicit definition is given in (3.5).

The paper is organized as follows. In the second section we use generalizations of the Hecke converse theorem to reveal connections between generalized Dirichlet series with certain properties (such as a meromorphic continuation to the entire plane) and functions which transform similarly as modular forms and are related to values of Dirichlet series at rational arguments.

In the third and fourth section we apply our results to some special cases such as the Dedekind zeta function of number fields and L-functions associated to modular forms of half-integral weight. In the last section we formulate some obvious questions which are motivated by our results.

Notation We will use the symbol ${\mathbf {1}}$ to denote the vector $(1, 1, \ldots , 1) \in \mathbb {R}^n$, where n shall be clear in the context. Also, for arbitrary $\varvec{\mathrm {a}}\in \mathbb {R}^n$, we write $s_{\varvec{\mathrm {a}}} = \langle \varvec{\mathrm {a}}, {\mathbf {1}}\rangle = \sum _{\nu =1}^n a_\nu$ as the sum of all entries in $\varvec{\mathrm {a}}$.

Let S be a set (or class) and $o := (o_1, \ldots , o_n) \in S \times \cdots \times S$ be a tuple. We will then use the notation $o_{\mathrm {inv}} = (o_n, \ldots , o_1)$ several times. Sometimes we will use the notation $\exp _\mu (x) := \mu ^x$.

2 Dirichlet series and general modular relations

The matter of this section is to explain the term Ramanujan identity and to summarize the concept in a formal definition. Like in the special case of modular forms there is a 1:1 correspondence between Dirichlet series with certain properties (such as a functional equation) and functions which are holomorphic on the upper half plane and are related to interesting rational functions. The examples given by Ramanujan only referred to values of L-functions at integer arguments. However, by including generalized Dirichlet series of the form

$$\begin{aligned} {D(s) = \sum _{\nu =1}^\infty a(\nu )\nu ^{-s/b}} \end{aligned}$$

for some $b \in \mathbb {N}$ it is possible to develop an analogous theory for L-functions at rational arguments. To formalize this theory we need the following.

Definition 2.1

Let $a\in \mathbb {R}^\times$, $b \in \mathbb {R}_{>0}$, $\varvec{\mathrm {a}}= (a_1, \ldots , a_n), \varvec{\mathrm {b}}= (b_1, \ldots , b_n)$ be in $\mathbb {R}^n$ and $\varvec{\mathrm {c}}= (c_1, \ldots , c_n), \varvec{\mathrm {d}}= (d_1, \ldots , d_n)$ be in $\mathbb {Z}^n$. We define the corresponding gamma factor by

$$\begin{aligned} {\gamma _{a,b,\varvec{\mathrm {a}},\varvec{\mathrm {b}},\varvec{\mathrm {c}},\varvec{\mathrm {d}}}(s) = ab^{s} \prod _{j=1}^n \Gamma \left( a_j + s\right) ^{c_j} \Gamma \left( b_j - s \right) ^{d_j}.} \end{aligned}$$

Observe that in the case $n=1$ we have Euler’s formula:

$$\begin{aligned} {\gamma _{1,1,0,1,1,1}(s) = \Gamma (s)\Gamma (1-s) = \frac{\pi }{\sin (\pi s)}.} \end{aligned}$$

It is obvious that products of gamma factors are again gamma factors and we obtain that the set $\mathfrak {W}$ of all gamma factors carries the structure of a multiplicative abelian group. We will simply write $\gamma (s)$ instead of $\gamma _{a,b,\varvec{\mathrm {a}},\varvec{\mathrm {b}},\varvec{\mathrm {c}},\varvec{\mathrm {d}}}(s)$ when the parameters are clear. We have the following formal trick.

Proposition 2.2

For $\mu = 1, 2, 3, \ldots$ we have multiplicative operators

$$\begin{aligned}&G_\mu : \mathfrak {W} \rightarrow \mathfrak {W}\\&\quad \gamma (s) \mapsto \prod _{j=1}^\mu \gamma \left( \frac{s+j-1}{\mu }\right) . \end{aligned}$$

Proof

It is well-known that

$$\begin{aligned} {G_\mu (\Gamma (a_j + s)) = (2\pi )^{(\mu -1)/2} \mu ^{1/2 - s - \mu a_j} \Gamma (\mu a_j + s) \in \mathfrak {W},} \end{aligned}$$

and similarly we obtain

$$\begin{aligned}{G_\mu (\Gamma (b_j - s)), G_\mu (ab^{s}) \in \mathfrak {W}.} \end{aligned}$$

Since $G_\mu$ is a multiplicative map (in fact, a group homomorphism) our assertion follows. $\square$

If we fix real vectors $\varvec{\mathrm {a}}, \varvec{\mathrm {b}}\in \mathbb {R}^n$ in the expression above, we obtain the subgroup $\mathfrak {W}_{\varvec{\mathrm {a}}, \varvec{\mathrm {b}}}$. We then have restricted homomorphisms

$$\begin{aligned} {G_\mu : \mathfrak {W}_{\varvec{\mathrm {a}}, \varvec{\mathrm {b}}} \rightarrow \mathfrak {W}_{\mu \varvec{\mathrm {a}}, \mu \varvec{\mathrm {b}}- (\mu - 1)\varvec{\mathrm {1}}}} \end{aligned}$$

by Remark 2.4. As we will see later, for some applications the above Gamma trick is still too restrictive. But by fixing $\varvec{\mathrm {c}}= (c_1, \ldots , c_n)$ and $\varvec{\mathrm {d}}= (d_1, \ldots , d_n)$ in $\mathbb {Z}^n$, we eventually obtain mappings

This is explained in greater detail in the following proposition. Note that $\mathfrak {W}_{\varvec{\mathrm {a}}, \varvec{\mathrm {b}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}$ is not a group with the operation declared above.

Proposition 2.3

(Generalized Gauß formula) We have mappings

given by

$$\begin{aligned} {(\gamma _{\alpha _j, \beta _j, \varvec{\mathrm {a}}, \varvec{\mathrm {b}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}(s))_{j=1}^\mu \mapsto \prod _{j=1}^\mu \gamma _{\alpha _j, \beta _j, \varvec{\mathrm {a}}, \varvec{\mathrm {b}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}\left( \frac{s + j - 1}{\mu }\right) .} \end{aligned}$$

We explicitly have

$$\begin{aligned} {\prod _{j=1}^\mu \gamma _{\alpha _j, \beta _j, \varvec{\mathrm {a}}, \varvec{\mathrm {b}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}\left( \frac{s + j - 1}{\mu }\right) = \gamma _{A,B,\mu \varvec{\mathrm {a}},\mu \varvec{\mathrm {b}}- (\mu -1)\varvec{\mathrm {1}},\varvec{\mathrm {c}},\varvec{\mathrm {d}}}(s),} \end{aligned}$$

where the real numbers A, B are given by

$$\begin{aligned} A= & {} \left( \prod _{j=1}^\mu \alpha _j \beta _j^{(j-1)/\mu } \right) (2\pi )^{(\mu -1)/2 \cdot (s_{\varvec{\mathrm {c}}} + s_{\varvec{\mathrm {d}}})} \\&\times \exp _\mu \left( \frac{s_{\varvec{\mathrm {c}}} + s_{\varvec{\mathrm {d}}}}{2} - (\langle \varvec{\mathrm {a}}, \varvec{\mathrm {c}}\rangle + \langle \varvec{\mathrm {b}}, \varvec{\mathrm {d}}\rangle )\mu + (\mu - 1)s_{\varvec{\mathrm {d}}} \right) \end{aligned}$$

and

$$\begin{aligned} {B = \left( \prod _{j=1}^\mu \beta _j \right) ^{\frac{1}{\mu }} \mu ^{s_{\varvec{\mathrm {d}}} - s_{\varvec{\mathrm {c}}}},} \end{aligned}$$

respectively. Recall that $s_{\varvec{\mathrm {v}}} = \left< \varvec{\mathrm {v}}, \varvec{\mathrm {1}}\right>$.

Proof

Expanding the product shows

$$\begin{aligned}&\prod _{j=1}^\mu \gamma _{\alpha _j, \beta _j, \varvec{\mathrm {a}}, \varvec{\mathrm {b}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}\left( \frac{s + j - 1}{\mu }\right) \\&\qquad \quad = \prod _{j=1}^\mu \alpha _j \beta _j^{(s + j - 1)/\mu } \prod _{\ell =1}^n \Gamma \left( a_\ell + \frac{s + j - 1}{\mu }\right) ^{c_\ell } \Gamma \left( b_\ell - \frac{s + j - 1}{\mu }\right) ^{d_\ell } \end{aligned}$$

and we use $\prod _{j=1}^\mu \Gamma (b_j - \frac{s+j-1}{\mu }) = \prod _{j=1}^\mu \Gamma (b_\ell - \frac{s}{\mu } - \frac{\mu -1}{\mu } + \frac{j-1}{\mu })$ to obtain

$$\begin{aligned} =&\prod _{j=1}^\mu \alpha _j \beta _j^{(s + j - 1)/\mu } \times \prod _{\ell =1}^n \left[ (2\pi )^{\frac{\mu -1}{2}} \mu ^{\frac{1}{2} - \mu a_\ell - s} \Gamma (\mu a_\ell + s)\right] ^{c_\ell }\\&\times \left[ (2\pi )^{\frac{\mu -1}{2}} \mu ^{\frac{1}{2} - \mu b_\ell + s + \mu - 1} \Gamma (\mu b_\ell - s - \mu + 1) \right] ^{d_\ell }. \end{aligned}$$

Sorting the terms leads us to

$$\begin{aligned} = \gamma _{A,B,\mu \varvec{\mathrm {a}}, \mu \varvec{\mathrm {b}}- (\mu - 1)\varvec{\mathrm {1}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}(s), \end{aligned}$$

as required. $\square$

Sometimes we will leave out the indices of G when the parameters should be clear.

Remark 2.4

Proposition 2.3 provides us with the explicit formula

$$\begin{aligned} {G_\mu (\gamma _{a,b,\varvec{\mathrm {a}}, \varvec{\mathrm {b}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}}(s)) = \gamma _{A_\mu , b \mu ^{-(s_{\varvec{\mathrm {c}}}+s_{\varvec{\mathrm {d}}})}, \mu \varvec{\mathrm {a}}, \mu \varvec{\mathrm {b}} - (\mu - 1)\varvec{\mathrm {1}}}(s),} \end{aligned}$$

where

$$\begin{aligned} {A = a^\mu b^{(\mu -1)/2} (2\pi )^{(\mu -1)/2 \cdot (s_{\varvec{\mathrm {c}}} + s_{\varvec{\mathrm {d}}})} \exp _\mu \left( \frac{s_{\varvec{\mathrm {c}}} + s_{\varvec{\mathrm {d}}}}{2} - (\langle \varvec{\mathrm {a}}, \varvec{\mathrm {c}}\rangle + \langle \varvec{\mathrm {b}}, \varvec{\mathrm {d}}\rangle )\mu + (\mu - 1)s_{\varvec{\mathrm {d}}} \right) .} \end{aligned}$$

The next definition comprises all relevant Dirichlet series for our purposes.

Definition 2.5

Let $b \in \mathbb {N}$. We say that a (generalized) Dirichlet series of the form

$$\begin{aligned}{D(s) = \sum _{\nu =1}^\infty a(\nu )\nu ^{-s/b}} \end{aligned}$$

has signature $((\gamma , \gamma ^*), \sigma , k)$ where $(\gamma , \gamma ^*) \in \mathfrak {W}^2$ and $k \in \mathbb {R}$, if the following conditions are all satisfied:

• (i) D(s) is absolutely convergent in the right half-plane $\{ s \in \mathbb {C}\mid \mathrm {Re}(s) > \sigma \}$ and has a meromorphic continuation to the entire complex plane with possible poles at arguments $s \in \mathbb {R}$.

• (ii) There is a dual (generalized) Dirichlet series $D^*(s)$ also absolutely convergent in $\{ s \in \mathbb {C}\mid \mathrm {Re}(s) > \sigma \}$ with a meromorphic continuation to the entire plane such that the completions

  $$\begin{aligned}{\widehat{D}(s) := \gamma (s) D(s)} \end{aligned}$$

  and

  $$\begin{aligned}{\widehat{D^*}(s) := \gamma ^*(s) D^*(s)} \end{aligned}$$

  are related by the functional equation

  $$\begin{aligned}{\widehat{D}(k - s) = \widehat{D^*}(s).} \end{aligned}$$

• (iii) The function $\widehat{D}(s)$ is bounded on every vertical strip $\{- \infty< \sigma _1< \mathrm {Re}(s)< \sigma _2 < \infty \} \cap \{ |\mathrm {Im}(s)| \geqslant 1\}$.

We denote the space of such generalized Dirichlet series D(s) by $\mathcal {D}((\gamma , \gamma ^*), \sigma , k)$. In the case $\gamma = \gamma ^*$, we simply write $\mathcal {D}(\gamma , \sigma , k)$.

From now on let us fix some gamma factors $\gamma , \gamma ^*$ with the property

$$\begin{aligned} \gamma (s), \gamma ^*(s) \ll _{\sigma _1, \sigma _2} |s|^{\nu _{\sigma _1, \sigma _2}} e^{- \frac{\pi }{2} |\mathrm {Im}(s)|}, \qquad \nu _{\sigma _1, \sigma _2} > 0, \end{aligned}$$

(2.1)

on every vertical strip $\sigma _1< \mathrm {Re}(s) < \sigma _2$. For lots of applications this follows by application of Stirling’s formula

$$\begin{aligned}{\Gamma (s) = \sqrt{2\pi } s^{s- \frac{1}{2}} e^{-s + H(s)}} \end{aligned}$$

in $\mathbb {C}_-$ with holomorphic H with the property

$$\begin{aligned} {\lim \limits _{\begin{array}{c} |s| \rightarrow \infty \\ - \pi + \delta< \mathrm {Arg}(s) < \pi - \delta \end{array}} H(s) = 0} \end{aligned}$$

for all fixed values $\delta \in (0, \pi )$. Let $S(f) \subset U$ denote the set of poles the meromorphic function f in its domain of definition U. For fixed $\sigma$ we define

$$\begin{aligned} {\theta _0 := \max \{ x \in S(\gamma ) \cup S(\gamma ^*) \mid x \leqslant \sigma \}, \qquad \theta _1 := \min \{x \in S(\gamma ) \cup S(\gamma ^*) \mid x > \sigma \}.} \end{aligned}$$

In the case that $\gamma , \gamma ^*$ have no pole z with $\mathrm {Re}(z) > \sigma$, we simply set $\theta _1 = \infty$. Note that we have a holomorphic inverse Mellin transform of $\gamma$

$$\begin{aligned} \mathcal {M}_\sigma ^{-1}(\gamma , x) = \frac{1}{2\pi i} \int \limits _{c - i\infty }^{c + i\infty } \gamma (s) x^{-s} \mathrm {d}s, \qquad \sigma< c < \theta _1, \end{aligned}$$

(2.2)

on the half plane $\mathrm {Re}(x) > 0$. By the usual argument including contour integration we see that (2.2) is independent from the choice of c. We can estimate the integral (2.2) uniformly for all $-i \tau \in W_\delta := \{ z \in \mathbb {C}^\times \mid |\mathrm {Arg}(z)| \leqslant \frac{\pi }{2} - \delta \}$ by

$$\begin{aligned} |\mathcal {M}_\sigma ^{-1}(\gamma , -i\tau )| \leqslant \frac{|\tau |^{-c}}{2\pi } \int \limits _{-\infty }^\infty |\gamma (c + it)| e^{\mathrm {Arg}(-i\tau )t} \mathrm {d}t\ll _{\gamma , c, \delta } |\tau |^{-c}. \end{aligned}$$

(2.3)

Definition 2.6

Let $f : \mathbb {H}\rightarrow \mathbb {C}$ be a holomorphic function. We say that f induces a modular identity (of the Ramanujan type) of signature $((\gamma , \gamma ^*), \sigma , k)$ (where $k \in \mathbb {R}$ and $\gamma , \gamma ^* \in \mathfrak {W}$ satisfies condition (2.1)) if the following conditions are satisfied:

• (i) We can expand f in series of the form

  $$\begin{aligned} f(\tau ) = \sum _{\nu = 1}^\infty \alpha (\nu )\mathcal {M}_\sigma ^{-1}(\gamma , -i\tau \nu ^{1/b}), \qquad b \in \mathbb {N}, \end{aligned}$$

  (2.4)

  such that $\alpha (\nu ) \ll \nu ^{\frac{\sigma }{b} - 1}$ in this case.

• (ii) There is a dual function $f^*$ with expansion

  $$\begin{aligned} {f^*(\tau ) = \sum _{\nu = 1}^\infty \alpha ^*(\nu )\mathcal {M}_\sigma ^{-1}(\gamma ^*, -i\tau \nu ^{1/{b^*}}), \qquad b^* \in \mathbb {N},} \end{aligned}$$

  $\alpha ^*(\nu ) \ll \nu ^{\frac{\sigma }{b^*} - 1}$, and also real numbers $k - \sigma< c_1, \ldots , c_\ell < \sigma$ and polynomials $P_1, \ldots , P_\ell$ with transformation property

  $$\begin{aligned} {f(-1/\tau ) = \tau ^k f^*(\tau ) + \sum _{j=1}^\ell P_j(\log (-i\tau )) \tau ^{c_j}.} \end{aligned}$$

We denote the space of such functions by $\mathcal {R}((\gamma , \gamma ^*), \sigma , k)$. Again, if $\gamma = \gamma ^*$ we write $\mathcal {R}(\gamma , \sigma , k)$. As in classical theory, we will sometimes call k the weight of f.

Theorem 2.7

Let $\gamma , \gamma ^*$ be gamma factors which satisfy (2.1), and $k \in \mathbb {R}$ with $k < 2\sigma$. Then we have an isomorphism between spaces

$$\begin{aligned} {\vartheta : \mathcal {D}((\gamma , \gamma ^*), \sigma , k) \rightarrow \mathcal {R}((\gamma , \gamma ^*), \sigma , k)} \end{aligned}$$

given by

$$\begin{aligned} {\vartheta : D \mapsto \left[ \tau \mapsto \frac{1}{2\pi i} \int \limits _{c - i\infty }^{c + i\infty } \gamma (s)D(s)(-i\tau )^{-s} \mathrm {d}s, \qquad \sigma< c < \theta _1\right] ,} \end{aligned}$$

with inverse

$$\begin{aligned} {\vartheta ^{-1} : f \mapsto \left[ s \mapsto \frac{1}{\gamma (s)} \int \limits _0^\infty f(ix)x^{s-1} \mathrm {d}x, \qquad \sigma< \mathrm {Re}(s) < \theta _1 \right] .} \end{aligned}$$

Note that the representation of $\vartheta ^{-1}(f)$ is not defined for all s but its meromorphic continuation is an element of $\mathcal {D}((\gamma , \gamma ^*), \sigma , k)$.

Proof

We omit a rigorous proof but sketch the main ideas. For the map $\vartheta$ let $\tau = iy$ with $y > 0$ and complete the integrals

$$\begin{aligned} \frac{1}{2\pi i}\int \limits _{\sigma + \varepsilon - i\infty }^{\sigma + \varepsilon + i\infty } \widehat{D}(s)y^{-s}\mathrm {d}s- \frac{1}{2\pi i}\int \limits _{k - \sigma - \varepsilon - i\infty }^{k - \sigma - \varepsilon + i\infty } \widehat{D}(s)y^{-s}\mathrm {d}s\end{aligned}$$

(2.5)

where $0< \varepsilon < \theta _1 - \sigma$, to a limit of closed contour integrals by adding horizontal segments to form a rectangle (the boundedness condition for the Dirichlet series on vertical strips allows us to use the Phragmen-Lindelöf principle (for details see for example [12] on p. 118) which means that the horizontal parts will vanish). Note that the coefficients $\alpha$ and $\alpha ^*$ satisfy the growth condition because of the convergence of the Dirichlet series. After the substitution $s \mapsto k - s$ in the right integral, expression (2.5) equals to

$$\begin{aligned} {\sum _{\nu =1}^\infty \alpha (\nu ) \mathcal {M}^{-1}_\sigma (\gamma , y \nu ^{1/b}) - y^{-k}\sum _{\nu =1}^\infty \alpha ^*(\nu ) \mathcal {M}^{-1}_\sigma (\gamma ^*, \nu ^{1/{b^*}}/y).} \end{aligned}$$

Finally, the residue theorem gives the desired error terms

$$\begin{aligned} {\sum _{j = 1}^\ell \mathrm {res}_{s = c_j}\left( \widehat{D}(s)y^{-s}\right) = \sum _{j=1}^\ell P_j(\log (y)) y^{-c_j},} \end{aligned}$$

and the result follows (after adjusting the objects notation) by analytic continuation.

For the other direction one obtains the Dirichlet series by construction (since the coefficients grow not to fast) by

$$\begin{aligned} {\int \limits _0^\infty f(ix)x^{s-1} \mathrm {d}x= \sum _{\nu =1}^\infty \alpha (\nu ) \int \limits _0^\infty \mathcal {M}_\sigma ^{-1}(\gamma , x\nu ^{1/b})x^{s-1} \mathrm {d}x= \gamma (s) D(s)} \end{aligned}$$

on the strip $\sigma< \mathrm {Re}(s) < \theta _1$. Note that switching integral and sum is allowed using absolute convergence and Lebesgues theorem (split the integral into two parts $I_0$ and $I_\infty$ from 0 to 1 and 1 to $\infty$, respectively, and choose values $\mathrm {Re}(s)> c_1 > \sigma$ and $c_2> \mathrm {Re}(s) > \sigma$ satisfying (2.3) for estimating the first and second integral). The dual integral is defined analogously and with the transformation property one obtains the functional equation back. In particular, since $c_j < \sigma$ for all $1 \leqslant j \leqslant \ell$, one has

$$\begin{aligned} \int \limits _0^\infty f(ix)x^{s-1} \mathrm {d}x&= \int \limits _1^\infty f(i/x) x^{-s-1} \mathrm {d}x+ I_\infty (s) \\&= \int \limits _1^\infty \left( (ix)^k f^*(ix) + \sum _{j=1}^\ell P_j(\log (x))x^{c_j}\right) x^{-s-1} \mathrm {d}x+ I_\infty (s) \\&= i^k I_\infty ^*(k-s) + \sum _{j=1}^\ell {\tilde{P}}_j\left( \frac{1}{s - c_j}\right) + I_\infty (s), \end{aligned}$$

where the dual integral converges since $k - \mathrm {Re}(s)< k - \sigma < \sigma$ and the ${\tilde{P}}_j$ are some polynomials. Hence

$$\begin{aligned} \gamma (s)D(s) - i^k I_\infty ^*(k - s) - \sum _{j=1}^\ell {\tilde{P}}_j\left( \frac{1}{s - c_j}\right) = I_\infty (s). \end{aligned}$$

(2.6)

With the same arguments (note that $k - \sigma < c_j$) one obtains

$$\begin{aligned} i^k \gamma ^*(s) D^*(s) - I_\infty (k-s) - \sum _{j=1}^\ell {\tilde{P}}_j\left( \frac{1}{k - s - c_j}\right) = i^k I_\infty ^*(s), \end{aligned}$$

(2.7)

and it follows that $I_\infty (s)$ and $I_\infty ^*(s)$ and hence D(s) and $D^*(s)$ have meromorphic continuations to the entire plane, since the vertical half planes $\{ \mathrm {Re}(s) > \max \{ k - \theta _1, \sigma \}\}$ and $\{ \mathrm {Re}(s) < \theta _1\}$ have a non-empty intersection, with possible poles only at real values. The functional equation becomes clear with (2.6) and (2.7) (after adjusting the dual by rescaling with the factor $i^k$).

The growth conditions are clear for vertical strips in $\{ \mathrm {Re}(s) > \sigma \}$ and $\{ \mathrm {Re}(s) < k - \sigma \}$ due to the functional equation. For the critical strip $\{ k - \sigma \leqslant \mathrm {Re}(s) \leqslant \sigma \}$ one uses the standard estimate of the integrals $I_\infty$ and $I^*_\infty$ along vertical lines. $\square$

For more about converse theorems the reader is referred to e.g. [4, pp. 336–338: Lemma 1 and Theorems 2 and 3] where general Dirichlet series $\sum _{n=1}^\infty a(n)e^{-\lambda _n s}$ (as usual, $\lambda _n$ is a real increasing sequence with $\lambda _n \rightarrow \infty$) and modular relations of the type

$$\begin{aligned} \sum _{n=0}^\infty a(n)\exp (-\lambda _n x) = x^{-\delta } \sum _{n=0}^\infty b(n)\exp \left( - \frac{\mu _n}{x} \right) \end{aligned}$$

are investigated. In Lemma 1, the effect of the residue integral on the modular error term is described in detail. Although Bochner assumes $\theta _1 = \infty$ for the Mellin integrals the arguments are similar.

We can now use the generalized Gauß formula to introduce a general method to extract analytic objects related to L-functions at rational arguments from those related to integer arguments. This is summed up in the next theorem.

Theorem 2.8

Let $\mu \in \mathbb {N}$ and ${\tilde{\gamma }} = (\gamma _j)_{1 \leqslant j \leqslant \mu }$ and ${\tilde{\gamma }}^* = (\gamma ^*_j)_{1 \leqslant j \leqslant \mu }$ be collections of gamma factors in $\mathfrak {W}_{\varvec{\mathrm {a}}, \varvec{\mathrm {b}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}$. We then have a map

Proof

Firstly, we show that the above map is indeed well-defined. To do so, we have to check that the image of some tuple $(D_1, \ldots , D_\mu )$ is a generalized Dirichlet series with signature $\left( \left( G_{\varvec{\mathrm {a}}, \varvec{\mathrm {b}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}^\mu ({\tilde{\gamma }}), G_{\varvec{\mathrm {a}}, \varvec{\mathrm {b}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}^\mu ({\tilde{\gamma }}_\mathrm {inv}^*)\right) , \mu \sigma , \mu k - \mu + 1 \right)$ as introduced in Definition 2.5. Since

$$\begin{aligned} {\mu \sigma< \mathrm {Re}(s) \implies \sigma < \mathrm {Re}\left( \frac{s}{\mu }\right) \leqslant \mathrm {Re}\left( \frac{s + j - 1}{\mu }\right) ,} \end{aligned}$$

the convergence part of condition (i) is clearly satisfied. As a product of meromorphic functions in the complex plane the resultant function is meromorphic too and still has poles only in $\mathbb {R}$ as every factor does. For part (ii) we use the functional equations of the individual factors:

$$\begin{aligned} {\widehat{\mathcal {T}_\mu ((D_j))}(\mu k - (\mu -1) - s) = \prod _{j=1}^\mu \widehat{D_j}\left( k - \frac{s+\mu -j}{\mu }\right) = \prod _{j=1}^\mu \widehat{D_{\mu -j+1}^*}\left( \frac{s+j-1}{\mu }\right) .} \end{aligned}$$

With

$$\begin{aligned} {\mathcal {T}_\mu ((D_j))^*(s) = \prod _{j=1}^\mu D_{\mu -j+1}^*\left( \frac{s+j-1}{\mu }\right) } \end{aligned}$$

we have found the dual which also converges absolutely for all s with $\mathrm {Re}(s) > \sigma$, with corresponding gamma factor $G_{\varvec{\mathrm {a}}, \varvec{\mathrm {b}}, \varvec{\mathrm {c}}, \varvec{\mathrm {d}}}^\mu ({\tilde{\gamma }}^*_\mathrm {inv})$. It is plain that (iii) is satisfied and this proves the theorem. $\square$

3 Application to Dedekind zeta functions of number fields

In this section, we will construct identities of higher degree by looking at the specific gamma factors $\gamma (s) = ab^s\Gamma ^n(s)$ for integers $n = 1, 2, 3, \ldots$.

Definition 3.1

Let $n \in \mathbb {N}$ be an integer. We define for all $\tau \in \mathbb {H}$

$$\begin{aligned} {W_n(\tau ) := \frac{1}{2\pi i} \int \limits _{c - i\infty }^{c + i\infty } \Gamma (s)^n (-i\tau )^{-s} \mathrm {d}s,} \end{aligned}$$

where $c > 0$ is some real number.

Let $K_1$ and $K_2$ be two number fields of degree n and the same signature $(r_1, r_2)$, where $r_1$ and $r_2$ denote the numbers of real and complex embeddings of $K_1$ and $K_2$, respectively. We now consider the special gamma factor

$$\begin{aligned} {\gamma _{K_1, K_2}(s)_n = \left( \frac{\sqrt{|d_{K_1} d_{K_2}|}}{ (2\pi )^n}\right) ^s \Gamma (s)^n.} \end{aligned}$$

Here, $d_{K_1}$ and $d_{K_2}$ denote the discriminants of $K_1$ and $K_2$, respectively. We are interested in the space $\mathcal {D}(\gamma _{K_1, K_2}, 1, k)$. But before starting, we just revise some basic facts.

Let K be a number field with degree n and signature $(r_1, r_2)$. We can then define its Dedekind zeta function by

$$\begin{aligned} {\zeta _K(s) := \sum _{\mathfrak {a}} \frac{1}{N(\mathfrak {a})^s},} \end{aligned}$$

where the sum extends over all non-zero ideals of the integral domain $\mathcal {O}_K$ and N is the norm of an ideal. It is a well known result by Hecke [8] that the corresponding function

$$\begin{aligned} {\xi _K(s) := \left( \frac{\sqrt{|d_K|}}{2^{r_2}\pi ^{n/2}} \right) ^s \Gamma \left( \frac{s}{2}\right) ^{r_1} \Gamma (s)^{r_2} \zeta _K(s)} \end{aligned}$$

has a holomorphic continuation to $\mathbb {C}\setminus \{0,1\}$ with simple poles for $s \in \{0,1\}$ and fulfills the functional equation

$$\begin{aligned}{\xi _K(1 - s) = \xi _K(s).} \end{aligned}$$

Proposition 3.2

Let $K_1$ and $K_2$ be two number fields of degree n and same signature $(r_1, r_2)$, $w > 0$ an odd integer and

$$\begin{aligned} {\psi _w(s; K_1, K_2) := \gamma _{K_1, K_2}(s)_n \zeta _{K_1}(s) \zeta _{K_2}(s + w).} \end{aligned}$$

Then we have the functional equation

$$\begin{aligned} \psi _w(1 - w - s; K_1, K_2) = (-1)^{r_1(w- 1)/2 + r_2}\psi _w(s; K_2, K_1). \end{aligned}$$

(3.1)

In other words, we have $\zeta _{K_1}(s)\zeta _{K_2}(s+w) \in \mathcal {D}(\gamma _{K_1, K_2}, 1, 1 - w)$, and

$$\begin{aligned} (\zeta _{K_1}(s)\zeta _{K_2}(s+w))^* = (-1)^{r_1(w- 1)/2 + r_2} \zeta _{K_2}(s)\zeta _{K_1}(s + w). \end{aligned}$$

(3.2)

Proof

We will first show that

$$\begin{aligned} \psi _w(s; K_1, K_2)= & {} \frac{1}{(2\sqrt{\pi })^{r_1}}\left( \frac{\sqrt{|d_{K_2}|}}{2^{r_2} \pi ^{n/2}}\right) ^{-w}\\&\quad \times \prod _{j=0}^{\frac{w-3}{2}} \left( \frac{s+1}{2} + j\right) ^{-r_1} \prod _{\ell =0}^{w-1} (s + \ell )^{-r_2} \times \xi _{K_1}(s) \xi _{K_2}(s + w). \end{aligned}$$

This is a simple calculation involving the duplication formula $\Gamma (s)\Gamma (s+\frac{1}{2}) = \Gamma (2s)2^{1-2s} \sqrt{\pi }$. We obtain

$$\begin{aligned}&\frac{1}{(2\sqrt{\pi })^{r_1}}\left( \frac{\sqrt{|d_{K_2}|}}{2^{r_2} \pi ^{n/2}}\right) ^{-w} \prod _{j=0}^{\frac{w-3}{2}} \left( \frac{s+1}{2} + j\right) ^{-r_1} \prod _{\ell =0}^{w-1} (s + \ell )^{-r_2} \times \xi _{K_1}(s) \xi _{K_2}(s + w) \\&\qquad \quad = \frac{1}{(2\sqrt{\pi })^{r_1}}\left( \frac{\sqrt{|d_{K_1} d_{K_2}|}}{ 2^{2r_2} \pi ^n }\right) ^s \Gamma \left( \frac{s}{2}\right) ^{r_1} \Gamma \left( \frac{s+1}{2}\right) ^{r_1} \Gamma (s)^{2r_2} \zeta _{K_1}(s) \zeta _{K_2}(s + w) \\&\qquad \quad = \frac{1}{(2\sqrt{\pi })^{r_1}} \left( \frac{\sqrt{|d_{K_1} d_{K_2}|}}{ 2^{r_1 + 2r_2} \pi ^n }\right) ^s (2\sqrt{\pi })^{r_1} \Gamma (s)^{r_1 + 2r_2} \zeta _{K_1}(s) \zeta _{K_2}(s+w) \end{aligned}$$

and since $n = r_1 + 2r_2$ we conclude

$$\begin{aligned}&= \left( \frac{\sqrt{|d_{K_1} d_{K_2}|}}{ (2\pi )^n}\right) ^s \Gamma (s)^n \zeta _{K_1}(s) \zeta _{K_2}(s + w), \end{aligned}$$

as required.

Now we show the functional equation by using the above representation in terms of $\xi _{K_j}$ with $j=1,2$. Obviously, the term $\xi _{K_1}(s) \xi _{K_2}(s + w)$ changes to $\xi _{K_2}(s)\xi _{K_1}(s+w)$ under the transformation $s \mapsto 1 - w - s$. We have

$$\begin{aligned} \prod _{j=0}^{\frac{w-3}{2}} \left( \frac{1 - w - s +1}{2} + j\right) ^{-r_1}&= (-1)^{r_1(w-1)/2}\prod _{j=0}^{\frac{w-3}{2}} \left( \frac{s+1}{2} + \frac{w-3}{2} - j\right) ^{-r_1} \\&= (-1)^{r_1(w-1)/2} \prod _{j=0}^{\frac{w-3}{2}} \left( \frac{s+1}{2} + j\right) ^{-r_1} \end{aligned}$$

and similarly

$$\begin{aligned} \prod _{\ell =0}^{w-1} (1 - w - s + \ell )^{-r_2}&= (-1)^{wr_2} \prod _{\ell = 0}^{w-1} (s + w - 1 - \ell )^{-r_2} \\&= (-1)^{wr_2} \prod _{\ell = 0}^{w-1} (s + \ell )^{-r_2}. \end{aligned}$$

Since $(-1)^{w} = -1$, the claim follows. $\square$

We are interested in formulas for L-functions at rational arguments. To gain those, we have to construct a proper generalized complete Dirichlet series.

Definition 3.3

Let $w > 1$ and $b > 0$ be integers with $w \equiv 1 \mod 2$. Also let ${\tilde{K}} = (K_1, K_1', K_2, K_2', \ldots , K_b, K_b')$ be a collection of number fields with the same degree n, such that $K_j$ and $K_j'$ have the same signature $(r_{1,j}, r_{2,j})$ for all $1\leqslant j \leqslant b$. Then we define

$$\begin{aligned} {\Phi _{w,b}(s; {\tilde{K}}) = \prod _{j=1}^b \psi _w\left( \frac{s+j-1}{b}; K_j, K_j'\right) .} \end{aligned}$$

For the sake of simplicity, we write $D^w_{K_1,K_2}(s) := \zeta _{K_1}(s)\zeta _{K_2}(s + w)$. Now one can apply Theorem 2.8 to the data to obtain the functional equation

$$\begin{aligned} \Phi _{w,b}(1 - bw - s; {\tilde{K}}) = (-1)^{\sum _{j=1}^b r_{1,j}(w-1)/2 + r_{2,j}}\Phi _{w,b}(s; {\tilde{K}}_\mathrm {inv}). \end{aligned}$$

(3.3)

For the convenience of the reader we want to demonstrate this general principle by the explicit case of real quadratic number fields. So assume that the above collection now only contains real quadratic number fields. A calculation shows

$$\begin{aligned} {G^b_{0,0,2,0}((\gamma _{K_j, K_j'})_{1 \leqslant j \leqslant b}) = \Delta b \left( \frac{2\pi b}{\root 2b \of {D}} \right) ^{-2s} \Gamma (s)^2 } \end{aligned}$$

where $D = \sqrt{|d_{K_1} \cdot d_{K_1'} \cdots d_{K_b} \cdot d_{K_b'}|}$ and $\Delta = \prod _{j=1}^b |d_{K_j} \cdot d_{K_j'}|^{\frac{j-1}{2b}}$ and hence we have

$$\begin{aligned} \Phi _{w,b}(s; {\tilde{K}}) = \Delta b \left( \frac{2\pi b}{\root 2b \of {D}} \right) ^{-2s} \Gamma (s)^2 \prod _{j=1}^b \zeta _{K_j}\left( \frac{s+j-1}{b}\right) \zeta _{K_j'}\left( \frac{s+j-1}{b} + w\right) . \end{aligned}$$

(3.4)

Obviously, the central object of studying yet is the generalized Dirichlet series

$$\begin{aligned} D_{{\tilde{K}}}^{w,b}(s) := \prod _{j=1}^b \zeta _{K_j}\left( \frac{s+j-1}{b}\right) \zeta _{K_j'}\left( \frac{s+j-1}{b} + w\right) = \sum _{\nu =1}^\infty c_{w,b}(\nu ; {\tilde{K}})\nu ^{-s/b}, \end{aligned}$$

(3.5)

where the generating coefficients $c_{w,b}(\nu ; {\tilde{K}})$ are defined by the product in the above equation.

Theorem 3.4

Let $w > 1$ and $b > 0$ be integers with $w \equiv 1 \mod 2$. Let ${\tilde{K}} = (K_1, K_1', \ldots , K_b, K_b')$ be a collection of real quadratic number fields as above. For all $\tau \in \mathbb {H}$ we define the (holomorphic) function

$$\begin{aligned} {E_{w,b}(\tau ; {\tilde{K}}) = 2\Delta b \sum _{\nu =1}^\infty c_{w,b}(\nu ; {\tilde{K}})K_0\left( 4\pi b \root 2b \of {\frac{\nu }{D}} \sqrt{- i \tau } \right) ,} \end{aligned}$$

Then, for all $\tau \in \mathbb {H}$, we have an identity

$$\begin{aligned} {E_{w,b}(\tau ; {\tilde{K}}) - (-i\tau )^{bw - 1} E_{w,b}(-1/\tau ; {\tilde{K}}_\mathrm {inv}) = \sum _{\alpha = 0}^{w+1} P_\alpha (\tau ) + \log (-i\tau )Q_\alpha (\tau ),} \end{aligned}$$

where the $P_i$ and $Q_j$ are rational functions with $P_\alpha \equiv Q_\alpha \equiv 0$ whenever $1 < \alpha$ and $\alpha \equiv 0 \mod 2$. The functions $P_i$ are explicitly given by

$$\begin{aligned} P_0(\tau )&= \sum _{\ell =1}^b (-i\tau )^{-\ell } A(\ell ) R_{K_{b-\ell +1}} (\ell - 1)!^2 \prod _{\begin{array}{c} j=1 \\ j \not = b-\ell +1 \end{array}}^b \zeta _{K_j} \left( \frac{\ell + j-1}{b} \right) \\&\quad \times \prod _{j=1}^b \zeta _{K_j'} \left( \frac{\ell + j-1}{b} + w\right) \\ P_1(\tau )&= \sum _{\ell = 1-b}^0 (-i\tau )^{-\ell } A(\ell ) \frac{\zeta '_{K_{1-\ell }}(0)\zeta _{K'_{1-\ell }}(w)}{b}\\&\quad \times \prod _{\begin{array}{c} j=1 \\ j \not = 1-\ell \end{array}}^b \zeta _{K_j}\left( \frac{\ell + j - 1}{b}\right) \zeta _{K'_j}\left( \frac{\ell + j - 1}{b} + w\right) \\ P_w(\tau )&= \sum _{\ell =1-bw}^{b-bw} (-i \tau )^{-\ell }A(\ell ) R_{K'_{b-bw +1 - \ell }} \frac{\zeta ''_{K_{b-bw+1-\ell }}(\ell )}{2b^2(-\ell )!^2} \\&\quad \times \prod _{\begin{array}{c} j=1 \\ j \not = b-bw +1 - \ell \end{array}}^b \zeta _{K_j}\left( \frac{\ell + j - 1}{b}\right) \zeta _{K'_{j}}\left( \frac{\ell + j -1}{b} + w\right) \end{aligned}$$

where $R_K := \mathrm {res}_{s=1} \zeta _K(s)$, and for all $2 \leqslant \alpha \leqslant w+1$ with $\alpha \equiv 1 \mod 2$ and $\alpha \not = w$

$$\begin{aligned} {P_\alpha (\tau ) = \sum _{\ell = 1 - b \alpha }^{b - b \alpha } (-i\tau )^{-\ell } \left[ \Psi _1(\ell ) + \Psi _2(\ell ) + \Psi _3(\ell )\right] } \end{aligned}$$

where

$$\begin{aligned}&\Psi _1(\ell ) = A(\ell ) (-1)^\ell \frac{H_{-\ell } - \gamma }{(-\ell )!^2} \prod _{j=1}^b \zeta _{K_j}\left( \frac{\ell +j -1}{b}\right) \zeta _{K_j'}\left( \frac{\ell +j-1}{b} + w\right) , \\&\Psi _2(\ell ) = A(\ell ) \frac{1}{b(-\ell )!^2} \left[ \sum _{\mu =1}^b \left( \zeta '_{K_\mu }\left( \frac{\ell +j-1}{b}\right) +\zeta '_{K'_\mu }\left( \frac{\ell +j-1}{b} + w \right) \right) Z_\mu (\ell )\right] \\&\Psi _3(\ell ) = -2\log \left( \frac{2\pi b}{\root 2b \of {D}}\right) A(\ell )\frac{1}{(-\ell )!^2} \prod _{j=1}^b \zeta _{K_j}\left( \frac{\ell +j -1}{b}\right) \zeta _{K_j'}\left( \frac{\ell +j-1}{b} + w\right) , \end{aligned}$$

with

$$\begin{aligned} {A(s) = \Delta b \left( \frac{2\pi b}{\root 2b \of {D}}\right) ^{-2s}} \end{aligned}$$

and

$$\begin{aligned} {Z_\mu (\ell ) = \prod _{\begin{array}{c} j=1 \\ j \not = \mu \end{array}}^b \zeta _{K_j}\left( \frac{s+j-1}{b}\right) \zeta _{K_j'}\left( \frac{s+j-1}{b} + w\right) .} \end{aligned}$$

The functions $Q_j$ satisfy $Q_0 \equiv Q_1 \equiv 0$ and

$$\begin{aligned} {Q_\alpha (\tau ) = - \sum _{\ell = 1-b\alpha }^{b-b\alpha }(-i\tau )^{-\ell }A(\ell )\frac{1}{(-\ell )!^2} \prod _{j=1}^b \zeta _{K_j}\left( \frac{\ell +j -1}{b}\right) \zeta _{K_j'}\left( \frac{\ell +j-1}{b} + w\right) } \end{aligned}$$

as $\alpha \geqslant 2$ and $\alpha \equiv 1 \mod 2$.

Proof

We remember that $2K_0(2\sqrt{x}) = W_2(x)$. From (3.3) we conclude

$$\begin{aligned} {D_{{\tilde{K}}}^{w,b}(s) \in \mathcal {D}((G^b_{0,0,2,0}((\gamma _{K_j, K_j'})_{1 \leqslant j \leqslant b}),G^b_{0,0,2,0}((\gamma _{K'_{b-j+1}, K_{b-j+1}})_{1 \leqslant j \leqslant b})), b, 1 - bw)} \end{aligned}$$

with dual series

$$\begin{aligned} {\left( {D_{{\tilde{K}}}^{w,b}}\right) ^*(s) = D_{{\tilde{K}}_\mathrm {inv}}^{w,b}(s).} \end{aligned}$$

Since we clearly have $1 - bw < 2b$, we can use Theorem 2.7. The calculations all base on investigating the residues of the completed Dirichlet series. For example, poles of first order are given in $s = 1, 2, \ldots , b$. The residues here are given by the summands of $P_0(\tau )$. The details and the further calculations are omitted. $\square$

Note that (1.2) follows by this new identity by setting $b = 1$ and $\alpha = 2\pi d_K^{-\frac{1}{2}} \sqrt{-i\tau }$ and $\beta = 2\pi d_K^{-\frac{1}{2}} \cdot \frac{1}{\sqrt{-i\tau }}$.

4 Application to L-functions for modular forms of half-integral weight

We can apply the developed methods to find new identities for L-functions assigned to modular forms of half-integral weight. We consider the Hecke group $\mathcal {H}(\lambda ) \subset \mathrm {SL}_2(\mathbb {R})$, which is by definition generated by the elements $S = \begin{pmatrix}0 &{} -1 \\ 1 &{} 0\end{pmatrix}$ and $T_\lambda = \begin{pmatrix}1 &{} \lambda \\ 0 &{} 1\end{pmatrix}$ where $\lambda > 0$ is some real number. It was shown by Hecke that $\mathcal {H}(\lambda )$ is discrete if and only if $\lambda \geqslant 2$ or $\lambda = 2\cos \left( \frac{\pi }{m}\right)$ with an integer $m \geqslant 3$. Let f be a cusp form of weight $k \in \frac{1}{2} + \mathbb {N}_0$ for $\mathcal {H}(\lambda )$. Then f has a Fourier expansion $f(\tau ) = \sum _{n=1}^\infty a(n)q^{n/\lambda }$ and satisfies the functional equation $f\left( - \frac{1}{\tau }\right) = (-i\tau )^k f(\tau )$. Furthermore, the coefficients a(n) shall be bounded by $a(n) \ll _f n^{\frac{k}{2}}$ (for $\lambda < 2$ this is always the case, for $\lambda \geqslant 2$ we assume it). The corresponding Hecke L-function $L_f(s) = \sum _{n=1}^\infty a(n)n^{-s}$ is absolutely convergent in the half-plane $\{ \mathrm {Re}(s) > \frac{k}{2} + 1\}$ and extends to a meromorphic function on all of $\mathbb {C}$. Kohnen and Raji show in [10], that $\phi _f(s) = L_f(s + k - 1)$ is an element of $\mathcal {D}(\gamma _{\mathrm {half}}, 2 - \frac{k}{2}, 2 - k)$ with corresponding gamma factor

$$\begin{aligned} {\gamma _{\mathrm {half}}(s) = \frac{1}{\pi }\left( \frac{2\pi }{\lambda }\right) ^{-s} \Gamma (s)\Gamma \left( \frac{1}{2} + s\right) \Gamma \left( \frac{1}{2} - s\right) = \left( \frac{2\pi }{\lambda }\right) ^{-s}\frac{\Gamma (s)}{\cos (\pi s)}.} \end{aligned}$$

Now we can assign f the series

$$\begin{aligned} {\mathcal {E}^*_f(z) = \sum _{n=1}^\infty a(n)n^{1-k} H(2\pi i n z/\lambda ),} \end{aligned}$$

where the function H is given by $H(z) = \frac{1}{\sqrt{\pi }} \left( e^z \Gamma \left( \frac{1}{2}, z \right) - \frac{1}{\sqrt{z}}\right)$, here, $\Gamma (\sigma , z) := \int _\sigma ^\infty e^{-t}t^{z-1} \mathrm {d}t$ denotes the incomplete Gamma function. Note that H is a holomorphic function on the upper half-plane and $H(z) = O(|z|^{- \frac{3}{2}})$. Given $a(n) \ll _f n^{\frac{k}{2}}$ it is easy to see that $\mathcal {E}^*_f$ is a holomorphic function on the upper half-plane. In [10], Kohnen and Raji used this series to start a cohomology theory in the case of half-integral weight. It is shown that

$$\begin{aligned} {\mathcal {E}^*_f(\tau ) - (i\tau )^{k-2} \mathcal {E}^*_f\left( - \frac{1}{\tau }\right) = P_f(\tau ) + \left( \frac{2\pi i \tau }{\lambda }\right) ^{-\frac{1}{2}} Q_f(\tau ),} \end{aligned}$$

where $P_f$ and $Q_f$ are polynomials of degree at most $k - \frac{1}{2}$. In the case $k \geqslant 3$ this result follows also by $D \in \mathcal {D}(\gamma _{\mathrm {half}}, 2 - \frac{k}{2}, 2 - k)$,

$$\begin{aligned} \mathcal {M}^{-1}_{\frac{1}{2}}\left( \Gamma (s)\sec (\pi s), x\right) = H(x) \end{aligned}$$

(4.1)

and Theorem 2.7 by studying the poles of $\hat{D}(s)$ at half-integral values. Note that the natural embedding

$$\begin{aligned} {\mathcal {D}\left( \gamma _{\mathrm {half}}, 2 - \frac{k}{2}, 2 - k\right) \hookrightarrow \mathcal {D}\left( \gamma _{\mathrm {half}}, \frac{1}{2}, 2 - k\right) } \end{aligned}$$

and hence the values $\sigma = \frac{1}{2}$ and $\theta _1 = \frac{3}{2}$ are used. We want to apply the main theorem to construct curious formulas for the functions $L_f$ at rational arguments.

Lemma 4.1

Let $\mu \in \mathbb {N}$. We obtain

$$\begin{aligned} {G^\mu (\gamma _{\mathrm {half}})(s) = \sqrt{\mu } \left( 2\pi \sqrt{\lambda } \right) ^{\mu - 1} \left( \frac{2\pi \mu }{\lambda }\right) ^{-s} \frac{\Gamma (s)}{\cos ^{(\mu - 1)}(\pi s)}.} \end{aligned}$$

Proof

This is routine, observe that

$$\begin{aligned} {\prod _{j=1}^\mu \cos \left( \pi \frac{s + j - 1}{\mu }\right) = (2\pi )^{1-\mu } \cos ^{(\mu -1)}(\pi s).} \end{aligned}$$

$\square$

Let $(f_j)_{1 \leqslant j \leqslant \mu }$ be a finite collection of cusp forms with same weight $k \in \frac{1}{2} + \mathbb {N}_0$. One can now use Theorem 2.8 to show that

$$\begin{aligned} {\prod _{j=1}^\mu \phi _{f_\mu }\left( \frac{s+j-1}{\mu }\right) \in \mathcal {D}\left( G^\mu (\gamma _{\mathrm {half}}), \mu \left( 2 - \frac{k}{2} \right) , \mu - \mu k + 1\right) .} \end{aligned}$$

At this point we obtain an infinite number of new identities, the details are omitted.

Example 4.2

Let $\mu = 3$. We consider the Dedekind eta function

$$\begin{aligned} {\eta (z) = q^{1/24} \prod _{n=1}^\infty (1 - q^n),} \end{aligned}$$

which is well known to be a holomorphic modular form of weight $k = \frac{1}{2}$ for $\mathrm {SL}_2(\mathbb {Z})$ with certain nebentypus character. Due to the above discussed results we find that

$$\begin{aligned} {\phi _\eta = L_\eta \left( s - \frac{1}{2}\right) \in \mathcal {D}\left( \gamma _\mathrm {half}, \frac{7}{4}, \frac{3}{2}\right) .} \end{aligned}$$

Hence

$$\begin{aligned} {\mathcal {T}_3(\phi _\eta ) \in \mathcal {D}\left( G^3(\gamma _\mathrm {half}), \frac{21}{4}, \frac{5}{2}\right) ,} \end{aligned}$$

where

$$\begin{aligned} {\gamma _3(s) := G^3(\gamma _{\mathrm {half}})(s) = - 96 \sqrt{3} \pi ^2 \left( \frac{\pi }{4}\right) ^{-s} \Gamma (s) \sec (\pi s).} \end{aligned}$$

With residue calculus and (4.1) we find

$$\begin{aligned} {\mathcal {M}^{-1}_{\frac{21}{4}}(\gamma _3, x) = - 96\sqrt{3} \pi ^{3/2} e^{\frac{\pi }{4}x} \Gamma \left( \frac{1}{2}, \frac{\pi x}{4}\right) + E(x),} \end{aligned}$$

where

$$\begin{aligned} {E(x) = - \frac{192\sqrt{3} \pi }{x^{1/2}}- \frac{384 \sqrt{3}}{x^{3/2}} + \frac{2304 \sqrt{3}}{\pi x^{5/2}} - \frac{23040 \sqrt{3}}{\pi ^2 x^{7/2}} + \frac{322560 \sqrt{3}}{\pi ^3 x^{9/2}}.} \end{aligned}$$

Put

$$\begin{aligned} {\phi _\eta \left( \frac{s}{3}\right) \phi _\eta \left( \frac{s+1}{3}\right) \phi _\eta \left( \frac{s+2}{3}\right) = \sum _{m=1}^\infty \lambda _{\eta , 3}(m)m^{-s/3},} \end{aligned}$$

then we obtain

$$\begin{aligned} {f(\tau ) = \sum _{m=1}^\infty \lambda _{\eta , 3}(m) \mathcal {M}^{-1}_{\frac{21}{4}}(\gamma _3, -i\tau m^{1/3}) \in \mathcal {R}\left( \gamma _3, \frac{21}{4}, \frac{5}{2}\right) .} \end{aligned}$$

The error term in the transformation law of $f(-1/\tau )$ is now related to products of values of $L_\eta$ at arguments $s \in \frac{1}{6} \mathbb {Z}$. The calculations are analogous to those made in [6] when proving Theorem 1.1.

5 Questions

It is natural to ask the following question at this stage.

Question 5.1

Is there a possibility to extract more detailed information about (products of) L-functions at rational arguments using the introduced techniques?

The most promising way is probably finding a cohomology theory just as in the case of modular forms of integer and half-integer weight to describe the period polynomials which have occurred.

A second question refers to results of Jin, Ma, Ono and Soundararajan in [9], who proved that the zeros of the period polynomial of a newform $f \in S_k(\Gamma _0(N))$ lie on the circle $|z| = 1/\sqrt{N}$.

Question 5.2

What can we say about the zeros of the error polynomials related to L-functions at rational arguments?