1 Introduction

Processing techniques for porous materials have great potential in applications ranging from nanoscience to catalysis and photo-catalysis, separation processes, energy conversion, and storage. The applications of these porous materials take place according to the hierarchy of the porous structure due to their pore size distribution and morphology [1]. Therefore, pore size control, microstructure, chemical composition, and morphology are the main control variables in their synthesis and processing. Advance research has not yet reached the level of complexity of porous natural materials (such as the butterfly wood, leaf, macaw feather, grass stem, kelp, coral, cotton, human bone, cuttlefish bone, and the sponge) with hierarchically porous structure made of interconnected pores with different lengths ranging from micropores (< 2 nm), mesopores (2–50 nm) to macropores (> 50 nm). Furthermore, the morphology of these examples of porous natural materials can have multi-porosity (a combination of two or more types of porosity) [1]. All these porous structures are challenging to reproduce and control. To date, there is no method to manufacture and control pore size distribution effectively for synthetic materials.

On the other hand, tridimensional (3D) printing (or additive manufacturing) [2] offers advantages, such as high precision, low cost, and customized geometry at the microporosity scale. Currently, 3D printing technology, such as new composite materials based on high-performance engineering thermoplastics (ET), provides a basis for increased thermal and mechanical performances to address the limitations of extrusion 3D printing [3]. Also, modifications to the 3D printing techniques allow obtaining diverse geometries of cellular continuous fiber-reinforced composites [4]. Another new method, roll-to-roll 3D printing, allows a faster and more massive commercial production scale of organic solar cells based on polymer/perovskite [5]. In addition, the other techniques have emerged apart from conventional additive manufacturing (or fused deposition modeling) like new laser sintering or stereo-lithography (among others) [6], doing possible new membranes for wastewater treatments, and separation of ionic species from pharmaceutical products [7].

Mathematical models in recent studies with SHE solved numerically in two and three dimensions through new numerical methods, such as first- and second-order semi-analytical Fourier spectral methods [15], meshless local collocation method [16], and unconditionally stable semi-implicit time discretization [17], minimization method of SHE functional [18]. These methods are computationally cheap and have a high-order time accuracy performance, which is compatible with the "mathematical design process, and 3D printing-assisted manufacturing" (explained in detail below). The numerical solution from these methods, obtained by computational simulation, presents the following morphologies: planar lamellar phase [15, 17], disordered nucleus phase [16], twisted lamellar phase [17], labyrinths [18], hexagonal [17, 18], and body-centered cubic (bcc) [18] phases. In contrast, in past studies [15, 19, 20], the SHE has been employed for explaining the pattern formation in hydrodynamic systems [19], Rayleigh–Bénard convection [21], and two labyrinths [22], isotropic, nematic, and smectic phases [20] in diblock copolymers. Furthermore, extended models of this equation have been proposed for research in that conditions emerge the pinning dynamics [23,24,25] and anisotropy [26] of hexagonal [23, 24], strips [25, 26], and labyrinths [27] phases, respectively.

Likewise, thanks to the various 3D printing techniques, prostheses, bone fillings, and scaffolds are manufactured for the tissue engineering area [8]. Fused deposition modeling refinement techniques allow generating of recyclable, lightweight polymeric structures or devices with hierarchical architectures, complex geometries of improved rigidity, and toughness due to bottom–up molecular control over the orientation of the injected polymer [9]. In addition, it is possible to produce hydrogel scaffolds based on dextran oxide/gelatin/cellulose nanoparticles for tissue repair [10] or composite scaffolds for bone regeneration based on polylactic acid due to their improved bio-functionality [11]. Composite scaffolds for bone regeneration based on polylactic acid due to its improved bio-functionality, either by 3D conventional additive manufacturing to obtain scaffolds with the morphology of bone tissue with sodium-alginate/hydroxyapatite coating [12] or by direct extrusion as a filament of a nanocomposite material based on graphite nanoplatelets/PLA/L-Arginine [13]. The novel inverse 3D printing method's application allows scaffolds with a rectangular distribution of uniform porosity of β-tricalcium phosphate, also for bone regeneration [14].

Even more, this work addresses the SHE extended again with the stabilizing quintic and destabilizing cubic terms [28,29,30,31,32] to obtain their bifurcations analysis [28, 31, 32] and the numerical solution in 3D [28, 29] to perform a porous simulated and controlled structure. The Materials and methods section proposes a new method of the mathematical design process and 3D printing-assisted manufacturing (MDP-3DPAM). In the "Numerical experiments: 3D computational simulation" section, the results of 3D numerical solutions of the quantic SHE models are presented. And, the section "Description of complex 3D computational models" is described and compared with natural systems. The porous materials’ prototypes obtained by fused deposition modeling and stereo-lithography UV-laser assisted are found in the next section. Finally, in the last sections, a discussion and conclusions of this paper are placed, and appendixes related to 3D computer simulations and 3D printing are presented.

2 Materials and methods

2.1 Materials

A 32 GB RAM computer running on the Kubuntu operating system achieved the numerical simulation patterns. Python 2.7 and its scientific extensions, such as NumPy, matplotlib, and mlab, were used [33]. The graphics of the numerical solution obtained were drawn in Mayavi in its second version [34]. A TEVO LITTLE MONSTER 3D with a 0.4 resolution nozzle and a Creality 3D id-002r printer achieved porous polymeric materials’ creation with PLA red color filament from 3D SOLUTECH and ELEGOO photopolymer transparent resin.

Hereinafter, the proposed method that allows obtaining polymeric materials with controlled porosity is described. This method is constituted by three stages (Mathematical modeling, Computational design, and 3D printing stages), which is named as mathematical design process and 3D printing assisted manufacturing (MDP-3DPAM), see Fig. 1.

Fig. 1
figure 1

Representative diagram of the three concatenated stages that constitute the method MDP-3DPAM

Full size image

2.2 Mathematical modeling stage: IPSA method outline

The numerical method employed for solving Eq. (A1) of Appendix A in the supporting information document is the implicit pseudo-spectral method described in [35], which is extended easily to \(3\mathrm{D}\) space. The spatial domain (discretized by a mesh of \({N}_{x}\times {N}_{y}\times {N}_{z}\) nodes) of this equation is periodic in all directions \((x, y, z),\) which is an approach that applies the discrete Fourier transform on the solution of the scalar field \(\varphi \left(\overrightarrow{r}, t\right)\). This method based on such discrete transforms provides optimal accuracy in that the rate of convergence for suitably smooth solutions is faster than any power of the mesh of \({N}_{x}\times {N}_{y}\times {N}_{z}\) nodes. The calculus of nonlinear terms is integrated using an exponential propagation procedure described in detail below, with the nonlinear terms handled explicitly, while a fully implicit approach is constructed. To better approximate, these terms can be treated as a linear system of differential equations modified by a nonlinear forcing term. The nonlinear terms are integrated by a predictor–corrector method. It can be shown that the overall technique is second-order accurate in time step bigger than with the finite difference methods. The implicit pseudo-spectral method is extended to array algorithms as follows. It is well known as the Fourier transform changes a gridded cubic space (GCS) with a mesh of \({N}_{x}\times {N}_{y}\times {N}_{z}\) nodes in a Fourier transformed space (FTS) with \({\left({q}_{x}\right)}_{i}\times {\left({q}_{y}\right)}_{j}\times {\left({q}_{z}\right)}_{k}\) nodes number, such that: \(-\left(\frac{{N}_{x}}{2}-1\right)\le \mathrm{i}\le {N}_{x}/2,-\left(\frac{{N}_{y}}{2}-1\right)\le \mathrm{j}\le {N}_{y}/2\) and \(-\left(\frac{{N}_{z}}{2}-1\right)\le k\le {N}_{z}/2\). The equations that define the coordinates of each point on the GCS mesh are: \({x}_{i}=\frac{(i-1){L}_{x}}{{N}_{x}}, i=1,...,{N}_{x},{y}_{j}=\frac{(j-1){L}_{y}}{{N}_{y}}, j=1,...,{N}_{y},{z}_{k}=\frac{(k-1){L}_{z}}{{N}_{z}}, k=1,...,{N}_{z},\) where \({L}_{x}, {L}_{y}\) Lx, and \({L}_{z}\) the spatial region dimensions in the x, y, and z directions. Furthermore, the points on the FTS mesh are such that: \(({q}_{x}{)}_{i}=2\uppi i/{L}_{x}, ({q}_{y}{)}_{j}=2\uppi j/{L}_{y}, ({q}_{z}{)}_{k}=2\uppi k/{L}_{z}\). An initial condition array from GCS was developed and then applied the numerical method described in Sect. 3.2 under the array of FTS of \({\left({q}_{x}\right)}_{i}\times {\left({q}_{y}\right)}_{j}\times {\left({q}_{z}\right)}_{k}\) nodes. The "NumPy" library for python distribution [33] allows evaluating simultaneously the implicit pseudo-spectral algorithm method in the FTS matrix utilizing an initial conditions matrix seed, in which the discrete Fourier transform is applied. NumPy library contains the FFT.py module that is a simple interface to the FFTPACK FORTRAN library, which is a powerful standard library for doing fast Fourier transforms of real and complex data sets.

As implementation example of this stage is solved numerically the spatial–temporal behavior of the fifth-order SHE (given by Eq. (A1) in Appendix A of support information). This equation is solved using the ISPA method developed in the previous section. Their numerical solution of Eq. (A4) was obtained by discretizing a square grid of mesh size \(\Delta x=0.5\) with \(128\times 128\times 128\) nodes, where periodic boundary conditions had been used. The values of control parameters are selected in Table B1 of Appendix B of the supporting information document. The numerical solution can be graphed in the Cartesian space, and each data value can be assigned with a different color. This arrangement of the numerical data has a specific morphology in the three-dimensional space, which we name as \(3D\) pattern that has a characteristic wavelength \({q}_{0}\). Based on the stability analysis of Appendix C of the supporting information document, we selected the critical wavenumber \({q}_{0}=2\pi /{\lambda }_{0}\) where wavelength \({\lambda }_{0}=2\pi\Delta x\), such that \({q}_{c}=1\). The temporal evolution of the system is performed with a time step \(\Delta t=0.1\) and \(T=t\Delta t\) adimensional time units with \(t\) iterations numbers. For each obtained \(3D\) patterns are employed, initial random conditions. The initial conditions for \(\phi (\overrightarrow{r},t)\) are random variables with values in the range \(\left[-\sqrt{\left|\alpha \right|},\sqrt{\left|\alpha \right|}\right]\) and a Gaussian distribution of zero averages and variance \(<{\phi }^{2}>=0.1\). For the observation of the 3D patterns, see Fig. 2.

Fig. 2
figure 2

Spatial–temporal dynamics solutions of fifth-order SHE. Where t represents the iterations steps number, and the values of control parameters are localized in Table B1 of Appendix B in the supporting information document

Full size image

2.3 Computational design stage

The method to create a computer-aided design (CAD) file from polymeric material resulting in a controlled pore size distribution object; Fig. 3 shows the process for developing materials with controlled microstructure and starting with the \(3\mathrm{D}\) pattern numerical solution obtained from the IPSAM algorithm based on SHE of quantic order, which is programmed in Python shell. If the reader wants to review a detailed description of the mathematical model, as well as the numerical method of the fast Fourier transform (FFT) to obtain a numerical solution for the fifth-order SHE, you can see the supporting information document (Appendix A). This \(3\mathrm{D}\) numerical solution is then analyzed on its.pkl file format by Mayavi2 software to obtain a.obj file so it can be afterward translated into standard triangle language extension (.stl). At this stage, the pore size is controlled as much as desired (see, for example, Fig. 4).

Fig. 3
figure 3

Workflow diagram of the mathematical design process and 3D printing-assisted manufacturing (MDP-3DPAM) in generating \(3D\) printed porous materials with controlled microstructure. The chart should be read from left to right. The linear stability analysis was done to identify points of interest for study pattern formation (see also Graphical Abstract)

Full size image
Fig. 4
figure 4

Microporous polymeric materials obtained by additive injection (patterns A–C) and stereo-lithography (pattern D) \(3D\) printing. The below panel is shown in a and c a face of patterns C and D, respectively. Images b) and d) obtained by stereoscopic microscopy are zooms of a face section of C and D patterns

Full size image

2.4 3D printing stage

The \(3\mathrm{D}\) models can be exported to any printer (Repeater Host in this case) software code generator for the final processing step, which also allows controlling the size and printing parameters for the impression in the materials analyzed in the next section. PLA material heated to 210 °C was used to achieve the final structures while printing by addictive manufacturer, while UV photopolymer resin was used to accomplish the other printing method known as stereo-lithography. Extruding different polymers allows the creation of solid structures with complex mechanical properties and controlled pore size distribution. The 3D printing process using mathematical models to design the pattern [12, 22] is an entirely new method to design and create new advanced materials.

3 Results

3.1 Numerical experiments: a 3D computational simulation

Obtained patterns from the numerical simulation are like the ones already reported in the literature. Figure 2 shows a phase change from isotropic to neumatic when turning on a control parameter (g = 2) which is like the behavior demonstrated by the third-order SH model [19,20,21, 36, 37]. Other behaviors like the numerical experiments reported in references [18, 22, 27] are consistent with the labyrinth phase shown in Fig. 2a. Moreover, when the control parameter \(g\) is turned on, there is a symmetry breaking that manifests itself in a pattern with island morphology like the patterns of the Ginzburg–Landau equation reported in [37,38,39,40]. This behavior is analogous to that reported in the typical SH model of quantic order when changing a control parameter to obtain a hexagonal phase from the gut phases [17, 18, 23,24,25,26,27]. A complete and detailed study of phase transitions and space–time dynamics is a motive for future studies. The linear stability analysis is presented in Appendix C of the supporting information document. Its study allows the selection of the control parameter values that are important for the development of this research.

3.2 Description of complex 3D computational models

Some \(3D\) structure patterns are obtained by computational simulation from the quintic SHE and can be used for the study of porous materials models in a similar way as reported in [41,42,43], which allows the processing of new porous polymeric materials as it will be shown in the next section. Figure 2a–c exhibits two phases separated into two \(3D\) structures that are negative and positive phases from the original simulated pattern of Fig. 2a. The positive phase morphology from the central image of Fig. 5a is very similar to the zeolite \(3D\) structure of the perovskite. In contrast, the \(3D\) structure from the central image of Fig. 5b is a biomimetic structure like the extracellular matrix from trabecular bone obtained by the method reported in other works [12, 22, 44, 45].

Fig. 5
figure 5

The negative and positive phases from the computational simulations are the first and second columns from left to right: a, b, and c colored with red, light-green, dark green, and white, respectively

Full size image

To finish this section, there is a structure comparison of the positive phase from the central image of Fig. 5c with the fingerprint photo of a real finger. Both 3D morphologies are similar in the shape of the grooves. This is consistent qualitatively with the slow dynamics of the skin of fingers and hands in the human body. The images from the third column on the right are natural structures obtained by SEM micrograph: (a) coral microstructure, (b) bone extracellular matrix (see [44, 45]), and (c) a fingerprint photo from the index finger.

3.3 Results of fused deposition modeling and stereo-lithography UV-laser assisted

Objects were printed in polylactic acid (PLA) filament, a thermoplastic polymer operated around 215 °C, but they are not limited only to this polymer; any polymer can be printed under certain conditions. The porosity of these materials can be directly controlled by varying the parameter \(\alpha\), chosen to simulate (see Table B1), which is related to the pattern morphology. In the second place, scaling this morphology in Blender to finally obtain a specific porous pattern with different pore size distributions and specific surface area due to the size scaling process. Instead of porous chemical composition structure dependence, as is shown in Fig. 4. These figures show the microporosity of the porous polymeric materials (see Fig. 4c and d) that were scaled to an eighth of their original size (see Fig. 4A), obtained by fused deposition modeling [Fig. 4A–C] and stereo-lithography UV-laser assisted [Fig. 4D, c and d], respectively.

The manufacture of polymeric porous materials by molten deposition modeling (or fabrication by filament fused) is realized to compare with stereolithographic 3D printing. Another advantage of using this 3D printing technique probes the universality of the new method proposed in this work: the mathematical design process and 3D printing-assisted manufacturing.

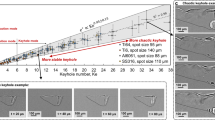
By direct observation, comparing Fig. 4b with Fig. 4d can be concluded that the macropores of the PLA porous material have an extensive size range of 600–1200 µm with bad definition, while the macropores of the resin have a larger size in a range of 300–500 µm. It can conclude that the 3D printing by stereo-lithography UV-laser assisted allows a better control to obtain a microporosity with the morphology of Fig. 4b. These polymeric matrices can bio-mimic the extracellular anisotropic matrix from the coronal cross-section of long trabecular bone [44, 45], under the chemical treatment of [12] in which the composite biomaterials are presented as promising scaffolds that can be degraded and absorbed by the human body, without showing biological rejection. Wolf's law [44, 45] will be subject to future studies to determine that the polymer morphology of Fig. 4c fulfills a hierarchical structure from the human proximal femur (e.g.). Figure 1D of Appendix D in the document of Supporting Information shows the open-pore system in the interior of the polymeric porous cube obtained by 3D printing. And the relationship between the print size and the pore size on one side of the 3D pattern, is presented in Appendix E, Fig. 1E (document of Supporting Information).

From the advancement of 3D printing as additive manufacturing (fabrication by fused filament), today, news techniques have emerged as Digital Light Processing (DLP) which allows printing facial prostheses [46] and meniscus implants for a knee in bland materials [47, 48] as the medical-grade silicone. Even more, using a machine learning algorithm [49] can optimize the processing of silicone materials, the formulation, and the central processing variables to manufacture bone scaffolds as polymeric porous materials with sodium-alginate/hydroxyapatite coating or silicone/hydroxyapatite composite materials. This hierarchical machine learning has been employed recently to determine the purity, composition, structure, dimensions, and mechanical properties of silicone implants that are affected using a 3D printer by DLP [49].

4 Discussion

A recent study [50] proposed an efficient numerical method for arbitrary-shaped porous structure generation for 3D printing, which is like published in the references [12, 22] (although it employed another numerical method). Nevertheless, in our work, scientific is proposed a new plan of computational design and manufacture of porous polymeric materials with controlled macroporosity. Although both works are similar concerning obtaining porous materials from mathematical models, our work proposes a general method that allows the use of any numerical method and 3D printing technique: the mathematical design process and 3D printing-assisted manufacturing MDP-3DPAM. For example, the new way proposed can be applied to the numerical methods employed in the references [12, 22]. While the manufacturing technique presented in the relation [50] is dependent on their numerical way: Fourier Fast Transform. This numerical method also is employed in the procedure MDP-3DPAM proposed, but with a subtle difference: in our process, the FFT is implemented in python in matrix form (objects "array"). Note that the Swift–Hohenberg equation cannot be solved by the FFT method proposed in [50]. Another fundamental difference between both works is that our proposed method allows control of porosity through the computational design stage, which can determine the pore size through the design and type of 3D printing. In the section "Results of fused deposition modeling and stereolithographic UV-laser assisted," the pore size is shown according to the 3D printing technique used to manufacture the porous material. Finally, the method for obtaining porous polymeric materials proposed in reference [50] has a single stage. In contrast, the method proposed in this paper consists of three interconnected phases: mathematical modeling, computational design, and 3D printing. In future work, they would be using the shape memory effect materials for 3D printing that can have various applications as cellular structure composite with a novel continuous fiber-reinforced printing path [4, 51].

5 Conclusions

The quintic order Swift–Hohenberg equation presented here is a more general equation than those reported in the references of this work, because it has been extended to a 3D model. Besides, its numerical solution is obtained in the three-dimensional space by a pseudo-spectral implicit method. The numerical method of the IPSA has been successfully applied to solve in the three-dimensional space the Swift–Hohenberg equation of quantic order with the FFT method employing an algorithm that is easy to reproduce and that also poses an acceptable calculation time.

The dynamics of the 3D simulations obtained by the numerical solution from the IPSA method can be well used to explain nonlinear behaviors that are far from equilibrium. Besides, it allows defying the underlying mechanism in the polymeric materials area. Some examples of this are the diblock copolymer blend phases and new computational models able to generate controlled 3D porous microstructures.

All the above has ended in a new methodology focused on implementing the numerical solutions as computational models able to generate controlled 3D microporous structures to process new polymeric porous materials like the ones that have been reported in [12, 22, 44, 45]. The advantage of this methodology is the pore size distribution control through the mathematical design process and assisted by 3D printing their easy implementation by different techniques: fused deposition modeling and stereo-lithography UV-laser assisted. Even this proposed method has universal properties as it is compatible with other numerical methods [16,17,18] and other 3D printing techniques [2,3,4,5,6,7].