Deformations and strain energy in fragments of tempered glass: experimental and numerical investigation

Abstract

The present paper is adding to the current knowledge by experimentally investigating the change of strain in a fragment of tempered glass. This is done by comparing the surface shape before and after fracture. The present work also aims at validating a FE-model for estimating the remaining strain energy and thereby the stress in a fragment post failure. The FE-model have been established in previous work Nielsen (Glass Struct Eng, 2016. doi:10.1007/s40940-016-0036-z) and is applied here on the specific geometry and initial state of the investigated fragments. This is done by measuring the residual stresses using a Scattered Light Polariscope before failure and thereby determining the initial stress state. The Geometry of the investigated fragment is found by means of a 3D scan. The surface topology of the fragment is found by letting a stylus traverse the surface and recording the shape. These information are then used for setting up a FE-model for calculating the stresses and strains left in the fragment after failure and compare the deformation to the measured.

1 Introduction

Tempered glass is widely used in the community and is part of our daily life. It is usually not possible to distinguish it from ordinary window glass (float glass) by the naked eye. However, when broken it reveals a characteristic feature; it shatters into relatively small fragments. In Fig. 1 fragments of broken tempered glass is seen. It is noted that the fragments often group into larger, quite fragile, chunks.

The fragmentation is driven by the amount of strain energy present in tempered glass, however, not all present energy is used in the process of fragmentation. This needs to be taken into account before any serious predictions between the residual stress state and the fragment size can be made.

This paper is describing a novel method for experimentally verifying previous calculations of the remaining strain energy in a fragment.

In order to understand the nature of the tempered glass and its fragmentation behaviour the tempering process might be a good place to start.

1.1 The tempering process

Tempered glass is ordinary float glass which has been heated to a temperature where it starts to be soft, unable to carry any stresses, and then quenched rapidly as sketched in Fig. 2.

Fig. 1

Fragments from broken tempered glass

Fig. 2

Tempered glass production, after Haldimann et al. (2008). Prior to heating and quenching, the glass is cleaned

During the quenching a temperature gradient will exist in the glass, the surface will contract and stiffen while the core is remaining soft and stress-free. When the temperature in the center is low enough for the material to become stiff, stresses will start to build up in the glass. When the glass reaches a uniform low temperature, say $25\,^{\circ }\hbox {C}$, the surface will be in compression and the core part in tension. If a cross-section far from edges is considered, the residual stresses will, almost, only be in-plane and varying near parabolic over the thickness. Since equilibrium is required, a rule of thumb can be derived from this stating that the residual compressive surface stress will be twice the tensile stress in the center and that the depth of zero stress is approximately 21% through the thickness, see Fig. 3.

Fig. 3

Section of tempered glass piece showing residual stress profile away from edges. The contour line represents zero stress

1.2 Survey of the correlation between strain energy and fragment size

Due to these residual stresses, tempered glass will contain strain energy even without any external loading. Assuming parabolic distribution over the thickness and a planar hydrostatic stress state everywhere in the plate, the strain energy per unit surface area (before failure), $U_0$, can be written as:

$$\begin{aligned} U_0=\frac{h(1-\nu )}{5E}\sigma _s^2 \end{aligned}$$

(1)

where h is the thickness, $\sigma _s^2$ is the surface residual stress, E and $\nu$ are the elastic constants. A derivation of this can be found in the literature, e.g. Barsom (1968), Gulati (1997), Nielsen (2016), Reich et al. (2012), Warren (2001).

Due to this strain energy, tempered glass will shatter if the residual stress equilibrium is disturbed sufficiently. This can be done either by scratching, cutting or drilling deep into the glass or simply loading it above its apparent strength.¹ The sudden release of strain energy will cause the glass to fragmenting at such high speed, that the fragments are accelerated and, if not hindered, they will move in an explosive manner, see e.g. Nielsen et al. (2009). There are primarily in-plane residual stresses in the tempered glass, the displacement of the glass fragments will therefore only be in the plane of the glass plate, Fig. 4.

Fig. 4

The process of failure in tempered glass, captured at 21,000 frames per second

Even though scientists have wondered about the fragmentation of tempered glass since the phenomenon was first scientifically described in the seventeenth century by authors such as Robert Hooke investigating the so-called Prince Rupert’s Droplets Hooke (1665), there is still not formulated a theoretical model predicting the fragment size as function of the initial residual stress state.

In 1965 an article by Akeyoshi and Kanai (1965) is published, investigating the relation between the residual stresses of tempered glass, the thickness of the glass and the tempering conditions. The experiments are conducted with a varying thickness from 2 to 8 mm and the central tensile stress is determined by applying a method of photo-elasticity (Fig. 5). As a sub-study the fragment density is compared to the thickness and the residual stresses of the glass. The fragment density is used as a measure for the degree of tempering. A non-linear relation is established, but it remains undetermined whether the origin of the relation comes from the thickness of the glass, the residual stresses or a combination. Also it is not described in detail how the number of fragments is determined nor how the residual stress is measured.

Fig. 5

The relation between number of fragments and the tensile residual stress, $\sigma _c$. Graph is reproduced from Akeyoshi and Kanai (1965) with unit of the abscissae changed to MPa and results from Eq. 4 added

Around the same time, Barsom (1968) establishes an analytical correlation between the maximum tensile stress and the average particle size by applying a method based on linear-elastic fracture mechanics. By assuming plane stress and that residual stresses of tempered glass can be modelled by a second-order polynomium, Barsom finds that the total elastic-strain energy relates to the central tensile stress to the power of 4. The idea is, that the stored energy dissipates during the fracture of tempered glass while generating fracture surfaces. From this, Barsom proceeds to establish a relation between the stored elastic energy and the area generated by the fracture process by applying linear-elastic fracture mechanics. It is assumed that the propagation of cracks is governed solely by the tensile stress, given that the cracks develop in the tensile zone before the compression zone of the glass. Barsom states that neutral stress planes are located approximately 0.21 h from the glass surface, where h is the thickness of the plate. The maximum tensile stress is then averaged over 58% of the thickness. This entails that the average tensile stress is equal to almost 70% of the maximum tensile stress. Therefore the strain-energy release rate, G, for a crack propagating due to residual stresses of the glass is a function of the mean tensile stress squared and the average mean free fracture path. Since the value of $G=0.93=16.61$ is known from previous studies, one can determine a value of the average mean free fracture path, which is assumed constant in the plate. By gained knowledge about the mean tensile stress and the strain-energy release rate combined with the assumption that a fragment of shattered tempered glass has a hexagonal cross section with sides equal to the length of the average mean free fracture path, Barsom finds that the center tensile stress, $\sigma _{c*}$, to the power of four multiplied with the mass of a glass fragment, M, normalized with the thickness, h, is constant:

$$\begin{aligned} \sigma _{c*}^4\cdot \left( \frac{M}{h}\right) =7.73\times 10^{12}~\frac{\mathrm {lb}^5}{\mathrm {in.}^9} \end{aligned}$$

(2)

In the above equation, the stress is expressed with a unit of mass divided by length squared.

Fig. 6

Center tensile stress $\sigma _c$ as a function of base area of fragment, A

The expression is rewritten with the center tensile stress in MPa, $\sigma _{c}$, as a function of the fragment base area, A, since $M=V~\rho =A~h~\rho$. From this it is clearly seen that the expression is independent of the thickness, h. A plot of the function is shown in Fig. 6

$$\begin{aligned} \sigma _c=105.81\left( \frac{1}{A} {\mathrm {MPa}}^4\,{\mathrm {mm}}^2\right) ^{1/4} \end{aligned}$$

(3)

This equation can also be re-written in order to give the average number of fragments (or particles) in a $50~\hbox {mm} \times 50~\hbox {mm}$ square, $N_{50}$, in order to compare with the results by Akeyoshi and Kanai (1965) given in Fig. 5. This is done by substituting $A=\frac{2500~\hbox {mm}^{2}}{N_{50}}$ in (3) and re-arranging:

$$\begin{aligned} N_{50}=\left( \frac{\sigma _c}{14.96~\hbox {MPa}}\right) ^4 \end{aligned}$$

(4)

Barsom (1968) performs an experimental fragmentation test and measures the particle weight of random fragments. It is not stated how the residual stresses are determined. However for stresses larger than 6000 psi (approximately 41 MPa) there is a good compliance between the analytical solution and the experimental data. Comparing with Fig. 5 it is seen that the shape of the equation seems reasonable, however, it lacks the dependency of the glass thickness, h.

Gulati (1997) establishes a so-called frangibility model. Again the model assumes that the residual stresses can be modelled with a second order polynomial, where the surface compression is twice the value of the central tensile stress. Like Barsom (1968) found, the initial stored elastic strain energy of the plate is found to vary linearly with the thickness of the plate and quadratically with the central tension. Like Barsom (1968), Gulati assumes that the fragmentation of glass is governed solely by the tensile stress. Also it is assumed that by initiation of the fracture process, only a fraction of the elastic strain energy is used to generate new fracture surfaces. Theses fracture surfaces are assumed smooth and perpendicular to the depth, and the developed fracture surfaces forms squared fragments. The assumption of squared fragments is based upon the assumption of uniform biaxial stresses. If $\hat{N}$ is the fragment density of the glass per unit surface area, then it is assumed that the side lengths of one fragment is $\frac{1}{\sqrt{\hat{N}}}$ and so that the area of fragmentation for one fragment must be $\frac{4h}{\sqrt{\hat{N}}}$. Combining this with the considerations on the elastic strain energy, Gulati finds that the fragment density depends on the central tension to the power of 4, but is independent of the thickness of the plate. A fragmentation test is performed on four glass plates with a thickness of 2.67 mm and varying level of tempering. A linear correlation between the fragment density and the measured central tensile stress to the power of four is found with good compliance to the frangibility model. A fragmentation test is also performed on a glass plate of 5.1 mm, and here it is found that the fragment density is not in compliance with the developed model. Gulati suggests that the fragment density is related to the plate thickness despite what the analytical model predicts. Gulati then concludes that the fragment density is nearly independent of the plate thickness under certain conditions; a thin plate or a high central tension. Gulati also estimates the fraction of used elastic strain energy and finds that 43% of the initial strain energy is used during fragmentation. Gulati applies the analytical model developed by Barsom (1968) to estimate the same fraction and finds that 35% of the initial strain energy is used.

Nielsen et al. (2009) presents a study of the fracture process of tempered glass. The fracture process is initiated with a diamond drill to transfer a minimum of energy to the test specimens. Among other things, the study shows that fracture in tempered glass takes place almost simultaneously in compressive and tensile zone. This is questioning the previous studies of Barsom (1968), Gulati (1997) where only the part of the strain energy originating from tensile stresses are assumed to be important in relation to the fracture process.

A recently published study by Nielsen (2016) provides a numerical calculation of the remaining stress state and strain energy in a tempered glass fragment. The model is based on a linear elastic finite element model. On the basis of more recent studies Nielsen et al. (2009), the author of the article suggests that it is more reasonable to apply the total strain energy of the tempered glass. From the study it is clearly shown that the initial stress state changes from being plane hydrostatic to becoming fully three dimensional in the fragment. Tables and calculation tools for estimating the remaining strain energy in the fragment with various parameters is provided. The study is based on a polygonal shape of the fragments with a varying number of sides ($n=\{3,4,5,\infty \}$).

1.3 Deformations of a cylindrical fragment

The release of strain energy and redistribution of stresses when the free surfaces of a fragment is formed must lead to deformations. Due to the variation of the initial residual stress over the thickness and poisson ratio, the deformations in the fragment are not trivial and easily evaluated. The surface parts where compressive stresses initially were present, tend to expand while the center part (initial tensile) do the opposite. This leads to that an intial straight line through the thickness and along the side of the fragment (before fragmentation) becomes curved after the fragmentation, as illustrated in Fig. 7. This curvature causes an out of plane deformation due to the rotation (the upper right corner in Fig. 7). All in all, this leads to a completely changed residual stress state with significant out-of-plane stresses.

In Fig. 7 is showing an axisymmetric FE model of one quarter of a cylindrical fragment. The full height of the fragment is 19 mm and the radius is 9.5 mm. The initial residual stress state was assumed parabolic with a compressive surface stress of −100 MPa and a center tensile stress of 50 MPa. The model is linear elastic assuming a Young’s modulus of 70 GPa and a Poisson’s ratio of 0.23. The mesh consists of 2500 second order axisymmetric displacement elements (CAX8). The density of the used mesh is fine enough for the results to be converged (a mesh consisting of only 100 elements would also be enough for determining the displacements).

The plot in Fig. 7 shows a deformed contour plot of the displacements in the 2-direction. It is also seen that the top surface of the fragment is curving. It is this deformation we will experimentally measure and compare to numerical results for a real fragment geometry in the following.

Fig. 7

Deformations for a cylindrically shaped fragment modelled axisymmetric in ABAQUS. Only 1/4 of the fragment is modelled due to symmetry

The work presented in here adds to the current knowledge, by investigating the strain energy in a given fragment by deformation measurements and comparison with a finite element model of the given fragment (by means of 3D scanning).

To provide an overview of the paper, the following list shortly states the steps in the investigation carried out.

• 1. Measure residual stresses in a glass plate.

• 2. Measure surface topology.

• 3. Break glass plate.

• 4. Measure surface topology (again).

• 5. 3D scanning a selected fragment.

• 6. Import geometry in ABAQUS and carry out the FE-analysis.

• 7. Compare results.

2 Experimental method and results

2.1 Measurement of residual stresses

Due to the optical properties of glass, it is possible to measure the residual stress by stress-optical methods. The so-called scattered light polariscope (SCALP-04) is based on this and is used in this investigation for measuring the residual stresses in the glass plate before failure. An elaborate explanation of the method can be found in e.g. Anton and Aben (2003) or Aben and Guillemet (1993).

Each test specimen is marked with three areas of $20~\hbox {mm}\times 20~\hbox {mm}$ as depicted in Fig. 8. Within each area four measurements of the residual stress are conducted in direction of both x and y.

Fig. 8

Placement of the three areas on the glass plate. All measures are in mm

The residual stresses are measured for the test specimen with a thickness of 19 mm. The mean principal stresses for each of the three fields can be seen in Table 1 and according to the manual of the SCALP-04 the accuracy of the measurements is approximately ±5%.

Table 1 Mean residual stresses within each measurement field

2.2 Measurement of surface topology

2.2.1 Measuring equipment: form TalySurf series 2

To determine the deformation of the glass surface within each field, a measurement of the surface profile is performed. This is done by Taylor Hobson’s Form TalySurf Series 2 as shown in Fig. 9.

Fig. 9

Test setup with test specimen in Form TalySurf Series 2. During the measurement, the test specimen is tilted (not shown)

A stylus traverses the surface, from which the metrology is wanted. A pickup converts the vertical movements of the stylus to an electrical signal which is then amplified and recorded.

The uncertainty of the measured vertical displacement is $\pm 0.145~\mu m$. The reported uncertainty is based on a standard uncertainty multiplied by a coverage factor, $k=2$, providing a level of confidence of approximately 95%.

2.2.2 Surface topology

The residual stress state of the test specimen is determined for an area of $20~\hbox {mm}\times 20~\hbox {mm}$.

The measurements of the surface topology are therefore executed over an area of $24~\hbox {mm}\times 24~\hbox {mm}$ aiming to center the area of determined residual stresses, see Fig. 10.

Fig. 10

Measurement scheme of surface topology. The measurement direction with high point density is referred to as primary measurement direction ($x_1$) and the other as secondary measurement direction ($x_2$). All measurements are in mm

The surface topology is measured two times. The first measurement is conducted with x as the primary measurement direction, $x_1$, and y as the secondary measurement direction, $x_2$. The specimen is then rotated $90^{\circ }$ and y is now the primary direction of measurements, $x_1$.

The primary direction of the measurement consists of 2400 points (100 points per mm), while the secondary direction only has 49 measurement points. Also the secondary measurement direction is affected by a sinusoidal movement of the stylus.

The primary and the secondary measurement directions are orthogonal. An example of measurements along the primary and secondary directions are shown in Fig. 11.

Fig. 11

Example of surface topology measurement before fragmentation. Top left a primary direction: before global levelling. Top right b secondary direction: before global levelling. Middle left c primary direction: after global levelling. Middle right d secondary direction: after global levelling. Bottom: sketch over the measurement directions within one $20~\hbox {mm} \times 20~\hbox {mm}$ area

In Fig. 11a it is clearly seen that the test specimen is tilted during the measurements. The software SPIP is used to level the measurements with the function Global levelling which is clearly seen by comparing Fig. 11a and c. This function calculates a first order plane of the measurements and then subtracts the first order plane. The measurements are conducted both before and after fragmentation of the glass. The measured data can be used to obtain a surface plot of the measured area, showing a mapped fragmentation pattern. The surface plots are used to compare the true fragmentation pattern to the measured one.

2.3 Fragmentation of tempered glass

After the first surface topology measurement of the glass plate, the test specimen is brought to failure. The fragment size is directly related to the stored elastic strain energy of the tempered glass and therefore it is essential that no energy is transferred to the glass during fragmentation as this will have an effect on the size of the glass fragments. The fragmentation of the tempered glass is therefore initiated by drilling with a diamond drill (with a diameter of 2.5 mm). By this method, the added energy when failure starts is minimized and assumed to be zero.

The fragmented glass must be held together to ensure the possibility of measuring the surface topology after fragmentation. Therefore the edges of the glass is taped. It is here assumed that the stiffness of the tape is low enough to allow the fragmentation and expansion of the glass freely.

The point of initiating the fragmentation of the test specimen is shown in Fig. 12. The point is placed relatively far away from the edges to ensure the stress distribution as depicted in Fig. 3. Also in reasonable distance to the measuring areas even though the method of initiating fragmentation by drilling should transfer a minimum of energy to the test specimen. When the test specimen is prepared, the drill is lowered to the surface of the glass and the drilling begins. The glass is expected to fragment, when the tensile stresses overcome the compressive stresses. During the drilling water is used to cool the drill and remove dust from the hole to prevent over-heating and excessive wear of the drill.

2.4 Identification of fragments

After the test specimen is fragmented, a surface topology measurement is conducted once again. Due to relatively large depth of cracks through field 1 and 2, it is not possible to recognize the fragmentation pattern from the topology measurements. However, this was possible for field 3 as shown in Fig. 13 where the identification of two specific fragments is given.

Fig. 12

Test setup for fragmentation of test specimen showing point of initiating fragmentation and diamond drill. All measures are in mm

Fig. 13

Identification of fragment pattern and individual fragments in field 3

After the surface topology measurements the glass fragments are separated, and fragments are chosen for further processing (3D scanning and numerical modelling). It is possible to identify and separate two fragments from field 3. These are labelled F3.1 and F3.2 in Fig. 13.

3 Numerical method

3.1 Modeling the geometry of a real fragment

In order to obtain an accurate model of the surface geometry of the fragment after fragmentation it is necessary to know the geometry of the fragment before failure. Obviously, this is not possible, however, if we assume that the fragments (deformed) geometry can be used for the fractured surfaces and the top and bottom surfaces can be modelled straight we obtain a relatively good estimate.

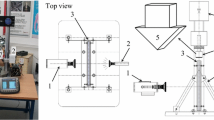
This geometry is obtained by the SeeMa Lab Structured Light Scanner. The scanner consists of both hardware components (including cameras, projector and rotation stage), and software for calibration, scanning and reconstruction.

Since the scanner uses structured light, the glass fragment must be covered to obtain a non-reflective and non-refractive surface. For this purpose, a chalk spray paint is applied as even and thin-layered as possible. Figure 14a shows the painted fragments.

Fig. 14

Fragment F3.1 depicted as a photograph b point cloud from 3D scan c faceted solid from both top and side view

The scanner depicts the surface of the fragment by rotating the fragment with steps of $40^{\circ }$ from $0^{\circ }$ to $359^{\circ }$. With every step, a point cloud is obtained and the steps are automatically aligned by the SeeMa software developed by the Eco3D group at Technical University of Denmark. Each fragment is scanned both horizontally and vertically and the two scans are aligned during post-processing. As the point clouds are aligned they can be reconstructed as a surface. In the software MeshLab, this can be done by Poisson Surface Reconstruction. The function generates a mesh build up by triangular shaped facets seeking to form a smooth surface. In Fig. 14 the physical fragment, point cloud and faceted solid is presented.

3.2 Creating a FE-model for the fragment

The FE-model of the real fragment is based on the geometry found by 3D scanning as discussed in the last section. Due to the linearity, the remaining stress-/strain state can be found by applying the initial planar-hydrostatic residual state, leaving all surfaces without any constraints. In order to avoid rigid body motions the model needs to be constrained in six points as illustrated in Fig. 15.

Fig. 15

Constraints and coordinate system on fragment

The properties used for the modeling are given in Table 2. It should be noted that the residual stresses are applied in the same manner as described in Nielsen (2016) using a non-physical thermal expansion coefficient and a specific temperature field as shortly sketched below:

$$\begin{aligned} \sigma (z)=\frac{E\alpha }{1-\nu }\varDelta T(z) \end{aligned}$$

(5)

where the temperature profile, $\varDelta T(z)$, is given from the measured stress profile.

Table 2 Finite element model parameters

The elements used are second order (displacement) 3D tetrahedral, named C3D10 in the finite element software ABAQUS. Due to the complexity of the geometry, a really coarse mesh was not possible. The convergence on the results were investigated for different meshes containing between 15,561 elements and 61,681 elements with a maximum deviation of less than 0.5%. A plot showing both the applied mesh and the transverse displacement for the fragment is given in Fig. 16.

Fig. 16

Contour plot of displacement in transverse direction (z)

4 Numerical results and discussion

In the following, the measurements of the two fragments F3.1 and F3.2 are given. The path of the measurments along the surface is sketched in Fig. 17

Fig. 17

Sketch of the paths along which the deformation was measured on the surface of the two fragments

Fig. 18

Fragment F3.1: topology measurement compared to finite element model. The vertical axis with variable, u, representing the deflection curves from the surface topology data (TM) and the numerical model. The different plots shows different sections in the surface

Fig. 19

Fragment F3.2: topology measurement compared to finite element model. The vertical axis with variable, u, representing the deflection curves from the surface topology data (TM) and the numerical model. The different plots shows different sections in the surface

4.1 Comparison with experiments

In Figs. 18 and 19 the topology measurements are compared to the finite element results for both fragments. Since the topology was only measured relatively the curves were brought to coincide at $x=0$. The experimental results yields the deformations in the thickness direction of the top-surface which can be compared to the FE-model. This alone does not validate the modelling of stresses and strains, however, with a prior knowledge of the stress distribution the correctness of the model is strongly supported.

For the comparison between the measurements and the model, a scattering degree of correlation is seen. Especially towards the edges of the fragments, deviations are observed. The kinks in the experimental curves are due to the transition to another fragment.

It is believed that this is due to that the software used for transforming the 3D scan into a FE-model did smoothing out the sharp edges. But also that the topology measurements were carried out before the fragment was isolated. From e.g. Nielsen et al. (2009) it is seen from a scanning electron image that the crack pattern in tempered glass is “bridged”. This effect indicates that the surfaces of the fragment was not completely free as assumed in the model. This also fits well with the plots where some scatter of the corrolation is seen. It would be recommended to separate the fragments before measuring the surface topology in the future.

Another issue is to find the exact same path across the fragment. In the plots, several measured paths (TM) are shown together with the FEM solution. The paths (TM) are across the fragment top-surface and are parallel with 0.5 mm distance All paths TM are along the primary measurement direction, $x_1$.

4.2 Parametric study on fragment deformation

In line with Nielsen (2016), a parametric study using a cylindrical fragment is carried out. The FE-model is setup in the same way as described in the before mentioned paper and similar to what is described in Sect. 3.2. In this paper the parametric study is focusing on the deformations of the top surface of the fragment. The parameter, s, used in the plots is a coordinate from the center $(s=0)$ to the edge of the fragment at the top surface.

4.2.1 Initial stress state versus deformation

This parametric study shows, as expected, a linear relation between the surface deformations and the initial residual stresses, see Fig. 20. As expected, the deformations are seen to increase with the magnitude of residual stresses. Due to linearity, all curves can be brought to coincide by simply dividing the displacement, $u_z$, with the initial stress, $\sigma _\infty$.

Fig. 20

Relation between initial residual compressive surface stress, $\sigma _{\infty }$, and surface deformation for a 19 mm high fragment with a radius of 9.5 mm

Fig. 21

Relation between glass thickness and surface deformation for a fragment with same diameter as thickness and an initial stress, $\sigma _\infty =100~\hbox {MPa}$

4.2.2 Glass thickness versus deformation

The thickness of the glass is obviously impacting the deformations of the surface of the fragment. This is shown in Fig. 21.

The effect is linear and if the parameter, s, is normalised and the same for the displacements, $u_z$, one single curve will be obtained.

4.2.3 Fragment size versus deformation

The deformation is also dependent on the size of the fragments as shown in Fig. 22. The parameter, s, is the coordinate from the center of the fragment to the edge. It is seen that fragments ranging from a radius of less than 2–19 mm is given. From the figure it is seen that the relation is not simple and that for large fragments there will be a small dent at the center of the fragment opposed to what is seen for the smaller fragments.

Fig. 22

Relation between fragment size and surface deformation

5 Conclusion

From the obtained results in the paper it can be concluded that it is possible to experimentally determine the change of surface shape of a fragment. From the results, a numerical model for estimating the deformations in a fragment of tempered glass is seen to provide reasonable results. The same model is also capable of calculating stresses/strains and other deformations.

In future work more experiments should be included and the scanning of the geometry could be done by the use of X-ray tomography in order to get a more precise scan without the need for spray paint on the fragment. The X-ray method would also allow for including internal cracks in the modeling of fragments.