Introduction

Quadrotors are four-rotor helicopters characterized by a nonlinear 6-DOF unstable dynamical model. To succeed autonomous navigation of the quadrotors it is necessary to design efficient control algorithms that will exhibit robustness to parametric uncertainties and to external disturbances. One can cite several results on quadrotors’ control. An approach for quadrotors’ control that is based on the transformation of their dynamical model in the linear canonical form and which is consequently directly associated with differential flatness theory has been given in [1]. Moreover, in [2] a flatness-based control approach is applied to quadrotors’ motion control. A predictive controller complemented by an \(H_{\infty }\) term for additional robustness has been analyzed and tested in the quadrotor’s flight control problem in [3, 4]. In [5] motion control of the quadrotor was implemented using controllers of the LQR-type and of the PID-type, while Kalman Filtering has been used to provide position estimates out of a visual measurements system. In [6] two control strategies are employed as baseline controllers for the quadrotor’s model: a LQR controller which is based on a linearized model of the quadrotor and a Sliding Mode Controller which is based on a nonlinear model of the quadrotor. Moreover, differential flatness theory has been used for trajectory planning. In [7] and in [8] adaptive control schemes have been proposed for the quadrotor’s model. The stability of the control loop is confirmed through the Lyapunov approach. In [9] quadrotor’s control with the use of a sliding-mode controller and a sliding-mode disturbance observer has been proposed.

In this paper a new control method is developed for quadrotors that is based on differential flatness theory together with the use of a disturbance observer that is also in accordance to differential flatness theory, the so-called Derivative-free nonlinear Kalman Filter. The differential flatness theory-based design of the controller uses a change of coordinates (diffeomorhism) that transforms the state-space equation of the quadrotor’s model into the linear canonical (Brunovsky) form [10–15]. For the linearized equivalent of the quadrotor it is easier to design a state feedback controller using techniques for linear feedback controllers’ synthesis. To provide the quadrotor’s control loop with additional robustness a disturbance observer is used. The disturbance observer applies the standard Kalman Filter recursion on the linearized model of the quadrotor. It is capable of estimating simultaneously the quadrotor’s linear and rotational velocities, as well as the vector of disturbances that affect the quadrotor’s model without the need to compute Jacobian matrices (derivative-free nonlinear Kalman Filter). The accurate estimation of the disturbance inputs enables to introduce an additional control term that compensates for the disturbances’ effects. The accurate tracking of reference trajectories that is performed by the quadrotor despite the existence of external disturbances is shown in simulation experiments.

Differential flatness theory has specific advantages when used in nonlinear control systems [10–15]. By enabling an exact linearization of the system’s dynamical model it makes possible to avoid the use of linear models of local validity in the controller’s design. The controller performs efficiently despite the change of operating points. After the design of such a state feedback controller, one can consider the inclusion in the control loop of supplementary control terms that will provide additional robustness. Thus one can design flatness-based adaptive fuzzy controllers or flatness-based sliding-mode controllers. As mentioned above, it is also possible to use a disturbance estimator-based auxiliary control input for compensating for the effects of disturbances in the feedback control loop. Moreover, the use of differential flatness theory in the design of state estimators and filters has also several strong points. One can perform estimation of the complete state vector of the system without the need to compute partial derivatives and Jacobian matrices. Moreover, by avoiding numerical errors which are due to approximate linearization of the system’s dynamic model (e.g. with the use of expansion in Taylor series) linear estimation algorithms can be implemented. In the case of Kalman Filter this means that one can perform state estimation with the use of the standard Kalman Filter recursion, thus preserving the method’s optimality features and providing state estimates of improved precision (e.g. comparing to Extended Kalman Filtering).

The structure of the paper is as follows: in “Kinematic of the Quadcopter” section the kinematic model of the quadrotor is analyzed. In “Euler-Lagrange-equations for the Quadrotor” section the dynamic model of the quadrotor is introduced, using the Euler-Lagrange approach. In “Differential Flatness Theory MIMO Systems”section, differential flatness theory for MIMO dynamical systems is analyzed and conditions for the transformation of such systems into the linear canonical form are provided. It is shown how one can design a state feedback controller for the linearized equivalent of the system and how a derivative-free implementation of nonlinear Kalman filtering can provide state estimation for the quadrotor’s model. In “Design of Flatness Based Controller for the Quadrotors Model”section, the design of a flatness-based controller for the quadrotor’s model is explained. In “Disturbances Estimation in Quadrotor with Kalman Filtering”section it is shown how one can perform estimation of disturbance forces exerted on the quadrotor’s model using a disturbance observer. The derivative-free nonlinear Kalman Filter is re-designed as a disturbance estimator, thus providing simultaneously estimations of the quadrotor’s velocities and of the external disturbance terms. In“Simulation Tests” experimental tests are performed to evaluate the performance of the proposed control scheme, based on differential flatness theory and the derivative-free nonlinear Kalman Filter. Finally, in “Conclusions” section concluding remarks are given.

Kinematic Model of the Quadcopter

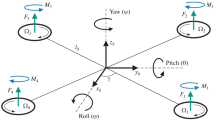
Two reference frames are defined [3, 4]. The first one \(B=[B_1,B_2,B_3]\) is attached to the quadcopter’s body, whereas the second \(E=[E_x,E_y,E_z]\) is considered to be an inertial coordinates system (Fig. 1). The Euler angles defining rotation round the axes of the body-fixed frame \(B_1\), \(B_2\) and \(B_3\) are defined as \(\theta \), \(\phi \) and \(\psi \), respectively. The two reference frames are connected to each other through a rotation matrix:

$$\begin{aligned} R=\begin{pmatrix} C{\psi }C{\theta } &{}\quad C{\psi }S{\theta }S{\phi }-S{\psi }C{\phi } &{} \quad C{\psi }S{\theta }C{\phi }+S{\psi }S{\phi } \\ S{\psi }C{\theta } &{}\quad S{\psi }S{\theta }S{\phi }+C{\psi }C{\phi } &{} S{\psi }S{\theta }C{\phi }-C{\psi }S{\phi } \\ -S{\theta } &{} \quad C{\theta }S{\phi } &{} \quad C{\theta }C{\phi } \end{pmatrix} \end{aligned}$$
(1)

where \(C=cos(\cdot )\) and \(S=sin(\cdot )\).

Fig. 1
figure 1

Reference axes for the quadcopter

Full size image

The connection between velocities in the two reference frames is as follows:

$$\begin{aligned} V_E=R{\cdot }{V_B} \end{aligned}$$
(2)

where \(V_E=[u_E,v_E,w_E]\) and \(V_B=[u_B,v_B,w_B]\) are the linear velocity vectors expressed in the two reference frames. About the angular velocities in the two reference frames the following relation holds

$$\begin{aligned} \dot{\eta }={W^{-1}}\omega \end{aligned}$$
(3)

that is

$$\begin{aligned} \begin{pmatrix} \dot{\phi } \\ \dot{\theta } \\ \dot{\psi } \end{pmatrix}= \begin{pmatrix} 1 &{} \quad sin(\phi )tan(\theta ) &{} \quad cos(\phi )tan(\theta ) \\ 0 &{} \quad cos(\phi ) &{} \quad -sin(\phi ) \\ 0 &{} \quad sin(\phi )sec(\theta ) &{} \quad cos(\phi )sec(\theta ) \end{pmatrix} \begin{pmatrix} p \\ q \\ r \end{pmatrix} \end{aligned}$$
(4)

where \(\eta =[\phi ,\theta ,\psi ]^T\) is the angular velocities vector in the inertial reference frame and \(\omega =[p,q,r]^T\) is the angular velocities vector in the body-fixed reference frame.

Euler-Lagrange Equations for the Quadcopter

The Euler-Lagrange equation for the quadcopter is formulated as follows

$$\begin{aligned} {{d} \over {dt}}\left( {{\partial {L}} \over {{\partial }\dot{q}_i}}\right) -{{{\partial }L} \over {{\partial }{q_i}}}= \begin{pmatrix} f_\xi \\ \tau _\eta \end{pmatrix} \end{aligned}$$
(5)

where the Lagrangian is defined as \(L(q,\dot{q})=E_{C_{trans}}+E_{C_{rot}}-E_p\), \(E_{C_{trans}}\) is the kinetic energy of the quadrotor due to translational motion, \(E_{C_{rot}}\) is the kinetic energy of the quadrotor due to rotational motion and \(E_p\) is the total potential energy of the quadrotor due to lift. The generalized state vector is \(q=[\xi ^T,\eta ^T]^T{\in }{R^6}\), \({\tau _\eta }{\in }{R^3}\) is the torques vector that causes rotation round the axes of the body-fixed reference frame, and \(f_{\xi }=R\hat{f}+\alpha _T\) is the translational force applied to the quadcopter due to the main control input \(U_1\) along the z-axis direction, while \(\alpha _T=[A_x,A_y,A_z]^T\) are the aerodynamic forces vector, defined along the axes of the inertial reference frame. Since the Lagrangian does not contain cross-coupling between the \(\dot{\xi }\) and the \(\dot{\eta }\) terms, the Lagrange-Euler equations can be divided into translational and rotational dynamics.

The translational dynamics of the quadcopter is given by

$$\begin{aligned} m\ddot{\xi }+mg{e_3}=f_{\xi } \end{aligned}$$
(6)

where \(e_3=[0,0,1]^T\) is the unit vector along the z axis of the inertial reference frame. Eq. (6) can be written using the following three equations

$$\begin{aligned} \ddot{x}= & {} {1 \over m}(cos(\psi )sin(\theta )cos(\phi )+sin(\psi )sin(\phi ))U_1+{A_x \over m} \nonumber \\ \ddot{y}= & {} {1 \over m}(sin(\psi )sin(\theta )cos(\phi )-cos(\psi )sin(\phi ))U_1+{A_y \over m} \nonumber \\ \ddot{z}= & {} -\,g+{1 \over m}(cos(\theta )cos(\phi )){U_1}+{{A_z} \over m} \end{aligned}$$
(7)

where m is the quadcopter’s mass and g is the gravitational acceleration.

The rotational dynamics of the quadcopter is given by

$$\begin{aligned} M(\eta )\ddot{\eta }+C(\eta ,\dot{\eta })\dot{\eta }={\tau _{\eta }} \end{aligned}$$
(8)

where the inertia matrix \(M(\eta )\) is defined as

$$\begin{aligned} M(\eta )=\begin{pmatrix} I_{xx} &{} \quad 0 &{}\quad -{I_{xx}}S{\theta } \\ 0 &{} {I_{yy}}{C^2}\phi +{I_{zz}}{S^2}\phi &{} \quad (I_{yy}-I_{zz})C{\phi }S{\phi }C{\theta } \\ -{I_{xx}}S{\theta } &{}\quad (I_{yy}-I_{zz})C{\phi }S{\phi }C{\theta } &{}\quad {I_{xx}}{S^2} {\theta }+{I_{yy}}{S^2}{\phi }{C^2}{\theta }+{I_{zz}}{C^2}{\phi }{C^2}{\theta } \end{pmatrix} \end{aligned}$$
(9)

and the Coriolis matrix is

$$\begin{aligned} C(\eta ,\dot{\eta })= \begin{pmatrix} c_{11} &{} \quad c_{12} &{} \quad c_{13} \\ c_{21} &{} \quad c_{22} &{} \quad c_{23} \\ c_{31} &{} \quad c_{32} &{} \quad c_{33} \end{pmatrix} \end{aligned}$$
(10)

where the elements of the matrix are

$$\begin{aligned} c_{11}= & {} 0 \nonumber \\ c_{12}= & {} ({I_{yy}}-{I_{zz}})(\dot{\theta }C{\phi }S{\phi }+\dot{\psi }{S^2}{\phi }C{\theta })\nonumber \\&+\,({I_{zz}}-{I_{yy}})\dot{\psi }{C^2}{\phi }C{\theta }\nonumber \\ c_{13}= & {} ({I_{zz}}-{I_{yy}})\dot{\psi }C{\phi }S{\phi }{C^2}\theta \nonumber \\ c_{21}= & {} ({I_{zz}}-{I_{yy}})(\dot{\theta }C{\phi }S{\phi }+\dot{\psi }{S^2}{\phi }C{\theta })\nonumber \\&+\,(I_{yy}-I_{zz}){\dot{\psi }}{C^2}{\phi }C{\theta }+{I_{xx}}\dot{\psi }C{\theta }\nonumber \\ c_{22}= & {} ({I_{zz}}-{I_{yy}}){\dot{\phi }}C{\phi }S{\phi }\nonumber \\ c_{23}= & {} -\,{I_{xx}}\dot{\psi }S{\theta }C{\theta }+{I_{yy}}\dot{\psi }{S^2}{\phi }C{\theta }S{\theta }+I_{zz}{\dot{\psi }}{C^2}{\phi }S{\theta }C{\theta }\nonumber \\ c_{31}= & {} ({I_{yy}}-{I_{zz}})\dot{\psi }{C^2}{\theta }S{\phi }C{\phi }-{I_{xx}}{\dot{\theta }}C{\theta } \nonumber \\ c_{32}= & {} ({I_{zz}}-{I_{yy}})(\dot{\theta }C{\phi }S{\phi }S{\theta }+\dot{\phi }{S^2}{\phi }C{\theta })\nonumber \\&+\,(I_{yy}-I_{zz})\dot{\phi }C^2{\phi }C{\theta }+{I_{xx}}\dot{\psi }S{\theta }C{\theta }\nonumber \\&-\,I_{yy}\dot{\psi }{S^2}{\phi }S{\theta }C{\theta }-I_{zz}\dot{\psi }C^2{\phi }S{\theta }C{\theta }\nonumber \\ c_{33}= & {} (I_{yy}-I_{zz})\dot{\phi }C{\phi }S{\phi }{C^2}\theta -{I_{yy}}\dot{\theta }{S^2}{\phi }C{\theta }S{\theta }\nonumber \\&-\,I_{zz}\dot{\theta }C^2{\phi }C{\theta }S{\theta }+I_{xx}\dot{\theta }C{\theta }S{\theta } \end{aligned}$$
(11)

Thus, the mathematical model that describes the quadrotor’s rotational motion is given by

$$\begin{aligned} \ddot{\eta }={M(\eta )^{-1}}(\tau _\eta -C(\eta ,\dot{\eta })\dot{\eta }) \end{aligned}$$
(12)

Denoting \(w={M(\eta )^{-1}}(\tau _\eta -C(\eta ,\dot{\eta })\dot{\eta })\), one has the following notation for the rotational dynamics

$$\begin{aligned} \begin{pmatrix} \ddot{\phi } \\ \ddot{\theta } \\ \ddot{\psi } \end{pmatrix}= \begin{pmatrix} w_a\\ w_b\\ w_c \end{pmatrix} \end{aligned}$$
(13)

Considering small variations of the heading angle of the quadrotor round \(\psi ={\pi \over 2}\), denoting \(w_1=U_1/m\) and taking also that the aerodynamic coefficients \(A_x,A_y,A_z<<m\), a simplified quadropter’s model is formulated as follows [1]

$$\begin{aligned} \begin{array}{lll} \ddot{x}={w_1}sin(\phi ) &{} \quad \ddot{y}={w_1}cos(\phi )sin(\theta ) &{} \quad \ddot{z}\;={w_1}cos(\phi )cos(\theta )-g \\ \ddot{\phi }=w_a &{} \quad \ddot{\theta }=w_b &{} \quad \ddot{\psi }=w_c \end{array} \end{aligned}$$
(14)

Differential Flatness Theory for MIMO Dynamical Systems

Basics of Differential Flatness Theory

Differential flatness theory will be used in the design of the quadrotor’s controller. Differential flatness theory can be applied to the generic class of systems \(\dot{x}=f(x,u)\). In this study, the interest is in dynamic models of the form

$$\begin{aligned} \dot{x}=f(x,t)+g(x,t)u \end{aligned}$$
(15)

The principles of the differential flatness theory have been extensively studied in the relevant bibliography [11, 12, 19]: A finite dimensional system is considered. This can be written in the form of an ordinary differential equation (ODE), i.e. \(S_i(w,\dot{w},\ddot{w},\ldots ,w^{(i)}), \ \ i=1,2,\cdots ,q\). The term w denotes the system variables (these variables are for instance the elements of the system’s state vector and the control input) while \(w^{(i)}\), \(i=1,2,\ldots ,q\) are the associated derivatives. Such a system is said to be differentially flat if there exists a set of m functions \(y=(y_1,\ldots ,y_m)\) of the system variables and of their time-derivatives, i.e. \(y_i=\phi (w,\dot{w},\ddot{w},\ldots ,w^{(\alpha _i)}), \ i=1,\ldots ,m\) satisfying the following two conditions [10, 20]:

  1. 1.

    There does not exist any differential relation of the form \(R(y,\dot{y},\ldots ,y^{(\beta )})=0\) which implies that the derivatives of the flat output are not coupled in the sense of an ODE, or equivalently it can be said that the flat output is differentially independent.

  2. 2.

    All system variables (i.e. the elements of the system’s state vector w and the control input) can be expressed using only the flat output y and its time derivatives \(w_i={\psi _i}(y,\dot{y},\ldots ,y^{(\gamma _i)}), \ i=1,\ldots ,s \). An equivalent definition of differentially flat systems is as follows:

Definition

The system \(\dot{x}=f(x,u)\), \(x{\in }{R^n}\), \(u{\in }{R^m}\) is differentially flat if there exist relations

$$\begin{aligned}&h: {R^n}{\times }{{(R^m)}^{r+1}}{\rightarrow }{R^m},\nonumber \\&\phi : {(R^m)^r}{\rightarrow }{R^n}\quad \ \text {and}\nonumber \\&\psi : (R^m)^{r+1}{\rightarrow }{R^m} \end{aligned}$$
(16)

such that

$$\begin{aligned} y= & {} h(x,u,\dot{u},\ldots ,u^{(r)}), \nonumber \\ x= & {} \phi (y,\dot{y},\ldots ,y^{(r-1)}), \ \text {and}\nonumber \\ u= & {} \psi (y,\dot{y},\ldots ,y^{(r-1)},y^{(r)}). \end{aligned}$$
(17)

This means that all system dynamics can be expressed as a function of the flat output and its derivatives, therefore the state vector and the control input can be written as

$$\begin{aligned} x(t)= & {} \phi (y(t),\quad \dot{y}(t),\ldots ,\quad y^{(r-1)}(t)),\quad \text {and}\nonumber \\ u(t)= & {} \psi (y(t),\quad \dot{y}(t),\ldots ,\quad y^{(r)}(t)) \end{aligned}$$
(18)

Classes of Differentially Flat Systems

For certain classes of dynamical systems it has been proven that they satisfy differential flatness properties. The following classes of nonlinear differentially flat systems are defined [14]:

  1. 1.

    Affine in-the-input systems: The dynamics of such systems is given by:

    $$\begin{aligned} \dot{x}=f(x)+{\sum _{i=1}^m}{g_i(x)}{u_i} \end{aligned}$$
    (19)

    From Eq. (19) it can be seen that the above state equation can also describe MIMO dynamical systems. Without out loss of generality it is assumed that \(G=[g_1,\ldots ,g_m]\) is of rank m. In case that the flat outputs of the aforementioned system are only functions of states x, then this class of dynamical systems is called 0-flat. It has been proven that a dynamical affine system with n states and \(n-1\) inputs is 0-flat if it is controllable.

  2. 2.

    Driftless systems: These are systems of the form

    $$\begin{aligned} \dot{x}={\sum _{i=1}^m}{f_i(x)}u_i \end{aligned}$$
    (20)

For driftless systems with two inputs, i.e.

$$\begin{aligned} \dot{x}={f_1(x)}{u_1}+{f_2(x)}{u_2} \end{aligned}$$
(21)

the flatness property holds, if and only if the rank of matrix \(E_{k+1}:=\{E_k,[E_k,E_k]\}, \ k{\ge }0\) with \(E_0:=\{f_1,f_2\}\) is equal to \(k+2\) for \(k=0,\ldots ,n-2\). It has been proven that a driftless system that is differentially flat, is also 0-flat.

Moreover, for flat systems with n states and \(n-2\) control inputs, i.e.

$$\begin{aligned} \dot{x}={\sum _{i=1}^{n-2}}{u_i}{f_i}(x) \ x{\in }R^n \end{aligned}$$
(22)

the flatness property holds, if controllability also holds. Furthermore, the system is 0-flat if n is even.

Conditions for Applying the Differential Flatness Theory to MIMO Systems

Application of the differential flatness theory to multi-input multi-output systems is of particular importance for the UAVs, such as quadrotors, because the latter stand also for MIMO systems. In order to demonstrate that a MIMO system satisfies the differential flatness properties, the flat outputs of the system have to be defined first. For nonlinear systems it is still an open problem to construct flat outputs. The following generic class of nonlinear systems is considered

$$\begin{aligned} \dot{x}=f(x,u) \end{aligned}$$
(23)

Such a system can be transformed to the form of an affine in the input system by adding an integrator to each input [15]

$$\begin{aligned} \dot{x}=f(x)+{\sum \nolimits _{i=1}^m}g_i(x){u_i} \end{aligned}$$
(24)

The following definitions are used [15–18]:

  1. (i)

    Lie Derivative: \({L_f}h(x)\) stands for the Lie derivative \({L_f}h(x)=({\nabla }h)f\) and the repeated Lie derivatives are recursively defined as \({L_f^0}h=h \ \ \text {for} \ i=0\), \({L_f^i}h={L_f}{{L_f^{i-1}}h}=\nabla {L_f^{i-1}h}f \ \ \text {for} \ i=1,2,\ldots \).

  2. (ii)

    Lie Bracket: \({ad_f^i}g\) stands for a Lie Bracket which is defined recursively as \({ad_f^i}g=[f,{ad_f^{i-1}}g]\) with \({ad_f^0}g=g\) and \({ad_f}g=[f,g]={{\nabla }g}f-{{\nabla }f}g\).

If the system of Eq. (24) can be linearized by a diffeomorphism \(z=\phi (x)\) and a static state feedback \(u=\alpha (x)+\beta (x)v\) into the following form

$$\begin{aligned}&\dot{z}_{i,j}=z_{i+1,j} \quad \ \text {for} \, \ 1{\le }j{\le }m \quad \ \text {and} \quad \ 1{\le }i{\le }v_j-1\nonumber \\&\quad \dot{z}_{v_{i,j}}={v_j} \end{aligned}$$
(25)

with \({\sum _{j=1}^m}{v_j}=n\), then \(y_j=z_{1,j}\) for \(1{\le }j{\le }m\) are the 0-flat outputs which can be written as functions of only the elements of the state vector x. To define conditions for transforming the system of Eq. (24) into the canonical form described in Eq. (25) the following theorem holds [15]

Theorem

For the nonlinear systems described by Eq. (24) the following variables are defined:

  1. (i)

    \(G_0=\text {span}[g_1,\ldots ,g_m]\).

  2. (ii)

    \(G_1=\text {span}[g_1,\ldots ,g_m,ad_f{g_1},\ldots ,ad_f{g_m}]\).

    \(\cdots \)

  3. (k)

    \(G_k=\text {span}\{{ad_f^j}{g_i} \ \text {for} \ 0{\le }j{\le }k, \ 1{\le }i{\le }m \}\).

Then, the linearization problem for the system of Eq. (24) can be solved if and only if

  1. (1)

    The dimension of \(G_i, \ i=1,\ldots ,k\) is constant for \(x{\in }X{\subseteq }R^n\) and for \(1{\le }i{\le }n-1\)

  2. (2)

    The dimension of \(G_{n-1}\) if of order n.

  3. (3)

    The distribution \(G_k\) is involutive for each \(1{\le }k{\le }{n-2}\).

Transformation of MIMO Nonlinear Systems into the Brunovsky Form

It is assumed now that after defining the flat outputs of the initial MIMO nonlinear system, and after expressing the system state variables and control inputs as functions of the flat output and of the associated derivatives, the system can be transformed in the Brunovsky canonical form:

$$\begin{aligned} \begin{array}{l} \dot{x}_1=x_2 \\ \dot{x}_2=x_3 \\ \cdots \\ \dot{x}_{r_1-1}=x_{r_1} \\ \dot{x}_{r_1}=f_1(x)+{\sum _{j=1}^p}{g_{1_j}(x)}u_j+d_1\\ \dot{x}_{r_1+1}=x_{r_1+2} \\ \dot{x}_{r_1+2}=x_{r_1+3} \\ \cdots \\ \dot{x}_{p-1}=x_{p} \\ \dot{x}_{p}=f_p(x)+{\sum _{j=1}^p}{g_{p_j}(x)}u_j+d_p\\ y_1=x_1 \\ y_2=x_2 \\ \cdots \\ y_p=x_{n-r_p+1} \end{array} \end{aligned}$$
(26)

where \(x=[x_1,\ldots ,x_n]^T\) is the state vector of the transformed system (according to the differential flatness formulation), \(u=[u_1,\ldots ,u_p]^T\) is the set of control inputs, \(y=[y_1,\ldots ,y_p]^T\) is the output vector, \(f_i\) are the drift functions and \(g_{i,j}, \ i,j=1,2,\ldots ,p\) are smooth functions corresponding to the control input gains, while \(d_j\) is a variable associated to external disturbances. In holds that \(r_1+r_2+\cdots +r_p=n\). Having written the initial nonlinear system into the canonical (Brunovsky) form it holds

$$\begin{aligned} y_i^{(r_i)}=f_i(x)+{\sum \nolimits _{j=1}^p}g_{ij}(x)u_j+d_j \end{aligned}$$
(27)

Next the following vectors and matrices can be defined

$$\begin{aligned} f(x)= & {} [f_1(x),\ldots ,f_n(x)]^T\nonumber \\ g(x)= & {} [g_1(x),\ldots ,g_n(x)]^T\quad \text {with} \ g_i(x)v\nonumber \\ \quad= & {} [g_{1i}(x), \ldots ,g_{pi}(x)]^T\\ A= & {} diag[A_1,\ldots ,A_p], \ \ B=diag[B_1,\ldots ,B_p] \nonumber \\ C^T= & {} diag[C_1,\ldots ,C_p], \ \ d=[d_1,\ldots ,d_p]^T\nonumber \end{aligned}$$
(28)

where matrix A has the MIMO canonical form, i.e. with elements

$$\begin{aligned}&A_i=\begin{pmatrix} 0 &{}\quad 1 &{}\quad \cdots &{}\quad 0 \quad \\ 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \quad \\ \vdots &{} \quad \vdots &{}\quad \cdots &{}\quad \vdots \quad \\ 0 &{}\quad 0 &{}\quad \cdots &{}\quad 1 \quad \\ 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \end{pmatrix}_{{r_i}\times {r_i}} \quad B_i=\begin{pmatrix} 0 \\ 0 \\ \cdots \\ 0 \\ 1 \end{pmatrix}_{{r_i}{\times }1} \nonumber \\&\quad C_i=\begin{pmatrix} 1\\ 0\\ \cdots \\ 0\\ 0 \end{pmatrix}_{1{\times }{r_i}} \end{aligned}$$
(29)

Thus, Eq. (27) can be written in state-space form

$$\begin{aligned}&\dot{x}=Ax+B[f(x)+g(x)u+\tilde{d}] \nonumber \\&\quad y={C^T}x \end{aligned}$$
(30)

which can be also written in the equivalent form:

$$\begin{aligned} \dot{x}= & {} Ax+Bv+B\tilde{d}\nonumber \\ y= & {} {C^T}x \end{aligned}$$
(31)

where the transformed control input is defined as \(v=f(x)+g(x)u\). By demonstrating differential flatness for the aerial vehicle’s model it is anticipated to express its dynamics in the canonical form defined by Eqs. (29), (30).

Design of Flatness-Based Controller for the Quadrotor’s Model

It will be shown, that the quadrotor’s model given in Eq. (14) is a differentially flat one, i.e. that all its state variables and the associated control inputs can be written as functions of a new variable called flat output and of its derivatives.

The following state variables are introduced \(x_1=x\), \(x_2=\dot{x}\), \(x_3=y\), \(x_4=\dot{y}\), \(x_5=z\), \(x_6=\dot{z}\), \(x_7=\phi \), \(x_8=\dot{\phi }\), \(x_9=\theta \), \(x_{10}=\dot{\theta }\), \(x_{11}=\psi \), \(x_{12}=\dot{\psi }\). Thus, one has the following state-space description for the quadrotor’s dynamic model

$$\begin{aligned} \begin{array}{cccc} \dot{x}_1=x_2 &{}\dot{x}_2={w_1}sin(x_7) &{}\dot{x}_3=x_4 &{}\dot{x}_4={w_1}cos(x_7)sin(x_9) \\ \dot{x}_5=x_6 &{}\dot{x}_6={w_1}cos(x_7)cos(x_9) &{}\dot{x}_7=x_8 &{}\dot{x}_8=w_a \\ \dot{x}_9=x_{10} &{}\dot{x}_{10}=w_b &{}\dot{x}_{11}=x_{12} &{}\dot{x}_{12}=w_c \end{array} \end{aligned}$$
(32)

The flat output of the system is taken to be the vector \(y_f=[x_1,x_3,x_5,x_7,x_9,x_{11}]^T\). It holds that

$$\begin{aligned} \begin{array}{cccc} x_1=[1 \ 0 \ 0 \ 0 \ 0 \ 0]y_f &{}\quad x_2=[1 \ 0 \ 0 \ 0 \ 0 \ 0]\dot{y}_f \\ x_3=[0 \ 1 \ 0 \ 0 \ 0 \ 0]{y_f} &{}\quad x_4=[0 \ 1 \ 0 \ 0 \ 0 \ 0]{\dot{y}_f} \\ x_5=[0 \ 0 \ 1 \ 0 \ 0 \ 0]y_f &{}\quad x_6=[0 \ 0 \ 1 \ 0 \ 0 \ 0]\dot{y}_f \\ x_7=[0 \ 0 \ 0 \ 1 \ 0 \ 0]y_f &{}\quad x_8=[0 \ 0 \ 0 \ 1 \ 0 \ 0]\dot{y}_f \\ x_9=[0 \ 0 \ 0 \ 0 \ 1 \ 0]y_f &{}\quad x_{10}=[0 \ 0 \ 0 \ 0 \ 1 \ 0]\dot{y}_f\\ x_{11}=[0 \ 0 \ 0 \ 0 \ 0 \ 1]y_f &{}\quad x_{12}=[0 \ 0 \ 0 \ 0 \ 0 \ 1]\dot{y}_f \end{array} \end{aligned}$$
(33)

According to Eq. (33) all state variables of the quadcopter can be written as functions of the flat output and its derivatives. Using this and Eq. (32) one also has that the control inputs of the quadcopter’s model, \(w_1\), \(w_a\), \(w_b\) and \(w_c\) can be written as functions of the flat output and its derivatives. Therefore, it is confirmed that the system is a differentially flat one.

Defining now the new control inputs

$$\begin{aligned} \begin{array}{ccc} v_1={w_1}sin(x_7) &{}v_2={w_1}cos(x_7)sin(x_9) &{}v_3={w_1}cos(x_7)cos(x_9) \\ v_4=w_a &{}v_5=w_b &{}v_6=w_c \end{array} \end{aligned}$$
(34)

one has the following state-space description for the system

$$\begin{aligned} \begin{pmatrix} \dot{y}_{f_1} \\ \ddot{y}_{f_1} \\ \dot{y}_{f_2} \\ \ddot{y}_{f_2} \\ \dot{y}_{f_3} \\ \ddot{y}_{f_3} \\ \dot{y}_{f_4} \\ \ddot{y}_{f_4} \\ \dot{y}_{f_5} \\ \ddot{y}_{f_5} \\ \dot{y}_{f_6} \\ \ddot{y}_{f_6} \\ \end{pmatrix}= \begin{pmatrix} 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \end{pmatrix} \begin{pmatrix} y_{f_1} \\ \dot{y}_{f_1} \\ y_{f_2} \\ \dot{y}_{f_2} \\ y_{f_3} \\ \dot{y}_{f_3} \\ y_{f_4} \\ \dot{y}_{f_4} \\ y_{f_5} \\ \dot{y}_{f_5} \\ y_{f_6} \\ \dot{y}_{f_6} \\ \end{pmatrix}+ \begin{pmatrix} 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 1 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 1 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \\ v_6 \end{pmatrix} \end{aligned}$$
(35)

and the measurement equation for this system becomes

$$\begin{aligned} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ z_5 \\ z_6 \\ \end{pmatrix}= \begin{pmatrix} 1 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \\ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \\ \end{pmatrix} \begin{pmatrix} y_{f_1} \\ \dot{y}_{f_1} \\ y_{f_2} \\ \dot{y}_{f_2} \\ y_{f_3} \\ \dot{y}_{f_3} \\ y_{f_4} \\ \dot{y}_{f_4} \\ y_{f_5} \\ \dot{y}_{f_5} \\ y_{f_6} \\ \dot{y}_{f_6} \end{pmatrix} \end{aligned}$$
(36)

Thus, using differential flatness theory the quadrotor’s model has been written in a MIMO linear canonical (Brunovsky) form, which is both controllable and observable.

After being written in the linear canonical form the quadrotor’s state-space equation comprises 6 subsystems of the form

$$\begin{aligned} \ddot{y}_{f_i}=v_i,\quad \ i=1,\ldots ,6 \end{aligned}$$
(37)

For each one of these subsystems a controller can be defined as follows

$$\begin{aligned} v_i\,{=}\,\ddot{y}_{f_i}^d-{k_{d_i}}(\dot{y}_{f_i}-\dot{y}_{f_i}^d)-{k_{p_i}}(y_{f_i}-y_{f_i}^d),\quad \ i\,{=}\,1,\ldots ,6 \end{aligned}$$
(38)

The control scheme is implemented in the form of two cascading loops. The inner control loop controls rotation angles, while the outer control loop sets the desired values of the rotation angles and in order to control position in the xyz-reference system. The computation of the reference setpoints for the rotation angles \(\phi _d(t)\), \(\theta _d(t)\) and \(\psi _d(t)\) and for the cartesian coordinates \(x_d(t)\),\(y_d(t)\) and \(z_d(t)\) takes into account the constraints imposed by the system dynamics.

Estimation of the Quadrotor’s Disturbance Forces and Torques with Kalman Filtering

It was shown that the initial nonlinear model of the quadrotor can be written in the MIMO canonical form of Eqs. (35) and (36). Next, it is assumed that the quadrotor’s model is affected by additive input disturbances, thus one has

$$\begin{aligned} \ddot{x}_1= & {} ({w_1}+d_1)sin(x_7) \nonumber \\ \ddot{x}_3= & {} ({w_1}+d_1)cos(x_7)sin(x_9) \nonumber \\ \ddot{x}_5= & {} ({w_1}+d_1)cos(x_7)cos(x_9) \nonumber \\ \ddot{x}_7= & {} {w_a}+{d_a} \nonumber \\ \ddot{x}_9= & {} {w_b}+{d_b} \nonumber \\ \ddot{x}_{11}= & {} {w_c}+{d_c} \end{aligned}$$
(39)

or using the new state variables \(y_{f_i} \ i=1,\ldots ,12\) of the differential flatness theory-based model and the transformed inputs \(v_i, i=1,\cdots ,6\) one has

$$\begin{aligned} \ddot{y}_{f_1}= & {} {v_1}+{d_1}sin(y_{f_7}) \nonumber \\ \ddot{y}_{f_3}= & {} {v_2}+{d_1}cos(y_{f_7})sin(y_{f_9}) \nonumber \\ \ddot{y}_{f_5}= & {} {v_3}+{d_1}cos(y_{f_7})cos(y_{f_9}) \nonumber \\ \ddot{y}_{f_7}= & {} {v_4}+{d_a} \nonumber \\ \ddot{y}_{f_9}= & {} {v_5}+{d_b} \nonumber \\ \ddot{y}_{f_{11}}= & {} {v_6}+{d_c} \end{aligned}$$
(40)

while by redefining the disturbance terms as \(\tilde{d}_1={d_1}sin(y_{f_7})\), \(\tilde{d}_2={d_1}cos(y_{f_7})sin(y_{f_9})\), \(\tilde{d}_3={d_1}cos(y_{f_7})cos(y_{f_9})\), \(\tilde{d}_4=d_a\), \(\tilde{d}_5=d_b\) and \(\tilde{d}_6=d_c\), the dynamics of the disturbed system can be written as

$$\begin{aligned} \ddot{y}_{f_1}= & {} v_1+\tilde{d}_1 \nonumber \\ \ddot{y}_{f_3}= & {} v_2+\tilde{d}_2 \nonumber \\ \ddot{y}_{f_5}= & {} v_3+\tilde{d}_3 \nonumber \\ \ddot{y}_{f_7}= & {} v_4+\tilde{d}_4 \nonumber \\ \ddot{y}_{f_9}= & {} v_5+\tilde{d}_5 \nonumber \\ \ddot{y}_{f_{11}}= & {} v_6+\tilde{d}_6 \end{aligned}$$
(41)

The system’s dynamics can be also written as \(\dot{y}_{f_1}=y_{f_2}\), \(\dot{y}_{f_2}={v_1}+\tilde{d}_1\), \(\dot{y}_{f_3}=y_{f_4}\), \(\dot{y}_{f_4}={v_2}+\tilde{d}_2\), \(\dot{y}_{f_5}=y_{f_6}\), \(\dot{y}_{f_6}={v_3}+\tilde{d}_3\), \(\dot{y}_{f_7}=y_{f_8}\), \(\dot{y}_{f_8}={v_4}+\tilde{d}_4\), \(\dot{y}_{f_9}=y_{f_{10}}\), \(\dot{y}_{f_{10}}={v_5}+\tilde{d}_5\), \(\dot{y}_{f_{11}}=y_{f_6}\), \(\dot{y}_{f_6}={v_6}+\tilde{d}_6\).

Without loss of generality, it is assumed that the dynamics of the disturbance terms are described by their second order derivative, i.e. \(\ddot{\tilde{d}}_i=f_{d_i}, \ i=1,\cdots ,6\). Next, the extended state vector of the system is defined so as to include disturbance terms as well. Thus one has the following state variables

$$\begin{aligned} \begin{array}{cccccc} z_{f_1}\,{=}\,y_{f_1} &{}z_{f_2}\,{=}\,y_{f_2} &{}z_{f_3}\,{=}\,y_{f_3} &{}z_{f_4}\,{=}\,y_{f_4} &{}z_{f_5}\,{=}\,y_{f_5}\\ z_{f_6}\,{=}\,y_{f_6}&{}z_{f_7}\,{=}\,y_{f_7} &{}z_{f_8}\,{=}\,y_{f_8} &{}z_{f_9}\,{=}\,y_{f_9} &{}z_{f_{10}}\,{=}\,y_{f_{10}}\\ z_{f_{11}}\,{=}\,y_{f_{11}} &{}z_{f_{12}}\,{=}\,y_{f_{12}} &{}z_{f_{13}}\,{=}\,\tilde{d}_1 &{}z_{f_{14}}\,{=}\,\dot{\tilde{d}}_1 &{}z_{f_{15}}\,{=}\,\ddot{\tilde{d}}_1\\ z_{f_{16}}\,{=}\,\tilde{d}_2 &{}z_{f_{17}}\,{=}\,\dot{\tilde{d}}_2 &{}z_{f_{18}}\,{=}\,\ddot{\tilde{d}}_2 &{}z_{f_{19}}\,{=}\,\tilde{d}_3 &{}z_{f_{20}}\,{=}\,\dot{\tilde{d}}_3\\ z_{f_{21}}\,{=}\,\ddot{\tilde{d}}_3 &{}z_{f_{22}}\,{=}\,\tilde{d}_4 &{}z_{f_{23}}\,{=}\,\dot{\tilde{d}}_4 &{}z_{f_{24}}\,{=}\,\ddot{\tilde{d}}_4 &{}z_{f_{25}}\,{=}\,\tilde{d}_5 \\ z_{f_{26}}\,{=}\,\dot{\tilde{d}}_6 &{}z_{f_{27}}\,{=}\,\ddot{\tilde{d}}_5 &{}z_{f_{28}}\,{=}\,\tilde{d}_6 &{}z_{f_{29}}\,{=}\,\dot{\tilde{d}}_6 &{}z_{f_{30}}\,{=}\,\ddot{\tilde{d}}_6 \end{array} \end{aligned}$$
(42)

Thus, the disturbed system can be described by a state-space equation of the form

$$\begin{aligned}&\dot{z}_f={A_f}{z_f}+{B_f}v \nonumber \\&z_{f}^{meas}={C_f}{z_f} \end{aligned}$$
(43)

where \({A_f}{\in }R^{{30}\times {30}}\), \({B_f}{\in }R^{{30}\times {6}}\) and \({C_f}{\in }R^{{6}\times {30}}\), with

(44)

For the aforementioned model, and after carrying out discretization of matrices \(A_f\) , \(B_f\) and \(C_f\) with common discretization methods one can implement the standard Kalman Filter algorithm using Eqs. (46) and (47). This is Derivative-free nonlinear Kalman filtering for the model of the quadcopter which, unlike EKF, is performed without the need to compute Jacobian matrices and does not introduce numerical errors due to approximative linearization with Taylor series expansion.

The dynamics of the disturbance terms \(\tilde{d}_i, \ i=1,\ldots ,6\) are taken to be unknown in the design of the associated disturbances’ estimator. Defining as \(\tilde{A}_d\), \(\tilde{B}_d\), and \(\tilde{C}_d\), the discrete-time equivalents of matrices \(\tilde{A}_f\), \(\tilde{B}_f\) and \(\tilde{C}_f\) respectively, one has the following dynamics:

$$\begin{aligned} \dot{\hat{z}}_f=\tilde{A}_f{\cdot }{\hat{z}_f}+\tilde{B}_f{\cdot }{\tilde{v}}+K\left( z_f^{meas}-{\tilde{C}_f}{\hat{z}_f}\right) \end{aligned}$$
(45)

where \(K{\in }R^{30{\times }6}\) is the state estimator’s gain. The associated Kalman Filter-based disturbance estimator is given by [19, 20]

Measurement update:

$$\begin{aligned}&K(k)={P^{-}(k)}{\tilde{C}_d^T}\left[ \tilde{C}_d{\cdot }P^{-}(k){\tilde{C}_d^T}+R\right] ^{-1} \nonumber \\&{\hat{z}_f(k)}={\hat{z}_f^{-}(k)}+K(k)\left[ z_f^{meas}(k)-\tilde{C}_d{\hat{z}_f^{-}(k)}\right] \nonumber \\&P(k)=P^{-}(k)-K(k){\tilde{C}_d}P^{-}(k) \end{aligned}$$
(46)

Time update:

$$\begin{aligned}&P^{-}(k+1)={\tilde{A}_d(k)}P(k){\tilde{A}_d^T}(k)+Q(k)\nonumber \\&{\hat{z}_f^{-}(k+1)}=\tilde{A}_d(k)\hat{z}_f(k)+\tilde{B}_d(k)\tilde{v}(k) \end{aligned}$$
(47)

To compensate for the effects of the disturbance forces it suffices to use in the control loop the modified control input vector

$$\begin{aligned} v=\begin{pmatrix} v_1-\hat{\tilde{d}}_1 \\ v_2-\hat{\tilde{d}}_2 \\ v_3-\hat{\tilde{d}}_3 \\ v_4-\hat{\tilde{d}}_4 \\ v_5-\hat{\tilde{d}}_5 \\ v_6-\hat{\tilde{d}}_6 \end{pmatrix} \quad \ \text {or}\quad \ v=\begin{pmatrix} v_1-\hat{z}_{13} \\ v_2-\hat{z}_{16} \\ v_3-\hat{z}_{19} \\ v_4-\hat{z}_{22} \\ v_5-\hat{z}_{25} \\ v_6-\hat{z}_{28} \end{pmatrix} \end{aligned}$$
(48)

Simulation Tests

Initial simulation experiments were concerned with flight control of the quadcopter in the disturbance-free case. The considered reference trajectories are shown in Fig. 2. The implementation of the flatness-based control enabled accurate tracking of the reference trajectories. Convergence has been succeeded for the linear position and velocity variables to the associated setpoints as it can be seen in Fig. 3a and b and in Fig. 4a. Moreover, there has been convergence of the angular position and velocity variables to the associated setpoints as it can be seen in Fig. 4a and in Fig. 5a and b.

Fig. 2
figure 2

Control of the quadrotor in the disturbance free-case: a trajectory of the quadrotor in the cartesian space, b projection of the quadrotor’s trajectory in the xy plane

Full size image
Fig. 3
figure 3

Control of the quadrotor in the disturbance free-case: a position and velocity along the x axis, b position and velocity along the y axis

Full size image
Fig. 4
figure 4

Control of the quadrotor in the disturbance free-case: a position and velocity along the z axis, b rotation angle \(\phi \) and associated angular speed

Full size image
Fig. 5
figure 5

Control of the quadrotor in the disturbance free-case: a rotation angle \(\theta \) and associated angular speed, b rotation angle \(\psi \) and associated angular speed

Full size image

Additional simulation experiments were concerned with control of the quadcopter in flight under disturbance forces and torques. The estimation of the disturbance forces and torques is shown in Fig. 6. The implementation of the flatness-based control enabled accurate tracking of the reference trajectories. There has been convergence of the linear position and velocity variables to the associated setpoints as it can be seen in Fig. 7a and b and in Fig. 8a. Moreover, there has been convergence of the angular position and velocity variables to the associated setpoints as it can be seen in Fig. 8b and in Fig. 9a and b.

Fig. 6
figure 6

Use of the derivative-free nonlinear Kalman Filter in estimation of disturbances: a associated with linear motion, b associated with the rotational motion of the aerial vehicle (blue line real value, green line estimated value)

Full size image
Fig. 7
figure 7

Control of the quadrotor in the presence of external disturbances a position and velocity along the x axis, b position and velocity along the y axis (blue line real value, green line estimated value, red line setpoint)

Full size image
Fig. 8
figure 8

Control of the quadrotor in the presence of external disturbances: a position and velocity along the z axis, b rotation angle \(\phi \) and associated angular speed (blue line real value, green line estimated value, red line setpoint)

Full size image
Fig. 9
figure 9

Control of the quadrotor in the presence of disturbances: a rotation angle \(\theta \) and associated angular speed, b rotation angle \(\psi \) and associated angular speed (blue line real value, green line estimated value, red line setpoint)

Full size image

Conclusions

The paper has examined a new control scheme for quadrotors that is based on the use of differential flatness theory and on disturbances estimation with the use of a new nonlinear filtering method, the so-called Derivative-free nonlinear Kalman Filter. It has been shown that the quadrotor’s model is a differentially flat one since all its state vector elements and control inputs can be expressed as functions of a vector variable that is the flat output of the system. Thus, the application of differential flatness theory introduces a transformation for the quadrotor’s state vector or equivalently a change of coordinates (diffeomorphism) that brings the system to the linear canonical (Brunovsky) form. It has been shown that the linearized equivalent of the quadrotor is in controllable and observable form. For this new model the design of a state feedback controller is easier. Moreover, by applying Kalman Filtering on the linearized equivalent of the system it is possible to produce estimates for the quadrotor’s state vector without the need of computation of Jacobian matrices and partial derivatives (unlike other nonlinear filtering methods such as the Extended Kalman Filter). Finally, by redesigning the derivative-free nonlinear Kalman Filter as a disturbance observer it becomes possible to estimate in real-time the external disturbances that affect the quadrotor’s model and consequently to compensate them with the inclusion in the control loop of auxiliary control terms. The efficiency of the proposed control scheme has been confirmed through simulation experiments.