Introduction

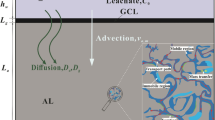
Groundwater is an important source for consumable water. Groundwater contribution in water supply is significant in many parts of the world. Contamination of groundwater is mainly due to contaminant transport through municipal solid waste landfills. In India 60 % of the waste is treated by landfills. Normally composite landfill liners have layers of geomembrane (GM), compacted clay liner (CCL) and geosynthetic clay liner (GCL) as barrier systems. The most commonly used composite liner is the one where a geomembrane is placed above a clay layer to restricting the transport through advection. A geomembrane is referred as a barrier when used inside an earth mass and liner when it is used as an interface [1]. A combination of geomembrane with thick compacted soil liner is adopted to overcome the limitation of geomembranes like very thin and limited adsorption capacity. This system is referred as geosynthetic clay liners. It requires less space, low material and construction cost and the performance is better than compacted soil liners. A detailed diagram is depicted in Fig. 1 showing the barrier system and its different components for the Kettleman Hill landfill [2]. This liner system is comparatively very complicated as it contains a protective soil layer, primary leachate collection system (PLCS), geotextile layer, granular layer and geonet layer for drainage of the leachate, high density polyethylene (HDPE) geomembrane layer, clay liner followed by secondary leachate collection system. All systems are not necessarily complicated like the Kettleman Hill landfill.

Fig. 1
figure 1

Schematic of barrier system (Rowe [2])

Full size image

The performance of different landfill liners should be assessed by developing an analytical or mathematical model. This highlights the importance of analytical and mathematical models for assessment of groundwater contamination through land filling. Guan et al. [3] recently developed an analytical solution for advective dispersive transport in two layered liner consisting of geosynthetic clay liner and soil liner. Numerical models like finite layer method, finite difference method and finite element method, find a great use in developing mathematical codes for observing contaminant transport through composite liners. Chai and Miura [4] developed two dimensional finite layer technique to observe the performance of liners when a geomembrane layer was introduced. Foose et al. [5] adopted finite-difference method for analyzing organic diffusion of contaminants, transported through composite liners. Kalbe et al. [6] used finite layer method to examine diffusion of acetone through composite liners. EI-Zein [7] applied finite element method for analyzing transport of contaminant through composite liners. In recent years meshfree methods are getting attention as their basic idea is to eliminate the structure of mesh and construct approximate solutions for the equation in terms of nodes [8]. Most common and successful meshfree method is the Element free Galerkin method (EFGM) and has been used for solving boundary value problems related to various field study [9–11].

It is evident from the available limited studies in the literature [3–7] that numerical modelling has a significant role in the analysis of migration of contaminant through composite liners. In the present study, steady state contaminant transport through geomembrane is assumed. On the basis of these assumptions, the one-dimensional model for contaminant transport through geomembrane considering diffusion is coupled with two dimensional model for contaminant transport through soil layer using EFGM. Lagrange multiplier has been used for enforcing the Dirichlet boundary conditions. EFGM can account for heterogeneous layer properties and different boundary conditions in a more realistic manner. The results obtained by the proposed method and those obtained by the analytical method are compared. Further a parametric study is performed to observe the effect of geomembrane overlaid on single and multi-layered system consisting of sand and clay on contaminant migration.

Contaminant Transport Through Geomembrane

Entire domain of landfill liner can be considered to be comprised of geomembrane and clay liner. In the present formulation geomembrane is modelled using one dimensional analysis and clay liner is modelled using usual two-dimensional analysis.

The stiffness and mass matrices calculated from the one dimensional analysis for geomembranes are added to the stiffness and mass matrices calculated from the two dimensional analysis of soil. The values of the stiffness and mass at the interface of the geomembrane and soil are replaced with the values of the stiffness and mass of the geomembrane.

The governing equations and boundary conditions for the solute transport through geomembranes and soil are as follows:

Governing equations for solute transport through geomembranes

$$\frac{{\partial C_{g} }}{\partial t} = D_{g} \frac{{\partial^{2} C_{g} }}{{\partial z^{2} }}$$
(1)

Governing equations for solute transport through soil liner

$$R\frac{\partial C}{\partial t} = D_{x} \frac{{\partial^{2} C}}{{\partial x^{2} }} + D_{z} \frac{{\partial^{2} C}}{{\partial z^{2} }} - v\frac{\partial C}{\partial z}$$
(2)

In which, C g is the concentration in geomembranes [M/L3], D g is the diffusion coefficient of geomembranes [L2/T], R is retardation factor given as \(R = 1 + \left( {{{\rho K_{d} } \mathord{\left/ {\vphantom {{\rho K_{d} } n}} \right. \kern-0pt} n}} \right)\), where n is the porosity, ρ is the bulk density [M/L3], K d is the distribution coefficient [L3/M], D x is the dispersion/diffusion coefficient in the x direction, D z is the dispersion/diffusion coefficient in the z direction.

Initial condition

$$C_{\text{g}} \left( {0,{\text{t}}} \right) = C_{0}$$

Boundary condition

$$\begin{aligned} C_{g} \left( {0,t} \right) & = C_{u} \left( t \right) \times S_{0,gm} \\ D_{g} \frac{{\partial C_{g} }}{\partial z} & = nD_{y} \frac{\partial C}{\partial z} \\ \end{aligned}$$
(3)

Variational principle is applied to transform governing differential equations of geomembrane and soil into EFGM formulation as follows.

Element Free Galerkin Method

EFGM uses only set of nodes to model the boundary and generate discrete equations. It employs moving least squares (MLS) approximants formulated [12] to approximate the function C(x) with C h(x) in which C(x) is the contaminant concentration at x, where x is a position coordinate. EFGM do not satisfy the Kronecker delta criterion and hence the Lagrangian multiplier technique [13] is used to enforce the Dirichlet boundary condition.

Moving Least Squares Approximations

According to the moving least squares proposed by Lancaster and Salkauskas [12], the approximation C h(x) of C(x) is:

$$C(x) \cong C^{h} (x) = \sum\limits_{i = 1}^{m} {p_{i} (x)a_{i} (x)} = P^{T} (x)a(x) \, \quad \forall x \in \varOmega$$
(4)

In which,

$$P^{T} = \left[ {1xy} \right]{\text{ and}}\;a^{T} \left( x \right) = \, \left[ {a_{0} \left( x \right),a_{1} \left( x \right),a_{2} \left( x \right) \ldots .a_{m} \left( x \right)} \right]$$
(5)

Function p(x) is a monomial basis function and a(x) is a vector of undetermined coefficients, whose values can vary according to the position of x in Ω and m is the order of the basis.

To determine a(x), the discrete L 2 norm given J has to be minimized with respect to a(x).

$$J = \sum\limits_{I = 1}^{n} {w(x - x_{I} )\left[ {C_{L}^{h} (x_{I} ,x) - C_{I} } \right]^{2} } \, = \sum\limits_{I = 1}^{n} {w(x - x_{I} )\left[ {P^{T} (x_{I} )a(x) - C_{I} } \right]^{2} }$$
(6)

where n is the number of nodes in neighbourhood of x for which weight function w(x − x I ) is non-zero and C I refers to nodal parameter of C at x = x I .

The minimum of J in Eq. (4) with respect to a(x) leads to the following set of linear equations

$$\left[ {A\left( x \right)} \right]\;\left\{ {a\left( x \right)} \right\} = \left[ {B\left( x \right)} \right]\;\left\{ C \right\}$$
(7)

In which,

$$\begin{aligned} A & = \sum\limits_{I = 1}^{n} {W_{I} P(x_{I} )P^{T} (x)} = W_{1} \left[ {\begin{array}{*{20}c} 1 & {x_{1} } & {y_{1} } \\ {x_{1} } & {x_{1}^{2} } & {x_{1} y_{1} } \\ {y_{1} } & {x_{1} y_{1} } & {y_{1}^{2} } \\ \end{array} } \right] + \cdots + W_{n} \left[ {\begin{array}{*{20}c} 1 & {x_{n} } & {y_{n} } \\ {x_{n} } & {x_{n}^{2} } & {x_{n} y_{n} } \\ {y_{n} } & {x_{n} y_{n} } & {y_{n}^{2} } \\ \end{array} } \right] \\ B(x) & = W_{I} p(x_{I} )p^{T} (x_{I} ) = \left[ {\begin{array}{*{20}c} {W_{1} } & {W_{2} } & \cdots & {W_{n} } \\ {x_{1} W_{1} } & {x_{2} W_{2} } & \cdots & {x_{n} W_{n} } \\ {y_{1} W_{1} } & {y_{2} W_{2} } & \cdots & {y_{n} W_{n} } \\ \end{array} } \right] \\ & {\text{where}}\quad W_{I} = w(x - x_{I} ) \times w(y - y_{I} ) \\ \end{aligned}$$
(8)
$$C^{T} = \, \left\{ {C_{ 1} ,C_{ 2} , \ldots C_{n} } \right\}$$
(9)

Then vector of undetermined coefficients a(x) is obtained by inverse operation.

$$\left\{ {a\left( x \right)} \right\} = \left[ {A\left( x \right)} \right]^{ - 1} \left[ {B\left( x \right)} \right]\;\left\{ C \right\}$$
(10)

By substituting Eq. (7) in Eq. (4), the MLS approximants can be defined as

$$C^{h} (x) = \sum\limits_{I = 1}^{n} {\varphi_{I} (x)C_{I} = \varphi (x)C}$$
(11)

where, \(\varphi\)(x) is shape function defined as

$$\varphi^{T} (x) = \left[ P \right]^{T} \left[ A \right]^{ - 1} \left[ B \right] = \left[ \gamma \right]^{T} \left[ B \right]$$
(12)

In which, \(\left[ \gamma \right]^{T} = \left[ P \right]^{T} \left[ A \right]^{ - 1}\)

$$\begin{aligned} \left[ \gamma \right]^{T} \left[ A \right] = \left[ P \right]^{T} \hfill \\ \left[ P \right] = \left[ A \right]^{T} \left[ \gamma \right] = \left[ A \right]\;\left[ \gamma \right] \hfill \\ \end{aligned}$$

Derivative of shape function with respect to direction i (x or y) is obtained from following steps.

$$\begin{aligned} \varphi_{,i}^{T} = \gamma_{,i}^{T} B + \gamma^{T} B_{,i} \hfill \\A\gamma _{{,i}} = P_{{,i}} - A_{{,i}} \gamma\end{aligned}$$
(13)
$$\begin{aligned} B_{I,x} (x) = \frac{dw}{dx}(x - x_{I} )p(x_{I} ) \\ \end{aligned}$$
(14)
$$\begin{aligned} B_{x} & = \left[ {\begin{array}{*{20}c} {W_{1}^{x} } & {W_{2}^{x} } & \cdots & {W_{n}^{x} } \\ {x_{1} W_{1}^{x} } & {x_{2} W_{2}^{x} } & \cdots & {x_{n} W_{n}^{x} } \\ {y_{1} W_{1}^{x} } & {y_{2} W_{2}^{x} } & \cdots & {y_{n} W_{n}^{x} } \\ \end{array} } \right]\;\;{\text{where}}\quad W_{r}^{x} = \frac{{dW_{r} }}{dx} = \frac{{\partial w(x - x_{r} )}}{\partial x}w(y - y_{r} ) \\ A_{,x} & = \sum\limits_{I = 1}^{n} {\frac{{dW_{I} }}{dx}P(x_{I} )P^{T} (x)} = \frac{{dW_{1} }}{dx}\left[ {\begin{array}{*{20}c} 1 & {x_{1} } & {y_{1} } \\ {x_{1} } & {x_{1}^{2} } & {x_{1} y_{1} } \\ {y_{1} } & {x_{1} y_{1} } & {y_{1}^{2} } \\ \end{array} } \right] + \cdots + \frac{{dW_{n} }}{dx}\left[ {\begin{array}{*{20}c} 1 & {x_{n} } & {y_{n} } \\ {x_{n} } & {x_{n}^{2} } & {x_{n} y_{n} } \\ {y_{n} } & {x_{n} y_{n} } & {y_{n}^{2} } \\ \end{array} } \right] \\ \end{aligned}$$
(15)

EFGM shape functions do not satisfy the Kronecker delta criterion Φ I (x J ) ≠ δ IJ . Therefore they are not interpolants, and the name approximants is used. For imposing essential boundary conditions Lagrangian multipliers are used [9].

Weight Function

An important ingredient in EFG method is the weight function used in Eq. (6). The weight function is non-zero over a small neighbourhood of x I , called support domains. The weight function should be smooth and continuous. The choice of weight function affects the approximation results. Present study considers quartic spline function given by

$$\begin{aligned} w(x - x_{I} ) = \left\{ \begin{array}{ll} {1 - 6r_{x}^{2} + 8r_{x}^{3} - 3r_{x}^{4} } &{r_{x} \le 1} \\ 0 & {r_{x} > 1} \\ \end{array} \right\} \hfill \\ w(y - y_{I} ) = \left\{ \begin{array}{ll} {1 - 6r_{y}^{2} + 8r_{y}^{3} - 3r_{y}^{4} } &{r_{y} \le 1} \\ 0 & {r_{y} > 1} \\ \end{array} \right\} \hfill \\ \end{aligned}$$

In which,

$$r_{x} = \frac{{d_{ix} }}{{d_{mI} }}\quad r_{y} = \frac{{d_{iy} }}{{d_{mI} }}\quad {\text{and}}\quad d_{ix} = \left| {x - x_{I} } \right|\quad d_{iy} = \left| {y - y_{I} } \right|$$

where d mI is the size of domain of influence of Ith node and is computed as d mI  = d max C I, where, d max is a scaling parameter which is typically 2.0–4.0 for static analysis. The distance c I is determined by searching for enough neighbour nodes for A to be regular.

The derivatives for weight function are as follows

$$\begin{aligned} \frac{{dw(x - x_{I} )}}{dx} = \left\{ \begin{array}{ll} ( - 12r_{i} + 24r_{i}^{2} - 12r_{i}^{3} ){\text{sign}}(x - x_{I} )& r_{i} \le 1 \\ 0 &r_{i} > 1 \\ \end{array} \right\} \hfill \\ \frac{{dw(y - y_{I} )}}{dy} = \left\{ \begin{array}{ll} ( - 12r_{i} + 24r_{i}^{2} - 12r_{i}^{3} ){\text{sign}}(y - y_{I} ) & r_{i} \le 1 \\ 0 &r_{i} > 1 \\ \end{array} \right\} \hfill \\ \end{aligned}$$
(16)

Solute Transport Through Geomembrane

Governing differential equation for solute transport through geomembranes is written in the following form to apply variational approach.

$$\frac{{\partial C_{g} }}{\partial t} - D_{g} \frac{{\partial^{2} C_{g} }}{{\partial x^{2} }} = 0$$
(17)

Equation (17) is multiplied throughout by C T g and integrated over the domain of geomembrane as explained below.

$$\int {C_{g}^{T} \left[ {\frac{{\partial C_{g} }}{\partial t} - D_{g} \frac{{\partial^{2} C_{g} }}{{\partial x^{2} }}} \right]} = 0$$
(18)
$$\int {C_{g}^{T} \frac{{\partial C_{g} }}{\partial t}dA - \int {D_{g} C^{T} \frac{{\partial^{2} C_{g} }}{{\partial y^{2} }}dA} } = 0$$
(19)
$$C_{g} = \varphi C_{g} {\kern 1pt} ;\quad C_{g}^{T} = C_{g}^{T} \varphi^{T}$$
(20)
$$\int_{\varOmega } {C_{g}^{T} \varphi^{T} \varphi \dot{C}_{g} dA} - \int_{{\varGamma_{E} }} {D_{g} C_{g}^{T} \frac{{\partial C_{g} }}{\partial x}} n_{s} d\varGamma \int { + \int\limits_{\varOmega } {D_{g} C_{g}^{T} \frac{{\partial \varphi^{T} }}{\partial x}\frac{\partial \varphi }{\partial x}C_{g} dA} } = 0$$
(21)
$$M\dot{C}_{g} + KC_{g} = 0$$
(22)

Using implicit time marching scheme

$$\begin{aligned} \frac{{MC_{g}^{t + \Delta t} - C_{g}^{t} }}{\Delta t} + KC_{g}^{t + \Delta t} = 0 \hfill \\ K\Delta tC_{g}^{t + \Delta t} + MC_{g}^{t + \Delta t} = MC_{g}^{t} \hfill \\ \end{aligned}$$
(23)

Solute Transport Through Soil Liner

Governing differential equation for solute transport through soil liner is written in the following form to apply variational approach.

$$R\frac{{\partial C_{{}} }}{\partial t} - D_{z} \frac{{\partial^{2} C_{{}} }}{{\partial z^{2} }} - D_{x} \frac{{\partial^{2} C_{{}} }}{{\partial x^{2} }} + v\frac{{\partial C_{{}} }}{\partial z} = 0$$
(24)

Equation (24) is multiplied throughout by C T and integrated over the domain of geomembrane as explained below.

$$\int\limits_{\varOmega }^{{}} {C^{T} D_{x} \frac{{\partial^{2} C}}{{\partial x^{2} }}dx - \int\limits_{\varOmega }^{{}} {C^{T} \mathop v\limits^{{}} \frac{\partial C}{\partial x}dx - \int\limits_{\varOmega }^{{}} {C^{T} R\frac{\partial C}{\partial t}dx - \int\limits_{\varOmega }^{{}} {C^{T} \lambda Cdx} } } } = 0$$
(25)
$$C = \varphi C;\quad C^{T} = C_{e}^{T} \varphi^{T}$$
(26)

Applying Green’s theorem,

$$\begin{aligned} &\int\limits_{{\varGamma_{E} }} {D_{x} C^{T} \frac{\partial C}{\partial x}n_{s} } d\varGamma - D_{x} \int\limits_{\varOmega }^{{}} {C_{e}^{T} \frac{{\partial \varphi^{T} }}{\partial x}\frac{\partial \varphi }{\partial x}C_{e} d\varOmega + \int\limits_{{\varGamma_{E} }} {D_{z} C^{T} \frac{\partial C}{\partial z}n_{s} d\varGamma } - D_{z} \int\limits_{\varOmega }^{{}} {C_{e}^{T} \frac{{\partial \varphi^{T} }}{\partial z}\frac{\partial \varphi }{\partial z}C_{e} d\varOmega } } \hfill \\& \quad +\, v\int\limits_{\varOmega }^{{}} {C_{e}^{T} \varphi^{T} \frac{\partial \varphi }{\partial x}C_{e} d\varOmega } - R\int\limits_{\varOmega }^{{}} {C_{e}^{T} \varphi^{T} \varphi \dot{C}_{e} d\varOmega -\, } \lambda \int\limits_{\varOmega }^{{}} {C_{e}^{T} \varphi^{T} \varphi C_{e} d\varOmega } = 0 \hfill \\ \end{aligned}$$
(27)

In order to enforce the essential boundary conditions following changes are incorporated.

$$\begin{aligned} &\int\limits_{{\varGamma_{E} }} {D_{x} C^{T} \frac{\partial C}{\partial x}n_{s} } d\varGamma - D_{x} \int\limits_{\varOmega }^{{}} {C_{e}^{T} \frac{{\partial \varphi^{T} }}{\partial x}\frac{\partial \varphi }{\partial x}C_{e} d\varOmega \,+\, \int\limits_{{\varGamma_{E} }} {D_{z} C^{T} \frac{\partial C}{\partial z}n_{s} d\varGamma } - D_{z} \int\limits_{\varOmega }^{{}} {C_{e}^{T} \frac{{\partial \varphi^{T} }}{\partial z}\frac{\partial \varphi }{\partial z}C_{e} d\varOmega } } \hfill \,+\, v\int\limits_{\varOmega }^{{}} {C_{e}^{T} \varphi^{T} \frac{\partial \varphi }{\partial x}C_{e} d\varOmega } - R\int\limits_{\varOmega }^{{}} {C_{e}^{T} \varphi^{T} \varphi \dot{C}_{e} d\varOmega - \,} \lambda \int\limits_{\varOmega }^{{}} {C_{e}^{T} \varphi^{T} \varphi C_{e} d\varOmega } \hfill \quad - \int\limits_{{\varGamma_{S} }} {\varXi^{T} (C - C_{0} )d\varXi - \int\limits_{{\varGamma_{S} }} {\varXi^{T} Cd\varXi } } = 0 \hfill \\ \end{aligned}$$
(28)
$$\begin{aligned} &\left[ K \right]\left\{ C \right\} + \left[ M \right]\left\{ C \right\}_{,t}\, + \,\left[ G \right]\left\{ \varXi \right\} = \left\{ Q \right\} \hfill \\ &\left[ {G^{T} } \right]\left\{ C \right\} = \left\{ q \right\} \hfill \\ \end{aligned}$$
(29)
$$\begin{gathered} {\rm where} \hfill \\ K_{{IJ}} = \int_{\varOmega } {[\varphi _{{I,x}}^{T} D_{x} \varphi _{{J,x}} + } \varphi _{{I,y}}^{T} D_{y} \varphi _{{J,y}} + \varphi _{I}^{T} v\varphi _{{J,x}} ]d\varOmega ;\quad M_{{IJ}} = \int\limits_{\varOmega } {\left[ {\varphi _{I}^{T} R\varphi _{J}^{{}} } \right]d\varOmega } ;\, \hfill \\ G_{{IK}} = \int\limits_{{\varGamma _{S} }} {\varphi _{I} N_{K} d\varGamma } ;\quad Q_{I} = \int\limits_{{\varGamma _{E} }} {\varphi _{I} D_{g} d\varGamma } ;\quad q_{{IK}} = \int\limits_{{\varGamma _{S} }} {N_{K} C_{0} d\varGamma } \; \hfill \\ \end{gathered}$$
(30)

Implicit time marching scheme

$$\begin{aligned} \left[ {\begin{array}{*{20}c} K & G \\ {G^{T} } & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} c \\ \lambda \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} f \\ q \\ \end{array} } \right] \hfill \\ f = M\left\{ C \right\};\quad \left[ K \right] = \Delta t\left[ K \right] \hfill \\ \end{aligned}$$
(31)

Algorithm

Based on the above mathematical formulation following steps are considered in the algorithm.

  1. 1.

    Set up nodal points and background cells

  2. 2.

    Set parameters for material properties like dispersion, velocity, retardation factor for matrix and fracture

  3. 3.

    Set up initial concentration C 0

  4. 4.

    Calculate nodes on for geomembranes and set up integration points and Jacobian

  5. 5.

    Loop over integration points

    1. i)

      Calculate weights at each node for given integration point x G

    2. ii)

      Calculate shape functions and derivatives at points x G

    3. iii)

      Assemble Stiffness matrix [K] and Mass matrix [M]

  6. 6.

    Set up integration points and Jacobian for each cell for matrix

  7. 7.

    Loop over integration points

    1. iv)

      Calculate weights at each node for given integration point x G

    2. v)

      Calculate shape functions and derivatives at points x G

    3. vi)

      Assemble Stiffness matrix [K] and Mass matrix [M] and skip the background cells at the interface of geomembrane and soil

    4. vii)

      For applying essential boundary in 2D, determine nodes on essential boundary and set up gauss points for the same. Integrate Lagrange multipliers along essential boundary to form G matrix and q vector. Enforce essential boundary using Lagrange multiplier

  8. 8.

    Constructing new stiffness [K New] and mass matrix [M New] by adding the stiffness and mass matrix of fracture and matrix

  9. 9.

    Applying the implicit time marching scheme on stiffness matrix [K New] and mass matrix [M New]

  10. 10.

    Assemble Global Stiffness matrix [K G] by adding stiffness matrix [K] and [G] matrix and obtain inverse the global stiffness matrix [K G]−1

  11. 11.

    Construct q K vector

  12. 12.

    Loop over time

    1. a)

      Construct {f} vector as \(\left\{ f \right\} = \left( {\left[ M \right] - 0.5\Delta t\left[ K \right]} \right)\left\{ C \right\}_{i - 1}\)

    2. b)

      Compute new concentrations {C i } by multiplying [K G]−1inverse and {f} vector.

    3. c)

      Set {C i−1} = {C i } for next time step.

Model Verification

The developed EFGM model considering coupling of one dimensional modelling of geomembrane and two-dimensional soil is verified with the results from Guan et al. [3]. The domain is presented in Fig. 2. Geomembrane is placed on top of the soil layer which in most cases is clay soil because as the combination of clay and geomembrane will retard the contaminant migration. Guan et al. [3] considered geosynthetic clay liner having thickness 0.0138 m overlying clay layer and analysed the model using analytical solution for one dimensional case. The material properties for Benzene are reported in Table 1. Variation of normalized concentration in time domain (years) is presented in Fig. 3. Sensitivity analysis is carried out with nodes varying from 21 × 11, 21 × 21, 21 × 6, 11 × 21 and 11 × 11. It can be observed from Fig. 3 that the results by EFGM using 21 × 21 nodes are in fairly good agreement with the results obtained by Guan et al. [3]. Figure 4 presents the normalized concentration profiles with distance for various values of D max ranging from 1.25 to 2.0. It can be observed that, the results obtained by 1.25 are in good agreement with the results obtained by Guan et al. [3]. Hence the model can be employed further for parametric study.

Fig. 2
figure 2

Domain of geomembrane and soil

Full size image
Table 1 Material properties from Guan et al. [3]
Full size table
Fig. 3
figure 3

Comparison of EFGM with Guan et al. [3]

Full size image
Fig. 4
figure 4

Comparison of EFGM with Guan et al. [3]

Full size image

Parametric Study

Parametric study has been performed to observe the effect of geomembrane on normalized concentration and effect of geomembrane on height of clay layer. To observe the effect three cases have been considered. In the first case geomembrane is placed over two layers of sand, in second case geomembrane is placed over two layers of sand and clay and lastly the geomembrane is placed over clay layer.

Geomembrane Overlain on Two Sand Layers

A hypothetical model considering two layers of sand is analyzed to observe the effect of geomembrane on normalized concentration. The domain of the geomembrane on top of two layers is presented in Fig. 5. The geomembranes are incorporated in the liner at different depth of 0.0 and 2.5 m. The material properties employed in the analysis are presented in Table 2 [2, 14]. 21 × 21 number of nodes considered to represent the entire domain.

Fig. 5
figure 5

Domain of geomembrane over two layers

Full size image
Table 2 Material properties for geomembrane and sand layers
Full size table

The variations in normalized concentration along the longitudinal distance (after 17.6 days) are presented in Fig. 6. It can be observed that when geomembrane is introduced, transport of contaminant in the subsurface is retarded. The contaminant reduced at a longitudinal distance of 3 m is 81 and 88 % when the geomembrane is placed at 0.0 and 2.5 m from the origin. Normalized concentration at a distance of 10 m from the source with respect to time has been presented in Fig. 7. It is observed that the time taken to reach the maximum normalized concentration of 0.9 is 82 days for both cases of location of geomembrane, whereas for the case of without geomembrane corresponding time is 29 days. The reduction of contaminant in the presence of geomembrane as a liner is possible because the hydraulic conductivity of geomembranes is negligible and diffusion coefficient is very low.

Fig. 6
figure 6

Effect of geomembrane on two sand layers

Full size image
Fig. 7
figure 7

Variation in concentration with time for geomembrane on two sand layers

Full size image

Geomembrane Overlain on Sand and Clay Layers

A hypothetical model having two layers, first layer sand and second layer clay is considered. The domain of the model is similar to the figure presented in Fig. 5. In this segment the concentration profile for the geomembrane, provided at 0.0 and 2.5 m is observed. The material properties are the same as reported in Table 3. The variations in normalized concentration with vertical distance are presented in Fig. 8. It can be observed that when geomembrane is introduced, transport of contaminant in the subsurface is retarded. The contaminant reduced at a longitudinal distance of 3 m is 78 and 88 % when the geomembrane is placed at 0.0 m and 2.5 m from the origin. Effect of geomembrane is more pronounce in the second case (geomembrane at 2.5 m), where a sudden drop in concentration is noticed below geomembrane.

Table 3 Material properties for geomembrane, sand and clay layers
Full size table
Fig. 8
figure 8

Effect of geomembrane on sand and clay layer

Full size image

Normalized concentration at a distance of 10 m from the source with respect to time has been presented in Fig. 9. It is observed that the time taken to reach the maximum normalized concentration of 0.9 is 126 days for both cases of location of geomembrane, whereas for the case of without geomembrane corresponding time is 91 days.

Fig. 9
figure 9

Variation in concentration with time for geomembrane on sand and clay layers

Full size image

Geomembrane Overlain on Clay Liner

In this section, geomembrane is placed over clay liner and the domain is similar to the domain shown in Fig. 10. The material properties employed for the analysis are reported in Table 4 [15]. The thickness of clay liner is adopted as 1 m and that of geomembrane is 0.015 m. The variations of concentration with longitudinal distance are presented in Fig. 11. It can be observed that, introduction of geomembrane over a clay liner improves the retardation of contaminant transport. The reduction of contaminant is approximately 89 % at a distance of 20 cm and it reduces further.

Fig. 10
figure 10

Domain of geomembrane over clay liner

Full size image
Table 4 Material properties for geomembrane overlying clay
Full size table
Fig. 11
figure 11

Effect of geomembrane on contaminant transport in clay

Full size image

Effect of Thickness of Clay Liner

As a design practice, minimum 45 cm thick clay liner is recommended to minimize infiltration through liner overlaid by geomembrane. So effect of thickness of the clay liner is examined by changing the thickness up to 2 m and comparing the reduction in contaminant transport. The material properties are the same as reported in Table 4 except the thickness of the clay liner and the total time. The thickness of the clay liner is varied as 0.5, 1, 1.5 and 2 m. Total time considered is 200 years. The variation of normalized concentration with normalized distance for the last time step (200 years) is presented in Fig. 12. It is observed that when the thickness of clay liner is increased from 0.5 m to 1 m, the concentration is reduced by 48.8 %, underlining significance of clay liner thickness. A sudden drop is observed in the concentration from top surface of geomembrane to bottom surface (0.025 m) corresponding to thickness of geomembrane, and dispersion in the matrix take place at a slow rate. With increase in the thickness, diffusion decreases as the plume moves from higher concentration level to lower concentration level.

Fig. 12
figure 12

Effect of thickness of clay liner on concentration

Full size image

Effect of thickness of clay layer on normalized concentration in time domain is described in Fig. 13. The values of concentration are presented for the last node. Normalized concentration reached at the last time step is 0.955, 0.489, 0.175 and 0.048 for thicknesses 0.5, 1, 1.5 and 2 m, respectively. It is observed that with increase in the thickness from 0.5 to 1 m results in 48.8, % reduction in concentration. Further increase in thickness to 1.5 and 2 m accounted for 81.7 and 94.9 % reduction in concentration, respectively. For 1 m thick clay liner, normalized concentrations are 0.038 and 0.196 after 50 and 100 years, respectively. Similarly, for 1.5 m thick clay liner, normalized concentrations are 0.00136, 0.0309 and 0.096 after 50, 100 and 150 years, respectively. For 2 m thick clay liner values are reduced further. It is to be noted that number of years required to achieve 10 % concentration are 14, 72, and 153 for 0.5, 1 and 1.5 m thickness clay liner, respectively. It can be concluded that 1 or 1.5 m thick clay liner are effective in preventing contaminant migration and depending upon time span proper thickness has to be selected. Similar results were reported by Foose et al. [16] and Chai and Miura [4]. The introduction of geomembrane as a liner above the clay liner, it helps in reduction of contaminant and reduction of height of clay liner making it a cost effective design.

Fig. 13
figure 13

Effect of thickness of clay liner on concentration in time domain

Full size image

Conclusions

In the present study, 1D model for contaminant transport through geomembrane considering diffusion is coupled with 2D model for contaminant transport through soil layer using EFGM. Numerical model can successfully predict contaminant transport through composite landfill liner with a more rational approach accounting for different layer properties. Effects of geomembrane layer and height of clay liner were critically observed in the parametric study. The location of geomembrane in the soil media has an effect on the contaminant transport. Normalized concentration is reduced after the use of geomembrane with soil. The thickness of clay liner has considerable bearing in the design of landfill liners. With increase in the thickness of clay liner, drastic reduction in the concentration is observed, underlining significance of clay liner thickness. It is also evident from the fact that time required to achieve 10 % concentration increases with increase in the thickness of clay liner.