Abstract
We provide a proof of Jacobson’s theorem on derivations of primitive rings with nonzero socle. Both Jacobson’s theorem and its formulation (in terms of the so-called differential operators on left vector spaces over a division ring) underlie our paper. We apply Jacobson’s theorem to describe derivations of standard operator rings on real, complex, or quaternionic left normed spaces. Indeed, when the space is infinite-dimensional, every derivation of such a standard operator ring is of the form \(A\rightarrow AB-BA\) for some continuous linear operator B on the space. Our quaternionic approach allows us to generalize Rickart’s theorem on representation of primitive complete normed associative complex algebras with nonzero socle to the case of primitive real or complex associative normed Q-algebras with nonzero socle. We prove that additive derivations of the Jordan algebra of a continuous nondegenerate symmetric bilinear form on any infinite-dimensional real or complex Banach space are in a one-to-one natural correspondence with those continuous linear operators on the space which are skew-adjoint relative to the form. Finally we prove that additive derivations of a real or complex (possibly non-associative) \(H^*\)-algebra with no nonzero finite-dimensional direct summand are linear and continuous.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Throughout this paper \(\Delta \) will denote a division ring and, given a left or right vector space X over \(\Delta \), we denote by L(X) the ring of all \(\Delta \)-linear operators on X.
Let X be a left vector space over \(\Delta \). Following [39, Definition IV.14.1], we say that a mapping \(T:X\rightarrow X\) is a differential operator on X if it is additive and there exists a ring derivation d of \(\Delta \) such that
It follows from (1.1) that every differential operator on X has a unique associated derivation. Examples of differential operators on X are all linear operators on X and all operators in \(\Delta I_X\), where \(\Delta I_X\) denotes the set of mappings of the form \(x\rightarrow \lambda x\) where \(\lambda \) runs over \(\Delta \). Actually the set \(\textrm{Diff}\hspace{0.55542pt}(X)\) of all differential operators on X is a Lie subring of the ring of all additive operators on X, and contains both L(X) and \(\Delta I_X\) as ideals. As a consequence, we are provided with the following.
Fact 1.1
Let X be a left vector space over \(\Delta \), and let T be a differential operator on X. Then \([A,T]:=AT-TA\) lies in L(X) whenever A does, and the mapping \(A\rightarrow [A,T]\) is a ring derivation of L(X).
Differential operators on right vector spaces over \(\Delta \) are defined analogously. Indeed, given a right vector space Y over \(\Delta \), a mapping \(T:Y\rightarrow Y\) is said to be a differential operator on Y if it is additive and there exists a ring derivation d of \(\Delta \) such that
We recall that a pairing over \(\Delta \) is a triple \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) where X is a left vector space over \(\Delta \), Y is a right vector space over \(\Delta \) and \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) is a bilinear form on \(X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\) which is non-degenerate; i.e. the conditions \(x\in X\) and \(\langle x,Y\rangle =0\) imply \(x=0\), and the conditions \(y\in Y\) and \(\langle X,y\rangle =0\) imply \(y=0\).
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \). Following [39, p. 87], we say that a differential operator T on X with associated derivation d has an adjoint in Y relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) if there exists a mapping \(T^\#:Y\rightarrow Y\) such that
It follows from (1.2) that the mapping \(T^\#\) is unique. If T is a differential operator on X with associated derivation d, and if T has an adjoint \(T^\#\), then it is immediate to verify that \(T^\#\) is a differential operator on Y with associated derivation \(-d\). As a consequence, if A belongs to \(L(X)\subseteq \textrm{Diff}\hspace{0.55542pt}(X)\), and if A has an adjoint \(A^\# \) relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \), then \(A^\# \) belongs to L(Y). The set of those linear operators on X which have adjoints relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) is a subring of L(X), which is denoted by \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). The subset of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) consisting of those operators in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) which have finite-dimensional range is an ideal of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), which is denoted by \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). By the structure theorem for primitive rings with nonzero socle [39, Section IV.9], up to isomorphisms, the primitive rings with nonzero socle are precisely the subrings of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) for some choice of the division ring \(\Delta \) and some choice of the pairing \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) over \(\Delta \). For such a ring  , the socle of
, the socle of  is \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\).
is \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\).
The pioneering and fundamental paper on pairings and their properties is that of Mackey [47]. Sometimes the sets of the form \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) for some pairing \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) over \(\Delta \) (regarded as algebras over the centre of \(\Delta \)) are called Mackey algebras. See for example the paper of Penkov and Serganova [51]. Recently derivations of some Mackey algebras and related Lie algebras were considered in the paper of Bezushchak [8].
Considering Fact 1.1, it is easily realized that the set \(\textrm{Diff} \hspace{0.55542pt}(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) of all differential operators on X having an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) is a (Lie) subring of the Lie ring \(\textrm{Diff}\hspace{0.55542pt}(X)\) containing both \(L (X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) and \(\Delta I_X\) as ideals. As a consequence, we have the following.
Fact 1.2
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \), and let T be a differential operator on X having an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \). Then [A, T] lies in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) whenever A does, and the mapping \(A\rightarrow [A,T]\) is a ring derivation of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\).
Conversely, according to [39, Proposition IV.14.1 and Theorem IV.14.3], we are provided with the following.
Theorem 1.3
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \),  be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and
be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and

be a derivation. Then there exists a differential operator T on X which has an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) and satisfies \(D(A)=[A,T]\) for every  .
.
Here, given a subring  of a ring
of a ring  , by a derivation from
, by a derivation from  to
to  we mean an additive mapping
we mean an additive mapping  satisfying
satisfying

Theorem 1.3 above is due to Jacobson [39]. As far as we know, Theorem 1.3 has been forgotten, and no application of it has appeared in the literature. In the case that \(\Delta \) is equal to \({\mathbb {R}}\) (the field of real numbers) or \({\mathbb {C}}\) (the field of complex numbers), and that X is a Banach space over \(\Delta \) naturally paired with its topological dual, Theorem 1.3 has been rediscovered by Šemrl [62, 63] (see also [57, Theorem 1.3]).
In Sect. 2, we provide the reader with a complete proof of Theorem 1.3, and derive some first applications of it.
In Sect. 3, we suppose that \(\frac{1}{2}\in \Delta \), and apply Theorem 1.3 to prove that this theorem remains true if  is merely assumed to be a Jordan subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and consequently
is merely assumed to be a Jordan subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and consequently  is assumed to be a derivation in the Jordan sense (Theorem 3.5). Precise definitions of a Jordan subring of a ring, and of a Jordan derivation from such a Jordan subring to the whole ring, will be given in this section.
is assumed to be a derivation in the Jordan sense (Theorem 3.5). Precise definitions of a Jordan subring of a ring, and of a Jordan derivation from such a Jordan subring to the whole ring, will be given in this section.
Throughout the remaining part of this paper \({\mathbb {H}}\) will denote the division real algebra of Hamilton’s quaternions, and almost always \({\mathbb {F}}\) will stand for either \({\mathbb {R}},{\mathbb {C}}\) or \({\mathbb {H}}\).
Let X be a left normed space over \({\mathbb {F}}\). We denote by  the subring of L(X) consisting of all continuous \({\mathbb {F}}\)-linear operators on X, and by
the subring of L(X) consisting of all continuous \({\mathbb {F}}\)-linear operators on X, and by  the ideal of
the ideal of  consisting of those operators in
consisting of those operators in  having finite-dimensional range. Standard operator rings (respectively, standard operator Jordan rings) on X are defined as those subrings (respectively, Jordan subrings) of
having finite-dimensional range. Standard operator rings (respectively, standard operator Jordan rings) on X are defined as those subrings (respectively, Jordan subrings) of  which contain
which contain  . We note that
. We note that  is a closed subalgebra of the real normed algebra
is a closed subalgebra of the real normed algebra  , where \(X_{\mathbb {R}}\) denotes the real normed space obtained from X by restricting the scalars. Therefore
, where \(X_{\mathbb {R}}\) denotes the real normed space obtained from X by restricting the scalars. Therefore  becomes naturally a real normed algebra when it is endowed with the operator norm.
becomes naturally a real normed algebra when it is endowed with the operator norm.
Now, to comment on Sect. 4, let us consider the following.
Theorem 1.4
Let X be an infinite-dimensional left normed space over \({\mathbb {F}}\), let  be a standard operator Jordan ring on X, and let
be a standard operator Jordan ring on X, and let  be a Jordan derivation. Then there exists
be a Jordan derivation. Then there exists  such that \(D(A)=[A,B]\) for every
such that \(D(A)=[A,B]\) for every  . As a consequence, D is continuous.
. As a consequence, D is continuous.
Throughout the remaining part of this paper \({\mathbb {K}}\) will stand for either \({\mathbb {R}}\) or \({\mathbb {C}}\). All forerunners of Theorem 1.4, known in the literature, deal only with the case that \({\mathbb {F}}= {\mathbb {K}}\). But, for any normed space X over \({\mathbb {K}}\),  is an algebra over \({\mathbb {K}}\) containing
is an algebra over \({\mathbb {K}}\) containing  as an algebra ideal, and hence we can think about the so-called standard operator algebras (respectively, standard operator Jordan algebras) on X, which are defined as those subalgebras (respectively, Jordan subalgebras) of
as an algebra ideal, and hence we can think about the so-called standard operator algebras (respectively, standard operator Jordan algebras) on X, which are defined as those subalgebras (respectively, Jordan subalgebras) of  which contain
which contain  . Now, ordering chronologically, Theorem 1.4 is known in the following particular cases:
. Now, ordering chronologically, Theorem 1.4 is known in the following particular cases:
-
(i)
(Chernoff [20]) \({\mathbb {F}}={\mathbb {K}}\),
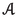 is a standard operator algebra on X, and D is a linear derivation. Clearly, in this case, the conclusion in the theorem remains true if the restriction that X is infinite-dimensional is removed.
is a standard operator algebra on X, and D is a linear derivation. Clearly, in this case, the conclusion in the theorem remains true if the restriction that X is infinite-dimensional is removed. -
(ii)
(Šemrl [62]) \({\mathbb {F}}={\mathbb {K}}\), X is a Hilbert space over \({\mathbb {K}}\),
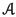 is a standard operator algebra on X, and D is a ring derivation. Moreover, in this case, the conclusion in the theorem does not remain true if the restriction that X is infinite-dimensional is removed.
is a standard operator algebra on X, and D is a ring derivation. Moreover, in this case, the conclusion in the theorem does not remain true if the restriction that X is infinite-dimensional is removed. -
(iii)
(Šemrl [63]) \({\mathbb {F}}={\mathbb {K}}\), X is complete,
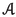 is a standard operator algebra on X, and D is a ring derivation.
is a standard operator algebra on X, and D is a ring derivation. -
(iv)
(Han [35]) \({\mathbb {F}}={\mathbb {K}}\),
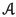 is a standard operator algebra on X, and D is a ring derivation.
is a standard operator algebra on X, and D is a ring derivation. -
(v)
(Vukman [68], see also [44]) \({\mathbb {F}}={\mathbb {K}}\),
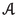 is a standard operator algebra on X, and D is linear. Clearly, in this case, the conclusion in the theorem remains true if the restriction that X is infinite-dimensional is removed. (In these papers, completeness of X is assumed but is never applied in the proofs.)
is a standard operator algebra on X, and D is linear. Clearly, in this case, the conclusion in the theorem remains true if the restriction that X is infinite-dimensional is removed. (In these papers, completeness of X is assumed but is never applied in the proofs.) -
(vi)
(The authors [57]) \({\mathbb {F}}={\mathbb {K}}\) and X is complete.
It is worth mentioning that, roughly speaking, the proof of forerunner (v) (respectively, (vi)) consists of a reduction to forerunner (i) (respectively, (iii)). Most part of Sect. 4 is devoted to prove Theorem 1.4. Our proof does not consist of a reduction to any of the forerunners listed above, but relies on an appropriate adaptation of the argument in the proof of Proposition 3.3 in the Boudi–Marhnine–Zarhouti paper [9] (see Theorem 4.10). By a normed pairing over \({\mathbb {F}}\) we mean any pairing \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), where X is a left normed space over \({\mathbb {F}}\), Y is a right normed space over \({\mathbb {F}}\), and the form \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle :X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\rightarrow {\mathbb {F}}\) is continuous. Now Theorem 4.10 just quoted asserts that, if \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is a normed pairing over \({\mathbb {F}}\), with X infinite-dimensional and complete, then  , and hence differential operators on X having an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) are continuous, and moreover they are linear whenever \({\mathbb {F}}={\mathbb {K}}\). As in the case of forerunner (ii) of Theorem 1.4, we realize that, also for \({\mathbb {F}}={\mathbb {H}}\), the conclusion in Theorem 1.4 does not remain true if the restriction that X is infinite-dimensional is removed (Remark 4.14).
, and hence differential operators on X having an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) are continuous, and moreover they are linear whenever \({\mathbb {F}}={\mathbb {K}}\). As in the case of forerunner (ii) of Theorem 1.4, we realize that, also for \({\mathbb {F}}={\mathbb {H}}\), the conclusion in Theorem 1.4 does not remain true if the restriction that X is infinite-dimensional is removed (Remark 4.14).
In Sect. 5, we generalize Rickart’s theorem on representation of primitive complete normed associative complex algebras with nonzero socle [52, Theorem 2.4.12] to the case of primitive real or complex associative normed Q-algebras with nonzero socle (Theorem 5.3). For the formulation and proof of this result, our quaternionic approach to normed pairings becomes crucial.
In Sect. 6, we describe additive derivations of Jordan algebras of a nondegenerate symmetric bilinear form on a vector space over any field of characteristic different from 2, by means of differential operators on the vector parts of such algebras (Proposition 6.2). With the help of Proposition 6.2 and Theorem 4.10, we prove that additive derivations of the Jordan algebra of a continuous nondegenerate symmetric bilinear form on any infinite-dimensional real or complex Banach space are in a one-to-one natural correspondence with those continuous linear operators on the space which are skew-adjoint relative to the form (Theorem 6.3). Moreover, neither the restriction that X is infinite-dimensional nor the one that X is complete can be removed (Remark 6.5 and Example 6.7). In particular, Theorem 6.3 provides us with a description of additive derivations of complete smooth normed commutative real algebras, JB-spin factors, quadratic Jordan \(H^*\)-algebras, and quadratic \(JB^*\)-algebras, whenever they are infinite-dimensional.
In the concluding section (Sect. 7) we prove that derivations of a (possibly non-associative) algebra  over an arbitrary field are differential operators on (the vector space underlying)
over an arbitrary field are differential operators on (the vector space underlying)  as soon as
as soon as  has zero annihilator and the centroid of
has zero annihilator and the centroid of  reduces to the scalar multiples of the identity operator on
reduces to the scalar multiples of the identity operator on  (Proposition 7.4). Considering this crucial result, we apply Theorem 4.10 once more (see Lemma 7.18), and adapt the argument in the proof of the main result in Villena’s paper [67] (see Proposition 7.19), to show that additive derivations of any real or complex (possibly non-associative) \(H^*\)-algebra with no nonzero finite-dimensional direct summand are linear and continuous (Corollary 7.24). Actually a better result, in the spirit of Theorem 4.1 in the Johnson–Sinclair paper [41], is obtained (see Theorem 7.22).
(Proposition 7.4). Considering this crucial result, we apply Theorem 4.10 once more (see Lemma 7.18), and adapt the argument in the proof of the main result in Villena’s paper [67] (see Proposition 7.19), to show that additive derivations of any real or complex (possibly non-associative) \(H^*\)-algebra with no nonzero finite-dimensional direct summand are linear and continuous (Corollary 7.24). Actually a better result, in the spirit of Theorem 4.1 in the Johnson–Sinclair paper [41], is obtained (see Theorem 7.22).
2 A proof of Jacobson’s theorem
§ 2.1 Given a pairing \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) over \(\Delta \) and \((x,y)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\), we denote by \(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y\) and \(y \hspace{1.111pt}{\otimes }\hspace{1.111pt}x\) the rank-one linear operators on X and Y defined by
for all \(v\in X\) and \(w\in Y\). The following properties are of direct verification:
-
(i)
\((x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y)^\#\!=y\hspace{1.111pt}{\otimes }\hspace{1.111pt}x\).
-
(ii)
\(A(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y)=Ax\hspace{1.111pt}{\otimes }\hspace{1.111pt}y\) for every \(A\in L(X)\).
-
(iii)
\((x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y)A=x\hspace{1.111pt}{\otimes }\hspace{1.111pt}A^\# y\) for every \(A\in L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\).
Moreover, we have the following description:
Let  be a ring, and let X be a faithful irreducible left
be a ring, and let X be a faithful irreducible left  -module. Let E(X) denote the ring of all additive mappings on X. Then the set
-module. Let E(X) denote the ring of all additive mappings on X. Then the set

is a division ring, which is called the associated division ring of  relative to X. It is clear that, if \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is a pairing over \(\Delta \), and if
relative to X. It is clear that, if \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is a pairing over \(\Delta \), and if  is a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), then X is a faithful irreducible left
is a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), then X is a faithful irreducible left  -module. Here, by the sake of completeness, we include a proof of the well-known fact that, in this case, \(\Delta I_X\) is the associated division ring of
-module. Here, by the sake of completeness, we include a proof of the well-known fact that, in this case, \(\Delta I_X\) is the associated division ring of  relative to X [39, Theorem II.4.1].
relative to X [39, Theorem II.4.1].
Lemma 2.2
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \) and  be a subring of \( L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{ \cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then the associated division ring of
be a subring of \( L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{ \cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then the associated division ring of  relative to X is equal to \(\Delta I_X\).
relative to X is equal to \(\Delta I_X\).
Proof
Since  , for any \(\lambda \in \Delta \), we have that \([A,\lambda I_X]=0\) for every
, for any \(\lambda \in \Delta \), we have that \([A,\lambda I_X]=0\) for every  . In order to prove the converse inclusion, let us fix \((x_0,y_0)\in X \hspace{1.111pt}{\times }\hspace{1.111pt}Y\) such that \(\langle x_0,y_0\rangle =1\). If \(B\in E(X)\) satisfies the condition \([A,B]=0\) for every
. In order to prove the converse inclusion, let us fix \((x_0,y_0)\in X \hspace{1.111pt}{\times }\hspace{1.111pt}Y\) such that \(\langle x_0,y_0\rangle =1\). If \(B\in E(X)\) satisfies the condition \([A,B]=0\) for every  , then for each \(x\in X\) we have
, then for each \(x\in X\) we have
and hence \(B= \langle B(x_0),y_0\rangle I_X \in \Delta I_X\).\(\square \)
We reformulate the above lemma as follows.
Corollary 2.3
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \), let  be as in Lemma 2.2, and let S be an additive operator on X such that \([A,S]=0\) for every
be as in Lemma 2.2, and let S be an additive operator on X such that \([A,S]=0\) for every  . Then \(S\in \Delta I_X\).
. Then \(S\in \Delta I_X\).
Now, following some ideas in Šemrl’s papers [62, 63], our proof of Theorem 1.3 goes as follows.
Proof of Theorem 1.3
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \), let  be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let
be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let

be a derivation. Fix \((x_0,y_0)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\) such that \(\langle x_0,y_0\rangle =1\), and consider the mapping \(T:X\rightarrow X\) given by
It is clear that T is additive. On the other hand, by \(\S \) 2.1 (ii), for each  and \(x\in X\) we have
and \(x\in X\) we have
Therefore, considering the definition of T, it is enough to valuate at \(x_0\) to realize that \(D(A)x=ATx-TAx\). Therefore \(D(A)=[A,T]\) (hence \([A,T]\in L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\)) for all  .
.
Let A and B be in  and \(\Delta I_X\), respectively. Since both A and [A, T] lie in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and \([L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle ),B]=0\), we obtain
and \(\Delta I_X\), respectively. Since both A and [A, T] lie in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and \([L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle ),B]=0\), we obtain
Therefore, since A is arbitrary in  , it follows from Lemma 2.2 that [B, T] lies in \(\Delta I_X\). Thus \([\Delta I_X,T] \subseteq \Delta I_X\) because B is arbitrary in \(\Delta I_X\).
, it follows from Lemma 2.2 that [B, T] lies in \(\Delta I_X\). Thus \([\Delta I_X,T] \subseteq \Delta I_X\) because B is arbitrary in \(\Delta I_X\).
Now consider the mapping \(d:\Delta \rightarrow \Delta \) determined by the condition
for every \(\lambda \in \Delta \). Then, clearly, d is a ring derivation of \(\Delta \). Moreover, for each \(\lambda \in \Delta \) and \(x\in X\) we have
It follows that T is a differential operator on X.
Finally, note that for each \(y\in Y\) we have
and hence we may consider the mapping \(y\rightarrow Sy:=[x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y, T]^\# y_0\) from Y to Y. Note also that \(E_0=x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y_0\) is an idempotent satisfying \(E_0x_0=x_0\), and hence
Therefore
hence \(\langle D(x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y_0)\hspace{1.111pt}x_0,y_0\rangle =0\), and so \(\langle Tx_0,y_0\rangle =0\). Now, for any \((x,y)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\), we see that
Hence S is an adjoint of T.\(\square \)
Remark 2.4
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \), let  be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), let
be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), let  be a derivation, and let T be the differential operator on X given by Theorem 1.3. It follows from Corollary 2.3 that, ‘essentially’, T is uniquely determined by D. Moreover, regarding the proof of Theorem 1.3 we have given, we realize that, for each \((x_0,y_0)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\) with \(\langle x_0,y_0\rangle =1\), the mapping \(x\rightarrow - D(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y_0)\hspace{1.111pt}x_0\) is a representative of T, and that (for such a choice of T) \([x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y, T]\) lies in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) for every \(y\in Y\), allowing to determine \(T^\# \) as the mapping \(y\rightarrow [x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y, T]^\# y_0\).
be a derivation, and let T be the differential operator on X given by Theorem 1.3. It follows from Corollary 2.3 that, ‘essentially’, T is uniquely determined by D. Moreover, regarding the proof of Theorem 1.3 we have given, we realize that, for each \((x_0,y_0)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\) with \(\langle x_0,y_0\rangle =1\), the mapping \(x\rightarrow - D(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y_0)\hspace{1.111pt}x_0\) is a representative of T, and that (for such a choice of T) \([x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y, T]\) lies in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) for every \(y\in Y\), allowing to determine \(T^\# \) as the mapping \(y\rightarrow [x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y, T]^\# y_0\).
Let X be a left vector space over \(\Delta \). Following [39, Definition IV.4.1], the (algebraic) dual \(X^*\) of X is defined as the set of all linear mappings from X to \(\Delta \). \(X^*\) has a natural structure of right vector space over \(\Delta \) for the operations
for all \(x\in X\), \(f,g\in X^*\), and \(\lambda \in \Delta \). It is clear that, by defining

 becomes a pairing over \(\Delta \). Let A be in L(X). Then for \(f\in X^*\) we have \(fA \in X^*\) and
becomes a pairing over \(\Delta \). Let A be in L(X). Then for \(f\in X^*\) we have \(fA \in X^*\) and
It follows that the mapping \(f\rightarrow fA\) from \(X^*\) to \(X^*\) is an adjoint of A relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \). Hence  . Therefore it is enough to apply Theorem 1.3 to obtain the converse of Fact 1.1 given by the first conclusion in Corollary 2.5 immediately below. The second conclusion in that corollary is straightforwardly checked by applying Corollary 2.3 to the left vector space X over \(\Delta \), naturally paired with its algebraic dual. For any ring
. Therefore it is enough to apply Theorem 1.3 to obtain the converse of Fact 1.1 given by the first conclusion in Corollary 2.5 immediately below. The second conclusion in that corollary is straightforwardly checked by applying Corollary 2.3 to the left vector space X over \(\Delta \), naturally paired with its algebraic dual. For any ring  , we denote by
, we denote by  the Lie ring of all derivations of
the Lie ring of all derivations of  .
.
Corollary 2.5
Let X be a left vector space over \(\Delta \). Then every ring derivation of L(X) is of the form \(A\rightarrow [A,T]\) for some differential operator T on X. More precisely: for each differential operator T on X, the mapping \(D_T:A\rightarrow [A,T]\) becomes a ring derivation of L(X), and the mapping \(T\rightarrow D_T\) is a surjective Lie anti-homomorphism from \(\textrm{Diff}\hspace{1.111pt}(X)\) to \(\textrm{Der}\hspace{0.55542pt}(L(X))\) with kernel \(\Delta I_X\).
Arguing similarly, with Fact 1.2 instead of Fact 1.1, we obtain the following.
Corollary 2.6
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \). Then, for each \(T\in \textrm{Diff}\hspace{0.55542pt}(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), the mapping \(D_T:A\rightarrow [A,T]\) becomes a ring derivation of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Moreover, the mapping \(T\rightarrow D_T\) is a surjective Lie anti-homomorphism from \(\textrm{Diff}\hspace{0.55542pt}(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) to \(\textrm{Der}\hspace{0.55542pt}(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle ))\) with kernel \(\Delta I_X\).
Lemma 2.7
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \), let  be a subring of L(X) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let
be a subring of L(X) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let  be a derivation vanishing on \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then \(D=0\).
be a derivation vanishing on \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then \(D=0\).
Proof
Let A be in  , and let (x, y) be in \(X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\). Then, by \(\S \) 2.1 (ii), \(A(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y)\) lies in \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Therefore, since D vanishes on \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\),
, and let (x, y) be in \(X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\). Then, by \(\S \) 2.1 (ii), \(A(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y)\) lies in \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Therefore, since D vanishes on \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\),
Since (x, y) is arbitrary in \(X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\), it is enough to apply \(\S \) 2.1 (ii) again (with D(A) instead of A) to conclude that \(D(A)=0\). Hence \(D=0\) because of the arbitrariness of  .\(\square \)
.\(\square \)
Proposition 2.8
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \),  be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and
be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and

be a derivation. Then there exists a unique derivation \({\widehat{D}}:L(X)\rightarrow L(X)\) extending D. Moreover
Proof
By Theorem 1.3, there is a differential operator T on X having an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) and satisfying \(D(A)=[A,T]\) for every  . Since T is a differential operator on X, it follows from Fact 1.1 that the mapping \({\widehat{D}}:B\rightarrow [B,T]\) is a derivation of L(X) extending D. But, since T has an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \), it follows from Fact 1.2 that the inclusion (2.1) holds. Finally, if \({\overline{D}}\) is any derivation of L(X) extending D, then \({\widehat{D}}-{\overline{D}}\) is a derivation of L(X) vanishing on \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), hence \({\widehat{D}}={\overline{D}}\) thanks to Lemma 2.7.\(\square \)
. Since T is a differential operator on X, it follows from Fact 1.1 that the mapping \({\widehat{D}}:B\rightarrow [B,T]\) is a derivation of L(X) extending D. But, since T has an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \), it follows from Fact 1.2 that the inclusion (2.1) holds. Finally, if \({\overline{D}}\) is any derivation of L(X) extending D, then \({\widehat{D}}-{\overline{D}}\) is a derivation of L(X) vanishing on \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), hence \({\widehat{D}}={\overline{D}}\) thanks to Lemma 2.7.\(\square \)
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \), and let  be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then the symmetric ring of quotients of
be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then the symmetric ring of quotients of  is \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), the maximal left ring of quotients of
is \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), the maximal left ring of quotients of  is L(X), and the extended centroid of
is L(X), and the extended centroid of  is isomorphic to the center of \(\Delta \) [5, Theorems 4.3.7 and 4.3.8]. Therefore Proposition 2.8 above also follows easily from the left version of [5, Proposition 2.5.1].
is isomorphic to the center of \(\Delta \) [5, Theorems 4.3.7 and 4.3.8]. Therefore Proposition 2.8 above also follows easily from the left version of [5, Proposition 2.5.1].
3 Considering Jordan derivations
By a non-associative ring we mean an additive group  endowed with a mapping \((A,B)\rightarrow AB\) from
endowed with a mapping \((A,B)\rightarrow AB\) from  which is additive in each of its variables. We recall that, given an element A in a non-associative ring
which is additive in each of its variables. We recall that, given an element A in a non-associative ring  , the operator \(U_A\) on
, the operator \(U_A\) on  is defined by
is defined by

In the case that  is in fact associative we see that \(U_A(B)=ABA\). Now let
is in fact associative we see that \(U_A(B)=ABA\). Now let  be an (associative) ring such that
be an (associative) ring such that  , and let
, and let  be a Jordan subring of
be a Jordan subring of  (i.e. an additive subgroup of
(i.e. an additive subgroup of  such that
such that
lies in  whenever \(A_1\) and \(A_2\) belong to
whenever \(A_1\) and \(A_2\) belong to  ). Then, for each \(A\in {\mathscr {A}}\), the operator \(U_A\) on the Jordan ring
). Then, for each \(A\in {\mathscr {A}}\), the operator \(U_A\) on the Jordan ring  satisfies that \(U_A(B)=ABA\) for every
satisfies that \(U_A(B)=ABA\) for every  , where juxtaposition means the associative product of
, where juxtaposition means the associative product of  .
.
Throughout this section we assume that \(\frac{1}{2}\in \Delta \), and \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) will stand for a pairing over \(\Delta \). Then, since 2 is a central element of \(\Delta \), so is \(\frac{1}{2}\), and therefore \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) are Jordan subrings of L(X).
Lemma 3.1
Let A be in L(X) such that \(U_B(A)=0\) for every \(B\in F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then \(A=0\).
Proof
By \(\S \) 2.1 (ii), for every \((x,y)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\) we have
hence \(\langle Ax,y\rangle =0\), and so \(A=0\).\(\square \)
The following corollary will not be applied in what follows, but has its own interest.
Corollary 3.2
Let A be in L(X) such that \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\hspace{1.111pt}{\bullet }\hspace{1.111pt}A=0\). Then \(A=0\).
Proof
For each \(B\in F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) we have
and so \(A=0\) thanks to Lemma 3.1.\(\square \)
Let  be a ring. Given
be a ring. Given  , we set
, we set
and we straightforwardly realize that
Now let  be a Jordan subring of
be a Jordan subring of  . A mapping
. A mapping  is a Jordan derivation from
is a Jordan derivation from  to
to  if it is additive and the equality
if it is additive and the equality
holds for all  .
.
Lemma 3.3
Let  be a Jordan subring of L(X) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let
be a Jordan subring of L(X) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let  be a Jordan derivation vanishing on \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then \(D=0\).
be a Jordan derivation vanishing on \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then \(D=0\).
Proof
Let A be in  , and let B be in \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then
, and let B be in \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then
But, by \(\S \) 2.1 (ii), we have

and then
Therefore, by applying (3.2) twice,
On the other hand, since
and \(D(B)=0\), it follows from (3.1) that
Now, using (3.3) and (3.4) we see that
Since B is arbitrary in \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), it is enough to apply Lemma 3.1 to obtain that \(D(A)=0\). But A is arbitrary in  .\(\square \)
.\(\square \)
Proposition 3.4
Let  be a Jordan subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let
be a Jordan subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let  be a Jordan derivation. Then there exists a unique derivation \({\widehat{D}}:L(X)\rightarrow L(X)\) extending D. Moreover
be a Jordan derivation. Then there exists a unique derivation \({\widehat{D}}:L(X)\rightarrow L(X)\) extending D. Moreover
Proof
Given \(A\in F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), it follows from Litoff’s Theorem [5, Theorem 4.3.11] that there exists an idempotent \(P \in F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) such that \(AP=PA=A\), hence
Since A is arbitrary in \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), it follows that
Therefore, by Herstein’s theorem [37] (see also [38, Theorem 3.3]), D is a derivation of \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then, by Proposition 2.8, there exists a unique derivation \({\widehat{D}}:L(X)\rightarrow L(X)\) such that \({\widehat{D}}(A)=D(A)\) for every \(A\in F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and moreover the inclusion (3.5) holds. Now the mapping \(A\rightarrow {\widehat{D}}(A)-D(A)\) is a Jordan derivation from  to L(X) vanishing on \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Therefore, by Lemma 3.3, \({\widehat{D}}\) is the unique derivation of L(X) which extends D.\(\square \)
to L(X) vanishing on \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Therefore, by Lemma 3.3, \({\widehat{D}}\) is the unique derivation of L(X) which extends D.\(\square \)
Now we can conclude the proof of the main result in this section, namely the following.
Theorem 3.5
Let  be a Jordan subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let
be a Jordan subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let  be a Jordan derivation. Then there exists an essentially unique differential operator T on X such that \(D(A)=[A,T]\) for every
be a Jordan derivation. Then there exists an essentially unique differential operator T on X such that \(D(A)=[A,T]\) for every  . Moreover, for each \((x_0,y_0)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\) with \(\langle x_0,y_0\rangle =1\), the mapping \(x\rightarrow - D(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y_0)x_0\) is a representative of T, and (for such a choice of \(T\) \()\) \([x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y, T]\) lies in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) for every \(y\in Y\), allowing to determine \(T^\# \) as the mapping \(y\rightarrow [x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y, T]^\# y_0\).
. Moreover, for each \((x_0,y_0)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\) with \(\langle x_0,y_0\rangle =1\), the mapping \(x\rightarrow - D(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y_0)x_0\) is a representative of T, and (for such a choice of \(T\) \()\) \([x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y, T]\) lies in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) for every \(y\in Y\), allowing to determine \(T^\# \) as the mapping \(y\rightarrow [x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y, T]^\# y_0\).
Proof
By Proposition 3.4, there exists a unique derivation
extending D. Therefore the proof is concluded by applying Theorem 1.3 and Remark 2.4 to \({\widehat{D}}\).\(\square \)
As a straightforward consequence of the above theorem (or of Proposition 3.4), we obtain the following.
Corollary 3.6
Let  be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let
be a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let  be a Jordan derivation. Then D is a derivation.
be a Jordan derivation. Then D is a derivation.
The above corollary is also a direct consequence of the recent paper by Lin [45], where a complete characterization of weak Jordan derivations of a prime ring into its maximal left ring of quotients is provided.
4 Derivations of standard operator rings on real, complex, or quaternionic normed spaces
4.1 Algebraic preliminaries
The following lemma is straightforward.
Lemma 4.1
Let  be an associative ring, let Z denote the centre of
be an associative ring, let Z denote the centre of  , and let d be a derivation of
, and let d be a derivation of  . Then Z is invariant under d. Therefore d induces a derivation of Z (namely, the restriction of d to Z, regarded as a mapping from Z to \(Z\) \()\) which will be denoted by \(d_Z\).
. Then Z is invariant under d. Therefore d induces a derivation of Z (namely, the restriction of d to Z, regarded as a mapping from Z to \(Z\) \()\) which will be denoted by \(d_Z\).
As always in this paper, \(\Delta \) denotes a division ring. As in the above lemma, we denote by Z the centre of \(\Delta \), and note that, in the current case, Z is a field.
Proposition 4.2
Let X be a left vector space over \(\Delta \), and let T be a differential operator on X. Suppose that \(\Delta \) has characteristic zero and is finite-dimensional over Z, and that T is Z-linear. Then there exist \(\mu \in \Delta \) and \(B\in L(X)\) such that \(T=\mu I_X+B\).
Proof
Let d be the ring derivation of \(\Delta \) associated to T. Since T is Z-linear, it follows that the ring derivation \(d_Z\) of Z in Lemma 4.1 is zero. This implies that d is Z-linear. Therefore, since \(\Delta \) has characteristic zero and is finite-dimensional over Z, it follows from [58, Theorem 2.5] that d is inner, say of the form \(d_\mu :\lambda \rightarrow [\mu , \lambda ]\) for some fixed \(\mu \in \Delta \). Now set \(B:=T-\mu I_X\). Then for all \(\lambda \in \Delta \) and \(x\in X\) we have
hence \(B\in L(X)\). But clearly \(T=\mu I_X+B\).\(\square \)
Lemma 4.3
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \). If X is infinite-dimensional, then there are sequences \(x_n\) and \(y_n\) in X and Y, respectively, such that \(\langle x_i,y_j\rangle =\delta _{ij}\) for all \(i,j\in {\mathbb {N}}\).
Proof
For \(y\in Y\) we set \(\ker \hspace{0.55542pt}(y):=\{u\in X\,{:} \, \langle u,y\rangle =0\}\). Starting with any couple \((x_1,y_1)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\) such that \(\langle x_1,y_1\rangle =1\), assume that the first n terms of the desired sequences have been constructed. Then \(P:=\sum _{i=1}^nx_i\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y_i\) and \(Q:=\sum _{i=1}^ny_i\hspace{0.55542pt}{\otimes }\hspace{1.111pt}x_i\) are linear projections on X and Y, respectively, such that \(\ker \hspace{0.55542pt}(P)=\bigcap _{1\leqslant i\leqslant n}\ker \hspace{0.55542pt}(y_i)\) and \(Q(Y)=\mathrm{\, lin}\hspace{0.55542pt}\{y_1,\ldots ,y_n\}\), which implies \(\langle \ker \hspace{0.55542pt}(P),Q(Y)\rangle =0\). Since P(X) is a finite-dimensional subspace of X, and X is infinite dimensional, there exists \(0\ne x_{n+1}\in \ker \hspace{0.55542pt}(P)\). Assume that \(\langle x_{n+1}, \ker \hspace{0.55542pt}(Q)\rangle =0\). Then, since \(\langle x_{n+1},Q(Y)\rangle =0\), we have \(\langle x_{n+1},Y\rangle =\langle x_{n+1}, Q(Y)+\ker \hspace{0.55542pt}(Q)\rangle =0\), and hence \(x_{n+1}=0\), which is not possible. Therefore there exists \(y_{n+1}\in \ker \hspace{0.55542pt}(Q)\) such that \(\langle x_{n+1},y_{n+1}\rangle =1\). Now we have \(\langle x_i,y_j\rangle =\delta _{ij}\) for all \(i,j\in \{1,\ldots ,n+1\}\). In this way, the \((n+1)\)-th terms of the desired sequences have been constructed.\(\square \)
To conclude this subsection, let us explain with more precision some facts on pairings, sketched in Sect. 1. Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a pairing over \(\Delta \). Let us say that a differential operator S on Y with associated derivation d has an adjoint in X relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) if there exists a (unique) mapping \(S^\#:X\rightarrow X\) such that \(\langle x,Sy\rangle =\langle S^\# x,y\rangle +d(\langle x,y\rangle )\) for all \((x,y)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\). Then the set \(\textrm{Diff}\hspace{0.55542pt}(Y,X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) of those differential operators on Y having an adjoint in X relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) is a Lie subring of the ring of all additive operators on Y, and the mapping \(\Phi :T\rightarrow T^\# \) from \(\textrm{Diff}\hspace{0.55542pt}(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) to \(\textrm{Diff} (Y,X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is a bijective Lie anti-homomorphism with inverse mapping the one \(S\rightarrow S^\# \) from \(\textrm{Diff}\hspace{0.55542pt}(Y,X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) to \(\textrm{Diff}\hspace{0.55542pt}(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Moreover, the inclusion \(\Delta I_X\subseteq \textrm{Diff} \hspace{0.55542pt}(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) holds, and for \(\lambda \in \Delta \) we have \((\lambda I_X)^\# \!=I_Y\lambda \), where \(I_Y\lambda \) denotes the mapping \(y\rightarrow y\lambda \) from Y to Y. Now set
Then \(L(Y,X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is a subring of L(Y), and the restriction of the mapping \(\Phi \) above to \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) becomes a bijective ring anti-homomorphism from \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) to \(L(Y,X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). These facts will be applied without notice in the proofs of Corollary 4.11, Proposition 4.12, and Theorem 5.3.
4.2 The main results
As we already said in Sect. 1, we denote by \({\mathbb {H}}\) the division real algebra of Hamilton’s quaternions (see for example [18, pp. 176–177 and Theorem 2.6.21] and [31, Chapter 7]). Then the centre of \({\mathbb {H}}\) is equal to \({\mathbb {R}}1\), and consequently identifies with \({\mathbb {R}}\). Let \(*\) stand for the standard involution of \({\mathbb {H}}\), and let \(\lambda \) be in \({\mathbb {H}}\). Then both \(\lambda +\lambda ^*\) and \(\lambda ^*\lambda \) lie in \({\mathbb {R}}\). Actually \(\lambda ^*\lambda \) is a nonnegative real number, and the mapping \(\lambda \rightarrow |\lambda |:=\sqrt{\lambda ^*\lambda }\) is an absolute value on \({\mathbb {H}}\). Given \(\lambda \in {\mathbb {H}}\) we set \(\textrm{Re} \hspace{0.55542pt}(\lambda ):=\frac{1}{2}(\lambda +\lambda ^*)\).
By a left quaternionic normed space we mean a left vector space X over \({\mathbb {H}}\) endowed with a subadditive mapping \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert :X\rightarrow {\mathbb {R}}\) such that \(\Vert x\Vert \,{=}\,0\) \(\Leftrightarrow \) \(x\,{=}\,0\), and \(\Vert \lambda x\Vert =|\lambda |\Vert x\Vert \) for all \(\lambda \in {\mathbb {H}}\) and \(x\in X\). Analogously right quaternionic normed spaces are defined. Since Soukhomlinoff’s pioneering paper [64], quaternionic normed spaces have been fully discussed in the literature (see [46, 50] and references therein), and appear naturally in the theory of complex Hilbert spaces [36, 7.5.5]. We note that, by restricting the scalars, every left or right quaternionic normed space becomes a normed space over \({\mathbb {R}}\). Let X be a left quaternionic normed space. Then the set \(X'\) of all continuous \({\mathbb {H}}\)-linear mappings from X to \({\mathbb {H}}\) is a vector subspace of the right quaternionic vector space \(X^*\) (the algebraic dual of X), and becomes a right quaternionic normed space under the norm
The right quaternionic normed space \(X'\) just introduced is called the (topological) dual of X.
Proposition 4.4
Let X be a left quaternionic normed space. Then the mapping \(\Phi :f\rightarrow \textrm{Re}\hspace{1.111pt}{ \circ }\hspace{0.55542pt}f\) becomes a surjective \({\mathbb {R}}\)-linear isometry from the dual \(X'\) of X to the dual \((X_{\mathbb {R}})'\) of \(X_{\mathbb {R}}\).
Proof
The facts that \(\textrm{Re} \hspace{1.66656pt}{\circ } f\) lies in \((X_{\mathbb {R}})'\) whenever f is in \(X'\) and that \(\Phi \) is \({\mathbb {R}}\)-linear are clear.
Let x and f be in X and \(X'\), respectively. Then we have
and hence \(|f(x)|\leqslant \Vert \Phi (f)\Vert \Vert x\Vert \). Since x is arbitrary in X, we deduce that \(\Vert f\Vert \leqslant \Vert \Phi (f)\Vert \). But the converse inequality is clear. Therefore, since f is arbitrary in \(X'\), we conclude that \(\Phi \) is an isometry.
Now let \(\phi \) be in \((X_{\mathbb {R}})'\). Take a canonical basis \(\{1,i,j,k\}\) of \({\mathbb {H}}\), so that \(i^2= j^2= k^2= -1\), \(ij = k = -ji\), \(jk = i = -kj\), and \(ki = j = -ik\). Define a mapping \(f:X\rightarrow {\mathbb {H}}\) by \(f(x):=\phi (x)-\phi (ix)\hspace{1.111pt}i-\phi (jx)j-\phi (kx)\hspace{1.111pt}k\). Then
and hence \(f(ix)=if(x)\). Analogously \(f(jx)=jf(x)\) and \(f(kx)=kf(x)\). Therefore, since clearly f is \({\mathbb {R}}\)-linear and continuous, it follows that f lies in \(X'\). Finally, since clearly \(\textrm{Re} \hspace{1.66656pt}{\circ } f=\phi \), and \(\phi \) is arbitrary in \((X_{\mathbb {R}})'\), we conclude that \(\Phi \) is surjective.\(\square \)
By a left (respectively, right) quaternionic Banach space we mean a left (respectively, right) quaternionic normed space which is a complete metric space relative to the distance \(\Vert u-v\Vert \). We note that, by restricting the scalars, every left or right quaternionic normed space becomes a normed space over \({\mathbb {R}}\). Therefore, as a byproduct of Proposition 4.4, we are provided with the following.
Corollary 4.5
The dual of any left quaternionic normed space is a right quaternionic Banach space in a natural way.
Lemma 4.6
Let X be a left normed space over \({\mathbb {F}}\), and let x be in X. Then there exists \(f\in X'\) such that \(\Vert f\Vert =1\) and \(f(x)=\Vert x\Vert \).
Proof
We may suppose that \({\mathbb {F}}={\mathbb {H}}\). Then, by the Hahn–Banach theorem applied to \((X_{\mathbb {R}})'\), there exists \(g\in (X_{\mathbb {R}})'\) such that \(\Vert g\Vert =1\) and \(g(x)=\Vert x\Vert \). Therefore, since the mapping  in Proposition 4.4 is a surjective \({\mathbb {R}}\)-linear isometry, it is enough to apply that proposition to realize that \(f:=\Phi ^{-1}(g)\in X'\) satisfies the conditions in the conclusion of the lemma.\(\square \)
in Proposition 4.4 is a surjective \({\mathbb {R}}\)-linear isometry, it is enough to apply that proposition to realize that \(f:=\Phi ^{-1}(g)\in X'\) satisfies the conditions in the conclusion of the lemma.\(\square \)
We note that Lemma 4.6 above follows from the main result in [64], as well as that the main result in [64] follows from Proposition 4.4.
By a normed pairing over \({\mathbb {F}}\) we mean any pairing \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), where X is a left normed space over \({\mathbb {F}}\), Y is a right normed space over \({\mathbb {F}}\), and the form \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) is continuous. If X (respectively, Y) is complete, then we say that \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is complete on the left (respectively, complete on the right). If \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is both complete on the left and complete on the right, then we simply say that it is a Banach pairing.
Lemma 4.7
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a normed pairing over \({\mathbb {F}}\), and let T be in \(\textrm{Diff} \hspace{0.55542pt}(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then there are mappings \(g:X\rightarrow {\mathbb {R}}_0^+\) and \(h:Y\rightarrow {\mathbb {R}}_0^+\) such that \(\Vert T(\langle x,y\rangle \hspace{1.111pt}x)\Vert \leqslant g(x)\hspace{1.111pt}h(y)\) for all \(x\in X\) and \(y\in Y\).
Proof
Let d denote the ring derivation of \({\mathbb {F}}\) associated to T, and set \(M:=\Vert \langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \Vert \). Let (x, y) be in \(X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\). Then, by (1.2), we have
Therefore, considering (1.1), we obtain
\(\square \)
Let X be a left normed space over \({\mathbb {F}}\). As we already said in Sect. 1, we denote by  the normed subalgebra of the \({\mathbb {R}}\)-algebra L(X) consisting of those operators in L(X) which are continuous, and by
the normed subalgebra of the \({\mathbb {R}}\)-algebra L(X) consisting of those operators in L(X) which are continuous, and by  the ideal of
the ideal of  consisting of those operators in
consisting of those operators in  whose range is finite-dimensional. The next lemma follows straightforwardly from the closed graph theorem.
whose range is finite-dimensional. The next lemma follows straightforwardly from the closed graph theorem.
Lemma 4.8
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a normed pairing over \({\mathbb {F}}\) complete on the left. Then  .
.
Remark 4.9
(a) Every additive operator on a vector space X over \({\mathbb {F}}\) is \({\mathbb {Q}}\)-linear, so such an operator T is \({\mathbb {R}}\)-linear if X is normed and T is continuous. Moreover, additive operators on a normed space X over \({\mathbb {F}}\) are continuous if (and only if) they are bounded on some neighborhood of zero. Indeed, since we can regard X as a normed space over \({\mathbb {R}}\), it is enough to consider the case that \({\mathbb {F}}={\mathbb {R}}\), and then to consult [1, pp. 36–37].
(b) If  is a (possibly non-associative) complex algebra with zero annihilator, and if D is an additive derivation of
is a (possibly non-associative) complex algebra with zero annihilator, and if D is an additive derivation of  , then, by [41, Remark 4.2], the equality \(D(iA)=i D(A)\) holds for all
, then, by [41, Remark 4.2], the equality \(D(iA)=i D(A)\) holds for all  . Consequently, \({\mathbb {R}}\)-linear derivations of any complex algebra with zero annihilator are \({\mathbb {C}}\)-linear. Therefore, by part (a) of the current remark, continuous additive derivations of any normed algebra over \({\mathbb {K}}\) with zero annihilator are linear. As a consequence, if d is a continuous ring derivation of \({\mathbb {K}}\), then \(d=0\). It is well known that nonzero derivations of \({\mathbb {R}}\) do exist [71, Chapter II, Section 17].
. Consequently, \({\mathbb {R}}\)-linear derivations of any complex algebra with zero annihilator are \({\mathbb {C}}\)-linear. Therefore, by part (a) of the current remark, continuous additive derivations of any normed algebra over \({\mathbb {K}}\) with zero annihilator are linear. As a consequence, if d is a continuous ring derivation of \({\mathbb {K}}\), then \(d=0\). It is well known that nonzero derivations of \({\mathbb {R}}\) do exist [71, Chapter II, Section 17].
Now we adapt the argument in the proof of [9, Proposition 3.3] to prove the following.
Theorem 4.10
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a normed pairing over \({\mathbb {F}}\) complete on the left, with X infinite-dimensional, and let T be in \(\textrm{Diff}\hspace{0.55542pt}(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then there exist \(\mu \in {\mathbb {F}}\) and \(A\in L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) such that \(T=\mu I_X+A\). As a consequence, T is continuous and, when \({\mathbb {F}}={\mathbb {K}}:={\mathbb {R}}\) or \({\mathbb {C}}\), T is linear.
Proof
Let d denote the ring derivation of \({\mathbb {F}}\) associated to T and, to derive a contradiction, assume that d is discontinuous. Then, by Remark 4.9 (a), d is unbounded on every neighborhood of zero. Let \(x_n\) and \(y_n\) be the sequences in X and Y, respectively, given by Lemma 4.3, and note that, replacing \(x_n\) with \(\Vert x_n\Vert ^{-1}x_n\) and \(y_n\) with \(y_n \Vert x_n\Vert \) if necessary, we may suppose that \(\Vert x_n\Vert =1\) for every \(n\in {\mathbb {N}}\). Let \(g:X\rightarrow {\mathbb {R}}_0^+\) and \(h:Y\rightarrow {\mathbb {R}}_0^+\) be the mappings given by Lemma 4.7, and for \(n\in {\mathbb {N}}\) set \(\alpha _n:=\max \hspace{1.111pt}\{1,h(y_n)\}\). Then there is \(\lambda _n\in {\mathbb {F}}\) such that \(|\lambda _n|\leqslant \frac{1}{2^n\alpha _n}\) and \(|d(\lambda _n)|>2^n\alpha _n\). Set \(x:=\sum _{k=1}^\infty \lambda _kx_k\). Then we have
Therefore, since the series \(\sum _n \frac{1}{2^n\alpha _n}\lambda _nTx\) converges, and the series \(\sum _n \frac{1}{2^n\alpha _n}d(\lambda _n)x\) diverges, it follows that the series \(\sum _n \frac{1}{2^n\alpha _n}T(\lambda _nx)\) diverges. But this is not possible because, since \(\lambda _n=\langle x,y_n\rangle \), we have \(T(\lambda _nx)=T(\langle x,y_n\rangle \hspace{1.111pt}x)\), so \(\Vert T(\lambda _nx)\Vert \leqslant g(x)\hspace{1.111pt}h(y_n)\leqslant g(x)\hspace{1.111pt}\alpha _n\) (by Lemma 4.7), and so the series \(\sum _n \frac{1}{2^n\alpha _n}T(\lambda _nx)\) is absolutely convergent.
Therefore d is continuous. If \({\mathbb {F}}={\mathbb {K}}\), then \(d=0\) (by Remark 4.9 (b)), so T is linear, hence T lies in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) (as it has an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \)), and the continuity of T follows from Lemma 4.8. Suppose that \({\mathbb {F}}={\mathbb {H}}\). Then, with the notation in Lemma 4.1, \(d_{\mathbb {R}}:{\mathbb {R}}\rightarrow {\mathbb {R}}\) is continuous, so \(d_{\mathbb {R}}=0\) (by Remark 4.9 (b) again), and so T is \({\mathbb {R}}\)-linear. Therefore, by Proposition 4.2, there exist \(\mu \in {\mathbb {F}}\) and \(A\in L (X)\) such that \(T=\mu I_X+A\), with \(A=T-\mu I_X\in L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) (as A has an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \)), and the continuity of T follows by applying Lemma 4.8 again.\(\square \)
Corollary 4.11
Let \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) be a normed pairing over \({\mathbb {F}}\) complete on the right, with X infinite-dimensional, let  be a Jordan subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let
be a Jordan subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and let

be a Jordan derivation. Then there exists \(B\in L (X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) such that \(D(A)=[A,B]\) for every  . As a consequence, if in fact \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is a Banach pairing, then D is continuous.
. As a consequence, if in fact \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is a Banach pairing, then D is continuous.
Proof
By Theorem 3.5, there exists a differential operator T on X having an adjoint \(T^\# \) relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) and satisfying \(D(A)=[A,T]\) for every  . But \(T^\# \) is a differential operator on Y having an adjoint (namely T) relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \). Therefore, by the complete-on-the-right version of Theorem 4.10, there exist \(\mu \in {\mathbb {F}}\) and \(C\in L(Y,X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) such that
. But \(T^\# \) is a differential operator on Y having an adjoint (namely T) relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \). Therefore, by the complete-on-the-right version of Theorem 4.10, there exist \(\mu \in {\mathbb {F}}\) and \(C\in L(Y,X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) such that  . Now
. Now  , where \(B:=C^\# \) lies in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Finally, since \(D(A)=[A,T]\) for every
, where \(B:=C^\# \) lies in \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Finally, since \(D(A)=[A,T]\) for every  , we conclude that \(D(A)=[A,B]\) for every
, we conclude that \(D(A)=[A,B]\) for every  .
.
The consequence follows from Lemma 4.8.\(\square \)
In the case that \({\mathbb {F}}\) is equal to \({\mathbb {R}}\) or \({\mathbb {C}}\), the next proposition is known in [47, Theorem II-4].
Proposition 4.12
Let X be a left normed space over \({\mathbb {F}}\), and for \((x,f)\in X\hspace{1.111pt}{\times }\hspace{1.111pt}X'\) set \(\langle x,f\rangle :=f(x)\). Then we have:
-
(i)
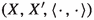 is a normed pairing over \({\mathbb {F}}\) complete on the right.
is a normed pairing over \({\mathbb {F}}\) complete on the right. -
(ii)
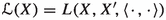 .
. -
(iii)
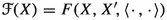 .
.
Proof
If \({\mathbb {F}}={\mathbb {K}}\), then assertion (i) is well known. Suppose that \({\mathbb {F}}={\mathbb {H}}\). Then, by Corollary 4.5, \(X'\) is a right Banach space over \({\mathbb {H}}\). Therefore to conclude the proof of (i) it is enough to show that the form \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) is nondegenerate. Let f be in \(X'\) such that \(\langle X,f\rangle =0\). Then clearly \(f=0\). Now let x be in X such that \(\langle x,X'\rangle =0\). Then, as a byproduct of Lemma 4.6, we have \(x=0\). Thus (i) has been proved.
Let F be in  . Then \(F\in L(X)\), and the topological transpose \(F'\), where \(F'(f):=f\hspace{1.111pt}{\circ }\hspace{1.111pt}F\) for every \(f\in X'\), is an adjoint of F relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \). Therefore F lies in
. Then \(F\in L(X)\), and the topological transpose \(F'\), where \(F'(f):=f\hspace{1.111pt}{\circ }\hspace{1.111pt}F\) for every \(f\in X'\), is an adjoint of F relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \). Therefore F lies in  . Conversely, let F be in
. Conversely, let F be in  . Then, by (i) and the complete-on-the-right version of Lemma 4.8, \(F^\# \) is continuous. Therefore, for all \(x\in X\) and \(f\in X'\) we have
. Then, by (i) and the complete-on-the-right version of Lemma 4.8, \(F^\# \) is continuous. Therefore, for all \(x\in X\) and \(f\in X'\) we have
Let x be in X. Then, by Lemma 4.6, there exists \(f\in X'\) such that \(\Vert f\Vert =1\) and \(f(Fx)=\Vert Fx\Vert \). Therefore, by (4.1), \(\Vert Fx\Vert \leqslant \Vert F^\# \Vert \Vert f\Vert \Vert x\Vert =\Vert F^\# \Vert \Vert x\Vert \). Since x is arbitrary in X, we conclude that F lies in  . Thus the proof of (ii) has been concluded.
. Thus the proof of (ii) has been concluded.
Assertion (iii) follows straightforwardly from (ii).\(\square \)
Proof of Theorem 1.4
Combine Corollary 4.11 and Proposition 4.12.\(\square \)
For the reader interested only in associative notions, we emphasize the straightforward consequence of Theorem 1.4 given by the following.
Corollary 4.13
Let X be an infinite-dimensional left normed space over \({\mathbb {F}}\), let  be a standard operator ring on X, and let
be a standard operator ring on X, and let  be a derivation. Then there exists
be a derivation. Then there exists  such that \(D(A)=[A,B]\) for every
such that \(D(A)=[A,B]\) for every  . As a consequence, D is continuous.
. As a consequence, D is continuous.
Remark 4.14
Let d be a (ring) derivation of \({\mathbb {R}}\). Then the mapping \(d_{\mathbb {C}}:a+ib\rightarrow d(a)+id(b)\) (\(a,b\in {\mathbb {R}}\)) is a derivation of \({\mathbb {C}}\). Similarly, if \(\{1,i,j,k\}\) is a canonical basis of \({\mathbb {H}}\), then the mapping
(\(\alpha , \beta , \gamma ,\delta \in {\mathbb {R}}\)) is a derivation of \({\mathbb {H}}\). Therefore, keeping in mind the existence of discontinuous derivations of \({\mathbb {R}}\) (Remark 4.9 (b)), the existence of discontinuous derivations of \({\mathbb {F}}:={\mathbb {R}},{\mathbb {C}}\), or \({\mathbb {H}}\) is assured.
Now let X be a finite-dimensional left normed space over \({\mathbb {F}}\). Then \(X={\mathbb {F}}^m\) for some positive integer m, and  (the ring of all \(m\hspace{1.111pt}{\times }\hspace{1.111pt}m\) matrices over \({\mathbb {F}}\)) is the unique standard operator Jordan ring on X. Moreover, given any derivation d of \({\mathbb {F}}\), the mapping \(d_m:(a_{i,j})\rightarrow (d(a_{i,j}))\) (\((a_{i,j})\in M_m({\mathbb {F}})\)) is a derivation of \(M_m({\mathbb {F}})\). It follows from the above paragraph that the restriction in Theorem 1.4 and Corollary 4.13 that X is infinite-dimensional cannot be removed.
(the ring of all \(m\hspace{1.111pt}{\times }\hspace{1.111pt}m\) matrices over \({\mathbb {F}}\)) is the unique standard operator Jordan ring on X. Moreover, given any derivation d of \({\mathbb {F}}\), the mapping \(d_m:(a_{i,j})\rightarrow (d(a_{i,j}))\) (\((a_{i,j})\in M_m({\mathbb {F}})\)) is a derivation of \(M_m({\mathbb {F}})\). It follows from the above paragraph that the restriction in Theorem 1.4 and Corollary 4.13 that X is infinite-dimensional cannot be removed.
To conclude this remark, let us incidentally note that derivations of \(M_m({\mathbb {F}})\) can be described in terms of derivations of \({\mathbb {R}}\). Indeed, according to [48, Example 19], each derivation of \(M_m({\mathbb {F}})\) decomposes as a sum of an inner derivation of \(M_m({\mathbb {F}})\) and a derivation of the form \(d_m\) for some derivation d of \({\mathbb {F}}\). (Even, in this result, \({\mathbb {F}}\) can be replaced with any unital ring; note also that, in the very particular case that \({\mathbb {F}}={\mathbb {K}}\), the result we are reviewing was rediscovered in [62, Theorem 2.2].) Moreover, it is easily realized that every derivation d of \({\mathbb {C}}\) can be written as \(d=(d_1)_{\mathbb {C}}+i(d_2)_{\mathbb {C}}\) for suitable derivations \(d_1,d_2\) of \({\mathbb {R}}\). Finally, according to [33, Theorem 3.1] or [34, Theorem 2.1], each derivation of \({\mathbb {H}}\) decomposes as a sum of an inner derivation of \({\mathbb {H}}\) and a derivation of the form \(d_{\mathbb {H}}\) for some derivation d of \({\mathbb {R}}\).
Definition 4.15
Let X be a nonzero left normed space over \({\mathbb {F}}\), and let \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) denote the norm of X as well as the dual norm on \(X'\) and the operator norm on the real algebra  . Arguing as in the proof of [18, Proposition 1.4.32], we realize that
. Arguing as in the proof of [18, Proposition 1.4.32], we realize that  is the smallest nonzero ring ideal of
is the smallest nonzero ring ideal of  . Generalizing a notion of Schatten [59, Definition V.1.3], by a norm ideal of operators on X we mean any nonzero \({\mathbb {R}}\)-algebra ideal
. Generalizing a notion of Schatten [59, Definition V.1.3], by a norm ideal of operators on X we mean any nonzero \({\mathbb {R}}\)-algebra ideal  of
of  endowed with a norm \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \) satisfying the following conditions:
endowed with a norm \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \) satisfying the following conditions:
-
(i)
\(\Vert x\hspace{1.111pt}{\otimes }\hspace{1.111pt}f\Vert =\vert \! \vert \! \vert x \vert \! \vert \! \vert \, \vert \! \vert \! \vert f \vert \! \vert \! \vert \) for all \(x\in X\) and \(f\in X'\) (here \(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}f\) has the meaning given in \(\S \) 2.1 particularized to the case that \(\Delta ={\mathbb {F}}\), \(Y=X'\), and X is naturally paired with \(X'\)).
-
(ii)
\(\Vert FAG \Vert \leqslant \vert \! \vert \! \vert F \vert \! \vert \! \vert \Vert A\Vert \, \vert \! \vert \! \vert G \vert \! \vert \! \vert \) for all
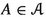 and
and 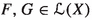 .
.
It follows from these conditions that, for  , \(x\in X\), and \(f\in X'\) with \(\vert \! \vert \! \vert x \vert \! \vert \! \vert =\vert \! \vert \! \vert f \vert \! \vert \! \vert =1\), we have
, \(x\in X\), and \(f\in X'\) with \(\vert \! \vert \! \vert x \vert \! \vert \! \vert =\vert \! \vert \! \vert f \vert \! \vert \! \vert =1\), we have
Hence \(\vert \! \vert \! \vert A \vert \! \vert \! \vert \leqslant \Vert A\Vert \) for every  . Therefore, keeping in mind (ii) again, we realize that
. Therefore, keeping in mind (ii) again, we realize that  is a real normed algebra.
is a real normed algebra.
Corollary 4.16
Let \((X,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| )\) be an infinite-dimensional left normed space over \({\mathbb {F}}\), let  be a norm ideal of operators on X, and let D be a ring derivation of
be a norm ideal of operators on X, and let D be a ring derivation of  . Then D is \({\mathbb {R}}\)-linear and \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \)-continuous.
. Then D is \({\mathbb {R}}\)-linear and \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \)-continuous.
Proof
Clearly  is a standard ring of operators on X. Therefore, by Corollary 4.13, there exists
is a standard ring of operators on X. Therefore, by Corollary 4.13, there exists  such that \(D(A)=[A,B]\) for every
such that \(D(A)=[A,B]\) for every  . As a first consequence, D is \({\mathbb {R}}\)-linear. Moreover, by requirement (ii) in Definition 4.15, for
. As a first consequence, D is \({\mathbb {R}}\)-linear. Moreover, by requirement (ii) in Definition 4.15, for  we have
we have  , and hence D is continuous (with
, and hence D is continuous (with  ).\(\square \)
).\(\square \)
Remark 4.17
With the notation and requirements in the above corollary, suppose that actually \({\mathbb {F}}={\mathbb {C}}\) and that in addition  is a complex subspace of
is a complex subspace of  . Then the above proof shows that D is \({\mathbb {C}}\)-linear.
. Then the above proof shows that D is \({\mathbb {C}}\)-linear.
5 Primitive associative normed Q-algebras with nonzero socle
This section is a homage to Rickart, who knew relevant forerunners of Lemmas 5.1 and 5.2, and of Theorem 5.3 below (see [52, Lemma 2.4.4, and Theorems 1.3.3 and 2.4.12]).
Lemma 5.1
Let  be a ring, let X be a faithful irreducible left
be a ring, let X be a faithful irreducible left  -module, let \(\Delta \) denote the associated division ring of
-module, let \(\Delta \) denote the associated division ring of  relative to X, and let us regard X as a left vector space over \(\Delta \). Suppose that actually
relative to X, and let us regard X as a left vector space over \(\Delta \). Suppose that actually  is (the ring underlying) an algebra over a field \({\mathfrak {F}}\). Then X becomes naturally a vector space over \({\mathfrak {F}}\), and \({\mathfrak {F}}\) is contained in the centre of \(\Delta \). Therefore \(\Delta \) is an algebra over \({\mathfrak {F}}\), and \(\Delta I_X\) consists only of \({\mathfrak {F}}\)-linear operators on X.
is (the ring underlying) an algebra over a field \({\mathfrak {F}}\). Then X becomes naturally a vector space over \({\mathfrak {F}}\), and \({\mathfrak {F}}\) is contained in the centre of \(\Delta \). Therefore \(\Delta \) is an algebra over \({\mathfrak {F}}\), and \(\Delta I_X\) consists only of \({\mathfrak {F}}\)-linear operators on X.
Proof
Since X is an irreducible left module over the ring  , and
, and  is an algebra over \({\mathfrak {F}}\), it follows from [39, Proposition I.9.2] that X can be regarded in one and only one way as an irreducible left module over the algebra
is an algebra over \({\mathfrak {F}}\), it follows from [39, Proposition I.9.2] that X can be regarded in one and only one way as an irreducible left module over the algebra  , i.e. X is an irreducible left module over the ring
, i.e. X is an irreducible left module over the ring  , and there is a unique multiplication \((\lambda , x) \rightarrow \lambda x\) from \({\mathfrak {F}} \hspace{1.111pt}{\times }\hspace{1.111pt}X\) to X converting \((X,+)\) into a vector space over \({\mathfrak {F}}\), and satisfying the bilinearity condition
, and there is a unique multiplication \((\lambda , x) \rightarrow \lambda x\) from \({\mathfrak {F}} \hspace{1.111pt}{\times }\hspace{1.111pt}X\) to X converting \((X,+)\) into a vector space over \({\mathfrak {F}}\), and satisfying the bilinearity condition

(compare [39, Definitions I.9.1 and I.9.3]). Now the first equality in (5.1) reads as that \({\mathfrak {F}}\) is included in \(\Delta \).
Let x be arbitrary in X. Then, by the irreducibility of X, there exists  such that \(Ax=x\). Now let \((\lambda ,\mu )\) be in \({\mathfrak {F}}\hspace{1.111pt}{\times }\hspace{0.55542pt}\Delta \). Then, since \(\lambda A\) lies in
such that \(Ax=x\). Now let \((\lambda ,\mu )\) be in \({\mathfrak {F}}\hspace{1.111pt}{\times }\hspace{0.55542pt}\Delta \). Then, since \(\lambda A\) lies in  , and \(B(\mu x)=\mu Bx\) for every
, and \(B(\mu x)=\mu Bx\) for every  , we have
, we have
Therefore, since x is arbitrary in X, we obtain that \(\mu \lambda =\lambda \mu \). Finally, since \((\lambda ,\mu )\) is arbitrary in \({\mathfrak {F}}\hspace{1.111pt}{\times }\hspace{0.55542pt}\Delta \), we conclude that \({\mathfrak {F}}\) is contained in the centre of \(\Delta \).\(\square \)
Lemma 5.2
Let \({\mathbb {F}}\) denote either \({\mathbb {C}}\) or \({\mathbb {H}}\), let X be a left vector space over \({\mathbb {F}}\), and let \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \) be a norm on X converting X into a real normed space and satisfying \(\Vert \lambda x\Vert \leqslant \vert \! \vert \! \vert \lambda \vert \! \vert \! \vert \Vert x\Vert \) for some \({\mathbb {R}}\)-algebra norm \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) on \({\mathbb {F}}\) and all \(\lambda \in {\mathbb {F}}\) and \(x\in X\). Then there exists an equivalent norm on X converting X into a normed space over \({\mathbb {F}}\).
Proof
For \(x\in X\), set \(\vert \! \vert \! \vert x \vert \! \vert \! \vert =\sup \hspace{1.111pt}\{\Vert \mu x\Vert \,{:}\,\mu \in {\mathbb {F}}\ \ \mathrm{such \ that} \ |\mu |=1\}\). Then it is easily checked that \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) is an equivalent norm on X converting X into a normed space over \({\mathbb {F}}\).\(\square \)
By an associative normed Q-algebra over \({\mathbb {K}}\) we mean any normed associative algebra over \({\mathbb {K}}\) such that the set of its quasi-invertible elements is open. Associative normed Q-algebras have become a classical topic in the theory of associative normed algebras, whose study goes back to Kaplansky [42] (see [18, Section 3.6.61] for additional information). Complete normed associative algebras are associative normed Q-algebras [18, Example 3.6.42], but the converse is not true. Thus, for example, every (possibly non closed) one-sided ideal of a complete normed associative algebra is an associative normed Q-algebra.
Theorem 5.3
Let  be a primitive associative normed Q-algebra over \({\mathbb {K}}={\mathbb {R}}\) or \({\mathbb {C}}\) having a nonzero socle. Let \({\mathbb {F}}\) stand for \({\mathbb {C}}\) if \({\mathbb {K}}={\mathbb {C}}\), and for \({\mathbb {R}},{\mathbb {C}}\), or \({\mathbb {H}}\) if \({\mathbb {K}}={\mathbb {R}}\). Then there exists a normed pairing \(((X,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| ),(Y,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| ), \langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) over \({\mathbb {F}}\) in such a way that
be a primitive associative normed Q-algebra over \({\mathbb {K}}={\mathbb {R}}\) or \({\mathbb {C}}\) having a nonzero socle. Let \({\mathbb {F}}\) stand for \({\mathbb {C}}\) if \({\mathbb {K}}={\mathbb {C}}\), and for \({\mathbb {R}},{\mathbb {C}}\), or \({\mathbb {H}}\) if \({\mathbb {K}}={\mathbb {R}}\). Then there exists a normed pairing \(((X,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| ),(Y,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| ), \langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) over \({\mathbb {F}}\) in such a way that  is a \({\mathbb {K}}\)-subalgebra of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), operators in
is a \({\mathbb {K}}\)-subalgebra of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), operators in  are \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous, and the mapping \(A\rightarrow A\) from
are \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous, and the mapping \(A\rightarrow A\) from  to
to  is continuous. Moreover, if the associative normed Q-algebra
is continuous. Moreover, if the associative normed Q-algebra  is in fact a complete normed algebra, then the pairing \(((X,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| ),(Y,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| ), \langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) above is a Banach pairing.
is in fact a complete normed algebra, then the pairing \(((X,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| ),(Y,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| ), \langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) above is a Banach pairing.
Proof
By [39, Section IV.9], there exist a division ring \(\Delta \) and a pairing \((X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) over \(\Delta \) such that  is a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then, since
is a subring of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then, since  is an algebra over \({\mathbb {K}}\), it follows from Lemmas 2.2 and 5.1 that X is a vector space over \({\mathbb {K}}\), that \(\Delta \) is an algebra over \({\mathbb {K}}\), and that \(\Delta I_X\) consists only of \({\mathbb {K}}\)-linear operators on X. Now, by [18, Corollary 3.6.44 (i) and its proof ], there exists a norm \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) on X converting X into a normed space (occasionally, a Banach space if we are dealing with the complete normed case) over \({\mathbb {K}}\), and with the properties that every operator
is an algebra over \({\mathbb {K}}\), it follows from Lemmas 2.2 and 5.1 that X is a vector space over \({\mathbb {K}}\), that \(\Delta \) is an algebra over \({\mathbb {K}}\), and that \(\Delta I_X\) consists only of \({\mathbb {K}}\)-linear operators on X. Now, by [18, Corollary 3.6.44 (i) and its proof ], there exists a norm \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) on X converting X into a normed space (occasionally, a Banach space if we are dealing with the complete normed case) over \({\mathbb {K}}\), and with the properties that every operator  is \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous with \(\vert \! \vert \! \vert A \vert \! \vert \! \vert \leqslant \Vert A\Vert \), and that \(\Delta I_X\) consists only of \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous \({\mathbb {K}}\)-linear operators on X. Moreover, a choice of such a norm \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) on X can be constructed by taking \(0\ne x_0\in X\), and defining
is \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous with \(\vert \! \vert \! \vert A \vert \! \vert \! \vert \leqslant \Vert A\Vert \), and that \(\Delta I_X\) consists only of \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous \({\mathbb {K}}\)-linear operators on X. Moreover, a choice of such a norm \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) on X can be constructed by taking \(0\ne x_0\in X\), and defining

On the other hand, since \(\Delta I_X\) consists only of \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous \({\mathbb {K}}\)-linear operators on X, we can convert \(\Delta \) into a normed algebra over \({\mathbb {K}}\) (under the operator norm corresponding to \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)), and apply the Gelfand–Mazur theorem [18, Proposition 2.5.40 and Corollary 1.1.43] to obtain that \(\Delta ={\mathbb {F}}\), with \({\mathbb {F}}\) as in the statement of the theorem. Now, if \({\mathbb {K}}={\mathbb {C}}\), or if \({\mathbb {K}}={\mathbb {R}}\) and \({\mathbb {F}}={\mathbb {R}}\), then \((X,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| )\) is a left normed (occasionally, Banach) space over \({\mathbb {F}}\) and the inequality \(\vert \! \vert \! \vert A \vert \! \vert \! \vert \leqslant \Vert A\Vert \) holds for every  . In the remaining cases (that \({\mathbb {K}}={\mathbb {R}}\) and \({\mathbb {F}}={\mathbb {C}}\) or \({\mathbb {H}}\)), it is enough to apply Lemma 5.2 to realize that, up to an equivalent renorming (we remain calling \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) the new norm), \((X,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| )\) becomes a left normed (occasionally, Banach) space over \({\mathbb {F}}\) and there is \(M>0\) such that the inequality \(\vert \! \vert \! \vert A \vert \! \vert \! \vert \leqslant M\Vert A\Vert \) holds for every
. In the remaining cases (that \({\mathbb {K}}={\mathbb {R}}\) and \({\mathbb {F}}={\mathbb {C}}\) or \({\mathbb {H}}\)), it is enough to apply Lemma 5.2 to realize that, up to an equivalent renorming (we remain calling \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) the new norm), \((X,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| )\) becomes a left normed (occasionally, Banach) space over \({\mathbb {F}}\) and there is \(M>0\) such that the inequality \(\vert \! \vert \! \vert A \vert \! \vert \! \vert \leqslant M\Vert A\Vert \) holds for every  . Therefore, in any case, \((X,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| )\) is a left normed (occasionally, Banach) space over \({\mathbb {F}}\) and there is \(K>0\) such that the inequality \(\vert \! \vert \! \vert A \vert \! \vert \! \vert \leqslant K\Vert A\Vert \) holds for every
. Therefore, in any case, \((X,\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| )\) is a left normed (occasionally, Banach) space over \({\mathbb {F}}\) and there is \(K>0\) such that the inequality \(\vert \! \vert \! \vert A \vert \! \vert \! \vert \leqslant K\Vert A\Vert \) holds for every  . Thus the mapping \(A\rightarrow A\) from
. Thus the mapping \(A\rightarrow A\) from  to
to  is continuous. We note that the change of the norm \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) we have done in some cases could affect equality (5.2), which should be replaced with a double inequality of the form
is continuous. We note that the change of the norm \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) we have done in some cases could affect equality (5.2), which should be replaced with a double inequality of the form

for some positive constants \(K_1,K_2\). In what follows we codify this incidence by writing \(\backsimeq \) instead of \(=\) in (5.2) and similar places.
In principle,  has no any natural norm. Nevertheless, since
has no any natural norm. Nevertheless, since  is antiisomorphic to
is antiisomorphic to  in a natural way, we can move the norm of
in a natural way, we can move the norm of  to
to  , and define \(\Vert A^\# \Vert :=\Vert A\Vert \) (
, and define \(\Vert A^\# \Vert :=\Vert A\Vert \) ( ), to realize that
), to realize that  becomes an associative normed Q-algebra (occasionally, a complete normed associative algebra) over \({\mathbb {K}}\).Footnote 1 Therefore, replacing in the above paragraph X with Y,
becomes an associative normed Q-algebra (occasionally, a complete normed associative algebra) over \({\mathbb {K}}\).Footnote 1 Therefore, replacing in the above paragraph X with Y,  with
with  , and Lemmas 2.2, 5.1, and 5.2 with their ‘right’ versions, we realize that there exists a norm \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) on Y converting Y into a right normed (occasionally, Banach) space over \({\mathbb {F}}\), and satisfying
, and Lemmas 2.2, 5.1, and 5.2 with their ‘right’ versions, we realize that there exists a norm \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \) on Y converting Y into a right normed (occasionally, Banach) space over \({\mathbb {F}}\), and satisfying

for every \(y\in Y\), where \(y_0\) is a prefixed nonzero element of Y.
Now, to conclude the proof of the theorem, it only remains to show that the form \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) is \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous. But this can be done by arguing as in the proof of [52, Lemma 2.4.11]. Indeed, let (x, y) be in \(X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\). Then \((x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y)^2= \langle x,y\rangle \hspace{1.111pt}x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y\), so \(|\langle x,y\rangle | \Vert x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y\Vert =\Vert (x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y)^2\Vert \leqslant \Vert (x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y)\Vert ^2\), and so \(|\langle x,y\rangle | \leqslant \Vert x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y\Vert \). Now let  be such that \(Ax_0=x\) and \(B^\# y_0=y\). Then \(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y=A(x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y_0)B\), and hence \(\Vert x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y\Vert \leqslant \Vert x_0\hspace{1.111pt}{\otimes }\hspace{1.111pt}y_0\Vert \Vert A\Vert \Vert B\Vert \). Taking the infimum over all such A and B, it follows from (5.2) (with \(\backsimeq \) instead of \(=\)) and (5.3) that there exists a positive constant L (independent of (x, y)) such that \(\Vert x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y\Vert \leqslant L\vert \! \vert \! \vert x \vert \! \vert \! \vert \vert \! \vert \! \vert y \vert \! \vert \! \vert \). It follows that \(|\langle x,y\rangle | \leqslant L\vert \! \vert \! \vert x \vert \! \vert \! \vert \vert \! \vert \! \vert y \vert \! \vert \! \vert \).\(\square \)
be such that \(Ax_0=x\) and \(B^\# y_0=y\). Then \(x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y=A(x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y_0)B\), and hence \(\Vert x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y\Vert \leqslant \Vert x_0\hspace{1.111pt}{\otimes }\hspace{1.111pt}y_0\Vert \Vert A\Vert \Vert B\Vert \). Taking the infimum over all such A and B, it follows from (5.2) (with \(\backsimeq \) instead of \(=\)) and (5.3) that there exists a positive constant L (independent of (x, y)) such that \(\Vert x\hspace{1.111pt}{\otimes }\hspace{1.111pt}y\Vert \leqslant L\vert \! \vert \! \vert x \vert \! \vert \! \vert \vert \! \vert \! \vert y \vert \! \vert \! \vert \). It follows that \(|\langle x,y\rangle | \leqslant L\vert \! \vert \! \vert x \vert \! \vert \! \vert \vert \! \vert \! \vert y \vert \! \vert \! \vert \).\(\square \)
A normed algebra  over \({\mathbb {K}}\) is said to have minimality of norm topology if every continuous algebra norm on
over \({\mathbb {K}}\) is said to have minimality of norm topology if every continuous algebra norm on  is equivalent to \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \). The next corollary follows straightforwardly from Theorem 5.3.
is equivalent to \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \). The next corollary follows straightforwardly from Theorem 5.3.
Corollary 5.4
Let  be a primitive associative normed Q-algebra over \({\mathbb {K}}={\mathbb {R}}\) or \({\mathbb {C}}\) having a nonzero socle and minimality of norm topology. Let \({\mathbb {F}}\) stand for \({\mathbb {C}}\) if \({\mathbb {K}}={\mathbb {C}}\), and for \({\mathbb {R}},{\mathbb {C}}\), or \({\mathbb {H}}\) if \({\mathbb {K}}={\mathbb {R}}\). Then there exist a normed pairing \((X,Y, \langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) over \({\mathbb {F}}\), and a \({\mathbb {K}}\)-subalgebra
be a primitive associative normed Q-algebra over \({\mathbb {K}}={\mathbb {R}}\) or \({\mathbb {C}}\) having a nonzero socle and minimality of norm topology. Let \({\mathbb {F}}\) stand for \({\mathbb {C}}\) if \({\mathbb {K}}={\mathbb {C}}\), and for \({\mathbb {R}},{\mathbb {C}}\), or \({\mathbb {H}}\) if \({\mathbb {K}}={\mathbb {R}}\). Then there exist a normed pairing \((X,Y, \langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) over \({\mathbb {F}}\), and a \({\mathbb {K}}\)-subalgebra  of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) and contained in
of \(L(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) containing \(F(X,Y,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) and contained in  , such that
, such that  is bicontinuously isomorphic to
is bicontinuously isomorphic to  endowed with the operator norm. Moreover, if the associative normed Q-algebra
endowed with the operator norm. Moreover, if the associative normed Q-algebra  is in fact a complete normed algebra, then the pairing \((X,Y, \langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) above is a Banach pairing.
is in fact a complete normed algebra, then the pairing \((X,Y, \langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) above is a Banach pairing.
The next corollary follows from [41, Theorem 4.1]. Nevertheless, the proof we are going to provide, by combining Corollary 4.11 and Theorem 5.3, has its own interest.
Corollary 5.5
Let  be an infinite-dimensional complete normed primitive associative real or complex algebra with nonzero socle. Then ring derivations of
be an infinite-dimensional complete normed primitive associative real or complex algebra with nonzero socle. Then ring derivations of  are linear and continuous.
are linear and continuous.
Proof
Let D be a ring derivation of  . Then representing
. Then representing  as in Theorem 5.3, and applying Corollary 4.11, we realize that D is linear and \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous. Now the \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \)-continuity of D follows from a closed graph argument. Indeed, let \(A_n\) be a sequence in
as in Theorem 5.3, and applying Corollary 4.11, we realize that D is linear and \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous. Now the \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \)-continuity of D follows from a closed graph argument. Indeed, let \(A_n\) be a sequence in  such that \(\Vert \cdot \Vert \)-\(\lim _{\,n}A_n=0\) and \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \)-
such that \(\Vert \cdot \Vert \)-\(\lim _{\,n}A_n=0\) and \(\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert \)- . Then, since the mapping \(A\rightarrow A\) from
. Then, since the mapping \(A\rightarrow A\) from  to
to  is continuous, we have \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-\(\lim _{\,n}A_n=0\) and \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-\(\lim _{\,n}D(A_n)=B\). But, since D is \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous, this implies \(B=0\).\(\square \)
is continuous, we have \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-\(\lim _{\,n}A_n=0\) and \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-\(\lim _{\,n}D(A_n)=B\). But, since D is \(\left| \! \left| \! \left| \, \cdot \, \right| \! \right| \! \right| \)-continuous, this implies \(B=0\).\(\square \)
6 Additive derivations of Jordan algebras of a bilinear form
Let  be a non-associative ring. The centre of
be a non-associative ring. The centre of  is defined as the subset of
is defined as the subset of  consisting of those elements
consisting of those elements  such that
such that

where, for  , \([A,B]:=AB-BA\) and
, \([A,B]:=AB-BA\) and
By a derivation of  we mean any additive mapping
we mean any additive mapping  satisfying
satisfying
for all  . For such a mapping D, one easily check that the equalities \(D([A,B])=[D(A),B]+[A,D(B)]\) and
. For such a mapping D, one easily check that the equalities \(D([A,B])=[D(A),B]+[A,D(B)]\) and
hold for all  . As a consequence, we are provided with the following more general version of Lemma 4.1.
. As a consequence, we are provided with the following more general version of Lemma 4.1.
Lemma 6.1
The centre of a non-associative ring  is invariant under any derivation of
is invariant under any derivation of  .
.
From now on \({\mathfrak {F}}\) will denote a field of characteristic different from 2. Let X be a vector space over \({\mathfrak {F}}\), and let \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) be a symmetric bilinear form on X. Then the direct sum \(\mathfrak F \hspace{1.111pt}{\oplus }\hspace{1.111pt}X\) becomes a unital Jordan algebra over \({\mathfrak {F}}\) under de product:
Such a Jordan algebra will be denoted by \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). It is well known that, if \(\dim \hspace{0.55542pt}(X)\geqslant 2\), and if \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) is nondegenerate, then \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is simple, and its centre is equal to \({\mathfrak {F}}\) (see for example [10, Satz VII.3.5]).
Proposition 6.2
Let X be a vector space over \({\mathfrak {F}}\), and let \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) be a nondegenerate symmetric bilinear form on X. We have:
-
(i)
If T is a differential operator on X with associated derivation \(d:{\mathfrak {F}} \rightarrow {\mathfrak {F}}\), and if \(-T\) is an adjoint of T relative to the pairing \((X,X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), then the mapping
$$\begin{aligned} D_{(d,T)}:\lambda +x\rightarrow d(\lambda )+Tx \end{aligned}$$is an additive derivation of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\).
-
(ii)
If \(\dim \hspace{0.55542pt}(X)\geqslant 2\), then every additive derivation of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is of the form \(D_{(d,T)}\) for some couple (d, T) as in assertion \(\mathrm{(i)}\).
Proof
The proof of assertion (i) is left to the reader.
Suppose that \(\dim \hspace{0.55542pt}(X)\geqslant 2\), and let D be an additive derivation of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). We claim that D diagonalizes relative to the direct sum \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )={\mathfrak {F}}\hspace{1.111pt}{\oplus }\hspace{1.111pt}X\). Indeed, \({\mathfrak {F}}\) is invariant under D, as \({\mathfrak {F}}\) is the centre of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) and Lemma 6.1 applies. Now note that, if \(x,y\in X\), then \(xy\in {\mathfrak {F}}\). Let x be in X. Then \(x^2\in {\mathfrak {F}}\), hence \(D(x^2)\in {\mathfrak {F}}\). Write \(D(x)=\lambda +y\) with \(\lambda \in {\mathfrak {F}}\) and \(y\in X\). Then we have \(D(x^2)=2D(x)x=2(\lambda x+yx).\) Therefore, since both \(D(x^2)\) and yx lie in \({\mathfrak {F}}\), and \(x\in X\), we conclude that \(\lambda x=0\), and this implies that \(D(x)\in X\). Thus, since x is arbitrary in X, we have shown that X is invariant under D. Now that the claim has been proved, let d denote the restriction of D to \({\mathfrak {F}}\), regarded as a mapping from \({\mathfrak {F}}\) to \({\mathfrak {F}}\), and let T denote the restriction of D to X, regarded as a mapping from X to X. Then, with the help of (6.1) and (6.2), it is routine to verify that d is a ring derivation of \({\mathfrak {F}}\), that T is a differential operator on X with associated derivation d, that \(-T\) is an adjoint of T relative to the pairing \((X,X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), and that \(D=D_{(d,T)}\) in the sense of assertion (i). In this way, assertion (ii) has been proved.\(\square \)
Now the main result in this section reads as follows.
Theorem 6.3
Let \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) be a continuous nondegenerate symmetric bilinear form on an infinite-dimensional Banach space X over \({\mathbb {K}}\). Then the additive derivations of the complete normed Jordan algebra \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )={\mathbb {K}}\hspace{1.111pt}{\oplus }\hspace{1.111pt}X\) are precisely the mappings of the form \(D_A:\lambda +x\rightarrow Ax\) for some  such that
such that
Proof
Since linear operators on X are precisely those differential operators on X whose associated derivation is zero, it follows from Proposition 6.2 (i) that, for each  satisfying (6.3), \(D_A\) is an additive derivation of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\).
satisfying (6.3), \(D_A\) is an additive derivation of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\).
Let D be any additive derivation of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). Then, by Proposition 6.2 (ii), \(D=D_{(d,T)}\) for some couple (d, T) as in Proposition 6.2 (i). But T is a differential operator on X having an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \). Therefore, by Theorem 4.10, T is linear and continuous. Now the proof that \(D=D_A\), for some  satisfying (6.3), is concluded by taking \(A=T\).\(\square \)
satisfying (6.3), is concluded by taking \(A=T\).\(\square \)
Remark 6.4
Let \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) be a continuous nondegenerate symmetric bilinear form on an infinite-dimensional Banach space X over \({\mathbb {K}}\). Then, as a byproduct of Theorem 6.3, additive derivations of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) are linear and continuous. But, considering Remark 4.9 (b), this is well known [9, Proposition 3.3].
Remark 6.5
Let m be a natural number, and let X be a vector space over \({\mathbb {K}}\) of dimension m, and let \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) be a nondegenerate symmetric bilinear form on X. Then identifying X with \({\mathbb {K}}^m\) by means of a suitable basis, we have
for a suitable \(p\in \{0,1, \ldots , m\}\) with \(p=m\) in the case that \({\mathbb {K}}={\mathbb {C}}\) (see for example [40, Section 6.3]). Note that, given any ring derivation d of \({\mathbb {K}}\), the mapping \({\widehat{d}}:X\rightarrow X\) defined by
is a differential operator on X whose associated derivation is d, and that \(-{\widehat{d}}\) is an adjoint of \({\widehat{d}}\) relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \). Now let T be any differential operator on X. Then, according to [57, Theorem 1.4] (a reformulation of [62, Theorem 2.2] via Fact 1.1), there exist \(C\in L (X)\) and a ring derivation d of \({\mathbb {K}}\) such that \(T=C+{\widehat{d}}\). Therefore, \(-T\) is an adjoint of T relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) if and only if \(-C\) is an adjoint of C relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \). In this way we have proved that the differential operators T on X such that \(-T=T^\# \) are precisely the operators of the form \(C+{\widehat{d}}\), where \(C\in L (X)\) satisfies \(-C=C^\# \), and d is a ring derivation of \({\mathbb {K}}\). As a byproduct, there are discontinuous choices of such operators T, and hence, applying Proposition 6.2 (i), we realize that there are discontinuous ring derivations of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\). It follows that the restriction in Theorem 6.3 that X is infinite-dimensional cannot be removed. Anyway, the italized assertion above, together with Proposition 6.2, provides us with a precise description of all additive derivations of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) in the case that \(m\geqslant 2\).
§ 6.6 By a smooth normed algebra we mean a norm-unital normed algebra whose closed unit ball has a unique tangent hyperplane at the unit. According to [18, Proposition 2.6.2], \({\mathbb {C}}\) is the unique smooth normed complex algebra. However, considering that the closed unit ball of every nonzero pre-Hilbert space has a unique tangent hyperplane at any of its norm-one points, it turns out straightforward that, given an arbitrary real pre-Hilbert space \((X,(\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt}))\), the Jordan algebra \(J(X,-(\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt}))\) becomes a smooth normed real algebra under the norm \(\Vert \lambda +x\Vert _2:=\sqrt{|\lambda |^2+\Vert x\Vert ^2}\). But, according to [18, Definition 2.6.4 and Theorem 2.6.9], every commutative smooth normed real algebra is of the form \((J(X,-(\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt})),\Vert \hspace{1.111pt}{\cdot }\hspace{1.111pt}\Vert _2)\) for some real pre-Hilbert space \((X,(\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt}))\). Therefore, in the complete infinite-dimensional case, it follows from Theorem 6.3 that additive derivations of such an algebra are the mappings of the form \(\lambda +x\rightarrow Ax\) for some  which is skew-adjoint relative to the \(C^*\)-algebra involution of
which is skew-adjoint relative to the \(C^*\)-algebra involution of  .
.
As the next example shows, the restriction of completeness cannot be removed in the above discussion.
Example 6.7
Let I be any infinite set, let X denote the real vector space of all families \((\lambda _i)_{i\in I}\) of real numbers having only a finite number of nonzero terms, and let \((\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt}):X\hspace{1.111pt}{\times }\hspace{1.111pt}X\rightarrow {\mathbb {R}}\) be defined by \(((\lambda _i)| (\mu _i)):=\sum _{i\in I}\lambda _i\mu _i\). Then \((X,(\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt}))\) is a real pre-Hilbert space, and hence \(J(X,-(\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt}))\) is an infinite-dimensional smooth normed commutative real algebra under the norm \(\Vert \lambda +x\Vert _2:=\sqrt{\lambda ^2+\Vert x\Vert ^2}\). Now take a nonzero derivation d of \({\mathbb {R}}\), and define a mapping \(T:X\rightarrow X\) by \(T((\lambda _i)):=(d(\lambda _i))\). Then T is a differential operator on X whose associated derivation is d, and \(-T\) is an adjoint of T relative to \((\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt})\). Therefore, according to Proposition 6.2 (i), the mapping \(D:\lambda +x\rightarrow Tx\) is an additive derivation of \(J(X,-(\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt}))\). However, since T is not linear, there is no  such that \(D(\lambda +x)= Ax\) for every \((\lambda , x)\in {\mathbb {R}}\hspace{1.111pt}{\times }\hspace{1.111pt}X\).
such that \(D(\lambda +x)= Ax\) for every \((\lambda , x)\in {\mathbb {R}}\hspace{1.111pt}{\times }\hspace{1.111pt}X\).
§ 6.8 JB-algebras are complete normed Jordan real algebras which, roughly speaking, behave like the self-adjoint parts of \(C^*\)-algebras endowed with the Jordan product \(A\hspace{1.111pt}{\bullet }\hspace{1.111pt}B =\frac{1}{2}(AB+BA)\). In fact JB-algebras are defined as those complete normed Jordan real algebras  satisfying \(\Vert A\Vert ^{2}\leqslant \Vert A^{2}+B^{2}\Vert \) for all
satisfying \(\Vert A\Vert ^{2}\leqslant \Vert A^{2}+B^{2}\Vert \) for all  . JB-algebras enjoy a deep and complete structure theory, which is nicely collected in the book of Hanche–Olsen and Størmer [36]. Additional information on JB-algebras can be found in [18, Section 3.1 and Subsection 3.4.1] and [19, Theorems 5.1.29 (i) and 5.1.38].
. JB-algebras enjoy a deep and complete structure theory, which is nicely collected in the book of Hanche–Olsen and Størmer [36]. Additional information on JB-algebras can be found in [18, Section 3.1 and Subsection 3.4.1] and [19, Theorems 5.1.29 (i) and 5.1.38].
In the structure theory of JB-algebras, the so-called JB-spin factors have special relevance. To introduce them, consider any real Hilbert space \((X,(\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt}))\) with \(\dim \hspace{0.55542pt}(X)\geqslant 2\). Then, according to [36, Lemma 6.1.3], \(J(X,(\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt}))\) is a JB-algebra under the norm \(\Vert \lambda +x\Vert _1:=|\lambda |+\Vert x\Vert \). Now, by definition, JB-spin factors are nothing other than the JB-algebras obtained by the procedure just described. Therefore, as in the case of infinite-dimensional complete smooth normed real algebras, discussed in \(\S \) 6.6, additive derivations of any infinite-dimensional JB-spin factor are the mappings of the form \(\lambda +x\rightarrow Ax\) for some  which is skew-adjoint relative to the \(C^*\)-algebra involution of
which is skew-adjoint relative to the \(C^*\)-algebra involution of  . This result can be also derived form Remark 6.4 and [66, Example 2.3].
. This result can be also derived form Remark 6.4 and [66, Example 2.3].
§ 6.9 Let  be an algebra over \({\mathbb {K}}\). We say that
be an algebra over \({\mathbb {K}}\). We say that  is quadratic if it is unital and, for every
is quadratic if it is unital and, for every  , \(a^2\) lies in the linear hull of \(\{{{\textbf {1}}},a\}\). As a consequence of [18, Proposition 2.5.13], the commutative quadratic algebras over \({\mathbb {K}}\) are precisely those of the form \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) for some vector space X over \({\mathbb {K}}\), and some symmetric bilinear form \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) on X.
, \(a^2\) lies in the linear hull of \(\{{{\textbf {1}}},a\}\). As a consequence of [18, Proposition 2.5.13], the commutative quadratic algebras over \({\mathbb {K}}\) are precisely those of the form \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) for some vector space X over \({\mathbb {K}}\), and some symmetric bilinear form \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt}, \hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) on X.
\(JB^*\)-algebras are defined as those complete normed Jordan complex algebras  endowed with a conjugate-linear algebra involution \(*\) satisfying \(\Vert U_{A}(A^*)\Vert =\Vert A\Vert ^{3}\) for every
endowed with a conjugate-linear algebra involution \(*\) satisfying \(\Vert U_{A}(A^*)\Vert =\Vert A\Vert ^{3}\) for every  . \(C^*\)-algebras, endowed with the Jordan product \(A\hspace{1.111pt}{\bullet }\hspace{1.111pt}B =\frac{1}{2}(AB+BA)\), become examples of \(JB^*\)-algebras. Thus, in some sense, \(JB^*\)-algebras generalize \(C^*\)-algebras. Actually, in a very precise sense, \(JB^*\)-algebras become the largest possible generalization of \(C^*\)-algebras (see [18, Definitions 3.3.1 and 3.5.29, and Proposition 3.5.31] and [19, Theorem 5.9.9 and Corollary 5.9.12]). Since Wright’s pioneering paper [69], \(JB^*\)-algebras have been studied in depth. The reader is referred to [18, 19, 56] for a full overview of their theory.
. \(C^*\)-algebras, endowed with the Jordan product \(A\hspace{1.111pt}{\bullet }\hspace{1.111pt}B =\frac{1}{2}(AB+BA)\), become examples of \(JB^*\)-algebras. Thus, in some sense, \(JB^*\)-algebras generalize \(C^*\)-algebras. Actually, in a very precise sense, \(JB^*\)-algebras become the largest possible generalization of \(C^*\)-algebras (see [18, Definitions 3.3.1 and 3.5.29, and Proposition 3.5.31] and [19, Theorem 5.9.9 and Corollary 5.9.12]). Since Wright’s pioneering paper [69], \(JB^*\)-algebras have been studied in depth. The reader is referred to [18, 19, 56] for a full overview of their theory.
From a purely algebraic point of view, quadratic Jordan complex \(H^*\)-algebras (see Definition 7.15 below) and quadratic \(JB^*\)-algebras are the same. Indeed, according to [22, Theorem 2 (3)] and [18, Corollary 3.5.7], in dimension \(\geqslant 3\) they are of the form \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\), where X is a complex Hilbert space, \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) is defined by \(\langle x,y\rangle :=(x\,{|}\,y^\natural )\) for all \(x,y\in X\), \(\natural \) denotes the essentially unique conjugation (i.e. isometric conjugate-linear involutive operator) on X [36, Lemma 7.5.6], and \((\lambda +x)^*:={\overline{\lambda }}+x^\natural \) for all \(\lambda \in {\mathbb {C}}\) and \(x\in X\). In the \(H^*\)-algebra case, the inner product is given by \((\lambda +x\,{|}\,\mu +y):=\lambda \overline{\mu }+(x\,{|}\,y)\), whereas, in the \(JB^*\)-algebra case, the norm of the algebra can be suitably reconstructed from \(\natural \) and the inner product of X in such a way that its topology extends those of \({\mathbb {C}}\) and X.
Now let X and \(\natural \) be as above, and for  define
define  by \(B^\natural x:=(Bx^\natural )^\natural \). Set \(\langle x,y\rangle :=(x\,{|}\,y^\natural )\) for all \(x,y\in X\). Then for
by \(B^\natural x:=(Bx^\natural )^\natural \). Set \(\langle x,y\rangle :=(x\,{|}\,y^\natural )\) for all \(x,y\in X\). Then for  satisfying (6.3) and all \(x,y\in X\) we have
satisfying (6.3) and all \(x,y\in X\) we have
and hence  . Since \(*\) and \(\natural \) commute on
. Since \(*\) and \(\natural \) commute on  , it follows from Theorem 6.3 that, when an infinite-dimensional quadratic Jordan complex \(H^*\)-algebra or an infinite-dimensional quadratic \(JB^*\)-algebra is regarded as in the above paragraph, the additive derivations of the algebra are precisely the mappings of the form \(\lambda +x\rightarrow Ax\), where
, it follows from Theorem 6.3 that, when an infinite-dimensional quadratic Jordan complex \(H^*\)-algebra or an infinite-dimensional quadratic \(JB^*\)-algebra is regarded as in the above paragraph, the additive derivations of the algebra are precisely the mappings of the form \(\lambda +x\rightarrow Ax\), where  is skew-symmetric relative to the involutive linear \(*\)-antiautomorphism \(\tau \) of
is skew-symmetric relative to the involutive linear \(*\)-antiautomorphism \(\tau \) of  defined by \(\tau (B):=(B^*)^\natural \).
defined by \(\tau (B):=(B^*)^\natural \).
We conclude this section with the following.
Corollary 6.10
Let Z be an infinite-dimensional reflexive real or complex Banach space. Set \(X:=Z\hspace{1.111pt}{\oplus }\hspace{1.111pt}Z'\) and \(\langle z+f,w+g\rangle :=f(w)+g(z)\) for all \(z,w\in Z\) and \(f,g\in Z'\). Then the additive derivations of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) are precisely the mappings of the form
where \(A:Z\rightarrow Z\),  , and \(C:Z\rightarrow Z'\) are continuous linear mappings such that
, and \(C:Z\rightarrow Z'\) are continuous linear mappings such that  and
and  .
.
Proof
It is clear that \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \) is a continuous nondegenerate symmetric bilinear form on X. For the sake of convenience, let us write
\(\bigr \langle \bigl ({\begin{matrix} z \\ f \end{matrix}}\bigr ), \bigl ({\begin{matrix} w \\ g \end{matrix}}\bigr )\bigr \rangle = f(w)+g(z),\) and, for  , \(H =\bigl ( {\begin{matrix} A &{} B \\ C &{} D \end{matrix}}\bigr )\), where \(A:Z\rightarrow Z\),
, \(H =\bigl ( {\begin{matrix} A &{} B \\ C &{} D \end{matrix}}\bigr )\), where \(A:Z\rightarrow Z\),  , \(C:Z\rightarrow Z'\) and
, \(C:Z\rightarrow Z'\) and  are continuous linear mappings such that \(H \bigl ({\begin{matrix} z \\ f \end{matrix}} \bigr ) = \bigl ({\begin{matrix} A &{} B \\ C &{} D \end{matrix}}\bigr )\bigl ( {\begin{matrix} z \\ f \end{matrix}}\bigr ) =\bigl ({\begin{matrix} Az+Bf \\ Cz+Df \end{matrix}}\bigr )\). By Theorem 6.3, derivations of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle ) \) are of the form
are continuous linear mappings such that \(H \bigl ({\begin{matrix} z \\ f \end{matrix}} \bigr ) = \bigl ({\begin{matrix} A &{} B \\ C &{} D \end{matrix}}\bigr )\bigl ( {\begin{matrix} z \\ f \end{matrix}}\bigr ) =\bigl ({\begin{matrix} Az+Bf \\ Cz+Df \end{matrix}}\bigr )\). By Theorem 6.3, derivations of \(J(X,\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle ) \) are of the form

for some  satisfying
satisfying

Therefore, writing H as a matrix as above, we have
or equivalently
Taking \(f=0\) and \(w=0\), we obtain \(g(Az) = - (Dg)(z)\), and hence \(D=-A'\). Taking \(f=g=0\), we get \((Cz)(w) = - (Cw)(z)\), and hence, identifying Z with \(Z''\) via the canonical injection, we see that \(C'\!=-C\). Analogously, taking \(z=w=0\), we obtain that \(B'\!=-B.\) \(\square \)
7 Additive derivations of non-associative \(H^*\)-algebras
7.1 Auxiliary results
In what follows  will denote a non-associative ring, and
will denote a non-associative ring, and  will stand for the associative ring of all additive mappings from
will stand for the associative ring of all additive mappings from  to
to  . The centroid of
. The centroid of  is defined as the subring of
is defined as the subring of  consisting of those
consisting of those  such that
such that
for all  , and is denoted by
, and is denoted by  . For
. For  and
and  , we write \(\lambda A\) instead of \(\lambda (A)\).
, we write \(\lambda A\) instead of \(\lambda (A)\).
Proposition 7.1
Let D be a derivation of  . Then there exists a derivation d of \(\Gamma (R)\) such that \(D(\lambda A)=\lambda D(A)+d(\lambda )A\) for every
. Then there exists a derivation d of \(\Gamma (R)\) such that \(D(\lambda A)=\lambda D(A)+d(\lambda )A\) for every  .
.
Proof
Note that the equalities (7.1) can be read as that a mapping  lies in
lies in  if and only if \([L_A,\lambda ]=0\) and \([R_A,\lambda ]=0\) for every
if and only if \([L_A,\lambda ]=0\) and \([R_A,\lambda ]=0\) for every  , where \(L_A\) and \(R_A\) denote the operators of left and right multiplication by A. Note also that the equality (6.1) is equivalent to \([D,L_A]=L_{D(A)}\) for every
, where \(L_A\) and \(R_A\) denote the operators of left and right multiplication by A. Note also that the equality (6.1) is equivalent to \([D,L_A]=L_{D(A)}\) for every  , or to \([D,R_A]=R_{D(A)}\) for every
, or to \([D,R_A]=R_{D(A)}\) for every  . These facts will be applied in what follows without notice.
. These facts will be applied in what follows without notice.
Let A and \(\lambda \) be in  and
and  , respectively. Then
, respectively. Then
and analogously \(0=[R_A,[D, \lambda ]]\). Therefore, since A is arbitrary in  , we realize that \([D,\lambda ]\) lies in
, we realize that \([D,\lambda ]\) lies in  . Thus
. Thus  because \(\lambda \) is arbitrary in
because \(\lambda \) is arbitrary in  . This allows us to consider the mapping
. This allows us to consider the mapping  defined by \(d(\lambda ):=[D,\lambda ]\). Clearly, d is a derivation of
defined by \(d(\lambda ):=[D,\lambda ]\). Clearly, d is a derivation of  . Moreover, for
. Moreover, for  and
and  we have
we have
\(\square \)
The annihilator of  is defined as the ideal of
is defined as the ideal of  consisting of those elements
consisting of those elements  such that
such that  , and is denoted by
, and is denoted by  . Now, arguing as in the case of algebras [18, Proposition 1.1.11 (i)], we obtain the following.
. Now, arguing as in the case of algebras [18, Proposition 1.1.11 (i)], we obtain the following.
Fact 7.2
If  has zero annihilator, then
has zero annihilator, then  is a commutative ring.
is a commutative ring.
In what follows \({\mathfrak {F}}\) will denote a field, and  will stand for an algebra over \({\mathfrak {F}}\). Usually, the algebra centroid
will stand for an algebra over \({\mathfrak {F}}\). Usually, the algebra centroid  of
of  is defined as the set of all linear operators \(\lambda \) on
is defined as the set of all linear operators \(\lambda \) on  satisfying the equalities (7.1) for all
satisfying the equalities (7.1) for all  . But, regarded
. But, regarded  as a non-associative ring, we may think about
as a non-associative ring, we may think about  in the sense defined above. To avoid any confusion, we will say that
in the sense defined above. To avoid any confusion, we will say that  is the additive centroid of
is the additive centroid of  .
.
Proposition 7.3
Suppose that  has zero annihilator. Then the additive centroid of
has zero annihilator. Then the additive centroid of  coincides with the algebra centroid of
coincides with the algebra centroid of  .
.
Proof
The inclusions  are clear. Moreover
are clear. Moreover  is the set of those operators in
is the set of those operators in  which commute with all elements in
which commute with all elements in  . Therefore, since
. Therefore, since  has zero annihilator, it follows from Fact 7.2 that
has zero annihilator, it follows from Fact 7.2 that  , as desired.\(\square \)
, as desired.\(\square \)
A proof of the above proposition, which avoids Fact 7.2, can be found in the argument of [41, Remark 4.2]. Indeed, let T be in  , let A, B be in
, let A, B be in  , and let \(\lambda \) be in \({\mathfrak {F}}\). Then
, and let \(\lambda \) be in \({\mathfrak {F}}\). Then
Therefore \(T(\lambda A)-\lambda T(A)=0\) because B is arbitrary in  and
and  has zero annihilator. The arbitrariness of
has zero annihilator. The arbitrariness of  and \(\lambda \in {\mathfrak {F}}\) yields
and \(\lambda \in {\mathfrak {F}}\) yields  , as desired.
, as desired.
Following [18, Definition 1.1.10], we say that  is central over \({\mathfrak {F}}\) if the algebra centroid of
is central over \({\mathfrak {F}}\) if the algebra centroid of  reduces to
reduces to  . Now, combining Propositions 7.1 and 7.3, we obtain the following
. Now, combining Propositions 7.1 and 7.3, we obtain the following
Proposition 7.4
Suppose that  is central over \({\mathfrak {F}}\) and has zero annihilator. Let D be an additive derivation of
is central over \({\mathfrak {F}}\) and has zero annihilator. Let D be an additive derivation of  . Then D is a differential operator on (the vector space of)
. Then D is a differential operator on (the vector space of)  .
.
The subalgebra of  generated by all operators of left and right multiplication on
generated by all operators of left and right multiplication on  by elements of
by elements of  is called the multiplication ideal of
is called the multiplication ideal of  , and is denoted by
, and is denoted by  .
.
Fact 7.5
The subring of  generated by all operators of left and right multiplication on
generated by all operators of left and right multiplication on  by elements of
by elements of  coincides with
coincides with  .
.
Proof
Let \({\mathfrak {S}}\) denote the subset of  consisting of all finite sums of products of the form
consisting of all finite sums of products of the form  , where \(n\in {\mathbb {N}}\) and, for \(1\leqslant i\leqslant n\), \(M_{A_i}\) is equal to either \(L_{A_i}\) or \(R_{A_i}\). Then \(\mathfrak S\) is a subring of
, where \(n\in {\mathbb {N}}\) and, for \(1\leqslant i\leqslant n\), \(M_{A_i}\) is equal to either \(L_{A_i}\) or \(R_{A_i}\). Then \(\mathfrak S\) is a subring of  containing all operators of left and right multiplication on
containing all operators of left and right multiplication on  by elements of
by elements of  , and is contained in any subring of
, and is contained in any subring of  containing such operators. Therefore \({\mathfrak {S}}\) is the subring of
containing such operators. Therefore \({\mathfrak {S}}\) is the subring of  generated by all operators of left and right multiplication on
generated by all operators of left and right multiplication on  by elements of
by elements of  . Since clearly
. Since clearly  , and \({\mathfrak {S}}\) is a subalgebra of
, and \({\mathfrak {S}}\) is a subalgebra of  (as \(\lambda M_A=M_{\lambda A}\) for all \(\lambda \in {\mathfrak {F}}\) and
(as \(\lambda M_A=M_{\lambda A}\) for all \(\lambda \in {\mathfrak {F}}\) and  ), the equality
), the equality  follows.\(\square \)
follows.\(\square \)
Lemma 7.6
Let D be an additive derivation of  , and let B be in
, and let B be in  . Then [B, D] lies in
. Then [B, D] lies in  .
.
Proof
The set  is a subring of
is a subring of  containing the generators of
containing the generators of  , and hence, by Fact 7.5, contains
, and hence, by Fact 7.5, contains  . Therefore
. Therefore  . \(\square \)
. \(\square \)
Set  . Then \({\mathscr {M}} ({\mathscr {A}})\) is the so-called multiplication algebra of
. Then \({\mathscr {M}} ({\mathscr {A}})\) is the so-called multiplication algebra of  , and is indeed the subalgebra of
, and is indeed the subalgebra of  generated by
generated by  and all operators of left and right multiplication on
and all operators of left and right multiplication on  by elements of
by elements of  .
.
Proposition 7.7
Suppose that  is central over \({\mathfrak {F}}\) and has zero annihilator. Let D be an additive derivation of
is central over \({\mathfrak {F}}\) and has zero annihilator. Let D be an additive derivation of  , and let B be in
, and let B be in  . Then [B, D] lies in
. Then [B, D] lies in  .
.
Proof
Write  with \(\lambda \in {\mathfrak {F}}\) and
with \(\lambda \in {\mathfrak {F}}\) and  . By Lemma 7.6,
. By Lemma 7.6,  . Moreover, by Proposition 7.4,
. Moreover, by Proposition 7.4,  . Therefore
. Therefore

\(\square \)
Direct summands of  are defined as those ideals
are defined as those ideals  of
of  that there is another ideal
that there is another ideal  of
of  satisfying
satisfying  . Now, arguing as in the case where \({\mathfrak {F}}={\mathbb {K}}:={\mathbb {R}}\) or \({\mathbb {C}}\), and derivations are assumed to be linear [19, Lemma 8.1.40], and noticing that both restrictions are unnecessary in the argument, we obtain the following.
. Now, arguing as in the case where \({\mathfrak {F}}={\mathbb {K}}:={\mathbb {R}}\) or \({\mathbb {C}}\), and derivations are assumed to be linear [19, Lemma 8.1.40], and noticing that both restrictions are unnecessary in the argument, we obtain the following.
Fact 7.8
Suppose that  has zero annihilator. Then direct summands of
has zero annihilator. Then direct summands of  are invariant under any additive derivation of
are invariant under any additive derivation of  .
.
From now on, we suppose that \({\mathfrak {F}}={\mathbb {K}}:={\mathbb {R}}\) or \({\mathbb {C}}\), and that  actually is a normed algebra.
actually is a normed algebra.
Fact 7.9
The inclusion  holds.
holds.
Proof
 is a subalgebra of L(A) containing the generators of
is a subalgebra of L(A) containing the generators of  . Therefore the result follows.\(\square \)
. Therefore the result follows.\(\square \)
Lemma 7.10
Suppose that  has zero annihilator. Let D be an additive derivation of
has zero annihilator. Let D be an additive derivation of  , and let
, and let  be a family of ideals of
be a family of ideals of  such that
such that  is dense in
is dense in  . We have:
. We have:
-
(i)
If D is linear on each
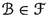 , then D is linear.
, then D is linear. -
(ii)
If actually the normed algebra
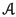 is complete, and if D is linear and continuous on each
is complete, and if D is linear and continuous on each 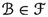 , then D is linear and continuous.
, then D is linear and continuous.
Proof
Suppose that D is linear on each  . Then for \(\lambda \in {\mathbb {K}}\),
. Then for \(\lambda \in {\mathbb {K}}\),  ,
,  , and
, and  we have
we have
(as AB lies in  ), and analogously \(B(D(\lambda A)-\lambda D(A))=0\). Therefore, since
), and analogously \(B(D(\lambda A)-\lambda D(A))=0\). Therefore, since  is arbitrary in
is arbitrary in  , and B is arbitrary in
, and B is arbitrary in  , and
, and  is dense in
is dense in  , we derive that \(D(\lambda A)-\lambda D(A)\) lies in the annihilator of
, we derive that \(D(\lambda A)-\lambda D(A)\) lies in the annihilator of  . Since
. Since  has zero annihilator, and \(\lambda \) is arbitrary in \({\mathbb {K}}\), and A is arbitrary in
has zero annihilator, and \(\lambda \) is arbitrary in \({\mathbb {K}}\), and A is arbitrary in  , the proof of (i) is concluded.
, the proof of (i) is concluded.
Now suppose that  is complete and that D is linear and continuous on each
is complete and that D is linear and continuous on each  . Then, by assertion (i) just proved, D is linear. Therefore, since
. Then, by assertion (i) just proved, D is linear. Therefore, since  is complete, to prove the continuity of D it is enough to show that D has closed graph. But this can be done by arguing as in the last paragraph of the proof of [19, Theorem 8.1.41]. Indeed, let \({{A}_{n}{}}\) be a sequence in
is complete, to prove the continuity of D it is enough to show that D has closed graph. But this can be done by arguing as in the last paragraph of the proof of [19, Theorem 8.1.41]. Indeed, let \({{A}_{n}{}}\) be a sequence in  such that \(\lim A_{n} = 0\) and \(\lim D(A_{n}) = A\) for some
such that \(\lim A_{n} = 0\) and \(\lim D(A_{n}) = A\) for some  . Then for
. Then for  and
and  we have
we have
and in the same way \(BA = 0.\) Therefore, since  is arbitrary in
is arbitrary in  , and B is arbitrary in
, and B is arbitrary in  , and
, and  is dense in
is dense in  , we derive that \(A=0\). Thus assertion (ii) has been proved.\(\square \)
, we derive that \(A=0\). Thus assertion (ii) has been proved.\(\square \)
Lemma 7.11
Let X be a normed space over \({\mathbb {K}}\), let T be a differential operator on X. Suppose that there exists a nonzero linear functional f on X (continuity of f is not required) such that fT is continuous. Then T is linear.
Proof
Let d denote the ring derivation of \({\mathbb {K}}\) associated to T. Take \(x\in X\) such that \(f(x)=1\). Then \(d(\lambda )=fT(\lambda x)-\lambda fTx\) for every \(\lambda \in {\mathbb {K}}\), and hence d is continuous. Therefore, by Remark 4.9 (b), \(d=0\).\(\square \)
Proposition 7.12
Let  be a topologically simple complete normed central algebra over \({\mathbb {K}}\), and let D be an additive derivation of
be a topologically simple complete normed central algebra over \({\mathbb {K}}\), and let D be an additive derivation of  . Suppose that there exists a nonzero continuous linear functional f on
. Suppose that there exists a nonzero continuous linear functional f on  such that fD is continuous. Then D is linear and continuous.
such that fD is continuous. Then D is linear and continuous.
Proof
By Proposition 7.4 and Lemma 7.11, D is linear. Let \({\mathfrak {S}}(D)\) denote the separating space of D. Then  is a closed subspace of
is a closed subspace of  [18, Lemma 1.1.57], and \({\mathfrak {S}}(D)\subseteq \ker \hspace{0.55542pt}(f)\), which implies that
[18, Lemma 1.1.57], and \({\mathfrak {S}}(D)\subseteq \ker \hspace{0.55542pt}(f)\), which implies that  . But it is straightforward that the separating space of any linear derivation of any normed algebra over \({\mathbb {K}}\) is an ideal of the algebra. Therefore \({\mathfrak {S}}(D)=0\), as
. But it is straightforward that the separating space of any linear derivation of any normed algebra over \({\mathbb {K}}\) is an ideal of the algebra. Therefore \({\mathfrak {S}}(D)=0\), as  is topologically simple. Then, by [18, Fact 1.1.56], D is continuous.\(\square \)
is topologically simple. Then, by [18, Fact 1.1.56], D is continuous.\(\square \)
Generalized complemented normed algebras over \({\mathbb {K}}\) are defined as those normed algebras over \({\mathbb {K}}\) having zero annihilator and satisfying the property that all their closed ideals are direct summands (compare [19, Fact 5.1.2]). For later application, we note that, as a consequence of [19, Lemma 5.1.1], generalized complemented normed algebras over \({\mathbb {K}}\) are semiprime. Moreover, according to [32] (see also [19, Theorem 8.2.44 (ii)]), if  is a generalized complemented complete normed algebra over \({\mathbb {K}}\) with zero weak radical, and if
is a generalized complemented complete normed algebra over \({\mathbb {K}}\) with zero weak radical, and if  stands for the family of its minimal closed ideals, then for each
stands for the family of its minimal closed ideals, then for each  there exists a unique summable family \(\{A_i\}_{i\in I}\) in
there exists a unique summable family \(\{A_i\}_{i\in I}\) in  such that
such that  for every \(i\in I\), and \(A=\sum _{i\in I}A_i\). (For the meaning of the weak radical of an algebra over \({\mathbb {K}}\), the reader is referred to [18, Definition 4.4.39].)
for every \(i\in I\), and \(A=\sum _{i\in I}A_i\). (For the meaning of the weak radical of an algebra over \({\mathbb {K}}\), the reader is referred to [18, Definition 4.4.39].)
Lemma 7.13
Let  be a generalized complemented complete normed algebra over \({\mathbb {K}}\) with zero weak radical, let
be a generalized complemented complete normed algebra over \({\mathbb {K}}\) with zero weak radical, let  stand for the family of its minimal closed ideals, let A be in
stand for the family of its minimal closed ideals, let A be in  , and let \(\{A_i\}_{i\in I}\) be the unique summable family in
, and let \(\{A_i\}_{i\in I}\) be the unique summable family in  such that
such that  for every \(i\in I\) and \(A=\sum _{i\in I}A_i\). Let
for every \(i\in I\) and \(A=\sum _{i\in I}A_i\). Let  be an additive derivation. Then the family \(\{D(A_i)\}_{i\in I}\) is summable in
be an additive derivation. Then the family \(\{D(A_i)\}_{i\in I}\) is summable in  with sum equal to D(A).
with sum equal to D(A).
Proof
Let \(\{B_i\}_{i\in I}\) be the unique summable family in  such that
such that  for every \(i\in I\) and \(D(A)=\sum _{i\in I}B_i\). It is enough to show that \(B_j=D(A_j)\) for every \(j\in I\). Let j be in I. Then both families \(\{A_i\}_{i\in I\hspace{1.111pt}{\setminus }\hspace{1.111pt}\{j\}}\) and \(\{B_i\}_{i\in I\setminus \{j\}}\) are summable in
for every \(i\in I\) and \(D(A)=\sum _{i\in I}B_i\). It is enough to show that \(B_j=D(A_j)\) for every \(j\in I\). Let j be in I. Then both families \(\{A_i\}_{i\in I\hspace{1.111pt}{\setminus }\hspace{1.111pt}\{j\}}\) and \(\{B_i\}_{i\in I\setminus \{j\}}\) are summable in  , and we have \(D(A)=B_j+\sum _{i\in I\setminus \{j\}}B_i\) and
, and we have \(D(A)=B_j+\sum _{i\in I\setminus \{j\}}B_i\) and
Therefore, since \(B_j\) and \(D(A_j)\) belong to  (the latest by Fact 7.8), and \(\sum _{i\in I{\setminus } \{j\}}B_i\) and \(D\bigl (\sum _{i\in I{\setminus } \{j\}}A_i\bigr )\) belong to
(the latest by Fact 7.8), and \(\sum _{i\in I{\setminus } \{j\}}B_i\) and \(D\bigl (\sum _{i\in I{\setminus } \{j\}}A_i\bigr )\) belong to  (the latest by Fact 7.8 again), and \({\mathscr {A}}_j\cap {\mathscr {B}}=0\) (by semiprimeness of
(the latest by Fact 7.8 again), and \({\mathscr {A}}_j\cap {\mathscr {B}}=0\) (by semiprimeness of  and [19, Fact 6.1.75]), it follows that \(B_j=D(A_j)\), as desired.\(\square \)
and [19, Fact 6.1.75]), it follows that \(B_j=D(A_j)\), as desired.\(\square \)
Proposition 7.14
Let  be a generalized complemented complete normed algebra over \({\mathbb {K}}\) with zero weak radical, and let
be a generalized complemented complete normed algebra over \({\mathbb {K}}\) with zero weak radical, and let  be an additive derivation. Let \({\mathscr {F}}\) denote the family of those minimal closed ideals
be an additive derivation. Let \({\mathscr {F}}\) denote the family of those minimal closed ideals  of
of  such that the restriction of D to
such that the restriction of D to  is discontinuous. Then
is discontinuous. Then  is finite.
is finite.
Proof
Let  denote the family of all minimal closed ideals of
denote the family of all minimal closed ideals of  . To derive a contradiction, assume that there exists an infinite sequence \(i_n\) of pair-wise different elements of I such that, for every \(n\in {\mathbb {N}}\), the restriction of D to
. To derive a contradiction, assume that there exists an infinite sequence \(i_n\) of pair-wise different elements of I such that, for every \(n\in {\mathbb {N}}\), the restriction of D to  is discontinuous. Then, by Remark 4.9 (a), for each \(n\in {\mathbb {N}}\) there is
is discontinuous. Then, by Remark 4.9 (a), for each \(n\in {\mathbb {N}}\) there is  such that \(\Vert B_n\Vert \leqslant \frac{1}{2^n}\) and \(\Vert D(B_n)\Vert \geqslant 1\). Now let \(\{A_i\}_{i\in I}\) be the family of elements of
such that \(\Vert B_n\Vert \leqslant \frac{1}{2^n}\) and \(\Vert D(B_n)\Vert \geqslant 1\). Now let \(\{A_i\}_{i\in I}\) be the family of elements of  defined by \(A_i:=0\) if \(i\ne i_n\) for every \(n\in {\mathbb {N}}\), and \(A_{i_n}:=B_n\) otherwise. Then, by [21, Proposition VII.9.18], the family \(\{A_i\}_{i\in I}\) is summable in
defined by \(A_i:=0\) if \(i\ne i_n\) for every \(n\in {\mathbb {N}}\), and \(A_{i_n}:=B_n\) otherwise. Then, by [21, Proposition VII.9.18], the family \(\{A_i\}_{i\in I}\) is summable in  . Set \(A:=\sum _{i\in I}A_i\), and note that
. Set \(A:=\sum _{i\in I}A_i\), and note that  for every \(i\in I\). It follows from Lemma 7.13 that the family \(\{D(A_i)\}_{i\in I}\) is summable in
for every \(i\in I\). It follows from Lemma 7.13 that the family \(\{D(A_i)\}_{i\in I}\) is summable in  , and hence, by [21, Corollary VII.9.6 and Proposition VII.9.8], the set \(\{i\in I\,{:}\,\Vert D(A_i)\Vert \geqslant 1\}\) is finite. But this is not possible because \(\Vert D(A_{i_n})\Vert \geqslant 1\) for every \(n\in {\mathbb {N}}\).\(\square \)
, and hence, by [21, Corollary VII.9.6 and Proposition VII.9.8], the set \(\{i\in I\,{:}\,\Vert D(A_i)\Vert \geqslant 1\}\) is finite. But this is not possible because \(\Vert D(A_{i_n})\Vert \geqslant 1\) for every \(n\in {\mathbb {N}}\).\(\square \)
7.2 The main result
Definition 7.15
We recall that semi-\(H^*\)-algebras are defined as those real or complex algebras X which are also Hilbert spaces, and are endowed with a conjugate-linear vector space involution \(*\) satisfying
\(H^*\)-algebras are defined as those semi-\(H^*\)-algebras whose involution \(*\) is an algebra involution. We remark that, up to the multiplication of the inner product by a suitable positive number, semi-\(H^*\)-algebras become complete normed algebras [18, Lemma 2.8.12 (i)].
Since the pioneering papers of Ambrose [2] and Kaplansky [43] determining associative complex and real \(H^*\)-algebras, respectively, the study of \(H^*\)-algebras into the most familiar classes of non-associative algebras (such a Jordan [7, 26, 27, 29, 30, 53, 54], Lie [3, 4, 6, 12, 24, 28, 49, 60, 61, 65], and Malcev algebras [13, 16, 70]), has attained a complete development, getting in particular the determination of those \(H^*\)-algebras in such classes. Nevertheless, concerning our current goal, we should pay attention to the approach to (semi-)\(H^*\)-algebras from a general non-associative point of view, such as is done in [6, 14,15,16,17, 25, 26, 54, 55, 67]. Anyway, for a full discussion of the theory of (semi-)\(H^*\)-algebras, the reader is referred to [18, Subsection 2.8.2], [19, Section 8.1], and [23].
From now on, X will denote a semi-\(H^*\)-algebra over \({\mathbb {K}}\). For  we denote by \(A^\bullet \) the unique operator in
we denote by \(A^\bullet \) the unique operator in  such that \((Ax\,{|}\,y)=(x\,{|}\,A^\bullet y)\) for all \(x,y\in X\). We adopt this notation because \(\bullet \) is a purely Hilbert-space notion, and hence, a priori, it has nothing to do with the involution \(*\) of X, and moreover the classical symbol \(A^*\) for the adjoint of A relative to \((\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt})\) could be confused with the (possibly discontinuous) linear operator on X defined by \(A^*x:=(Ax^*)^*\). Nevertheless, given \(x\in X\), the equalities (7.2) read as that
such that \((Ax\,{|}\,y)=(x\,{|}\,A^\bullet y)\) for all \(x,y\in X\). We adopt this notation because \(\bullet \) is a purely Hilbert-space notion, and hence, a priori, it has nothing to do with the involution \(*\) of X, and moreover the classical symbol \(A^*\) for the adjoint of A relative to \((\hspace{1.111pt}{\cdot }\hspace{1.111pt}|\hspace{1.111pt}{\cdot }\hspace{1.111pt})\) could be confused with the (possibly discontinuous) linear operator on X defined by \(A^*x:=(Ax^*)^*\). Nevertheless, given \(x\in X\), the equalities (7.2) read as that  and \((R_x)^\bullet =R_{x^*}\). Therefore, since
and \((R_x)^\bullet =R_{x^*}\). Therefore, since  (by Fact 7.9), and \(\bullet \) is a conjugate-linear algebra involution on
(by Fact 7.9), and \(\bullet \) is a conjugate-linear algebra involution on  taking the set of generators of
taking the set of generators of  into such a set, we obtain the following well-known result.
into such a set, we obtain the following well-known result.
Fact 7.16
 is a \(\bullet \)-invariant subalgebra of
is a \(\bullet \)-invariant subalgebra of  .
.
Since topologically simple complex semi-\(H^*\)-algebras are central over \({\mathbb {C}}\) [19, Lemma 8.1.29] and have zero annihilator, we can combine Proposition 7.4, Fact 1.1, and Propositions 7.7 and 7.12 (in this order) to obtain the following.
Proposition 7.17
Suppose that \({\mathbb {K}}={\mathbb {C}}\) and that X is topologically simple. Let T be an additive derivation of X. We have:
-
(i)
T is a differential operator on X.
-
(ii)
The mapping \(A\rightarrow [T,A]\) is a ring derivation of L(X) leaving
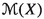 invariant.
invariant. -
(iii)
If there exists some nonzero element \(y\in X\) such that the mapping \(x \rightarrow (Tx \,{|}\, y)\) is continuous, then T is linear and continuous.
As for any Hilbert space, given \(x,y\in X\), we denote by \(x\hspace{1.111pt}{\odot }\hspace{1.111pt}y\) the continuous linear operator on X defined by \((x\hspace{1.111pt}{\odot }\hspace{1.111pt}y)\hspace{1.111pt}z:=(z\,{|}\, y)\hspace{1.111pt}x\) for every \(z\in X\).
Lemma 7.18
Suppose that \({\mathbb {K}}={\mathbb {C}}\), that X is topologically simple and infinite-dimensional, and that there exists an operator in  whose range is one-dimensional. Then additive derivations of X are linear and continuous.
whose range is one-dimensional. Then additive derivations of X are linear and continuous.
Proof
By Fact 7.9, the operator in  whose existence has been assumed should be of the form \(x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}y_0\) for some nonzero \(x_0,y_0\in X\). Then, since \((x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}y_0)(x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}y_0)^\bullet =(x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}y_0)(y_0\hspace{1.111pt}{\odot }\hspace{1.111pt}x_0)=\Vert y_0\Vert ^2x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}x_0\), it follows from Fact 7.16 that \(x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}x_0\) lies in
whose existence has been assumed should be of the form \(x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}y_0\) for some nonzero \(x_0,y_0\in X\). Then, since \((x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}y_0)(x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}y_0)^\bullet =(x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}y_0)(y_0\hspace{1.111pt}{\odot }\hspace{1.111pt}x_0)=\Vert y_0\Vert ^2x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}x_0\), it follows from Fact 7.16 that \(x_0\hspace{1.111pt}{\odot }\hspace{1.111pt}x_0\) lies in  . Moreover, we may suppose that \(\Vert x_0\Vert =1\). Set
. Moreover, we may suppose that \(\Vert x_0\Vert =1\). Set  . Then Y is a nonzero ideal of X, so it is dense in X because X is topologically simple. We note that,
. Then Y is a nonzero ideal of X, so it is dense in X because X is topologically simple. We note that,

Indeed, taking  such that \(y=Ax_0\), it follows from Fact 7.16 that
such that \(y=Ax_0\), it follows from Fact 7.16 that

Now let T be any additive derivation of X. Then, by Proposition 7.17 (ii), the mapping \(D:A\rightarrow [T,A]\) is a ring derivation of L(X) leaving  invariant. On the other hand, by Proposition 7.17 (i), T is a differential operator on X. Let d denote the ring derivation of \({\mathbb {C}}\) associated to T, and set \(S:=T-(Tx_0\,{|}\,x_0)I_X\). Then S is a differential operator on X whose associated derivation is d, and satisfies that \((Sx_0\,{|}\,x_0)=0\) and that \(D(A)=[S,A]\) for every \(A\in L(X)\). Let (x, y) be in \(X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\). It follows that
invariant. On the other hand, by Proposition 7.17 (i), T is a differential operator on X. Let d denote the ring derivation of \({\mathbb {C}}\) associated to T, and set \(S:=T-(Tx_0\,{|}\,x_0)I_X\). Then S is a differential operator on X whose associated derivation is d, and satisfies that \((Sx_0\,{|}\,x_0)=0\) and that \(D(A)=[S,A]\) for every \(A\in L(X)\). Let (x, y) be in \(X\hspace{1.111pt}{\times }\hspace{1.111pt}Y\). It follows that
Therefore, taking inner products with \(x_0\), we obtain
Now note that, considering (7.3) and that  is D-invariant, we have that
is D-invariant, we have that  , and that then, by Fact 7.16, also
, and that then, by Fact 7.16, also  . Therefore, \((D(x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y))^\bullet x_0\in Y\), and (7.4) reads as
. Therefore, \((D(x_0\hspace{0.55542pt}{\otimes }\hspace{1.111pt}y))^\bullet x_0\in Y\), and (7.4) reads as
where \(S^\bullet :Y\rightarrow Y\) is the mapping defined by \(S^\bullet y:=-(D(x_0\hspace{1.111pt}{\otimes }\hspace{1.111pt}y))^\bullet x_0\).
Consider a set copy \({\widehat{Y}}\) of Y with sum, product by scalars, and norm defined by \(\widehat{y_1}+\widehat{y_2}:=\widehat{y_1+y_2}\), \(\lambda {\widehat{y}}:=\widehat{{\overline{\lambda }}y}\), and \(\Vert {\widehat{y}}\Vert :=\Vert y\Vert \), respectively, and for \((x,{\widehat{y}})\in X\hspace{1.111pt}{\times }\hspace{1.111pt}{\widehat{Y}}\), set \(\langle x,{\widehat{y}}\rangle =(x\,{|}\,y)\). Then \((X,{\widehat{Y}},\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle )\) is a normed pairing over \({\mathbb {C}}\), complete on the left. (In verifying this, the unique point which could be non clear is the one that \(\langle x,{\widehat{Y}}\rangle =0\) implies \(x=0\); but this follows from the fact that Y is dense in X.) Moreover (7.5) reads as
where \(S^\# {\widehat{y}}:=\widehat{S^\bullet y}\). Thus the differential operator S on X has an adjoint relative to \(\langle \hspace{1.111pt}{\cdot }\hspace{1.111pt},\hspace{0.55542pt}{\cdot }\hspace{1.111pt}\rangle \), and hence, by Theorem 4.10, is linear and continuous. Finally, since \(T=S+(Tx_0\,{|}\, x_0)I_X\), T is linear and continuous.\(\square \)
The proof of the next proposition follows Villena’s argument in the proof of the main result in [67] (see also [19, Theorem 8.1.41]), with the appropriate changes.
Proposition 7.19
Suppose that \({\mathbb {K}}={\mathbb {C}}\) and that X is topologically simple and infinite-dimensional. Let T be an additive derivation of X. Then T is linear and continuous.
Proof
Suppose that there exists some nonzero element \(y\in X\) such that the mapping \(x \rightarrow (Tx \,{|}\, y)\) is continuous. Then, by Proposition 7.17 (iii), T is linear and continuous. Therefore, to conclude the proof of the proposition it is enough to discuss the case that, for every nonzero \(y\in X\), the mapping \(x \rightarrow (Tx \,{|}\, y)\) is discontinuous. Actually we are going to show that this case cannot happen.
To derive a contradiction, assume that, for every nonzero \(y\in X\), the mapping \(x \rightarrow (Tx \,{|}\, y)\) is discontinuous. Then, by Remark 4.9 (a), for every nonzero \(y\in X\), the mapping \(x \rightarrow (Tx \,{|}\, y)\) is unbounded on any neighborhood of zero. Moreover, clearly T is discontinuous, and hence, by Lemma 7.18, the inequality \(\dim A(X)>1\) holds for every nonzero  . It follows from [19, Corollary 8.1.34 and Proposition 8.1.38] that there exist sequences \( {y}_{n}\) in X and \( A_{n}\) in
. It follows from [19, Corollary 8.1.34 and Proposition 8.1.38] that there exist sequences \( {y}_{n}\) in X and \( A_{n}\) in  such that \(A_{n}\cdots A_{1}y_{n} \ne 0\) and \(A_{n+1}\cdots A_{1}y_{n}=0\) for every \(n\in {\mathbb {N}}\), and clearly we may suppose that \(\Vert y_{n}\Vert =\Vert A_{n}\Vert =1\) for every \(n\in {\mathbb {N}}\).
such that \(A_{n}\cdots A_{1}y_{n} \ne 0\) and \(A_{n+1}\cdots A_{1}y_{n}=0\) for every \(n\in {\mathbb {N}}\), and clearly we may suppose that \(\Vert y_{n}\Vert =\Vert A_{n}\Vert =1\) for every \(n\in {\mathbb {N}}\).
Now, according to Proposition 7.17 (ii), let D denote the ring derivation of  defined by \(D(A):=[T,A]\) for every
defined by \(D(A):=[T,A]\) for every  . Then, considering Fact 7.16 and the above paragraph, we can construct inductively a sequence \({x}_{n}\) in X with the property that for every \(n\in {\mathbb {N}}\) we have \( \Vert x_{n} \Vert \leqslant 2^{-n}\) and
. Then, considering Fact 7.16 and the above paragraph, we can construct inductively a sequence \({x}_{n}\) in X with the property that for every \(n\in {\mathbb {N}}\) we have \( \Vert x_{n} \Vert \leqslant 2^{-n}\) and
Now we consider the element \(x\in X\) defined by \(x:=\sum ^{\infty }_{j=1}A_{1}^\bullet \cdots A_{j}^\bullet x_{j}\), and for \(n\in {\mathbb {N}}\) we write \(z_{n}:=x_{n+1}+\sum ^{\infty }_{j=n+2}A_{n+2}^\bullet \cdots A_{j}^\bullet x_{j}\). Then we have
where for the last equality we have used that \(A_{n+1}\cdots A_{1}y_{n} = 0.\) Therefore, since \( \Vert z_{n} \Vert \leqslant 1,\) we obtain
Now the impossible fact that \( \Vert Tx \Vert \geqslant n\) for every \(n\in {\mathbb {N}}\) is the desired contradiction.\(\square \)
Corollary 7.20
Suppose that X is topologically simple and infinite-dimensional. Let T be an additive derivation of X. Then T is linear and continuous.
Proof
If \({\mathbb {K}}={\mathbb {C}}\), then the result follows from Proposition 7.19.
Suppose that \({\mathbb {K}}={\mathbb {R}}\). Then, by [19, Theorem 8.1.88], either X is a topologically simple complex semi-\(H^*\)-algebra, regarded as a real semi-\(H^*\)-algebra, or there exists a couple \((Z,\natural )\), where Z is a topologically simple complex semi-\(H^*\)-algebra and \(\natural \) is an isometric involutive conjugate-linear algebra \(*\)-automorphism of Z, such that \(X=\{z\in Z\,{:}\,z^\natural =z\}\). If the first possibility happens, then the result follows by applying Proposition 7.19 again. Suppose that \(X=\{z\in Z\,{:}\,z^\natural =z\}\) for \((Z,\natural )\) as above. Then, since \(Z=X\hspace{1.111pt}{\oplus }\hspace{1.111pt}iX\), we may define an additive derivation \({\overline{T}}:Z\rightarrow Z\) by setting \({\overline{T}}(x_1+ix_2):=Tx_1+iTx_2\) (\(x_1,x_2\in X\)). By applying Proposition 7.19 once more, we obtain that \({\overline{T}}\) is \({\mathbb {C}}\)-linear and continuous. Therefore, since T is the restriction of \({\overline{T}}\) to X, T is \({\mathbb {R}}\)-linear and continuous.\(\square \)
We recall that closed ideals of any semi-\(H^*\)-algebra over \({\mathbb {K}}\) are direct summands [19, Proposition 8.1.13 (i)]. Considering this result, together with [19, Lemma 8.2.18], we obtain the following.
Fact 7.21
Suppose that X has zero annihilator. Then X is a generalized complemented complete normed algebra over \({\mathbb {K}}\) with zero weak radical.
Now the main result in this section reads as follows.
Theorem 7.22
Suppose that X has zero annihilator. Let T be an additive derivation of X. Then there exist T-invariant closed \(*\)-ideals Y and Z of X such that \(X=Y\hspace{1.111pt}{\oplus }\hspace{1.111pt}Z\), T is linear and continuous on Y, Z is finite-dimensional, and T is discontinuous on Z.
Proof
Let M be an infinite-dimensional minimal closed ideal of X. Then, by [19, Proposition 8.1.13 (iv)–(v)], M is an infinite-dimensional topologically simple semi-\(H^*\)-algebra over \({\mathbb {K}}\) in a natural way. On the other hand, by Fact 7.8, M is invariant under T, and hence the restriction of T to M can be seen as an additive derivation of M. It follows from Corollary 7.20 that T is continuous on M.
Let \(\{M_i\}_{i\in I}\) denote the family of all minimal closed ideals of X, and let J stand for the set of those \(i\in I\) such that T is discontinuous on \(M_i\). It follows from Fact 7.21, Proposition 7.14, and the above paragraph that J is finite, and that \(M_i\) is finite-dimensional whenever \(i\in J\). Moreover, by Fact 7.8 and Remark 4.9 (b), T is linear on \(M_i\) whenever i belongs to \(I\hspace{1.111pt}{\setminus }\hspace{1.111pt}J\). Now set \(Y:=\overline{\sum _{i\in I{\setminus } J}M_i}\) and \(Z:=\sum _{i\in J}M_i\). Then Y and Z are T-invariant closed \(*\)-ideals of X (by Fact 7.8 and [19, Proposition 8.1.13 (v)]), T is linear and continuous on Y (by Lemma 7.10 (ii)), Z is finite-dimensional, T is discontinuous on Z, and \(X=Y\hspace{1.111pt}{\oplus }\hspace{1.111pt}Z\) (by [19, Theorem 8.1.16 and Fact 6.1.75]).\(\square \)
Fact 7.23
Suppose that X has no nonzero finite-dimensional direct summand. Then X has zero annihilator.
Proof
Let Y be any finite-dimensional subspace of \(\textrm{Ann}\hspace{0.55542pt}(X)\). Then Y is a closed ideal of X, hence a finite-dimensional direct summand. Therefore \(Y=0\), as X has no nonzero such a direct summand. Thus \(\textrm{Ann}\hspace{0.55542pt}(X)\) has no nonzero finite-dimensional subspace, and hence \(\textrm{Ann}\hspace{0.55542pt}(X)=0\).\(\square \)
Combining Theorem 7.22 and Fact 7.23, we obtain the following.
Corollary 7.24
Suppose that X has no nonzero finite-dimensional direct summand. Then additive derivations of X are linear and continuous.
In relation to the following remark, we note that alternative (so, in particular, associative) or Jordan semi-\(H^*\)-algebras with zero annihilator are \(H^*\)-algebras [19, Proposition 8.1.23 (ii) and Corollary 8.1.80], and that, for associative algebras, semisimplicity and J-semisimplicity mean the same [18, Definition 4.4.12].
Remark 7.25
(a) As far as we know, even the particularization of Theorem 7.22 to the case that X is associative (respectively, Jordan) has not been noticed in the literature. Nevertheless, such a particularization can be easily obtained from previously known results. Indeed, associative (respectively, Jordan) complex \(H^*\)-algebras with zero annihilator are J-semisimple [19, Corollary 8.1.146] (respectively, [19, Proposition 8.1.145]). Therefore, by [41, Theorem 4.1] (respectively, [9, Theorem 3.5]), the particularization of Theorem 7.22 to the case that X is complex and associative (respectively, Jordan) follows. Finally, reducing the real case to the complex one by means of [19, Proposition 8.1.77], we obtain the associative (respectively, Jordan) version of Theorem 7.22.
(b) The particularization of Corollary 7.24 to the case that X is alternative follows from the associative version of that corollary because alternative \(H^*\)-algebras over \({\mathbb {K}}\) with no nonzero finite-dimensional direct summand are associative. Indeed, let X be an alternative \(H^*\)-algebra over \({\mathbb {K}}\) with no nonzero finite-dimensional direct summand. Then, by Fact 7.23, X has zero annihilator, and hence, as in the proof of Theorem 7.22, each minimal closed ideal of X is an infinite-dimensional topologically simple alternative \(H^*\)-algebra over \({\mathbb {K}}\) in a natural way, and the sum of all minimal closed ideals of X is dense in X. Therefore, since every infinite-dimensional topologically simple alternative \(H^*\)-algebra over \({\mathbb {K}}\) is associative [11, Theorems 8.2 and 8.4] (see also [19, pp. 551–552]), we conclude that X is associative, as desired.
(c) Let m be a natural number. Then \(M_m({\mathbb {K}})\) becomes an \(H^*\)-algebra over \({\mathbb {K}}\) under the inner product \(((a_{i,j})\,{|}\,(b_{i,j})):=\sum _{i,j}a_{i,j}\overline{b_{i,j}}\) and the involution \((a_{i,j})^*:=(\overline{a_{j,i}})\). It follows from Remark 4.14 that, even in the associative case, the possibility that the direct summand Z in Theorem 7.22 be nonzero can happen.
Theorem 7.22 would follow straightforwardly from Fact 7.21 if the following conjecture were proved.
Conjecture 7.26
Let X be a generalized complemented complete normed algebra over \({\mathbb {K}}\) with zero weak radical, and let T be an additive derivation of X. Then there exist T-invariant closed ideals Y and Z of X such that \(X=Y\hspace{1.111pt}{\oplus }\hspace{1.111pt}Z\), T is linear and continuous on Y, Z is finite-dimensional, and T is discontinuous on Z.
Conjecture 7.26 above holds if X is associative and commutative. Indeed, in this case, by [18, Proposition 4.4.65 (ii)], the requirement that X has zero weak radical is equivalent to the semisimplicity of X, and the Johnson–Sinclair theorem [41] applies. Nevertheless we do not know if Conjecture 7.26 holds in the case that X is associative but not commutative (see [18, Remark 4.4.68 (a)]). Anyway, looking at the proof of Theorem 7.22, and considering [19, Theorem 8.2.44], one can realize that (the general case of) Conjecture 7.26 is equivalent to the simpler one which follows.
Conjecture 7.27
Let X be an infinite-dimensional topologically simple complete normed algebra over \({\mathbb {K}}\) with zero weak radical. Then additive derivations of X are continuous.
Notes
This nice idea is taken from the paragraph immediately before [52, Lemma 2.4.11].
References
Aczél, J., Dhombres, J.: Functional Equations in Several Variables. Encyclopedia of Mathematics and Its Applications, vol. 31. Cambridge University Press, Cambridge (1989)
Ambrose, W.: Structure theorems for a special class of Banach algebras. Trans. Amer. Math. Soc. 57(3), 364–386 (1945)
Balachandran, V.K.: Simple \(L^*\)-algebras of classical type. Math. Ann. 180, 205–219 (1969)
Balachandran, V.K.: Automorphisms of \(L^*\)-algebras. Tohoku Math. J. 22, 163–173 (1970)
Beidar, K.I., Martindale III, W.S., Mikhalev, A.V.: Rings with Generalized Identities. Monographs and Textbooks in Pure and Applied Mathematics, vol. 196. Marcel Dekker, New York (1996)
Beltiţă, D.: Smooth Homogeneous Structures in Operator Theory. Chapman & Hall/CRC Monographs and Surveys in Pure and Applied Mathematics, vol. 137. Chapman & Hall/CRC, Boca Raton (2006)
Bensebah, A.: \({JV}\)-algèbres et \({JH}^*\)-algèbres. Canadian Math. Bull. 34(4), 447–455 (1991)
Bezushchak, O.: Automorphisms and derivations of algebras of infinite matrices. Linear Algebra Appl. 650, 42–59 (2022)
Boudi, N., Marhnine, H., Zarhouti, C.: Additive derivations on Jordan Banach pairs. Comm. Algebra 32(9), 3609–3625 (2004)
Braun, H., Koecher, M.: Jordan-Algebren. Die Grundlehren der Mathematischen Wissenschaften, vol. 128. Springer, Berlin (1966)
Cabrera, M.: \(H^*\)-Álgebras no Asociativas Reales. \(H^*\)-Álgebras de Malcev Complejas y Reales. Ph.D. thesis, la Universidad de Granada (1988)
Cabrera, M., El Marrakchi, A., Martínez, J., Rodríguez, A.: An Allison–Kantor–Koecher–Tits construction for Lie \(H^*\)-algebras. J. Algebra 164, 361–408 (1994)
Cabrera-García, M., Martínez-Moreno, J., Rodríguez-Palacios, A.: Mal’cev \(H^*\)-algebras. Math. Proc. Cambridge Phil. Soc. 103(3), 463–471 (1988)
Cabrera, M., Martínez, J., Rodríguez, A.: Nonassociative real \(H^*\)-algebras. Publ. Mat. 32(2), 267–274 (1988)
Cabrera, M., Mohammed, A.A.: Totally multiplicatively prime algebras. Proc. Roy. Soc. Edinburgh Sect. A 132(5), 1145–1162 (2002)
Cabrera García, M., Rodríguez Palacios, A.: Extended centroid and central closure of semiprime normed algebras: a first approach. Comm. Algebra 18(7), 2293–2326 (1990)
Cabrera García, M., Rodríguez Palacios, A.: Nonassociative ultraprime normed algebras. Quart. J. Math. Oxford Ser. (2) 43(1), 1–7 (1992)
Cabrera García, M., Rodríguez Palacios, Á.: Non-Associative Normed Algebras. Vol. 1: The Vidav–Palmer and Gelfand–Naimark Theorems. Encyclopedia of Mathematics and its Applications, vol. 154. Cambridge University Press, Cambridge (2014)
Cabrera García, M., Rodríguez Palacios, Á.: Non-Associative Normed Algebras. Vol. 2: Representation Theory and the Zel’manov Approach. Encyclopedia of Mathematics and its Applications, vol. 167. Cambridge University Press, Cambridge (2018)
Chernoff, P.R.: Representations, automorphisms and derivations of some operator algebras. J. Funct. Anal. 12, 275–289 (1973)
Choquet, G.: Cours d’analyse. Topologie. Masson et Cie, Paris, Tome II (1964)
Cuenca Mira, J.A.: Sobre \(H^*\)-álgebras no asociativas. Teoría de estructura de las \(H^*\)-álgebras de Jordan no conmutativas semisimples. PhD Thesis, Universidad de Granada (1982)
Cuenca, J.A.: Structure of \(H^*\)-algebras. In: Makhlouf, A. (ed.) Algebra and Applications, Vol. 1: Non-associative Algebras and Categories. Chapter 5, pp. 155–198. Wiley-ISTE (2021)
Cuenca Mira, J.A., García Martín, A., Martín González, C.: Structure theory for \(L^*\)-algebras. Math. Proc. Cambridge Phil. Soc. 107(2), 361–365 (1990)
Cuenca Mira, J.A., Rodríguez Palacios, Á.: Isomorphisms of \(H^*\)-algebras. Math. Proc. Cambridge Phil. Soc. 97(1), 93–99 (1985)
Cuenca Mira, J.A., Rodríguez Palacios, Á.: Structure theory for noncommutative Jordan \(H^*\)-algebras. J. Algebra 106, 1–14 (1987)
Cuenca Mira, J.A., Sánchez Sánchez, A.: Structure theory for real noncommutative Jordan \(H^*\)-algebras. J. Algebra 164(2), 481–499 (1994)
de la Harpe, P.: Classification des \(L^*\)-algèbres semi-simples réelles séparables. C. R. Acad. Sci. Paris Sér. A-B 272, A1559-1561 (1971)
Devapakkiam, C.V.: Hilbert space methods in the theory of Jordan algebras. I. Math. Proc. Cambridge Philos. Soc. 78(2), 293–300 (1975)
Devapakkiam, C.V., Rema, P.S.: Hilbert space methods in the theory of Jordan algebras. II. Math. Proc. Cambridge Philos. Soc. 79(2), 307–319 (1976)
Ebbinghaus, H.-D., Hermes, H., Hirzbruch, F., Koecher, M., Mainzer, K., Neukirch, J., Prestel, A., Remmert, R.: Numbers. Graduate Texts in Mathematics, vol. 123. Springer, New York (1991)
Fernández López, A., Rodríguez Palacios, Á.: A Wedderburn theorem for nonassociative complete normed algebras. J. London Math. Soc. 33(2), 328–338 (1986)
Ghahramani, H., Ghosseiri, M.N., Heidari Zadeh, L.: Generalized derivations and generalized Jordan derivations of quaternion rings. Iran. J. Sci. Technol. Trans. A Sci. 45(1), 305–308 (2021)
Ghahramani, H., Ghosseiri, M.N., Safari, S.: On derivations, biderivations and superbiderivations of quaternion rings. Rend. Circ. Mat. Palermo (2) 70(2), 665–674 (2021)
Han, D.: Continuity and linearity of additive derivations of nest algebras on Banach spaces. Chin. Ann. Math. Ser. B 17(2), 227–236 (1996)
Hanche-Olsen, H., Størmer, E.: Jordan Operator Algebras. Monographs and Studies in Mathematics, vol. 21. Pitman, Boston (1984)
Herstein, I.N.: Jordan derivations of prime rings. Proc. Amer. Math. Soc. 8, 1104–1119 (1957)
Herstein, I.N.: Topics in Ring Theory. The University of Chicago Press, Chicago (1969)
Jacobson, N.: Structure of Rings. American Mathematical Society Colloquium Publications, vol. 37. American Mathematical Society, Providence (1964)
Jacobson, N.: Basic Algebra. I. 2nd edn. W.H. Freeman and Company, New York (1985)
Johnson, B.E., Sinclair, A.M.: Continuity of derivations and a problem of Kaplansky. Amer. J. Math. 90(4), 1067–1073 (1968)
Kaplansky, I.: Topological rings. Amer. J. Math. 69, 153–183 (1947)
Kaplansky, I.: Dual rings. Ann. Math. 49, 689–701 (1948)
Kosi-Ulbl, I., Rodríguez Palacios, Á., Vukman, J.: A generalization of a theorem of Chernoff on standard operator algebras. Monatsh. Math. 195(4), 675–685 (2021)
Lin, J.-H.: Weak Jordan derivations of prime rings. Linear Multilinear Algebra 69(8), 1422–1445 (2021)
Luna-Elizarrarás, M.E.: On interactions of quaternionic and complex structures of linear spaces. Adv. Appl. Clifford Algebras 31(4), 60 (2021)
Mackey, G.W.: On infinite-dimensional linear spaces. Trans. Amer. Math. Soc. 57, 155–207 (1945)
Mathis, D.: Differential polynomial rings and Morita equivalence. Comm. Algebra 10(18), 2001–2017 (1982)
Neher, E.: Generators and relations for 3-graded Lie algebras. J. Algebra 155(1), 1–35 (1993)
Ng, C.-K.: On quaternionic functional analysis. Math. Proc. Cambridge Philos. Soc. 143(2), 391–406 (2007)
Penkov, I., Serganova, V.: Categories of integrable \(sl(\infty )\)-, \(o(\infty )\)-, \(sp(\infty )\)-modules. In: Representation Theory and Mathematical Physics. Contemporary Mathematics, vol. 557, pp. 335–357. American Mathematical Society, Providence (2011)
Rickart, C.E.: General Theory of Banach Algebras. The University Series in Higher Mathematics. van Nostrand Co., Princeton (1960)
Rodríguez Palacios, Á.: Jordan axioms for \(C^*\)-algebras. Manuscripta Math. 61(3), 279–314 (1988)
Rodríguez Palacios, Á.: Continuity of densely valued homomorphisms into \(H^*\)-algebras. Quart. J. Math. Oxford 46(181), 107–118 (1995)
Rodríguez Palacios, Á.: Conditional expectations in complete normed complex algebras satisfying the von Neumann inequality. J. Math. Anal. Appl. 506(1), 125563 (2022)
Rodríguez Palacios, Á., Cabrera García, M.: Non-associative \(C^*\)-algebras. In: Makhlouf, A. (ed.) Algebra and Applications, Vol. 1: Non-Associative Algebras and Categories. Chapter 4, pp. 111–154. Wiley-ISTE (2021)
Rodríguez Palacios, Á., Cabrera García, M.: Standard operator Jordan rings on Banach spaces, and their derivations. Oper. Matrices 16(2), 429–446 (2022)
Schafer, R.D.: An Introduction to Nonassociative Algebras. Corrected reprint of the 1966 original. Dover, New York (1995)
Schatten, R.: Norm Ideals of Completely Continuous Operators. 2nd printing. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 27. Springer, Berlin (1970)
Schue, J.R.: Hilbert space methods in the theory of Lie algebras. Trans. Amer. Math. Soc. 95, 69–80 (1960)
Schue, J.R.: Cartan decompositions for \(L^{\ast }\)-algebras. Trans. Amer. Math. Soc. 98, 334–349 (1961)
Šemrl, P.: Additive derivations of some operator algebras. Illinois J. Math. 35(2), 234–240 (1991)
Šemrl, P.: Ring derivations on standard operator algebras. J. Funct. Anal. 112(2), 318–324 (1993)
Soukhomlinoff, G.: Über Fortsetzung von linearen Funktionalen in linearen komplexen Räumen und linearen Quaternionräumen. Rec. Math. Moscou 3, 353–358 (1938) (in Russian, German summary)
Unsain, I.: Classification of the simple separable real \(L^*\)-algebras. J. Differential Geometry 7, 423–451 (1972)
Upmeier, H.: Derivations of Jordan \(C^*\)-algebras. Math. Scan. 46(2), 251–264 (1980)
Villena, A.R.: Continuity of derivations on \(H^*\)-algebras. Proc. Amer. Math. Soc. 122(3), 821–826 (1994)
Vukman, J.: Identities related to derivations and centralizers on standard operator algebras. Taiwanese J. Math. 11(1), 255–265 (2007)
Wright, J.D.M.: Jordan \(C^*\)-algebras. Michigan Math. J. 24(3), 291–302 (1977)
Zalar, B.: Continuity of derivations on Mal’cev \(H^*\)-algebras. Math. Proc. Cambridge Philos. Soc. 110(3), 455–459 (1991)
Zariski, O., Samuel, P.: Commutative Algebra. Vol. I. Graduate Texts in Mathematics, vol. 28. Springer, New York (1975)
Acknowledgements
The authors would like to thank the referee for careful reading of the paper and useful suggestions.
Funding
Funding for open access publishing: Universidad de Granada/CBUA
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors have been partially supported by the Junta de Andalucía Grant FQM199.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rodríguez Palacios, Á., Cabrera García, M. Jacobson’s theorem on derivations of primitive rings with nonzero socle: a proof and applications. European Journal of Mathematics 9, 67 (2023). https://doi.org/10.1007/s40879-023-00667-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40879-023-00667-4
Keywords
- Primitive ring
- Differential operator
- Additive derivation
- Standard operator ring
- Quaternionic normed space
- \(H^*\)-algebra



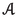 is a standard operator algebra on X, and D is a linear derivation. Clearly, in this case, the conclusion in the theorem remains true if the restriction that X is infinite-dimensional is removed.
is a standard operator algebra on X, and D is a linear derivation. Clearly, in this case, the conclusion in the theorem remains true if the restriction that X is infinite-dimensional is removed.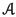 is a standard operator algebra on X, and D is a ring derivation. Moreover, in this case, the conclusion in the theorem does not remain true if the restriction that X is infinite-dimensional is removed.
is a standard operator algebra on X, and D is a ring derivation. Moreover, in this case, the conclusion in the theorem does not remain true if the restriction that X is infinite-dimensional is removed.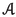 is a standard operator algebra on X, and D is a ring derivation.
is a standard operator algebra on X, and D is a ring derivation.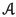 is a standard operator algebra on X, and D is a ring derivation.
is a standard operator algebra on X, and D is a ring derivation.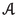 is a standard operator algebra on X, and D is linear. Clearly, in this case, the conclusion in the theorem remains true if the restriction that X is infinite-dimensional is removed. (In these papers, completeness of X is assumed but is never applied in the proofs.)
is a standard operator algebra on X, and D is linear. Clearly, in this case, the conclusion in the theorem remains true if the restriction that X is infinite-dimensional is removed. (In these papers, completeness of X is assumed but is never applied in the proofs.)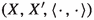 is a normed pairing over
is a normed pairing over 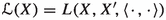 .
.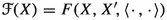 .
.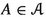 and
and 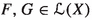 .
.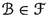 , then D is linear.
, then D is linear.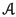 is complete, and if D is linear and continuous on each
is complete, and if D is linear and continuous on each 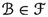 , then D is linear and continuous.
, then D is linear and continuous.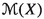 invariant.
invariant.