On The Role of Constitutive Modeling and Computational Parameters in the Numerical Simulation of Dynamic Tensile Extrusion Test

Abstract

In Dynamic Tensile Extrusion (DTE) test, the material is subjected to extreme conditions, such as severe plastic deformations, high pressures, and large variations of temperature and strain rate. Although the numerical simulation of this test is ideal for constitutive model validation, there are several computational features to assess before performing further analyses. This work aims to evaluate the influence of constitutive modeling and computational parameters on the predicted material jet in the simulation of DTE tests on Oxygen-Free High Conductivity Copper at different extrusion velocities. Dynamic transient analyses have been performed with implicit finite element code using a single-step Houbolt procedure. To begin with, three constitutive models (the Mechanical Threshold Stress, modified Johnson–Cook, and Zerilli-Armstrong) were selected and model parameters have been identified on available uniaxial tensile test data at different temperature and strain rates. Successively, the effect of friction, damping, remeshing, and extrusion die modeling has been investigated by performing parametric numerical simulations at 400 m/s extrusion velocity and an optimum set of computational parameters was determined. Finally, constitutive models' performance has been verified by comparing the predicted size, shape, and number of extruded fragments at different velocities with experimental data. The ability to correctly predict the size and shape of the last temporally forming fragment appears to be directly related to the ability of the constitutive model to accurately describe the material response in the viscous drag regime.

Introduction

In many engineering applications (i.e. armor and anti-armor technology, hot metalworking, foreign object damage, blast protection, etc.) materials are required to perform under severe operative conditions. In these circumstances, numerical simulation becomes an essential tool for a reliable and robust design. The ability of the computational simulation tools to anticipate structures and components performance depends strongly on the capacity of the constitutive models to accurately describe material behavior under conditions involving large plastic deformation, strain rate, temperature, and pressure [1]. Usually, information about the material constitutive response is obtained with traditional laboratory characterization tests which can only probe material response over a limited range of variability of loading conditions. This requires that material model performances must be validated against tests characterized by complex load paths with arbitrary combinations and gradients of the constitutive variables [2]. These tests provide a large amount of information about the material response and fracture behavior in conditions closer to real case scenarios and, with the definition of appropriate validation metrics, they offer essential support to advanced modeling development [3]. In impact dynamics, examples of validation tests used to probe material response and to validate constitutive modeling are the Taylor anvil test, the Taylor symmetric test (rod-on-rod, ROR), and the Drop Tower test [4,5,6,7,8,9]. Recently, to investigate the material behavior in conditions similar to those experienced in shaped charge devices, Gray et al. [10] introduced a new test known as Dynamic Tensile Extrusion (DTE) test. In this test, a projectile, made of the material of interest, is accelerated in a high-pressure gas-gun and launched into a conical die, properly designed to obtain a velocity difference between the tip and tail of the sample, promoting the dynamic extrusion of the material. Since the die exit bore is smaller than the specimen diameter, the sample undergoes severe tensile adiabatic deformation under strain rates ranging from 10⁵ s⁻¹ to 10⁶ s⁻¹ while being subjected to high pressure and shear stress waves (3–5 GPa). The DTE test has been used to investigate dynamic material response and the role of microstructural features during jet formation in metals and alloys [10,11,12,13,14], and polymers [15,16,17]. This test provided a fundamental understanding of the correlation between microstructure and the deformation process at very high strain rates. Escobedo et al. [11] showed that dynamic extrusion of high purity zirconium was accomplished by a combination of twinning and slip which results in different tensile ductility depending on the initial texture. Differently, Cao et al. [18] found that, in high purity tantalum, the initial texture does not influence total elongation and microstructural evolution but it promotes instabilities and break-ups during the test. In pure metals, such as OHFC copper [10] and pure aluminum [14], material ductility was found to be strongly influenced by the initial grain size $d$, decreasing with increasing the initial grain size for coarse-grain microstructure $\left( {d > 10\mu {\text{m}}} \right)$. Inversely, DTE tests performed on fine-grained $\left( {d = 1 \div 10\mu {\text{m}}} \right)$ and ultra-fine grained $\left( {d < 1\mu {\text{m}}} \right)$ copper showed an increases in the material ductility as the initial grain size increases [19]. Furthermore, it was shown that the occurrence of dynamic recrystallization, driven by large plastic strain and elevated temperate caused by adiabatic heating, could contribute in increasing material ductility [12, 20].

From a numerical point of view, the simulation of validation tests such as the DTE is quite challenging and it requires a thorough assessment of several computational features: coupled thermomechanical models, dynamic transients, contact interaction between different bodies, estimation of friction coefficients, and stress wave propagation [8]. Different modeling approaches can be found in the literature. Park et al. [20] performed numerical simulations of DTE tests on CG and UFG copper in the explicit FEM code LS-DYNA, the overall shape and number of fragments were used as validation metrics. They aimed to evaluate the adiabatic temperature rise during the test and they found that the local temperature could reach $0.6{\text{T}}_{{\text{m}}}$ before fragmentation, high enough to promote recrystallization in UFG Copper. Bonora, Testa, Ruggiero, Iannitti, Mortazavi and Hörnqvist [21] performed extensive numerical simulations of DTE tests on high purity copper at different impact velocities, using implicit FEM code MSC MARC with a direct integration method for solving the equations of motion showing the correlation between the ability to predict the shape and number of extruded fragments and the selected material constitutive model. Burkett [22] carried out Eulerian hydrocode simulations of tests on both copper and tantalum and investigated the performance of different constitutive models. The experimental and predicted size of the extruded fragments and the velocity history of the projectile were compared. The use of macroscopic validation metrics (such as fragments number, shape, and dimensions) has been commonly used [14, 23], but microscopic metrics, such as the prediction of grain orientation change during the test, have been proposed as well [12, 24, 25].

The novelty of the present paper is in the investigation the role of material modeling and computational parameters in the numerical simulation of the DTE performed on OHFC copper. Indeed, an extensive sensitivity analysis was carried out to define the optimum configuration for the simulation of such test and to minimize results uncertainties due to an inaccurate selection of numerical parameters. The influence of those parameters has been investigated together with different material models, whose performances have been calibrated at a reference velocity and verified for other testing velocities.

Material and Testing

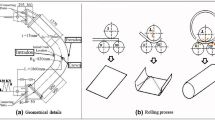
Bonora et al. [21] performed DTE tests on oxygen-free high conductivity copper (OFHC commercial pure 99.98%). In that study, specimens were machined from a half-hardened bar and annealed at 450 °C for ½ h in an inert Argon atmosphere. Electron backscattered diffraction (EBSD) analysis showed a random texture with an initial grain size of 47 mm [12]. DTE tests at different impact velocity, ranging from 350 to 420 m/s, were performed in vacuum, using a single-stage light gas gun. The extrusion die and bullet-shape sample geometries are reported in Fig. 1. Texture evolution investigation revealed that discontinuous dynamic recrystallization has occurred at least at the end of the fragment that remains in the extrusion die. Extruded fragments were soft-recovered in a ballistic gel [26]. As validation metrics for future numerical simulation analyses, the number, shape, and size of the fragments were recorded and reported. These data have been used in this work for computational model verification and validation [3].

Fig. 1

Technical drawing of a extrusion die b sample [21]. Units are in mm

Constitutive Modeling and Material Parameters Identification

In the literature, several continuum-scale material models to describe material behavior at high strain rates, large plastic deformation, dynamic pressure, and temperature have been proposed [27]. In general, these models might be divided into two main groups: phenomenological and physically based. While models in the first group are basically mathematical expressions providing a good fit for a set of experimental test results, those in the latter group are developed considering the deformations mechanisms at the microscopic scale. Physically-based constitutive models are usually characterized by more complex formulations and require the identification of a large number of parameters if compared to empirical models. However, they allow an accurate description of the material response over a wider range of the constitutive variables. In this work, the performance of three different material models has been investigated: the physically-based Mechanical Threshold Stress (MTS), a modified version of the phenomenological Johnson–Cook model (MJC), and the Zerilli and Armstrong (ZA) pseudo-physically based model.

Identification of Material Model Parameters

The identification of the material model parameters requires test results performed under different combinations of strain rate and temperature. The influence of strain rate and temperature on the mechanical properties of OFHC Copper was extensively studied in the literature [28,29,30,31]. The hardening law parameters were identified on the uniaxial tensile test performed at 0.001/s and room temperature; the reference flow curve of the material in such conditions was evaluated from the experimental data reported in [21]. The strain rate sensitivity parameters were evaluated by fitting the flow stress data reported in [32], at a constant level of plastic strain, as a function of the logarithm of the strain rate. Lastly, the thermal effect on the material response was evaluated from the data presented in [33, 34] for different levels of strain rate and plastic deformation.

These experimental data have been used for objective identification of the model parameters required by each model. For each model, the starting values of such parameters were evaluated from the results presented in literature for the material under investigation. An iterative constrained optimization procedure was carried in MATLAB, using a least-square-based optimization method. The objective functions were: (a) the reference flow curve, (b) true stress versus strain rate values for fixed value of plastic strain and temperature (c) true stress versus temperature values for fixed value of plastic strain and strain rate. The aim of the optimization procedure was to identify, for each model, the optimum set of material parameters which minimized the error between the experimental data and the model prediction, calculated as follows:

$$Error = \left| {\left| {\frac{{\sigma_{EXP} - \sigma_{MODEL} }}{{\sigma_{EXP} }}} \right|} \right|$$

(1)

In which $\sigma_{EXP}$ and $\sigma_{MODEL}$ are the the experimental and computed values of true stress respectively.

Modified Johnson–Cook Model (MJC)

The success of the phenomenological Johnson–Cook (JC) model is due to its simplicity in parameters identification. Indeed, the effects of work hardening, strain rate, and temperature are separated and represented by simple functions requiring few material constants that can be easily determined using tensile tests at different strain rates and temperatures [4]. For the material flow curve, in the original JC model, a power-law is assumed while the strain rate effect is accounted for by a logarithmic function. This model was initially intended to describe the strain rate effect on the flow stress in the range controlled by thermal activation. To extend the model predictive capability over a wider strain rate range, a modified version of the original model formulation, in which the strain rate effect on the flow stress is given by a power law, has been proposed. Thus, the MJC model is given as,

$$\sigma_{y} = \left\{ {\sigma_{a} + \mathop \sum \nolimits_{i = 1}^{2} Q_{i} \left[ {1 - \exp \left( { - \frac{{\varepsilon_{p} }}{{C_{i} }}} \right)} \right]} \right\}\left( {1 + \dot{\varepsilon }_{p}^{*} } \right)^{C} \left( {1 - T^{*m} } \right)$$

(2)

where $\sigma_{a}$ is the yield stress, $Q_{i}$ is the hardening saturation value, $C_{i}$ is the hardening exponent, and $C$ and $m$ represent the strain rate and thermal sensitivity respectely; the first right-hand side term describes the work-hardening of the material, and the other two terms define the strain rate and temperature effect, respectively. The normalized equivalent plastic strain rate $\dot{\varepsilon }_{p}^{*}$ is defined as,

$$\dot{\varepsilon }_{p}^{*} = \frac{{\dot{\varepsilon }_{p} }}{{\dot{\varepsilon }_{ref} }}$$

(3)

$\dot{\varepsilon }_{ref}$ is a user-defined reference strain rate, and the homologous temperature $T^{*}$ is,

$$T^{*} = \frac{{T - T_{r} }}{{T_{m} - T_{r} }}$$

(4)

where $T$ is the temperature, $T_{r}$ is the reference temperature and $T_{m}$ is the melting temperature. In contrast with the original Johnson–Cook model, the work-hardening is given as a two-terms Voce’s equation which predicts that stress saturates for large strain. In copper, this condition is representative of equilibrium between strain hardening and dynamic recovery at large plastic strains [35]. The power-law function of the strain rate can be used to describe the variation of the strain rate sensitivity in different regimes. For low values of $\dot{\varepsilon }_{0}$, the model describes the transition from the athermal to the thermal activation regime, while for large $\dot{\varepsilon }_{0}$ values the model can be used to account for the rapid increase of strain rate sensitivity in the viscous drag controlled regime. If the $\dot{\varepsilon }_{0}$ parameter is determined by fitting the data over the whole strain rate range, this model provides an approximation of the effective variation of the yield stress.

In Table 1, the MJC model parameters are summarized. The comparison of the flow curve and experimental data, for the reference low-strain rate, is shown in Fig. 2a. In Fig. 2b, the model predicted strain rate sensitivity for a reference plastic strain of 0.15 is compared with experimental data from Follansbee and Kocks [32]. Figure 2c shows the model predictive capabilities at different temperatures and at different levels of plastic strain both in adiabatic and isotherm conditions. In Fig. 3, the model predicted normalized stress at 0.2 plastic strain, for a strain rate ranging from 10^–4/s up to 10⁵/s, is compared with experimental data from different sources [28, 29, 31,32,33]. Here, it is evident that if the fitting procedure is performed to match experimental data at high strain rates, the linear dependence of the yield stress on the logarithm of the strain rate cannot be described by the model.

Table 1 Summary of MJC model parameters

Fig. 2

MJC model parameters identification: a flow curve and b strain rate sensitivity for 0.15 of plastic strain c temperature effect

Fig. 3

MJC model parameters verification: strain rate sensitivity at 0.2 of plastic strain. The experimental data are reported in [28, 29, 31,32,33]

The predictive capabilities of the MJC model were further investigated by comparing experimental flow curves at different strain rates and temperatures with calculated ones, Fig. 4. In these calculations, the adiabatic temperature rise was considered as follows:

$$\Delta T = \frac{\chi }{{\rho c_{P} }}\int {\sigma d\varepsilon }$$

(5)

where $\rho$ is the material density (8.96 g/cm³), $c_{P}$ the specific heat (0.383 J/gK) and $\chi$ is the Taylor-Quinney factor, which represents the fraction of plastic work converted into heat, assumed to be 0.95 [36].

Fig. 4

Comparison of experimental and MJC model computed flow curves at different temperatures and strain rates: a 2000s⁻¹ [30] and b 4000 s.⁻¹ [33]

ZA—Zerilli-Armstrong Model

ZA [5] developed a dislocation-mechanics-based constitutive model accounting for the effects of strain hardening, strain rate, hardening and thermal softening on activation energy. They proposed two different simple relations for BCC and FCC materials since the two structures exhibit a significant difference on the plastic strain dependence of the activation area. While BCC metals show a negligible dependence of the activation volume on the plastic strain, in FCC materials, such as copper, the activation volume decreases with plastic strain due to the increase of dislocation interactions. For FCC materials, Zerilli-Armstrong constitutive relation is written as:

$$\sigma_{y} = \sigma_{a} + B\varepsilon_{p}^{n} \exp \left[ { - \left( {\alpha_{0} - \alpha_{1} \log \dot{\varepsilon }_{p}^{ } } \right)T} \right]$$

(6)

where $\sigma_{a}$ is the yield stress, $B$ and $n$ are the hardening coefficient and exponent, $\alpha_{0}$ and $\alpha_{1}$ are material constants which model the thermal and strain rate sensitivity. The first term on the right-hand side is the athermal component of the yield stress which is influenced by initial solutes, dislocation density, and grain size. The latter term is the thermally activated component of the flow stress, in which material work-hardening is described by a power-law relation and it depends on both strain rate and temperature. In the original formulation [5], a prescribed value of 0.5 was assigned to the work-hardening exponent $n$, but a better agreement with the experimental data can be achieved by changing this parameter. Indeed, to account for flow stress saturation in copper, a value less than 0.5 could be used [35]. The identified parameters for strain rate and temperature effect, listed in Table 2, are quite close to those reported in [5] for the same material. However, as shown in Fig. 5, the model does not provide a thorough representation of the experimental data. This might be linked to the approximation of the power-law for describing material work-hardening, as previously stated. Furthermore, the linear representation of the flow stress dependence with $\log \dot{\varepsilon }_{p}$ at a constant strain, assumed in [8], poorly describes the behavior of the material under investigation at very high strain rates. In Figs. 6 and 7 the results computed with the ZA model are compared to further experimental data.

Table 2 Summary of ZA model parameters

Fig. 5

ZA model parameters identification: a flow curve and b strain rate sensitivity for 0.15 of plastic strain c temperature effect

Fig. 6

ZA model parameters verification: strain rate sensitivity at 0.2 of plastic strain. The experimental data are reported in [28, 29, 31,32,33]

Fig. 7

Comparison of experimental and ZA model computed flow curves at different temperatures and strain rates: a 2000s⁻¹ [30] and b 4000 s.⁻¹ [33]

MTS—Mechanical Threshold Stress Model

Follansbee and Kocks [32] proposed a constitutive model based on dislocation mechanics. In this model, the Mechanical Treshold Stress (MTS) $\hat{\sigma }$, an internal state variable to account for microstructural evolution during deformation, is introduced. The flow stress of the material is represented as the sum of two terms:

$$\sigma_{y} = \hat{\sigma }_{a} + \frac{G}{{G_{0} }}\left[ {s\left( {\dot{\varepsilon }_{p}^{ } ,T} \right) \cdot \hat{\sigma }} \right]$$

(7)

in which $\hat{\sigma }_{a}$ is the athermal component of the yield stress which describes dislocations’ interaction with long-range obstacles, such as grain boundaries. The second term, instead, represents the rate-dependent interaction of dislocations with short-range obstacles such as dislocation forests in pure FCC structures. The thermally activated regime is strongly dependent on strain rate $\dot{\varepsilon }_{p}$, absolute temperature $T$, and structure, accounted for by the MTS $\hat{\sigma }$. $G$ is the temperature-dependent shear modulus given as,

$$G = G_{0} - \frac{{b_{1} }}{{e^{{b_{2} /T}} - 1}}$$

(8)

where $G_{0}$ is the shear modulus at a reference temperature, $b_{1}$ and $b_{2}$ are material constants which are determined according to the expressions given in [10]. The term $s$ represents the ratio between the applied stress and the MTS at a constant structure that, according to thermal activation controlled and drag controlled kinetics relationships, can be written as,

$$s\left( {\dot{\varepsilon }_{p}^{ } ,T} \right) = \left[ {1 - \left( {\frac{{kT\ln \frac{{\dot{\varepsilon }_{0}^{ } }}{{\dot{\varepsilon }_{p}^{ } }}}}{{Gb^{3} g_{0} }}} \right)^{\frac{1}{q}} } \right]^{\frac{1}{p}}$$

(9)

where $\dot{\varepsilon }_{0}^{{}}$ is a material constant, $g_{0}$ the normalized activation energy, $b$ is the magnitude of the Burger’s vector, $k$ is Boltzmann’s constant. The average shape of the obstacles profile is defined by the $p$ and $q$ constants.

The evolution of the structure along arbitrary paths of strain, strain rate, and temperature is formulated in a differential form that balances dislocation accumulation and dynamic recovery phenomena occurring during plastic deformation. It is assumed that the structure evolution can be described as,

$$\theta = \theta_{0} \left[ {1 - F\left( {\frac{{\hat{\sigma }_{ } - \hat{\sigma }_{a} }}{{\hat{\sigma }_{es} - \hat{\sigma }_{a} }}} \right)} \right]$$

(10)

in which the strain hardening rate $\theta = d\hat{\sigma }/d\varepsilon_{p}$ depends on the athermal work-hardening rate $\theta_{0}$ and on the saturation MTS $\hat{\sigma }_{es}$, which can be written as follows,

$$\hat{\sigma }_{es} = \hat{\sigma }_{es0} \left( {\frac{{\dot{\varepsilon }_{p}^{ } }}{{\dot{\varepsilon }_{es0}^{ } }}} \right)^{{\frac{kT}{{Gb^{3} A}}}}$$

(11)

$$\theta_{0} = a_{0} + a_{1} \ln \left( {\frac{{\dot{\varepsilon }_{p}^{ } }}{{\varepsilon_{0}^{ } }}} \right) + a_{2} \sqrt {\frac{{\dot{\varepsilon }_{p}^{ } }}{{\varepsilon_{0}^{ } }}}$$

(12)

where $A$,$\dot{\varepsilon }_{es0}$,$a_{0}$,$a_{1}$,$a_{2}$,$\varepsilon_{0}$ are material constants and $\hat{\sigma }_{es0}$ is the MTS at 0 K. The function $F$ is chosen to fit the experimental data. For OFHC copper, a modified version of the Voce-type equation was proposed:

$$\frac{{\partial \hat{\sigma }}}{{\partial \varepsilon_{p} }} = \theta_{0} \left[ {1 - \frac{{\tanh \left( {2{{\hat{\sigma }} \mathord{\left/ {\vphantom {{\hat{\sigma }} {\hat{\sigma }_{es} }}} \right. \kern-\nulldelimiterspace} {\hat{\sigma }_{es} }}} \right)}}{\tanh \left( 2 \right)}} \right]$$

(13)

The identification of material constants requires many experimental tests, that should include strain rate and temperature jumps. For copper, the model parameters identified in [37] were initially assumed and later adjusted to ensure a better description of the flow curve and the viscous drag phenomenon. The MTS model parameters for OFHC copper are summarized in Table 3.

Table 3 Summary of MTS model parameters

The comparison between the model results and experimental data is presented in Figs. 8, 9, and 10. Despite a greater formulation complexity and more material parameters to identify, the MTS model results in a better agreement with the experimental data over a wider range of temperatures and strain rates. Indeed, the MTS error in the prediction of the experimental data presented in Fig. 10 is 4.2%, while, for the same experimental set, the MJC and the ZA exhibited errors of 13.5% and 19.2% respectively.

Fig. 8

MTS model parameters identification: a flow curve and b strain rate sensitivity for 0.15 of plastic strain c temperature effect

Fig. 9

MTS model parameters verification: strain rate sensitivity at 0.2 of plastic strain. The experimental data are reported in [28, 29, 31,32,33]

Fig. 10

Comparison of experimental and MTS model computed flow curves at different temperatures and strain rates: a 2000s⁻¹ [30] and b 4000 s.⁻¹ [33]

Numerical Simulation Of Dynamic Tensile Extrusion (Dte) Test

Finite Element Model and Analisys

DTE tests on OFHC copper at different impact velocities were simulated using the finite element method (FEM) code MSC Marc v2021. A coupled thermo-mechanical analysis was carried out to consider the thermal softening due to the conversion of plastic work into heat in quasi-adiabatic conditions. Simulations were performed under large displacement and finite strain formulation using the Lagrangian updating technique while a single-step Houbolt procedure was chosen for the dynamic transient analysis. Since the problem is axisymmetric, a bi-dimensional model was developed using four-node, isoparametric elements with bilinear interpolation functions in an axisymmetric formulation.

Both the bullet-like sample and the extrusion die were modeled as elastoplastic deformable bodies, although an investigation of the influence of the die modeling on the overall result has been carried out. For the sample, the different constitutive models presented in the previous section (MJC, ZA, MTS) were implemented via user subroutines. The extrusion die was simulated as elastic–plastic material using a standard JC constitutive model and model parameters employed in [21] were assumed in this work. A parametric investigation was performed prescribing an initial velocity to the bullet-type sample accordingly to experimental tests.

Post mortem microstructural analysis revealed that dynamic recrystallization, which acts as a local stress-relief factor, preventing voids nucleation and causing rupture [38], has occurred in the extruded fragments ends [12]. Thus, to simulate extrusion jet fragmentation, a simple maximum plastic strain criterion was used. In particular, elements are removed when the average total equivalent plastic strain over the element Gauss points exceeds 700%. This limit value was selected to avoid unphysical deformation due to remeshing of the necked ligament between the forming fragments.

Friction

Friction plays an important role during the travelling of the sample in the extrusion die. In general, friction is a complex physical phenomenon that involves the characteristics of the surface, such as surface roughness, temperature, normal stress, and relative velocity. The actual physics of friction and its numerical representation continue to be topics of research and a limited library of friction models are usually made available to the user in commercial numerical codes.

In this work, the interaction between the die and the specimen was modeled as deformable-deformable contact algorithm. For friction a bilinear shear formulation, which states that the frictional stress is a fraction of the equivalent stress in the material, was used. In the bilinear model, it is assumed that that the shear (friction) stress $\sigma_{t}$ in a node is proportional to the applied shear (friction) force and limited by,

$$\sigma_{t} = \min \left( {\mu \sigma_{n} ,\mu {{\sigma_{eq} } \mathord{\left/ {\vphantom {{\sigma_{eq} } {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}} \right)$$

(14)

where $\sigma_{n}$ is the normal stress, $\sigma_{eq}$ the equivalent of stress and $\mu$ is the friction coefficient which was calibrated and kept constant during the analysis. Element damping was also employed to damp out unwanted high-frequency chatter in the structure and to improve convergence. Element damping in MSC MARC scales down the element mass $M_{i}$ and stiffness $K_{i}$ matrices in the following way,

$$C = \mathop \sum \limits_{i = 1}^{n} \upsilon_{i} M_{i} + \left( {\beta_{i} + \gamma_{i} \frac{\Delta t}{\pi }} \right)K_{i}$$

(15)

where, $M_{i}$ is the mass of i-th element and $K_{i}$ is the stiffness matrices. $\upsilon_{i}$, $\beta_{i}$ and $\gamma_{i}$ are the numerical damping coefficients and $\Delta t$ is the time increment. Here, $\alpha_{i}$ and $\beta_{i}$ were assumed to be equal to zero, and only element stiffness damping $\gamma_{i}$ was considered.

Remeshing

Since the sample in the extrusion die is undergoing extreme distortion, remeshing is strictly necessary when using Lagrangian finite element formulation. In this work, Advancing Front Mesher (AFM) was used. This feature creates a 2D quadrilateral mesh starting from the outline of the geometry and then advancing inwards. To create the new mesh, a strain change criterion was chosen with a limit value of 0.5. In Fig. 11, the initial mesh is shown.

Fig. 11

Initial mesh for DTE showing the bullet-shaped sample and the extrusion die. The red-line indicates axisymmetry condition

Material Models

The three selected material models, i.e. MJC, ZA and MTS, are not available in the MSC MARC material library. Thus, they have been implemented via user subroutine WKSLP. This user subroutine, present in the code library, allows the user to define the yield stress for the material and the corresponding work-hardening slope directly as a function of equivalent plastic strain, strain rate and temperature. The user needs to define the value of the slope of the equivalent stress vs. equivalent plastic strain. The current yield stress can be defined also. The specification of the latter is optional. If the value of the current yield is not given here, MSC MARC calculates it from the initial yield value and the work-hardening slopes defined in this user subroutine. The user subroutine is called as required by Marc during the elastic–plastic calculations. The number of times it is called per increment depends on the number of points going plastic, on the nonlinearity of the work-hardening curve, and on temperature dependence. For the integration of the stage II hardening in the MTS model, a Runge–Kutta algorithm was implemented.

Results and Discussion

DTE tests have been performed at 350, 380, 400, and 420 m/s. Results in terms of retrieved fragments are shown in Fig. 12. Hereafter, fragments are numbered starting from the left, where fragment 1 is the one that remains in the die, fragment 4 is last of the jet sequence although being the first formed during the extrusion process. In the numerical simulation of the DTE, several computational parameters can affect the results in terms of the predicted number, shape, and size of the fragments making it difficult to discriminate the effective material constitutive model performance. Thus, a sensitivity analysis was performed with the twofold objective to evaluate the influence of such parameters and determine an optimum set that minimizes the influence on the material model response. To begin with, the DTE test performed at 400 m/s was used as the reference case for computational model calibration. Successively, the effective material model predictive capability was assessed by predicting DTE behavior at different impact velocities and comparing computational results with experiments.

Fig. 12

DTE tests recovered fragments at different impact velocities [21]

Model Calibration

A parametric investigation of the influence of computational parameters on numerical simulation results was carried out for the reference case of 400 m/s impact velocity. To quantitatively investigate the effect of these parameters, the error in the estimation of each fragment length was calculated as follows:

$$Error (\% ) = \frac{{l_{FEM} - l_{EXP} }}{{l_{EXP} }} \cdot 100$$

(16)

in which $l_{EXP}$ and $l_{FEM}$ are the measured length in the experiment and the numerical predicted length, respectively.

Damping Effect

In the simulation, the use of damping for the sample elements was found to have a strong effect on the predicted length of the extruded fragments. Increasing the damping coefficient, the length and the number of the extruded fragments decreases, as a result of a higher attenuation of the material response. The damping coefficient $\gamma_{i}$ was varied between 0 (no damping) and 10. In Fig. 13a–c, the error in the predicted fragment length for each constitutive model is summarized. For the MTS model, the best solution is found without damping ($\gamma_{i} = 0$). Instead, for both MJC and ZA models, the minimization of the overall error was achieved for $\gamma_{i} = 1.2$. With the increase in damping coefficient, the error with the MTS model in the length of the predicted fragments diverges almost immediately, while the other two material models show some difficulty in accurately predicting the length of the second fragment in particular. This behavior may be a consequence of the differential formulation of stage II hardening in the MTS model which ensures higher response stability to strain rate jumps [10]. The length of Fragment 1 appeared to be the least affected by the damping coefficient: the reflection of release and compressive waves in this portion of the material is indeed less significant than in the tip.

Fig. 13

Effect of bullet damping on predicted fragment lengths a MTS model, b MJC model, c ZA model. Die damping coefficient was set to 1.2

Friction Effect

The effect of the choice of the friction coefficient was investigated by performing a parametric investigation varying the friction coefficient $\mu$ between 0 (no friction) and 0.3. This upper bound value was determined as the value at which the error in the predicted length of at least two fragments was diverging, becoming larger than 100%. Results for the three material models are shown in Fig. 14. The friction coefficient seems to have a major influence on the size of the second and third fragments: increasing the friction coefficient the expected length of these two fragments decreases. When the friction coefficient becomes large, the formation of fragments is inhibited: friction reduces the jet velocity of the second and third fragments, limiting the extrusion process. This is clearly represented in Fig. 15, in which the computed velocities profile, for two material points in the middle of the first and third fragments, are compared for different friction coefficients. From these results, the variation of the momentum for the first fragment with friction is negligible, resulting in a limited influence on the fragment length. In addition, the assumption of no-friction has to be excluded since the predicted shape and size of the fragments are far away from the experiments. For the MJC and MTS models, the minimum error in the predicted lengths of the fragments was obtained for a friction coefficient of 0.08. This value also provided the best representation of the experimental data with the ZA model, although the formation of the second fragment was not predicted. This value is significantly lower than the kinetic friction value reported in the literature for copper on steel under clean surface conditions ($\mu = 0.31$) [39].

Fig. 14

Effect of friction on predicted fragment lengths a MTS model, b MJC model, c ZA model. The bullet damping coefficient was set to 1.2 for the MJC and ZA models, and 0.0 for the MTS model

Fig. 15

Profile velocities for different friction coefficients at the middle of the first and third fragment with the MTS model

Remeshing Effect

Since the test sample undergoes extremely large plastic deformation, remeshing is unavoidable when using implicit finite element codes. Unfortunately, remeshing inevitably affects the results. When a new mesh is generated, the correspondence between nodes is not guaranteed and the interpolation of the results on the new mesh might lead to computational inaccuracy, artificial smoothing of state variables gradients, loss of information, and error propagation [40]. The Advancing Front Mesher, which was used in the present study, support loads and boundary conditions on the outline, offering full support for the geometry preservation including hard and soft entities. There are some limited capabilities for mesh density control, with curvature control and refinement boxes, but it supports trimming and crack propagation. The criterion to trigger remeshing may also influence the results. In Fig. 16, the qualitative comparison of the predicted jet with different remeshing criteria is shown for the MTS and MJC models. For the ZA model, the results exhibited a similar trend with respect to the MJC. The two investigated remeshing criterial are a strain change-based criterion and angle change-based criterion. In the first, a new mesh is generated when the level of plastic strain accumulated in a Gauss-point exceed a user-defined value. In the latter, the remeshing is triggered when the internal angle of an element changes according to a used-defined value. The limit values for the generation of a new mesh were selected to follow the deformation process without an excessive element distortion that may cause numerical errors that propagate in the subsequent remeshing operations. A limit value of 0.5 was selected for the strain change criterion, while a value of 20° for the angle change criterion. As shown, results seem to depend on the combination of the remeshing criterion and material model. For the MTS model, the two criteria provide similar results, while for the MJC model, the angle deviation criterion results in a reduction in the length of the second fragment and a variation of its shape as well.

Fig. 16

Qualitative evaluation of the influence of remeshing criteria for MTS and MJC constitutive model. Contour plots indicate the Total Equivalent Plastic Strain

Extrusion Die Modeling Effect

The way how the extrusion die is simulated plays a crucial role in the numerical results of DTE. In previous studies, the extrusion die has been simulated in different ways: rigid body [10], elastic-perfectly plastic material [22] or elastic–plastic material with strain rate effect [21]. The choice of the extrusion die constitutive modeling affects the stress wave dynamics during the extrusion process with possible effect on the predicted extruded material jet. When the extrusion die is modelled as a deformable material, it is necessary to also calibrate the numerical damping to be used. A sensitivity analysis of the extrusion die modeling was carried out assuming the MTS model for the test sample. In Fig. 17, the comparison of the predicted fragments for 400 m/s impact for different combination of selected constitutive model and damping factor for the die is shown. For reference, the results without damping for the elastic and elastic–plastic die models are also given. All simulations were carried out with a constant friction coefficient of 0.08. Analyses show that assuming the die as a rigid body leads to predicted extruded jet far off the experimental results. A better agreement with experiments is found for the case of elastic and elastic–plastic material behavior where the error can be minimized tuning the damping coefficient. Interestingly, without damping coefficient, the error in the predicted lengths of the extruded fragments was significantly higher for the elastic–plastic die than the elastic one, Fig. 18. This indicates that stress waves in the elastic–plastic die require to be damped more than that calculated for the purely elastic case. Although the yield stress for the die is 1500 MPa, which is appropriate for a high strength tool steel, this value is exceeded in region close to the exit bore for impact velocities larger than 350 m/s. Probably, it is the stress wave generation and propagation in this region that has a major influence in the formation of the jet fragments. An optimum configuration was obtained modeling the die as elastic–plastic material with a damping coefficient of 1.2.

Fig. 17

Influence of the die modeling on fragment shape for the MTS model. Contour plots indicate the Total Equivalent Plastic Strain

Fig. 18

Effect of die modeling on predicted fragment lengths for the MTS model

Constitutive Models Assessment

A qualitative comparison of the shape and size of the predicted fragments with the experimental results with the three material models and optimized numerical parameters is shown in Fig. 19. The MTS model seems to provide better and more accurate results compared to the other two. The MJC model provided good results despite its simplicity. while the ZA model failed in predicting the formation of the second fragment with a friction coefficient of 0.08, although the predicted length of the fragment in between is comparable to the sum of the lengths of the two experimental fragments.

Fig. 19

Qualitative comparison between the experimental and numerical fragments for the impact velocity of 400 m/s. Contour plots indicate the Total Equivalent Plastic Strain

In Fig. 20, quantitative measurements of the fragment’s length, diameter, and shape are reported and compared with numerical results for MTS and MJC models. Although both models show a good agreement with the experimental results, the shape of the fragments is predicted more accurately with the MTS.

Fig. 20

Quantitative comparison between the experimental and numerical fragments for the impact velocity of 400 m/s with MTS and MJC models

Material Model Verification

Finally, material models’ predictive capability has been verified by performing numerical simulation of DTE at impact velocities other than the reference case of 400 m/s. As before, for each material model, quantitative validation metrics and qualitative results regarding the extruded jet (Figs. 21, 22, 23, 24) have been compared with experimental data. In Fig. 21, the error in the predicted fragment size as a function of the impact velocity is shown. Here, MTS model seems to be capable to anticipate the characteristics of the jet fragmentation with better accuracy than other two models over the entire velocity range investigated experimentally. However, all material models seem to show some difficulties in predicting the size of the second fragment for impact velocity 400 m/s and higher. This fragment is the last to be formed during the dynamic extrusion but, according to the numerical simulation results, the portion of the jet material involved in its formation is deforming at very high strain rate levels during the whole jet extrusion process. This is shown in Fig. 25, where the computed maps of the strain rate at different time instants, from the extrusion to the fragment formation, are given. The portion of jetted material, corresponding to the second fragment, deforms at strain rates that for copper are dominated by viscous phonon drag [41]. In Fig. 26, the comparison between the strain rate evolution versus plastic strain, for two sample points located at about half the length of the second and third fragment, is shown. This information has been extracted from the numerical simulation of the test at 420 m/s with the MTS model and the investigated in the material points are presented in Fig. 25. According to this, the strain rate in both fragments is similar, but the second fragment deforms at about twice the plastic strain, thus it remains at a high strain rate for a longer time. The material constitutive response in this regime is not accurately described by the MJC and ZA models which show the larger error in the predicted length of the second fragment. Furthermore, all the material models considered here, predict a linear increase of the yield stress with the strain rate not considering that viscous drag is limited [21, 42].

Fig. 21

Error in predicted fragment size at different impact velocities a MTS model b MJC model c ZA model

Fig. 22

Summary of predicted fragments at different impact velocities with the MTS model. The contour plot indicates the Total Equivalent Plastic Strain

Fig. 23

Summary of predicted fragments at different impact velocities with the MJC model. The contour plot indicates the Total Equivalent Plastic Strain

Fig. 24

Summary of predicted fragments at different impact velocities with the ZA model. The contour plot indicates the Total Equivalent Plastic Strain

Fig. 25

Computed maps of the strain rate at different time instants, from extrusion to fragmentation. The red and yellow circles represent the sample points for monitoring the strain rate evolution with respect to plastic strain during the test

Fig. 26

Comparison of FEM predicted strain rate evolution versus plastic deformation for two points in the middle of the second and third fragments

Conclusions

In this work, the performance of three different constitutive models and the influence of numerical parameters for the simulation of the DTE test on OFHC Copper were investigated. A sensitivity analysis was carried out to investigate the effect of computational parameters for the simulation of the 400 m/s test. The second and third fragments were found to be the most affected by numerical parameters, and an optimum set, regardless of bullet constitutive modeling, was identified to perform further analysis. For each constitutive model, the predicted extruded jet is overall in good agreement with the experimental data. The results show that the physically-based MTS model allows a better description of the phenomenon at different testing velocities, with good accuracy in predicting both size and shape of fragments, although a large number of material constants are required. The ZA model does not predict the formation of the third fragment at 400 m/s, with the largest errors for other velocities as well. The MJC model cannot predict the length of the second fragment at 420 m/s and the error in the prediction of the fragments’ lengths is higher than MTS. However, given its simplicity, the model offers a good trade-off between accuracy and complexity. Interestingly, the ability to correctly predict the size and shape of the last temporally forming fragment appears to be directly related to the ability of the constitutive model to accurately describe the material response in the viscous drag regime. This opens a window for the DTE and its possible use for material model assessment in the very high strain rate-large plastic strain regime.