Influence of Strength and Thermo-mechanical Properties of Solid Constituents on Temperature of Two Shock Loaded Porous Materials

Abstract

The temperature response of copper and silicon dioxide porous materials under impact loading is investigated experimentally and numerically. The gas gun experiments employ high speed pyrometry for measurement of the thermal emission from the shock compressed porous materials through a transparent polymer window. The numerical analysis uses a two-phase thermodynamically consistent model with consideration of strain rate sensitive flow stress. The objective of the study is to assess the contribution from the two phases constituting the porous materials to the temperature shock response. The numerical investigation includes an analysis of plastic deformation of the condensed phase, material compaction, and the inter-phase heat exchange for two porous materials with distinctively different thermal, mechanical, and strength properties of the solid constituents. Using a phenomenological approach that employs conventional equations of state for the phases and viscoelastic constitutive equations for the solid constituents, results of the modeling of the materials under shock compression correlates the measured temperature of the powders if the gaseous phase is taken into account. A detailed one-dimensional analysis evaluates possible contributions of the thermo-mechanical and kinetic properties, including compaction resistance, strength, and strain rate sensitivity to the thermal emission. It is shown that the adiabatic compression of the gaseous phase and heat exchange can make a notable contribution towards the evaluated temperature. The analysis suggests that the two-phase consideration accounting for the rate sensitive strength of the solid phase is highly desirable for an accurate assessment of the thermal shock response of porous materials under mechanical and thermal non-equilibrium.

Introduction

Porous materials, including a variety of structural and reactive materials, are important for a large number of dynamic applications, such as shock wave mitigation and shock absorption. Whereas the mechanical contribution of the gaseous phase of a porous material appears negligible at shock compression, in reality the interstitial gas is both a mechanical mediator and a contributor of thermal energy due to the adiabatic shock compression of the gas. At the same time, strength of the condensed constituents affects the porous material compaction and the rate sensitivity of the flow stress influences the rise time of shock wave thus affecting the pore compression and having an impact on the adiabatic heating due to pore collapse.

The effect of extreme heat release in porous materials is routinely used for the thermodynamic analysis of the constituting condensed materials in the high temperature zone of the phase diagram for the design of appropriate Equations of State (EOSs). Wide-range EOSs can appropriately describe the shock response of condensed materials, including the approach of kinetically variable EOSs (e.g., P-λ model by Grady [1]). However, when describing porous materials via models based on the condensed phase EOSs (e.g., P-α model by Hermann [2]), the thermal response may not be adequate, requiring extra effort or EOS modifications for an accurate description of the shock response [3, 4].

Experimental pyrometry [5] in the near infra-red region has been used in the present work for assessment of the thermal radiation output of two distinct inorganic powders, namely silicon dioxide and copper. The technique evaluates the emission by comparing the ratios of the wavelength bandwidth outputs, corresponding to three colors in the near infra-red part of the spectrum, with a calibration curve from a greybody emitter. Temporal resolution of the pyrometer is sufficient for evaluating the shock response of porous material (powder) samples, which are loaded by flyer plates launched by a gas gun. The corresponding experimental measurements are used in the present paper for analysis of the contribution of various mechanical and thermo-physical parameters of the two powders to the thermal emission.

Meso-mechanical modeling reported in the literature enables one to analyze in detail the effects of pore distribution and shape at loading comparable with the strength level [6] or to describe the temperature spikes in the interstitial space [7,8,9], but cannot give useful information for the measurable thermal emission. Therefore, a phenomenological approach [10], omitting the details exhibited at the micro- and meso-level might help in assessment of the thermal energy output. At the same time, when accounting for the processes at the micro- and meso-level, the corresponding constitutive equations can appropriately describe the influence of relevant internal variables on the output within the phenomenological approach. Majority of the existing phenomenological models for two-phase materials ignore the effect of interstitial air because of its negligible effect at quasi-static loading, whereas in dynamic conditions, the effect of heating due to the pore collapse has been observed explicitly in shock experiments [11]. Therefore, the present study specifically accounts for the adiabatic compression of the interstitial gas and analyzes its contribution into the emitted thermal energy.

The present numerical analysis employs the two-phase approach, resulting in a model [12] formulated as a system of hyperbolic equations, based on the non-equilibrium irreversible thermodynamics applied to the systems of conservation laws [13]. The model was originally developed for low porosity materials with moderate inter-phase heat exchange [10] and further progressed to a model [14] accounting for extreme thermal effects in highly porous materials while neglecting the strength effects. The further model [12] takes into account both the extreme thermal effects and strength effects, which is used in the present work. This model is thermodynamically consistent and validated by description of Hugoniots of both moderately porous [10] and highly porous materials with anomalous Hugoniot response [12, 14]. The role of the thermal effects governed in the model by a heat exchange kinetic has been analyzed and clarified in [15]. The model [12] allows a description of the material response in a phenomenological sense, as a whole, while averaging the thermodynamic parameters, along with the description of response of the individual phases. This model is used in the present paper for the analysis of the phase contributions to the thermal emission for the copper and quartz porous materials investigated experimentally. The model employs individual EOSs for the condensed and gaseous phases and has been implemented in the CTH hydrocode [16], with the implementation reported elsewhere [17].

A more detailed parametric study for one of the two materials considers the effects of parameters responsible for several mechanisms of the material compression, specifically, plastic deformation of the solid phase including strain rate effects, compaction controlled by solid particle deformation and fracture, and inter-phase heat exchange. The results of the numerical analysis correlate well with the temperature trend observed in the present experiments. The parametric study indicates that the influence of the interstitial gas may significantly contribute to the observed difference in the thermal emission between the two powders analyzed. Specifically, the strain rate sensitivity, promoting or resisting the pore collapse, can be a significant factor along with the inter-phase heat exchange, with both affecting the temperature.

Experiments

Planar high velocity impact gas gun tests, which provide a calibrated shock wave load, have been conducted to evaluate the effect of the thermo-mechanical properties of the material constituents on the thermal output of porous materials during the shock compression.

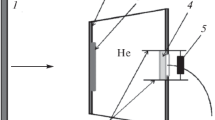
A 10 mm thick, 28 mm diameter polymethylmethacrylate (PMMA) flyer plate housed in a sabot (Fig. 1), is accelerated in a 30 mm bore gas gun to a velocity of 400 m/s. The flyer plate collides with a target assembly (‘Target Cell’) containing the porous sample which is covered by a 3 mm aluminum plate and backed by a 13 mm transparent PMMA window (‘Acrylic Lid’) as shown in Fig. 1. The emitted thermal radiation is collected and transmitted by a fiber optic cable to the pyrometer.

Fig. 1

Experimental set-up of the high velocity impact experiment

Micrographs and scanning electron microscopy (SEM) images of the investigated powders are shown in Fig. 2. It is seen that the particle shapes for a typical sample are quite regular for the silicon dioxide powder and very irregular for the copper powder with large length-to-width ratios. The copper powder particles are agglomerated from smaller particles in the submicron range. The maximum and minimum dimensions of the clustered particles vary from tens of microns to a hundred microns as seen in the 10 micron scale image in Fig. 2c.

Fig. 2

Micrographs of the materials: silicon dioxide powder at 1 mm scale (a) and copper powder at 20 μm scale (b), along with a 10 μm detailed view of the copper powder (c)

The thermal output was assessed by a three-color pyrometer in the near infrared wavelength region, which allows estimation of the temperature. The thermal emission is collected from an 8 mm diameter circle area of the sample surface at the sample-window interface. The central wavelengths of the 50 nm width bandpass filters are 900, 1075, and 1550 nm. The wavelengths were chosen to avoid spectral lines for the selected test materials: copper and quartz (silicon dioxide). Temporal resolution of the pyrometer system was 100 ns. A schematic of the pyrometer is shown in Fig. 3. The pyrometer has been calibrated with a source of effective temperature 2800 K. The measured temperatures are obtained by fitting the thermal radiation response with a greybody radiation spectrum (Planck curve) at each time step. Emissivity is assumed constant with respect to wavelength at each time step, however, it can vary with time [18, 19]. A comparison of the output from the porous materials, which are composed of thermally distinctive constituents, allows estimation of the constituent influence on the thermal response and necessitates understanding the output difference via constitutive modeling.

Fig. 3

Schematic of the three-color pyrometer used in the present experiments

The measured temperatures from the pyrometry data (sampled at 2G Samples/s and averaged over 100 points) for the silicon dioxide and copper powders are shown in Fig. 4. It should be noted that the origin time for the observed temperatures shown in Fig. 4 is aligned with the signal rise, not with the instance of collision of the flyer plate with the target assembly. The temporal resolution of the signals is not sufficient to measure the initial collapse of the gaseous pores adjacent to the window interface, which is on the order of 10 ns as shown by [11]. The measured temperatures characterize a more integral response of the powders to the shock wave interacting with the PMMA window, which will be discussed in detail in the subsequent sections.

Fig. 4

Measured temperatures for silicon dioxide (curve S) and copper (curve C) powders

Model

A two-phase model developed earlier [12] is based on the principles of extended irreversible thermodynamics with the principles specified for the systems of conservation laws in [13]. Under the assumption of a single velocity for the two phases, the governing laws of the model can be formulated in the conventional form for conservation of mass, momentum, and energy. The model takes into account strength effects for the condensed constituents. To achieve this, rate sensitive constitutive equations for weighted small elastic deviatoric deformations, e_ij, introduced for decoupling of bulk from deviatoric response (see [12]), are also included in the model formulation. At the same time, the model specifies individual phases with the parameters responsible for the inter-phase exchanges: mass concentration of the first phase c related to possible phase transitions; volumetric concentration θ of the first phase related to the compaction (representing porosity in case of gaseous first phase), entropy disbalance χ related to the inter-phase energy exchange, and strain disbalance parameters λ_ij related to the inter-phase shear work exchange (relating to the irreversible deformation of the solid phase in case of a porous material). Using these inter-phase exchange variables, specific parameters of the phases, density, entropy (identified by subscripts with the phase number below), and elastic deformations (identified by corresponding superscripts in parentheses below), can be calculated from the averaged parameters and internal variables of porous material as follows:

$$\rho_{1} = \rho \frac{c}{\theta },\quad \rho_{2} = \rho \frac{1 - c}{{1 - \theta }},\quad s_{1} = \frac{s + \chi }{{2c}},\quad s_{2} = \frac{s - \chi }{{2\left( {1 - c} \right)}},\quad e_{ij}^{(1)} = \frac{\theta }{c}\left( {e_{ij} + \lambda_{ij} \left( {1 - \theta } \right)} \right),\quad e_{ij}^{(2)} = \frac{1 - \theta }{{1 - c}}\left( {e_{ij} - \lambda_{ij} \theta } \right).$$

As a result, the standard system of conservation laws with constitutive viscoelastic Maxwell-type equations for the deformations complemented with constitutive equations for the inter-phase exchange parameters (internal variables) takes the following form [12]:

$$\begin{gathered} \frac{\partial \rho }{{\partial t}} + \frac{{\partial \rho u_{k} }}{{\partial x_{k} }} = 0,\quad \frac{{\partial \rho u_{i} }}{\partial t} + \frac{{\partial \left( {\rho u_{i} u_{k} - s_{ik} } \right)}}{{\partial x_{k} }} + \frac{\partial p}{{\partial x_{i} }} = 0, \hfill \\ \frac{{\partial \rho \left( {E + {{u^{2} } \mathord{\left/ {\vphantom {{u^{2} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}{\partial t} + \frac{{\partial \left[ {\rho u_{k} \left( {E + {{u^{2} } \mathord{\left/ {\vphantom {{u^{2} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) - s_{ik} u_{i} + pu_{k} } \right]}}{{\partial x_{k} }} = 0, \hfill \\ \frac{{\partial \rho e_{ij} }}{\partial t} + \frac{{\partial \rho e_{ij} u_{k} }}{{\partial x_{k} }} - \frac{1}{2}\frac{{\partial u_{i} }}{{\partial x_{j} }} - \frac{1}{2}\frac{{\partial u_{j} }}{{\partial x_{i} }} + \frac{1}{3}\frac{{\partial u_{k} }}{{\partial x_{k} }}\delta_{ij} = - \left( {\theta \varphi_{ij}^{\left( 1 \right)} + \left( {1 - \theta } \right)\varphi_{ij}^{\left( 2 \right)} } \right) - \rho \lambda_{ij} \psi_{0} , \hfill \\ \frac{dc}{{dt}} = - E_{c} \varphi_{0} ,\quad \frac{d\theta }{{dt}} = - \left( {E_{\theta } + \lambda_{ij} s_{ij} } \right)\;\psi_{0} ,\quad \frac{d\chi }{{dt}} = - E_{\chi } \omega_{0} ,\quad \frac{{d\lambda_{ij} }}{dt} = - \frac{{\varphi_{ij}^{\left( 1 \right)} - \varphi_{ij}^{\left( 2 \right)} }}{\rho }. \hfill \\ \end{gathered}$$

(1)

Here, s_ij are the stress deviator components, δ_ij are components of the unit tensor, p is pressure, and u_i are velocity components. To provide thermodynamic correctness of the model, the right hand sides are chosen in (1) such that the entropy growth rate would be non-negative with arbitrary non-negative functions φ₀, ψ₀, and ω₀ [12]. The functions φ_ij⁽¹⁾ and φ_ij⁽²⁾ are responsible for the irreversible response of the first and second phases, respectively (assuming the first phase is gaseous, this is applicable only to the second condensed phase for the case of a porous material) and they are determined from a given yield limit dependence on strain rate [12]. Internal energy E is defined for the porous medium as E(ρ, e_ij, s, c, θ, χ, λ_ij) = cE⁽¹⁾(ρ₁, e_ij⁽¹⁾, s₁) + (1 – c)E⁽²⁾(ρ₂, e_ij⁽²⁾, s₂) from internal energies of the corresponding phases E⁽¹⁾ and E⁽²⁾. The compaction kinetic is taken for the copper powder from [14] and for the silicon dioxide powder, which behaves very similarly to the calcite sand at compaction, from [20].

Dependent thermodynamic variables can be calculated from the thermodynamic identity: TdS = dE – pdV – s_ijde_ij – Λdc – Πdθ – Q_ijdλ_ij – Ψdχ, where V = 1/ρ and T is temperature, using the chain rule:

$$T = E_{s} ,\quad p = \rho^{2} E_{\rho } ,\quad s_{ij} = E_{{e_{ij} }} ,\quad \Lambda = E_{c} ,\quad \Pi = E_{\theta } ,\quad Q_{ij} = E_{{\lambda_{ij} }} ,\quad \Psi = E_{\chi } .$$

The chosen EOSs for the powders are a Mie-Grüneisen consistent EOS for the condensed phase [21] and the ideal gas EOS for the gaseous phase. Key parameters of the EOS for the condensed phases are taken to be ρ₀ = 4 g/cm³, ρ₀₀ = 8.9 g/cm³, K = 138 GPa, G = 40.8 GPa for copper and ρ₀ = 1.37 g/cm³, ρ₀₀ = 2.65 g/cm³, K = 43.6 GPa, G = 31.2 GPa for silicon dioxide, where ρ₀₀ is initial density of the corresponding solid constituents, ρ₀ is initial density of powders taken from those used in the present experiments, and K and G are bulk and shear modulus (the material constants of different phases are denoted by the same symbols for brevity). The rate functions φ_ij⁽¹⁾ are reduced to zero for the gaseous phase and φ_ij⁽²⁾ require rate sensitive yield limits controlling the solid phase viscosity [22], which vary for the present constitutive equation from 10 to 30 MPa for quartz [20] and from 240 to 280 MPa (at a constant strain) for copper [23] over a strain rate range of 10^–2 to 10³ 1/s. The procedure for fitting two key parameters for the plastic rate function φ_ij⁽²⁾ of the Maxwell-type viscoelastic constitutive equation, using two yield limit points Y₁ and Y₂ versus two corresponding strain rate dε₁/dt and dε₂/dt, is described in [24], the subscripts for yield limit and strain rate refer to the point number of a dataset for the second phase only. A dependence of the rate sensitive flow stress expanded over the range from 10^–5 to 10⁵ 1/s for the abovementioned baseline case of quartz is shown as curve 2 in Fig. 5a.

Fig. 5

Dependences of yield limit versus strain rate for the solid phase of silicon dioxide powder (a) with crosses used as input data for the constitutive stress relaxation functions φ_ij⁽²⁾. The porosity θ versus pressure p (pressure equilibrium curves) for the silicon dioxide (curve 1) and copper (curve 2) porous materials (b)

In order to understand how rate sensitivity in various materials affects the heat exchange in the materials, different hypothetical rate sensitivity dependencies can be considered, for example, for a silicon dioxide material, in addition to the curve 2 assessed in the experiments [20]. For various rate sensitivities of the yield limit, examples are shown in Fig. 5a for the least rate sensitive cases, presented by curves 4 and 5, corresponding to the minimum and maximum yield limit values of the range considered in the present work, up to the most rate sensitive case shown by curve 3 (at Y₁ = 5 MPa and Y₂ = 50 MPa) with the sensitivity increased up to the case of curve 3 via intermediate cases shown by curves 1 and 2 (the latter corresponding to the given yield limits in the baseline case). These dependencies of yield limit versus strain rate shown in Fig. 5a will be used in the parametric analysis in a subsequent section.

The rate function ψ₀ of the constitutive equation for the porosity parameter θ is material specific and can be determined from Split Hopkinson Pressure Bar (SHPB) tests or from special tests enabling one to measure porosity in shock response experiments. This function has a critical component, equilibrium porosity (the residual porosity of a porous material after specified load), represented by pressure equilibrium curves [10, 14], which depict effective pressure, p_cr, for transition from uncompacted (pre-test) to compacted states. The effective pressure is characterized by the value on the order of 250 MPa for the silicon dioxide powder [20] and a porosity-dependent value tapering from 100 MPa up to 2 GPa for the copper powder [14] obtained from the experimental data [25]. The corresponding fitted pressure equilibrium curves used for the copper and quartz porous materials are shown in Fig. 5b and they are used as input data for the compaction rate function ψ₀. The relatively abrupt behavior of the pressure equilibrium curve for sand observed in [10] can be explained by brittle fracture of the silicon dioxide particles. Similar behavior for a sand has also been observed in [26]. At the same time, the relatively gradual compaction seen as curve 2 in Fig. 5b is caused by the ductile deformation of metallic powders under compaction, which is observed for a number of metallic powders such as aluminum [27, 28], copper [25], and a porous iron [29].

The kinetic ω₀ is controlled by the heat conductivity coefficients of the phases and is essentially influenced by the particle diameter d. Namely, the heat exchange kinetic ω = E_χω₀ is associated with a balance of the total energy E + u²/2, where an energy intake into the solid phase, l₀, is related to ω as ω = – (l₀/T₁ + l₀/T₂)/ρ, as derived in [14]. The heat exchange source term l₀ is proportional to the interface heat exchange through the unit area – h (T₁ – T₂) controlled by the heat transfer coefficient and the total interface surface area within a unit of representative volume. The latter is proportional to the number of particle interfaces, which in turn is inversely proportional to the particle diameter d (specifically, for particles with characteristic diameter d having corresponding averaged area proportional to d² with the number of particles to be inversely proportional to d³, this will result in the total gas–solid interface area proportional to d²/d³ = 1/d). Taking h = Nk_eff/d, k_eff = k₁k₂/[θk₂ + (1 – θ)k₁] from [30] and integrating with the interface area within the representative volume, the kinetic ω₀ can be written as follows

$$\omega_{0} = A\frac{h}{\rho d}\frac{{T_{1} + T_{2} }}{{T_{1} T_{2} }}\; = \frac{AN}{{\rho d^{2} }}\frac{{k_{1} k_{2} }}{{\theta k_{2} + \left( {1 - \theta } \right)k_{1} }}\frac{{T_{1} + T_{2} }}{{T_{1} T_{2} }}\;,$$

(2)

where, k₁ and k₂ are the heat conductivity coefficients of the corresponding phases, A = 1 is a form factor affected by the particle morphologies, and N = 10³ is the Nusselt number. The heat conductivity coefficients for the condensed constituents are taken to be k₁ = 0.025 W/(m K) for air, k₂ = 2 W/(m K) for silicon dioxide, and k₂ = 400 W/(m K) for copper. The heat exchange kinetic in the form (2) has been used in previous publications [9, 12, 14, 17, 20, 30] with different proportionality coefficients in relation to the particle diameter.

The present phenomenological approach deals with the rate specifications of the inter-phase exchange, which is described by the rate functions in the system of Eq. (1) on right hand sides constituting the present two-phase model. Within this approach, three mechanisms can be identified which affect the thermal energy emission during the high strain-rate loading, controlled in the model by the rate functions. In absence of mass exchange for the present case of inert porous materials (φ₀ = 0), the irreversible deformation of the solid phase of the porous mixture is controlled by the rate sensitive flow stress, managed by the stress relaxation functions φ_ij⁽²⁾. This presents the first possible micro-structure related mechanism associated with the plastic work dissipation. The inter-phase momentum exchange with related pressure relaxation is represented by the rate function ψ₀, which is responsible for the process of compaction and associated with particle rearrangements and fracture. This is also a source of entropy and temperature rise, which provides us with the second mechanism of additional heating at the meso-level. The third mechanism is associated with direct inter-phase heat exchange driven mostly by heat convection and conduction, integrated into the rate function ω₀ in (2). The role of each of the mechanisms on the temperature rise will be analyzed in a subsequent section via a variation of key parameters responsible for the inter-phase exchange rates.

The present model has been validated for a number of porous materials such as aluminum and quartz [10], and aluminum and copper at various porosities [12]. The model has been implemented in the shock physics Eulerian code CTH, developed by Sandia National Laboratories [16], and the two-phase model implementation [17] has been validated for calcite sand [20]. However, the above studies were mainly focused on the Hugoniot response of the materials and the thermal effects have not been specifically addressed, which is the objective of the present analysis.

Numerical Modeling of the Experiments

Experiments for the set-up shown in Fig. 1 are simulated in the present section. When representing the porous material, properties of the gaseous phase are taken to be those of air. Properties of the condensed phases are selected to be those of copper or quartz (silicon dioxide) depending on the powder analyzed. As mentioned above, mass exchange is absent in the present case, so φ₀ = 0 in (1).

The numerical set-up representing the experiment is shown in Figs. 6 and 7 at t = 0. The 2 mm thick powder sample (lightest grey) is encased in an aluminum cell (dark grey) with 3 mm thickness at the impact face and backed by a 13 mm thick PMMA window (W), shown in grey. A porous aluminum liner (dashed area) allows for changing the gaseous conditions (atmospheric air in the present tests) through the ports (uncolored) adjacent to the liner. The cell, corresponding to the ‘Target Cell’ in Fig. 1, is impacted by a 10 mm thick PMMA flyer plate (F) with a velocity of 400 m/s.

Fig. 6

Calculated temperature for the copper powder (lightest grey) using the set-up shown at t = 0. Temperature color maps are in the sub-section containing the sample below the full set-up grayscale maps (Color figure online)

Fig. 7

Calculated temperature for the silicon dioxide powder (lightest grey) using the set-up shown at t = 0. Temperature color maps are in the sub-section containing the sample below the full set-up grayscale maps (Color figure online)

The characteristic particle size, d, used in the heat exchange rate function ω₀ in (2), is taken to be 90 μm for the copper powder and 200 μm for the silicon dioxide quartz sand. The CTH calculation of temperature profiles employing the present two-phase model are shown in Fig. 6 for the copper powder and in Fig. 7 for the silicon dioxide powder at t = 2, 4 and 6 μs. The profiles in the full set-up (upper section of the graphs) in Figs. 6 and 7 are shown in grayscale and a narrow section of the set-up containing the same temperature profiles within the sample area shows these profiles in color map under the main graph. Due to a relatively low sound velocity in the porous samples for the present thickness-to-diameter ratio of the samples, the profiles show a strong influence of the lateral waves affecting the wave propagation along the direction of impact, thus resulting in non-one-dimensionality. However, the two-dimensional numerical set-up represents the experimental one closely. Therefore, the numerical results can be directly compared with the experimental results because of the one-to-one representation. It is seen from the axial distribution in Fig. 8, specifically at a later stage, that the high-temperature region in the copper powder (Fig. 6) is narrow when comparing with that in the silicon dioxide (Fig. 7) where this region is spread through the whole thickness of the sample, in particular, when reaching the observation point after t = 6 μs lying on the symmetry axis at the sample-window interface.

Fig. 8

Calculated temperature distribution along the assembly axis for the silicon dioxide (curve 1 in black) and copper (curve 2 in red) powders (Color figure online)

In order to illustrate the powder heating, the temperature profile along the symmetry axis can be extracted for observation of the thermal pulse propagation in detail. The results of the extraction visualizing a section of the axis containing the sample cross-section in Fig. 8 demonstrate that the initial temperature spike at t = 1 μs, when the shock wave enters the sample after having propagated through the cell material C, heats up the copper powder with the thermal pulse of less amplitude (curve 2 in Fig. 8) than the silicon dioxide powder (curve 1 in Fig. 8). As the wave propagates through the sample and reflects from the window, the thermal pulses in the porous materials attenuate, however, this takes a longer time in the silicon dioxide powder due to a stronger pulse. As a result, when arriving at the interface between the sample and the PMMA window W at t = 6 μs, the pulse in the copper powder is weaker and shorter in duration.

These calculation results can be summarized as time history curves taken as temperature at the intersection of the symmetry axis of the set-up assembly with the sample-window interface, corresponding to the fiber optic probe observation point. The resulting curves, as seen in Fig. 9, confirm the conclusions of the discussion above, showing a more decayed and shorter thermal pulse in the copper powder. These results correlate reasonably with the trend of the experimental observations shown in Fig. 4. The origin time in Fig. 9 is aligned with the time of impact of the flyer plate against sample, thus resulting in comparable calculated durations of the high-temperature emission with the experimental ones shown in Fig. 4. It is interesting to note that the present modification of the heat exchange kinetic (2), using the total surface of the phase interface in a representative volume as a factor, allows for correlation of the calculated temperatures with the experiment using the same free parameters of the kinetic (the form factor and the Nusselt number).

Fig. 9

Calculated temperatures at the point lying on the assembly symmetry axis at the sample-window interface for the copper (curve C) and silicon dioxide (curve S) powders

In order to understand the reasons of such behavior of the thermal pulse, we will conduct calculations in the next section for a schematic set-up describing the conventional Sod shock tube problem representing shock wave propagation through a porous sample due to planar plate impact.

Parametric Analysis

Using the present modeling approach, this section investigates possible contributions to the thermal output in a porous material due to the internal and inter-phase exchange processes. As mentioned previously, the mass concentration parameter c is constant in the present case due to the absence of any phase transition in the simulations. Therefore, the subject of the analysis is the three factors that are associated with the mechanisms governed by the different constitutive equations in (1) for parameters θ, λ_ij, and χ. The corresponding rate functions ψ₀, φ_ij⁽²⁾, and ω₀ in (1) are associated with the material compaction, plastic deformation of the solid phase, and inter-phase heat exchange, respectively. These functions can be controlled in the most influential way via several key parameters, which are: effective compaction pressure p_cr in ψ₀, a set of the rate sensitive yield limits of the solid phase Y₁ and Y₂ against two different strain rates in φ_ij⁽²⁾, and characteristic particle diameter d in ω₀.

As a model one-dimensional set-up, we consider a high-velocity impact of a 10 mm thick PMMA plate with a velocity of 400 m/s against a 10 mm silicon dioxide porous sample. The silicon dioxide powder is taken for the present modeling because of an easier interpretable compaction behavior (curve 1 in Fig. 5b) characterized mainly by the effective compaction pressure p_cr. Numerical results at t = 1.5 μs after the collision, when the shock wave is approaching the free surface of the target sample, are shown below in Figs. 10, 11, 12 and 13. Dashed lines in the plots indicate locations of the material interfaces, including the free surface coordinates in the vicinity of x = 0 (for the flyer plate) and x = 2 cm (for the powder sample).

Fig. 10

Calculated temperature profiles (curves 1) of simulated silicon dioxide powder along with stress profiles (curves 2) at t = 1.5 μs. Scales for the curves 2 in (a–c) are on the right side of the plots. Porosity parameter (d) where the curves (1–3) correspond to the cases (a–c). The selected values of the key parameter p_cr are: 10 MPa (a); 250 MPa (b); and 750 MPa (c)

Fig. 11

Calculated stress (curves 1), porosity (curves 2), temperature (curves 3), and temperature in the solid phase (curves 4) for a low rate sensitivity case, Y₁ = 15 MPa and Y₂ = 25 MPa (a, b), and for a high rate sensitivity case, Y₁ = 5 MPa and Y₂ = 50 MPa (c, d). Scales for the curves 2 and 4 are on the right side of the plots

Fig. 12

Calculated stress (curves 1) and temperature (curves 2) at a nearly constant flow stress of 5 MPa (a) and 50 MPa (b). Calculated temperature (curves 1) and temperature of the solid phase (curves 2) for the porous materials with characteristic particle dimensions of 100 μm (c) and 400 μm (d). Scales for the curves 2 are on the right side of the plots

Fig. 13

Calculated temperature (curves 1) and stress (curves 2) in the pressure non-equilibrium case at p_cr = 1 GPa, for a low rate sensitivity case, Y₁ = 15 MPa and Y₂ = 25 MPa (a), nominal rate sensitivity, Y₁ = 10 MPa and Y₂ = 30 MPa (b), and a high rate sensitivity case, Y₁ = 5 MPa and Y₂ = 50 MPa (c). Density of the gaseous phase (d) where the curves (1–3) correspond to the cases (a–c). Scales for the curves 2 (a, b) are on the right side of the plots

Firstly, we evaluate the contribution of the compaction process in the porous material controlled by parameter p_cr to the temperature increase. Analyzing this mechanism, an increase in the compaction resistance can be forced by increasing p_cr from 10 MPa, via the nominal value of 250 MPa, up to 750 MPa. In addition to an elastic precursor propagating through the solid phase, the numerical results shown in Fig. 10 demonstrate the formation of an extra wave step associated with the material compaction, where the stress level behind this step corresponds to the characteristic compaction pressure p_cr. It is seen in Fig. 10a–c that this increase in p_cr prevents the material to compacting up to a higher loading pressure by particle destruction thus retaining the pores between the particles and reducing pore compression and collapse. The calculations in Fig. 10 show that the porosity changes only in the principle stress wave behind the ‘compaction’ wave. It is seen in Fig. 10 that the stress increment from the state behind the compaction wave till the level in the principal wave decreases with the increase of p_cr thus decreasing the corresponding mass change related to the total porosity variation. This results in the noticeable reduction in the porosity θ in Fig. 10d (curves 1 and 2) on one side, and in a very moderate decrease of θ in Fig. 10d (curve 3) on the other side. Because of this behavior, the powder temperature is seen to increase significantly (Fig. 10a, b) when the pores can collapse and thus the heating due to adiabatic compression is a major contributor to the temperature rise. The difference between the temperature levels in Fig. 10a and b seems to contradict this trend, however, the corresponding stress profiles show a possible involvement of the second mechanism not yet analyzed. Specifically, the ramping of the principal stress wave due to development of the ‘compaction’ wave correlates with the loading strain rate, which is faster in Fig. 10b, resulting in a higher temperature. In order to confirm this we will analyze the second mechanism associated with the internal resistance to shear stress (strength) in the solid phase next.

The second mechanism, associated with the inelastic shock dissipation in the solid phase, is analyzed by varying the flow stress against strain rate. Referring to the diagram in Fig. 5a, we first consider the rate sensitivities corresponding to the curves 1–3 in the diagram with the baseline value of p_cr = 250 MPa. The calculation, corresponding to the baseline case for yield limits Y₁ = 10 MPa and Y₂ = 30 MPa, at the strain rates of 10^–2 and 10³ 1/s chosen above, has already been conducted and was shown in Fig. 10b and d as curve 2. Calculations for the low rate sensitivity case, corresponding to curve 1 in Fig. 5a (Y₁ = 15 MPa and Y₂ = 25 MPa), represent the case with a relatively small viscosity resulting in a steep shock front. On the other side, calculations for the high rate sensitivity case, corresponding to curve 3 in Fig. 5a (Y₁ = 5 MPa and Y₂ = 50 MPa), represent the case with a large viscosity resulting in a shallow shock front. The corresponding results of the calculations for the low and high rate sensitivity cases are shown in Fig. 11a–d, respectively. From comparison of these three cases, it is seen that the rise time in the stress wave is consistently increasing from the lowest rate sensitivity (Fig. 11a, b) to the highest one (Fig. 11c, d). While the total energy is being conserved, it is seen that the energy is dissipating over a wider zone in the sample with the rate sensitivity increase.

This change in dissipation is related to the inter-phase exchange rates, thus affecting the rate of temperature equilibration between the phases. As shown before and seen in Figs. 10 and 11, the porosity is changing only behind the front of the ‘compaction’ wave. This porosity variation follows the principal plastic wave within a narrow (Fig. 11a) or a relatively wide (Fig. 11c) zone, depending on the rate sensitivity of strength in the solid phase. Because of the mass conservation both for the porous material and for the phases in the present case of no mass exchange, the porosity reduction necessitated by the mass conservation in the case of low rate sensitivity occurs within this narrow zone in contrast to the reduction within the wide zone in the case of high rate sensitivity. This results in a more significant pore collapse (curve 2 in Fig. 11a) in the low sensitivity case than in the high rate sensitivity case (curve 2 in Fig. 11c). The latter reduces the pore collapse effect, seen as an increase in porosity (curve 2 in Fig. 11a, curve 2 in Fig. 10d, and curve 2 in Fig. 11c) and thus decreases the adiabatic heating. Curves 4 in Fig. 11 show that in the case of loading in a steeper wave (Fig. 11a, b), the temperature in the solid phase tends to rise quicker than in the case of Fig. 11c and d.

Continuing with an analysis of the second mechanism, we consider possible influence of the flow stress magnitude. This is not a trivial problem for the case of a significant rate sensitivity due to the present highly non-linear rheological relation φ_ij⁽²⁾: as a result, a shift of points Y₁ and Y₂ does not transfer conformly the flow stress–strain rate curves, such as those shown in Fig. 5a, if following the fitting procedure [24]. However, the problem of the strength magnitude can be simplified if only low rate sensitivity dependencies are taken for the analysis such as those represented by curves 4 and 5 in Fig. 5a, with Y₁ = 4.9 MPa and Y₂ = 5.1 MPa for curve 4 and Y₁ = 49 MPa and Y₂ = 51 MPa for curve 5. The corresponding calculation results are shown in Fig. 12a and b, respectively. It is seen that the strength level, at least not in the range of the characteristic compaction pressure p_cr and at the loads essentially above the yield limit, has no significant effect on temperature (curves 1 in Fig. 12a, b) via direct plastic work dissipation. This can be explained by the fact that the majority of relevant plastic work occurs within the principal shock wave, whereas the yield limit variation affects only the elastic precursor, as seen from the corresponding stress profiles (curves 2 in Fig. 12a, b).

Finally, the third mechanism associated with the inter-phase heat exchange can be effectively controlled by the characteristic particle diameter d. In order to analyze the role of this mechanism on the thermal pulse evolution in the powder, d was varied from a value of 100 μm (Fig. 12c) via the nominal value of 200 μm (Fig. 10b) up to 400 μm (Fig. 12d). The porosity and stress observed in these calculations (not shown in the plots) confirm that the smaller particle diameter, d, results in a quicker equilibration via faster inter-phase energy exchange. The corresponding temperature equilibration for small d (Fig. 12c) simulates the trend of transition from the inter-phase thermal non-equilibrium for a larger d (Fig. 12d) to a relative thermal equilibrium (Fig. 12c) with obvious smaller temperature difference than in the cases d = 200 μm and d = 400 μm. The faster thermal equilibration at smaller d results in a more significant absorption of the thermal energy produced during the adiabatic compression of the interstitial gas by the solid phase and, as a result, reducing the overall temperature increase of the porous material.

From the calculations above it is seen that the strain rate sensitivity of strength and the heat exchange mechanisms seem to be in competition and it is not obvious which of the mechanisms is of prime importance to the temperature rise: a more localized dissipation in a steeper wave or a higher adiabatic compression of the gaseous phase. In order to understand this, we consider a hypothetical case with the characteristic compaction pressure, p_cr, that is deliberately higher (p_cr = 1 GPa) than the pressure level in the principal wave. In this case, the compression of the gaseous phase cannot be achieved due to compaction resulting in the change of porosity during the loading. Therefore, pressure relaxation for the pressure in the solid phase, that is higher than pressure in the interstitial gas, cannot occur. As a result, the only source of the temperature rise in this case is compression of separate phases at the pressure non-equilibrium. Results of the calculations for the three rate sensitivity cases considered above are shown in Fig. 13.

It is seen that temperature is increasing with the dissipation from (a) to (c) in Fig. 13, which is unusual to what could be expected in a homogeneous material. In the two-phase material this behavior can be explained by a gradual loading in the case of a large dissipation zone (Fig. 13c) which provides the regime of quasi-isentropic compression. This compression may result in the pore collapse due to the loading path allowing the volume reduction to infinitely small values whereas the minimal volume is finite at a nearly shock compression in Fig. 13a (for an analysis of compression of a porous material in two similar compression regimes corresponding to temperature non-equilibrium and temperature equilibrium Hugoniots, see [15]). As a result, the adiabatic compression of the interstitial gas to a smaller volume (Fig. 13d) at a pressure comparable with that in the principle shock wave results in a higher temperature at the quasi-isentropic loading (Fig. 13c). Nevertheless, this calculated temperature difference and the overall temperature magnitude are significantly less when comparing with the case when the adiabatic compression is involved directly due to the pore collapse.

Summarizing, the most influential mechanism of the three analyzed is likely to be the inter-phase heat exchange and contribution to the material temperature via the adiabatic compression of the gaseous phase. Plastic deformation of the solid phase does not contribute significantly to the temperature rise by itself. However, strength of the solid phase may not be negligible as a factor affecting compaction via breakage and rearrangement of particles and thus indirectly contributing to the adiabatic compression of the gaseous phase. As shown above, all three mechanisms are associated with the pore compression and collapse via compaction at the meso-level and with the viscosity growing with an increase of the yield limit rate sensitivity at the micro-level thus influencing the heat exchange rate.

To finalize the analysis, we calculate the same plane impact problem with the copper powder sample. We take the compaction kinetic specified above as shown in Fig. 5b (curve 2) and the input parameters for the material used in the calculation of the previous section. Evolution of profiles for the physical variables at t = 1, 2, and 3 μs after the collision of the flyer plate with the sample are shown in Fig. 14. It should be noted that due to flyer plate movement, the free surface of the plate and the contact interface are moving as well, which results in multiple dashed lines because of time superposition of the three frames.

Fig. 14

Calculated temperatures (a), stresses (b), porosity (c), and temperatures of the solid phase (d) for copper powder at t = 1 μs (1); 2 μs (2); and 3 μs (3)

It is seen that the ductile character of the copper powder compaction curve, resulting in a tapering compaction wave that merges with the principle wave and thus significantly increasing effective viscosity (Fig. 14b) in the shock wave, results in a delayed pore collapse (Fig. 14c). In addition to a smaller characteristic particle diameter compared with the previously analyzed silicon dioxide powder, a relatively high heat conductivity of the copper results in a gradual increase of temperature in the solid phase and in an accelerated temperature equilibration (Fig. 14d). This results in a smaller overall temperature increase due to the thermal energy absorption by the solid phase, similarly to the previous analysis in Fig. 13c and d utilizing the simpler silicon dioxide system that possesses a more schematic shape of the compaction curve.

Summarizing, the calculations demonstrate that the thermal emission due to the pore collapse controlled by the inter-phase head exchange and the higher loading rate (strain rate) might be the strongest contributors to the powder temperature increase under dynamic loading.

Discussions and Conclusions

The present study shows that the reasoning behind the lower observed temperature in the copper powder when compared with the silicon dioxide powder is in agreement with the two-phase nature of the porous materials. These reasons can be explained with the help of the numerical analysis conducted in the previous section. Specifically, a higher strength of the copper particles, which results in a higher p_cr, a lower strain rate in the principle wave dominated by the ductility shape of the pressure equilibrium curve (effective compaction pressure), and a closer proximity to the thermal equilibrium due to smaller characteristic dimensions of the copper particles and a higher thermal conductivity of copper result in a lower temperature, which follows from the analysis outlined above.

In summary, taking the gaseous phase into account, which may be the decisive factor in the temperature rise [11], provides a very important contribution to the high temperatures observed in the shock compression of powders and which is very difficult to model within a single-phase approach. Comparing the present experimental and calculated temperatures, it is seen that the two-phase approach correlates well with the experimental observations. Specifically, trends in the temperature magnitude and thermal pulse duration can be described well using the multi-phase consideration with conventional EOSs for the phases. The correct trends reproduced by the two-phase modeling may make it unnecessary to consider next order physical effects on the atomic and molecular levels for the condensed constituents, which are used in many advanced EOSs for porous materials in single-phase considerations with the objective to fit hydrocode calculations to experimental observations. It should be noted that the ideal gas EOS is used in the present work for the description of the air compression. Because of this, molecule dissociation and ionization are not taken into account in the extreme temperature conditions. Therefore, the present consideration cannot claim to be predictive and can only be reserved for description of the temperature trends and for a comparison amongst different powders.