Introduction

Nearly 50 years ago, Sakharov et al. [1] proposed an experimental approach to investigate the stability of a shock front and to determine the viscosity of a shocked material. Briefly, an explosive was used to generate a shock wave into a metal piece with a sinusoidal perturbation machined into its surface. This generated a non-planar shock wave that traveled through the metal piece and into the sample. The amplitude of the perturbation was monitored as a function of sample thickness. The perturbation was found to decay with propagation distance, and, because of the converging–diverging nature of the flow, the perturbation could actually invert in phase one or more times. The initial experiments were performed on an aluminum alloy, but Mineev and Savinov [2] reported results for aluminum, lead, and sodium chloride. Interestingly, some of those early results for aluminum included initially distended forms, albeit at pressures likely to lead to melting. In contrast, Mineev and Zaidel [3] studied the liquids water and mercury. More recently, Mineev and Funtikov [4–6] have published additional results utilizing the technique.

In the early work of this type, the material was treated as a viscous fluid [7] in order to extract a viscosity value. While mercury and water are liquids initially and should remain so under shock loading, aluminum is a solid and remains so for the regime studied as it begins to melt at approximately 125 GPa on the principal Hugoniot [8]. The discussion in Mineev and Savinov [2] suggests that they recognized that aluminum was solid in their experiments, so the choice of treating the material as a fluid may have been one of expediency in that they could generate solutions for the viscous fluid problem analytically. The viscous fluid analysis of Zaidel [7] was reexamined and refined by Miller and Ahrens [9]. They pointed out some difficulties with the treatment of the boundary conditions in the problem but obtained results that were broadly consistent with the earlier work.

More recently, Abramson [10] compared the results for viscosity of water obtained through different static and dynamic techniques. By reinterpreting the results of cylinder acceleration experiments [11–13] as having significantly higher Reynolds number than previously thought, he found consistent values for all of the techniques except for the perturbation decay approach. This led him to conclude that the approach measures not viscosity but “yields information on some other dissipative process.” Thus, the experimental observations of perturbation decay in water are not fully understood at this time.

Beginning with the work of Liu et al. [14], a group of researchers in China began to utilize a modified version of the earlier approach but incorporating a two-stage gas gun to generate the shock wave loading. This has the advantage over the explosive drive of providing well-posed initial conditions for the problem. They utilize shorting pins and, later, optical probes [15] to measure shock arrival at an array of points along the perturbation and at different thicknesses of the wedge sample. They have applied the technique to aluminum [14, 16, 17] as well as iron [18, 19]. Although their initial work employed the analytical solution of Miller and Ahrens [9], Ma et al. [20] used a finite difference model to estimate the viscosity. They obtained somewhat different results, especially for high velocities, and attributed this to assumptions made for the initial conditions of the analytical solution. They found their results were independent of the artificial viscosity used in the finite difference calculations, and Ma et al. [17] found the results obtained were insensitive to the bulk viscosity utilized.

Although the possible effect of material strength on the viscosities determined for solids by this approach was recognized earlier, Li et al. [18] took this a step farther by suggesting that the perturbation decay experiment measures an effective viscosity that “represents both the influence of material strength and viscosity in the damping process.” Xiao-Juan et al. [21] took the next logical step of performing analyses including both viscosity and material strength. For a shock in aluminum of 101 GPa, they found a viscosity of 2800 Pa-s compared to 3500 Pa-s when strength was ignored (i.e., fluid-like behavior was assumed). Unfortunately, 101 GPa is fairly close to the melt temperature of aluminum, which could lead to a reduced effect of strength in that experiment. On the other hand, shock-release experiments on aluminum [22] suggest that the strength remains relatively high even at that pressure. It would be interesting to see if strength plays a more significant role at much lower pressures where the material is far from melt.

In this paper, an exploratory study using a modified form of the perturbation decay experiment to probe the behavior of shocked granular materials is reported. With the exception of the very early work [1, 2] in the area, no results on granular materials have been reported, and those results were for metal powders in regimes quite different than those considered here. While planar shock experiments (c.f. [23, 24]) can provide the dynamic longitudinal stress-density response of granular materials, the lateral component of stress is not measured so the strength (deviatoric) response of the material is not known. The problem of measuring the strength of materials at high pressures and strain rates is not unique to granular materials (see review article by Vogler and Chhabildas [25]), but applying existing techniques to granular materials presents additional difficulties not present in fully dense materials. It is hoped that the perturbation decay experimental approach described here will prove to be useful in probing the strength response of granular materials so that their dynamic behavior can be better understood.

In order to better understand the experiments and interpret the experimental results, simulations using two distinct approaches are presented. First, because any realistic problems will only be tractable using continuum modeling tools, simulations are performed using available continuum models for compaction and strength within an Eulerian framework. These models are relatively inexpensive from a computational standpoint, but the model parameters are entirely empirical. Therefore, parametric studies of the effect of varying the model parameters are conducted, and variations in the experimental parameters are also explored. Ultimately, it is expected that the experimental results can be used to calibrate continuum models, though the models used here may not be ideal for that purpose. The second modeling approach used is to perform mesoscale simulations in which individual particles are resolved. Such models have been used with some success on other problems involving granular materials and should be, at least to some degree, predictive of material behavior. Thus, the mesoscale model can be used to explore directly the effect of material properties such as volume fraction and particle diameter. Favorable comparison with experimental data will also improve confidence in the mesoscale modeling tools for use in problems beyond the planar loading cases for which they have mainly been used.

The paper is laid out as follows. Initial experiments as well as continuum and mesoscale modeling results are presented. “Experimental Methods” section provides details of the experimental setup, while “Modeling Techniques” section contains details of the modeling approaches utilized. In “Experimental Results” section, results for initial perturbation decay experiments on a granular material are presented. These results demonstrate the feasibility of the approach and provide motivation for future experimental development. Results from simulations of the experiments in which continuum and mesoscale models are used are presented in “Continuum Simulation Results” and “Mesoscale Simulation Results” sections, respectively, and the simulation results are compared to those from experiments. The continuum and mesoscale simulations are utilized to explore sensitivities of the results to material parameters as well as to aid in interpreting the experiments. The experimental and modeling results are discussed and conclusions are drawn in “Closure” section.

Experimental Methods

The experimental configurations utilized in the initial perturbation decay experiments on granular tungsten carbide (WC) are presented in this section.

Material

The experiments were conducted on a granular WC produced by Kennametal Inc. of Latrobe, Pennsylvania. This is the same material studied in quasi-static compaction and plate impact loading by Vogler et al. [23]. As in that study, particles of nominal sizes of 20–32 µm were sieved from the as-received material. The WC has a crystalline density of 15.6 g/cm\(^{3}\). The particle morphology can be seen in Fig. 1. The blocky nature of the particles is due to the processing approach utilized in their manufacture.

Fig. 1
figure 1

SEM image of the sieved WC powder used in this investigation

Full size image

Experimental Configuration

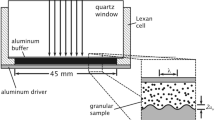
A modified version of the experimental configuration for plate impact experiments on granular materials [23, 24] was used as shown schematically in Fig. 2. The target consists of an aluminum driver, a hollow Lexan body, and a backing fused silica window. These three parts form the capsule that was filled with the WC powder. Densities of approximately 9.1 and 8.9 g/cm\(^{3}\) (approximately 58 % of crystalline density) were found using the mass of the powder in the cell and the estimated cell volumes for experiments PD-1 and PD-2, respectively, which is slightly higher than in previous experiments [23]. The inner surface of the fused silica window was coated with a thin layer of aluminum to provide a reflective surface for the interferometer. A thin (0.54 mm) aluminum buffer was glued onto the aluminum-coated surface between the WC and the fused silica window to protect the reflector from the abrasive WC powder. The target was impacted by a projectile faced with a thick aluminum plate and launched using a smooth bore compressed gas gun. The impact velocity and tilt of the projectile were characterized using pins protruding slightly from the surface of the target.

Fig. 2
figure 2

Cross-section view of the experimental configuration for the perturbation decay experiments with close-up view of the driver plate with sinusoidal perturbation

Full size image

The most important feature of the target was the sinusoidal wavy pattern cut into the driver plate as shown in the inset in Fig. 2. The perturbation wavelength \(\lambda \) was nominally 2 mm, while the amplitude from peak to valley (2\(a_{o}\)) was 0.50 mm. The wavelength and amplitude were chosen to be large relative to the WC particles and small relative to the sample size (around 44 mm), with the amplitude chosen to be a fraction of the wavelength. Although initial simulations indicated that these dimensions were suitable, neither has been optimized. Two different approaches were used to create the sinusoidal perturbation. In experiment PD-1, the pattern was cut with a fly-cutting tool. While this produced the desired pattern, a small curvature in the “peaks” and “valleys” of the pattern was introduced due to the tooling used. In contrast, a wire EDM technique was used to create the pattern in experiment PD-2. This resulted in the straight pattern seen in Fig. 3. Profilometric characterization of the patterns indicated that they had the desired wavelength to 2–3 % and amplitude to within 5 %. For an individual part, though, the wavelength and amplitude were consistent to within about 1 %. Deviations from a sinusoidal shape were small and are not considered significant for this preliminary study.

Fig. 3
figure 3

Photograph of the aluminum driver with the sinusoidal perturbation cut using wire EDM. The notch at the edge of the plate is used to ensure proper orientation of the piece during assembly

Full size image

The primary diagnostic used in these experiments was the line-VISAR [26, 27], an optical interferometer that can resolve velocity histories along a narrow line. The line-VISAR was oriented perpendicular to the perturbation peaks as shown in Fig. 2. By resolving the velocity history along a line across a few wavelengths, the evolution of the perturbation after traveling through the granular WC sample can be measured.

Modeling Techniques

Three different approaches were utilized in simulating the perturbation decay phenomena observed experimentally. Each has been used previously with some degree of success to simulate the dynamic behavior of the granular WC used in this investigation. The first of these involves continuum calculations with the finite volume code CTH [28]. The second utilizes the same code but employs it in a two-dimensional (2-D) mesoscale approach in which individual grains are modeled explicitly as circular rods of infinite length. The third is the same as the second except that the mesoscale simulations are three-dimensional (3-D) spheres. As one would expect, the computational costs increase greatly from the continuum calculations, in which scales of order 1 mm must be resolved accurately, to the 2-D mesoscale calculations, in which features of order 10 µm must be resolved. Similarly, 3-D simulations were significantly more expensive than the 2-D calculations.

Continuum Models

The continuum calculations include the aluminum impactor with a prescribed initial velocity, the aluminum driver, and the granular sample. A schematic of the simulation is shown in Fig. 4. Note that \(x=0\) corresponds to the peak of the perturbations in the driver. Due to the symmetries of the problem, only half of a wavelength was modeled; rigid boundary conditions were applied at the bottom and top of the simulation domain. Lagrangian tracer points were distributed along the \(y=0\) and \(y=\lambda /2\) lines as a means to determine the amplitude of the perturbation propagating in the sample.

Fig. 4
figure 4

Schematic of continuum simulations

Full size image

A simple Mie-Grüneisen [29] equation of state (EOS) was utilized for the aluminum along with the Johnson–Cook strength model. When a fused silica window is included in the simulation, it is treated with a tabular EOS [30]. The granular sample was treated in a continuum fashion using the P-\(\lambda \) model [31–33] to describe the compaction process. Compaction—the removal of porosity from the sample—is assumed to be controlled entirely by the pressure in the material and is treated as a transition between two states using

$$\begin{aligned} v(P) = \big (1-\lambda (P)\big )v_{e}(P) + \lambda (P)v_{h}(P) \end{aligned}$$
(1)

where \(v_{e}\) is termed the elastic (isostrain) response of the material, essentially an estimate for the material response of the porous material without void crushing, and \(v_{h}\) is the hydrodynamic response of the material constituents, in this case taken as the shock Hugoniot of fully dense WC. The parameter \(\lambda \) increases monotonically and irreversibly from 0 to 1 as pressure increases and is assumed to follow a functional form given by

$$\begin{aligned} \lambda (P) = 1 - e^{-(P/P_{c})^{n}} \end{aligned}$$
(2)

where \(P_{c}\) is the compaction pressure, and the parameter n controls how abruptly the compaction occurs as pressure increases. Calibration of the model was done using planar impact data [23]. Parameters for the P-\(\lambda \) model are given in Table 1.

The strength behavior of the WC sample was described using two models: an elastic-perfectly plastic (EPP) idealization, and a pressure-dependent yield strength Y given by

$$\begin{aligned} Y = Y_{\infty } + (Y_{o} - Y_{\infty })exp\bigg [-\frac{dY}{dP}\frac{P}{Y_{\infty } - Y_{o}}\bigg ]. \end{aligned}$$
(3)

In negative (tensile) pressure, \(Y = Y_{o}\). The pressure-dependent model will be referred to as the Geo strength model. The strength at zero pressure, \(Y_{o}\), is chosen to be a small value to reflect the lack of strength in loose granular materials, while the strength at high pressures \(Y_{\infty }\) is set equal to the elastic limit measured for fully dense WC in shock experiments [34]. Variation of strength with pressure dY / dP is set based on strength measurements for granular WC in pressure-shear experiments [35]. Parameters for the strength models are given in Table 2. The strength model includes no thermal effects, though the shear modulus will go to zero if the EOS indicates that the material has melted. Bulk melting of the sample material is not expected for the cases considered here, but higher impact velocities or greater sample distentions would be expected to lead to melting. Furthermore, due to the heterogeneous nature of granular materials some fraction of the material might melt even when the average temperature does not reach the melt temperature [36].

Table 1 Material EOS and P-\(\lambda \) compaction model parameters used in simulations
Full size table
Table 2 Strength model parameters used in simulations
Full size table

2-D Mesoscale Models

Previously, two-dimensional mesoscale models have been used to simulate the dynamic loading of granular WC [37, 38]. These simulations were done in the spirit of the work of Benson and coworkers (e.g. [39]) utilizing very simple geometries and material models within an Eulerian modeling framework. Briefly, the models consist of circles of material arranged randomly in the domain of the sample. As with the continuum models, some simulations included the full aluminum driver and impactor, but for most simulations alternative means of driving the simulations were used for computational efficiency. Part of the simulation domain is shown in Fig. 5. Note that the particles were distributed randomly in a rectangular domain. The aluminum driver with the sinusoidal perturbation was inserted first into the simulation domain, which resulted in some of the circular particles being partially cut off by the aluminum driver. Since the wavelength is large compared to the particle diameter and only a few particles were cut, this should not affect the results significantly. The top and bottom of the domain were linked using periodicity conditions to mimic a sample with multiple repeating perturbations. The domain shown in the figure is only one wavelength, but in many cases domains of two or four wavelengths were used as discussed later. In most of the simulations, a uniform particle diameter of 32 µm was used as has been done previously, but the effect of variations in particle diameter is explored to a limited degree.

Fig. 5
figure 5

Initial configuration for 2-D mesoscale simulations showing one wavelength of the perturbation. Shocks are driven from left to right, and measurements of velocity histories are made at the center of each particle. Colors of particles are for visualization purposes only

Full size image

As was done previously, the WC particles were modeled with a simple Mie-Grüneisen EOS [29] and an elastic-perfectly plastic strength model. EOS parameters for WC in the mesoscale simulations are the same as those given in Table 1 for the continuum simulations, though no compaction model is used. Strength model parameters are found in Table 2. Aluminum and fused silica were treated in the same manner as in the continuum simulations.

The studies of Borg and Vogler showed that many aspects of the behavior of granular WC including the stress-density response, the shock rise time, and wave attenuation [40] could be reproduced with this 2-D modeling approach provided the strength of the individual particles was adjusted to an appropriate value. Thus, the perturbation decay configuration examined here provides a means to test the validity of the 2-D mesoscale model in a regime different from that for which it was calibrated.

3-D Mesoscale Models

Borg and Vogler [36] have recently extended the mesoscale approach to 3-D using spherical particles. They found that the 3-D calculations gave similar results to the 2-D simulations, though it was necessary to use a sliding algorithm to treat the interactions between individual particles. Since the flow of material in the perturbation decay configuration is no longer nominally 1-D, there might be important differences between the 2-D and 3-D mesoscale simulations that justify the additional computational expense of the 3-D simulations. The EOS and strength models were the same as those used in the 2-D calculations. The 3-D domain used in the simulations is shown in Fig. 6. Note that the domain is 0.25 mm thick (\(\lambda / 8\)). This thickness was chosen to be relatively small so that the computation is not too expensive, but it still represents nearly ten particles diameters. Due to the additional computational expense of the 3-D simulations, the simulations were always conducted without modeling the entire aluminum impactor.

Fig. 6
figure 6

Initial configuration for 3-D mesoscale simulations. Shocks are driven from left to right, and measurements of velocity histories are made at the center of each particle. Colors are assigned for each of the individual materials used to define the particles

Full size image

In the study of Borg and Vogler [36], it was found that the 3-D simulations displayed a small-amplitude precursor not seen in the experiments. This was found to be an artifact of the Eulerian modeling approach that led to cells containing material from two particles to form a solid bond between the particles that could transmit waves elasticly. Real interfaces between particles, of course, allow frictional sliding between the particles. To emulate this numerically, a sliding algorithm for the particles was enabled. To facilitate this, the particles in the model are randomly assigned to one of ten distinct materials for modeling purposes, and the sliding algorithm sets the shearing velocity gradients to zero for numerical cells containing more than one material. This gives a rough approximation of frictionless sliding. The initial assignment of materials is done so that any two particles of the same material have at least one particle diameter distance between them, though it is possible that two particles of the same material could come into contact during the course of particle motion. The case utilizing the numerical sliding algorithm is referred to as “intergranular sliding,” while the case without it is referred to as “stiction.”

Experimental Results

Two experiments have been conducted using the configuration described in “Experimental Methods” section with projectile velocity of 327 m/s and 874 m/s, respectively. These will be referred to as experiments PD-1 and PD-2. In both, the thickness of the samples was approximately 3 mm from the deepest points in the sinusoidal imperfections to the aluminum buffer. Based on previous experimental and modeling work on shock loading of granular WC, the pressure in the sample was estimated to be 1.6 GPa for PD-1 and 5.5 GPa for PD-2, which correspond approximately to densities of 12.0 g/cm\(^{3}\) (77 % dense) and 14.8 g/cm\(^{3}\) (95 % dense), respectively.

The primary diagnostic in these experiment was the line-VISAR oriented across the sinusoidal imperfections. The streak camera image for PD-1 is shown in Fig. 7. The horizontal direction of the image corresponds to time, while the vertical axis is distance along the line illuminated on the sample. The spatial and temporal scales of the image are 63 pixels/mm and 209 pixels/µs, respectively. The velocity per fringe of the interferometer was 0.131 km/s/fringe. Initially, one sees streaks that are uniform with time as the shock generated by the projectile impact has not yet arrived at the plane being monitored. Shock arrival is seen as a sudden change in the shape of the fringes across the region monitored, but it was not possible to correlate the timing of the streak image to projectile impact. The shock front is not homogeneous, displaying a spatially periodic pattern of converging and diverging flow indicating that the sinusoidal perturbation has persisted in the sample despite traveling through about 2.5 mm of granular WC. The front does not appear to be fully sinusoidal in nature, which is consistent with the results of Sakharov et al. [1], but it is not clear if this reflects the real material behavior or is an artifact due to the nature of the diagnostic. After the shock arrival, there is a very complicated fringe pattern that is, at least to some degree, both spatially and temporally periodic. While, in principal, it should be possible to analyze the velocity histories for the positions monitored [41, 42], the spatial variation of shock arrival time is the main focus of interest. The differences in time were found to range from 30-70 ns, a relatively large amount of scatter that is largely due to the difficulty in determining the shock arrival time for any given position. In part, this was due to lack of optimization of the sweep of the streak camera, but the ramped nature of the wave at this impact velocity [23] also complicates the issue. It proved difficult to assign error bars to these values for \(\Delta t\) because of the ramping, but each measurement is estimated to be accurate to \(\pm 20\) ns.

Fig. 7
figure 7

Streak camera image from the line-VISAR for experiment PD-1, which had a projectile velocity of 327 m/s

Full size image

The streak image for experiment PD-2 is shown in Fig. 8. With a streak time of 4 µs and the magnification of the interferometer, the spatial and temporals scales of the image are 141 pixels/mm and 421 pixels/µs, respectively. The velocity per fringe of the interferometer was 0.256 km/s/fringe. While the image is qualitatively similar to that for PD-1, a couple of significant differences are noted. First, there is a strong loss of light when the shock arrives in PD-2, probably because of the stronger shock. Second, the size of the perturbation is well-resolved with many pixels of the streak camera covering that time. These two factors result in more repeatable measurements of shock amplitude across the image with values of 69–80 ns found. It is estimated that an individual peak or valley can be determined to \(\pm 2\) pixels or better, suggesting that each measurement of \(\Delta t\) is accurate to \(\pm 10\) ns or better.

Fig. 8
figure 8

Streak camera image from the line-VISAR for experiment PD-2, which had a projectile velocity of 874 m/s

Full size image

Continuum Simulation Results

Results from continuum and mesoscale simulations are presented in this section. Because the experimental data for PD-2 has less scatter, more attention is given to that experiment.

Continuum Simulations

Contours of pressure from a continuum simulation using the pressure-dependent yield surface are shown in Fig. 9. Shortly after impact, the shock wave travels through the aluminum driver and begins to interact with the sample. In Fig. 9a at 0.04 µs after impact, the shock has reached the granular sample in the valley of the perturbation but is still traveling through the driver toward the perturbation peak. After the shock fully enters the sample, the perturbation amplitude gradually decays as the wave propagates as shown in the figure. However, even after traveling through nearly 3 mm of the sample, the perturbation is still evident as shown in Fig. 9d. Also shown in the figure is the interface between the driver and sample. While there is some change in the shape of the interface as the shock passes, its shape remains relatively unchanged after the shock is well past.

Fig. 9
figure 9

Contour plots of pressure from CTH simulations of impact at 874 m/s with the pressure-dependent strength model and the P-\(\lambda \) compaction model at a 0.22, b 0.50, c 1.00, and d 2.00 µs after impact. The dashed lines denote the interface of between the driver and the sample, and the pressure scale is inset in the first image

Full size image

The strain and strain rate experienced by the sample during the experiment can be estimated using [2]

$$\begin{aligned} \epsilon = \frac{2 \pi a_{o}}{\lambda } \end{aligned}$$
(4)

and

$$\begin{aligned} \dot{\epsilon } = \frac{4 \pi ^{2} a_{o} U_{s}}{\lambda ^{2}} \end{aligned}$$
(5)

Using the geometric parameters and the shock velocity from the simulation of \(U_{s} = 1.28\) km/s, values of \(\epsilon = 0.8\) and \(\dot{\epsilon } = 3\times 10^{6}\) s\(^{-1}\) are obtained. Of course, strain and strain rate are nonuniform in this problem, so these relationships only provide rough estimates. Examining the continuum simulations, peak equivalent plastic strain rates (as usually defined) are three to four times those give by Eq. 5, and the volumetric strain rate associated with compaction are not accounted for in the the equation or in the plastic strain from the simulation. Regardless, these represent fairly high values of strain. The strain rates are well above those obtained in Hopkinson bar experiments, somewhat higher than those in most oblique impact experiments, and comparable to those of ramp wave experiments on the Z machine [43].

The evolution of the perturbation amplitude as it propagates through the sample is shown in Fig. 10 for the continuum simulations with a pressure dependent strength (Geo model) and a constant value (EPP) of strength. The amplitude of the perturbation is defined as the time \(\Delta t\) between when the peaks and valleys arrive at a fixed value of x. In this and all other plots, the horizontal distance is normalized by the perturbation wavelength \(\lambda \), while the perturbation amplitude \(\Delta t\) is normalized by the amplitude of the perturbation in the driver \(2a_{o}\) divided by the shock velocity in the sample \(U_{s}\). This quantity represents a first approximation of the initial perturbation amplitude, but the perturbation will always be smaller than this value since a finite time is required for the wave to propagate through the driver. Although it is possible to generate a better approximation for the initial perturbation that accounts for the wave propagation in the driver, this version is used due to its simplicity. Similarly, other normalizations could be used; e.g., the amplitude \(2a_{o}\) could be used rather than the wavelength \(\lambda \) to normalize the horizontal position, but it is not obvious that this provides more useful results.

Fig. 10
figure 10

Perturbation decay from continuum simulations for an impact velocity of 874 m/s for two strength models compared to the experimental results from PD-2. Five values of Y are shown for the EPP strength model, while the baseline plus high and low values of dY / dP are shown for the Geo model

Full size image

Initially, both cases decay at a similar rate with distance, and in the EPP simulations it decays to small negative value (the phase has inverted) by a distance of about 2 mm (\(x/\lambda \approx 1\)). In contrast, the Geo model decays more slowly and still has an amplitude of about 70 ns at a distance of 4 mm. Also shown for comparison are the experimental data points from PD-2 with error bars corresponding to an uncertainty of approximately 10 ns for each measurement. The amplitudes measured are rather tightly clumped and agree well with the Geo model for the propagation distance tested. Unfortunately, additional data are not available for comparison with the simulation results for other propagation distances.

Also shown in the plot are the perturbation evolutions for four additional strength values for the EPP model, \(Y=0, 0.2, 0.3,\) and 0.4 GPa. As the value of Y increases, the decay levels off earlier and at a larger amplitude. Varying the value of dY / dP in the Geo model to 0.1 or 0.3 from the nominal value of 0.2 has a similar effect to varying the value of Y in the EPP model. For the 874 m/s impact in experiment PD-2 with a pressure of about 5.5 GPa, the Geo model gives a strength value of around 1.0 GPa, which is higher than the values used for the EPP model because values that high would result in a strong elastic precursor in the propagating wave.

The simulations shown were conducted at a spatial resolution of 10 µm. Although the EPP simulations did not display any noticeable dependence upon the resolution, a small amount was seen for the Geo simulations. As the cell size is reduced, the perturbation decays more slowly, about 6 % less for a 2.5 µm resolution simulation.

As the wave propagates, the perturbation imprinted in it decays. Also, the interface between the aluminum driver and the granular WC sample evolves in a manner similar to a Richtmyer–Meshkov (RM) instability [44]. As expected, the perturbation amplitude at that interface grows due to the passage of the shock wave, though the amplitude ceases to grow after the wave has traveled a sufficient distance from the interface. The amount of growth that occurs is dependent upon the strength of the materials at the interface; thus, simulations with the EPP model for \(Y=0.1\) GPa show greater growth than when the Geo model is used, about 29 % for the former and 8 % for the latter. In both cases, the shape remains sinusoidal in character, but the peaks are flattened out slightly and the valleys become more steep. The presence of strength in the driver and sample appears to be responsible for stopping the growth [45], though even the small strength of the aluminum is sufficient to stop the growth by itself. However, if even the strength of the aluminum is removed from the simulation, then phenomena such as spikes and bubbles do emerge. It should be emphasized that the RM and perturbation decay experimental configurations are fundamentally different, though there are some similarities. RM experiments involve monitoring the interface between two dissimilar materials, while perturbation decay experiments focus on the evolution of the wave propagating in the second material. The evolution of the interface will affect the wave propagating into the second material, but after it has traveled a sufficient distance the wave is no longer influenced by the interface.

Sensitivity to Simulation Parameters

The sensitivity of the results to other model parameters and aspects of the simulations was examined next. First, the P-\(\lambda \) model parameter \(P_{c}\) was varied from its nominal values of 1.6 GPa to 1.2 and 2.0 GPa, while n was varied from 0.7 to 0.5 and 0.9. This had only a slight effect on the perturbation decay. Similarly, the constants in the simulations for linear and quadratic artificial viscosity were reduced by half, but this had only a slight effect on the perturbation decay results, consistent with previous work [20]. Real viscosity as typically used for fluids is not available within the modeling framework used here, and its use for granular materials is questionable in any event.

The effect of the initial perturbation parameters is examined in Fig. 11. Increasing the value of \(2a_{o}\) results in a more rapid decay of the perturbation and decay to lower normalized values, though in absolute value the amplitude is about the same for all cases for \(x>3\) mm. This appears to be due to greater convergence effects for larger amplitudes that cause the valley portions of the wave to catch up more rapidly. As wavelength is increased for a constant amplitude, decay becomes less rapid as convergence effects become less important. When both \(\lambda \) and \(a_{o}\) are varied simultaneously so their ratio remains constant, the results are unchanged from the baseline case. Additional examination of the results shows that including an additional non-dimensional parameter related to the degree of convergence, \((a_{o}/\lambda )^{2}\), in the normalization of x collapses all of these results in Fig. 11 reasonably well, though further study of scaling for the amplitude and wavelength is needed.

Fig. 11
figure 11

Perturbation decay from continuum simulations for varying perturbation a amplitudes and b wavelengths

Full size image

Varying the impact velocity in the simulations has a small effect on the normalized results as can be seen in Fig. 12 for the EPP and Geo models. For the EPP model with \(Y=0.1\) GPa, the results have a nearly constant vertical offset that increases with impact velocity. This arises due to varying differences in the shock velocities of the sample and the aluminum driver with increasing pressure. Alternate normalizations accounting for both velocities would nearly collapse all of these results. For the Geo model, the same effect is seen for \(x/\lambda <0.5\). For larger distances, though, the results invert position because the Geo model gives higher strengths, and, thus, less rapid decay for increased pressures/velocities. The experimental results for both PD-1 and P-2 are included in the figure. Even allowing for the larger uncertainties in the results for PD-1, there is a much larger difference between the two experiments than is predicted from the continuum models, though the trend of less rapid perturbation decay seen in the Geo model simulations is consistent with that of the experiments.

Fig. 12
figure 12

Perturbation decay from continuum simulations for varying impact velocities with a the Geo strength model and b the EPP model with Y=0.1 GPa along with experimental results from PD-1 and PD-2

Full size image

The Role of Measurement Location

In the simulation results presented in this section, the wave amplitudes were determined using Lagrangian tracers in the material. In the experiments presented in “Experimental Results” section, however, the measurements were made at the interface of a buffer and window backing the sample. Therefore, the effect of different approaches for measuring perturbation amplitude are examined using the continuum model as shown in Fig. 13. If simulations are performed with a 0.5 mm aluminum buffer and a fused silica window with measurements made at their interface, then the apparent amplitude \(\Delta t\) is reduced significantly as seen in the figure. The cause of this can be seen in Fig. 14, which shows the perturbed wave interacting with the buffer and window. Because the wave speed in the buffer is much higher than in the sample, the waves converge in the buffer before the valley of the wave reaches the buffer. The thicker the buffer is, the more pronounced the effect will be. In the specific case of the sample thickness in PD-2, measuring at the buffer/window interface results in an error of about 32 % in the apparent perturbation amplitude.

Fig. 13
figure 13

Perturbation decay from continuum simulations with different approaches to measuring the perturbation amplitude: in situ evaluation, using a buffered window, using a buffer with a free surface, or directly at the sample/window interface

Full size image
Fig. 14
figure 14

Contours of pressure illustrating the interaction between the perturbed wave front and the interface with the sample (dark grey) and buffer (light grey) at a 0.970 µs and b 1.020 µs after impact

Full size image

Modifying the setup by removing the fused silica window so that measurements are made at a free surface produces results that are little-changed from those for the buffered window. Finally, if the buffer is removed and measurements made at the sample/window interface, then amplitudes very similar to those for the in situ case are found. The error introduced by making measurements after the wave travels through a buffer depends upon the thickness of the buffer relative to the other dimensions of the problem \(\lambda \) and a(x) as well as on the wave speed in the buffer relative to that of the sample. As the wave speeds of the granular sample are very low, almost any metal used for the buffer will present a problem. It is possible that the results on liquids such as water [3] were affected somewhat by the use of the buffer. The use of polymer buffers, which have low wavespeeds, and significantly longer wavelengths (10 or 20 mm) than those used here mitigate the effect somewhat, though the experimental details provided by the authors are not sufficient to fully evaluate the effects. In general, these results suggest that care should be taken in designing the experiments. The issue of buffers will be discussed further for the mesoscale simulations in “Mesoscale Simulation Results” section.

Finally, the shapes of the perturbation obtained by determining the wave arrival time for a fixed x position are shown in Fig. 15. Both the in situ and buffered window cases have sinusoidal forms, albeit of different amplitude as discussed above. Also shown are arrival times as a function of position extracted from the streak image shown in Fig. 8. Since multiple wavelengths are captured in the image, different symbols indicate the wave shape for the individual sections of the image. In contrast to the simulations, the experimental wave shapes are more flattened at the peaks of the wave that arrive earlier and more sharp at the lagging valleys of the wave. A slight flattening at the peaks is also observed in the simulations when the measurements are made with a buffered window. As the characteristics of the line-VISAR that lead to loss of light return in the image are not well understood, it is probably inappropriate to conclude too much from this comparison.

Fig. 15
figure 15

Wave shape from experiment PD-2 compared to continuum simulation results. Simulation results for in situ evaluation and using a buffered window are shown

Full size image

Alternate Driver Configurations

While the continuum simulations are relatively inexpensive computationally, mesoscale simulations resolving individual grains are much more expensive, especially 3-D simulations. To reduce this cost, alternate approaches that do not explicitly model the full impactor and driver were explored. From a computational standpoint, the simplest approach is to replace the deformable impactor and driver with a rigid driver moving with a prescribed velocity \(u_{p}\), which can be extracted from the late-time mass velocities in the full simulations. As can be seen in the Fig. 16, though, this gives significantly larger amplitudes at small propagation distances and slightly smaller amplitudes for intermediate distances. As a first approximation, one can scale the amplitude of the rigid driver by

$$\begin{aligned} a_{s} = a_{o} \bigg [1-\frac{U_{s}}{U_{Al}}\bigg ]. \end{aligned}$$
(6)

where \(a_{s}\) is the scaled rigid amplitude and \(U_{Al}\) is the shock velocity in aluminum for the given impact conditions. This accounts, in part, for the time required for the shock to travel through the deformable driver from the valleys to the peaks. As can be seen in the figure, this scaling improves agreement with the full simulation, but some differences remain.

Fig. 16
figure 16

Perturbation decay from continuum simulations utilizing different approaches for driving the sample: the full impactor, a rigid driver with prescribed velocity, a scaled rigid driver, and a hybrid combination of rigid piston and deformable driver

Full size image

A third “hybrid” option was also examined. This involves a deformable aluminum driver backed by a flat rigid piston moving at a prescribed velocity. The deformable piece is 1 mm at its thinnest (i.e. the valleys of the driver). This approach provides the best agreement with the full simulation, differing noticeably only for very small (\(x/\lambda <0.3\)) distances. Since those distances will probably be difficult to probe experimentally, this is not a significant limitation.

Mesoscale Simulation Results

While the continuum calculations shown in “Continuum Simulation Results” section capture the removal of porosity in the granular WC in an empirical manner, the 2-D and 3-D mesoscale simulations in this section explicitly resolve the removal of porosity from the sample, albeit in an idealized geometry and using very simple models for the material response. This makes it possible to gain additional insight into the material properties and deformation processes that most affect behavior. Because of the greater computational expense associated with the 2-D and, especially, the 3-D mesoscale models, the hybrid drive is preferred. Results from the continuum and 2-D mesoscale models indicate that the hybrid drive gives results consistent with simulating the full driver and impactor, and all mesoscale results presented here utilized the hybrid driver.

Two-Dimensional Mesoscale Simulations

Images from a 2-D mesoscale simulation at conditions similar to the experiment PD-2 are shown in Fig. 17. In the first image, motion of the rigid piston has begun to load the granular sample in the valley of the driver but has not yet reached the driver peaks. Shortly after this image, the driver will be fully loaded and the wave will be propagating completely in the sample. At a somewhat later time shown in the second image, the wave has propagated into the sample, and the perturbation amplitude has decreased somewhat. As in the continuum simulations shown in Fig. 9, the convergent/divergent nature of the flow can be seen as a high pressure (red) region near the valley and a less obvious low pressure region near the peaks. In contrast to the continuum results which are spatially smooth, these results reveal their granular nature in two features: force chains in the direction of wave propagation and an uneven front to the propagating front, both of which have been observed in previous work on planar loading of granular WC [37]. Although the wave front is, in general, not parallel to the y-axis, the front otherwise seems to behave in a manner very similar to that seen previously for the planar loading case [37]. Thus, although it was not examined in depth, particle motion perpendicular to the local shock front appears to play a significant role in the current case as well as the planar case. In the third image, the wave has propagated further with the perturbation decreasing in amplitude. The high-pressure in the valley of the driver has persisted, suggesting that it is locked into the material and will persist indefinitely, but there is no obvious high pressure region near the valley in the wavefront.

Fig. 17
figure 17

Plots of pressure for a section of a 2-D mesoscale simulations of perturbation decay for impact at 874 m/s at a 0.20, b 1.00, and c 2.50 µs after impact. The black region in the left of c is the rigid piston used in the hybrid approach. The pressure scale is inset in the first image

Full size image

While in the continuum calculations it was sufficient to monitor two series of points along the wave propagation direction, one along the valley and the other along the peak, in order to determine the perturbation amplitude, the stochastic nature of these mesoscale calculations means that another approach is required. Therefore, the approach of monitoring each particle used by Vogler et al. [46] was modified as follows. A single Lagrangian tracer was placed at the center of each particle, and its velocity was monitored. When the tracer reached a velocity of half of the late time velocity (which is the piston velocity for simulations with rigid or hybrid drivers), the particle is considered to be in motion. The coordinates of those particles that began to move within a specified time interval \(\delta t\) were used to fit a sine wave as illustrated in Fig. 18. A value of \(\delta t = 50\) ns was used as a compromise between having sufficient particles to obtain a valid fit and sampling over too long a time so that the wave shape is inaccurate. Other functional forms were tried for the fitting, but the sine was found to give the best results. It should be noted that the approach used for determining wave amplitude in the mesoscale simulations results in a spatial amplitude \(\Delta x\) at a fixed time for the perturbation rather than the temporal amplitude \(\Delta t\) at a specific position obtained in the experiments and the continuum simulations. However, if the wave evolves slowly, the two are equivalent and can be related to one another through the shock velocity in the sample \(U_{s}\).

Fig. 18
figure 18

Particles that begin motion over time intervals of \(\delta t = 50\) ns for three propagation distances as well as the sine waves fit to each

Full size image

A mesoscale simulation represents a specific realization of potential random particle arrangements for the given particle size, volume fraction, and domain. When multiple realizations of particle arrangements were simulated, the results were found to have a surprisingly large variability. This contrasts with previous work [37, 46, 47] in which the properties of planar waves showed minimal variability between different realizations. One possible explanation for this is that the planar wave involves all of the particles in the wavefront in the same manner, while the perturbed wave causes the front to experience varying conditions along the length: converging flow near the valleys, diverging flow near the peaks, and shearing between the two. If one of these aspects influences the perturbation evolution more than the others, then a relatively small region of the domain will control the decay. In order to obtain more consistent results across multiple simulations, domains of height \(W = 4\lambda \) (Figs. 17 and 18 show only a fourth of the total domain) were used in the 2-D calculations. This domain size was found to give repeatable results without being too computationally expensive.

The perturbation decay for the 2-D mesoscale model is shown in Fig. 19 along with the continuum and experimental results previously presented. The perturbation decays much more slowly than in the continuum cases, apparently resulting in a significantly larger amplitude than seen in the experiment. However, if the actual buffered window configuration used in the experiments is incorporated into the mesoscale simulations, the results are affected dramatically, even more so than was the case for the continuum model. Across the range examined for the buffered case, there is no significant change in the apparent \(\Delta t\). For the sample thickness of experiment PD-2, the windowed results are about 50 % lower than the in situ value and, in fact, agree well with the experimental results. The stochastic nature of the mesoscale model results in some scatter in the value of \(\Delta t\) found for a given position, but the scatter is comparable to that seen in experiment PD-2. The wave shapes from the buffered window for the 2-D mesoscale simulations show larger variability than the experimental variability shown in Fig. 15. This is consistent with the need to utilize multiple wavelengths in the simulations in order to achieve repeatable results.

Unlike in the continuum simulations, the perturbation at the interface between the driver and sample does not grow significantly with the passage of the shock, but local perturbations on the scale of one to a few grains are seen. If Y in the mesoscale simulations is set to zero, though, some indications of turbulent flow are observed in the sample region.

Fig. 19
figure 19

Perturbation decay from a mesoscale simulation compared with continuum and experimental results from PD-2. Simulation results include measurement in situ and at a buffer/window interface

Full size image

As was done with the continuum model, the effect of variations in the mesoscale model parameters on the perturbation decay was examined. The value of \(Y=8\) GPa for the WC particles has been used as a baseline value since it has previously been used to calibrate the mesoscale model to planar compaction results [40]. Varying the value of this parameter can affect the perturbation decay result significantly as seen in Fig. 20. For values near zero, the results are similar to the continuum results at small values of Y (see Fig. 10), though \(\Delta t\) is never negative in this case. As Y is increased, the perturbation decays more slowly until a value of about 4 GPa is reached. For strengths from 4 to 12 GPa, the perturbation changes only slightly. However, the minimal decay is found around 6 GPa; values of Y above that lead to slightly higher attenuation. Interestingly, this means that the 2-D mesoscale model gives nearly the same response for all credible values of Y for granular WC for this piston velocity. At different piston velocities, the same trend is found, though the value of Y that gives the minimal attenuation is found to increase with piston velocity. Apparently, for sufficiently high strength most of the material behaves elastically so that changes in Y affect behavior little. For very high values of Y, partially filled cells between particles are sufficiently strong (strength in partially filled cells being a based on the volume average of the material present) that they influence behavior, causing a slightly more rapid decay.

Fig. 20
figure 20

Perturbation decay from 2-D mesoscale simulations for various values of the flow stress Y

Full size image

Varying the impact or piston velocity had only a small effect on the perturbation decay in the continuum simulations (see Fig. 12). This is also true for the mesoscale simulations as seen in Fig. 21. Although the noise in the decay for each simulation makes it less obvious, the trends are the same as those from the continuum model with the Geo strength model. For small values of \(x/\lambda \), the normalized \(\Delta t\) decreases as velocity increases because the shock velocities of aluminum and granular WC become more similar. For larger values of \(x/\lambda \), the perturbation amplitude increases with piston velocity. In the Geo model, the strength is explicitly a function of pressure; in the mesoscale model, the strength of the individual grains is not pressure dependent but the overall strength of the material increases with velocity because there is less residual porosity.

Fig. 21
figure 21

Perturbation decay from mesoscale simulations with varying varying piston velocities for the hybrid driver configuration compared with continuum simulation results and experimental results from PD-1 and PD-2

Full size image

Varying the perturbation wavelength \(\lambda \) and amplitude \(a_{o}\) has similar effects to those observed for the continuum model (see Fig. 11): increases in amplitude lead to more rapid decay, and shorter wavelengths decay more rapidly. Incorporating the parameter \((a_{o}/\lambda )^{2}\) into the normalization of the horizontal axis collapses the results for different amplitudes very well, but the results for varying \(\lambda \) are not collapsed as well.

While the particle diameter is not a parameter in the continuum model, it can readily be varied in the mesoscale model. Results for the baseline value for D of 32 µm along with results for 48, 64, and 96 µm are shown in Fig. 22. Perhaps surprisingly, even relatively modest changes in the particle diameter noticeably affect the perturbation decay leading to more rapid decay as D increases. While \(a_{o} \gg D\) for the baseline case, granular materials produce nonuniformities sometimes referred to as stress bridges or force chains that can lead the main wave by a few particle diameters. Once the amplitude has decayed somewhat from its original value, a(x) may be only a few particle diameters. Thus, the decaying perturbation starts to look like the transient nonuniformities that are always present in the wavefront; since those transient nonuniformities come and go according to random variations in the particle arrangements, this fluctuation seems to lead to more rapid perturbation decay. Indeed, for small values of x the results for 32, 48, and 64 µm particles are only slightly different. Also note that for \(D = 96\) µm, the perturbation amplitude becomes negative. The perturbation amplitudes after that seem to be due to fitting a sine wave with prescribed wavelength to random transient fluctuations in the wavefront rather than being due to the initial perturbation. Sufficiently small particles should not show any dependence on D; indeed, the results for \(D = 24\) µm are nearly identical to those for 32 µm. Similarly, a simulation incorporating variability in the particle size with an average diameter of 32 µm and a normal distribution of sizes with standard deviation of 10 µm gave the same results as the calculation with a uniform diameter of 32 µm. The mechanism of random variability leading to perturbation decay seems to be inherent in the random nature of the granular material and, thus, is not captured by the continuum calculations. In real ceramics such as WC, particles are expected to fracture, so that the particle size distribution can change during loading. As this effect is not captured in a realistic way in these mesoscale simulations, it is not clear how that would affect the perturbation decay. It will be interesting to see if a significant effect of initial particle size is observed experimentally.

Fig. 22
figure 22

Perturbation decay from mesoscale simulations with varying particle diameters compared with continuum simulation results and experimental results from PD-2

Full size image

Finally, the effect of volume fraction was examined. Volume fractions of both 45 and 65 % were compared to the baseline value of 55 %. Slightly faster attenuation was observed for the 45 % case, and it was even more rapid for the 65 % case. Unfortunately, the simulations were conducted in the hybrid configuration with constant piston velocity, so neither the stress nor the final density was held constant. Beyond the effects due to stress and density levels, it seems that the wave front heterogeneities may be more pronounced for higher volume fractions. As there are still open questions on the effect of initial volume fraction, further work is needed in this area.

Three-Dimensional Mesoscale Simulations

In many respects, the 3-D mesoscale models give similar results to their 2-D counterparts. As was seen by [36], 3-D simulations run without utilizing the numerical slide option (stiction case) exhibited a small-amplitude precursor not seen in experiments. Leaving aside the precursor in that case, when slices of the 3-D model are examined, they appear quite similar to images of the 2-D model. As seen previously, the wave front has a raggedness at the scale of a few particle diameters, and development of force chains is evident. The 3-D results were analyzed in the same manner as the 2-D simulations, and those results are shown in Fig. 23 along with result from the 2-D mesoscale and continuum model. The 2-D model and 3-D model with stiction give similar results, suggesting that the dimensionality of the problem is not a critical aspect. Although only a single wavelength is included in the simulation, the scatter from realization to realization was relatively small. This reflects that fact that 3-D simulations have over twice as many particles as the 4\(\lambda \) simulations in 2-D due to the finite thickness in the z-direction. Averaging in the z-direction provides a similar effect to averaging over multiple wavelengths in the y-direction.

Fig. 23
figure 23

Perturbation decay from 3-D mesoscale simulations with stiction and intergranular sliding treatments of particle interactions for the hybrid driver configuration compared with simulation results using continuum and 2-D mesoscale models as well as experimental results from PD-2

Full size image

When the intergranular sliding option is used to approximate sliding between materials, the decay occurs slightly less rapidly as seen in the figure. Since intergranular sliding approximates frictionless sliding and the stiction case involves bonding between particles, the two should represent the bounds on intergranular behavior. More realistic cases including frictional effects should fall between the two, suggesting a limited role for friction. Additional results using a Lagrangian modeling framework allowing for more realistic modeling of friction will be reported separately.

Closure

In this paper, initial experimental results for granular WC utilizing a modified version of the perturbation decay experiment performed on a gas gun are presented. The results demonstrate the experiments are feasible and can, in principal, be conducted over a wide range of impact velocities. Low impact velocities such as that in PD-1 which result in dispersed waves may create some difficulties in interpreting the results, but arbitrarily high velocities (e.g., those achievable on a two-stage gun) present no conceptual difficulties.

Although the line-VISAR used in these experiments provides a means to measure the perturbation amplitude after the wave has traveled through the sample, it is significantly limited in that only a single sample thickness can be tested. This makes it very difficult to trace the full evolution of the perturbation amplitude. In the initial study by Sakharov et al. [1], amplitudes at many sample thicknesses were obtained using a flash-gap technique, slitting, and a streak camera. A similar approach for instrumenting the current experiments would be desirable.

In addition to the experimental results, simulations utilizing three different modeling approaches are presented. One of the main findings from the simulations is that the presence of a buffer between the sample and measurement site strongly affects the perturbation amplitude measured. Thus, any redesigned target should not include a buffered window or anything that will have a similar effect. This constraint may make the setup of Sakharov et al. [1] unsuitable, but there are other configurations that can be explored. While evaluating the perturbation amplitude in situ suggests that the continuum model matches the results from experiment PD-2, considering the effects of the buffered window suggests instead that the mesoscale model agrees with the experimental data. Additional data are needed, though, to evaluate whether the mesoscale model accurately reproduces the perturbation decay over a broad range of sample thicknesses, impact velocities, perturbation characteristics, etc.

Parametric studies with the models provide additional insight. The perturbation decay in both the continuum and mesoscale simulations was found to be most influenced by material strength, though the effect is manifested somewhat differently in the two case. In the continuum simulations, higher strength slows the decay of the perturbation. In the mesoscale simulations higher strength again slows the perturbation decay but only until a critical value of Y is reached. When Y approaches the longitudinal stress in the material, the perturbation evolution remains nearly constant with further increases. Varying the impact velocity has only a modest effect on the evolution for both the continuum and mesoscale models. On the other hand, variations in the perturbation wavelength \(\lambda \) and amplitude \(a_{o}\) affect the evolution significantly when the amplitude and distance are normalized as done here, suggesting a relatively stringent test of models for granular material behavior. Empirically, including the ratio of the perturbation amplitude and wavelength \(a_{o}/\lambda \) in the normalization seems to collapse the data reasonably well since this captures to some degree the degree of convergence/divergence due to the perturbation. In the initial papers on the topic [1, 2], it was found that solids showed varying results for different values of \(\lambda \), while porous materials that were, presumably, melted by the shock collapsed onto a single curve. Thus, it may be that the strength of solid materials leads to the dependence seen in the previous and current results. Somewhat surprisingly, mesoscale simulations indicate the particle size will affect the perturbation decay significantly, though experimental confirmation of this is needed. Some sensitivity to the initial volume fraction is also predicted.

Although the limited data available are not sufficient to draw strong conclusions about the validity of the modeling approaches, the results of PD-2 suggest that the existing calibration of the pressure-dependent strength model is somewhat inaccurate. It may be sufficient to adjust the model parameters somewhat, or an entirely different functional form may be required. On the other hand, the data from experiment PD-2 agrees well with the 2-D mesoscale model results. If the mesoscale models agree with additional data of this type, it will greatly increase confidence in the predictive capabilities of such models for different dynamic problems.

These initial results for perturbation decay in granular materials helps identify a number of issues to be addressed in future work. From the experimental standpoint, the foremost considerations are removing the buffer from the measurement site and increasing the data return for a single experiment. These two goals may constrain the potential solutions somewhat, but it appears that it should be possible to address both. Once the experiment itself has been refined, a number of issues can be explored such as those related to the effects of impact velocity / pressure; granular material properties like particle size and morphology; the material studied; and the presence of a second granular or liquid phase. The modeling tools, especially the mesoscale model, can provide predictions about the effects of most of these parameters. However, because the mesoscale model is based on an Eulerian modeling approach, it does not account for particle-particle contact or friction. Nor does it model particle fracture in a physically realistic way. Therefore, simulations using a particle-based Lagrangian approach [48] will be explored separately to address those issues.