1 Introduction

This work describes the development of a computer program for the dimensioning of foils of a hydrofoil boat, unique in the fact that it does not only deal with foil design, like most software, but with the hydrofoil boat hull as a whole, in an attempt to contribute to the concept and preliminary design of these boats that can be processed autonomously or integrated to an existing computer system.

Hydrofoil boats are craft that have complete hydrodynamic support by submerged foils at their operation speeds. The basic working principle is to lift the hull out of the water to reduce the resistance (only on foils) and installed power, and to reduce the motions in seakeeping. According to Johnston [8], the first boat of this kind was from 1894, successfully tested by the Meachan brothers in Chicago. Also, in Italy, 1905, Enrico Forlanini built a “hydro-aeroplane” that reached 38 kt [11].

Hydrofoil boats are ones of the well-known High-Performance Craft or Vessels (HPC), Advanced Marine Vehicles in the 70s. In comparison with other HPC, the seakeeping of hydrofoil boats is the best, only comparable with SWATHs (Small Waterplane Area Twin Hulls), which are better at low or no speeds (where the hydrofoil boat still didn’t take off), but cannot reach the approximately 50+ kt of hydrofoil boats. This maximum speed is lower than the ones of some planing boats, mono or multi hulls, WIGs (Wings in Ground Effect), about 200 kt and hovercraft (Air Cushion Vehicles and Surface Effect Ships), about 80 kt, but the seakeeping at high speeds is incomparably better. The load capacity is smaller than hovercraft and far greater than WIGs, comparable to planing boats. The maneuverability is by far the best of all and does not compromise course keeping. They can also be catamarans, for better deck area.

This type of concept is better recommended for high-speed operations at high seastates (but not only to) with lower resistance and very good course keeping and maneuverability, which is ideal for light military boats, ferry boats in rough waters and more recently, applied to pleasure and leisure (even for sailing) boats. The software presented here was a development of Fonteles [5] to dimension foils of a hydrofoil boat, using several references and analytical empirical formulation on hydrofoils, applying a method created by Calkins and published by Schachter and Vianna [15], for fully submerged foils, adding to the method surface piercing foils formulation and dimensioning. This program is part of a suite for the determination of the dynamic equilibrium of high-speed craft, in turn part of a computational system under development [18], programmed to perform a design methodology proposed by Schachter et al. [14], the Solution-Focused Design process, as a development from Schachter [16] and Keane et al. [9]. It is integrated, specially encoded to allow for processing conflicting naval architecture design modules out of a usual sequence, thus enabling to creatively test different design options, focused on the solution.

The suite, of which this program is part of, deals with the dynamic equilibrium (lift, drag, balance) of planing and hydrofoil boats, as well as other high-performance vessels and also allows for propeller selection.

The programmed method of this work, part of the mentioned suite, for hydrofoil boat preliminary design, works both integrated to the system and autonomously, as a single software. As mentioned, it applies the cited method and additional implementations, that from a stipulated foil configuration, from a pre-defined high-speed hull form, dimensions interactively the foils, calculating Lift and Drag, subject to constraints such as Structural Resistance and Cavitation, as a function of thickness to chord (t/c) and load factor (W/S).

It is an absolute novel computer program, since all others in existence compute either theoretically or with CFD the foils alone or interacting with a hull, only as given, one configuration per run, but never in a design integrated and interactive fashion, it applies a hydrofoil boat design methodology, with foil dimensioning for equilibrium, take-off, angle of attack determination and variation, etc. Also, due to the design multidisciplinary approach mentioned, for consistency, the formulation adopted is, as mentioned, analytical empirical, experimental based.

2 The design method and formulation

As cited, the design method of this program for dimensioning the foils for a hydrofoil boat were created by Calkins (advanced marine vehicles design—class notes, COV-705, PEnO-COPPE/UFRJ, 1976), uses several formulations, mainly by Du Cane [3], and was presented by Schachter and Vianna [15].

The method was conceived to optimize the main features of foil dimensioning design, which are: Lift and Drag to, respectively, counteract the weight and for the propulsion, and the ratio of Lift on Drag coefficients, CL/CD, should be maximized, subject to structural strength and cavitation limits constraints. These parameters were all solved for two important hydrofoil design factors, thickness on chord ratio (t/c) and a load coefficient (W/S, weight on foil area), so they could be brought together in the optimization graph of Fig. 1.

Fig. 1
figure 1

Features, limits and operation point

Full size image

This method shown in the graph was created to use a generic, self-designed foil section, and therefore allowing the freedom to vary the foil thickness, t. For the most common cases, where tested and tabulated profiles, such as NACA, e.g., are used, t/c is constant, optimized for a maximum CL/CD, thus represented by a straight line in the graph (Fig. 2). Another fundamental design factor to be considered is the load coefficient W/S. This is a ratio taken from experience from hydrofoil boats, with values of practical limits between the foils leaving the water and the boat being too heavy to take-off. These practical values of W/S vary from 3800 to 5700 kgf/m2 (800 to 1200 PSI), and the program uses the range 3000 to 7000 kgf/m2 for better curve adjustments and visualization.

Fig. 2
figure 2

Real case situation, using a NACA foil

Full size image

There are, of course, other design factors to be considered in a concept design of a hydrofoil boat, such as stability, structural design, propulsion, etc., but these are out of the scope of this work.

The foils are dimensioned to work up to the cruise speed, with the take-off speed determination, showing several graphs of all results.

The lift of the foils is varied by the speed and their submersion; therefore the lift is calculated at each knot along the take-off process. The take-off speed is defined in the program by the subtraction of the lift of the foils from the weight, until the speed the lift equals the weight (Fig. 3).

Fig. 3
figure 3

Take-off speed determination

Full size image

The displacement at each knot is used to compute the resistance of the hull, using Holtrop [7] up to Fn = 0.4 and Savitsky [12] above, which is added to the foil drag to provide the Resistance/Power vs Speed curve.

2.1 Foil lift

According to Sphaier (Hydrodynamics II—class notes (in Portuguese), PEnO-COPPE/UFRJ, 2003), a symmetrical body moving at a constant speed, in the direction of the axis of symmetry, through a viscous liquid, must overcome a resistance in the opposite direction of the movement.

In the case of a non-symmetrical body, or when the flow is not in the direction of the axis of symmetry the resulting force is not only in the opposite direction of the movement, but also, perpendicular to the direction, as in Fig. 4.

Fig. 4
figure 4

Lift and drag forces on a foil [10]

Full size image

This perpendicular force is called Lift Force and the horizontal, Drag Force. The proper choice of forms of a body can be harnessed in engineering, so that when moving the body in an environment the generated force can support the vessel’s weight. These bodies are called hydrodynamic profiles or hydrofoils.

The first characteristic to be studied is the form. From only one dimension it is possible to identify the profile, in this case, the chord, c. In order to study the hydrodynamic problem an angle of attack has to be set.

The fluid is characterized by specific gravity and dynamic viscosity. The geometry of the hydrodynamic problem is only completely determined by identifying the angle of attack.

The kinematics of the movement is characterized by speed incident flow. The dynamics of the phenomenon is determined by inertial and viscous forces:

  • c—chord, distance between profile extremes.

  • \(\alpha\)—angle of attack taken from the base line of the profile.

  • \(v\)—flow speed.

  • \(\rho\)—specific gravity of the fluid.

  • \(\mu\)—dynamic viscosity.

  • L—lift force.

By this definition, the Lift force should be written as:

$$L=f(c,v,\uprho ,\upmu ,\mathrm{ form})$$
(1)

With these parameters, applying dimensional analysis, there are three groups:

$${C}_{L}=\frac{L}{\rho {V}^{2}c}$$
(2)
$${R}_{e}=\frac{\rho {V}^{2}c}{\mu }$$
(3)
$$\propto$$
(4)

where \({C}_{\rm{L}}\) is the lift coefficient and \({R}_{\rm{e}}\) is the Reynolds number. With the above non-dimensional groups the following relation can be drawn:

$${C}_{\rm{L}}=\frac{L}{\rho {V}^{2}c}={f}_{1}({R}_{\rm{e}},\propto )$$
(5)

The definition of function \({f}_{1}\) is given by experimenting on smaller profiles and the results extrapolated to the prototype size. From these experiments it is possible to build the curves relating forces coefficient and the angle of attack as well as the relation between the drag and lift coefficient, see Fig. 5.

Fig. 5
figure 5

Relation between lift and drag coefficients, CL and CD [10]

Full size image

The Lift Force exists because of a difference between the pressure at the upper side of the hydrofoil and the bottom side. This pressure gradient is caused by a difference in the flow speed of these parts.

For each angle of attack there is a different pressure distribution at the upper and the bottom side. Integrating this distribution, it is possible to find the Lift and the Drag Forces.

The Lift Force per unit of length is:

$$L={\int }_{\text{A}}^{B}\left({p}_{\text{u}}-{p}_{\text{b}}\right)dx$$
(6)

Assuming \({u}_{\text{u}}={u}_{\text{b}}\) and utilizing Eüler Integration Equation:

$$L=\frac{\rho }{2}{\int }_{\text{A}}^{B}\left[{\left(V+{u}_{\text{u}}\right)}^{2}-{\left(V-{u}_{\text{b}}\right)}^{2}\right]{\text{d}}x$$
(7)
$$L=\frac{\rho }{2}{\int }_{\text{A}}^{B}\left[2V\left({u}_{\text{u}}+{u}_{\text{b}}\right)+{u}_{\text{u}}^{2}-{u}_{\text{b}}^{2}\right]{\text{d}}x$$
(8)

In a circular flow around the body there is no force acting:

$$L=-\frac{\rho }{2}{\int }_{\text{A}}^{B}\left[{u}_{\text{u}}^{2}-{u}_{\text{b}}^{2}\right]{\text{d}}x=0$$
(9)

So:

$$L=\rho V\left[{\int }_{\text{A}}^{B}{u}_{\text{u}}{\text{d}}x+{\int }_{\text{A}}^{B}{u}_{\text{b}}{\text{d}}x\right]$$
(10)
$$L=\rho V\left[{\int }_{\text{A}}^{B}u.{\text{d}}x{\left.\right|}_{\text{u}}+{\int }_{\text{A}}^{B}u.{\text{d}}x{\left.\right|}_{\text{b}}\right]=\rho V\Gamma$$
(11)

So the lift force due to a vortex can be written as:

$$L=\rho V\Gamma$$
(12)

From the integration of pressures it is possible to conclude that there is a sustaining force and that it is linked to the existence of a circulation around the body (Fig. 6).

Fig. 6
figure 6

Flow around the body

Full size image

The program calculates the Lift Force (L) as:

$$L = 1/2\uprho {V}^{2} S {C}_{\mathrm{L}} (\mathrm{kgf})$$
(13)

where ρ is the specific gravity of the fluid (kgf s2/m4), S is the foil area (m2), as the span (b) times the chord (c) of the foil.

The lift coefficient (CL) is defined as:

$${C}_{\mathrm{L}} = {C}_{\mathrm{L\alpha }} {\mathrm{\alpha }}_{\mathrm{T}}$$
(14)

where CLα is the slope of the lift curve and αT is the total angle of attack (Fig. 7). The lift coefficient CL in normal conditions varies linearly with the total angle of attack (αT) and has a slope (CLα) value of 2π, for two-dimensional thin foils. NACA provides tabulated CL for their foils.

Fig. 7
figure 7

Hydrofoil section geometry [3]

Full size image
$${{C}}_{\mathrm{L}} = 2\uppi {{\alpha }}_{\mathrm{T}}$$
(15)

The correction for the angular coefficient, CLα, of the lift curve for fully submerged foils taken to a reasonable practical minimum (to interact with drag components) are a correction for the Aspect Ratio (AR), b2/S, experimental results proposed by Calkins (1976), and applied successfully by Schachter [17], for fully submerged foils (16) and for surface piercing foils (17), being hf the foil submersion;

$${{AR}}_{\mathrm{corrected}} ={ AR }/{ AR}+2$$
(16)
$${{AR}}_{\mathrm{corrected}} =\frac{\left[{AR }\left(1+\frac{{{h}}_{\mathrm{f}}}{{b}}\right)\right]}{\{[{AR }(1+{{h}}_{\mathrm{f}}/{b})] +2\}}$$
(17)

and a correction for the Free Surface Effect (K), from Wadlin et al. [20], presented by Du Cane [3]:

$$K\, = \,\frac{{\left[ {\left( {4\left( {h_{f} /c} \right)} \right)^{2} \, + \,1} \right]}}{{\left[ {\left( {4\left( {h_{f} /c} \right)} \right)^{2} \, + \,2} \right]}}$$
(18)

Leading to the correction of the angular coefficient of the lift curve as (ARcorrected accordingly to fully submerged or surface piercing):

$${C}_{{\text{L}}\alpha} = 2\uppi {AR}_{\mathrm{corrected}}\frac{\left[{\left(4 \frac{{h}_{f}}{c}\right)}^{2}+1\right]}{\left[{\left(4 \frac{{h}_{f}}{c}\right)}^{2}+2\right]}$$
(19)

2.2 Foil drag

The force mentioned in Sect. 2.1, that opposes the movement is the Drag Force. Following the same reasoning behind the formulation of the lift force, the non-dimensional groups are related in an analogous way:

$${C}_{\text{D}}=\frac{D}{\rho {V}^{2}c}={f}_{2}({R}_{e},\propto )$$
(20)

The function \({f}_{2}\) is defined with experimental testing as is the \({f}_{1}\) function. The viscosity of a real fluid has a negligible effect on the lift of thin foils, but not on the drag.

The drag (D) calculation is analogous to the lift.

$$D = 1/2\uprho {V}^{2} S {C}_{\mathrm{D}} (\mathrm{kgf})$$
(21)

The drag coefficient CD, has 4 main components, frictional and viscous pressure (CD0), wavemaking, CDW and induced drag CDi (only fully submerged). The struts are considered to be vertical with frictional drag, for Sst = hf c, added to the total drag.

$${C}_{\mathrm{D}} = {C}_{\mathrm{D}0} + {{C}}_{\mathrm{DW}} + {{C}}_{\mathrm{Di}}$$
(22)

The formulation is given by Du Cane [3]. The coefficient Cf is from the ATTC flat plate friction table, including the known correction for high-speed craft ΔCf, which in the case of foils is 0.0008:

$${C}_{\mathrm{D}0}=2\left({C}_{\mathrm{f}} + {\Delta }_{\mathrm{Cf}}\right)\left(1+1.2\frac{{t}}{{c}}\right)+0.11 \left({C}_{\mathrm{L}0}- {C}_{\mathrm{L}}\right)$$
(23)

The wavemaking component, presented by Du Cane, from Vladimirov [19], is a function of CLα, the inclination of the lift coefficient curve (as all drag), the chord’s Froude number (Fnc) and the foil submersion (hf) and chord (c):

$${C}_{\mathrm{DW}} = {\left({C}_{{\text{L}}\alpha }\right)}^{2}\frac{1}{2}{\mathrm{Fn}}_{\mathrm{c}}^{2}\mathrm{EXP}\left[-2\left(\frac{{h}_{f}}{\mathrm{c}}\right){\mathrm{Fn}}_{\mathrm{c}}^{2}\right]$$
(24)

According to Hoerner [6], the lift induced drag, also known as ‘drag due to lift’, can be estimated with the realistic supposition of elliptic transversal loading, which is, as theory indicates, the optimum lift distribution over the span for maximum lift and minimum induced drag. The equivalent stream deflected by such a foil is that of a cylinder with the same diameter of the span b. Thus:

$$L\;{\mathrm{or}}\;F =\uprho \left(\frac{\uppi }{4}\right){b}^{2} V w$$
(25)

w is the vertical downwash velocity at some distance behind the foil (Fig. 8), and the average downwash angle is:

Fig. 8
figure 8

Induced drag, a component of ‘lift` force [10]—modified)

Full size image
$$w/V = 2 {C}_{\mathrm{L}} /{ \pi AR }= 2 {{\alpha }}_{\mathrm{i}}$$
(26)

The lift induced drag can be deduced from the induced angle (αi), which is assumed to be an average flow deflection of half of the final theoretical downwash angle α of a wing. As in Fig. 8, the ‘F’ force produced normal to the induced angle, tilted backward from the Lift force L.

$${{\alpha }}_{\mathrm{i}} \sim \mathrm{ tan }{{\alpha }}_{\mathrm{i}} = {C}_{\mathrm{L}} /\uppi AR$$
(27)

And in the flow direction, the induced drag’s minimum coefficient:

$${C}_{\mathrm{Di}} = {C}_{\mathrm{L}}\mathrm{tan}{{\alpha }}_{\mathrm{i}}= {C}_{\mathrm{L}}^{2} /{ \pi AR}$$
(28)

As formulated by Du Cane [3] from Hoerner [6], the induced component can be calculated as a function of CLα, biplane factor (σ) and an adjusted aspect ratio (ARa):

$${C}_{\mathrm{Di}} = {\left({C}_{{\mathrm{L}}\alpha }\right)}^{2} (1 +\upsigma ) / (\uppi {AR}_{\mathrm{a}})$$
(29)

The biplane factor (σ) for Prandtl wings of finite, limited span, that produce a “trailing-vortex” drag, is expressed by Du Cane. For wings in the air, σ = 0, but is significant in the water, with the foil approaching the free surface, and although of complex determination, was simplified by Eames and Jones [4] for high Froude numbers, which is the case for hydrofoil boats (see Fig. 9):

Fig. 9
figure 9

Foil configuration, varying from inverted T through π, up to U shape, as ‘a’ increases. (h = hf)—[3]

Full size image
$$\upsigma = {AR}_{\mathrm{a}} / [{AR}_{\mathrm{a}} + 12 ({h}_{\mathrm{f}}/c)]$$
(30)
$${AR}_{\mathrm{a}} = b/c [1 +(a/b{)}^{3} {h}_{\mathrm{f}}/b]$$
(31)

It should be noted that for surface piercing foils there is always a portion of the foils out of the water. Therefore, the induced drag CDi does not apply for these foils and in the program the wetted area S is interactively recalculated for each speed, at each elevation.

2.3 Foil angle of attack (αT)

From Eqs. (13) and (14),

$${{\alpha }}_{\mathrm{T}} = {C}_{\mathrm{L}}/{C}_{{\mathrm{L}}\alpha}$$
(32)

2.4 Structural limit

For the structural strength constraint limit, the bending moment was used, since it is more critical than the shear force. A formulation was developed to obtain a minimum t/c, as a function of W/S that satisfied this constraint.

This formulation can be used for inverted T, inverted π and U foil configurations. The inverted T deduction will be presented here, the others are analogous. The load distribution in an inverted T foil is (Fig, 10):

Fig. 10
figure 10

Loads on an inverted T foil

Full size image

That can be considered as studded (cantilever) beams (Fig. 11):

Fig. 11
figure 11

Studded beam

Full size image

And the Moment can be written as:

$${M}_{(\mathrm{max})} = w {L}^{2} / 2 = w {b}^{2} / 8$$
(33)

For surface piercing foils the foil spans (b) are adjusted to their dihedral and inclination angles.

The inertia (I) was taken from a generic flat-ogival foil (Fig. 12), which is a reasonable approximation for any foil.

$${I}={{\uppi}}{c}{{t}}^{3}/64$$
(34)
Fig. 12
figure 12

Flat-ogival foil

Full size image

And the Yield Stress (σy) is,

$${\upsigma }_{{y}}={{\varvec{M}}}_{({\varvec{m}}{\varvec{a}}{\varvec{x}})}\frac{{z}}{{I}}\left({\text{the}}\;{\text{Section}}\;{\text{Modulus}}\;{\text{being}}\frac{{z}}{{I}}\right)$$
$$=[({w}{{b}}^{2}/8){t}/2]/(64/\uppi {c}{{t}}^{3})$$
(35)

Creating a constant with the numbers and π, and solving for t/c, considering that W/S = wb/bc, the formulation becomes:

$${t}/{c }= \sqrt{[(1.27\frac{{W}}{{S}}{{b}}^{2}) / ({\upsigma }_{\mathrm{y}}{{c}}^{2})]}$$
(36)

Working a general equation from studded (T) to bi-anchored (U) beams, with a correction for strut spacing (bS) from 0 to b and W/S in IS units (SF: safety factor):

$${t}/{c}=\sqrt{0.85{{b}}_{\mathrm{s}}^{2}+\frac{2\left\{1.27{\left[\frac{{b}-{{b}}_{{S}}}{2}\right]}^{2}{g}\left(\frac{{W}}{{S}}\right)\right\}}{\left(\frac{{\upsigma }_{\mathrm{y}}{{c}}^{2}}{\mathrm{SF}}\right)}}$$
(37)

2.5 Cavitation limit

Considering a hydrofoil at a small angle of attack in a two-dimensional, steady, non-viscous flow, the velocity ahead of section as \({V}_{0}\) and total pressure as \({p}_{o}\), are as shown in Fig. 13.

Fig. 13
figure 13

Flow and pressure around an airfoil [10]

Full size image

According to Bernoulli’s Theorem:

$$\frac{{p}_{0}}{w}+\frac{{\left({V}_{0}\right)}^{2}}{2g}={\text{constant}}$$
(38)

Or:

$${p}_{0}+\frac{1}{2}\rho {\left({V}_{0}\right)}^{2}={\text{constant}}$$
(39)

At any point P, where the pressure and velocity are \({p}_{1}\) and \({V}_{1}\):

$${p}_{1}+\frac{1}{2}\rho {\left({V}_{1}\right)}^{2}={p}_{0}+\frac{1}{2}\rho {\left({V}_{0}\right)}^{2}$$
(40)

And the difference in pressure:

$$\Delta p={p}_{1}-{p}_{0}=\frac{1}{2}\rho ({V}_{0}^{2}-{V}_{1}^{2})$$
(41)

If \({V}_{1}>{V}_{0}\), the flow is accelerating, then the pressure at point P has decreased.

At some point S near the nose section, the flow is divided, losing all velocity and momentum in the direction of the motion; therefore the velocity in point S is zero:

$$\Delta p={p}_{S}-{p}_{0}=\frac{1}{2}\rho {\left({V}_{0}\right)}^{2}$$
(42)

S is called the stagnation point and the dynamic stagnation is:

$$q=\frac{1}{2}\rho {\left({V}_{0}\right)}^{2}$$
(43)

The fluid above the dividing streamline passes over the upper surface with increased velocity resulting in a decrease in pressure, while the fluid below is slowed down resulting in an increased pressure, this difference in pressures generates the Lift force.

At some point in the upper section the pressure will be:

$$\Delta p={p}_{1}-{p}_{0}=\frac{1}{2}\rho ({V}_{0}^{2}-{V}_{1}^{2})$$
(44)

Rearranging:

$${p}_{1}={p}_{0}+ \Delta p$$
(45)

If:

$$\Delta p= -{p}_{0} \Rightarrow {p}_{1}=0$$
(46)

In the case of a \({p}_{1}\) reaching zero, the streamline will break and form bubbles since water does not bear tension.

In fact, this happens before the pressure becomes zero, but when it assumes values under the vapor pressure of water (\({p}_{v}\)) at which the water begins to “boil” and form cavities.

The cavitation criteria:

$${p}_{v}={p}_{0}+\Delta p$$
(47)

Or:

$$\Delta p= -({p}_{0}-{p}_{v})$$
(48)

Dividing by the dynamic pressure, the cavitation will begin when:

$$-\frac{\Delta p}{q} \ge \frac{{p}_{0}-pv}{q}$$
(49)

The expression:

$$\sigma =\frac{{p}_{0}-{p}_{v}}{q}$$
(50)

Is called the cavitation number, \(\sigma\). This number can be calculated in any particular case, because: \({p}_{0}\) is the sum of the hydrostatic and the atmospheric pressures, \({p}_{v}\) is dependent on the temperature and \(q\) upon density and speed.

\(\Delta p/q\) is a function of the geometry of a particular section and its angle of attack. An ordinary pressure distribution is shown in Fig. 13. Drawing the line \({(p}_{0}-{p}_{v})/q\), one can see if cavitation would occur.

For the constraint of the cavitation limit, the method works out a formulation to obtain a t/c, as a function of W/S, where the foil does not cavitate. For such, a practical and approximated formulation, proposed by Du Cane, was used, that provides an incipient cavitation number (σI), as:

$${\upsigma }_{\mathrm{I}}= {{A}}_{\mathrm{f}}{ t}/{c }+ {{B}}_{\mathrm{f}} {{C}}_{\mathrm{L}}$$
(51)

This formulation assumes that the total pressure distribution is approximately the summation of individual contributions, it is for thin foils (t/c < 0.2) and αT = 0. ‘Af’ is a practical profile factor (see Table 1).

Table 1 Profile factors Af [3]
Full size table
$${{B}}_{\mathrm{f}} = 1 / (1 +{ a})$$
(52)

where ‘a’ is the camber or taper (mean line) height, as ‘f’ in Fig. 7. ‘Bf’ varies from 0.5 to 2/π.

From Eq. (13), CL is:

$${{C}}_{\mathrm{L}} ={ L }/ 1/2\uprho {{V}}^{2}{ S }=({W}/{S})/{q}$$
(53)

where L (lift) = W (weight); \({q }={1/2 \rho }{{V}}^{2}\)

Hence,

$${\upsigma }_{\mathrm{I}}= {{A}}_{\mathrm{f}}{ t}/{c }+ {{B}}_{\mathrm{f}} \left({W}/{S}\right)/{q}$$
(54)

The incipient cavitation number also is the atmospheric pressure (pa) minus the vapor pressure (pv) plus the hydrostatic pressure (ρghf), over q. Equaling Eq. (54) to this expression, attributing values for pa, pv and ρ at 15 °C, for g = 9.81 m/s2, and solving for t/c, the expression of the maximum t/c to avoid cavitation becomes:

$$\frac{{t}}{{c}}= \frac{\left[69.06 + 10.045 {{h}}_{\mathrm{f}}- {{B}}_{\mathrm{f}} \left({W}/{S}\right)\right]}{{{A}}_{\mathrm{f}}{ q}}$$
(55)

2.6 Determination of (CL/CD)max

For the design using a generic foil, the maximum Lift to Drag Coefficient Ratio, (CL/CD)max is obtained from Eqs. (53) and (22):

$${\left(\frac{{{C}}_{\mathrm{L}}}{{{C}}_{\mathrm{D}}}\right)}_{\mathrm{max}}=[({W}/{S})/{q}] / ({{C}}_{\mathrm{D}0} + {{C}}_{\mathrm{DW}} + {{C}}_{\mathrm{DI}})$$
(56)

(For surface piercing foils, CDi = 0.0).

For a tabulated foil section, such as NACA, the t/c found in the design process is already for a (CL/CD)max.

3 Design sequence

As mentioned, this program dimensions the foils of a pre-defined high-speed hull, adequate for being a hydrofoil boat. This can be done either in the computer design system this software is integrated with, or by a hull defined with other software (stand-alone mode).

The hydrofoil boat program, as part of the dynamic equilibrium computation suite, uses for resistance (or drag) calculations, in both cases, and automatically in the suite, the Holtrop method when Froude numbers are below 0.4 and the Savitsky method for Froude numbers of 0.4 onwards.

The program is processed interactively, in the following sequence:

  1. 1.

    The parameters required can be obtained either directly from a system’s file or as user input: design displacement (Δ), center of gravity (LCG, VCG), cruise speed (V), distance from propeller thrust (T) to VCG, length between perpendiculars (LPP), breadth (BOA) and breadth at chine (BC), depth (D), deadrise angle (β), shaft inclination (ε), chine height at transom, strut height margin, foil structural strength safety factor (SF) and the boat’s Hydrostatics table.

  2. 2.

    In the ‘Wave Height’ area the user defines the design operating Seastate.

  3. 3.

    In the foil definition area, for the Rear and Front Foils, the user selects the Foil Profile, its Material, Configuration (inverted T or π, U or V surface piercing), the longitudinal position of each foil (for the determination of the load on the foils) and the surface roughness.

  4. 4.

    In the Foil Geometry area the design starts. The user inputs both foils geometries (spans, strut spans, inclinations), and their feasibility or not is shown in real time for modifications.

  5. 5.

    By clicking in ‘Calculate’, the computed information of the foils can be verified in the Rear and Front Foil Definition area (areas, chords, Lift, angles of attack, Structural Strength, Cavitation, for a range of W/S), pointing out the optimized foils.

  6. 6.

    With the foils defined, the next step is the take-off procedure, which allows for two options: either prescribing the maximum foil angle of attack (for the earliest take-off) or the desired take-off speed. It is a graphical procedure with lift of the foils vs decreased draft of the hull. The design criteria for angles of attack of this procedure is to use a constant angle of attack until take-off, and then decrease it at each knot in order to keep the lift (equal to the weight) constant until the cruise speed is reached. Graphs of lift, drag, angle of attack vs speed and other are presented.

  7. 7.

    From the imported Hydrostatics, the Resistance (Drag) and Power vs Speed graphs are shown.

4 A brief description of the program

The hydrofoil boat foils dimensioning through the optimization program for their preliminary design is, as already shown, a part of a dynamic equilibrium determination suite and is fully integrated, using its subroutines. It is also integrated with the greater system, that uses the Solution-Focused Design methodology [14], through files that interleave to and from each other. The program follows the system’s same philosophy: a minimum of screens, a logical sequence of required data, self-explained (names and units) and all necessary data (input and output) on the same screens and ease to change from one screen to another, with consistency of data on modifications.

The hull references, as in the whole system, are the stern, the baseline and the centerline, for all data. Besides the design functions of the program, there are the general commands of the whole suite, which are consistent with the other programs of the system.

The program has the usual general commands, besides units, speed, fluid and other properties settings, report generating, main characteristics and input data interleaving from one type of boat to another, etc.

There are four design stages groups that are processed in sequence: Foil Geometry (input), Rear and Front Foil Definition, Foil Resistance (Take-off) and Resistance, Power and Operation.

The Foil Geometry input process is highly interactive, and the user can change at any time the foil geometry and even any parameters from the Data Entry.

There are settings for the type configuration and drawing of fully submerged foils (Inverted T or π, or U) and surface piercing foils, such Dihedral Angle, Foil Height and Submergence, to form geometries like V, double V, flat bottom V and W types, to allow their drawing and for the adoption of the appropriate formulation for each type. Some examples can be seen in Figs. 14, 15 and 16.

Fig. 14
figure 14

Foil geometry definition of fully submerged foils (inverted T and π)

Full size image
Fig. 15
figure 15

Foil geometry definition of surface piercing foils (double V and W)

Full size image
Fig. 16
figure 16

Foil geometry definition of surface piercing foils (V and flat bottom V)

Full size image

5 Precision check

In order to verify the reliability of the program, few estimates based on real hydrofoil boats were made using the program to see if they gave the same results, as measured, as a precision check of the program calculations.

Information was gathered from datasheets and images of real existing hydrofoil boats, such as the Boeing JETFOIL 929 115 for fully submerged foils (Fig. 17) and the Rodriques RHS70 for surface piercing foils (Fig. 18).

Fig. 17
figure 17

Boeing JETFOIL 929 115

Full size image
Fig. 18
figure 18

Rodriques RHS70

Full size image

Some information was not available in the literature, such as the Section Profile, Angle of Attack at the calculated (cruise) speed and the position of the center of gravity of the boat. These parameters had to be estimated or worked backwards (for the LCG, e.g., from the displacement and the foils’ positions).

5.1 Fully submerged

For the JETFOIL 929 115, the following particulars were gathered:

LOA = 27.4 m,

Breadth = 9.5 m,

Draft = 5.2 m,

Speed = 43 Kt,

Displacement = 117 t,

VCG = 2.6 m,

LCG = 13.7 m.

(Aft foil ~ 3 m and Fwd foil ~ 21.3 m from the stern).


The JETFOIL uses an inverted T foil forward and a U foil aft. From the data and images used,


Fwd span (bf) =  ~ 3.6 m.

Aft span (ba) =  ~ 9.5 m.

Chord (c) =  ~ 1.15 m (Fwd and Aft).


Estimated foil material: Steel,

Estimated Section Profile: NACA 63-215.


The comparison parameter was the calculated foil from the program (Table 2).

Table 2 JETFOIL 929 115: precision check
Full size table

5.2 Surface piercing

For the Rodriques RHS70, the following particulars were gathered:

LOA = 22 m,

Breadth = 4.8 m,

Draft = 2.7 m,

Speed = 32.4 Kt,

Displacement = 31.5 t,

VCG = 1.35 m,

LCG = 11 m.

(Aft foil ~ 1 m and Fwd foil ~ 15 m, from the stern).

There were considered two dihedral foils, the Forward as a double V one (as the Front of Fig. 15) and the Aft as a flat bottom V (as the Rear of Fig. 16), as set in Table 3.

Table 3 Surface piercing RHS70 foils entry data
Full size table

Estimated foil material: Steel,

Estimated Section Profile: NACA 66-206 for the Forward foil and NACA 64-209 for the Aft foil.

The comparison parameter was the calculated foil from the program (Table 4).

Table 4 Rodriques RHS70: precision check
Full size table

These discrepancies seem reasonable, as this is an initial dimensioning of the foils.

6 Design example

A design example is presented here to demonstrate the method and the design process.

It is a conceptual design of a fully submerged hydrofoil patrol boat, with the main particulars shown below, with the hull based on a planing boat developed previously in the system.

6.1 Data input and foil geometry

This planing boat has LPP = 40 m, B = 8.5 m and D = 6.1 m and the data is as shown below:


Displacement (Δ) = 210.566 t,

LCG = 12.365 m,

VCG = 2.875 m,

f = 2.875 m (thrust to VCG distance),

Breadth at Chine = 8.5 m,

Deadrise angle (β) = 18.45 deg (dominant),

ε = 0.0 (shaft inclination angle—n.a.),

Chine height at transom = 0.971 m.


This hydrofoil patrol boat was specified to have a 40 Kt cruise speed, to operate in Seastate 4 (Significant wave height (h1/3) of 2.1 m), a Strut height margin of 0.2 was used, and a structural strength (SF) foil safety factor of 2.0 was specified.

For the foils, the Rear one was an inverted π shaped at 3 m from the stern and the Front one, an inverted T, 33 m from the stern. Both were selected made of Steel and with a Section Profile NACA 66-206. The steel roughness was chosen to be 0.15 mm.

In the Foil Geometry definition, as in Fig. 14, the wingspan of the Rear foil is 10 m, with a strut span of 8.5 m (inverted π shape), while the Front foil’s wingspan is 7.0 m and the strut span, zero (inverted T shape), see Table 5.

Table 5 Foil geometry spans input
Full size table

These inputs gave consistent feasible foil calculations, as the Rear and Front foils names in the top of the columns were within W/S practical ranges, after optimized. For the selected foil section, the program suggests and computes 95% of the stall angle (8°, for the NACA 66-206 profile) for the maximum angle of attack (αTmax), but this can be overwritten.

6.2 Results of the design example

6.2.1 Foils chords and angles of attack

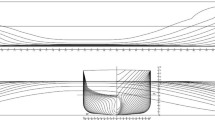
The program’s calculations for the design cruise speed took part and the plot of ‘t/c vs W/S’ was done (Fig. 19). There Eq. (55) of t/c to avoid cavitation was calculated for each W/S and plotted in blue and Eq. (37) of t/c for structural resistance limit in red. The t/c curve for maximum CL/CD, as mentioned in Sect. 2, is a constant horizontal line since a NACA foil is being used, instead of a generic one. For the design NACA 66-206 foil, this tabulated value is 6%, see green line.

Fig. 19
figure 19

Rear foil optimization

Full size image

The interception for the Rear foil was with the structural limit, at W/S of 5239 kgf/m2, and all values are shown in Table 6, where the marked columns are interpolated, giving an optimized Rear foil, with: Chord = 2.765 m and αT = 2.928 deg.

Table 6 Rear foil definition (where: Cav. Lim. cavitation limit, Struc. Lim. structural limit)
Full size table

The exact same procedure is done by the program in a plot and a table similar to those of Fig. 19 and Table 6, for the Front Foil, where the ‘t/c vs W/S’ plot produces an interception also with the structural limit of W/S = 4961 kgf/m2, with an optimized Front foil, of: Chord = 1.893 m and αT = 2.993 deg.

The Rear and Front Foil Definition Tables, such as in Table 6 also produce, as mentioned, for each value of W/S, the foil Area, the Chord, Strut Immersion, foil Aspect Ratio, Calkins correction (Eq. 16), Wadlin correction (Eq. 18), final Corrected Aspect Ratio, CLα, required CL, αT, each point in the plots similar to Fig. 19 of t/c values for Cavitation Limit (Cav. Lim.), for Structural Limit (Str. Lim.) and for maximum CL/CD.

6.2.2 Take-off, lift and drag results

Soon after, the Take-off calculations take part. The selected configurations with their chords and angles of attack were used to first compute the Take-off speed. In Fig. 20 the Take-off from an initial angle was computed, being the angle the suggested value of 95% of the Stall Angle (7.6°) of the selected profile and the Take-off process was chosen to start with the Forward foil.

Fig. 20
figure 20

Take-off speed determination

Full size image

The Lift force (Eq. 13) was calculated for the chords and angles of attack obtained, knot by knot (see blue curve), until both lifts added the boat’s weight (red curve). After this point is reached, the angles of attack are reduced at each knot to keep the lift constant. Then, as mentioned, the lift is subtracted from the weight at the lower speeds in order to find the planing hull lift, starting at its displacement and ending out of the water, see green curve. The Take-off speed is the speed where the hull leaves the water or the foil lift equals the weight, in this design example, 25 kt.

The required angle of attack decay of the foils, in order to maintain constant lift equal to the weight is shown in the first graph of Fig. 21, from zero to the 25 kt Take-off speed (green), and onto the design cruise speed of 40 kt (yellow).

Fig. 21
figure 21

Foil resistance—angles of attack and foils lift and drag curves

Full size image

The ‘Lift and Drag vs Speed’ graph is shown in the second plot of Fig. 21. The values of this graph are shown in Table 7, where the Lift and Drag is calculated for each knot for the Rear Foil and the Front Foil, showing values of CLα and CD (CD0 + CDi + CDw), where the Pre-Take-Off condition of fixed angle of attack as well as the Cruising Condition at 40 kt with its angles of attack are shown in Table 8.

Table 7 Foil resistance—foil lift and drag calculations
Full size table
Table 8 Pre take-off and cruising data
Full size table

6.2.3 Resistance, power and operation results

Finally, the Resistance and Power Curves are drawn. Their calculated values are shown in Tables 8 and 9, and the curves displayed in Fig. 22. For each knot the following parameters, with their nomenclature, are calculated (Table 9):

Table 9 Resistance, power and operation calculations
Full size table
Fig. 22
figure 22

Resistance, power and operation—total resistance and effective horsepower comparisons

Full size image

δDisp: displacement condition,

LWL: waterline length,

Q: Taylor Number—V(kt)/√L(ft),

Fn: Froude Number—V/√gL,

Tf, Ta: draft forward and aft,

BWL: waterline breadth,

SW: hull wetted area,

LCB: center of buoyancy,

CM: midship section coefficient,

Cwp: waterplane area coefficient,

At: transom area,

Hull and Foil RT: hull resistance and foil drag,

Pl.Bt RT and EHP: planing boat drag and EHP.

These calculations and curves are, as had already been explained, for the whole hydrofoil boat: hull, foils, and both together. It should be noticed that until 14 kt the method applied is Holtrop [7], since Fn < 0.4 (see the 7th line of Table 9), and for 15 kt on, Savitsky [12], in the planing boat calculations. The Resistance and Power vs Speed curves of the original planing boat, still without foils, is presented for comparison. The typical behavior of hydrofoil boats can be seen in Fig. 22, as the final result of all calculations. In yellow there are independent bare hull results of the planing boat (without foils), from the pre-planing regime (Fn < 0.4) up to the pure planing regime (Fn > 0.89 or Q > 3.0). The blue curve is for the foils drag. The red curve is for the hull resistance alone (coincides with the yellow before it leaves the water), a resistance curve derived, as explained, from a different draft at each knot, due to the foil lift on the hull. The draft decreases until the hull leaves the water—the foil lift at the initial fixed angle of attack equals the boat’s weight and the hull resistance equals zero. And finally there is the complete hydrofoil drag curve in green, with its ‘hump speeds’ up to 25 kt, when the boat takes off. The cruise speed of 40 kt is also shown. All these drags are calculated at the angles of attack found and plotted in Fig. 21. The last graph, shown in the lower part of Fig. 22, is the plot of the Effective Horsepower calculation for both the bare hull planing boat (in red) and the hydrofoil boat (in blue) for comparison, to confirm that hydrofoil boats need less propulsion power than planing boats of the same size, at the same speed.

In Fig. 23 a perspective view of the conceptual design of the hydrofoil patrol boat is presented. This was taken from the General Arrangement produced in the design.

Fig. 23
figure 23

Perspective drawing of the hydrofoil patrol boat conceptual design

Full size image

7 Conclusion

The development of a computer program that dimensions hydrofoil boats has been presented. It is integrated to a full computer naval architectural design system, but can also be used autonomously. It is in a suite that calculates the dynamic equilibrium, resistance and propulsion for these craft and also planing boats, displacement and high-speed displacement boats, complimenting and making use of their calculations and results.

It is the only software known, and therefore innovative, to optimize and determine, from the selection of foils section profiles, configurations and material, the dimensions of the foils, their full integration with the hull used, take-off speed determination, lift and drag vs speed curves, angles of attack at each speed, resistance and power vs speed for propulsion. In other words, it doesn’t only dimension the foils or foils with the hull, in separate runs per configuration, like it could be adapted for CFD software; it does it in a whole boat design integrated manner, finding the optimal foils dimensions and their angles of attack at each speed, finding the take-off speed. All in minutes, instead of days or weeks of work. In fact, since the traditional way of designing hydrofoil boats can get complex, the method of Schachter and Vianna [15] used here is also a breakthrough.

The analytical empirical formulation encoded, well based in the literature, provides a good level of reliability (as the precision check and the design example showed) and added to the previous ones provides a unique, novel, set of tools for the hydrodynamic design of high-speed or high-performance (as it is called today) craft.

The program’s ergonomics, consistent with the other modules for dynamic equilibrium and in the integrated design system, based on the mentioned Solution-Focused Design methodology, provide interfaces with menus easy to use, logical design sequence, with explicit units, placing inputs visually close to outputs, allowing for changes to evaluate alternatives along the design in real time, at any time, in any order, with inconsistency warning, all very quickly, which is rare in existing software in the market, that require either input files or complicated settings in different tabs. It also produces comprehensive graphics with tables showing all calculations of all parameters.

It is believed this software may be useful, mainly as it is being noticed a return of this kind of craft in the market, for recreational and military boats.