Hochschild cohomology: some applications in representation theory of algebras

Abstract

We present a survey of results concerning the use of Hochschild cohomology in representation theory of algebras.

1 Introduction

These notes are an expanded version of a 50-min talk given at the CIMPA-UNESCO-MESR-MINECO-BRAZIL research school on algebraic and geometric aspects of representation theory, in Curitiba-Brazil, in February 2013. During this school there were introductory mini-courses on homological algebra (Mariano Suárez-Álvarez), representation theory of algebras (Patrick Le Meur) and Auslander–Reiten theory (Ibrahim Assem), amongst others. The title of the talk was “Hochschild cohomology: definitions and examples”. It was intended to serve as an introduction to the use of Hochschild cohomology in representation theory of algebras, and its audience was advanced undergraduate or beginning graduate students with little background in either, representation theory of algebras or homological algebra. This fact is reflected in these notes: they give the standard definitions about Hochschild cohomology groups and the Gerstenhaber algebra structure on their sum, in Sect. 2. Section 3 is devoted to a quick survey of the use of Hochschild cohomology in representation theory. In it, we focus on simple connectedness of algebras, we review some results concerning the Gerstenhaber algebra structure on ${\textsf {HH}}^{*}(A)$, and, finally, illustrate the use of ${\textsf {HH}}^{*}(A)$ as derived invariant. Other important applications of Hochschild cohomology, via support varieties, as developed in [24, 46], are not included here, due to space/time restrictions.

2 Hochschild cohomology: general facts

In this section we present general facts and constructions about Hochschild (co)homology groups: the definition of the groups, some classical interpretations, as well as the products defined on the sum of the cohomology groups.

Let $\Bbbk$ be a commutative field. Unless otherwise explicitly specified, the tensor products are taken over the field $\Bbbk$, so $\otimes$ stands for $\underset{\Bbbk }{\otimes }$. In the sequel A, is a finite dimensional associative algebra over $\Bbbk$, with 1. The multiplication is given by a map $\mu :A \otimes A \rightarrow A$, satisfying the usual axioms, and one usually writes $\mu (a\otimes b) = ab$. The opposite algebra $A^{op}$ has the same underlying vector space, but the multiplication is $\mu ^{op} = \mu \circ \tau$, where $\tau :A \otimes A \rightarrow A\otimes A$ is the flip given by $\tau (a\otimes b) = b\otimes a$. The enveloping algebra $A^e$ of A is the tensor product of algebras $A^e = A \otimes A^{op}$.

Unless otherwise stated, we consider left-modules over algebras, that is vector spaces M together with a left A-action $\mu _M: A\otimes M \rightarrow M$ satisfying the usual axioms. Right A-modules can be equivalently considered as left $A^{op}$-modules. The right action will be denoted $\mu _M^{*} : M \otimes A \rightarrow M$. Further, $A-A$-bimodules are equivalently considered as left $A^e$-modules via $(a\otimes b)m = amb$.

2.1 Hochschild cohomology groups

In order to define the Hochschild complex, we need to define the nth tensor power of A wit itself, as follows

$$\begin{aligned} A^{\otimes n} = \left\{ \begin{array}{ll}A &{}\quad \text{ if } \quad n=1\\ A\otimes A^{\otimes n-1} &{}\quad \text{ if } \quad 1<n. \end{array} \right. \end{aligned}$$

The Hochschild complex of A is then defined by:

$$\begin{aligned} C_n(A) = \left\{ \begin{array}{ll} 0 &{}\quad \text{ if } \quad n<-1\\ A^{\otimes (n+2)} &{}\quad \text{ if } \quad -1 \leqslant n \end{array} \right. \end{aligned}$$

and $b_{n-1} :C_{n+1}(A) \rightarrow C_n(A)$ by

Note that each $b_n$ is a map of $A^e$-modules.

Definition 2.1.1

Let A be an algebra, and M a left $A^e$-bimodule (equivalently an $A-A$-bimodule).

• (a) The ith Hochschild cohomology group of A with coefficients in M, denoted by ${\textsf {H}}^{i}(A;M)$ is the ith cohomology group of the complex obtained upon applying ${\textsf {Hom}}_{A^e}(-,\,M)$ to the Hochschild complex. In case $M=A$, we will write ${\textsf {HH}}^{i}(A)$ instead of ${\textsf {H}}^{i}(A;M)$.

• (b) The ith Hochschild homology group of A with coefficients in M, denoted by ${\textsf {H}}_i(A;M)$ is the ith homology group of the complex obtained upon applying $M \underset{A^e}{\otimes } -$ to the Hochschild complex.

In what follows we will be mainly interested in the cohomology groups ${\textsf {HH}}^{i}(A)$.

Proposition 2.1.2

The Hochschild complex is a projective resolution of A as an $A^e$-module.

Proof

(sketch):

• One has $C_n(A) = A\otimes A^{\otimes n} \otimes A \simeq A\otimes A^{op} \otimes A^{\otimes n} \simeq A^e \otimes A^{\otimes n}.$ Since $A^{\otimes n}$ is $\Bbbk$-projective, the $A^e$-module $C_n(A)$ is projective.

• Define $s_n:C_{n-1}(A) \rightarrow C_n(A)$ by $s_n({\mathbf {x}}) = 1\otimes {\mathbf {x}}$. A straightforward computation shows that $((-1)^n s_n)_n$ defines a contracting homotopy, showing that the complex is exact. $\square$

It follows from the preceding proposition that ${\textsf {H}}^{i}(A;M) = {\textsf {Ext}}_{A^e}^{i}(A,\,M)$ and that ${\textsf {H}}_i(A;M) = {\textsf {Tor}}^{A^e}_i (M,A)$. Thus, the Hochschild (co)homology groups can be equivalently computed using other more convenient projective resolutions of $_AA_A$. Note that the Hochschild complex involves vector spaces whose dimensions grow very fast. Thus for concrete computations one often uses smaller resolutions (see [37, §4]).

In order to give interpretations of the lower degrees cohomology groups, the following will be useful.

Proposition 2.1.3

The Hochschild cohomology groups ${\textsf {H}}^{i}(A;M)$ are the cohomology groups of the complex

with $d^0(m)=[m,-]$, that is $\delta ^0(m)(a) = am-ma$, and, for $f\in \mathsf{Hom}_{\Bbbk }(A^{\otimes n},\,M)$,

Argument Indeed, a direct verification shows that the map $\varphi : {\textsf {Hom}}_{A^e}(A^{\otimes n+2},\,M) \rightarrow {\textsf {Hom}}_{\Bbbk }(A^{\otimes n},\,M)$ given by $\varphi (f)({\mathbf {x}}) = 1\otimes {\mathbf {x}} \otimes 1$ is a morphism of complexes, which moreover is bijective. Further the differential d is induced by b, by using the map $\varphi$. $\square$

With these results in mind we can give the standard interpretations of the cohomology groups corresponding to the lower degrees.

• (a) We have that ${\textsf {H}}^{0}(A;M) = \left\{ m\in M|\ [m,-] = 0\right\} = \left\{ m\in M|\ am =ma,\, \forall a \in A\right\}$ is the set of the elements of M commuting with all the elements in A. In particular, ${\textsf {HH}}^{0}(A)$ is the centre of A.

• (b) We have that ${\textsf {H}}^{1}(A;M) = \displaystyle \frac{{\textsf {Ker}}\ d^1}{{\textsf {Im}}\ d^0}$. But $f\in {\textsf {Ker}}\ d^1$ if and only if $d^1f(a_1\otimes a_2)=0$ for every $a_1,a_2$ in A, that is

  $$\begin{aligned} 0 = a_1f(a_2) - f(a_1 a_2) + f(a_1)a_2 \end{aligned}$$

  or equivalently

  $$\begin{aligned} f(a_1a_2) = a_1f(a_2) + f(a_1)a_2. \end{aligned}$$

  Such a map is said to be a derivation of A in M. Thus, ${\textsf {Ker}}\ d^1$ is the set of all such derivations.

  On the other hand, $f\in {\textsf {Im}}\ d^0$ if and only if there exists $m\in M$ such that $f(a) = am-ma$ for every $a\in A$. Such derivations are called inner derivations of A in M. Hence

  

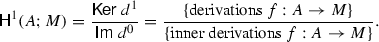
Remark 2.1.4

The interpretations given above are very classical. In a similar vein, one can establish a bijective correspondence between elements in ${\textsf {H}}^{2}(A;M)$ and split extensions of A by M (see [37]). In another direction, the second and the third Hochschild cohomology groups of an algebra A are related to the rigidity properties of A, see for instance [26].

2.2 Products in cohomology

Besides the fact that the groups ${\textsf {HH}}^{i}(A)$ are interesting in themselves, their sum ${\textsf {HH}}^{*}(A) = \bigoplus \limits _{i\geqslant 0} {\textsf {HH}}^{i}(A)$ has a rich additional structure defined by Gerstenhaber [25].

The Yoneda splicing of extensions makes of ${\textsf {HH}}^{*}(A)$ a graded commutative algebra (see [11, p.40]). This product coincides with the cup-product defined at the cochain level (see below). In addition, there is a bracket on ${\textsf {HH}}^{*}(A)$, that upon a 1-degree shift, makes it into a graded Lie algebra. We now briefly exhibit these constructions.

Given two cochains $f\in {\textsf {Hom}}_{\Bbbk }(A^{\otimes n},\,A)$ and $g\in {\textsf {Hom}}_{\Bbbk }(A^{\otimes m},\,A)$, their cup-product is the cochain $f\cup g \in {\textsf {Hom}}_{\Bbbk }(A^{\otimes n+m},\,A)$ defined by

$$\begin{aligned} f\cup g =\mu (f\otimes g). \end{aligned}$$

Let $d^\bullet$, as in Proposition 2.1.3. One readily verifies that

$$\begin{aligned} f \cup g = d f \cup g + (-1)^m f \cup d g \end{aligned}$$

and that in fact the product defined at the cochain level induces a product, still denoted $\cup$, in cohomology:

$$\begin{aligned} \cup :{\textsf {HH}}^{n}(A) \otimes {\textsf {HH}}^{m}(A) \rightarrow {\textsf {HH}}^{n+m}(A). \end{aligned}$$

This product is graded commutative: if we let ${\mathbf {f}}$ and ${\mathbf {g}}$ be the cohomology classes of the cochains f and g, then ${\mathbf {f}} \cup {\mathbf {g}} = (-1)^{nm}{\mathbf {g}}\cup {\mathbf {f}}$. Further, $\cup$ coincides with the Yoneda splicing of extensions.

Let us now consider the bracket. As before, let f and g be cochains of degrees n and m. Define the cochain $f \circ g\in {\textsf {Hom}}_{\Bbbk }(A^{\otimes n+m-1},\,A)$ by

Finally, define

$$\begin{aligned}{}[f ,g ] = f\circ g - (-1)^{(n-1)(m-1)} g\circ f. \end{aligned}$$

Again, a direct computation shows that

$$\begin{aligned} d[f ,g] = [f,dg] + (-1)^{m-1}[df,g]. \end{aligned}$$

This ensures that the bracket $[-,-]$ induces an operation at the cohomology level:

$$\begin{aligned}{}[-,-] :{\textsf {HH}}^{n}(A) \otimes {\textsf {HH}}^{m}(A) \rightarrow {\textsf {HH}}^{n+m-1}(A). \end{aligned}$$

Endowed with this bracket, the shifted sum ${\textsf {HH}}^{*+1}(A)$ becomes a graded Lie algebra.

Remark 2.2.1

• (a) The bracket of two elements of degree 1 is their commutator. Consequently, ${\textsf {HH}}^{1}(A)$ is a Lie algebra on its own.

• (b) Each ${\textsf {HH}}^{n}(A)$ is a Lie module over ${\textsf {HH}}^{1}(A)$.

Further, the the bracket and the cup-product are compatible: if ${\mathbf {f}},{\mathbf {g}}$ and ${\mathbf {h}}$ denote elements of degrees n, m and p, then

$$\begin{aligned}{}[{\mathbf {f}}\cup {\mathbf {g}},{\mathbf {h}}] = [{\mathbf {f}},{\mathbf {h}}]\cup {\mathbf {g}} + (-1)^{n(p-1)}{\mathbf {f}}\cup [{\mathbf {g}},{\mathbf {h}}]. \end{aligned}$$

Thus, ${\textsf {HH}}^{*}(A)$ is said to be a Gerstenhaber algebra.

3 Some applications in representation theory

In this section we turn our attention to some results illustrating the use of Hochschild cohomology in representation theory of algebras, as well as some more precise knowledge about the structure of ${\textsf {HH}}^{*}(A)$ for particular classes of algebras. For the remaining part of the paper, we assume that the field $\Bbbk$ is algebraically closed and that our algebras are Morita-reduced (or basic).

We start considering simple connectedness of algebras and some geometric properties of the Auslander–Reiten quiver $\Gamma (A-{\textsf {mod}})$. We then consider the Gerstenhaber algebra structure on ${\textsf {HH}}^{*}(A)$ and give a brief account it. Finally we turn our attention to the fact that this structure is is a derived invariant, and give an application.

3.1 Simple connectedness

Basic algebras over algebraically closed fields can be written as bound quiver algebras $A=\Bbbk Q/I$. The quiver Q is uniquely determined by A, whereas I is an ideal of the path algebra $\Bbbk Q$ which depends on the choice of bases of some vector spaces (see [6, Chap.II]). In case Q has no oriented cycles it is said to be acyclic, and the algebra A is said to be triangular. To the pair (Q, I) is associated its fundamental group $\pi _1(Q,I)$, using the so-called minimal relations and the associated homotopy relation on the set of closed walks on Q, as defined in [35]. This fundamental group is not an invariant of the algebra, one may have $\Bbbk Q / I_1 \simeq \Bbbk Q / I_2$ but $\pi _1(Q,I_1) \not \simeq \pi _1(Q,I_2)$ (see [9, 18]). Following [7], an algebra A is said to be simply connected if it is triangular and whenever $A \simeq \Bbbk Q/I$, one has that $\pi _1(Q,I)$ is trivial. For algebras of finite representation type this notion coincides with that of [13], namely that the Auslander–Reiten quiver $\Gamma (A-{\textsf {mod}})$ is a connected 2-dimensional simplicial complex. Note however that another definition of simple connectedness, which does not assume that Q has no oriented cycles is used in [2, 33].

In [4, 23], it has been established that if $A \simeq \Bbbk Q/I$, then there exists a monomorphism $\sigma :{\textsf {Hom}}_{}(\pi _1(Q,I),\,\Bbbk ^+) \rightarrow {\textsf {HH}}^{1}(A)$. In [4, 3.2] it was shown that $\sigma$ is a monomorphism whenever Q has no oriented cycles, and in [23] this hypothesis was proven to be unnecessary, and, further, additional conditions under which $\sigma$ is an isomorphism have been established. Among others, $\sigma$ is an isomorphism in case A in an algebra of finite representation type having no oriented cycles in its quiver ([23, Corollary3,p438]).

The map $\sigma$ can be interpreted as a cohomological version of the Hurewicz map from algebraic topology (see [41, 4.27], for instance).

The relation between Hochschild cohomology and simple connected algebras was already noticed in [45]. In that paper (a slightly less general version of) the following problem is stated:

Problem

For which classes of algebras it is true that simple connectedness is equivalent to the vanishing of the first Hochschild cohomology group of the algebra (with coefficients in itself)?

This problem has motivated several investigations. We summarize some results in the following theorem:

Theorem 3.1.1

Let A be an algebra, then A is simply connected if and only if ${\mathsf{HH}}^{1}(A) = 0$ whenever A is:

• (a) Of finite-representation type (Buchweitz–Liu [16]),

• (b) A shod algebra (Coelho–Lanzilotta–Savioli [22]),

• (c) A weakly shod algebra (Assem–Lanzilotta [5] for the tame case, and Le Meur [32] for the general case),

• (d) A piecewise hereditary algebra (Le Meur [33]),

• (e) A standard Laura algebra (Assem–Bustamante–Le Meur [2]),

• (f) A special biserial algebra (Assem–Bustamante–Le Meur [3]).

Note that the triangularity assumption in the definition of simple connectedness is needed. Indeed, Buchweitz and Liu noticed that without it the vanishing of $\pi _1(Q,I)$ and that of ${\textsf {HH}}^{1}(A)$ are not equivalent, even for algebras of finite-representation type. Up to this moment we have only considered simple connectedness of an algebra and its connections to the first Hochschild cohomology group. Even if in some cases (for instance if A of finite representation type) this group can provide some information about the geometry of $\Gamma (A-{\textsf {mod}})$, it is not enough to give a complete description. For instance, oriented cycles are not detected by ${\textsf {HH}}^{1}(A)$, but by the higher cohomology groups, as the following result, due to Happel, establishes ([29, 5.4]). Recall that an algebra A is said to be representation-directed if no indecomposable $A-$module $M_0$ belongs to an oriented cycle $M_0 \rightarrow M_1 \rightarrow \cdots \rightarrow M_t \rightarrow M_0$ of non-zero non isomorphisms.

Theorem 3.1.2

Let A be a representation directed algebra. Then $\mathsf{HH}^{i}(A) = 0$ for every $i\geqslant 2$. $\square$

Example 3.1.3

Consider the quiver Q

Let $I_1 = \langle \alpha \beta ,\gamma \delta \rangle ,\, I_2 = \langle \alpha \beta - \gamma \delta \rangle ,\ I_3=\langle \alpha \beta \rangle ,$ and set $A_i = \Bbbk Q/I_i$ for $i\in \{1,2,3\}$. The algebras $A_i$ are all of finite representation type. Their Auslander–Reiten quivers are depicted in Fig. 1.

Fig. 1

The Auslander–Reiten quivers. As usual, dotted lines denote the meshes. a $\Gamma (A_1-{\textsf {mod}})$ is not simply connected, there is a “hole” in it. b $\Gamma (A_2-{\textsf {mod}})$ is simply connected, as is the algebra $A_2$. c In $\Gamma (A_3)-{\textsf {mod}}$ the two copies of the simple module $S_2$ are to be identified, giving rise to an oriented cycle

One has that $\pi _1(Q,I_2)$ is trivial, as is ${\textsf {HH}}^{1}(A_2)$. In fact one can easily compute, using Happel’s long exact sequence [29, 5.3] for instance, that ${\textsf {HH}}^{i}(A_3) = 0$ for every $i\geqslant 1$. Note that $\Gamma (A_2-{\textsf {mod}})$ is simply connected.

On the other hand, $\pi _1(Q,I_1) \simeq \pi _1(Q,I_3) \simeq \mathbb {Z}$ and ${\textsf {HH}}^{1}(A_1) \simeq {\textsf {HH}}^{1}(A_3) \simeq \Bbbk$. The Auslander–Reiten quivers $\Gamma (A_1-{\textsf {mod}})$ and $\Gamma (A_3-{\textsf {mod}})$ are not simply connected, they both have an infinite cyclic fundamental group. However in $\Gamma (A_3-{\textsf {mod}})$ there is an oriented cycle, whereas $A_1$ is representation-directed. Again, using Happel’s long exact sequence one can compute

$$\begin{aligned} {\textsf {HH}}^{i}(A_1) = \left\{ \begin{array}{ll}\Bbbk &{}\quad \text{ if }\;\; i\leqslant 1 \\ 0 &{}\quad \text{ otherwise, } \end{array} \right. \quad \text{ and }\quad {\textsf {HH}}^{i}(A_3) = \left\{ \begin{array}{ll}\Bbbk &{}\quad \text{ if }\;\; i\leqslant 2 \\ 0 &{}\quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

The non zero element in ${\textsf {HH}}^{2}(A_3)$ is the class of the map $f:A_3\otimes A_3 \rightarrow A_3$ given by $f(\alpha \otimes \beta ) = \gamma \delta$ (we identify an arrow with its class modulo $I_3$).

3.2 Multiplicative structures

In general there are few classes of algebras for which one has an explicit description of the structure of ${\textsf {HH}}^{*}(A)$. As Green and Solberg point out in [27, p.2], “for a finite dimensional algebra A the ring structure of ${\textsf {HH}}^{*}(A)$ has often been observed to be trivial. One knows that for many self-injective algebras there are non-zero products in ${\textsf {HH}}^{*}(A)$.” For instance, by a result of Cibils and Solotar [21] one knows that in case G is a finite abelian group (whose order is invertible in $\Bbbk$) then ${\textsf {HH}}^{*}(\Bbbk G) \simeq \Bbbk G \otimes {\textsf {H}}^{*}(G,\Bbbk )$, as rings (see also [44]).

More recently, Snashall and Taillefer described in [47] the ring structure of ${\textsf {HH}}^{*}(A)$ for some self-injective special biserial algebras, and Román and Redondo considered string algebras of finite global dimension in [38].

The Lie structure on ${\textsf {HH}}^{*}(A)$ has been studied in even fewer cases. In [48], Strametz studied the Lie algebra structure of ${\textsf {HH}}^{1}(A)$ for monomial algebras. Also, Sánchez-Flores in [42] has considered algebras whose radical is 2-niltpotent, and, in [43], the group algebra of a cyclic group.

Recall that an algebra A is said to be a string algebra if there exists a bound quiver (Q, I) such that

S1:

The ideal I is generated by a set of paths of length at least two,

S2:

Each vertex of Q is the source and the target of at most two arrows, and

S3:

For every arrow $\sigma$ in Q, there exists at most one arrow $\beta$ and one arrow $\gamma$ such that $\alpha \beta \in I$ and $\gamma \alpha \in I$.

Further a string algebra $A \simeq \Bbbk Q / I$ is said to be gentle if in addition

G1:

The ideal I is generated by a set of paths of length two and

G2:

For every arrow $\sigma$ in Q, there exists at most one arrow $\beta$ and one arrow $\gamma$ such that $\alpha \beta \not \in I$ and $\gamma \alpha \not \in I$.

String algebras are of tame representation type. They have been extensively studied and are well-understood from the representation theoretic point of view. The subclass of gentle algebras includes, for instance, all the iterated tilted, cluster-tilted and m-cluster tilted algebras of types $\mathbb {A}$ and $\tilde{\mathbb {A}}$.

We can now state:

Theorem 3.2.1

([17, 38]) Let $A\simeq \Bbbk Q /I$ be a triangular string algebra. Then

• (a) The cup product of elements of positive degree in $\mathsf{HH}^{*}(A)$ is trivial, and

• (b) If A is gentle, then the bracket of elements of degrees strictly greater than 1 is trivial.

$\square$

Statement (b), as well as a weaker version of statement (a) was proved in [17]. Statement (a) has been proved by Redondo and Román [38] in the general case. Also, in a more recent paper [39], they described the Gerstenhaber algebra associated to a quadratic string algebra, giving conditions on (Q, I) leading to non-trivial structures in ${\textsf {HH}}^{*}(A)$.

and with more restrictive hypothesis in [17] from where we borrow statement (b), and the following example.

Example 3.2.2

Let $A=\Bbbk Q / I$ where A is the quiver

and I is the ideal generated by all the paths of length 2. This is a string algebra which is not gentle, and one can compute

$$\begin{aligned} {\textsf {HH}}^{i}(A) = \left\{ \begin{array}{ll} 1 &{}\quad \text{ if } \;\; i\in \{0,2,3,4\},\\ 2 &{}\quad \text{ if } \;\; i=1\\ 0 &{}\quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

The generators of ${\textsf {HH}}^{i}(A)$, for $i\leqslant 2$ are the (classes of) the maps defined by $f_2(\alpha _3 \otimes \alpha _2) = \beta ,\ f_3(\alpha _4\otimes \beta \otimes \alpha _1) = \gamma$ and $f_4(\alpha _4\otimes \alpha _3 \otimes \alpha _2\otimes \alpha _1) = \gamma$. In this example one can compute that $[{\textsf {HH}}^{n}(A);{\textsf {HH}}^{m}(A)] = {\textsf {HH}}^{n+m-1}(A)$.

In light of Green and Solberg’s remark quoted previously, statement (a) in the last theorem, as well as results from [20, 34] and other empirical observations, one can ask:

Problem

Given a monomial triangular algebra $A=\Bbbk Q/I$, is it true that the ring structure of ${\textsf {HH}}^{*}(A)$ is trivial?

3.3 Derived invariance

Recall that two algebras $A_1$ and $A_2$ are said to be derived equivalent if the derived categories of their modules categories $\mathcal {D}(A_1-{\textsf {mod}})$ and $\mathcal {D}(A_2-{\textsf {mod}})$ are equivalent as triangulated categories. When studying module categories, one is often interested in them up to derived equivalence. It is thus interesting to have tools allowing to decide whether or not two algebras are derived equivalent.

There are several known derived invariants, as, for instance, the determinant of the Cartan matrix. Interpreting tilting as an equivalence of derived categories, Happel showed in [28] that Hochschild cohomology is also a derived invariant. By a result of Rickard in [40] this is indeed the case for all derived equivalences (not only for those coming from tiltings). Since the cup-product of the cohomology ring ${\textsf {HH}}^{*}(A)$ can be interpreted as the composition of maps in $\mathcal {D}(A^e-{\textsf {mod}})$ (see [30, §2]), the multiplicative structure is preserved. Further, by a result of Keller [30], the bracket is also preserved under derived equivalence, thus the whole Gerstenhaber algebra structure on ${\textsf {HH}}^{*}(A)$ is a derived invariant.

Let $H\simeq \Bbbk Q$ be a triangular hereditary algebra. The derived category $\mathcal {D}(H-{\textsf {mod}})$ is triangulated, and we denote by [1] its translation functor. For an integer n, we denote by [n] the composition of [1] with itself n times, thus $[1]^n = [n]$. In addition, $\mathcal {D}(H-{\textsf {mod}})$ has Auslander–Reiten triangles, and, as usual, the Auslander–Reiten translation is denoted by $\tau$.

Let m be a natural number. The m-cluster category of H is the quotient category $\mathcal {C}_m(H):=\mathcal {D}^b(H)/ \tau ^{-1} [m]$ which carries a natural triangulated structure, see [31]. The endomorphism algebras of the so-called m-cluster tilting objects are called m-cluster tilted algebras (see [49]) in $\mathcal {C}_m(H)$ are called m-cluster tilted algebras of type Q. In case $m=1$, this definition specializes to that of a cluster tilted algebra, a class intensively studied since its definition in [14].

Buan and Vatne gave in [15] a criterion to decide whether two cluster tilted algebras of type $\mathbb {A}$ are themselves derived equivalent or not. This has been done using the Cartan matrix as derived invariant. Later, Bastian [10], gave an analogous classification for the $\tilde{\mathbb {A}}$ case (these two classes of algebras are known to be gentle, after [1]). She used another finer derived invariant for gentle algebras, the function $\phi$ introduced by Avella-Alaminos and Geiss [8]. Without going into the details, we shall only say that given a gentle bound quiver (Q, I), there is associated a map $\phi : \mathbb {N} \times \mathbb {N} \rightarrow \mathbb {N}$ constructed essentially by counting some particular sequences of paths. For instance, $\phi (0,t)$ counts the number of cycles of length t such that the composition of any two consecutive arrows lies in I.

In [12] a more general question has been considered, namely the characterization of the algebras that are derived equivalent to cluster tilted algebras of type $\mathbb {A}$ or $\tilde{\mathbb {A}}$. Again, in that paper the map $\phi$ is of central importance, and the characterizations therein are given in terms of the form of this map. In another direction, results analogous to those of [15] have been established for m-cluster tilted algebras of type $\mathbb {A}$ by Murphy [36]: he described these algebras by quivers and relations, and gave a criterion permitting to decide whether two m-cluster tilted algebras of type $\mathbb {A}$ are derived equivalent or not. Again, he used the Cartan matrix as in [15]. In [19], the author and Gubitosi classified the algebras derived equivalent to m-cluster tilted algebras of type $\mathbb {A}$, but using the Hochschild cohomology ring as a derived invariant, we now take this direction.

Recall that given a connected quiver Q, its Euler characteristic, $\chi (Q)=|Q_1|-|Q_0|+1$, is the rank of its first homology group, Q being viewed as a graph. In [19] it is shown that a connected algebra $A=\Bbbk Q/I$ is derived equivalent to a connected component of an m-cluster tilted algebra of type $\mathbb {A}$ if and only if (Q, I) is a gentle bound quiver having $\chi (Q)$ oriented cycles of length $m+2$, each of which has full relations (meaning that the composition of two consecutive arrows of the cycle belongs to the ideal), such algebras are called m-branched. Specializing to the case $m=1$, the results of [12, 15] are recovered. Although it is not known if the function $\phi$ is a complete invariant in general, in [19] (see also [12]) it is shown that this is indeed the case for algebras derived equivalent to m-cluster tilted algebras of type $\mathbb {A}$. Further, the invariant pair (r, s) of an m-branched algebra $A=\Bbbk Q / I$ is defined in [19] as follows: The integer s is the rank of the Grothendieck group $K_0(A)$, while r is the Euler characteristic of Q, which in addition parametrizes the structure of the Hochschild cohomology ring ${\textsf {HH}}^{*}(A)$. In case A is connected, it is also the rank of the fundamental group $\pi _1(Q,I)$ of the bound quiver (Q, I), which is free in this context. In [19] the following theorem is proved.

Theorem 3.3.1

Let $A=\Bbbk Q / I$ and $A'=\Bbbk Q'/I'$ be connected m-branched algebras. Then the following conditions are equivalent.

• (a) A and $A'$ are derived equivalent,

• (b) A and $A'$ are tilting-cotilting equivalent,

• (c) A and $A'$ have the same invariant pair,

• (d) $\mathsf{HH}^{*}(A) \simeq \mathsf{HH}^{*}(A')$ and $K_0(A) \simeq K_0(A')$,

• (e) $\phi _A = \phi _{A'}$.

• (f) $\pi _1(Q,I) \simeq \pi _1(Q',I')$ and $|Q_0| = |Q'_0|$.

$\square$

We end with an example

Example 3.3.2

Let (Q, I) and $(Q',I')$ be the bound quivers

The algebra $A= \Bbbk Q/I$ is derived equivalent to a cluster tilted algebra of type $\mathbb {A}_6$, though it is not itself a cluster tilted algebra. The algebra $A'=\Bbbk Q/I'$ is a 3-cluster tilted algebra of type $\mathbb {A}_6$. In both cases the determinant of the Cartan matrix is 2. In contrast, in case the characteristic of $\Bbbk$ is not 2, then ${\textsf {HH}}^{6}(A) \simeq \Bbbk$, whereas ${\textsf {HH}}^{6}(A')=0$; and ${\textsf {HH}}^{10}(A)=0$ whereas ${\textsf {HH}}^{10}(A')\simeq \Bbbk$.