New Bounds on the Double Total Domination Number of Graphs

Abstract

Let G be a graph of minimum degree at least two. A set $D\subseteq V(G)$ is said to be a double total dominating set of G if $|N(v)\cap D|\ge 2$ for every vertex $v\in V(G)$. The minimum cardinality among all double total dominating sets of G is the double total domination number of G. In this article, we continue with the study of this parameter. In particular, we provide new bounds on the double total domination number in terms of other domination parameters. Some of our results are tight bounds that improve some well-known results.

1 Introduction

Throughout this article, we consider $G=(V(G),E(G))$ as a simple graph of minimum degree at least two. A set $D\subseteq V(G)$ is said to be a dominating set if every vertex in $V(G){\setminus } D$ is adjacent to at least one vertex in D. The domination number of G, denoted by $\gamma (G)$, is the minimum cardinality among all dominating sets of G. Among the most studied domination variants can be found those where the dominating sets are defined by an added condition that is imposed on every vertex of G. In this article, we continue with the study of one of these variants, namely double total domination number.

Given a graph G, a set $D\subseteq V(G)$ is said to be a double total dominating set if $|N(v)\cap D|\ge 2$ for every $v\in V(G)$. The double total domination number of G, denoted by $\gamma _{\times 2,t}(G)$, is the minimum cardinality among all double total dominating sets of G. We define a $\gamma _{\times 2,t}(G)$-set as a double total dominating set of cardinality $\gamma _{\times 2,t}(G)$. We remark that this parameter is also called in the literature as 2-tuple total domination number or total 2-domination number.

The double total domination number has been well studied by the research community. For instance, in [1, 4, 17, 19, 21, 22], some combinatorial results were presented, and in [2, 3, 18, 23], some studies on certain product graphs were carried out. Our goal is to making some new remarkable contributions to this domination parameter. In particular, we provide new bounds on the double total domination number of a graph of minimum degree at least two. Such bounds can also be seen as relationships between the double total domination number and several classical domination parameters like double domination number, 2-domination number, independence number, among others. Some of our results are tight bounds that improve some well-known results.

1.1 Additional Definitions and Previous Results

Given a graph G, we denote by ${\text {n}}(G)=|V(G)|$ its order, by ${\text {m}}(G)=|E(G)|$ its size, and by $\varDelta (G)$ and $\delta (G)$ its maximum and minimum degrees, respectively. Given a vertex $v\in V(G)$, $N(v)=\{u\in V(G): uv\in E(G)\}$ and $N[v]=N(v)\cup \{v\}$. As usual, given a set $D\subseteq V(G)$, $N(D)= \cup _{v\in D} N(v)$ and $N[D]= N(D)\cup D$. The distance d(u, v) between two vertices u and v, in a connected graph G, equals the minimum length of a (u, v)-path in G. The diameter of G, denoted by ${\text {diam}}(G)$, is the maximum distance among all pairs of vertices of G. We say that a graph G is H-free if G does not contain the graph H as an induced subgraph. Given two disjoint graphs $G_1$ and $G_2$, the join graph $G_1+G_2$ is the graph obtained from $G_1$ and $G_2$, with vertex set $V(G_1+G_2)=V(G_1)\cup V(G_2)$ and edge set $E(G_1+G_2)=E(G_1)\cup E(G_2)\cup \{uv: u\in V(G_1), v\in V(G_2)\}$. We will use the notation $P_n$, $C_n$, $K_n$, and $N_n$ for path graphs, cycle graphs, complete graphs, and empty graphs of order n, respectively. We end this subsection with some definitions and terminology on domination invariants which will be further used.

A set $I\subseteq V(G)$ is said to be an independent set of G if $N(v)\cap I=\emptyset$ for every $v\in I$. The maximum cardinality among all independent sets is the independence number of G and is denoted by $\alpha (G)$. We define an $\alpha (G)$-set as an independent set of cardinality $\alpha (G)$. Moreover, a set $W\subseteq V(G)$ is said to be a vertex cover of G if $V(G){\setminus } W$ is an independent set of G. The minimum cardinality among all vertex covers of G is the vertex cover number of G and is denoted by $\beta (G)$. We define a $\beta (G)$-set as a vertex cover of cardinality $\beta (G)$. In 1959, Gallai [10] proved that $\alpha (G)+\beta (G) = {\text {n}}(G)$ for every nontrivial graph G. We remark that the previous relation is a well-known result in graph theory.

Two well-established domination parameters are the total domination number and the 2-domination number. A set $D\subseteq V(G)$ is said to be a total dominating set of G if $|N(v)\cap D|\ge 1$ for every vertex $v\in V(G)$. The total domination number of G, denoted by $\gamma _t(G)$, is the minimum cardinality among all total dominating sets of G. We define a $\gamma _{t}(G)$-set as a total dominating set of cardinality $\gamma _{t}(G)$ (see [16, 20]). Moreover, a set $S\subseteq V(G)$ is said to be a 2-dominating set of G if $|N(v)\cap S|\ge 2$ for every vertex $v\in V(G){\setminus } S$. The 2-domination number of G, denoted by $\gamma _2(G)$, is the minimum cardinality among all 2-dominating sets of G. We define a $\gamma _{2}(G)$-set as a 2-dominating set of cardinality $\gamma _{2}(G)$.

Combinations between domination parameters are probably the most used features in different versions of domination invariants. For instance, the double domination is just a combination of the total domination and the 2-domination. A set $D\subseteq V(G)$ is said to be a double dominating set of a graph G with no isolated vertex if $|N[v]\cap D|\ge 2$ for every vertex $v\in V(G)$. The double domination number of G, denoted by $\gamma _{\times 2}(G)$, is the minimum cardinality among all double dominating sets of G. We define a $\gamma _{\times 2}(G)$-set as a double dominating set of cardinality $\gamma _{\times 2}(G)$. For more information about 2-domination and double domination in graphs, we suggest the chapter [11] due to Hansberg and Volkmann and the recent works [7, 9]. A double dominating set $D\subseteq V(G)$ is a total outer-independent dominating set of G if $V(G){\setminus } D$ is an independent set. The total outer-independent domination number of G, denoted by $\gamma _{t,oi}(G)$, is the minimum cardinality among all total outer-independent dominating sets of G. We define a $\gamma _{t,oi}(G)$-set as a total outer-independent dominating set of cardinality $\gamma _{t,oi}(G)$ (see [5, 6, 8, 24]).

By definition, all the previous parameters are, in one way or another, related to each other. The following result shows the most natural relationships that exist between them.

Proposition 1

The following inequality chains hold for any graph G with $\delta (G)\ge 2$.

• (i) $\max \{\gamma _2(G),\gamma _t(G)\}\le \gamma _{\times 2}(G)\le \min \{\gamma _{\times 2,t}(G),\gamma _{t,oi}(G)\}.$

• (ii) $\gamma _2(G)\le \beta (G)={\text {n}}(G)-\alpha (G)\le \gamma _{t,oi}(G).$

Fig. 1

Sets of black-coloured vertices form a $\gamma _{\times 2,t}(G_1)$-set and a $\gamma _{\times 2,t}(G_2)$-set, respectively

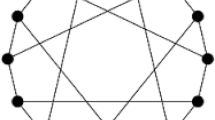
For instance, for the graphs shown in Fig. 1 we have the following.

• (a) $\gamma _t(G_1)=\alpha (G_1)=4<\gamma _2(G_1)=\gamma _{\times 2}(G_1)=\gamma _{\times 2,t}(G_1)=6<\gamma _{t,oi}(G_1)=8.$

• (b) $\gamma _t(G_2)=\gamma _2(G_2)=4<\alpha (G_2)=\gamma _{\times 2}(G_2)=\gamma _{t,oi}(G_2)=6<\gamma _{\times 2,t}(G_2)=8.$

We suggest the books [12, 15] in case the reader is not familiar with another some basic concepts, notation and terminology of graphs.

2 Bounds and Relationships with Other Parameters

The following upper bounds for the double total domination number were established by Bermudo et al. in [1] and independently by Bonomo et al. in [4].

Theorem 1

( [1, 4]) The following statements hold for any graph G with $\delta (G)\ge 2$.

• (i) $\gamma _{\times 2,t}(G)\le 2\gamma _{\times 2}(G)-1.$

• (ii) $\gamma _{\times 2,t}(G)\le 3\gamma _2(G)-2.$

Since $\gamma _{2}(G)\le \gamma _{\times 2}(G)$, the next theorem improves the upper bound given in Theorem 1-(i) whenever $\gamma _2(G)\le \gamma _{\times 2}(G)-2$.

Theorem 2

For any graph G with $\delta (G)\ge 2$,

$$\begin{aligned} \gamma _{\times 2,t}(G)\le \gamma _{\times 2}(G)+\gamma _2(G). \end{aligned}$$

Proof

Let D be a $\gamma _{\times 2}(G)$-set and X a $\gamma _{2}(G)$-set. We next define a set $S\subseteq V(G)$ of minimum cardinality among the sets satisfying the following properties.

• (i) $D\cup X\subseteq S$.

• (ii) If $x\in D\cap X$, then either $N(x){\setminus } (D\cup X)=\emptyset$ or $S\cap N(x){\setminus } (D\cup X)\ne \emptyset$.

From (i), we deduce that S is a double dominating set of G and by the minimality of |S| we have that $|S|\le |D\cup X|+|D\cap X|=|D|+|X|$. To conclude that S is a double total dominating set of G, we only need to prove that $|N(x)\cap S|\ge 2$ for every $x\in S$. Let $v\in S$. First, we notice that if $v\in S{\setminus } (D\cap X)$, then $|N(v)\cap S|\ge 2$ because D and X are 2-dominating sets of G. Now, suppose that $v\in D\cap X$. Since $\delta (G)\ge 2$ and $|N(v)\cap S|\ge |N(v)\cap D|\ge 1$, by (ii) we deduce that $|N(v)\cap S|\ge 2$. Hence, S is a double total dominating set of G, as desired. Therefore, $\gamma _{\times 2,t}(G)\le |S|\le |D|+|X|= \gamma _{\times 2}(G)+\gamma _{2}(G)$, which completes the proof. $\square$

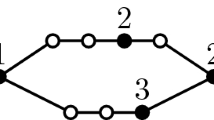
To show clear examples where the difference between the bounds given by Theorems 2 and 1 can be as large as desired, we can take the graph $H_r$ defined as follows.

Fig. 2

Sets of black-coloured vertices form a $\gamma _{\times 2,t}(H_3)$-set

For any integer $r\ge 2$, the graph $H_r$ is defined as the graph obtained from the path $P_r$ and the graph H given in Fig. 2 by taking one copy of $P_r$ and r copies of H and identifying the $i^{th}$ vertex of $P_r$ with the vertex $v\in V(H)$ in the $i^{th}$ copy of H for every $i\in \{1, 2,\ldots , r\}$. Figure 2 shows the graph $H_3$. Notice that for the graph $H_r$, it follows that $|V(H_r)|=6r$, $\gamma _{\times 2}(H_r)=3r$ and $\gamma _{2}(H_r)=2r$. Therefore, if we take r large enough, then the difference between the bounds given by Theorems 2 and 1 can be as large as desired.

We next proceed to show that the bound given in Theorem 1-(ii) has room for improvement. To this purpose, we need to state the following result due to Cabrera Martínez and Rodríguez-Velázquez [9].

Theorem 3

([9]) For any graph G with no isolated vertex,

$$\begin{aligned} \gamma _{\times 2}(G)\le \gamma (G)+\min \{\alpha (G),\gamma _2(G)\}. \end{aligned}$$

By combining Theorems 2 and 3 , we obtain the next result, which clearly improves the bound $\gamma _{\times 2,t}(G)\le 3\gamma _{2}(G)-2$ whenever $\gamma (G)\le \gamma _{2}(G)-3$.

Theorem 4

For any graph G with $\delta (G)\ge 2$,

$$\begin{aligned} \gamma _{\times 2,t}(G)\le \gamma (G)+\min \{\alpha (G)+\gamma _2(G),2\gamma _2(G)\}\le \gamma (G)+2\gamma _2(G). \end{aligned}$$

From Theorem 2 and Proposition 1, we deduce the bound $\gamma _{\times 2,t}(G)\le \gamma _{\times 2}(G)+{\text {n}}(G)-\alpha (G)$. We next show that this previous inequality can be improved for two specific families of graphs. Emphasize that $K_{1,3}+e$ is the graph obtained by adding an edge to the complete bipartite graph $K_{1,3}$.

Theorem 5

The following statements hold for any graph G.

• (i) If G is a $K_{1,3}$-free graph with $\delta (G)\ge 4$, then

  $$\begin{aligned} \gamma _{\times 2,t}(G)\le {\text {n}}(G)-\alpha (G). \end{aligned}$$

• (ii) If G is a $\{K_{1,3},K_{1,3}+e\}$-free graph with $\delta (G)=3$, then

  $$\begin{aligned} \gamma _{\times 2,t}(G)\le \gamma (G)+{\text {n}}(G)-\alpha (G). \end{aligned}$$

Proof

Let G be a $K_{1,3}$-free graph with $\delta (G)\ge 3$ and S a $\beta (G)$-set. First, we shall prove that S is a double dominating set of G. Notice that S is a 2-dominating set of G because $V(G){\setminus } S$ is an independent set. Now, if there exists a vertex $v\in S$ such that $N(v)\cap S=\emptyset$, then the set formed by v and any three neighbours induces a $K_{1,3}$, which is a contradiction. Therefore, every vertex in S has at least one neighbour in S, which implies that S is a double dominating set of G, as required.

Now, suppose that $\delta (G)\ge 4$. If there exists a vertex $v\in S$ such that $|N(v)\cap S|=1$, then the set formed by v and any three vertices in $N(v){\setminus } S$ induces a $K_{1,3}$, which is a contradiction. Hence, every vertex in S has at least two neighbours in S, which implies that S is a double total dominating set of G. Therefore, $\gamma _{\times 2,t}(G)\le |S|=\beta (G)={\text {n}}(G)-\alpha (G)$, which completes the proof of (i).

Finally, we suppose that G is a $\{K_{1,3},K_{1,3}+e\}$-free graph with $\delta (G)=3$. Let D be a $\gamma (G)$-set. Now, we define $W'\subseteq V(G)$ as a set of minimum cardinality among all sets $W\subseteq V(G)$ such that the following conditions are satisfied.

• (a) $S\cup D\subseteq W$.

• (b) If $x\in S\cap D$, then choose one vertex $w\in N(x){\setminus } S$ (if any) and set $w\in W$.

Now, we proceed to prove that $W'$ is a double total dominating set of G. By definition, we deduce that $W'$ is a double dominating set of G, and by the minimality of $|W'|$ we have that $|W'|\le |D|+|S|$. It remains to show that $|N(v)\cap W'|\ge 2$ for every vertex $v\in W'$. Suppose, to the contrary, that there exists a vertex $v\in W'$ such that $N(v)\cap W'=\{v'\}$. Now, by definitions of $W'$ and S, it is easy to check that $v\in S{\setminus } D$, $v'\in S\cap D$ and there exists a vertex $w\in N(v')\cap W'{\setminus } S$ such that $vw\notin E(G)$. Let $u,u'\in N(v){\setminus } \{v'\}$. Notice that $u,u'\in N(v')$ because G is a $\{K_{1,3},K_{1,3}+e\}$-free graph and $uu'\notin E(G)$. Moreover, applying the same reasoning with the vertices $v',v,u,w$, we deduce that $w\in N(v)$ because $wu\notin E(G)$, which is a contradiction. Hence, $W'$ is a double total dominating set of G, and so,

$$\begin{aligned} \gamma _{\times 2,t}(G)\le & {} |W'|\le |D|+|S|\\= & {} \gamma (G)+{\text {n}}(G)-\alpha (G). \end{aligned}$$

Therefore, the proof is complete. $\square$

Next, we discuss the relationship between the double total domination number and the total outer-independent domination number.

Theorem 6

The following statements hold for any graph G with $\delta (G)\ge 2$.

• (i) $\gamma _{\times 2,t}(G)\le 2\gamma _{t,oi}(G)-\delta (G)+1.$

• (ii) If G is a $K_{1,3}$-free graph with $\delta (G)\ge 4$, then $\gamma _{\times 2,t}(G)\le \gamma _{t,oi}(G).$

Proof

Let D be a $\gamma _{t,oi}(G)$-set, $v\in V(G){\setminus } D$, $D'=D\cup \{v\}$ and $D_0=\{v\in D: |N(v)\cap D'|=1\}$. Observe that $|D_0|\le |D|-|N(v)|\le |D|-\delta (G)$. Now, we define $D''\subseteq V(G)$ as a set of minimum cardinality among all sets $W\subseteq V(G)$ such that the following conditions are satisfied.

• (a) $D'\subseteq W$.

• (b) $|N(x)\cap W|\ge 2$ for every vertex $x\in D$.

By definition, it is straightforward that $D''$ is a double total dominating set of G. In addition, every vertex in $D_0$ has at least one neighbour in $D''{\setminus } D$. Hence, and by the minimality of $D''$, we deduce that $|D''{\setminus } D'|\le |D_0| \le |D|-\delta (G)$. Therefore,

$$\begin{aligned} \gamma _{\times 2,t}(G)&\le |D''|\\&=|D'|+|D''{\setminus } D'|\\&\le 2|D|-\delta (G)+1\\&= 2\gamma _{t,oi}(G)-\delta (G)+1. \end{aligned}$$

Therefore, (i) holds. Finally, (ii) follows by Theorem 5-(i) and Proposition 1-(ii), which completes the proof. $\square$

The bound given in (i) is achieved for the graph $G\cong K_2+N_r$, where $r\in {\mathbb {Z}}^+$. In this case, we have that $\gamma _{\times 2,t}(G)=3$ and $\gamma _{t,oi}(G)=\delta (G)=2$.

Next we derive new bounds on the double total domination number. The first result improves the bound $\gamma _{\times 2,t}(G)\ge \gamma _t(G)+1$ (see [4]) whenever ${\text {diam}}(G)\ge 5$.

Theorem 7

The following statements hold for any connected graph G with $\delta (G)\ge 2$.

• (i) $\gamma _{\times 2,t}(G)\ge \gamma _t(G)+\left\lceil \frac{{\text {diam}}(G)+1}{5}\right\rceil .$

• (ii) If G is a $K_{1,3}$-free graph with ${\text {diam}}(G)=2$, then $\gamma _{\times 2,t}(G)\le \varDelta (G)+\delta (G)+1$.

Proof

Let D be a $\gamma _{\times 2,t}(G)$-set. Let $P=v_0v_1\cdots v_k$ be a diametrical path of G (in this case, $k={\text {diam}}(G)$) and $S=\{v_0, v_5, \ldots ,v_{5\lfloor k/5\rfloor }\}$. Hence, $d(x,y)\ge 5$ for any different vertices $x,y\in S$. Now, let $D'\subset D$ be a set of cardinality |S| such that $|N[x]\cap D|=1$ for every $x\in S$. Observe that by the definitions of D and S, the set $D'$ is well defined. In addition, and by the definitions of S and $D'$, we have that $d(x,y)\ge 3$ for any different vertices $x,y\in D'$.

With all of the above in mind, let us proceed to prove that $D''=D{\setminus } D'$ is a total dominating set of G. Suppose to the contrary that there exists $v\in V(G)$ such that $N(v)\cap D''=\emptyset$. This implies that $N(v)\cap D'\ne \emptyset$. Now, recall that $|N(v)\cap D|\ge 2$ by definition of D. Since $d(x,y)\ge 3$ for any different vertices $x,y\in D'$, we deduce that $|N(v)\cap D'|=1$. Then, this implies that $|N(v)\cap D''|=|N(v)\cap (D{\setminus } D')|\ge 1$, which is a contradiction. Therefore, $D''$ is a total dominating set of G, which implies that

$$\begin{aligned} \gamma _t(G)\le |D''|=|D{\setminus } D'|=|D|-|S|=\gamma _{\times 2,t}(G)-\left\lceil ({\text {diam}}(G)+1)/5\right\rceil . \end{aligned}$$

Hence, the proof of (i) is complete.

In order to prove (ii), we assume that G is a $K_{1,3}$-free graph with ${\text {diam}}(G)=2$. Let $v\in V(G)$ be a vertex of minimum degree and $u\in V(G){\setminus } N[v]$. Notice that $N(u)\cap N(v)\ne \emptyset$. We proceed to prove that $W=N[v]\cup N[u]$ is a double total dominating set of G. By definition, we have that $|N(x)\cap W|\ge 2$ for every $x\in \{u,v\}$. Now, notice that $N[u]\cap N(x)\ne \emptyset$ and $N[v]\cap N(x)\ne \emptyset$ for every $x\in V(G){\setminus } \{u,v\}$. This implies that $|N(x)\cap W|\ge 2$ for every $x\in W{\setminus } \{u,v\}$, and that $N(x)\cap W\ne \emptyset$ for every $x\in V(G){\setminus } W$. We only need to prove that $|N(x)\cap W|\ge 2$ for every $x\in V(G){\setminus } W$. Suppose to the contrary that there exists $x'\in V(G){\setminus } W$ such that $|N(x')\cap W|=1$. As ${\text {diam}}(G)=2$, there exists a vertex $w\in N(v)\cap N(u)$ such that $N(x')\cap W=\{w\}$, and then, the set formed by w, u, v and $x'$ induces a $K_{1,3}$, which is a contradiction. Hence, every vertex in $V(G){\setminus } W$ has at least two neighbours in W. Thus, W is a double total dominating set of G, which implies that

$$\begin{aligned}&\gamma _{\times 2,t}(G)\le |W|\le |N[u]\cup N[v]|\\&\quad \le |N[v]|+|N[u]|-|N(u)\cap N(v)|\le \varDelta (G)+\delta (G)+1. \end{aligned}$$

Therefore, the proof is complete. $\square$

The bounds above are tight. For instance, the bound given in (i) is achieved by the graph $G_1$ shown in Figure 1. In this case, we have that $\gamma _{\times 2,t}(G_1)=6$, $\gamma _t(G_1)=4$ and ${\text {diam}}(G_1)=6$. Moreover, the bound given in (ii) is achieved for the cycle $C_5$.

We continue with a new lower bound for the double total domination number in terms of the order, the maximum degree, and the total domination number of G.

Theorem 8

For any graph G with $\delta (G)\ge 2$,

$$\begin{aligned} \gamma _{\times 2,t}(G)\ge \left\lceil \frac{2{\text {n}}(G)+\gamma _t(G)}{\varDelta (G)+1}\right\rceil . \end{aligned}$$

Proof

In order to deduce the result, we need to introduce the following definitions. Let $f: V(G)\rightarrow \{0,1,2\}$ be a function and $V_i^f=\{v\in V(G): f(v)=i\}$ for every $i\in \{0,1,2\}$. The weight of f is defined to be

$$\begin{aligned} \omega (f)=\sum _{v\in V(G)}f(v)=|V_1^f|+2|V_2^f|. \end{aligned}$$

We say that f is a double dominating function on G if $\sum _{u\in N(v)}f(u)\ge 2$ for every vertex $v\in V_0^f\cup V_1^f$, and if the subgraph induced by $V_1^f\cup V_2^f$ has no isolated vertex. Observe that for any double dominating function f, the set $V_1^f\cup V_2^f$ is a total dominating set of G. Hence,

$$\begin{aligned} \gamma _t(G)\le |V_1^f\cup V_2^f|=|V_1^f|+|V_2^f|=\omega (f)-|V_2^f|. \end{aligned}$$

(1)

Let D be a $\gamma _{\times 2,t}(G)$-set and let g be a double dominating function of minimum weight among all double dominating functions on G. Observe that the function $g'$, defined by $g'(x)=1$ whenever $x\in D$ and $g'(x)=0$ otherwise, is a double dominating function on G. Hence, $\omega (g)\le \omega (g')=|D|=\gamma _{\times 2,t}(G).$ Moreover, notice that

$$\begin{aligned} \varDelta (G)\omega (g)&=\varDelta (G)\sum _{x\in V(G)}g(x)\\&\quad \ge \sum _{x\in V(G)}|N(x)|g(x)= \sum _{x\in V(G)}\sum _{u\in N(x)}g(u)\\&\quad \ge 2\left( |V_0^g|+|V_1^g|\right) +|V_2^g|=2{\text {n}}(G)-|V_2^g|. \end{aligned}$$

From (1) and the previous two inequality chains, we deduce that

$$\begin{aligned} 2{\text {n}}(G)+\gamma _t(G)&\le \varDelta (G)\omega (g)+|V_2^g|+\omega (g)-|V_2^g|\\&=(\varDelta (G)+1)\omega (g)\\&\le (\varDelta (G)+1)\gamma _{\times 2,t}(G). \end{aligned}$$

Therefore, $\gamma _{\times 2,t}(G)\ge \left\lceil \frac{2{\text {n}}(G)+\gamma _t(G)}{\varDelta (G)+1}\right\rceil$, which completes the proof. $\square$

The bound above is tight. For instance, it is achieved for the graph $G_1$ shown in Fig. 1. In this case, $\gamma _{\times 2,t}(G_1)=6$, $\gamma _t(G_1)=4$, ${\text {n}}(G_1)=12$ and $\varDelta (G_1)=4$.

It is well known that $\gamma _{\times 2,t}(G)\ge (4{\text {n}}(G)-2{\text {m}}(G))/2$ for any graph G of minimum degree $\delta (G)\ge 2$ (see [11]). The next result improves this previous lower bound whenever $\delta (G)\ge 3$.

Theorem 9

For any graph G with $\delta (G)\ge 2$,

$$\begin{aligned} \gamma _{\times 2,t}(G)\ge \left\lceil \frac{(\delta (G)+2){\text {n}}(G)-2{\text {m}}(G)}{\delta (G)}\right\rceil . \end{aligned}$$

Proof

Let D be a $\gamma _{\times 2,t}(G)$-set and ${\overline{D}}=V(G){\setminus } D$. Hence,

$$\begin{aligned} 2{\text {m}}(G)&=\sum _{v\in D} |N(v)\cap D|+2\sum _{v\in {\overline{D}}} |N(v)\cap D|+\sum _{v\in {\overline{D}}} |N(v)\cap {\overline{D}}|\\&=\sum _{v\in D} |N(v)\cap D|+\sum _{v\in {\overline{D}}} |N(v)\cap D|+\sum _{v\in {\overline{D}}} |N(v)|\\&\quad \ge 2|D|+2({\text {n}}(G)-|D|)+\delta (G)({\text {n}}(G)-|D|)\\&=(\delta (G)+2){\text {n}}(G)-\delta (G)|D|, \end{aligned}$$

which implies that $|D|\ge \left\lceil \frac{(\delta (G)+2){\text {n}}(G)-2{\text {m}}(G)}{\delta (G)}\right\rceil .$ Therefore, the proof is complete. $\square$

Fig. 3

Graph $G_{2,3}\in {\mathcal {G}}$

Let ${\mathcal {G}}$ be the family of graphs $G_{2,r}$ defined as follows. For any integer $r\ge 3$, the graph $G_{2,r}$ is obtained from two different copies of a complete bipartite graph $G_1\cong G_2\cong K_{2,r}$, such that $V(G_{2,r})=V(G_1)\cup V(G_2)$, $V(G_1)=\{u,u',u_1,\ldots , u_r\}$, $V(G_2)=\{v,v',v_1,\ldots , v_r\}$, u and $u'$ (resp., v and $v'$) are the vertices of degree r of $G_1$ (resp., $G_2)$ and $E(G_{2,r})=E(G_1)\cup E(G_2)\cup \{uv,uv',u'v,u'v'\}$. Figure 3 shows the graph $G_{2,3}$. Notice that $\gamma _{\times 2,t}(G_{2,r})=4$, ${\text {n}}(G_{2,r})=2r+4$, ${\text {m}}(G_{2,r})=4r+4$ and $\delta (G_{2,r})=2$ for every graph $G_{2,r}\in {\mathcal {G}}$. Hence, the bound given in Theorem 9 is achieved for the graphs $G_{2,r}$ belonging to family ${\mathcal {G}}$. Moreover, this bound is also achieved for the graph $G_2$ shown in Figure 1. In this case, we have that $\gamma _{\times 2,t}(G_2)=8$, ${\text {n}}(G_2)=10$, ${\text {m}}(G_2)=12$ and $\delta (G_2)=2$.

3 Open Problems

• (a) In the light of Theorem 3 and the bound obtained in Theorem 2, it is natural to ask whether $\gamma _{\times 2,t}(G)\le \gamma _{\times 2}(G)+\alpha (G)$. Moreover, it is straightforward that the bound holds whenever $\gamma _2(G)\le \alpha (G)$. However, we conjecture that this inequality is satisfied for every graph G with $\delta (G)\ge 2$.

• (b) After numerous attempts, we have not been able to find examples of graphs that reach the bounds given in Theorems  2, 4 and 5 . In this sense, we propose to find examples of graphs for which the equalities are reached, or to improve these bounds.

• (c) We have shown that $\gamma _{\times 2,t}(G)\ge \gamma _t(G)+\left\lceil ({\text {diam}}(G)+1)/5\right\rceil$ for any connected graph G with $\delta (G)\ge 2$. We propose the problem of characterizing all connected graphs for which this equality holds, or providing necessary or sufficient conditions to achieve it.