Rational Solutions to the KPI Equation as Multi-lumps with a One Degree of Summation

Abstract

In this paper, we construct solutions to the Kadomtsev–Petviashvili equation (KPI) by using a Darboux transformation with particular genera-ting functions limited to one degree of summation. With this choice, we get rational solutions expressed in terms of a wronskian of order N depending on $N(D+5)$ real parameters. In this case, we construct explicitly multi-parametric rational solutions to the KPI equation and we study the patterns of their modulus in the plane (x, y) and their evolution according to time and parameters.

Introduction

The Kadomtsev–Petviashvili equation (KPI)

$$\begin{aligned} (4u_{t} - 6uu_{x} + u_{xxx})_{x} - 3u_{yy} = 0, \end{aligned}$$

(1)

where as usual, subscripts x, y and t denote partial derivatives was proposed first by Kadomtsev and Petviashvili [1] in 1970. This equation describes weakly nonlinear waves in media. It is the subject of countless researches beginning with Petviashvili [2] in 1976, then in 1977 with Manakov, Zakharov, Bordag and Matveev [3], with Krichever [4, 5], Matveev in 1979 [6], Freeman and Nimmo [7, 8] in 1983 among others.

Some recent works related to this study can be cited. Tian, Xu and Zhang successfully proposed an effective and direct approach to study the symmetry-preserving discretization for a class of generalized higher order equations, and proposed an open problem about symmetries and the multipliers of conservation law [9]. Li and Tian systematically solved the Cauchy problem of the general n-component nonlinear Schrödinger equations based the Riemann-Hilbert method, and have given the N-soliton solutions. Moreover, they proposed a conjecture about the law of nonlinear wave propagation [10]. Wang, Tian and Cheng successfully derived the three-component coupled Hirota hierarchy, and firstly obtained the explicit soliton solutions of the equations via dressing method [11]. Yang, Tian and Li successfully solved the soliton solutions of the focusing nonlinear Schrödinger equation with multiple high-order poles under nonzero boundary conditions for the first time [12]. Wu and Tian successfully solved the long-time asymptotic problem of the solution to the non local short pulse equation with the Schwartz-type initial data, without solitons [13]. With respect to soliton resolution conjecture, Li, Tian, Yang and Fan have done some interesting work in deriving the solutions of Wadati–Konno–Ichikawa equation and complex short pulse equation with the help of Dbar-steepest descent method. They solved the long-time asymptotic behavior of the solutions of these equations, and proved the soliton resolution conjecture and the asymptotic stability of solutions of these equations [14,15,16].

Here, we use an extended Darboux transformation and some specific generating functions to construct rational solutions to the KPI equation in terms of a second derivative with respect to x of a logarithm of a wronskian of order N. These solutions depend on a degree of summation S and a degree of degree of derivation D. In this study, we choose $S=1$. So we obtain N order solutions depending in general on $N(D+5)$ real parameters which are rational in x, y and t. In the following, we restrict ourselves to the case where the order N is equal to 1.

We construct some explicit rational solutions of order 1, depending on several real parameters, and the representations of their modulus in the plane of the coordinates (x, y) according to parameters and time t.

Multi-parametric Rational Solutions of Order N to the KPI Equation

We consider the Kadomtsev-Petiaviasvili (KPI) equation

$$\begin{aligned} (4u_{t} - 6uu_{x} + u_{xxx})_{x} - 3u_{yy} = 0. \end{aligned}$$

We consider the wronskian of order N of the functions $f_{1},\ldots ,f_{N}$ denoted as $W(f_{1},\ldots ,f_{N})$, and defined by $\det (\partial _{x}^{i-1}f_{j})_{1 \le i \le N, \, 1 \le j\le N}$, $\partial _{x}^{i}$ being the partial derivative of order i with respect to x and $\partial _{x}^{0} f_{j}$ being the function $f_{j}$.

We consider $a_{j}$, $b_{jsd}$, $d_{js}$, $e_{js}$, $g_{js}$, $h_{js}$, arbitrary real numbers with $c_{js} = g_{js} + i h_{js}$.

We consider the following elementary functions $f_{js}$ defined by

$$\begin{aligned} f_{js}(x,y,t) = e^{i c_{js}x -i c_{js}^{2}y + i c_{js}^{3}t + d_{js} + ie_{js} } = e^{i (g_{js} + i h_{js})x -i (g_{js} + i h_{js})^{2}y + i (g_{js} + i h_{js})^{3}t + d_{js} + ie_{js} }. \end{aligned}$$

(2)

Then, we have the following statement :

Theorem 2.1

Let $\psi _{j}$, be the functions defined by

$$\begin{aligned} \psi _{j}(x,y,t) = a_{j} + \sum _{s=1}^{S} \sum _{d=0}^{D} b_{jsd} \partial _{c_{js}}^{d} e^{i c_{js}x - i c_{js}^{2}y + i c_{js}^{3}t + d_{js} + ie_{js} }= a_{j} + \sum _{s=1}^{S} \sum _{d=0}^{D} b_{jsd} \partial _{c_{js}}^{d} f_{js}(x,y,t). \end{aligned}$$

(3)

Then the function u defined by

$$\begin{aligned} u(x,y,t) = - 2 \partial ^{2}_{x} \ln (W(\psi _{1}(x,y,t),\ldots ,\psi _{N}(x,y,t)) \end{aligned}$$

(4)

is a solution to the (KPI) equation (1) depending on real $N(S(D+5)+1)$ parameters $a_{j}$, $b_{j,s,d}$, $g_{j,s}$, $h_{j,s}$, $d_{j,s}$, $e_{j,s}$, $1\le j \le N$, $1\le s \le S$, $0\le d \le D$.

Proof

The (KPI) equation (1)

$$\begin{aligned} (4u_{t} - 6uu_{x} + u_{xxx})_{x} - 3u_{yy} = 0, \end{aligned}$$

can be seen as the compatibility condition of these two equations

$$\begin{aligned} \left\{ \begin{array}{l} \phi _{t} = -\phi _{3x} +\dfrac{3}{2} u \phi _{x} + v \phi ,\\ \phi _{y} = i \phi _{xx} - i u \phi . \end{array} \right. \end{aligned}$$

(5)

We use here the classical Darboux transforamtion defined by

$$\begin{aligned} D(f) = \partial _{x}f - \dfrac{\partial _{x}\varphi _{1}}{\varphi _{1}}f, \end{aligned}$$

(6)

where $\varphi _{1}$ is a solution of (5) with $u=u_{1}$ and $v=v_{1}$.

Each solution $\phi$ to this system gives a solution u to the KPI equation. We use the covariance of this system [17] with respect to the Darboux transformation. It means that if $\phi ,\phi _{1},\ldots ,\phi _{N}, \phi$ are solutions of the system (5) respectively associated to u and v, then $\phi [N]$ defined by $\phi [N] = \dfrac{W(\phi _{1},\ldots ,\psi _{N}, \phi )}{W(\phi _{1},\ldots ,\phi _{N})}$ is another solution of this system (5) where in particular u replaced by $u[N] = u- 2 (\ln W(\phi _{1}, \ldots ,\phi _{N})_{xx}$ giving a new solution to the KPI equation.

If we choose $u=0$ and $v=0$ then the functions $\psi _{j}$ defined in (3) verify the following system

$$\begin{aligned} \left\{ \begin{array}{l} \psi _{t} = -\psi _{3x},\\ \psi _{y} = i \psi _{xx}. \end{array} \right. \end{aligned}$$

(7)

Then the solution of the system (7) associated can be written as $\varphi (x,y,t) = \dfrac{W(\psi _{1},\ldots ,\psi _{N}, \psi )}{W(\psi _{1},\ldots ,\psi _{N})}$ and $u_{N}$ can be expressed as

$$\begin{aligned} u[N] = - 2 (\ln W(\psi _{1}, \ldots ,\psi _{N}))_{xx}, \end{aligned}$$

which proves the result. $\hfill\square$

We will call the order N of the wronskian, the order of the solution. The number S of terms of the summation will be call the degree of the summation of the solution and D the degree of derivation of the solution.

In the following, we restrict ourselves to the study with $S=1$.

So we will use some simplified notations.

We consider $b_{jd}$, $d_{j}$, $e_{j}$, $g_{j}$, $h_{j}$, arbitrary real numbers with $c_{j} = g_{j} + i h_{j}$.

We consider the following elementary functions $f_{j}$ defined by

$$\begin{aligned} f_{j}(x,y,t) = e^{i c_{j}x -i c_{j}^{2}y + i c_{j}^{3}t + d_{j} + ie_{j} } = e^{i (g_{j} + i h_{j})x -i (g_{j} + i h_{j})^{2}y + i (g_{j} + i h_{j})^{3}t + d_{j} + ie_{j} }. \end{aligned}$$

(8)

Then, we have the following statement :

Theorem 2.2

Let $\phi _{j}$, be the functions defined by

$$\begin{aligned} \phi _{j}(x,y,t) = \sum _{d=0}^{D} b_{jd} \partial _{c_{j}}^{d} e^{i c_{j}x - i c_{j}^{2}y + i c_{j}^{3}t + d_{j} + ie_{j} }= \sum _{d=0}^{D} b_{jd} \partial _{c_{j}}^{d} f_{j}(x,y,t). \end{aligned}$$

(9)

Then the function u defined by

$$\begin{aligned} u(x,y,t) = - 2 \partial ^{2}_{x} \ln (W(\phi _{1}(x,y,t),\ldots ,\phi _{N}(x,y,t)) \end{aligned}$$

(10)

is a rational solution to the (KPI) equation (1) depending on real $N(D+5)$ parameters $b_{j,d}$, $g_{j}$, $h_{j}$, $d_{j}$, $e_{j}$, $1\le j \le N$, $0\le d \le D$.

Proof

From the previous result, by choosing $S=1$, $a_{j}=1$, we already know that (10) is a solution to the KPI equation.

It remains to prove that this solution is rational.

$\partial _{c_{j}}^{d} f_{j}(x,y,t)$ can be written as $p_{jd}(x,y,t) f_{j}(x,y,t)$ where $p_{jd}(x,y,t)$ is a polynomial in x, y and t and so

$$\begin{aligned} \phi _{j}(x,y,t) = \sum _{d=0}^{D}b_{jd}p_{jd}(x,y,t)f_{j}(x,y,t) = f_{j}(x,y,t) \sum _{d=0}^{D} b_{jd} p_{jd}(x,y,t)= P_{j}(x,y,t) f_{j}(x,y,t), \end{aligned}$$

where $P_{j}(x,y,t)$ is a polynomial in x, y and t.

The derivation with respect to x of $\phi _{j}(x,y,t)$ then is equal to $\partial _{x}^{k} \phi _{j}(x,y,t) = Q_{j,k}(x,y,t) f_{j} (x,y,t)$ where $Q_{j,k}(x,y,t)$ is a polynomial in x, y and t. We denote $Q_{j,0}(x,y,t)$ the polynomial $P_{j}(x,y,t)$

The wronskian $W(\phi _{1},\ldots ,\phi _{N})$ can be written as

$$\begin{aligned} \left| \begin{array}{cccc} Q_{1,0}(x,y,t) f_{1} (x,y,t) &{} Q_{2,0}(x,y,t) f_{2} (x,y,t) &{} \dots &{} Q_{N,0}(x,y,t) f_{N} (x,y,t) \\ Q_{1,1}(x,y,t) f_{1} (x,y,t) &{} Q_{2,1}(x,y,t) f_{2} (x,y,t) &{} \dots &{} Q_{N,1}(x,y,t) f_{N} (x,y,t) \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ Q_{1,N-1}(x,y,t) f_{1} (x,y,t) &{} Q_{2,N-1}(x,y,t) f_{2} (x,y,t) &{} \dots &{} Q_{N,N-1}(x,y,t) f_{N} (x,y,t) \\ \end{array} \right| \end{aligned}$$

It can be rewritten as

$$\begin{aligned} W(\phi _{1},\ldots ,\phi _{N}) = \prod _{k=1}^{N}f_{k} (x,y,t) \left| \begin{array}{cccc} Q_{1,0}(x,y,t) &{} Q_{2,0}(x,y,t) &{} \dots &{} Q_{N,0}(x,y,t) \\ Q_{1,1}(x,y,t) &{} Q_{2,1}(x,y,t) &{} \dots &{} Q_{N,1}(x,y,t) \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ Q_{1,N-1}(x,y,t) &{} Q_{2,N-1}(x,y,t) &{} \dots &{} Q_{N,N-1}(x,y,t) \\ \end{array} \right| \end{aligned}$$

or as the product

$$\begin{aligned} W(\phi _{1},\ldots ,\phi _{N}) = \prod _{k=1}^{N}f_{k} (x,y,t) \times \Delta \end{aligned}$$

where $\Delta$ is a polynomial in x, y ans t.

$$\begin{aligned} \ln \prod _{k=1}^{N}f_{k} (x,y,t) = \sum _{k=1}^{N} \ln f_{k}(x,y,t) = \sum _{k=1}^{N} ic_{k}x -ic_{k}^2y + ic_{k}^{3}t + d_{k} + i e_{k} \end{aligned}$$

and so

$$\begin{aligned} \partial _{x}^{2} \ln \prod _{k=1}^{N}f_{k} (x,y,t) =0 \end{aligned}$$

So we have

$$\begin{aligned} u(x,y,t) = -2 \partial _{x}^{2} \ln W(\phi _{1}(x,y,t), \ldots , \phi _{N}(x,y,t)) = -2 \partial _{x}^{2} \ln \Delta = \dfrac{\Delta _{2x} \Delta - \Delta _{x}^{2}}{\Delta ^{2}} \end{aligned}$$

is a rational solution to the KPI equation, which proves the result. $\hfill\square$

Rational Solutions of Order 1 with a Degree of Derivation Equal to 1 ($D=1$) Depending on 6 Real Parameters

The case $D=0$ is not interesting because we get the solution $u=0$.

In the case $D=1$, solutions to the KPI equation can be written as

$$\begin{aligned} u_{}(x,y,t) = -2 \frac{ {b_{{1,1}}}^{2} }{( ib_{{1,1}}x+b_{{1,0}}+3\,itb_{{1,1}}{g_{{1}}}^{2}-3\,itb_{{1,1}}{h_{{1 }}}^{2}-2\,iyb_{{1,1}}g_{{1}}+2\,yb_{{1,1}}h_{{1}}-6\,tb_{{1,1}}g_{{1} }h_{{1}} )^{2}}. \end{aligned}$$

In this case, we observe lumps whose intensities depend on 6 real parameters. If $b_{1,1}=0$, we get the solution $u=0$.

We give some figures in the (x, y) plane of coordinates.

Fig. 1

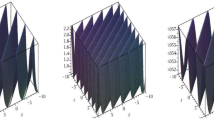
Solutions of order 1 to KPI, on the left for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; in the center for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $g_{1}=0$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; on the right for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $g_{1}=1$, $h_{1}=0$, $d_{1}=1$, $e_{1}=1$

Fig. 2

Solutions of order 1 to KPI, on the left for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; in the center for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $g_{1}=0$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; on the right for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $g_{1}=1$, $h_{1}=0$, $d_{1}=1$, $e_{1}=1$

In Fig. 1 and 2, we obtain lumps whose modulus depends on the values of parameters and we remark that these structures are more sensitive to $g_{1}$ and $h_{1}$ parameters than to others.

Rational Solutions of Order 1 with a Degree of Derivation Equal to 2 ($D=2$) Depending on 7 Real Parameters

In this case, we take $D=2$; the solutions to the KPI equation can be written as

$$\begin{aligned} u_{}(x,y,t) = -2 \frac{n(x,y,t)}{d_{}(x,y,t)^{2}} \end{aligned}$$

with

$n(x,y,t) = -2\,{b_{{1,2}}}^{2}{x}^{2}+ ( 12\,t{b_{{1,2}}}^{2}{h_{{1}}}^{2}+8 \,y{b_{{1,2}}}^{2}g_{{1}}-12\,t{b_{{1,2}}}^{2}{g_{{1}}}^{2} +8\,iy{b_{{ 1,2}}}^{2}h_{{1}}-24\,it{b_{{1,2}}}^{2}g_{{1}}h_{{1}}+2\,ib_{{1,1}}b_{ {1,2}} ) x+72\,i{t}^{2}{b_{{1,2}}}^{2}g_{{1}}{h_{{1}}}^{3}-12\,i t{b_{{1,2}}}^{2}g_{{1}}-6\,itb_{{1,1}}b_{{1,2}}{h_{{1}}}^{2}-2\,b_{{1,0 }}b_{{1,2}} +108\,{t}^{2}{b_{{1,2}}}^{2}{g_{{1}}}^{2}{h_{{1}}}^{2}+24\, ty{b_{{1,2}}}^{2}{g_{{1}}}^{3}+6\,itb_{{1,1}}b_{{1,2}}{g_{{1}}}^{2}+4 \,yb_{{1,1}}b_{{1,2}}h_{{1}}-16\,i{y}^{2}{b_{{1,2}}}^{2}g_{{1}}h_{{1}} -12\,tb_{{1,1}}b_{{1,2}}g_{{1}}h_{{1}}-18\,{t}^{2}{b_{{1,2}}}^{2}{g_{{ 1}}}^{4} +12\,t{b_{{1,2}}}^{2}h_{{1}}+{b_{{1,1}}}^{2}+8\,{y}^{2}{b_{{1, 2}}}^{2}{h_{{1}}}^{2}-24\,ity{b_{{1,2}}}^{2}{h_{{1}}}^{3} +4\,iy{b_{{1, 2}}}^{2}-72\,i{t}^{2}{b_{{1,2}}}^{2}{g_{{1}}}^{3}h_{{1}}-72\,ty{b_{{1, 2}}}^{2}g_{{1}}{h_{{1}}}^{2}-4\,iyb_{{1,1}}b_{{1,2}}g_{{1}}-18\,{t}^{2 }{b_{{1,2}}}^{2}{h_{{1}}}^{4} +72\,ity{b_{{1,2}}}^{2}{g_{{1}}}^{2}h_{{1 }}-8\,{y}^{2}{b_{{1,2}}}^{2}{g_{{1}}}^{2}$ and

$d(x,y,t) = b_{{1,2}}{x}^{2}+ ( 6\,tb_{{1,2}}{g_{{1}}}^{2}+12\,itb_{{1,2}}g_{ {1}}h_{{1}}-6\,tb_{{1,2}}{h_{{1}}}^{2}-4\,yb_{{1,2}}g_{{1}}-4\,ib_{{1, 2}}yh_{{1}}-ib_{{1,1}} ) x+9\,{t}^{2}b_{{1,2}}{g_{{1}}}^{4}+12\, ityb_{{1,2}}{h_{{1}}}^{3}-54\,{t}^{2}b_{{1,2}}{g_{{1}}}^{2}{h_{{1}}}^{ 2}-36\,ib_{{1,2}}t{g_{{1}}}^{2}yh_{{1}} +9\,{t}^{2}b_{{1,2}}{h_{{1}}}^{ 4}-12\,tyb_{{1,2}}{g_{{1}}}^{3}-6\,ib_{{1,2}}tg_{{1}}+36\,tyb_{{1,2}}g _{{1}}{h_{{1}}}^{2}+2\,iyb_{{1,1}}g_{{1}}+4\,{y}^{2}b_{{1,2}}{g_{{1}}} ^{2}+36\,i{t}^{2}b_{{1,2}}{g_{{1}}}^{3}h_{{1}}-4\,{y}^{2}b_{{1,2}}{h_{ {1}}}^{2}+2\,iyb_{{1,2}}+6\,tb_{{1,1}}g_{{1}}h_{{1}}-36\,ib_{{1,2}}{t} ^{2}g_{{1}}{h_{{1}}}^{3}+8\,i{y}^{2}b_{{1,2}}g_{{1}}h_{{1}}+6\,tb_{{1, 2}}h_{{1}}+3\,itb_{{1,1}}{h_{{1}}}^{2}-2\,yb_{{1,1}}h_{{1}}-3\,ib_{{1, 1}}t{g_{{1}}}^{2}-b_{{1,0}}$

We give some figures in the (x, y) plane of coordinates.

Fig. 3

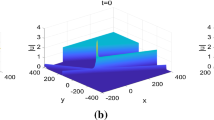
Solutions of order 1 to KPI, on the left for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=0$, $e_{1}=1$; in the center for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $g_{1}=1$, $h_{1}=0$, $d_{1}=1$, $e_{1}=1$; on the right for $t=10$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $g_{1}=0.01$, $h_{1}=10^2$, $d_{1}=1$, $e_{1}=1$

Fig. 4

Solutions of order 1 to KPI, on the left for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $g_{1}=0.01$, $h_{1}=0.01$, $d_{1}=0$, $e_{1}=1$; in the center for $t=1$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; on the right for $t=10^3$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $g_{1}=0.01$, $h_{1}=10^2$, $d_{1}=1$, $e_{1}=1$

In Figs. 3 and 4, we get lumps whose modulus depends on the values of parameters. These structures are more sensitive to $g_{1}$ and $h_{1}$ parameters than to others. In this case, we observe a maximum of two isolated lumps, as shown for example in the Fig. 4 in the center.

Solutions of Order 1 with a Degree of Derivation Equal to 3 ($D=3$) Depending on 8 Real Pdarameters

In the case $D=3$, we observe multi lumps. As in the previous cases, these structures are more sensitive to $g_{1}$ and $h_{1}$ parameters than to others.

The solutions to the KPI equation can be written as

$$\begin{aligned} u_{}(x,y,t) = -2 \frac{n(x,y,t)}{d_{}(x,y,t)^{2}}. \end{aligned}$$

with

$n(x,y,t) =3\,{b_{{1,3}}}^{2}{x}^{4}+ ( -36\,t{b_{{1,3}}}^{2}{h_{{1}}}^{2}+ 36\,t{b_{{1,3}}}^{2}{g_{{1}}}^{2}-24\,y{b_{{1,3}}}^{2}g_{{1}} +72\,it{b _{{1,3}}}^{2}g_{{1}}h_{{1}}-24\,iy{b_{{1,3}}}^{2}h_{{1}}-4\,ib_{{1,2}} b_{{1,3}} ) {x}^{3}+ ( 216\,ity{b_{{1,3}}}^{2}{h_{{1}}}^{3} +162\,{t}^{2}{b_{{1,3}}}^{2}{g_{{1}}}^{4}-36\,itb_{{1,2}}b_{{1,3}}{g_{ {1}}}^{2}-648\,i{t}^{2}{b_{{1,3}}}^{2}g_{{1}}{h_{{1}}}^{3}-972\,{t}^{2 }{b_{{1,3}}}^{2}{g_{{1}}}^{2}{h_{{1}}}^{2}+162\,{t}^{2}{b_{{1,3}}}^{2} {h_{{1}}}^{4}-2\,{b_{{1,2}}}^{2} +648\,i{t}^{2}{b_{{1,3}}}^{2}{g_{{1}}} ^{3}h_{{1}}+648\,ty{b_{{1,3}}}^{2}g_{{1}}{h_{{1}}}^{2} +36\,itb_{{1,2}} b_{{1,3}}{h_{{1}}}^{2}-24\,yb_{{1,2}}b_{{1,3}}h_{{1}}-648\,ity{b_{{1,3 }}}^{2}{g_{{1}}}^{2}h_{{1}}+144\,i{y}^{2}{b_{{1,3}}}^{2}g_{{1}}h_{{1}} -216\,ty{b_{{1,3}}}^{2}{g_{{1}}}^{3} +72\,tb_{{1,2}}b_{{1,3}}g_{{1}}h_{ {1}}-72\,{y}^{2}{b_{{1,3}}}^{2}{h_{{1}}}^{2}+72\,{y}^{2}{b_{{1,3}}}^{2 }{g_{{1}}}^{2} +24\,iyb_{{1,2}}b_{{1,3}}g_{{1}} ) {x}^{2}+ ( 1728\,it{y}^{2}{b_{{1,3}}}^{2}{g_{{1}}}^{3}h_{{1}}-1728\,it{y} ^{2}{b_{{1,3}}}^{2}g_{{1}}{h_{{1}}}^{3}$$+648\,i{t}^{2}b_{{1,2}}b_{{1,3} }{g_{{1}}}^{2}{h_{{1}}}^{2} +144\,ityb_{{1,2}}b_{{1,3}}{g_{{1}}}^{3}- 3240\,i{t}^{2}y{b_{{1,3}}}^{2}{g_{{1}}}^{4}h_{{1}}+6480\,i{t}^{2}y{b_{ {1,3}}}^{2}{g_{{1}}}^{2}{h_{{1}}}^{3}-432\,tyb_{{1,2}}b_{{1,3}}{g_{{1} }}^{2}h_{{1}}-4860\,{t}^{3}{b_{{1,3}}}^{2}{g_{{1}}}^{4}{h_{{1}}}^{2} + 4860\,{t}^{3}{b_{{1,3}}}^{2}{g_{{1}}}^{2}{h_{{1}}}^{4}+432\,t{y}^{2}{b _{{1,3}}}^{2}{h_{{1}}}^{4}+96\,i{y}^{3}{b_{{1,3}}}^{2}{h_{{1}}}^{3}+8 \,iy{b_{{1,2}}}^{2}h_{{1}} +432\,t{y}^{2}{b_{{1,3}}}^{2}{g_{{1}}}^{4}- 648\,{t}^{2}y{b_{{1,3}}}^{2}{g_{{1}}}^{5}+288\,{y}^{3}{b_{{1,3}}}^{2}g _{{1}}{h_{{1}}}^{2}-432\,ityb_{{1,2}}b_{{1,3}}g_{{1}}{h_{{1}}}^{2}+36 \,t{b_{{1,3}}}^{2}-48\,i{y}^{2}b_{{1,2}}b_{{1,3}}{g_{{1}}}^{2}+48\,i{y }^{2}b_{{1,2}}b_{{1,3}}{h_{{1}}}^{2}-24\,it{b_{{1,2}}}^{2}g_{{1}}h_{{1 }}-108\,i{t}^{2}b_{{1,2}}b_{{1,3}}{g_{{1}}}^{4}-108\,i{t}^{2}b_{{1,2}} b_{{1,3}}{h_{{1}}}^{4}-288\,i{y}^{3}{b_{{1,3}}}^{2}{g_{{1}}}^{2}h_{{1} }-648\,i{t}^{2}y{b_{{1,3}}}^{2}{h_{{1}}}^{5} +1944\,i{t}^{3}{b_{{1,3}}} ^{2}{g_{{1}}}^{5}h_{{1}}-6480\,i{t}^{3}{b_{{1,3}}}^{2}{g_{{1}}}^{3}{h_ {{1}}}^{3}+1944\,i{t}^{3}{b_{{1,3}}}^{2}g_{{1}}{h_{{1}}}^{5}+96\,{y}^{ 2}b_{{1,2}}b_{{1,3}}g_{{1}}h_{{1}} +432\,{t}^{2}b_{{1,2}}b_{{1,3}}{g_{{ 1}}}^{3}h_{{1}}-432\,{t}^{2}b_{{1,2}}b_{{1,3}}g_{{1}}{h_{{1}}}^{3}+144 \,tyb_{{1,2}}b_{{1,3}}{h_{{1}}}^{3}-2592\,t{y}^{2}{b_{{1,3}}}^{2}{g_{{ 1}}}^{2}{h_{{1}}}^{2} +6480\,{t}^{2}y{b_{{1,3}}}^{2}{g_{{1}}}^{3}{h_{{1 }}}^{2}-3240\,{t}^{2}y{b_{{1,3}}}^{2}g_{{1}}{h_{{1}}}^{4}-12\,t{b_{{1, 2}}}^{2}{g_{{1}}}^{2}+12\,t{b_{{1,2}}}^{2}{h_{{1}}}^{2} +8\,y{b_{{1,2}} }^{2}g_{{1}}-6\,ib_{{1,0}}b_{{1,3}}+2\,ib_{{1,1}}b_{{1,2}}+324\,{t}^{3 }{b_{{1,3}}}^{2}{g_{{1}}}^{6}-324\,{t}^{3}{b_{{1,3}}}^{2}{h_{{1}}}^{6} -96\,{y}^{3}{b_{{1,3}}}^{2}{g_{{1}}}^{3} ) x+13608\,{t}^{3}y{b_{ {1,3}}}^{2}{g_{{1}}}^{5}{h_{{1}}}^{2}-22680\,{t}^{3}y{b_{{1,3}}}^{2}{g _{{1}}}^{3}{h_{{1}}}^{4}-2160\,{t}^{3}b_{{1,2}}b_{{1,3}}{g_{{1}}}^{3}{ h_{{1}}}^{3} +648\,{t}^{3}b_{{1,2}}b_{{1,3}}g_{{1}}{h_{{1}}}^{5}$$+2880\, t{y}^{3}{b_{{1,3}}}^{2}{g_{{1}}}^{3}{h_{{1}}}^{2}-1440\,t{y}^{3}{b_{{1 ,3}}}^{2}g_{{1}}{h_{{1}}}^{4}-216\,{t}^{2}yb_{{1,2}}b_{{1,3}}{h_{{1}}} ^{5}-96\,i{y}^{3}b_{{1,2}}b_{{1,3}}g_{{1}}{h_{{1}}}^{2}+72\,ity{b_{{1, 2}}}^{2}{g_{{1}}}^{2}h_{{1}}-144\,it{y}^{2}b_{{1,2}}b_{{1,3}}{g_{{1}}} ^{4}-144\,it{y}^{2}b_{{1,2}}b_{{1,3}}{h_{{1}}}^{4} +4536\,{t}^{3}y{b_{{ 1,3}}}^{2}g_{{1}}{h_{{1}}}^{6}+1620\,i{t}^{3}b_{{1,2}}b_{{1,3}}{g_{{1} }}^{4}{h_{{1}}}^{2}-1620\,i{t}^{3}b_{{1,2}}b_{{1,3}}{g_{{1}}}^{2}{h_{{ 1}}}^{4}-1440\,it{y}^{3}{b_{{1,3}}}^{2}{g_{{1}}}^{4}h_{{1}} +2880\,it{y }^{3}{b_{{1,3}}}^{2}{g_{{1}}}^{2}{h_{{1}}}^{3}+3888\,i{t}^{2}{y}^{2}{b _{{1,3}}}^{2}{g_{{1}}}^{5}h_{{1}}-12960\,i{t}^{2}{y}^{2}{b_{{1,3}}}^{2 }{g_{{1}}}^{3}{h_{{1}}}^{3}+3888\,i{t}^{2}{y}^{2}{b_{{1,3}}}^{2}g_{{1} }{h_{{1}}}^{5}-4536\,i{t}^{3}y{b_{{1,3}}}^{2}{g_{{1}}}^{6}h_{{1}} + 22680\,i{t}^{3}y{b_{{1,3}}}^{2}{g_{{1}}}^{4}{h_{{1}}}^{3}-13608\,i{t}^ {3}y{b_{{1,3}}}^{2}{g_{{1}}}^{2}{h_{{1}}}^{5}+1080\,i{t}^{2}yb_{{1,2}} b_{{1,3}}g_{{1}}{h_{{1}}}^{4} +864\,it{y}^{2}b_{{1,2}}b_{{1,3}}{g_{{1}} }^{2}{h_{{1}}}^{2}+216\,i{t}^{2}yb_{{1,2}}b_{{1,3}}{g_{{1}}}^{5}+1944 \,i{t}^{4}{b_{{1,3}}}^{2}{g_{{1}}}^{7}h_{{1}}-13608\,i{t}^{4}{b_{{1,3} }}^{2}{g_{{1}}}^{5}{h_{{1}}}^{3}+13608\,i{t}^{4}{b_{{1,3}}}^{2}{g_{{1} }}^{3}{h_{{1}}}^{5}-1944\,i{t}^{4}{b_{{1,3}}}^{2}g_{{1}}{h_{{1}}}^{7} + 648\,i{t}^{3}y{b_{{1,3}}}^{2}{h_{{1}}}^{7}-108\,i{t}^{3}b_{{1,2}}b_{{1 ,3}}{g_{{1}}}^{6}+108\,i{t}^{3}b_{{1,2}}b_{{1,3}}{h_{{1}}}^{6}-288\,it {y}^{3}{b_{{1,3}}}^{2}{h_{{1}}}^{5}+192\,i{y}^{4}{b_{{1,3}}}^{2}{g_{{1 }}}^{3}h_{{1}}-192\,i{y}^{4}{b_{{1,3}}}^{2}g_{{1}}{h_{{1}}}^{3}-72\,i{ t}^{2}{b_{{1,2}}}^{2}{g_{{1}}}^{3}h_{{1}} +72\,i{t}^{2}{b_{{1,2}}}^{2}g _{{1}}{h_{{1}}}^{3}+32\,i{y}^{3}b_{{1,2}}b_{{1,3}}{g_{{1}}}^{3}+36\,it b_{{1,1}}b_{{1,3}}g_{{1}}-9720\,{t}^{2}{y}^{2}{b_{{1,3}}}^{2}{g_{{1}}} ^{4}{h_{{1}}}^{2}+9720\,{t}^{2}{y}^{2}{b_{{1,3}}}^{2}{g_{{1}}}^{2}{h_{ {1}}}^{4}$$+648\,{t}^{3}b_{{1,2}}b_{{1,3}}{g_{{1}}}^{5}h_{{1}}-432\,i{t} ^{2}{b_{{1,3}}}^{2}g_{{1}}h_{{1}}-16\,i{y}^{2}{b_{{1,2}}}^{2}g_{{1}}h_ {{1}}+144\,ity{b_{{1,3}}}^{2}h_{{1}}-18\,itb_{{1,0}}b_{{1,3}}{g_{{1}}} ^{2}+18\,itb_{{1,0}}b_{{1,3}}{h_{{1}}}^{2} +6\,itb_{{1,1}}b_{{1,2}}{g_{ {1}}}^{2}-6\,itb_{{1,1}}b_{{1,2}}{h_{{1}}}^{2}-648\,{t}^{2}{y}^{2}{b_{ {1,3}}}^{2}{h_{{1}}}^{6}-288\,{y}^{4}{b_{{1,3}}}^{2}{g_{{1}}}^{2}{h_{{ 1}}}^{2}+108\,{t}^{2}{b_{{1,2}}}^{2}{g_{{1}}}^{2}{h_{{1}}}^{2}+32\,{y} ^{3}b_{{1,2}}b_{{1,3}}{h_{{1}}}^{3} +24\,ty{b_{{1,2}}}^{2}{g_{{1}}}^{3} -12\,yb_{{1,0}}b_{{1,3}}h_{{1}}+4\,yb_{{1,1}}b_{{1,2}}h_{{1}}-6804\,{t }^{4}{b_{{1,3}}}^{2}{g_{{1}}}^{6}{h_{{1}}}^{2}+17010\,{t}^{4}{b_{{1,3} }}^{2}{g_{{1}}}^{4}{h_{{1}}}^{4}-6804\,{t}^{4}{b_{{1,3}}}^{2}{g_{{1}}} ^{2}{h_{{1}}}^{6} +{b_{{1,1}}}^{2}+36\,tb_{{1,0}}b_{{1,3}}g_{{1}}h_{{1} }-12\,tb_{{1,1}}b_{{1,2}}g_{{1}}h_{{1}}-96\,{y}^{3}b_{{1,2}}b_{{1,3}}{ g_{{1}}}^{2}h_{{1}}-72\,ty{b_{{1,2}}}^{2}g_{{1}}{h_{{1}}}^{2}-2160\,i{ t}^{2}yb_{{1,2}}b_{{1,3}}{g_{{1}}}^{3}{h_{{1}}}^{2}-2\,b_{{1,0}}b_{{1, 2}}-36\,{y}^{2}{b_{{1,3}}}^{2}-12\,it{b_{{1,2}}}^{2}g_{{1}}-12\,itb_{{ 1,2}}b_{{1,3}}-12\,iyb_{{1,1}}b_{{1,3}}-36\,tb_{{1,1}}b_{{1,3}}h_{{1}} +144\,ty{b_{{1,3}}}^{2}g_{{1}}-648\,{t}^{3}y{b_{{1,3}}}^{2}{g_{{1}}}^{ 7}+648\,{t}^{2}{y}^{2}{b_{{1,3}}}^{2}{g_{{1}}}^{6}-288\,t{y}^{3}{b_{{1 ,3}}}^{2}{g_{{1}}}^{5}+576\,t{y}^{2}b_{{1,2}}b_{{1,3}}{g_{{1}}}^{3}h_{ {1}}-576\,t{y}^{2}b_{{1,2}}b_{{1,3}}g_{{1}}{h_{{1}}}^{3}-1080\,{t}^{2} yb_{{1,2}}b_{{1,3}}{g_{{1}}}^{4}h_{{1}} +2160\,{t}^{2}yb_{{1,2}}b_{{1,3 }}{g_{{1}}}^{2}{h_{{1}}}^{3}+12\,iyb_{{1,0}}b_{{1,3}}g_{{1}}-4\,iyb_{{ 1,1}}b_{{1,2}}g_{{1}}-24\,ity{b_{{1,2}}}^{2}{h_{{1}}}^{3}+4\,iy{b_{{1, 2}}}^{2}+216\,{t}^{2}{b_{{1,3}}}^{2}{h_{{1}}}^{2}+243\,{t}^{4}{b_{{1,3 }}}^{2}{g_{{1}}}^{8}+243\,{t}^{4}{b_{{1,3}}}^{2}{h_{{1}}}^{8} +48\,{y}^ {4}{b_{{1,3}}}^{2}{h_{{1}}}^{4}-18\,{t}^{2}{b_{{1,2}}}^{2}{g_{{1}}}^{4 }-18\,{t}^{2}{b_{{1,2}}}^{2}{h_{{1}}}^{4}-8\,{y}^{2}{b_{{1,2}}}^{2}{g_ {{1}}}^{2} +8\,{y}^{2}{b_{{1,2}}}^{2}{h_{{1}}}^{2}+12\,t{b_{{1,2}}}^{2} h_{{1}}-216\,{t}^{2}{b_{{1,3}}}^{2}{g_{{1}}}^{2}+48\,{y}^{4}{b_{{1,3}} }^{2}{g_{{1}}}^{4}$

and

$d(x,y,t) =ib_{{1,3}}{x}^{3}+ ( 9\,itb_{{1,3}}{g_{{1}}}^{2}-18\,tb_{{1,3}}g_ {{1}}h_{{1}}-9\,itb_{{1,3}}{h_{{1}}}^{2}-6\,iyb_{{1,3}}g_{{1}} +6\,yb_{ {1,3}}h_{{1}}+b_{{1,2}} ) {x}^{2}+ ( 27\,i{t}^{2}b_{{1,3}}{ g_{{1}}}^{4}-108\,{t}^{2}b_{{1,3}}{g_{{1}}}^{3}h_{{1}}-162\,i{t}^{2}b_ {{1,3}}{g_{{1}}}^{2}{h_{{1}}}^{2} +108\,{t}^{2}b_{{1,3}}g_{{1}}{h_{{1}} }^{3}+27\,i{t}^{2}b_{{1,3}}{h_{{1}}}^{4}-36\,ityb_{{1,3}}{g_{{1}}}^{3} +108\,tyb_{{1,3}}{g_{{1}}}^{2}h_{{1}}+108\,ityb_{{1,3}}g_{{1}}{h_{{1}} }^{2}-36\,tyb_{{1,3}}{h_{{1}}}^{3}+12\,i{y}^{2}b_{{1,3}}{g_{{1}}}^{2}- 24\,{y}^{2}b_{{1,3}}g_{{1}}h_{{1}}-12\,i{y}^{2}b_{{1,3}}{h_{{1}}}^{2}$$+ 6\,tb_{{1,2}}{g_{{1}}}^{2}+12\,itb_{{1,2}}g_{{1}}h_{{1}}-6\,tb_{{1,2}} {h_{{1}}}^{2}+18\,tb_{{1,3}}g_{{1}}+18\,itb_{{1,3}}h_{{1}}-4\,yb_{{1,2 }}g_{{1}}-4\,iyb_{{1,2}}h_{{1}}-6\,yb_{{1,3}}-ib_{{1,1}} ) x-54 \,{t}^{2}b_{{1,2}}{g_{{1}}}^{2}{h_{{1}}}^{2}-b_{{1,0}}-162\,{t}^{3}b_{ {1,3}}g_{{1}}{h_{{1}}}^{5} +54\,{t}^{2}yb_{{1,3}}{h_{{1}}}^{5}-4\,{y}^{ 2}b_{{1,2}}{h_{{1}}}^{2}-162\,{t}^{3}b_{{1,3}}{g_{{1}}}^{5}h_{{1}}+9\, {t}^{2}b_{{1,2}}{h_{{1}}}^{4}+4\,{y}^{2}b_{{1,2}}{g_{{1}}}^{2}-8\,{y}^ {3}b_{{1,3}}{h_{{1}}}^{3}-2\,yb_{{1,1}}h_{{1}}+9\,{t}^{2}b_{{1,2}}{g_{ {1}}}^{4} +54\,{t}^{2}b_{{1,3}}{g_{{1}}}^{3}+12\,{y}^{2}b_{{1,3}}g_{{1} }-54\,i{t}^{2}b_{{1,3}}{h_{{1}}}^{3}+12\,i{y}^{2}b_{{1,3}}h_{{1}}+27\, i{t}^{3}b_{{1,3}}{g_{{1}}}^{6}-27\,i{t}^{3}b_{{1,3}}{h_{{1}}}^{6}-8\,i {y}^{3}b_{{1,3}}{g_{{1}}}^{3}+3\,itb_{{1,1}}{h_{{1}}}^{2}-6\,itb_{{1,2 }}g_{{1}}-3\,itb_{{1,1}}{g_{{1}}}^{2}+2\,iyb_{{1,1}}g_{{1}} +6\,tb_{{1, 2}}h_{{1}}+2\,iyb_{{1,2}}-6\,itb_{{1,3}}+36\,i{t}^{2}b_{{1,2}}{g_{{1}} }^{3}h_{{1}}-36\,i{t}^{2}b_{{1,2}}g_{{1}}{h_{{1}}}^{3}+12\,ityb_{{1,2} }{h_{{1}}}^{3}+8\,i{y}^{2}b_{{1,2}}g_{{1}}h_{{1}}-405\,i{t}^{3}b_{{1,3 }}{g_{{1}}}^{4}{h_{{1}}}^{2}-54\,i{t}^{2}yb_{{1,3}}{g_{{1}}}^{5}+405\, i{t}^{3}b_{{1,3}}{g_{{1}}}^{2}{h_{{1}}}^{4} +36\,it{y}^{2}b_{{1,3}}{g_{ {1}}}^{4}+36\,it{y}^{2}b_{{1,3}}{h_{{1}}}^{4}+24\,i{y}^{3}b_{{1,3}}g_{ {1}}{h_{{1}}}^{2}+162\,i{t}^{2}b_{{1,3}}{g_{{1}}}^{2}h_{{1}}+24\,{y}^{ 3}b_{{1,3}}{g_{{1}}}^{2}h_{{1}}-162\,{t}^{2}b_{{1,3}}g_{{1}}{h_{{1}}}^ {2} +54\,tyb_{{1,3}}{h_{{1}}}^{2}+6\,tb_{{1,1}}g_{{1}}h_{{1}}-12\,tyb_{ {1,2}}{g_{{1}}}^{3}+540\,{t}^{3}b_{{1,3}}{g_{{1}}}^{3}{h_{{1}}}^{3}-54 \,tyb_{{1,3}}{g_{{1}}}^{2}-108\,ityb_{{1,3}}g_{{1}}h_{{1}}-270\,i{t}^{ 2}yb_{{1,3}}g_{{1}}{h_{{1}}}^{4}-216\,it{y}^{2}b_{{1,3}}{g_{{1}}}^{2}{ h_{{1}}}^{2} +540\,i{t}^{2}yb_{{1,3}}{g_{{1}}}^{3}{h_{{1}}}^{2}-36\,ity b_{{1,2}}{g_{{1}}}^{2}h_{{1}}+36\,tyb_{{1,2}}g_{{1}}{h_{{1}}}^{2}-144 \,t{y}^{2}b_{{1,3}}{g_{{1}}}^{3}h_{{1}}+270\,{t}^{2}yb_{{1,3}}{g_{{1}} }^{4}h_{{1}}+144\,t{y}^{2}b_{{1,3}}g_{{1}}{h_{{1}}}^{3}-540\,{t}^{2}yb _{{1,3}}{g_{{1}}}^{2}{h_{{1}}}^{3}$.

We give some figures in the (x, y) plane of coordinates.

Fig. 5

Solutions of order 1 to KPI, on the left for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $g_{1}=0$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; in the center for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $g_{1}=1$, $h_{1}=0$, $d_{1}=1$, $e_{1}=1$; on the right for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $g_{1}=0.01$, $h_{1}=0.01$, $d_{1}=1$, $e_{1}=1$

Fig. 6

Solutions of order 1 to KPI, on the left for $t=0$, $b_{1,0}=10^3$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; in the center for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=10^3$, $g_{1}=1$, $h_{1}=0$, $d_{1}=1$, $e_{1}=1$; on the right for $t=0$, $b_{1,0}=1$, $b_{1,1}=10^3$, $b_{1,2}=1$, $b_{1,3}=10^3$, $g_{1}=0.01$, $h_{1}=0.01$, $d_{1}=1$, $e_{1}=1$

In Figs. 5 and 6, we get lumps depending on 8 real parameters. These structures are more sensitive to $g_{1}$ and $h_{1}$ parameters than to others. In this case, we observe a maximum of three distinct isolated lumps, as shown for example in the Fig. 6 to the left.

Solutions of Order 1 with a Degree of Derivation Equal to 4 ($D=4$) Depending on 9 Real Parameters

In the case $D=4$, the expression of the solutions with all parameters being too long, we present only one of them with particular values of parameters. For example we choose :

$b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$.

So, the solution to the KPI equation, with these choices of parameters, can be written as

$$\begin{aligned} u_{}(x,y,t) = -2 \frac{n(x,y,t)}{d_{}(x,y,t)^{2}} \end{aligned}$$

with

$n(x,y,t) = -4\,{x}^{6}+ ( 48\,y-144\,it+6\,i+48\,iy ) {x}^{5}+ ( 72\,it+5-84\,iy-480\,i{y}^{2}+2160\,{t}^{2}+1440\,iyt-252\,t+60\,y- 1440\,yt ) {x}^{4} + ( -17280\,iy{t}^{2}+3168\,yt-3888\,i{t} ^{2}+192\,it-40\,iy+1440\,iyt+17280\,i{t}^{3}-24\,t-64\,y-1280\,{y}^{3 }+192\,i{y}^{2}-672\,{y}^{2}-17280\,{t}^{2}y-1728\,{t}^{2}+11520\,t{y} ^{2}+1280\,i{y}^{3} ) {x}^{3} + ( -77760\,{t}^{4}-23040\,t{y }^{3}+103680\,{t}^{3}y+24\,iy+384\,i{y}^{2}-6912\,t{y}^{2}+288\,{y}^{2 }+103680\,i{t}^{2}{y}^{2}+28512\,{t}^{3}+2112\,{y}^{3}+960\,i{y}^{3}+ 432\,yt-15552\,i{y}^{2}t+38880\,iy{t}^{2}+2160\,i{t}^{2}+10+3840\,{y}^ {4}-15552\,i{t}^{3}-2304\,iyt-103680\,i{t}^{3}y+72\,t-23040\,it{y}^{3} -12960\,{t}^{2}y-2376\,{t}^{2} ) {x}^{2}$$+ ( -16\,y-84\,t- 256\,{y}^{3}+96\,{y}^{2}+3024\,{t}^{2}-4\,i-28512\,{t}^{3}+138240\,{t} ^{2}{y}^{3}-1536\,{y}^{4}+62208\,{t}^{4}-3072\,{y}^{5}-40\,iy-1472\,i{ y}^{3}+101088\,i{t}^{4}-3456\,i{y}^{4}-864\,i{t}^{2}-186624\,i{t}^{5}- 3072\,i{y}^{5}-168\,i{y}^{2}-12096\,i{t}^{3}+34560\,it{y}^{3}+311040\, i{t}^{4}y-138240\,i{t}^{2}{y}^{3}+9792\,i{y}^{2}t+720\,iyt-9504\,iy{t} ^{2}+46080\,it{y}^{4}-62208\,i{t}^{2}{y}^{2}-51840\,i{t}^{3}y-196992\, {t}^{3}y +114048\,{t}^{2}{y}^{2}-11520\,t{y}^{3}+48\,it-1008\,yt+31104 \,{t}^{2}y-6336\,t{y}^{2}+311040\,{t}^{4}y-414720\,{t}^{3}{y}^{2} ) x-936\,{t}^{2}-7776\,{t}^{3}-131328\,{t}^{2}{y}^{3}-704\,{y}^ {4}+22032\,{t}^{4}-768\,{y}^{5}-12\,{y}^{2}-1-8\,y+72\,t-336\,{y}^{3}- 622080\,i{t}^{4}{y}^{2}-7776\,iy{t}^{2} +269568\,i{t}^{3}{y}^{2}-13824 \,it{y}^{4}+373248\,i{t}^{5}y+276480\,i{t}^{3}{y}^{3}-18432\,it{y}^{5} -24192\,i{t}^{2}{y}^{2}+117504\,i{t}^{3}y-6912\,it{y}^{3}-357696\,i{t} ^{4}y-34560\,i{t}^{2}{y}^{3}+2592\,i{y}^{2}t-139968\,{t}^{5}+186624\,{ t}^{6}+2048\,i{y}^{6}-88128\,i{t}^{4}+1536\,i{y}^{4}-288\,i{t}^{2} + 93312\,i{t}^{5}+2304\,i{y}^{5}+32\,i{y}^{2}+2592\,i{t}^{3}+24\,iy-12\, it+63936\,{t}^{3}y-69120\,{t}^{2}{y}^{2}+16512\,t{y}^{3}-373248\,{t}^{ 5}y +276480\,{t}^{3}{y}^{3}-138240\,{t}^{2}{y}^{4}+18432\,t{y}^{5}-144 \,i{y}^{3}+192\,yt+1728\,{t}^{2}y+1296\,t{y}^{2}+77760\,{t}^{4}y+ 165888\,{t}^{3}{y}^{2}+25344\,t{y}^{4}$

and

$d(x,y,t) = -{x}^{4}+ ( -24\,it+8\,y+8\,iy+i ) {x}^{3}+ ( 216\,{t} ^{2}+144\,ity-144\,ty-48\,i{y}^{2}-54\,t+36\,it-18\,iy+6\,y+1 ) {x}^{2} + ( 864\,i{t}^{3}-864\,{t}^{2}y-864\,i{t}^{2}y+576\,t{y}^{ 2}+64\,i{y}^{3}-64\,{y}^{3}-432\,{t}^{2}-540\,i{t}^{2}+504\,ty+72\,ity -72\,{y}^{2}+48\,i{y}^{2}+30\,it+42\,t-10\,y-4\,iy-i ) x-1-2\,y + 12\,t+112\,{y}^{3}+24\,{y}^{2}-144\,{t}^{2}+4\,iy+16\,i{y}^{3}+468\,i{ t}^{2}+20\,i{y}^{2}-1296\,i{t}^{3}-384\,i{y}^{3}t-720\,i{y}^{2}t-252\, iyt+2376\,i{t}^{2}y+1728\,i{t}^{2}{y}^{2}-1728\,iy{t}^{3}+1512\,{t}^{3 }+64\,{y}^{4}-1296\,{t}^{4}-12\,it +1728\,{t}^{3}y-384\,t{y}^{3}-96\,ty -216\,{t}^{2}y-576\,t{y}^{2}$.

We get multi lumps. We present some figures in the (x, y) plane :

Fig. 7

Solutions of order 1 to KPI, on the left for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; in the center for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $g_{1}=1$, $h_{1}=0$, $d_{1}=1$, $e_{1}=1$; on the right for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $g_{1}=10^3$, $h_{1}=0,01$, $d_{1}=1$, $e_{1}=1$

Fig. 8

Solutions of order 1 to KPI, on the left for $t=0$, $b_{1,0}=10^3$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; in the center for $t=0$, $b_{1,0}=10^2$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $g_{1}=1$, $h_{1}=0$, $d_{1}=0,01$, $e_{1}=0,01$; on the right for $t=1$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $g_{1}=10^3$, $h_{1}=0,01$, $d_{1}=1$, $e_{1}=1$

In Figs. 7 and 8, we get lumps depending on 9 real parameters. These structures are more sensitive to $g_{1}$ and $h_{1}$ parameters than to others. In this case, we observe a maximum of four distinct isolated lumps, as shown for example in the Fig. 8 in the center. In Fig. 8, on the right, there are four isolated lumps aligned on a non rectilinear curve.

Solutions of Order 1 with a Degree of Derivation Equal to 5 ($D=5$) Depending on 10 Real Parameters

In the case $D=5$, the expression of the solutions with all parameters being too long, we present only one of them with particular values of parameters. For example we choose :

$b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $b_{1,5}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$.

The solution to the KPI equation can be written as

$$\begin{aligned} u_{}(x,y,t) = -2 \frac{n(x,y,t)}{d_{}(x,y,t)^{2}} \end{aligned}$$

with

$n(x,y,t) = 5\,{x}^{8}+ ( 240\,it-80\,y-80\,iy-8\,i ) {x}^{7}+ ( 3360\,ty-5040\,{t}^{2}-3360\,ity-112\,y+576\,t+1120\,i{y}^{2}-8+192\,i y-240\,it ) {x}^{6} + ( -4032\,ity+8640\,{t}^{2}+96\,iy- 60480\,i{t}^{3}+4\,i-168\,t+60480\,{t}^{2}y+60480\,i{t}^{2}y-960\,i{y} ^{2}-4480\,i{y}^{3}-40320\,t{y}^{2}-12672\,ty+192\,y+2304\,{y}^{2}+ 4480\,{y}^{3}+14688\,i{t}^{2}-576\,it ) {x}^{5} + ( -5+40\,y -372\,t-14080\,{y}^{3}-1560\,{y}^{2}+12960\,{t}^{2}+97920\,it{y}^{2}- 604800\,i{t}^{2}{y}^{2}-276480\,i{t}^{2}y+134400\,it{y}^{3}+604800\,i{ t}^{3}y+13920\,ity+60480\,{t}^{2}y+57600\,t{y}^{2}-4480\,i{y}^{3}+132 \,it$$+129600\,i{t}^{3}-15840\,i{t}^{2}-124\,iy-1920\,i{y}^{2}+134400\,t {y}^{3}-604800\,{t}^{3}y-480\,ty-190080\,{t}^{3}-22400\,{y}^{4}+453600 \,{t}^{4} ) {x}^{4}+ ( -24\,y+216\,t+2240\,{y}^{3}-992\,{y} ^{2}-19008\,{t}^{2}-3360\,ity-108480\,it{y}^{2}+1036800\,i{t}^{2}{y}^{ 2}-537600\,it{y}^{4}+1612800\,i{t}^{2}{y}^{3}+109440\,i{t}^{2}y- 3628800\,i{t}^{4}y-491520\,it{y}^{3} +483840\,i{t}^{3}y+20\,i+4838400\, {t}^{3}{y}^{2}-3628800\,{t}^{4}y-1612800\,{t}^{2}{y}^{3}-351360\,{t}^{ 2}y+69120\,t{y}^{2}-1399680\,i{t}^{4}+2177280\,i{t}^{5}+72\,it+138240 \,i{t}^{3} +15040\,i{y}^{3}+35840\,i{y}^{5}-288\,i{t}^{2}+43520\,i{y}^{ 4}+40\,iy+1152\,i{y}^{2}+107520\,t{y}^{3}-1520640\,{t}^{2}{y}^{2}+ 2903040\,{t}^{3}y+8928\,ty+319680\,{t}^{3}+25600\,{y}^{4}-1036800\,{t} ^{4}+35840\,{y}^{5} ) {x}^{3}+ ( 10+120\,y-288\,t+7552\,{y} ^{3}+528\,{y}^{2}+9144\,{t}^{2}-15552\,it{y}^{2} +829440\,i{t}^{2}{y}^{ 2}+691200\,it{y}^{4}+967680\,i{t}^{2}{y}^{3}-11197440\,i{t}^{3}{y}^{2} +185760\,i{t}^{2}y+16174080\,i{t}^{4}y-9676800\,i{t}^{3}{y}^{3}- 13063680\,i{t}^{5}y+645120\,it{y}^{5}+193920\,it{y}^{3}-3732480\,i{t}^ {3}y-3744\,ity+21772800\,i{t}^{4}{y}^{2}-8294400\,{t}^{3}{y}^{2}- 1013760\,t{y}^{4}-2177280\,{t}^{4}y +5806080\,{t}^{2}{y}^{3}+207360\,{t }^{2}y-76032\,t{y}^{2}-6531840\,{t}^{6}-240\,it+2695680\,i{t}^{4}- 71680\,i{y}^{6}-4665600\,i{t}^{5}-313632\,i{t}^{3}-2240\,i{y}^{3}- 98304\,i{y}^{5} +10800\,i{t}^{2}-44160\,i{y}^{4}-96\,iy+144\,i{y}^{2}- 516480\,t{y}^{3}+2134080\,{t}^{2}{y}^{2}-1866240\,{t}^{3}y-9676800\,{t }^{3}{y}^{3}+4838400\,{t}^{2}{y}^{4}-645120\,t{y}^{5}+13063680\,{t}^{5 }y-3168\,ty-66528\,{t}^{3}+5971968\,{t}^{5}+23040\,{y}^{4}-777600\,{t} ^{4}+21504\,{y}^{5} ) {x}^{2} + ( -136\,y+156\,t-896\,{y}^{3 }+24192\,it{y}^{2}-1168128\,i{t}^{2}{y}^{2}+368640\,it{y}^{4}-5264640 \,i{t}^{2}{y}^{3}+15240960\,i{t}^{3}{y}^{2}-29030400\,i{t}^{4}{y}^{3}+ 26127360\,i{t}^{6}y-64224\,i{t}^{2}y-3870720\,i{t}^{2}{y}^{5}-10782720 \,i{t}^{4}y+19353600\,i{t}^{3}{y}^{4}+28753920\,i{t}^{3}{y}^{3}- 5225472\,i{t}^{5}y+258048\,it{y}^{5}$$+184320\,it{y}^{3}+2090880\,i{t}^{ 3}y+1680\,ity-31104000\,i{t}^{4}{y}^{2}-7464960\,i{t}^{2}{y}^{4}-384\, {y}^{2}+1584\,{t}^{2}-4\,i-4147200\,{t}^{3}{y}^{2}+1044480\,t{y}^{4}+ 29030400\,{t}^{4}{y}^{3}-52254720\,{t}^{5}{y}^{2} +26127360\,{t}^{6}y+ 860160\,t{y}^{6}-3870720\,{t}^{2}{y}^{5}+17625600\,{t}^{4}y-2776320\,{ t}^{2}{y}^{3}+67104\,{t}^{2}y-7776\,t{y}^{2}-40960\,{y}^{7}+11197440\, {t}^{6}+13810176\,i{t}^{6}-533952\,i{t}^{4}+61440\,i{y}^{6}-2239488\,i {t}^{5} +408\,it-11197440\,i{t}^{7}-7776\,i{t}^{3}-1792\,i{y}^{3}+32256 \,i{y}^{5}-3744\,i{t}^{2}-6656\,i{y}^{4}+40960\,i{y}^{7}-40\,iy-48\,i{ y}^{2}+145920\,t{y}^{3}-93312\,{t}^{2}{y}^{2}-1372032\,{t}^{3}y+ 39813120\,{t}^{4}{y}^{2}-3870720\,{t}^{3}{y}^{3}-5529600\,{t}^{2}{y}^{ 4} +1548288\,t{y}^{5}-46282752\,{t}^{5}y+192\,ty-106272\,{t}^{3}- 10419840\,{t}^{5}-90112\,{y}^{6}-16896\,{y}^{4}+1824768\,{t}^{4}-75264 \,{y}^{5} ) x+224\,{y}^{3}-936\,{t}^{2}+8398080\,{t}^{8}+20480\, {y}^{8}+108\,{y}^{2}-15303168\,i{t}^{6}+11197440\,i{t}^{7}+67392\,i{t} ^{3}+656\,i{y}^{3} +13568\,i{y}^{5}+432\,i{t}^{2}+2176\,i{y}^{4}+8192\, i{y}^{7}+4520448\,{t}^{3}{y}^{2}+17664\,t{y}^{4}-295488\,i{t}^{4}+ 16384\,i{y}^{6}+3592512\,i{t}^{5}-132\,it-491520\,t{y}^{6}-774144\,{t} ^{2}{y}^{5}-5857920\,{t}^{4}y-972288\,{t}^{2}{y}^{3}-22752\,{t}^{2}y+ 4656\,t{y}^{2}+49152\,{y}^{7}-13436928\,{t}^{7} +2612736\,{t}^{6}+ 17694720\,{t}^{3}{y}^{4}-51425280\,{t}^{4}{y}^{3}+44789760\,{t}^{5}{y} ^{2}+5225472\,{t}^{6}y-1-8\,y+72\,t-4608\,t{y}^{3}-181440\,{t}^{2}{y}^ {2}+798336\,{t}^{3}y-36028800\,{t}^{4}{y}^{2}+16243200\,{t}^{3}{y}^{3} -1382400\,{t}^{2}{y}^{4}-408576\,t{y}^{5} +21026304\,{t}^{5}y-245760\,t {y}^{7}+7741440\,{t}^{3}{y}^{5}-29030400\,{t}^{4}{y}^{4}+34836480\,{t} ^{5}{y}^{3}-22394880\,{t}^{7}y+672\,ty+24\,iy+22394880\,i{t}^{7}y-3888 \,it{y}^{2}+266688\,i{t}^{2}{y}^{2}-240384\,it{y}^{4} +1163520\,i{t}^{2 }{y}^{3}-905472\,i{t}^{3}{y}^{2}-5806080\,i{t}^{4}{y}^{3}-53747712\,i{ t}^{6}y-17856\,i{t}^{2}y+5750784\,i{t}^{2}{y}^{5}-3312576\,i{t}^{4}y- 13824000\,i{t}^{3}{y}^{4}+55240704\,i{t}^{5}{y}^{2}-663552\,it{y}^{6}- 245760\,it{y}^{7}-7741440\,i{t}^{3}{y}^{5} +34836480\,i{t}^{5}{y}^{3}+ 2580480\,i{t}^{2}{y}^{6}-10160640\,i{t}^{3}{y}^{3}+30730752\,i{t}^{5}y -740352\,it{y}^{5}-52992\,it{y}^{3}-245376\,i{t}^{3}y-1200\,ity- 52254720\,i{t}^{6}{y}^{2}+272\,i{y}^{2}-7464960\,i{t}^{4}{y}^{2} + 5368320\,i{t}^{2}{y}^{4}-29376\,{t}^{3}+1197504\,{t}^{5}+50688\,{y}^{6 }+2896\,{y}^{4}-768528\,{t}^{4}+7168\,{y}^{5}$

and

$d(x,y,t) = i{x}^{5}+ ( -30\,t-10\,iy+10\,y+1 ) {x}^{4}+ ( -360\,i {t}^{2}+240\,ity+240\,ty-80\,{y}^{2}+60\,t+84\,it-28\,y-8\,iy-i ) {x}^{3} + ( 2160\,{t}^{3}-2160\,{t}^{2}y+2160\,i{t}^{2}y- 1440\,it{y}^{2}+160\,{y}^{3}+160\,i{y}^{3}-1296\,{t}^{2}+1080\,i{t}^{2 }-1224\,ity+144\,ty+168\,i{y}^{2}+120\,{y}^{2}+54\,t-96\,it+18\,iy-6\, y-1 ) {x}^{2} + ( 6480\,i{t}^{4}-8640\,{t}^{3}y-8640\,i{t}^{ 3}y+8640\,{t}^{2}{y}^{2}-1920\,t{y}^{3}+1920\,it{y}^{3}-320\,i{y}^{4}- 7344\,i{t}^{3}-6480\,{t}^{3}+864\,i{t}^{2}y+11664\,{t}^{2}y+2880\,it{y }^{2}-3456\,t{y}^{2}-544\,i{y}^{3}+64\,{y}^{3} +2232\,{t}^{2}+540\,i{t} ^{2}+528\,ity-1104\,ty-108\,i{y}^{2}+72\,{y}^{2}-30\,it-42\,t+10\,y+4 \,iy+i ) x+2\,y-12\,t+720\,it{y}^{2}-232\,{y}^{3}-24\,{y}^{2}- 216\,{t}^{2}-12960\,i{t}^{4}-828\,i{t}^{2}+1+1920\,t{y}^{4}+12960\,{t} ^{4}y-5760\,{t}^{2}{y}^{3}-5544\,{t}^{2}y +2856\,t{y}^{2}+5184\,t{y}^{3 }-12960\,{t}^{2}{y}^{2}-1728\,{t}^{3}y+128\,i{y}^{5}+104\,i{y}^{3}+ 9936\,i{t}^{3}+320\,i{y}^{4}-4\,iy+216\,ty-14688\,i{t}^{2}{y}^{2}+252 \,ity-5760\,i{t}^{2}{y}^{3}-12960\,i{t}^{4}y-8136\,i{t}^{2}y +384\,it{y }^{3}+31968\,i{t}^{3}y+17280\,i{t}^{3}{y}^{2}-20\,i{y}^{2}+12\,it-1512 \,{t}^{3}-7776\,{t}^{5}-384\,{y}^{4}+14256\,{t}^{4}-128\,{y}^{5}$.

We present some figures in the (x, y) plane :

Fig. 9

Solutions of order 1 to KPI, on the left for $t=0$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $b_{1,5}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; in the center for $t=0$, $b_{1,0}=10^3$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $b_{1,5}=1$, $g_{1}=0$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; on the right for $t=0$, $b_{1,0}=10^3$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $b_{1,5}=1$, $g_{1}=1$, $h_{1}=0$, $d_{1}=1$, $e_{1}=1$

Fig. 10

Solutions of order 1 to KPI, on the left for $t=0$, $b_{1,0}=10^3$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $b_{1,5}=1$, $g_{1}=10^3$, $h_{1}=0,01$, $d_{1}=1$, $e_{1}=1$; in the center for $t=0$, $b_{1,0}=10^2$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $b_{1,5}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$; on the right for $t=1$, $b_{1,0}=1$, $b_{1,1}=1$, $b_{1,2}=1$, $b_{1,3}=1$, $b_{1,4}=1$, $b_{1,5}=1$, $g_{1}=1$, $h_{1}=1$, $d_{1}=1$, $e_{1}=1$

In Figs. 9 and 10, we get lumps depending on 10 real parameters. In this case, we observe a maximum of five distinct isolated lumps, as shown for example in the Fig. 10 in the center. In Fig. 10, on the right, there are five lumps aligned on a non rectilinear curve.

Conclusion

By means of a Darboux transformation with particular generating functions, we construct multi-parametric solutions to the KPI equation expressed in terms of a wronskian of order N. These solutions depend on the order of the determinant N, the degree of summation S and the degree of derivation D. In this study, to get rational solutions, we restrict ourselves to the case where $S=1$. In the general case, these rational solutions can be written as a second derivative with respect to x of a logarithm of a wronskian of order N, depending on $N(D+5)$ real parameters. For a rational solution of order N, the numerator is a polynomial in x, y and t of degree $2N-2$ and the denominator a polynomial of degree 2N in x, y and t.

We only give the explicit expressions of the solutions in the simple case of order $N=1$ and degrees of summation between $S=1$ and $S=5$.

All these solutions are different from these constructed with another approach given by the present author [18,19,20,21,22].

It would be relevant to study the cases of order greater or equal to 2 and to realize an exhaustive classification of the solutions to the KPI equation.

We postpone this study to another publication.