Heat and Mass Transfer Analysis of a Three-Dimensional MHD Convective Flow with Sinusoidal Suction in the Presence of Radiation Absorption and Diffusion Thermo Effect

Abstract

The significance of the radiation absorption effect on MHD flow and heat transfer problems has become more important in many industrial applications. Particularly at a high operating temperature, the radiation effect becomes quite significant. Therefore, the primary motive of the current study is to explore the radiation absorption effect along with the diffusion thermo effect on a three-dimensional MHD convective flow of a radiating fluid in the presence of sinusoidal suction. To derive the non-dimensional governing equations, the regular perturbation approach is employed. The effect of various rheological parameters on the velocity, temperature, and concentration fields, as well as skin friction, the Nusselt number, and the Sherwood number, is depicted graphically. Finally, it is highlighted that both radiation absorption and the Dufour effect contribute to the enhancement of shear stress and heat transfer rate at the plate. Furthermore, it has been established that increasing the Reynolds number decelerates the momentum transfer rate while enhancing both the heat and mass transfer rates.

Introduction

During the last few decades, investigators have paid close curiosity to the study of coupled heat and mass transfer flow. This is mostly due to its various applications in the scientific, technical, and industrial sectors. These applications cover a wide range of topics, including chemical processing machinery, oceanic circulation, emergency cooling systems of advanced nuclear reactors, cooling techniques for plastic sheets, fog formation and dissipation, food processing and drying, temperature distribution, moisture control in agricultural fields, and polymer production. A huge volume of studies has been conducted on different aspects of heat and mass transfer with the MHD effect, a few of them are Riaz et al. [1], Javaherdeh et al. [2], Mahanthesh et al. [3], Kataria and Patel [4], Chamkha and Rashad [5], Krishna et al. [6] etc.

A few other works that addressed the three-dimensional MHD convective flow together with sinusoidal suction velocity under various physical situations can be found in Ahmed [7], Zafar et al. [8], Rana et al. [9], Jain and Gupta [10], Rana and Latif [11] etc.

The importance of radiation absorption on the flow of fluids is quite relevant from the perspective of science. Such a phenomenon has been detected in planetary atmospheres while absorbing radiation from neighbouring stars. Additionally, this effect is significant in many industrial applications, encompassing oil reservoirs, thermal insulation, catalytic reactors, reactor safety measures, geothermal systems, etc. To emphasize the relevance of the effects caused by radiation absorption, numerous articles have been published, for instance, Ibrahim et al. [12], Narayana [13], Hernandez and Zueco [14], Venkateswarlu and Narayana [15], Krishna [16] and Azifuzzaman et al. [17]. Convective flow with thermal radiation occurs in many industrial processes, including heating or cooling chambers, energy operations, evaporation from vast reservoirs, solar power technologies, etc. Recently, Anwar et al. [18], Asifa et al. [19], Anwar et al. [20], Wahid et al. [21], and Anwar et al. [22] examined the free convective flow of a radiating fluid in the presence of a magnetic field.

Despite being of lesser magnitude than the effects defined by Fourier's and Fick's laws, the Dufour and Soret effects often go unnoticed in several studies. However, there are many scenarios where exceptions are made. The Dufour effect is essential and unavoidable in several instances, as reported by Eckert and Drake [23]. Studies such as Waini et al. [24], Postelnicu [25], and Kandasamy et al. [26], Kune et al. [27], Zhao et al. [28], Huang and Yih [29] and Reddy et al. [30] delved into various facets of the Dufour effect.

The main goal of the current study is to investigate the three-dimensional MHD mixed convective flow of a radiating fluid with sinusoidal suction velocity, radiation absorption, and the Dufour effect. Numerous publications that have examined different facets of the radiation absorption effect may have been discovered up to this point. However, to our knowledge, none of the research to date has looked at how radiation absorption and diffusion-thermo affect the three-dimensional heat and mass transfer flow of a radiating fluid with sinusoidal suction. The consideration of the radiation absorption effect on a three-dimensional flow with sinusoidal suction velocity makes our problem differ from any other previously existing model, which is also the novelty of the present study.

Basic Equations

The equations for the steady, incompressible, viscous, electrically conducting radiating fluid over an infinite vertical plate under the influence of diffusion-thermo and radiation absorption effects are as follows:

Mass continuity equation (Ahmed [7]):

$$\overrightarrow{\nabla }.\overrightarrow{q}=0.$$

(1)

Momentum equation (Ahmed [7]):

$$\left(\overrightarrow{q}.\overrightarrow{\nabla }\right)\overrightarrow{q}=-\frac{1}{\uprho }\overrightarrow{\nabla }p+\upnu {\nabla }^{2}\overrightarrow{q}+\frac{\overrightarrow{J}\times \overrightarrow{B}}{\uprho }+\overrightarrow{g}.$$

(2)

Energy equation (Ahmed [7]):

$$\uprho {C}_{p}\hspace{0.17em}\left(\overrightarrow{q}.\overrightarrow{\nabla }\right)T=\upkappa {\nabla }^{2}T+\frac{\uprho {D}_{M}{K}_{T}}{{C}_{S}}{\nabla }^{2}C-\overrightarrow{\nabla }.{\overrightarrow{q}}_{r}+\overline{\mathrm{Q} }\left(C-{C}_{\infty }\right).$$

(3)

Species continuity equation (Ahmed [7]):

$$\left(\overrightarrow{q}\cdot \overrightarrow{\nabla }\right)C={D}_{M}{\nabla }^{2}C-\overline{\mathrm{K} }\left(C-{C}_{\infty }\right).$$

(4)

Ohm's Law for moving conductor:

$$\overrightarrow{J}=\upsigma \left(\overrightarrow{E}+\overrightarrow{q}\times \overrightarrow{B}\right).$$

(5)

All the symbols are provided in the nomenclature section.

Problem Formulation

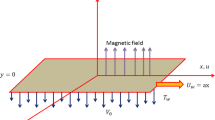
Consider a steady three-dimensional convective hydromagnetic flow of a viscous, incompressible, electrically conducting fluid past a semi-infinite vertical plate. A coordinate reference frame is introduced in which the $\overline{x }$-axis is set parallel to the plate, the $\overline{y }$-axis is orthogonal to the plate, and the $\overline{z }$-axis is orthogonal to the $\overline{x }$-$\overline{y }$ plane. Let $\overrightarrow{q}=(\overline{u },\overline{v },\overline{w }$) be the fluid velocity and $\overrightarrow{B}=\left(0,{B}_{0},0\right)$ be the uniform magnetic field imposed orthogonal to the plate. Figure 1 portrays the physical model of the flow problem.

Fig. 1

Schematic diagram of the problem

Our study is confined to the assumptions listed below:

• 1. Except for the density in the buoyancy force term, all fluid properties are taken to be constant.

• 2. No external electric field is taken into account.

• 3. It is presumed that the plate is electrically non-conducting.

• 4. ${T}_{w}>{T}_{\infty }$ and ${C}_{w}>{C}_{\infty }.$

• 5. It is assumed that the magnetic Reynolds number is sufficiently low so that the effect of the induced magnetic field is considered negligible when compared to the applied magnetic field.

The plate experiences a sinusoidal suction velocity defined by

$${\overline{v} }_{w}=-{V}_{0}\left(1+\upepsilon \hspace{0.17em}\mathrm{cos}\frac{\uppi \overline{z}}{L }\right)$$

(6)

where ${V}_{0}>0$ is the undisturbed part of the suction velocity, $L$ is the wavelength of the periodic suction, and $\upepsilon \left(\ll 1\right)$ is the amplitude of the suction velocity.

Based on the previously mentioned assumptions and utilizing the Boussinesq approximations, Eqs. (1–4) can be simplified to the following expression:

Equation of continuity:

$$\frac{\partial \overline{v} }{\partial \overline{y} }+\frac{\partial \overline{w} }{\partial \overline{z} }=0.$$

(7)

Momentum equations:

$$\overline{v }\frac{\partial \overline{u} }{\partial \overline{y} }+\overline{w }\frac{\partial \overline{u} }{\partial \overline{z} }=g\upbeta \left(T-{T}_{\infty }\right)+g\overline{\upbeta }\left(C-{C}_{\infty }\right)+\upnu \left(\frac{{\partial }^{2}\overline{u} }{\partial {\overline{y} }^{2}}+\frac{{\partial }^{2}\overline{u} }{\partial {\overline{z} }^{2}}\right)-\frac{\upsigma {B}_{0}^{2}\overline{u}}{\uprho },$$

(8)

$$\overline{v }\frac{\partial \overline{v} }{\partial \overline{y} }+\overline{w }\frac{\partial \overline{v} }{\partial \overline{z} }=-\frac{1}{\uprho }\frac{\partial \overline{p} }{\partial \overline{y} }+\upnu \left(\frac{{\partial }^{2}\overline{v} }{\partial {\overline{y} }^{2}}+\frac{{\partial }^{2}\overline{v} }{\partial {\overline{z} }^{2}}\right),$$

(9)

$$\overline{v }\frac{\partial \overline{w} }{\partial \overline{y} }+\overline{w }\frac{\partial \overline{w} }{\partial \overline{z} }=-\frac{1}{\uprho }\frac{\partial \overline{p} }{\partial \overline{z} }+\upnu \left(\frac{{\partial }^{2}\overline{w} }{\partial {\overline{y} }^{2}}+\frac{{\partial }^{2}\overline{w} }{\partial {\overline{z} }^{2}}\right)-\frac{\upsigma {B}_{0}^{2}\overline{w}}{\uprho }.$$

(10)

Energy equation:

$$\overline{v}\frac{\partial T }{\partial \overline{y} }+\overline{w}\frac{\partial T }{\partial \overline{z} }=\frac{\upkappa }{\uprho {C}_{p}}\left(\frac{{\partial }^{2}T}{\partial {\overline{y} }^{2}}+\frac{{\partial }^{2}T}{\partial {\overline{z} }^{2}}\right)+\frac{{D}_{M}{K}_{T}}{{C}_{S}{C}_{p}}\left(\frac{{\partial }^{2}C}{\partial {\overline{y} }^{2}}+\frac{{\partial }^{2}C}{\partial {\overline{z} }^{2}}\right)-\frac{1}{\uprho {C}_{p}}\hspace{0.17em}\overrightarrow{\nabla }.{\overrightarrow{q}}_{r}+\frac{\overline{Q}}{\uprho {C }_{p}}\left(C-{C}_{\infty }\right).$$

(11)

Species continuity equation:

$$\overline{v}\frac{\partial C }{\partial \overline{y} }+\overline{w}\frac{\partial C }{\partial \overline{z} }={D}_{M}\left(\frac{{\partial }^{2}C}{\partial {\overline{y} }^{2}}+\frac{{\partial }^{2}C}{\partial {\overline{z} }^{2}}\right)-\overline{K }\left(C-{C}_{\infty }\right).$$

(12)

By employing the Rosseland approximation (\cite{venkateswarlu2015}), the radiative heat flux $\overrightarrow{{q}_{r}}$ can be determined for an optically thick non-gray gas by the following expression:

$${\overrightarrow{q}}_{r}=-\frac{4{\upsigma }^{*}}{3{\upkappa }^{*}}\hspace{0.17em}\overrightarrow{\nabla }{T}^{4}.$$

(13)

Since, within the fluid flow $\left|T-{T}_{\infty }\right|\ll 1,$ therefore ${T}^{4}$ can be expressed as

$${T}^{4}=\{{T}_{\infty }+\left(T-{T}_{\infty }\right){\}}^{4}\approx 4T{T}_{\infty }^{3}-3{T}_{\infty }^{4}.$$

(14)

Utilizing the Eqs. (13) and (14), Eq. (11) transforms to

$$\overline{v}\frac{\partial T }{\partial \overline{y} }+\overline{w}\frac{\partial T }{\partial \overline{z} }=\frac{\upkappa }{\uprho {C}_{p}}\left(\frac{{\partial }^{2}T}{\partial {\overline{y} }^{2}}+\frac{{\partial }^{2}T}{\partial {\overline{z} }^{2}}\right)+\frac{{D}_{M}{K}_{T}}{{C}_{S}{C}_{p}}\left(\frac{{\partial }^{2}C}{\partial {\overline{y} }^{2}}+\frac{{\partial }^{2}C}{\partial {\overline{z} }^{2}}\right)+\frac{16{\upsigma }^{*}{T}_{\infty }^{3}}{3{\upkappa }^{*}\uprho {C}_{p}}\hspace{0.17em}{\nabla }^{2}T+\frac{\overline{Q}}{\uprho {C }_{p}}\left(C-{C}_{\infty }\right).$$

(15)

The appropriate boundary conditions for the given problem are as follows (Ahmed [7])

$$\overline{u }=U,\hspace{1em}\overline{v }={\overline{v} }_{w},\hspace{1em}\overline{w }=0,\hspace{1em}T={T}_{w},\hspace{1em}C={C}_{w}\hspace{1em}{\text{at}}\hspace{1em}\overline{y }=0$$

(16)

$$\overline{u }\to 0,\hspace{1em}\overline{v }\to -{V}_{0},\hspace{1em}\overline{w }\to 0,\hspace{1em}T\to {T}_{\infty },\hspace{1em}C\to {C}_{\infty },\hspace{1em}\overline{p }\to {\overline{p} }_{\infty }\hspace{1em}{\text{as}}\hspace{1em}\overline{y }\to \infty $$

(17)

Some dimensionless quantities are introduced as follows

$$y=\frac{\overline{y}}{L },\hspace{1em}z=\frac{\overline{z}}{L },\hspace{1em}u=\frac{\overline{u}}{U },\hspace{1em}v=\frac{\overline{v}}{{V }_{0}},\hspace{1em}w=\frac{\overline{w}}{{V }_{0}},\hspace{1em}\uptheta =\frac{T-{T}_{\infty }}{{T}_{w}-{T}_{\infty }},\hspace{1em}\upphi =\frac{C-{C}_{\infty }}{{C}_{w}-{C}_{\infty }},$$

$$\begin{aligned} &{\text{Pr}}=\frac{\upmu {C}_{p}}{\upkappa },\hspace{1em}{\text{Sc}}=\frac{\upnu }{{D}_{M}},\hspace{1em}{\text{Du}}=\frac{{K}_{T}{D}_{M}\hspace{0.17em}\left(C-{C}_{\infty }\right)}{\upnu {C}_{s}{C}_{p}\hspace{0.17em}\left({T}_{w}-{T}_{\infty }\right)},\\&{\text{Gr}}=\frac{Lg\upbeta \hspace{0.17em}\left({T}_{w}-{T}_{\infty }\right)}{U{V}_{0}},\hspace{1em}{\text{Gm}}=\frac{Lg\overline{\upbeta }\hspace{0.17em}\left({C}_{w}-{C}_{\infty }\right)}{U{V}_{0}},\end{aligned}$$

$$M=\frac{\upsigma {B}_{0}^{2}\upnu }{\uprho {V}_{0}^{2}},\hspace{1em}{\text{Re}}=\frac{{V}_{0}L}{\upnu },\hspace{1em}N=\frac{\upkappa {\upkappa }^{*}}{4{\upsigma }^{*}{T}_{\infty }^{3}},\hspace{1em}{Q}_{l}=\frac{\overline{Q }L\hspace{0.17em}\left({C}_{w}-{C}_{\infty }\right)}{\uprho {C}_{p}{V}_{0}\hspace{0.17em}\left({T}_{w}-{T}_{\infty }\right)},\hspace{1em}\upgamma =\frac{L\overline{K}}{{V }_{0}},$$

$$p=\frac{\overline{p} }{\uprho {\left(\frac{\upnu }{L}\right)}^{2}},\hspace{1em}{p}_{\infty }=\frac{{\overline{p} }_{\infty }}{\uprho {\left(\frac{\upnu }{L}\right)}^{2}}.$$

Based on the non-dimensional quantities, the Eqs. (7–10), (12), and (15) are reduced to

$$\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0,$$

(18)

$$v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}={\text{Gr}}\hspace{0.17em}\uptheta +{\text{Gm}}\hspace{0.17em}\upphi +\frac{1}{\text{Re}}\left(\frac{{\partial }^{2}u}{\partial {y}^{2}}+\frac{{\partial }^{2}u}{\partial {z}^{2}}\right)-M\hspace{0.17em}{\text{Re}}\hspace{0.17em}u,$$

(19)

$$v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}=-\frac{1}{{\text{Re}}^{2}}\hspace{0.17em}\frac{\partial p}{\partial y}+\frac{1}{\text{Re}}\left(\frac{{\partial }^{2}v}{\partial {y}^{2}}+\frac{{\partial }^{2}v}{\partial {z}^{2}}\right),$$

(20)

$$v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}=-\frac{1}{{\text{Re}}^{2}}\hspace{0.17em}\frac{\partial p}{\partial z}+\frac{1}{\text{Re}}\left(\frac{{\partial }^{2}w}{\partial {y}^{2}}+\frac{{\partial }^{2}w}{\partial {z}^{2}}\right)-M\hspace{0.17em}{\text{Re}}\hspace{0.17em}w,$$

(21)

$$v\frac{\partial\uptheta }{\partial y}+w\frac{\partial\uptheta }{\partial z}=\frac{1}{\text{Pr Re}}\left(1+\frac{4}{3N}\right)\left(\frac{{\partial }^{2}\uptheta }{\partial {y}^{2}}+\frac{{\partial }^{2}\uptheta }{\partial {z}^{2}}\right)+\frac{\text{Du}}{{\text{Re}}}\left(\frac{{\partial }^{2}\upphi }{\partial {y}^{2}}+\frac{{\partial }^{2}\upphi }{\partial {z}^{2}}\right)+{Q}_{l}\upphi ,$$

(22)

$$v\frac{\partial\upphi }{\partial y}+w\frac{\partial\upphi }{\partial z}=\frac{1}{\text{Sc Re}}\left(\frac{{\partial }^{2}\upphi }{\partial {y}^{2}}+\frac{{\partial }^{2}\upphi }{\partial {z}^{2}}\right)-{\gamma \phi }.$$

(23)

The corresponding boundary conditions are

$$u=1,\hspace{1em}v=-1-\epsilon \mathrm{cos}\pi z,\hspace{1em}w=0,\hspace{1em}\uptheta =1=\upphi \hspace{1em}{\text{at}}\hspace{1em}y=0,$$

(24)

$$u\to 0,\hspace{1em}v\to -1,\hspace{1em}w\to 0,\hspace{1em}\uptheta \to 0,\hspace{1em}\upphi \to 0,\hspace{1em}p\to {p}_{\infty }\hspace{1em}{\text{as}}\hspace{1em}y\to \infty .$$

(25)

Solution Methodology

To solve Eqs. (18–23), we assume the solution of the following form:

$$f\left(y,z\right)={f}_{0}\left(y\right)+\upepsilon {f}_{1}\left(y,z\right)+O\left({\upepsilon }^{2}\right).$$

(26)

where $f$ stands for $u, v, w,$ $\uptheta ,\upphi$ and $p$ with ${p}_{0}={p}_{\infty },$ and ${w}_{0}=0$. Substituting (26) into Eqs. (18–23) and equating the coefficients of ${\upepsilon }^{0}$ and $\upepsilon$, and ignoring the higher order terms of ${\upepsilon }^{2}$, we have the following equations.

Zeroth-order equations:

$$\frac{d{v}_{0}}{dy}=0,$$

(27)

$${v}_{0}\frac{d{u}_{0}}{dy}={\text{Gr}}\hspace{0.17em}{\uptheta }_{0}+{\text{Gm}}\hspace{0.17em}{\upphi }_{0}+\frac{1}{\text{Re}}\frac{{d}^{2}{u}_{0}}{d{y}^{2}}-M\hspace{0.17em}{\text{Re}}\hspace{0.17em}{u}_{0},$$

(28)

$${v}_{0}\frac{d{\uptheta }_{0}}{dy}=\frac{1}{\text{Pr Re}}\left(1+\frac{4}{3N}\right)\frac{{d}^{2}{\uptheta }_{0}}{d{y}^{2}}+\frac{\text{Du}}{{\text{Re}}}\frac{{d}^{2}{\upphi }_{0}}{d{y}^{2}}+{Q}_{l}{\upphi }_{0},$$

(29)

$${v}_{0}\frac{d{\upphi }_{0}}{dy}=\frac{1}{\text{Sc Re}}\frac{{d}^{2}{\upphi }_{0}}{d{y}^{2}}-\upgamma {\upphi }_{0},$$

(30)

The corresponding zeroth order boundary conditions are

$${u}_{0}=1,\hspace{1em}{v}_{0}=0,\hspace{1em}{\uptheta }_{0}=1={\upphi }_{0}\hspace{1em}{\text{at}}\hspace{1em}y=0,$$

(31)

$${u}_{0}=0,\hspace{1em}{v}_{0}=-1,\hspace{1em}{\uptheta }_{0}=0={\upphi }_{0}\hspace{1em}{\text{as}}\hspace{1em}y\to \infty .$$

(32)

First-order equations:

$$\frac{\partial {v}_{1}}{\partial y}+\frac{\partial {w}_{1}}{\partial z}=0,$$

(33)

$$-\frac{\partial {u}_{1}}{\partial y}+{v}_{1}{u}_{0}^{{^{\prime}}}={\text{Gr}}\hspace{0.17em}{\uptheta }_{1}+{\text{Gm}}\hspace{0.17em}{\upphi }_{1}+\frac{1}{\text{Re}}\left(\frac{{\partial }^{2}{u}_{1}}{\partial {y}^{2}}+\frac{{\partial }^{2}{u}_{1}}{\partial {z}^{2}}\right)-M\hspace{0.17em}{\text{Re}}\hspace{0.17em}{u}_{1},$$

(34)

$$-\frac{\partial {v}_{1}}{\partial y}=-\frac{1}{{\text{Re}}^{2}}\frac{\partial {p}_{1}}{\partial y}+\frac{1}{\text{Re}}\left(\frac{{\partial }^{2}{v}_{1}}{\partial {y}^{2}}+\frac{{\partial }^{2}{v}_{1}}{\partial {z}^{2}}\right),$$

(35)

$$-\frac{\partial {w}_{1}}{\partial z}=-\frac{1}{{\text{Re}}^{2}}\frac{\partial {p}_{1}}{\partial z}+\frac{1}{\text{Re}}\left(\frac{{\partial }^{2}{w}_{1}}{\partial {y}^{2}}+\frac{{\partial }^{2}{w}_{1}}{\partial {z}^{2}}\right)-M\hspace{0.17em}{\text{Re}}\hspace{0.17em}{w}_{1},$$

(36)

$$-\frac{\partial {\uptheta }_{1}}{\partial y}+{v}_{1}{\uptheta }_{0}^{{^{\prime}}}=\frac{\Lambda }{\text{Re Pr}}\left(\frac{{\partial }^{2}{\uptheta }_{1}}{\partial {y}^{2}}+\frac{{\partial }^{2}{\uptheta }_{1}}{\partial {z}^{2}}\right)+\frac{\text{Du}}{{\text{Re}}}\left(\frac{{\partial }^{2}{\upphi }_{1}}{\partial {y}^{2}}+\frac{{\partial }^{2}{\upphi }_{1}}{\partial {z}^{2}}\right)+{Q}_{l}{\upphi }_{1},$$

(37)

$$-\frac{\partial {\upphi }_{1}}{\partial y}+{v}_{1}{\upphi }_{0}^{{^{\prime}}}=\frac{1}{\text{Sc Re}}\left(\frac{{\partial }^{2}{\upphi }_{1}}{\partial {y}^{2}}+\frac{{\partial }^{2}{\upphi }_{1}}{\partial {z}^{2}}\right)-\upgamma {\upphi }_{1}.$$

(38)

Subjected to the boundary conditions:

$${u}_{1}=0,\hspace{1em}{v}_{1}=-\mathrm{cos}{\pi }z,\hspace{1em}{w}_{1}=0,\hspace{1em}{\uptheta }_{1}=0={\upphi }_{1}\hspace{1em}{\text{at}}\hspace{1em}y=0,$$

(39)

$${u}_{1}\to 0,\hspace{1em}{v}_{1}\to 0,\hspace{1em}{w}_{1}=0,\hspace{1em}{\uptheta }_{1}\to 0,\hspace{1em}{\upphi }_{1}\to 0,\hspace{1em}{p}_{1}\to 0\hspace{1em}{\text{as}}\hspace{1em}y\to \infty $$

(40)

Solutions of Zeroth-Order Equations

The solutions of Eqs. (27–30) under the conditions (31), (32) are

$${v}_{0}=-1$$

(41)

$${\upphi }_{0}={e}^{-\uplambda y},$$

(42)

$${\uptheta }_{0}=\left(1+{\Lambda }_{1}\right)\hspace{0.17em}{e}^{-\frac{\text{Pr Re}}{\Lambda }y}-{\Lambda }_{1}\hspace{0.17em}{e}^{-\uplambda y},$$

(43)

$${u}_{0}={A}_{0}\hspace{0.17em}{e}^{-\upxi y}+{A}_{4}\hspace{0.17em}{e}^{-\upgamma y}+{A}_{5}\hspace{0.17em}{e}^{-\uplambda y}.$$

(44)

Cross-Flow Solution

To find out the solution of Eqs. (33), (35), and (36) for ${v}_{1},{ w}_{1},$ and ${p}_{1}$, we consider the following transformations

$${v}_{1}=-\uppi \hspace{0.17em}{v}_{11}\left(y\right)\mathrm{cos}{\pi }z,$$

(45)

$${w}_{1}={v}_{11}^{{^{\prime}}}\left(y\right)\mathrm{sin}{\pi }z,$$

(46)

$${p}_{1}={\text{Re}}^{2}\hspace{0.17em}{p}_{11}\left(y\right)\mathrm{cos}{\pi }z.$$

(47)

Here “prime” denotes the differentiation with respect to y.

On substitution of Eqs. (45–47), Eq. (33) is trivially satisfied, and Eqs. (35) and (36) transform to the following form

$${v}_{11}^{{^{\prime}}{^{\prime}}}+{\text{Re}}\hspace{0.17em}{v}_{11}^{{^{\prime}}}-{\uppi }^{2}{v}_{11}=-\frac{\text{Re}}{\uppi }\hspace{0.17em}{p}_{11}^{{^{\prime}}},$$

(48)

$${v}_{11}^{{^{\prime}}{^{\prime}}{^{\prime}}}+{\text{Re}}\hspace{0.17em}{v}_{11}^{{^{\prime}}{^{\prime}}}-\left({\uppi }^{2}+M\hspace{0.17em}{\text{Re}}^{2}\right){v}_{11}^{{^{\prime}}}=-{\text{Re}}\hspace{0.17em}\uppi \hspace{0.17em}{p}_{11}.$$

(49)

with relevant boundary conditions

$${v}_{11}=\frac{1}{\uppi },\hspace{1em}{v}_{11}^{{^{\prime}}}=0\hspace{1em}{\text{at}}\hspace{1em}y=0,$$

(50)

$${v}_{11}\to 0,\hspace{1em}{v}_{11}^{{^{\prime}}}\to 0,\hspace{1em}{p}_{11}\to 0\hspace{1em}{\text{as}}\hspace{1em}y\to \infty .$$

(51)

Subjecting to the boundary conditions (50) and (51), the solution of the Eqs. (48) and (49) are obtained as follows

$${v}_{11}={K}_{0}\hspace{0.17em}\left(\overline{\upeta }\hspace{0.17em}{e}^{-\upeta y}-\upeta \hspace{0.17em}{e}^{-\overline{\upeta }y }\right),$$

(52)

$${p}_{11}=\frac{{K}_{0}\hspace{0.17em}\upeta \hspace{0.17em}\overline{\upeta } }{\uppi \hspace{0.17em}{\text{Re}}}\left({\upeta }_{1}\hspace{0.17em}{e}^{-\upeta y}+\overline{\upeta }\hspace{0.17em}{e}^{-\overline{\upeta }y }\right).$$

(53)

Therefore, the solutions for the velocity components ${v}_{1}$, ${w}_{1}$ and pressure ${p}_{1}$ are as follows

$${v}_{1}=-\uppi \hspace{0.17em}{K}_{0}\hspace{0.17em}\left(\overline{\upeta }\hspace{0.17em}{e}^{-\upeta y}-\upeta \hspace{0.17em}{e}^{-\overline{\upeta }y }\right)\hspace{0.17em}\mathrm{cos}{\pi }z,$$

(54)

$${w}_{1}={K}_{0}\hspace{0.17em}\upeta \hspace{0.17em}\overline{\upeta }\hspace{0.17em}\left({e}^{-\overline{\upeta }y }-{e}^{-\upeta y}\right)\mathrm{sin}{\pi }z,$$

(55)

$${p}_{1}=\frac{{\text{Re}}\hspace{0.17em}{K}_{0}\hspace{0.17em}\upeta \hspace{0.17em}\overline{\upeta }}{\uppi }\left({\upeta }_{1}\hspace{0.17em}{e}^{-\upeta y}+\overline{\upeta }\hspace{0.17em}{e}^{-\overline{\upeta }y }\right)\mathrm{cos}{\pi }z.$$

(56)

Solutions for First Order Velocity, Temperature, and Concentration Field

To obtain the solutions for ${u}_{1}$,${\uptheta }_{1}$, and ${\upphi }_{1}$ from the Eqs. (34), (37), and (38), we assume the following expressions for ${u}_{1},{\uptheta }_{1}, \,\,\mathrm{and}\,\,{\upphi }_{1}.$

$${u}_{1}={u}_{11}\hspace{0.17em}\mathrm{cos}{\pi }z,\hspace{1em}{\uptheta }_{1}={\uptheta }_{11}\hspace{0.17em}\mathrm{cos}{\pi }z,\hspace{1em}{\upphi }_{1}={\upphi }_{11}\hspace{0.17em}\mathrm{cos}{\pi }z$$

(57)

Based on Eq. (57), Eqs. (34), (37), and (38) are transformed to

$${\upphi }_{11}^{{^{\prime}}{^{\prime}}}+\text{Sc Re}\hspace{0.17em}{\upphi }_{11}^{{^{\prime}}}-\left({\uppi }^{2}+\upgamma \text{Sc Re}\right){\upphi }_{11}=-\uppi \hspace{0.17em}\text{Sc Re}\hspace{0.17em}{v}_{11}\hspace{0.17em}{\upphi }_{0}^{{^{\prime}}},$$

(58)

$$\Lambda {\uptheta }_{11}^{{^{\prime}}{^{\prime}}}+\text{Pr Re}{\uptheta }_{11}^{{^{\prime}}}-{\uppi }^{2}\hspace{0.17em}\Lambda {\uptheta }_{11}=-\uppi \hspace{0.17em}\text{Pr Re}\hspace{0.17em}{v}_{11}\hspace{0.17em}{\uptheta }_{0}^{{^{\prime}}}-\text{Pr Du}\hspace{0.17em}\left({\upphi }_{11}^{{^{\prime}}{^{\prime}}}-{\uppi }^{2}\hspace{0.17em}{\upphi }_{11}\right)$$

$$-\text{Pr Re}\hspace{0.17em}{Q}_{l}\hspace{0.17em}{\upphi }_{11},$$

(59)

$${u}_{11}^{{^{\prime}}{^{\prime}}}+{\text{Re}}\hspace{0.17em}{u}_{11}^{{^{\prime}}}-\left({\uppi }^{2}+M\hspace{0.17em}{\text{Re}}^{2}\right)\hspace{0.17em}{u}_{11}=-\text{Gr Re}\hspace{0.17em}{\uptheta }_{11}-\text{Gm Re}\hspace{0.17em}{\upphi }_{11}-\uppi \hspace{0.17em}{\text{Re}}\hspace{0.17em}{v}_{11}\hspace{0.17em}{u}_{0}^{{^{\prime}}}.$$

(60)

With the conditions,

$${u}_{11}=0,\hspace{1em}{\uptheta }_{11}=0,\hspace{1em}{\upphi }_{11}=0,\hspace{1em}{\text{at}}\hspace{1em}y=0,$$

(61)

$${u}_{11}\to 0,\hspace{1em}{\uptheta }_{11}\to 0,\hspace{1em}{\upphi }_{11}\to 0,\hspace{1em}{\text{as}}\hspace{1em}y\to 0.$$

(62)

Solving (58–60), subjecting to the conditions (61) and (62), we get.

$${\phi }_{11}=\lambda \mathrm{ Sc Re }\pi {K}_{0}\left[{A}_{8}{e}^{-\omega y}+{A}_{6} {e}^{-\left(\eta +\lambda \right)y}+{A}_{7} {e}^{-y\left(\overline{\eta }+\lambda \right)}\right].$$

(63)

$${\theta }_{11} ={F}_{0} {e}^{-\overline{\omega }y}+{F}_{1} {e}^{-y\left(\eta +\gamma \right)}+{F}_{2} {e}^{-y\left(\eta +\lambda \right)}+{F}_{3} {e}^{\left(-\left(\overline{\eta }+\gamma \right)y\right)}+$$

$${F}_{4}{e}^{-y\left(\overline{\eta }+\lambda \right)}+{F}_{5} {e}^{-\omega y}.$$

(64)

$$\begin{aligned}{u}_{11}=&{I}_{0}{e}^{-\alpha y}+{I}_{1} {e}^{-y\left(\eta +\xi \right)}+{I}_{2} {e}^{-y\left(\eta +\gamma \right)}+{I}_{3} {e}^{-y\left(\eta +\lambda \right)}+{I}_{4} {e}^{-y\left(\overline{\eta }+\xi \right)}+{I}_{5} {e}^{-y\left(\overline{\eta }+\gamma \right)}\\& +{I}_{6} {e}^{-y\left(\overline{\eta }+\lambda \right)}+{I}_{7} {e}^{-\overline{\omega }y}+{I}_{8} {e}^{-\omega y}.\end{aligned}$$

(65)

For engineering purposes, the coefficient of skin friction $\tau$, the heat transfer coefficient characterized by Nusselt number Nu, or the rate of mass transfer corresponding to Sherwood number Sh at the plate in the non-dimensional form are as follows

$$\tau =-{\left.\frac{\partial u}{\partial y}\right]}_{y=0}, {\text{Nu}}=-{\left.\frac{\partial \theta }{\partial y}\right]}_{y=0}, {\text{and}}\hspace{1em}{\text{Sh}}=-{\left.\frac{\partial \phi }{\partial y}\right]}_{y=0}.$$

(66)

Results and Discussions

The analytical results obtained in the previous section for velocity, temperature, and concentration, as well as for skin friction, Nusselt number, and Sherwood number, are explored graphically for various parameters that are involved in flow problems and flow characteristics. For the computations, we have fixed the following parameters: $\mathrm{Pr }= 0.71$, which corresponds to air, $\mathrm{Sc}=0.6$ refers to the water vapor diffused in dry air, and $\upepsilon =0.01$, $z=0, \mathrm{Gr} =5 =\mathrm{ Gm}$ are chosen arbitrarily.

Figure 2 reveals that escalating the value of the Dufour number Du improves the velocity profiles. As the Dufour effect intensifies, the thermal buoyancy force within the velocity field strengthens, leading to an acceleration of fluid velocity.

Fig. 2

Velocity profiles for distinct Du

Figure 3 illustrates that the fluid velocity within the boundary layer region is reduced by augmenting the magnetic field parameter. This deceleration is attributed to the presence of the Lorentz force, which opposes the fluid motion. The impact of Reynolds number on velocity and temperature distributions are spotted in Figs. 4 and 5, respectively. These figures make it obvious that the velocity and temperature distributions are decreasing functions of the Reynolds number. In general, rising values of the Reynolds number accelerate fluid velocity; however, in our investigation, the reverse phenomena might be seen. This is because, as the Reynolds number grows, the suction effect takes precedence over viscosity, causing the fluid velocity to decrease.

Fig. 3

Velocity profiles for distinct M

Fig. 4

Velocity profiles for distinct Re

Fig. 5

Temperature profiles for distinct Re

The effects of the radiation absorption parameter ${Q}_{l}$ on fluid velocity and temperature are highlighted in Figs. 6 and 7, respectively. These outcomes indicate that velocity and temperature distributions accelerate due to distinct augmenting values of radiation absorption ${Q}_{l}$. Physically, as ${Q}_{l}$ is raised, conduction over absorption radiation becomes more dominant. Consequently, this amplifies the buoyancy force and leads to an increase in the thickness of both the hydrodynamic and thermal boundary layers. The influence of the Dufour number Du on temperature distributions is portrayed in Fig. 8. It can be seen from this figure that fluid temperature enhances with increasing Dufour number Du. As we increase the magnitude of Du, the concentration gradients within the temperature field become more pronounced. This results in an elevation of temperature and an expansion of the thermal boundary layer's thickness.

Fig. 6

Velocity for different ${Q}_{l}$

Fig. 7

Temperature for different ${Q}_{l}$

Fig. 8

Temperature for distinct Du

Figures 2, 4, 5, 6, 7, 8 further demonstrates that the temperature and fluid velocity both first rise in a thin layer next to the plate before falling asymptotically and tend to their minimum value at $y=0$, demonstrating that the buoyancy force has a significant impact on the flow close to the plate and that this impact is negligible in the free stream.

The concentration distributions for distinct values of chemical reaction γ and Reynolds number Re are displayed in Figs. 9 and 10. These results reveal that the concentration profiles are inversely proportional with chemical reaction parameter $\upgamma$ and Reynolds number Re. The primary explanation is that as chemical reaction parameters increase, the number of solute molecules experiencing chemical reactions rises, which causes a decline in the concentration field. As an outcome, a destructive chemical reaction dramatically minimizes the thickness of the solutal boundary layer.

Fig. 9

Concentration for distinct γ

Fig. 10

Concentration profiles for Re

The effects of the Dufour effect (Du), radiation absorption parameter ${Q}_{l}$, and magnetic parameter M on skin friction coefficients are illustrated in Figs. 11, 12, 13. These figures reveal that the shear stress or drag force experienced by the plate is increased due to the presence of the Dufour effect and radiation absorption effect. However, the shear stress or drag force is reduced when the magnetic field is applied.

Fig. 11

Impact of Du on skin friction

Fig. 12

Impact of ${Q}_{l}$ on skin friction

Fig. 13

Impact of $M$ on skin friction

Figures 14 and 15 clearly indicate that the heat transfer rate, represented by the Nusselt number, demonstrates an upward trend for both the radiation absorption effect and the Dufour effect. These outcomes reflect that heat transfer by convection plays a more significant role than heat transfer by conduction for both the radiation absorption and the Dufour effect.

Fig. 14

Impact of ${Q}_{l}$ on Nusselt number

Fig. 15

Impact of Du on Nusselt number

Figures 16 and 17 assert that the Sherwood number, which measures the rate of mass transfer at the plate, increases for both the chemical reaction parameter $\upgamma$ and Schmidt number Sc. These findings explored the fact that, under the impact of a chemical reaction and Schmidt number, mass transfer by convection is faster than mass transfer by diffusion. Figures 11, 12, 13, 14, 15, 16, 17 further indicate that the growing value of the Reynolds number shrinks the skin friction while increasing the Nusselt and Sherwood numbers. Physically, it reveals that low viscosity slows the momentum transfer rate while boosting heat and mass transfer rates at the plate.

Fig. 16

Sherwood number for γ

Fig. 17

Sherwood number for Sc

Conclusions

This theoretical study investigates how radiation absorption and diffusion thermo affect a three-dimensional MHD convective flow of a radiating fluid with sinusoidal suction velocity and chemical reaction. The perturbation technique is employed to compute the set of governing equations. The previous section includes a graphical illustration of the effects of different factors on velocity, temperature, concentration, skin friction, and Nusselt and Sherwood numbers. Based on the previous results and discussion section, some of the significant findings of our study are as follows:

• The growing values of the Dufour number and radiation absorption parameter accelerate the fluid velocity and temperature profiles within the boundary layer region.

• As the Reynolds number expands, the hydrodynamic, thermal, and solutal boundary layer thickness shrinks asymptotically.

• Both the drag force and the rate of heat transfer at the wall are accelerated by the existence of radiation absorption and Dufour effects.

• The amplification of the chemical reaction parameter has accelerated the mass transfer rate at the plate.

• Additionally, it can be identified that the drag force at the wall asymptotically declines as the Reynolds number rises, although the rate of heat and mass transfer exhibits a completely opposite behaviour.

Appendix I

$$ \begin{aligned} \lambda =&\, \frac{{{\text{Sc Re}} + \sqrt {\left( {\text{Re Sc}} \right)^{2} +4\gamma \,{\text{Re Sc}}} }}{2}, \lambda_{1} = \frac{{1 + \sqrt {1 +4M} }}{2}, \\ \overline{\lambda }_{1} = &\,\frac{{1 - \sqrt {1 + 4M}}}{2}, \xi = {\text{Re}}\lambda_{1} ,\overline{\xi } ={\text{Re}}\overline{\lambda }_{1} ,\end{aligned}$$

$$ \Lambda = 1 + \frac{4}{3N}, \Lambda_{0} = {\text{Pr Du}}{\lambda^{2}} + Q_{l} \,{\text{Pr Re}}, \lambda_{1} = \frac{{\Lambda_{0} }}{{\lambda^{2} \Lambda - {\text{Pr Re }}\lambda}}, \gamma_{1} = \frac{{\text{Pr Re}}}{\Lambda }, $$

$$\begin{aligned} {\upeta } = &\,\frac{{{\upxi } + \sqrt {{\upxi }^{2} + 4{\uppi }^{2} } }}{2},{\overline{\eta }} = \frac{{{\overline{\xi }} - \sqrt {\overline{\xi }^{2} + 4{\uppi }^{2} } }}{2}, \\K_{0} = &\,\frac{1}{{{\uppi }\left({{\overline{\eta }} - {\upeta }} \right)}}, {\upeta }_{1} = {\upeta }^{2} - {\upeta }\,{\text{Re}} - \left( {{\uppi }^{2} +M\,{\text{Re}}^{2} } \right),\end{aligned} $$

$$ \overline{{{\upeta }_{1} }} = - \overline{\eta }^{2} + {\overline{\eta }}\,{\text{Re}} + \left( {{\uppi }^{2} + M\,{\text{Re}}^{2} } \right),{\upomega } = \frac{{{\text{Sc Re}} + \sqrt {\left( {\text{Sc Re}} \right)^{2} + 4\left( {{\uppi }^{2} + {\upgamma }\,{\text{Sc Re}}} \right)} }}{2}, $$

$$\begin{aligned}{\overline{\omega }} = &\,\frac{{{\text{Pr Re}} + \sqrt {\left({\text{Pr Re}} \right)^{2} + 4{\Lambda }^{2} \,{\uppi }^{2} } }}{2},R\left( D \right) = D^{2} + {\text{Re}}\,D - M\,{\text{Re}}^{2} ,\\A_{1} = &\,\frac{{1 + {\Lambda }_{1} }}{{R\left( { - {\upgamma }_{1} }\right)}},A_{2} = \frac{{{\Lambda }_{1} }}{{R\left( { - {\uplambda }} \right)}}, \end{aligned}$$

$$ A_{3} = \frac{1}{{R\left( { - {\uplambda }} \right)}},\quad A_{0} = 1 + {\text{Gr Re}}\,\left( {A_{1} - A_{2} } \right) + {\text{Gm Re}}\,A_{3} ,\quad A_{4} = - {\text{Gr Re}}\,A_{1} , $$

$$ A_{5} = {\text{Re}}\,\left( {{\text{Gm}}\,A_{2} - {\text{Gr}}\,A_{3} } \right),\quad f\left( D \right) = D^{2} + {\text{Sc Re}}\,D - \left( {{\uppi }^{2} + {\upgamma }\,{\text{Sc Re}}} \right),\quad A_{6} = \frac{{{\overline{\eta }}}}{{f\left( { - {\upeta } - {\uplambda }} \right)}}, $$

$$ A_{7} = \frac{{\upeta }}{{f\left( { - {\overline{\eta }} - {\uplambda }} \right)}},\quad A_{8} = - A_{6} - A_{7} ,\quad {\upgamma }_{2} = {\text{Pr Re}}\,{\uppi }\,K_{0} ,\quad B_{1} = {\upgamma }_{2} \,{\overline{\eta }}\,{\upgamma }_{1} \,\left( {1 + {\Lambda }_{1} } \right), $$

$$ B_{2} = - {\upgamma }_{2} \,{\overline{\eta }}\,{\Lambda }_{1} {\uplambda },B_{3} = - {\upgamma }_{2} \,{\upeta }\,{\upgamma }_{1} \,\left( {1 + {\Lambda }_{1} } \right),{ }\gamma_{3} = {\upgamma }_{2} \,{\text{Du Sc}}\,{\uplambda },\quad B_{5} = - {\upgamma }_{3} \,{\upomega }^{2} \,A_{8} , $$

$$ B_{6} = - {\upgamma }_{3} \,\left( {{\upeta } + {\uplambda }} \right)^{2} \,A_{6} ,B_{7} = - {\upgamma }_{3} \,\left( {\overline{\eta }^{2} + {\uplambda }} \right)^{2} \,A_{7} ,\quad {\Gamma }_{0} = {\text{Pr}}\,\left( {{\uppi }^{2} \,Du - {\text{Re}}\,Q_{l} } \right), $$

$$ \begin{aligned}{\Gamma }_{1} =&\, {\Gamma }_{0} \,{\uplambda }\,{\uppi }\,{\text{Re Sc}}\,K_{0} , B_{8} = {\Gamma }_{1} A_{8} ,B_{9} = {\Gamma }_{1}A_{6} ,{ }\\B_{10} = &\,{\Gamma }_{1} A_{7} , {\Omega }\left( D \right) ={\Lambda }\,D^{2} + {\text{Pr Re}}\,D - {\Lambda }\,{\uppi }^{2} ,\end{aligned}$$

$$\begin{aligned} E_{1} =&\,B_{2} + B_{6} + B_{9} ,E_{2} = B_{4} + B_{7} + B_{10} ,\\E_{3} =&\,B_{5} + B_{8} ,{ }F_{1} = \frac{{B_{1} }}{{{\Omega }\left( { -{\upeta } - {\upgamma }_{1} } \right)}},{ }F_{2} = \frac{{E_{1}}}{{{\Omega }\left( { - {\upeta } - {\uplambda }} \right)}},\end{aligned}$$

$$\begin{aligned} F_{3} =&\,\frac{{B_{3} }}{{{\Omega }\left( { - {\overline{\eta }} - {\upgamma }_{1} } \right)}},\quad F_{4} = \frac{{E_{2} }}{{{\Omega }\left( { -{\overline{\eta }} - {\upgamma }_{1} } \right)}},\\ F_{5} =&\,\frac{{E_{3} }}{{{\Omega }\left( { - {\upomega }} \right)}},\quad F_{0} = - \mathop \sum \limits_{i = 1}^{5} F_{i} ,\quad {\Gamma }_{2} = {\uppi }\,{\text{Re}}\,K_{0} ,\end{aligned}$$

$$\begin{aligned}{\upalpha } = &\,\frac{{{\text{Re}} + \sqrt {{\text{Re}}^{2} + 4\left({{\uppi }^{2} + M\,{\text{Re}}^{2} } \right)} }}{2},\quad G_{1} ={\Gamma }_{2} \,{\overline{\eta }}\,{\upxi }\,A_{0} ,\\ G_{2} =&\,{\Gamma }_{2} \,{\overline{\eta }}\,{\upgamma }_{1} \,A_{4} ,\quad G_{3} = {\Gamma }_{2} \,{\overline{\eta }}\,{\uplambda }\,A_{5} ,\end{aligned}$$

$$ \begin{aligned}G_{4} =&\,- {\Gamma }_{2} \,{\upeta }\,{\upxi }\,A_{0} ,{ }G_{5} = - {\Gamma }_{2} \,{\upeta }\,{\upgamma }_{1} \,A_{4} ,{ }G_{6} = - {\Gamma }_{2} \,{\upeta }\,{\uplambda }\,A_{5} ,\\ G_{7} =&\, - {\text{Gr Re}}\,F_{0} ,{ }G_{8} = { } - {\text{Gr Re}}\,F_{1} ,G_{9} = -{\text{Gr Re}}\,F_{2} ,\\ G_{10} =&\, - {\text{Gr Re}}\,F_{3} ,{}G_{11} = - {\text{Gr Re}}\,F_{4} ,{ }G_{12} = - {\text{Gr Re}}\,F_{5} ,\end{aligned} $$

$$ {\Gamma }_{3} = {\text{Gm}}\;{\text{Re}}^{2} \,{\uplambda }\,{\uppi }\,{\text{Sc}}\,K_{0} , G_{13} = - {\Gamma }_{3} \,A_{8} ,\quad G_{14} = - {\Gamma }_{3} \,A_{6} ,\quad G_{15} = {\Gamma }_{3} \,A_{7} , $$

$$ G_{16} = G_{2} + G_{8} ,\quad G_{17} = G_{3} + G_{9} + G_{14} ,{ }G_{18} = G_{5} + G_{10} ,\quad G_{19} = G_{6} + G_{11} + G_{15} , $$

$$ G_{20} = G_{12} + G_{13} ,\quad G\left( D \right) = D^{2} + {\text{Re}}\,D - \left( {{\uppi }^{2} + M\,{\text{Re}}^{2} } \right),{ }I_{1} = \frac{{G_{1} }}{{G\left( { - {\upeta } - {\upxi }} \right)}}, $$

$$\begin{aligned} I_{2} =&\,\frac{{G_{16} }}{{G\left( { - {\upeta } - {\upgamma }_{1} }\right)}},\quad I_{3} = \frac{{G_{17} }}{{G\left( { - {\upeta } -{\uplambda }} \right)}},\quad I_{4} = \frac{{G_{4} }}{{G\left( { -{\overline{\eta }} - {\upxi }} \right)}},\\ I_{5} = &\,\frac{{G_{18}}}{{G\left( { - {\overline{\eta }} - {\upgamma }_{1} }\right)}},\quad I_{6} = \frac{{G_{19} }}{{G\left( { -{\overline{\eta }} - {\uplambda }} \right)}},\end{aligned}$$

$$ I_{7} = \frac{{G_{7} }}{{G\left( { - {\overline{\omega }}} \right)}},\quad I_{8} = \frac{{G_{20} }}{{G\left( { - {\upomega }} \right)}},\quad I_{0} = - \mathop \sum \limits_{k = 1}^{8} I_{k} $$