Abstract
This article’s main objective is to derive the existence criterion for positive solutions and establish Hyers-Ulam (HU) stability of the fractional differential equations (FDEs).This equation is studies with nonlocal conditions. We explore the reuslt by using the Atangana-Baleanu fractional derivative in the Caputo’s sense. We study the FDEs with two different order fractional derivatives and the p-Laplacian operator. The FDEs will be converted into the equivalent solution in the integral equation form via the Green function for these goals. This problem’s existence and uniqueness (EU) criterion is established by utilizing some known fixed point techniques. The uniqueness of the solution is also investigated via the Banach contraction principle. The positiveness of the solution is investigated with the help of the Green function, whether it is decreasing or increasing function. For the application of the problem, an example is also presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The fractional differential equations (FDEs) have been widely deployed to diverse areas of aeronautical engineering, biology, physics, mechanics, and chemistry. Mainly, FDEs have a lot of application in the modeling of numerous phenomena in different fields of engineering and science such as heat conduction, signals, fluid mechanics, and hydrodynamics[1, 2]. FDEs that globalize the usual notion of derivative and integral operators to derivatives and integrals of arbitrarily (fractional) order. In the last few years, the notion of FDEs received more attention due to their considerable interest in various fields [3,4,5]. Recently, FDEs with multiple types of derivatives like Caputo derivative, Riemann-Liouville (R-L) derivative, Hilfer fractional derivative, Hadamard derivative have been studied by many researchers. Recently, Caputo and Fabrizio [6] developed a derivative based on the exponential decay law, which helped to explore the area of FDEs. The influence of this derivative is that this derivative does not have singularity since the exponential kernel function is used. The FDEs using this new derivative have been established with significant results [7, 8]. But, the associated integral with the Caputo and Fabrizio derivative is in the term of classical order. Atangana and Baleanu established the new derivative with Mittag Leffler (ML) function to fix this problem. Atangana-Baleanu derivative and its considerable results in diverse fields we suggest the reader refer [9].
There has been a growing interest in the evolution of sequential FDEs with the p-Laplacian operator in many fields of research. The turbulent flow is a fundamental mechanics problem in a porous medium. For solving this type of issue, Leibenson [10] developed the p-Laplacian operator as follows:
Later on, many important results have been established related to (1) with various type of boundary conditions see the reader [11,12,13,14,15]. Many researchers have described the EU results for FDEs with the p-Laplacian operator; for example, Li and He [16] established the positive solutions for FDEs involving the p-Laplacian operator with four-point boundary conditions. The existence of upper and lower solutions is proved using the monotone iterative method:

where \(1< \chi ,\varsigma ^*\le 2\) and \( {\mathcal {D}}^{\varsigma ^*} ,{\mathcal {D}}^{\chi } \) are fractional derivative in the form of Riemann-Liouville differentiations. The following is the integral boundary value problem involving a fractional p-Laplacian equation in the form of mixed fractional derivatives[17]:

where \(1< \chi ,\varsigma ^*\le 2\) and \( {\mathcal {D}}^{\varsigma ^*} ,{\mathcal {D}}^{\chi } \) are fractional derivative in the form of Riemann-Liouville differentiations,  denotes the
denotes the  -Laplacian operator and satisfies the
-Laplacian operator and satisfies the  . The following is the integral boundary value problem involving a fractional p-Laplacian equation in the form of mixed fractional derivatives[17]:
. The following is the integral boundary value problem involving a fractional p-Laplacian equation in the form of mixed fractional derivatives[17]:

where \(f \in C([0, 1] \times {\mathbb {R}}^{2},{\mathbb {R}})\) is a nonlinear function, \( ~^{\mathcal {C}}_{0}\mathcal {D}^{{\chi }}, ~^{\mathcal {C}}_{0}\mathcal {D}^{\varsigma ^*} \) be the derivatives of fractional order \({ \chi }\) and \(\varsigma ^*\) are the Caputo fractional such that \(0<\varsigma ^*, \chi \le 1\), \(\nu , \epsilon _{1}, j \in {\mathbb {R}}, \xi , \alpha \in [0, 1].\) The HU stability and existence of positive solution for a class of singular FDEs in Caputo sense with nonlinear p-Laplacian operator is discussed by Khan et al. [18]. Aslam et al. explored the EU and HU stability results for singular delay FDEs with p-Laplacian fractional boundary conditions[19]. Matar et al. studied the existence criterion for nonperiodic FDEs in the form of generalized Caputo sense with the p-Laplacian[20]. The EU result for Langevin FDEs by using the Bielecki norm with the modified argument is investigated by Faruk Develi [21]. A particular form of the equations is derived, and the uniqueness of the solutions is studied by utilizing the Burton’s method. Seda Igret Araz [22] presented a new general condition for the EU of solutions for the integro FDEs by using the notion of fractal-fractional derivative and AB- integral under contraction mapping. Devi et al. [23] analyzed the stability and EU of solutions for a general FDEs with the help of green function and nonlocal conditions by utilizing the fixed point technique. Khan et al.[24] and Xiaoyan Li [25] investigated the existence and HU stability for a nonlinear singular FDEs with ML-kernel involving local conditions. However, several FDEs are yet to be investigated and enlarged to real space problems. The theory of FDEs with various boundary conditions is still in the beginning phase, and many characteristics of this theory need to be investigate. A boundary condition is a direction, some sequence of values of the unknown solution. Recently, the notion of boundary value problem for FDEs with the positive solution is studied very little in Banach space until now. Also, there are very few papers on FDEs with the p-Laplacian operator involving AB-fractional derivative in Caputo’s sense.
Motivated by the above discussions, our primary objective is to investigate the EU of solutions for singular FDEs in Banach space. The main contribution of this article is the singular FDEs is discussed with nonlocal integral boundary conditions instead of local conditions. Moreover, the accomplished solution in this manuscript are generalized and improve the existing literature works.
where \( ~^{\mathcal {ABC}}_{0}\mathcal {D}^{{\chi }}, ~^{\mathcal {ABC}}_{0}\mathcal {D}^{\varsigma ^*} \) be the derivatives of fractional order \({ \chi }\) and \(\varsigma ^*\) in the left AB-derivative Caputo’s sense respectively and  is continuous function. The orders \(0< \chi \le 1, 1<\varsigma ^*\le 2 , \delta >0,<\epsilon _{1}<1 \) and
is continuous function. The orders \(0< \chi \le 1, 1<\varsigma ^*\le 2 , \delta >0,<\epsilon _{1}<1 \) and  be the
be the  -Laplacian operator and satisfies the
-Laplacian operator and satisfies the  .
.
The scheme of the remaining article is as planned out as follows: we recall some notations and basic definitions which are desired in the discussion in the next section. \( 2^{nd}\) section would introduce certain properties of the green function to find the desired results. \( 3^{rd}\) is devoted to deriving the EU results through the fixed point technique. Further, we also establish the HU stability in \( 4^{th}\) part. At the end, we discuss an application to analyze our outcome more apparently.
Basic results and Preliminaries
Definition 2.1
[2] For \(\chi >0,\) The R-L fractional integral of order \( \chi \in {\mathbb {R}}\) for a continuous function  is defined as
is defined as
provided that such integral exists.
Definition 2.2
[1] For \(\chi \ge 0\),  is a integrable and continuous function, the R-L fractional derivative of order \(\chi \) is defined as
is a integrable and continuous function, the R-L fractional derivative of order \(\chi \) is defined as
where \([\chi ]\) represent the gratest-integer.
Definition 2.3
[1] For n-times continuously differentiable function  , Caputo fractional derivative of order \( \chi \in {\mathbb {R}} ~(\chi >0)\) is defined as
, Caputo fractional derivative of order \( \chi \in {\mathbb {R}} ~(\chi >0)\) is defined as
where \([\chi ]\) represent the gratest-integer.
Definition 2.4
[27] Let \(0<\chi \le 1 \) and  , where \(0\le a<b\), the Caputo AB-fractional derivative and the R-L AB-fractional derivative of order \(\chi \) are defined as
, where \(0\le a<b\), the Caputo AB-fractional derivative and the R-L AB-fractional derivative of order \(\chi \) are defined as
and
respectively, where \(E_{\chi }\) is called the Mittag-Leffler function and given by

and \(B(\chi )\) is a normalizing positive function satisfying \(B(0)=B(1)=1\).
Definition 2.5
[27] Let \(0<\chi \le 1 \) and  , where \(0 \le a<b\), the associated AB-fractional integral is
, where \(0 \le a<b\), the associated AB-fractional integral is
where \(I^{\chi }\) is the R-L fractional integral defined in (3).
Lemma 2.1
[26] The fractional derivative AB-integral of the fuction  is given by
is given by
where \(I^{\chi ^*}\) is the R-L fractional integral defined in (3).
Lemma 2.2
[2] Let  and
and  , then
, then
for the \(a_{j}\in {\mathbb {R}}\) for \(j=0,1,2,\ldots ,k-1.\)
Theorem 2.3
[29, 30](Guo-Krasnosel’skii Theorem ) Consider \({{\mathcal {Y}}}^{*}\) be a Banach space and let a cone \({\mathfrak {P}}^{*}\in {\mathcal {Y}}^{*} \). Assume that \(\mathcal {A}^{*}_1,\mathcal {A}^{*}_2\) are two bounded subset of \({\mathcal {Y}}^{*}\) such that \(0\in \mathcal {A}^{*}_{1},~ \overline{\mathcal {A}^{*}_1}\subset \mathcal {A}^{*}_{2}\). Then, a operator \(\mathcal {G}^{*}:{\mathfrak {P}}^{*}\cap (\overline{\mathcal {A}^{*}_2} \setminus \mathcal {A}^{*}_{1})\longrightarrow {\mathfrak {P}}^{*},\) which is completely continuous and satisfying the following

Then \( \mathcal {G}^{*}\) has a fixed point in \({\mathfrak {P}}^{*}\cap (\overline{\mathcal {A}^{*}_{2}} \setminus \mathcal {A}^{*}_{1}).\)
Lemma 2.4
[23, 24] For the  -Laplacian operator
-Laplacian operator  , the following conditions are hold true \((1)\, \text { If }\, |\gamma _{1}|, |\gamma _{2}|\ge \mu>0,~1<{\mathcal {p}}\le 2,~\gamma _{1},\gamma _{2}>0\), then
, the following conditions are hold true \((1)\, \text { If }\, |\gamma _{1}|, |\gamma _{2}|\ge \mu>0,~1<{\mathcal {p}}\le 2,~\gamma _{1},\gamma _{2}>0\), then

\((2)\,\text { If }\, {\mathcal {p}}> 2,|\gamma _{1}|, |\gamma _{2}|\le \mu ^{*}>0\), then

Green function
Theorem 3.1
Let  and \( \varsigma ^* \in (1,2)\) such that
and \( \varsigma ^* \in (1,2)\) such that  then FDEs (2) with \(\phi ^{*}_p\) operator has the following integral form
then FDEs (2) with \(\phi ^{*}_p\) operator has the following integral form
where the Green’s function  is definied by
is definied by
Proof
Taking the integral operator \(^{\mathcal{AB}\mathcal{}}\mathcal {I}^{\chi }\) to both sides (2) and using Lemma (2.1) the given equation (2) becomes
As given condition  , put the value of \(b_0=0\), then (11) convert in
, put the value of \(b_0=0\), then (11) convert in
Applying q-Laplacian opertaor further (12) get the form
Again using Lemma (2.1), then (13) becomes
where \( a_{j}\in {\mathbb {R}}\) for \(j=0,1.\)
Using boundary conditions  in (14), \( \implies a_1=0 \) and
in (14), \( \implies a_1=0 \) and  , implies that
, implies that  .
.
Putting value of constants \(a_0\) and \(a_1\) in (14), we get
where  is defined in (10). \(\square \)
is defined in (10). \(\square \)
Lemma 3.2
 be the Green’s function specified in (10) satisfies the following properties:
be the Green’s function specified in (10) satisfies the following properties:
 ;
;
\((\mathcal {B}_{2})~~\)The function  is decreasing multivalued function and
is decreasing multivalued function and  ;
;
 .
.
Proof
To assess \((\mathcal {B}_{1})\), we will discuss the following cases 
Case 1. For \( \kappa \le t\), then
Case 2. When \(t\le \kappa \), we evaluate
From (16) and (17), verified that  .
.
Now, to evaluate \((\mathcal {B}_{2})\), we suppose that 
Case 1. For \( \kappa \le t\), then
Case 2. When \(t\le \kappa \), we find that
From equation (18) and (19), we observe  , accordingly,
, accordingly,  is decreasing function. Therefore, we have for
is decreasing function. Therefore, we have for 
and for 
For \((\mathcal {B}_{3})\), we assume that
Case 1. For  , then with the condition
, then with the condition  , we have
, we have
Case 2. For  , then
, then
Consequently, from equations (22) and (23), proof of condition \(\mathcal {B}_{3}\) is completed.
Existence result
Here, we establish the existence criterion for FDEs (2) by inserting the below mentioned conditions.
Consider \({\mathcal {Y}}^{*}=\mathcal { C[0,1]}\) be the Banach space endowed with the  . Suppose that \({\mathfrak {P}}^{*}\in {\mathcal {Y}}^{*} \) be a cone having non-negative functions,
. Suppose that \({\mathfrak {P}}^{*}\in {\mathcal {Y}}^{*} \) be a cone having non-negative functions,  . Let
. Let  , the given equation (2), using Theorem (3.1) has alternative form
, the given equation (2), using Theorem (3.1) has alternative form
Let us define a operator \({\mathfrak {F}}^{*}:{\mathfrak {P}}^{*}\setminus \{0\}\rightarrow {\mathcal {Y}}^{*}\) assosiated with problem (2), such that
By using Theorem 3.1,  be a fixed point of \( {\mathfrak {F}}^{*}\) i.e.,
be a fixed point of \( {\mathfrak {F}}^{*}\) i.e.,
To find the desired result we define the some assumptions:
-
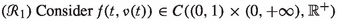 and
and 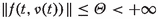 .
. -
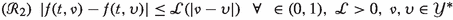 .
.
Theorem 4.1
Let us consider that conditions \( (\mathcal {R}_{1}) -(\mathcal {R}_{2})\) are satisfied and  . Then \({\mathfrak {F}}^{*}\) is completely continuous.
. Then \({\mathfrak {F}}^{*}\) is completely continuous.
Proof
For any  , using Lemma 3.2 and (25), we have
, using Lemma 3.2 and (25), we have
Now using \(\mathcal {B}_{3}\) of Lemma 3.2 we have
For continuity of \({\mathfrak {F}}^{*},\) we shows that  as
as  , let us contrive
, let us contrive
By continuity of function  , we have
, we have  . This implies that \({\mathfrak {F}}^{*}\) is a continuous operator. \(\square \)
. This implies that \({\mathfrak {F}}^{*}\) is a continuous operator. \(\square \)
Now, we discuss the uniform boundedness of \({\mathfrak {F}}^{*} \) on \((\overline{\mathcal {A}^{{*}}_2(r)}) \setminus \mathcal {A}^{{*}}_1(r).\)
By (25) and using \((\mathcal {R}_{1})-(\mathcal {R}_{2})\), for any  , we get
, we get
Consequently, \( {\mathfrak {F}}^{*} \) is uniformly bounded.
Next, we verify that compactness of operator \({\mathfrak {F}}^{*} \), for this firstly we discuss the equicontinuity of \({\mathfrak {F}}^{*} \).
For  , we have
, we have
Thus, \({\mathfrak {F}}^{*}\) is an equicontinuous operator on \((\overline{\mathcal {A}^{{*}}(r_2)}) \setminus \mathcal {A}^{{*}}(r_1)\) and by Arzela Ascoli theorem \({\mathfrak {F}}^{*}\) is compact on \((\overline{\mathcal {A}^{{*}}(r_2)}) \setminus \mathcal {A}^{{*}}(r_1).\) Thus \({\mathfrak {F}}^{*}\) is completely continuous.
Let us calculate the height functions for  for
for 
Theorem 4.2
Suppose that assumptions \((\mathcal {R}_{1})-(\mathcal {R}_{2})\), are satisfied and \(\exists ~~ {\mathfrak {K}}_1,{\mathfrak {K}}_2\in \mathbb {R}^{{+}}\) such that any of the below mentioned condition hold:
or
Then the given equation (2) has a positive solution  .
.
Proof
Let us consider the case  . If
. If  then
then  and
and  . Using (32),
. Using (32),  , we devise
, we devise
If  then
then  . Using (32) and
. Using (32) and  . From the Green function property with
. From the Green function property with  , we have
, we have
Thus  is a fixed point of \({\mathfrak {F}}^{*}\). By using Lemma 3.2 and Theorem 2.3, for
is a fixed point of \({\mathfrak {F}}^{*}\). By using Lemma 3.2 and Theorem 2.3, for  and
and  , we have
, we have  . Therefore
. Therefore  is positive solution. \(\square \)
is positive solution. \(\square \)
Uniqueness result
Theorem 4.3
Let us consider assumptions \((\mathcal {R}_1)~\text {and}~ (\mathcal {R}_2)\) are satisfied. If
where
Then there exist unique solution for the given equation (2) on (0, 1).
Proof
For \(q\ge 2 \).
For each  , we have
, we have

but in (37) assumed that \(\varDelta ^{*}<1.\) Therefore \({\mathfrak {F}}^{*}\) is contraction map. Accordingly, by Banach contraction mapping principle that there exist a unique fixed point for operator \({\mathfrak {F}}^{*}\). Hence we conclude that, unique solution exist for (2). \(\square \)
Hyers-Ulam stability
Here, we analysis the HU stability of (2). We define the HU stability as following:
Definition 5.1[28] The integral equation (9) is said to be HU stable if there exists non negative constant \(\varLambda \), for for every \(\gamma ^{*}>0\) satisfying the following:
If,
then there exist a function \(\upsilon (t)\), which is continuous and satisfying the given below equation:
implies
Theorem 5.1
The FDE (2) with  operator is HU stable for \(q\ge 2\) provided that \((\mathcal {R}_1)\text {and}~ (\mathcal {R}_2)\) are satisfied.
operator is HU stable for \(q\ge 2\) provided that \((\mathcal {R}_1)\text {and}~ (\mathcal {R}_2)\) are satisfied.  satisfies
satisfies
under the condition  , where
, where  be the approximate solution (42).
be the approximate solution (42).
Proof
Let  be the solution of (2) and \(\upsilon (t)\) be the approximate solution and satisfying (42). Consider that
be the solution of (2) and \(\upsilon (t)\) be the approximate solution and satisfying (42). Consider that
and  . We prove that the integral equation (9) is HU stable, with assumptions \((\mathcal {R}_1) \text {and}~ (\mathcal {R}_2).\) we have
. We prove that the integral equation (9) is HU stable, with assumptions \((\mathcal {R}_1) \text {and}~ (\mathcal {R}_2).\) we have

Let
By using Gronwall inequality, we get
Hence the equation (9) is HU stable. As a result, the FDE (2) is HU stable. \(\square \)
Example
Here, we present some example to illustrate our results.
Example 6.1
Assume that a singular FDEs with  laplacian operator:
laplacian operator:
where  .
.
 , then we have
, then we have

Assume \({\mathfrak {K}}_1=0.0001\), \({\mathfrak {K}}_2=1\) and  and using Theorem 4.2. Then,
and using Theorem 4.2. Then,
Now,  , we have
, we have
Using Theorem 4.2, given equation (47) has a solution  which satisfies
which satisfies  .
.
Conclusion
The main goal of this article was to illustrate extensive applications of AB-fractional derivative in various problem. This derivative opened the scope of exploration of the analytical, theoretical, and quantitative behaviour for various problem due to nonlocal kernel. The EU of FDEs is investigated by employed point theorem. The HU stability is also estimated. An example is also proposed to demonstrate the accomplished solution.
Data Availibility
Not applicable
References
Podlubny, I.: Fractional differential equations. 198, (1998) Academic Press, Son Diego https://doi.org/10.2307/2653160
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, vol. 204. Elsevier Science Limited, Amsterdam (2006)
Agrawal, O.P.: Solution for a fractional diffusion-wave equation defined in a bounded domain. Nonlinear Dyn. 29(14), 145–155 (2002)
Atangana, A.: Derivative with a new parameter: theory, methods and applications. Academic Press, San Diego (2015)
Jarad, F., Abdeljawad, T., Hammouch, Z.: On a class of ordinary differential equations in the frame of atanganabaleanu fractional derivative. Chaos Solitons Fractals. 117, 16–20 (2018)
Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl. 1, 73–85 (2015)
Atangana, A.: On the new fractional derivative and application to nonlinear fisher’s reaction-diffusion equation. Appl Math Comput. 273, 948–956 (2016)
Atangana, A., Alkahtani, B.S.: Analysis of the kellersegel model with a fractional derivative without singular kernel. Entropy 17, 4439–4453 (2015)
Atangana, A.: Modelling the spread of COVID-19 with new fractal-fractional operators: can the lockdown save mankind before vaccination. Chaos Solitons Fract. 136, 109860 (2020)
Leibenson, L.S.: General problem of the movement of a compressible fluid in a porous medium. Izv. Akad. Nauk. Kirg. SSSR 9, 7–10 (1983)
Devi, A., Kumar, A.: Existence of solutions for fractional Langevin equation involving generalized Caputo derivative with periodic boundary conditions. In: AIP Conference Proceedings, 2214: pp. 020026-1–020026-10, (2020) https://doi.org/10.1063/5.0003365
Devi, A., Kumar, A., Abdeljawad, T., Khan, A.: Existence and stability analysis of solutions for fractional Langevin equations with nonlocal integral and anti-periodic type boundary conditions. Fractals. 28, 1–12 (2020)
Bedi, P., Kumar, A., Abdeljawad, T., Khan, A.: Existence of mild solutions for impulsive neutral Hilfer fractional evolution equations. Adv. Diff. Equ. 2020(1), 1–16 (2020)
Bedi, P., Kumar, A., Abdeljawad, T., Khan, A.: S-asymptotically \(\omega \)-periodic mild solutions and stability analysis of Hilfer fractional evolution equations, Evol. Equ. Control Theory. (2020)
Devi, A., Kumar, A., Abdeljawad, T., Khan, A.: Stability analysis of solutions and existence theory of fractional Langevin equation. Alexindria Eng. J. 60, 3641–3647 (2021)
Li, X., He, M.: Monotone iterative method for fractional p-Laplacian differential equations with four-point boundary conditions. Adv. Differ. Equ. 2020(686), 1–13 (2020)
Liu, Z., Lu, L.: On the solvability of a fractional differential equation model involving the p-Laplacian operator. Electron. J. Qual. Theory Differ. Equ. 2012(70), 1–18 (2012)
Khan, H., Chen, W., Sun, H.: Analysis of positive solution and Hyers-Ulam stability for a class of singular fractional differential equations with p-Laplacian in Banach space. Math. Meth. Appl. Sci. 41, 3430–3440 (2018)
Aslam, M., Gómez-Aguilar, JF., Rahman, G., Murtaza, R.: Existence, uniqueness, and Hyers–Ulam stability of solutions to nonlinear p-Laplacian singular delay fractional boundary value problems. Math Meth Appl Sci. 1–15 (2021)
Matar, M.M., Abbas, M.I., Alzabut, J., Kaabar, M.K.A., Etemad, S., Rezapour, S.: Investigation of the p-Laplacian nonperiodic nonlinear boundary value problem via generalized Caputo fractional derivatives. Adv. Defer. Equ. 2021(68), 1–18 (2021)
Develi, F.: Existence and Ulam–Hyers stability results for nonlinear fractional Langevin equation with modified argument. Math. Meth. Appl. Sci. 1–9 (2021)
Araz, S.I.: Ulam-Hyers stability of fractional Langevin equations. Appl. Math. Comput. 258, 72–83 (2015)
Devi, A., Kumar, A., Baleanu, D., Khan, A.: On stability analysis and existence of positive solutions for a general non-linear fractional differential equations. Adv. Differ. Equ. 2020(1), 1–16 (2020)
Khan, A., Khan, H., Gómez-Aguilar, J.F., Abdeljawad, T.: Existence and Hyers-Ulam stability for a nonlinear singular fractional differential equations with Mittag-Leffler kernel. Chaos, Solitons Fractals. 127, 422–427 (2019)
Li, X.: Comment for Existence and Hyers-Ulam stability for a nonlinear singular fractional differential equations with Mittag-Leffler kernel. Chaos Solitons Fractals. 142, 110439 (2021)
Abdalla, B., Abdeljawad, T.: On the oscillation of Caputo fractional differential equations with Mittag-Leffler nonsingular kernel. Chaos Solitons Fractals. 127, 173–177 (2019)
Atangana, A., Baleanu, D.: New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Preprint arXiv:1602.03408; (2016)
Hyers, D.H.: On the stability of the linear functional equation. Proc. Natl. Acad. Sci. U.S.A. 27, 222–224 (1941)
Krasnoselsky, M.A.: Two remarks on the method of successive approximation. Uspekhi Mathematicheskikh Nauk. 10, 123-127 (1955). url: http://mi.mathnet.ru/eng/umn7954
Guo, D., Lakshmikantham, V.: Nonlinear Problems in Abstract Cones, p. 5. Academic press, Cambridge, Vol (2014)
Acknowledgements
The first author acknowledge with thanks to Council of Scientific and Industrial Research (CSIR)- New Delhi, India for suporting this research work under grant no. 09/1051(0031)/2019-EMR-1 and Department of Mathematics and Statistics, Central University of Punjab, Bathinda, India.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
Both the authors have made equally contributions to the publication of this article. Both the authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Devi, A., Kumar, A. Stability results and existence for fractional differential equation involving Atangana-Baleanu derivative with nonlocal integral conditions. Int. J. Appl. Comput. Math 8, 228 (2022). https://doi.org/10.1007/s40819-022-01406-1
Accepted:
Published:
DOI: https://doi.org/10.1007/s40819-022-01406-1
Keywords
- Hyers-Ulam stability
- Atangana-Baleanu fractional derivative
- p-Laplacian operator
- Fixed point theorem
- EU of solutions
- Nonlocal conditions



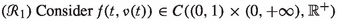 and
and 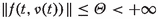 .
.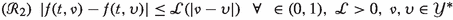 .
.