Introduction

Magnetohydrodynamics (MHD) has found ever-increasing applications in modern smart technologies. The application of magnetic fields (static or alternating) has been shown to manipulate successfully the material characteristics of electro-conductive polymers which are finding new applications in aerospace, offshore and naval industries. Interesting studies in this regard addressing various systems employing magnetic polymers include environmental engineering [1], thin film fabrication processes [2] and design of shock dissipation systems with magnetic elastomers [3]. Coating applications and energy systems enhancement with smart magnetic polymers have also grown substantially in recent years. Relevant technologies in this regard are nuclear engineering [4], medical engineering exploiting stimuli-based polymers [5] and hydromagnetic energy generation [6]. In the context of coating applications, it is critical to regulate heat transfer conditions which lead to improved bonding and homogeneity in engineered polymeric surfaces. Many studies have therefore examined the transport phenomena (i.e. coupled heat and momentum transfer) from different geometrical shapes including cones, pipes, disks and truncated bodies and spheres. The spherical geometry is particularly relevant to chemical engineering processes. Investigators have applied a variety of different material models for the coatings and also numerical methods to solve the associated boundary value problems. Salleh et al. [7] used the Crank–Nicolson method to analyze flow from a circular cylinder with Newtonian heating. Hayat et al. [8] used homotopy analysis method (HAM) to simulate the MHD flow of Powell–Eyring fluid by a stretching cylinder. Makanda et al. [9] analyzed the radiative heat flux effect on hydromagnetic dissipative Casson slip fluid flow from a horizontal circular cylinder in porous media.

The above studies were confined to Newtonian fluids. However, generally polymers are known to exhibit non-Newtonian characteristics. Engineers have therefore developed a variety of constitutive models to analyse the shear stress–strain characteristics of these fluids, including viscoplastic, viscoelastic, micro-structural and power-law models. Both purely fluid flow and heat transfer from a sphere to non-Newtonian fluids have been reported in a number of theoretical investigations. Malik et al. [10] used the Runge–Kutta Fehlberg method to obtain numerical solutions for steady thermal boundary layer flow of a Casson nanofluid flowing over a vertical radially exponentially-stretching cylinder. Rao and Sekhar [11] investigated MHD flow past a circular cylinder with applied magnetic field. Subba Rao et al. [12] investigated slip effects on Casson fluid flow from an Isothermal sphere. They analyzed the behavior of fluid on velocity and temperature distributions when thermal and velocity slips are considered. Grigoriadis et al. [13] analysed the MHD flow past a circular cylinder using the immersed boundary method. Subba Rao et al. [14] used the finite difference method to analyze boundary layer flow of non-Newtonian fluid from an inclined plate with thermal slip boundary condition. Bhatnagar [15] presented analytical solutions for thermal convection in elastic-viscous flow from a spinning, insulated sphere, correlating his findings with experiments on polysiloxane, and observing that the secondary flow breaks down into two regimes wherein heat convection dominates dissipation effects due to viscoelasticity of the polymer. These studies however did not consider the Williamson model. This is a shear-thinning non-Newtonian model which quite accurately simulates polymer viscoelastic flows over a wide spectrum of shear rates. In Williamson fluids the viscosity is reduced with rising shear stress rates. This model has found some popularity in engineering simulations. Prasannakumara et al. [16] used the Runge–Kutta–Fehlberg shooting algorithm to analyse reactive-radiative flow of Williamson viscoelastic nanofluid from a stretching sheet in a permeable material. Khan and Khan [17] investigated Blasius, Sakiadis, stretching and stagnation point flows of Williamson fluid using the homotopy analysis method, over a range of Weissenberg numbers. Bég et al. [18] presented extensive numerical solutions for hydromagnetic pumping of a Williamson fluid using a modified differential transform method, observing that a change in Weissenberg number strongly modifies the pressure difference and axial velocity. Further studies of transport phenomena in Williamson fluids include Rao and Rao [19] and Dapra and Scarpi [20].

In the present investigation, we consider the magnetohydrodynamic convection boundary layer flow of a Williamson polymeric fluid external to a stationary solid horizontal circular cylinder with Newtonian heating. Magnetic fields have been found to profoundly influence heat transfer and velocity characteristics in curved body flows. Relevant examples include Bég et al. [21] (for cylindrical geometries), Alkasasbeh et al. [22] who addressed radiative effects also, Subba Rao et al. [23] who considered porous medium drag effects and Kasim et al. [24] who used a viscoelastic model. Slip effects have been shown to be prominent in certain polymeric flow processes. Momentum (hydrodynamic) slip relates to the non-adherence of the polymer to a solid boundary and arises in polymer melts, emulsions, petro-chemical suspensions and also foams [25,26,27,28,29,30,31,32,33]. The presence of momentum slip invalidates the classical “no-slip” boundary condition. Thermal slip may also arise in heat transfer problems and can also significantly modify both velocity and temperature characteristics both at the solid surface and deeper into the boundary layer. Several researchers have examined multi-physical flows with velocity and/or thermal slip effects including Jamil and Khan [34], Tripathi et al. [35] (for viscoelastic fluids), Bég et al. [36] for magnetohydrodynamic heat and mass transfer and Devi and Devi [37] for swirling disk hydromagnetic flows with cross diffusion. Sreenadha et al. [38] have studied analytically the wall slip effects in peristaltic propulsion and heat transfer of Williamson fluids in inclined conduits. The present study employs a finite difference numerical method due to Keller for solving the two-dimensional steady flow and heat transfer in a Williamson polymeric liquid boundary layer from a cylinder. Verification of the computations is conducted for the special case of non-magnetic, Newtonian flow in the absence of Newtonian heating with earlier published literature. Newtonian heating is however physically more realistic for materials processing operations, as studied in our paper. It captures better the wall thermal conditions in non-Newtonian sheet processing. It allows conjugate heat transfer to be simulated at the wall and avoids under-prediction encountered with conventional thermal boundary conditions. Therefore the heat transfer from the surface is taken to be proportional to the local surface temperature in Newtonian heating and this mimics quite well physically observed phenomena in thermal materials processing. The hot stretching wall can be better simulated than with standard thermal boundary conditions and this improves the correlation between our mathematical model and manufacturing processes involving thermal treatment of non-Newtonian liquids (polymers). Newtonian heating was introduced as a term by Merkin [39] and has been successfully employed by many authors in polymeric and magnetic material flow simulations including Ramzan et al. [40], Awais et al. [41] and Uddin et al. [42]. These studies all confirmed that very different and better results are achieved with Newtonian boundary conditions for heating compared with conventional thermal wall conditions. The present study finds applications in electro-conductive thermal polymer processing systems.

Magnetohydrodynamic Viscoelastic Thermofluid Model

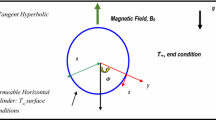
The regime under investigation is illustrated in Fig. 1. Steady, incompressible hydromagnetic Williamson non-Newtonian boundary layer flow and heat transfer from a cylindrical body under radial magnetic field is considered. For an incompressible Williamson fluid, the continuity (mass conservation) and momentum equations are given as:

$$\begin{aligned} \hbox {div V}= & {} 0, \end{aligned}$$
(1)
$$\begin{aligned} {\uprho }\frac{\hbox {dV}}{\hbox {dt}}= & {} \hbox {divS} +\uprho \hbox {b}, \end{aligned}$$
(2)

where \({\uprho }\) is the density of the fluid, \(\hbox {V}\) is the velocity vector, \(\hbox {S}\) is the Cauchy stress tensor, b represents the specific body force vector, and \(\hbox {d/dt}\) represents the material time derivate. The constitutive equations of the Williamson fluid model [16,17,18,19,20] are given as:

$$\begin{aligned} \hbox {S}= & {} -\hbox {pI}+ \uptau \end{aligned}$$
(3)
$$\begin{aligned} \tau= & {} \left[ {\mu _\infty +\frac{(\mu _0 -\mu _\infty )}{1-\Gamma \dot{\gamma }}} \right] A_{1}, \end{aligned}$$
(4)

Here \(\hbox {p}\) is the pressure, \(\hbox {I}\) is the identity vector, \(\tau \)is the extra stress tensor, \(\mu _0 \) are the limiting viscosities at zero and at infinite shear rate, \(\varGamma \) is the time constant (>0), \(\hbox {A}_{1} \) is the first Rivlin–Erickson tensor and \(\dot{\upgamma }\) is defined as follows:

$$\begin{aligned} \dot{\gamma }= & {} \sqrt{\frac{1}{2}\pi }, \end{aligned}$$
(5)
$$\begin{aligned} \pi= & {} { trace}(A_1^2 ) \end{aligned}$$
(6)

Here we considered the case for which \(\mu _\infty =0\) and \(\Gamma \dot{\gamma } <1.\) Thus Eq. (4) can be written as:

$$\begin{aligned} \tau = \left[ {\frac{(\mu _0 -\mu _\infty )}{1-\Gamma \dot{\gamma }}} \right] A_1, \end{aligned}$$
(7)

Or by using binomial expansion we get:

$$\begin{aligned} \tau =\mu _0 \left[ {1+\Gamma \dot{\gamma }} \right] A_1. \end{aligned}$$
(8)

The x-coordinate is measured along the circumference of the horizontal cylinder from the lowest point and the y-coordinate is measured normal to the surface, with ‘a’ denoting the radius of the horizontal cylinder. \(\Phi =x/a\) is the angle of orientation of the y-axis with respect to the vertical \(0\le \Phi \le \pi \). The gravitational acceleration, g acts downwards. Both the horizontal cylinder and the fluid are maintained initially at the same temperature. Instantaneously they are raised to a temperature \(T_w >T_\infty \) i.e. the ambient temperature of the fluid which remains unchanged.

Fig. 1
figure 1

Magnetohydrodynamic non-Newtonian heat transfer from a cylinder

Full size image

The two-dimensional mass, momentum and energy boundary layer equations governing the flow in an (x, y) coordinate system may be shown to take the form:

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 \end{aligned}$$
(9)
$$\begin{aligned}&\displaystyle u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\nu \frac{\partial ^{2}u}{\partial y^{2}}+\sqrt{2}\nu \Gamma \frac{\partial u}{\partial y}\frac{\partial ^{2}u}{\partial y^{2}}+g\beta (T-T_\infty )\sin \left( {\frac{x}{a}} \right) -\frac{\sigma B_0^2 }{\rho }u \end{aligned}$$
(10)
$$\begin{aligned}&\displaystyle u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y} =\alpha \frac{\partial ^{2}T}{\partial y^{2}}\qquad \end{aligned}$$
(11)

The boundary conditions for the considered flow with velocity and thermal slip are:

$$\begin{aligned} \hbox {At }y= & {} 0, u=0, v=0, -k\frac{\partial T}{\partial y}=h_w (T_w -T)\nonumber \\ \hbox {As }y\rightarrow & {} \infty , u\rightarrow 0, v\rightarrow 0, T\rightarrow T_\infty \end{aligned}$$
(12)

The stream function \(\psi \) is defined by \(u=\frac{\partial \psi }{\partial y}\) and \(v=-\frac{\partial \psi }{\partial x}\), and therefore, the continuity equation is automatically satisfied. In order to write the governing equations and the boundary conditions in dimensionless form, the following non-dimensional quantities are introduced:

$$\begin{aligned} \xi= & {} \frac{x}{a},\quad \eta =\frac{y}{x}Gr^{1/4},\quad f(\xi , \eta ) =\frac{\psi }{\nu \xi Gr^{1/4}},\quad \theta (\xi , \eta )=\frac{T-T_\infty }{T_w -T_\infty } \nonumber \\ \Pr= & {} \frac{\nu }{\alpha },\quad Gr=\frac{g\beta _1 (T_w -T_\infty )a^{3}}{\nu ^{3}},\quad W_e =\frac{\sqrt{2 } \nu \Gamma x Gr^{3/4}}{a^{3}},\quad M=\frac{\sigma B_0^2 a^{2}}{\rho \nu \sqrt{Gr}}\qquad \end{aligned}$$
(13)

The emerging momentum and heat (energy) conservation equations in dimensionless from assume the following form:

$$\begin{aligned}&\displaystyle {f}^{\prime \prime \prime }+f{f}^{\prime \prime }-{f}^{{\prime }^{2}}+W_e {f}^{\prime \prime }{f}^{\prime \prime \prime }+ \frac{\sin \xi }{\xi }\theta -M{f}^{\prime }=\xi \left( {{f}^{\prime }\frac{\partial {f}^{\prime }}{\partial \xi }-{f}^{\prime \prime }\frac{\partial f}{\partial \xi }} \right) \end{aligned}$$
(14)
$$\begin{aligned}&\displaystyle \frac{{\theta }^{\prime \prime }}{\Pr }+f{\theta }^{\prime }=\xi \left( {{f}^{\prime }\frac{\partial \theta }{\partial \xi }-{\theta }^{\prime }\frac{\partial f}{\partial \xi }} \right) \end{aligned}$$
(15)

The transformed dimensionless boundary conditions are reduced to:

$$\begin{aligned} \hbox {At }\eta= & {} 0, \quad f=0, \quad {f}^{\prime }=0, \quad \theta =1+\frac{{\theta }^{\prime }}{\gamma }\nonumber \\ \hbox {As } \eta\rightarrow & {} \infty ,\quad {f}^{\prime }\rightarrow 0, \quad \theta \rightarrow 0 \end{aligned}$$
(16)

The skin-friction coefficient (cylinder surface shear stress) and the local Nusselt number (cylinder surface heat transfer rate) can be defined, respectively, using the transformations described above with the following expressions:

$$\begin{aligned} Gr^{-3/4}C_f= & {} \xi {f}^{\prime \prime }(\xi , 0)+\frac{W_e }{2}\xi ({f}^{\prime \prime }(\xi , 0))^{2} \end{aligned}$$
(17)
$$\begin{aligned} Gr^{-1/4}Nu= & {} -{\theta }^{\prime }(\xi , 0) \end{aligned}$$
(18)

All parameters are defined in the nomenclature.

Computational Solution with Keller Box Implict Method

The transformed, nonlinear, multi-physical boundary value problem defined by Eqns. (14)–(16) can be solved via a number of numerical schemes. Here we implement a popular, second order accurate implicit finite difference method originally developed by Keller [43]. Recent studies featuring this method in the context of magnetohydrodynamic and rheological flows include Sajid et al. [44] who studied ferrofluid flows in curved conduits, Gaffar et al. [45] who investigated hydromagnetic tangent hyperbolic non-Newtonian convection from a cone and radiative-convective Casson slip boundary layer flows by Subba Rao et al. [46]. In the Keller box scheme, the multi-degree, multi-order coupled partial differential equations defined in (14) and (15) are first reduced to a system of first order equations. These equations are then discretized with the finite difference approximations with appropriate step lengths in each coordinate direction. Introducing the new variables:

$$\begin{aligned} u(x,y)= & {} {f}^{\prime }, v(x,y)={f}^{\prime \prime }, s(x,y)=\theta \end{aligned}$$
(19)
$$\begin{aligned} {f}^{\prime }= & {} u \end{aligned}$$
(20)
$$\begin{aligned} u^{\prime }= & {} v \end{aligned}$$
(21)
$$\begin{aligned} {\theta }^{\prime }= & {} t \end{aligned}$$
(22)

Equations (14)–(15) reduce then to the form:

$$\begin{aligned}&\displaystyle {v}^{\prime }+fv+W_e v{v}^{\prime }-u^{2}+ \frac{\sin \xi }{\xi }s-Mu=\xi \left( {u\frac{\partial u}{\partial \xi }-v\frac{\partial f}{\partial \xi }} \right) \end{aligned}$$
(23)
$$\begin{aligned}&\displaystyle \frac{{t}^{\prime }}{\Pr }+ft=\xi \left( {u\frac{\partial s}{\partial \xi }-t\frac{\partial f}{\partial \xi }} \right) \end{aligned}$$
(24)

where primes denote differentiation with respect to \(\eta \). In terms of the dependent variables, the boundary conditions (16) become:

$$\begin{aligned} \hbox {At }\eta= & {} 0,\,f=0,\, {f}^{\prime }=0,\, \theta =1+\frac{{\theta }^{\prime }}{\gamma }\nonumber \\ \hbox {As }\eta\rightarrow & {} \infty ,\, {f}^{\prime }\rightarrow 0,\, \theta \rightarrow 0 \end{aligned}$$
(25)

A two-dimensional computational mesh (grid) is imposed on the \(\xi -\eta \) plane as shown in Fig. 2. The stepping process is defined by:

$$\begin{aligned} \eta _{^{0}}= & {} 0, \quad \eta _{^{j}} =\eta _{^{j-1}} +h_j \quad j=1,2,\ldots ,J\quad \eta _J \equiv \eta _\infty \end{aligned}$$
(26)
$$\begin{aligned} \xi ^{0}= & {} 0, \quad \xi ^{n}=\xi ^{n-1}+k_n \quad n=1,2,\ldots ,N. \end{aligned}$$
(27)

where \(k_{n}\) and \(h_{j}\) denote the step distances in the \(\xi \) and \(\eta \) directions respectively.

Fig. 2
figure 2

Keller box element and boundary layer mesh

Full size image

If \(g_j^n \) denotes the value of any variable at \(\left( {\eta _j, \xi ^{n}} \right) \), then the variables and derivatives of Eqs. (20)–(24) at \(\left( {\eta _{j-1/2}, \xi ^{n-1/2}} \right) \) are replaced by:

$$\begin{aligned} g_{j-1/2}^{n-1/2}= & {} \frac{1}{4}\left( {g_j^n +g_{j-1}^n +g_j^{n-1} +g_{j-1}^{n-1} } \right) , \end{aligned}$$
(28)
$$\begin{aligned} \left( {\frac{\partial g}{\partial \eta }} \right) _{j-1/2}^{n-1/2}= & {} \frac{1}{2h_j }\left( {g_j^n -g_{j-1}^n +g_j^{n-1} -g_{j-1}^{n-1} } \right) , \end{aligned}$$
(29)
$$\begin{aligned} \left( {\frac{\partial g}{\partial \xi }} \right) _{j-1/2}^{n-1/2}= & {} \frac{1}{2k^{n}}\left( {g_j^n -g_{j-1}^n +g_j^{n-1} -g_{j-1}^{n-1} } \right) , \end{aligned}$$
(30)

The finite-difference approximation of Eqs. (20)–(24) for the mid-point \(\left( {\eta _{j-1/2}, \xi ^{n}} \right) \) assume the form given below:

$$\begin{aligned}&\displaystyle h_j^{-1} \left( {f_j^n -f_{j-1}^n } \right) =u_{j-1/2}^n, \end{aligned}$$
(31)
$$\begin{aligned}&\displaystyle h_j^{-1} \left( {u_j^n -u_{j-1}^n } \right) =v_{j-1/2}^n, \end{aligned}$$
(32)
$$\begin{aligned}&\displaystyle h_j^{-1} \left( {s_j^n -s_{j-1}^n } \right) =t_{j-1/2}^n, \end{aligned}$$
(33)
$$\begin{aligned}&\displaystyle \left( {v_j -v_{j-1} } \right) +(1+\alpha ) \frac{h_j }{4}\left[ {\left( {f_j +f_{j-1} } \right) \left( {v_j +v_{j-1} } \right) } \right] - \frac{\left( {1+\alpha } \right) h_j }{4}\left( {u_j +u_{j-1} } \right) ^{2} \nonumber \\&\displaystyle + \frac{Ah_j }{2}\left( {s_j +s_{j-1} } \right) +\frac{W_e }{2}\left( {v_j +v_{j-1} } \right) \left( {v_j -v_{j-1} } \right) \nonumber \\&\displaystyle - \frac{Mh_j }{2}\left( {u_j +u_{j-1} } \right) - \frac{\alpha h_j }{2}f_{j-1/2}^{n-1} \left( {v_j +v_{j-1} } \right) \nonumber \\&\displaystyle + \frac{\alpha h_j }{2}v_{j-1/2}^{n-1} \left( {f_j +f_{j-1} } \right) = \left[ {R_1 } \right] _{j-1/2}^{n-1} \end{aligned}$$
(34)
$$\begin{aligned}&\displaystyle \frac{1}{\Pr }\left( {t_j -t_{j-1} } \right) +\left( {1+\alpha } \right) \frac{h_j }{4}\left[ {\left( {f_j +f_{j-1} } \right) \left( {t_j +t_{j-1} } \right) } \right] -\frac{\alpha h_j }{4}\left[ {\left( {u_j +u_{j-1} } \right) \left( {s_j +s_{j-1} } \right) } \right] \nonumber \\&\displaystyle +\frac{\alpha h_j }{2}s_{j-1/2}^{n-1} \left( {u_j +u_{j-1} } \right) -\frac{\alpha h_j }{2}u_{j-1/2}^{n-1} \left( {s_j +s_{j-1} } \right) -\frac{\alpha h_j }{2}f_{j-1/2}^{n-1} \left( {t_j +t_{j-1} } \right) \nonumber \\&\displaystyle + \frac{\alpha h_j }{2}t_{j-1/2}^{n-1} \left( {f_j +f_{j-1} } \right) = \left[ {R_2 } \right] _{j-1/2}^{n-1} \end{aligned}$$
(35)

Here the following abbreviations apply:

$$\begin{aligned} \alpha= & {} \frac{\xi ^{n-1/2}}{k_n },\quad A=\frac{\sin \left( {\xi ^{n-1/2}} \right) }{\xi ^{n-1/2}}\end{aligned}$$
(36)
$$\begin{aligned} \left[ {R_1 } \right] _{j-1/2}^{n-1}= & {} -h_j \left[ {\begin{array}{l} \left( {\frac{v_j -v_{j-1}}{h_j }} \right) +\left( {1-\alpha } \right) \left( {f_{j-1/2} v_{j-1/2}} \right) +W_e v_{j-1} {v}^{\prime }_{j-1/2} \\ +\left( {1-\alpha } \right) \left( {u_{j-1/2} } \right) ^{2}+A\left( {s_{j-1/2}} \right) -M\left( {u_{j-1/2} } \right) \\ \end{array}} \right] \end{aligned}$$
(37)
$$\begin{aligned} \left[ {R_2 } \right] _{j-1/2}^{n-1}= & {} -h_j \left[ {\frac{1}{\Pr }\left( {\frac{t_j -t_{j-1}}{h_j }} \right) +\left( {1-\alpha } \right) \left( {f_{j-1/2}t_{j-1/2}} \right) +\alpha \left( {u_{j-1/2}s_{j-1/2}} \right) } \right] \nonumber \\ \end{aligned}$$
(38)

The boundary conditions take the form:

$$\begin{aligned} f_0^n =u_0^n =0,\quad \theta _0^n =1,\quad u_J^n =0,\quad v_J^n =0,\quad \theta _J^n =0 \end{aligned}$$
(39)

The emerging non-linear system of algebraic equations is linearized by means of Newton’s method and then solved by the block-elimination method. The accuracy of computations is influenced by the number of mesh points in both directions. After experimenting with various grid sizes in the \(\eta \)-direction (radial coordinate) a larger number of mesh points are selected whereas in the \(\xi \) direction (tangential coordinate) significantly less mesh points are utilized. \(\eta _{{ max}}\) has been set at 16 and this defines a sufficiently large value at which the prescribed boundary conditions are satisfied. \(\xi _{{ max}}\) is set at 1.0 for this flow domain. Mesh independence is therefore achieved in the present computations. The computer program of the algorithm is executed in MATLAB running on a PC.

Table 1 Variations of the local heat transfer coefficient \(-{\theta }^{\prime }(\xi , 0)\) for various values of \(\xi \) with \(W_e =0.0,\gamma =0.0, M=0.0\)
Full size table
Fig. 3
figure 3

a Effect of We on velocity profiles. b Effect of We on temperature profiles

Full size image
Fig. 4
figure 4

a Effect of Pr on velocity profiles. b Effect of Pr on temperature profiles

Full size image
Fig. 5
figure 5

a Effect of M on velocity profiles. b Effect of M on temperature profiles

Full size image
Fig. 6
figure 6

a Effect of \(\gamma \) on velocity profiles. b Effect of \(\gamma \) on temperature profiles

Full size image
Fig. 7
figure 7

a Effect of \(\xi \) on velocity profiles. b Effect of \(\xi \) on temperature profiles

Full size image

Validation of Keller Box Solutions

The present Keller box solutions have been validated for the special case of non-magnetic \((M=0)\) Newtonian flow (\(We = 0\)) in the absence of Newtonian heating effect \((\gamma =0)\). This case was considered earlier by Nazar et al. [47]. In addition to prescribing \(M=We=\gamma =0\) in the present model, it is also possible to make a comparison as the momentum equation and boundary conditions assume the following reduced form:

$$\begin{aligned}&f^{///}+ff^{//}-f^{/2}+\frac{\sin \xi }{\xi }\theta =\xi \left( {f^{/}\frac{\partial f^{/}}{\partial \xi }-f^{//}\frac{\partial f}{\partial \xi }} \right) \end{aligned}$$
(40)
$$\begin{aligned}&\hbox {At }\eta =0;f=0;f^{/}=0,\theta =1\\&\hbox {At }\eta \rightarrow \infty :f^{/}\rightarrow 0;\theta \rightarrow 0 \end{aligned}$$
Fig. 8
figure 8

a Effect of We on skin friction coefficient results. b Effect of We on Nusselt number coefficient results

Full size image
Fig. 9
figure 9

a Effect of \(\gamma \) on skin friction coefficient results. b Effect of \(\gamma \) on Nusselt number coefficient results

Full size image
Fig. 10
figure 10

a Effect of M on skin friction coefficient results. b Effect of M on Nusselt number coefficient results

Full size image

The energy equation (15) is identical to that considered in Nazar et al. [47]. The comparison of solutions is documented in Table 1. Excellent correlation is achieved and confidence in the present solutions is therefore justifiably high.

Results and Discussion

Extensive computations have been conducted using the Keller box code to study the influence of the key thermo-physical parameters on velocity, temperature, skin friction and Nusselt number. In the present computations, the following default parameters are prescribed (unless otherwise stated): \(\xi =1.0, M=1.0, We=0.3, \Pr =7.0, \gamma =0.5\). These are visualized in Figs. 3a, b, 4, 5, 6, 7, 8, 9 and 10a–b.

Figure 3a, b illustrate the influence of Weissenberg number (We) on velocity and temperature profiles. We arises only in the momentum Eq. (14) in the mixed derivative \(We {f}^{\prime \prime } {f}^{\prime \prime \prime }\). Weissenberg number (We) measures the relative effects of viscosity to elasticity. Weissenberg number of zero corresponds to a purely Newtonian fluid, and infinite Weissenberg number corresponds to a purely elastic solid. Intermediate values correlate quite well with actual polymeric viscoelastic properties. With increasing We, there is a general increase through the boundary layer in velocity magnitudes. The boundary layer flow is therefore accelerated as viscous effects are depleted since resistance to the flow is reduced.

The momentum boundary layer is therefore depleted with greater Weissenberg number. We note that in Fig. 3a the magnetic body force parameter, M, is set at unity implying that the Lorentzian magnetic drag and viscous hydrodynamic force are of the same magnitude. Figure 3b shows that a consistent elevation is computed in temperature of the viscoelastic fluid with greater values of Weissenberg number, We. The acceleration in the flow aids in momentum development which also assists in thermal diffusion, leading to heating of the boundary layer. Thermal boundary layer thickness is therefore enhanced with increasing We values i.e. decreasing viscosity and increasing elastic effects. Effectively therefore Newtonian fluids (We =0) achieve lower velocities and temperatures than Williamson fluids. Similar trends have been reported by Hayat et al. [48] and Khan and Khan [17].

Figure 4a, b depict the evolution in velocity and temperature characteristics with transverse coordinate i.e. normal to the cylinder surface for various Prandtl numbers, Pr. Relatively high values of Pr are considered since these physically correspond to industrial polymers [49, 50]. Prandtl number embodies the ratio of momentum diffusivity to thermal diffusivity in the boundary layer regime. It also represents the ratio of the product of specific heat capacity and dynamic viscosity, to the fluid thermal conductivity. For polymers momentum diffusion rate greatly exceeds thermal diffusion rate. The low values of thermal conductivity in most polymers also result in a high Prandtl number. With increasing Pr from 7 to 100 there is evidently a substantial deceleration in boundary layer flow i.e. a thickening in the momentum boundary layer (Fig. 4a). The effect is most prominent close to the cylinder surface. Also Fig. 4b shows that with greater Prandtl number the temperature values are strongly decreased throughout the boundary layer transverse to the cylinder surface. Thermal boundary layer thickness is therefore significantly reduced. The asymptotically smooth profiles in the free stream (high \(\eta \) values) confirm that an adequately large infinity boundary condition has been imposed in the Keller box numerical code.

Figure 5a, b present the evolution in velocity and temperature functions with a variation in magnetic body force parameter (M). The radial magnetic field generates a transverse retarding body force. This decelerates the boundary layer flow and velocities are therefore reduced as observed in Fig. 5a. The momentum development in the viscoelastic coating can therefore be controlled using a radial magnetic field. The effect is prominent throughout the boundary layer from the cylinder surface to the free stream. Momentum (hydrodynamic) boundary layer thickness is therefore increased with greater magnetic field. Figure 5b shows that the temperature is strongly enhanced with greater magnetic parameter. The excess work expended in dragging the polymer against the action of the magnetic field is dissipated as thermal energy (heat). This energizes the boundary layer and increases thermal boundary layer thickness. Again the influence of magnetic field is sustained throughout the entire boundary layer domain. These results concur with other investigations of magnetic non-Newtonian heat transfer including Kasim et al. [24] and Megahed [51].

Figure 6a, b present the response in velocity and temperature distributions to a modification in the Newtonian heating parameter (\(\gamma \)). A marked depletion in velocity (Fig. 6a) accompanies an increase in Newtonian heating effect and this trend is sustained throughout the boundary layer. The Heating parameter indirectly influences the momentum field via coupling to the energy equation (Newtonian heating is only simulated in the wall thermal boundary condition in Eq. 16). With greater Newtonian heating effect, there is also a very profound depletion in temperature at the cylinder surface and in close proximity to it (Fig. 6b). However, this effect weakens considerably with further distance from the cylinder surface and is effectively eliminated before reaching the free stream. Temperature profiles decay from a maximum at the cylinder surface to the free stream. All profiles converge at a large value of transverse coordinate, again showing that a sufficiently large infinity boundary condition has been utilized in the numerical computations. Again the absence of Newtonian heating effect achieves higher temperatures indicating that without this modification in the thermal boundary condition at the wall (cylinder surface) the temperature is over-predicted, which can be critical to heat treatment of polymeric coatings [50].

Table 2 Variations of \(C_f\) and Nu for different \(\hbox {We}, {\upgamma }\) and \(\xi \)
Full size table
Table 3 Variations of \(C_f\) and Nu for different \(\hbox {We}, {\upgamma }\) and \(\xi \)
Full size table
Table 4 Variations of \(C_f\) and Nu for different values of \(\gamma , \Pr \)
Full size table
Table 5 Variations of \(C_f\) and Nu for different values of \(\gamma , \Pr \)
Full size table

Figure 7a, b illustrate the influence of the stream wise (tangential) coordinate, \(\xi \), on the velocity and temperature distributions. A weak deceleration in the boundary layer flow is experienced with greater \(\xi \), values i.e. with progressive distance along the cylinder surface from the lower stagnation point \((\xi =0)\), as shown in Fig. 7a. Momentum boundary layer thickness is therefore increased marginally with \(\xi \) values. Conversely a weak enhancement in temperature is computed in Fig. 7b, with increasing \(\xi \) values. Thermal boundary layer thickness is increased therefore as we progress from the lower stagnation point on the cylinder surface around the cylinder periphery upwards.

Figure 8a, b presents the variation in surface shear stress (skin friction) and Nusselt number (wall heat transfer gradient) with Weissenberg number with both thermal and velocity slip present. In consistency with the near-wall behaviour computed for the velocity field in Fig. 3a, there is a significant elevation in skin friction with increasing We values. With progressively greater We values the elasticity in the polymer is increased. This aids in momentum development and accelerates the boundary layer flow. A similar trend has been computed in the studies by Hayat et al. [48]. The Weissenberg number indicates the degree of anisotropy or orientation generated by the deformation, and is appropriate to describe flows with a constant stretch history, and therefore appropriate for polymers. A strong reduction in Nusselt number arises with an elevation in Weissenberg number i.e. heat is transferred from the cylinder surface to the boundary layer. This concurs with Fig. 3b wherein temperature (and thermal boundary layer thickness) are found to be enhanced with Wiessenberg number. The cylinder surface is therefore effectively cooled with greater Weissenberg numbers.

Figure 9a, b present the distributions in skin friction and Nusselt number with Newtonian heating effect (\(\gamma \)). Both skin friction and Nusselt number are strongly reduced with an increase Newtonian heating. The boundary layer is therefore decelerated and heated with stronger Newtonian heating. With Newtonian heating absent therefore the skin friction is maximized at the cylinder surface. The inclusion of Newtonian heating, which is encountered in various slippy polymer flows, is therefore important in more physically realistic simulations.

Figure 10a, b illustrate the influence of magnetic parameter (M) on skin friction and Nusselt number. A significant depletion is caused in skin friction (Fig. 10a) with greater magnetic field, which corresponds to a retardation of the boundary layer flow. The maximum skin friction therefore is achieved only in the absence of a radial magnetic field i.e. M = 0. For \(M<\) 1, the magnetic body force is exceeded by the viscous hydrodynamic force in the regime. For \(M>\) 1 the contrary is the case. The reduction in Nusselt number with greater M values implies that the transfer of heat from the boundary layer to the wall (cylinder surface) is reduced. This physically indicates therefore that greater heat is conveyed away from the cylinder surface to the fluid which explains the higher temperatures associated with strong magnetic field in the earlier computations (Fig. 5b). Magnetic field is therefore a potent mechanism for controlling thermal and velocity characteristics in electrically-conducting polymer dynamics.

Tables 2, 3, 4 and 5 present numerical values for the influence of the various parameters on skin friction and Nusselt number functions. These confirm the trends already elaborated in Figs. 9a, b and 10 and furthermore provide benchmarks against which other researchers may validate extensions of the present model.

Conclusion

Motivated by applications in thermal processing of magnetic polymers in coating systems, a mathematical model has been developed for the magnetohydrodynamic flow and heat transfer in an electro-conductive viscoelastic Williamson fluid from a cylindrical body under radial magnetic field. To simulate slippery polymer interfacial effects, both thermal and momentum slip have been incorporated into the model. The normalized, nonlinear two-dimensional, steady state boundary layer equations for momentum and heat (energy) have been solved with a finite difference scheme, with verification of computational accuracy demonstrated via benchmarking with earlier non-magnetic, no slip, Newtonian solutions in the literature. The present computations have shown that increasing Weissenberg number accelerates the near-wall flow and also increases temperatures (i.e. reduces Nusselt number). Stronger magnetic parameter serves to decelerate the flow and to elevate temperatures i.e. decreases Nusselt numbers. With greater momentum slip the flow is accelerated near the cylinder surface whereas temperatures are depressed i.e. Nusselt numbers are increased. With greater thermal slip surface skin friction and Nusselt number are both significantly suppressed. The present work has ignored transient and porous medium effects in viscoelastic flow [52] which will be considered in the future.