Unsteady MHD Free Convection Flow of Nanofluid Past an Accelerated Vertical Plate with Variable Temperature and Thermal Radiation

Abstract

An analytical study is performed to study the problem of nanofluid flow and heat transfer due to the exponentially accelerated motion of an infinite vertical plate in the presence of (i) magnetic field, (ii) thermal radiation and (iii) variable temperature at the plate. A range of nanofluids containing nanoparticles of aluminium oxide, copper, titanium oxide and silver with nanoparticle volume fraction range $\le$0.04 are considered. The partial differential equations governing the flow are solved by Laplace transform technique. Excellent validation of the present results is achieved with existing results in the literature. The effects of various parameters occurring into the problem such as nanoparticle volume fraction, nanofluid type, magnetic parameter, radiation parameter, accelerating parameter and thermal Grashof number on the velocity and temperature profiles, skin friction coefficient and Nusselt number are easily examined and discussed via the closed forms obtained which may be further used to verify the validity of obtained numerical solutions for more complicated transient free convection nanofluid flow problems.

Introduction

In many manufacturing processes, such as hot rolling, wire drawing, extrusion of metals fibre drawing and crystal growing, heat transfer occurs between a moving material and the ambient medium. In the case of wire drawing and continuous casting processes, the material is cooled by passing it through a colder ambient medium like water or, in some cases, just quiescent ambient air. Stokes [1] studied the problem of the flow of an incompressible viscous fluid past an impulsively started infinite horizontal plate, in its own plane. It is also known as Rayleigh’s problem in the literature. Soundalgekar [2] presented an exact solution to the flow of a viscous fluid past an impulsively started infinite isothermal vertical plate in its own plane by the usual Laplace-transform technique. He discussed the effects of heating or cooling of the plate on the flow field through the Grashof number. The fluid considered in this study was pure air or water. Such a study is found useful in filtration processes, the drying of porous materials in textile industries, etc. Also in many applications in space technology the plate temperature does not remain uniform but varies with time. Soundalgekar and Patil [3] presented the exact analysis of Stokes problem for an infinite vertical plate, whose temperature varies linearly with time. In recent years hydromagnetic flows and heat transfer have become more important because of numerous applications, for example, metallurgical processes in cooling of continuous strips through a quiescent fluid, thermonuclear fusion, aerodynamics, etc. The effect of variable temperature on the Stokes problem for an infinite vertical plate in the presence of transverse magnetic field was analyzed by Soundalgekar et al. [4].

Convective flows with radiation are also encountered in many industrial processes such as heating and cooling of chambers, energy processes, evaporation from large reservoirs, solar power technology and space vehicle re-entry. England and Emery [5] investigated thermal radiation effects of an optically thin gray gas bounded by a stationary vertical plate. The problem of radiation free convective flow of an optically thin gray gas past a semi-infinite vertical plate was studied by Soundalgekar and Takhar [6]. The effect radiation on mixed convection along an isothermal vertical plate was considered by Hossain and Takhar [7]. Radiation and chemical reaction effects on unsteady MHD free convection flow of a dissipative fluid past an infinite vertical Plate with Newtonian heating were analyzed by Rajesh et al. [8]. In many industrial applications, the flow past an exponentially accelerated infinite vertical plate plays an important role. From this point of view, Singh and Kumar [9] studied free convection effects on flow past an exponentially accelerated vertical plate. Effects of mass transfer on exponentially accelerated infinite vertical plate with constant heat flux and uniform mass diffusion were analyzed [10]. Rajesh and Varma [11] investigated radiation and mass transfer effects on MHD free convection flow past an exponentially accelerated vertical plate with variable temperature. Later, Rajesh and Varma [12] studied heat source effects on MHD flow past an exponentially accelerated vertical plate with variable temperature through a porous medium. Also Unsteady convective flow past an exponentially accelerated infinite vertical porous plate with Newtonian heating and viscous dissipation was recently analyzed by Rajesh and Chamkha [13].

On other hand, it is well known that conventional heat transfer fluids, including oil, water, and ethylene glycol mixture are poor heat transfer fluids, since the thermal conductivity of these fluids plays an important role on the heat transfer coefficient between the heat transfer medium and the heat transfer surface. An innovative technique for improving heat transfer by using ultra fine solid particles in the fluids has been used extensively during the last several years. A nanofluid, which is a term introduced by Choi [14], is a base fluid with suspended metallic nano-scale particles called nanoparticles. Because traditional fluids used for heat transfer applications such as water, mineral oils and ethylene glycol have a rather low thermal conductivity, nanofluids with relatively higher thermal conductivities have attracted enormous interest from researchers due to their potential in enhancement of heat transfer with little or no penalty in pressure drop. Daungthongsuk and Wongwises [15] studied the effect of thermo physical properties models on the predicting of the convective heat transfer coefficient for low concentration nanofluid. Abu-Nada and Oztop [16] studied effects of inclination angle on natural convection in enclosures filled with Cu-water nanofluid. The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid was discussed by Nield and Kuznetsov [17]. The problem of mixed convection MHD flow of a nanofluid past a stretching permeable surface in the presence of Brownian motion and thermophoresis effects was studied by Chamkha et al. [18]. Also Chamkha et al. [19] presented non similar solution for natural convective boundary layer flow over a sphere embedded in a porous medium saturated with a nanofluid. Gorla et al. [20] studied Heat transfer in the boundary layer on a stretching circular cylinder in a nanofluid. Later, the problem of mixed convection past a vertical wedge embedded in a porous medium saturated by a nanofluid was analysed by Gorla et al. [21]. Free convection boundary layer flow of a non-Newtonian fluid over a permeable vertical cone embedded in a porous medium saturated with a nanofluid was discussed by Rashad et al. [22]. Chamkha et al. [23] analyzed the unsteady boundary-layer flow of a nanofluid over a horizontal stretching plate in the presence of melting effect. Also the problem of mixed convection boundary-layer flow over an isothermal vertical wedge embedded in a porous medium saturated with a nanofluid was studied by Chamkha et al. [24]. The problem of heat and mass transfer of unsteady natural convection flow of some nanofluids past a vertical infinite flat plate with radiation effect was studied by Turkyilmazoglu and Pop [25]. Loganathan et al. [26] studied the effects of radiation on an unsteady natural convective flow of a nanofluid past an infinite vertical plate. Recently Turkyilmazoglu [27] analyzed unsteady convection flow of some nanofluids past a moving vertical flat plate with heat transfer by the usual Laplace transform technique.

The objective of this paper is to study the problem of nanofluid flow and heat transfer due to the exponentially accelerated motion of an infinite vertical plate with variable temperature in the presence of magnetic field and thermal radiation. In the current analysis, the inertial term is neglected taking into account the fact that the medium is highly viscous.

The partial differential equations governing the flow are solved by Laplace transform technique. The velocity and temperature profiles, as well as skin friction coefficient and Nusselt number are examined and discussed for various parameters occurring in the problem.

Fig. 1

The physical model and coordinate system

Mathematical Analysis

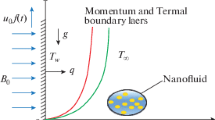
The unsteady, laminar, two-dimensional, boundary layer flow of a viscous incompressible electrically conducting nanofluid past an exponentially accelerated vertical plate in the presence of an applied magnetic field and thermal radiation is considered. The x-axis is taken along the plate in the vertically upward direction, and the y-axis is taken normal to the surface of the plate as shown in Fig. 1. The gravitational acceleration g acts downward. Initially, both the plate and the nanofluid are stationary at the same temperature ${T}_\infty ^{'}$. They are maintained at this condition for all ${t'}\le 0$. At time ${t'}>0$, the plate is exponentially accelerated with a velocity $u=u_0 \exp ({a'}{t'})$ in its own plane. At the same time the plate temperature is raised linearly with time t. We assume that the uniform magnetic field with intensity of $B_0$ acts in the normal direction to the plate and the effect of induced magnetic field is negligible, which is valid when the magnetic Reynolds number is small. The viscous dissipation, Ohmic heating and Hall effects are neglected as they are also assumed to be small. The fluid is water based nanofluid containing different types of nanoparticles: aluminium oxide (Al$_2$O$_3$), copper (Cu), titanium oxide (TiO$_2$) and silver (Ag). In this study, nanofluids are assumed to behave as single-phase fluids with local thermal equilibrium between the base fluid and the nanoparticles suspended in them so that no slip occurs between them. A schematic representation of physical model and coordinate system is depicted in Fig. 1. The thermo physical properties of the nanoparticles [28] are given in Table 1. The basic unsteady momentum and thermal energy equations according to the model for nanofluids given by Tiwari and Das [29] satisfying Boussinesq’s approximation [30] in the presence of magnetic field and thermal radiation are as follows:

$$\begin{aligned}&\frac{\partial u}{\partial {t'}}=\frac{\mu _{nf} }{\rho _{nf} }\frac{\partial ^{2}u}{\partial y^{2}}+\frac{\left( {\rho \beta } \right) _{nf} }{\rho _{nf} }g\left( {{T'}-{T}_\infty ^{'} } \right) -\frac{\sigma B_0^2 u}{\rho _{nf} } \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial {T'}}{\partial {t'}}=\frac{\kappa _{nf} }{\left( {\rho C_p } \right) _{nf} }\frac{\partial ^{2}{T'}}{\partial y^{2}}-\frac{1}{\left( {\rho C_p } \right) _{nf} }\frac{\partial q_r }{\partial y} \end{aligned}$$

(2)

Table 1 Thermo-physical properties of water and nanoparticles

The initial and boundary conditions for the problem are

$$\begin{aligned}&{t'}\le 0: u=0, \qquad {T'}={T}_\infty ^{'} \qquad \hbox {for all y}\nonumber \\&{t'}>0: u=u_0 \exp ({a'}{t'}), \qquad {T'}={T}_\infty ^{'} +\left( {{T}_w^{'} -{T}_\infty ^{'} } \right) A{t'} \qquad \hbox {at}\qquad y=0\nonumber \\&u\rightarrow 0, \qquad {T'}\rightarrow {T}_\infty ^{'} \qquad \hbox {as} \qquad y\rightarrow \infty \end{aligned}$$

(3)

where $A=\frac{u_0^2 }{\nu _f }$.

Here u is the velocity along x-axis; ${t'}$ is the time; g is the acceleration due to gravity; ${T'}$ Temperature of the fluid; ${T}_\infty ^{'}$ temperature of the fluid far away from the plate; ${T}_w^{'}$ Temperature of the plate, $\rho _{nf}$ is the effective density of the nanofluid, $\mu _{nf}$ is the effective dynamic viscosity of the nanofluid, $\beta _{nf}$ is the thermal expansion of the nanofluid, $\kappa _{nf}$ is the thermal conductivity of the nanofluid.

For nanofluids the expressions of density $\rho _{nf}$, thermal expansion coefficient $\left( {\rho \beta } \right) _{nf}$ and heat capacitance $\left( {\rho C_p } \right) _{nf}$ are given by

$$\begin{aligned} \rho _{nf}= & {} \left( {1-\phi } \right) \rho _f +\phi \rho _s\nonumber \\ \left( {\rho \beta } \right) _{nf}= & {} \left( {1-\phi } \right) \left( {\rho \beta } \right) _f +\phi \left( {\rho \beta } \right) _s\nonumber \\ \left( {\rho C_p } \right) _{nf}= & {} \left( {1-\phi } \right) \left( {\rho C_p } \right) _f +\phi \left( {\rho C_p } \right) _s \end{aligned}$$

(4)

The effective thermal conductivity of the nanofluid according to Hamilton and Crosser [31] model is given by

$$\begin{aligned} \frac{\kappa _{eff} }{\kappa _f }=\frac{\kappa _s +\left( {n-1} \right) \kappa _f -\left( {n-1} \right) \phi \left( {\kappa _f -\kappa _s } \right) }{\kappa _s +\left( {n-1} \right) \kappa _f +\phi \left( {\kappa _f -\kappa _s } \right) } \end{aligned}$$

(5)

where “n” is the empirical shape factor for the nanoparticle. In particular “n” $=$ 3 for spherical shaped nanoparticles and “n” $=$ 3/2 for cylindrical ones. $\phi$ is the solid volume fraction of nanoparticles, $\mu$ is the dynamic viscosity, $\nu$ is the kinematic viscosity, $\beta$ is the thermal expansion coefficient, $\rho$ is the density and $\kappa$ is the thermal conductivity. Here the subscripts nf, f and s represent the thermo physical properties of the nanofluids, base fluid and the solid nanoparticles, respectively.

To simulate uni-directional radiative heat flux, we implement the Rosseland approximation [32], which leads to the following expression for radiative heat flux $q_r$:

$$\begin{aligned} q_r =-\frac{4\sigma _s }{3k_e }\frac{\partial {T}^{'4}}{\partial y} \end{aligned}$$

(6)

where $\sigma _s$ is the Stefan–Boltzmann constant and $k_e$ is the mean absorption coefficient, respectively. It should be noted that by using the Rosseland approximation we limit our analysis to optically thick nanofluids. If temperature differences within the flow are sufficiently small such that ${T}^{'4}$ may be expressed as a linear function of the temperature, then the Taylor series for ${T}^{'4}$ about ${T}_\infty ^{'}$, after neglecting higher order terms, is given by:

$$\begin{aligned} {T}^{'4}\cong 4{T}_\infty ^{'3}{T'}-3{T}_\infty ^{'4} \end{aligned}$$

(7)

In view Eqs. (6) and (7), Eq. (2) reduces to

$$\begin{aligned} \frac{\partial {T'}}{\partial {t'}}=\frac{\kappa _{nf} }{\left( {\rho C_p } \right) _{nf} }\frac{\partial ^{2}{T'}}{\partial y^{2}}+\frac{16\sigma _s {T}_\infty ^{'3} }{3k_e \left( {\rho C_p } \right) _{nf} }\frac{\partial ^{2}{T'}}{\partial y^{2}} \end{aligned}$$

(8)

The following dimensionless parameters are defined:

$$\begin{aligned} u= & {} \frac{u}{u_0 }, t=\frac{{t'}u_0^2 }{\nu _f }, Y=\frac{yu_0 }{\nu _f }, T=\frac{{T'}-{T}_\infty ^{'} }{{T}_w^{'} -{T}_\infty ^{'} }, G_r =\frac{g\beta _f \nu _f \left( {{T}_w^{'} -{T}_\infty ^{'} } \right) }{u_0^3 },\nonumber \\ P_r= & {} \frac{\nu _f }{\alpha _f }, M=\frac{\sigma B_0^2 \nu _f }{\rho _f u_0^2 }, \quad a=\frac{{a'}\nu _f }{u_0^2 }, N=\frac{\kappa _f k_e }{4\sigma _s {T}_\infty ^{'3}} \end{aligned}$$

(9)

With the non-dimensional variables (9), Eqs. (1) and (8) become

$$\begin{aligned} \frac{\partial U}{\partial t}= & {} \frac{1}{\left( {1-\phi +\phi \frac{\rho _s }{\rho _f }} \right) }\left( {\frac{1}{\left( {1-\phi } \right) ^{2.5}}\frac{\partial ^{2}U}{\partial Y^{2}}+\left( {1-\phi +\phi \frac{\left( {\rho \beta } \right) _s }{\left( {\rho \beta } \right) _f }} \right) GrT-MU} \right) \qquad \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial T}{\partial t}= & {} \frac{1}{\left( {1-\phi +\phi \frac{\left( {\rho C_p } \right) _s }{\left( {\rho C_p } \right) _f }} \right) }\left( {\frac{\kappa _{nf} }{\kappa _f }+\frac{4}{3N}} \right) \frac{1}{P_r }\frac{\partial ^{2}T}{\partial Y^{2}} \end{aligned}$$

(11)

The initial and boundary conditions in non-dimensional quantities are given by

$$\begin{aligned}&t\le 0: U=0, \qquad T=0\qquad \hbox {for all }Y\nonumber \\&t>0: U=\exp ({at}), \qquad T=t \quad \hbox {at} \quad Y=0\nonumber \\&U\rightarrow 0, \qquad T\rightarrow 0 \quad \hbox {as} \quad Y\rightarrow \infty \end{aligned}$$

(12)

Let

$$\begin{aligned} E_1= & {} \left( {\frac{\kappa _{nf} }{\kappa _f }+\frac{4}{3N}} \right) \frac{1}{\left( {1-\phi +\phi \frac{\left( {\rho C_p } \right) _s }{\left( {\rho C_p } \right) _f }} \right) },\quad E_2 =\frac{1}{\left( {1-\phi } \right) ^{2.5}}\frac{1}{\left( {1-\phi +\phi \frac{\rho _s }{\rho _f }} \right) }\nonumber \\ E_3= & {} \frac{\left( {1-\phi +\phi \frac{\left( {\rho \beta } \right) _s }{\left( {\rho \beta } \right) _f }} \right) }{\left( {1-\phi +\phi \frac{\rho _s }{\rho _f }} \right) }, \quad E_4 =\frac{1}{\left( {1-\phi +\phi \frac{\rho _s }{\rho _f }} \right) } \end{aligned}$$

(13)

Now Eqs. (10) and (11) in terms of $E_1$, $E_2$, $E_3$ and $E_4$ are

$$\begin{aligned}&\frac{\partial U}{\partial t}=E_2 \frac{\partial ^{2}U}{\partial Y^{2}}+E_3 GrT-E_4 MU \end{aligned}$$

(14)

$$\begin{aligned}&\frac{\partial T}{\partial t}=E_1 \frac{1}{P_r }\frac{\partial ^{2}T}{\partial Y^{2}} \end{aligned}$$

(15)

Equations (14) and (15) subjected to the initial and boundary conditions in Eq. (12) are solved using Laplace transform technique and the solutions are given by

$$\begin{aligned} T= & {} \left( {t+\frac{Y^{2}P_r }{2E_1 }} \right) erfc\left( {\frac{Y\sqrt{P_r }}{2\sqrt{E_1 t}}} \right) -Y\sqrt{\frac{tP_r }{\pi E_1 }}\exp \left( {-\frac{Y^{2}P_r }{4E_1 t}} \right) \end{aligned}$$

(16)

$$\begin{aligned} U= & {} \frac{\exp \left( {at} \right) }{2}\left[ {\begin{array}{l} \exp \left( {-Y\sqrt{\frac{ME_4 +a}{E_2 }}} \right) erfc\left( {\frac{Y}{2\sqrt{E_2 t}}-\sqrt{(ME_4 +a)t}} \right) \\ +\exp \left( {Y\sqrt{\frac{ME_4 +a}{E_2 }}} \right) erfc\left( {\frac{Y}{2\sqrt{E_2 t}}+\sqrt{(ME_4 +a)t}} \right) \\ \end{array}} \right] \nonumber \\&-\frac{G_r E_3 }{E_2 \left( {\frac{P_r }{E_1 }-\frac{1}{E_2 }} \right) Z^{2}}\left[ {\begin{array}{l} \frac{1}{2}\left[ {\begin{array}{l} \exp \left( {-Y\sqrt{\frac{ME_4 }{E_2 }}} \right) erfc\left( {\frac{Y}{2\sqrt{E_2 t}}-\sqrt{ME_4 t}} \right) \\ +\exp \left( {Y\sqrt{\frac{ME_4 }{E_2 }}} \right) erfc\left( {\frac{Y}{2\sqrt{E_2 t}}+\sqrt{ME_4 t}} \right) \\ \end{array}} \right] \\ +Z \left( {\begin{array}{l} \frac{t}{2}\left[ {\begin{array}{l} \exp \left( {Y\sqrt{\frac{ME_4 }{E_2 }}} \right) erfc\left( {\frac{Y}{2\sqrt{E_2 t}}+\sqrt{ME_4 t}} \right) \\ +\exp \left( {-Y\sqrt{\frac{ME_4 }{E_2 }}} \right) erfc\left( {\frac{Y}{2\sqrt{E_2 t}}-\sqrt{ME_4 t}} \right) \\ \end{array}} \right] \\ -\frac{Y}{4\sqrt{ME_2 E_4 }}\left[ {\begin{array}{l} \exp \left( {-Y\sqrt{\frac{ME_4 }{E_2 }}} \right) erfc\left( {\frac{Y}{2\sqrt{E_2 t}}-\sqrt{ME_4 t}} \right) \\ -\exp \left( {Y\sqrt{\frac{ME_4 }{E_2 }}} \right) erfc\left( {\frac{Y}{2\sqrt{E_2 t}}+\sqrt{ME_4 t}} \right) \\ \end{array}} \right] \\ \end{array}} \right) \\ -\frac{\exp \left( {Zt} \right) }{2}\left[ {\begin{array}{l} \exp \left( {-Y\sqrt{\frac{ME_4 +Z}{E_2 }}} \right) erfc\left( {\frac{Y}{2\sqrt{E_2 t}}-\sqrt{(ME_4 +Z)t}} \right) \\ +\exp \left( {Y\sqrt{\frac{ME_4 +Z}{E_2 }}} \right) erfc\left( {\frac{Y}{2\sqrt{E_2 t}}+\sqrt{(ME_4 +Z)t}} \right) \\ \end{array}} \right] \\ \end{array}} \right] \nonumber \\&+\frac{G_r E_3 }{E_2 \left( {\frac{P_r }{E_1 }-\frac{1}{E_2 }} \right) Z^{2}}\left[ {\begin{array}{l} erfc\left( {\frac{Y\sqrt{P_r }}{2\sqrt{E_1 t}}} \right) \\ +Z \left( {\left( {t+\frac{Y^{2}P_r }{2E_1 }} \right) erfc\left( {\frac{Y\sqrt{P_r }}{2\sqrt{E_1 t}}} \right) -Y\sqrt{\frac{tP_r }{\pi E_1 }}\exp \left( {-\frac{Y^{2}P_r }{4E_1 t}} \right) } \right) \\ -\frac{\exp \left( {Zt} \right) }{2}\left[ {\begin{array}{l} \exp \left( {-Y\sqrt{\frac{ZP_r }{E_1 }}} \right) erfc\left( {\frac{Y\sqrt{P_r }}{2\sqrt{E_1 t}}-\sqrt{Zt}} \right) \\ +\exp \left( {Y\sqrt{\frac{ZP_r }{E_1 }}} \right) erfc\left( {\frac{Y\sqrt{P_r }}{2\sqrt{E_1 t}}+\sqrt{Zt}} \right) \\ \end{array}} \right] \\ \end{array}} \right] \end{aligned}$$

(17)

Where $Z=\frac{\left( {\frac{ME_4 }{E_2 }} \right) }{\left( {\frac{P_r }{E_1 }-\frac{1}{E_2 }} \right) }$, $erf(s)=\frac{2}{\sqrt{\pi }}\int _0^s {\exp \left( {-s^{2}} \right) } ds$, and $erfc(s)=1-erf(s)$

Physical quantities of practical interest are the skin friction coefficient $C_f$, and the Nusselt number Nu, which are defined, respectively, as follows:

$$\begin{aligned} C_f =\frac{\tau _w }{\rho _f u_0^2 }, \quad Nu=\frac{q_w L_{ref} }{\kappa _f \left( {{T}_w^{'} -{T}_\infty ^{'} } \right) } \end{aligned}$$

(18)

Where $\tau _w$ and $q_w$are the skin-friction or shear stress and the heat flux from the surface of the plate, respectively, and they are given by

$$\begin{aligned} \tau _w =\mu _{nf} \left( {\frac{\partial u}{\partial y}} \right) _{y=0} , \quad q_w =-\kappa _{nf} \left( {\frac{\partial {T'}}{\partial y}} \right) _{y=0} \end{aligned}$$

(19)

Using non-dimensional variables (9), we get

The skin friction coefficient

$$\begin{aligned} C_f= & {} \frac{1}{\left( {1-\phi } \right) ^{2.5}}\left( {\frac{\partial U}{\partial Y}} \right) _{Y=0} \nonumber \\= & {} \frac{1}{\left( {1-\phi } \right) ^{2.5}}\left[ {\begin{array}{l} -\exp \left( {at} \right) \left[ {\sqrt{\frac{ME_4 +a}{E_2 }}erf\left( {\sqrt{\left( {ME_4 +a} \right) t}} \right) +\frac{1}{\sqrt{\pi E_2 t}}\exp \left( {-\left( {ME_4 +a} \right) t} \right) } \right] \\ -\frac{G_r E_3 }{E_2 \left( {\frac{P_r }{E_1 }-\frac{1}{E_2 }} \right) Z^{2}}\left( {\begin{array}{l} -\left[ {\sqrt{\frac{ME_4 }{E_2 }}erf\left( {\sqrt{ME_4 t}} \right) +\frac{1}{\sqrt{\pi E_2 t}}\exp \left( {-ME_4 t} \right) } \right] \\ +Z\left( {\begin{array}{l} -t\left[ {\sqrt{\frac{ME_4 }{E_2 }}erf\left( {\sqrt{ME_4 t}} \right) +\frac{1}{\sqrt{\pi E_2 t}}\exp \left( {-ME_4 t} \right) } \right] \nonumber \\ -\frac{1}{2\sqrt{ME_2 E_4 }}erf\left( {\sqrt{ME_4 t}} \right) \\ \end{array}} \right) \\ +\exp \left( {Zt} \right) \left[ {\begin{array}{l} \sqrt{\frac{ME_4 +Z}{E_2 }}erf\left( {\sqrt{\left( {ME_4 +Z} \right) t}} \right) \\ +\frac{1}{\sqrt{\pi E_2 t}}\exp \left( {-\left( {ME_4 +Z} \right) t} \right) \\ \end{array}} \right] \\ \end{array}} \right) \\ +\frac{G_r E_3 }{E_2 \left( {\frac{P_r }{E_1 }-\frac{1}{E_2 }} \right) Z^{2}}\left( {-\sqrt{\frac{P_r }{\pi E_1 t}}-2Z\sqrt{\frac{tP_r }{\pi E_1 }}+\exp \left( {Zt} \right) \left[ {\begin{array}{l} \sqrt{\frac{ZP_r }{E_1 }}erf\left( {\sqrt{Zt}} \right) \\ +\sqrt{\frac{P_r }{\pi E_1 t}}\exp \left( {-Zt} \right) \\ \end{array}} \right] } \right) \\ \end{array}} \right] \\ \end{aligned}$$

(20)

And the Nusselt number

$$\begin{aligned} Nu=-\frac{\kappa _{nf} }{\kappa _f }\left( {\frac{\partial T}{\partial Y}} \right) _{Y=0} =\frac{2\kappa _{nf} }{\kappa _f }\sqrt{\frac{tP_r }{\pi E_1 }} \end{aligned}$$

(21)

Results and Discussion

In order to get the physical insight into the problem, extensive numerical computations are conducted for various values of the governing thermo-physical parameters and depicted in tables and graphs. We consider four different types of nanofluids containing aluminium oxide (Al$_2$ O$_3$), copper (Cu), titanium oxide (TiO$_2$) and silver (Ag) nanoparticles with water as a base fluid. The nanoparticle volume fraction is considered in the range of $0\le \phi \le 0.04$, as sedimentation takes place when the nanoparticle volume fraction exceeds 8 %. In this study, we have considered spherical nanoparticles with thermal conductivity [33] and dynamic viscosity [34] shown in Model I in Table 2. The Prandtl number, Pr of the base fluid is kept constant at 6.2. When $\phi = 0$ this study reduces the governing equations to those of a regular fluid i.e. nanoscale characteristics are eliminated. In order to check the accuracy of the present results, the temperature profiles of the present study (in the absence of nanoparticle volume fraction and thermal radiation) are compared with existing results in literature by Muthukumaraswamy et al. [35] in Fig. 2 and they are found to be in excellent agreement.

Table 2 Thermal conductivity and dynamic viscosity for various shapes of nanoparticles

Fig. 2

Comparison of temperature profiles of present study with Muthukumaraswamy et al. [35]

Fig. 3

Effect of magnetic parameter (M) on the velocity profiles

Fig. 4

Effect of radiation parameter (N) on the velocity profiles

Fig. 5

Effect of accelerating parameter (a) on the veocity profiles

Fig. 6

Effect of thermal Grashof number (Gr) on the velocity profiles

Fig. 7

Development of the velocity profiles with time (t)

Fig. 8

Effect of nanoparticle volume fraction $(\phi )$ on the velocity profiles

The velocity profiles of Al$_2$O$_3$-water nanofluid with coordinate Y for different values of magnetic parameter (M), radiation parameter (N), exponential accelerated parameter (a), thermal Grashof number (Gr), time (t), nanoparticle volume fraction ($\phi )$ when Pr $=$ 6.2 are presented in Figs. 3, 4, 5, 6, 7 and 8. It is found in Fig. 3 that, as the magnetic parameter M increase, the flow rate of Al$_2$O$_3$-water nanofluid retard and thereby giving rise to a decrease in the velocity profiles. The reason behind this phenomenon is that application of magnetic field to an electrically conducting nanofluid gives rise to a resistive type force called the Lorentz force. This force has the tendency to slow down the motion of the nanofluid in the boundary layer. It is seen in Fig. 4 that, the velocity of Al$_2$O$_3$-water nanofluid decreases with an increase in the thermal radiation parameter N. From the definition given in Eq. (9), $N=\frac{\kappa _f k_e }{4\sigma _s {T}_\infty ^{'3}}$, as N increases thermal conduction contribution dominates and thermal radiative contribution recedes. Therefore for higher values of N, a lower radiative flux is present and this exerts a decelerating influence on nanofluid boundary layer flow.

It is observed in Fig. 5 that, the velocity increases with increasing exponential accelerated parameter. Figure 5 also reveals that when we take exponential accelerating parameter equal to zero the whole problem converted into nanofluid flow over impulsively started plate with variable temperature in the presence of radiation and magnetic field. The parameter $G_r =\frac{g\beta _f \nu _f \left( {{T}_w^{'} -{T}_\infty ^{'} } \right) }{u_0^3 }$ denotes the relative influence of thermal buoyancy force and viscous force in the boundary layer regime. With large values of this parameter, buoyancy dominates and for small values viscosity dominates. It is noticed in Fig. 6 that, the velocity of Al$_2$O$_3$-water nanofluid increases with the increase in thermal Grashof number Gr. This means that buoyancy force accelerates velocity field. An increase in the value of thermal Grashof number has the tendency to induce much flow in the boundary layer due to the effect of thermal buoyancy. As time (t) progress, the velocity profiles of Al$_2$O$_3$-water nanofluid increases with time; this is seen in Fig. 7. It is observed in Fig. 8 that, the velocity profiles of Al$_2$O$_3$-water nanofluid increases with the increase in the nanoparticle volume fraction $\phi$. Further, it is seen in Fig. 8 that, the velocity of the Al$_2$O$_3$-Water nanofluid is more than that for pure water (Newtonian viscous fluid).

Fig. 9

Effect of radiation parameter (N) on the temperature profiles

Fig. 10

Development of temperature profiles with time (t)

Fig. 11

Effect of nanoparticle volume fraction $(\phi )$ on the temperature profiles

The temperature profiles of Al$_2$O$_3$-water nanofluid with coordinate Y for different values of radiation parameter (N), time (t), and nanoparticle volume fraction $(\phi )$ when Pr $=$ 6.2, are shown in Figs. 9, 10 and 11. It is found in Fig. 9 that, the temperature of Al$_2$O$_3$-water nanofluid decreases with increasing values of N. The reason behind this is that, greater N values imply lower thermal radiative flux which manifests in a reduction in temperatures. Evidently a reduction in radiative flux effectively suppresses the rate of energy transport to the fluid and results in a cooling of the boundary layer regime and thinner thermal boundary layer. Like the velocity, the temperature is also found to increase with a progress in time; this is clear in Fig. 10. It is found in Fig. 11 that, the temperature of the nanofluid also increases with increase in nanoparticle volume fraction $\phi$. This is attributable to the fact that an increase in nanoparticle volume fraction leads to an increase in the thermal conductivity of the nanofluid and hence accentuates thermal diffusion, manifesting in a thickening in thermal boundary layer thickness. It is also seen in Figs. 3, 4, 5, 6, 7, 8, 9, 10 and 11 that, velocity and temperatures of nanofluid descend from a maximum at the plate surface in a monotonic fashion to zero with increasing coordinate Y for all M, N, a, Gr, t, and $\phi$.

Table 3 Effects of the nanoparticle volume fraction for different types of nanofluids on skin friction coefficient when Pr  $=$  6.2, M  $=$  4, Gr  $=$  5, N  $=$  3, a  $=$  0.5, t  $=$  0.5

Table 4 Effects of the magnetic parameter for different types of nanofluids on skin friction coefficient when Pr  $=$  6.2, Gr  $=$  5, N  $=$  3, a  $=$   0.5,$\phi$= 0.04, t  $=$  0.5

Table 5 Effects of the radiation parameter for different types of nanofluids on skin friction coefficient when t $=$ 0.5, Pr  $=$  6.2, M  $=$  4, Gr  $=$  5, a  $=$  0.5, $\phi = 0.04$

Table 6 Effects of the thermal Grashof number for different types of nanofluids on skin friction coefficient when t  $=$  0.5, Pr  $=$  6.2, M  $=$  4, N  $=$  3, a  $=$  0.5, $\phi = 0.04$

Table 7 Effects of the accelerating parameter for different types of nanofluids on skin friction coefficient when t  $=$  0.5, Pr  $=$  6.2, M   $=$  4, Gr  $=$  5, N  $=$  3, $\phi = 0.04$

Table 8 Effects of the nanoparticle volume fraction for different types of nanofluids on Nusselt number when t  $=$  0.5, Pr  $=$  6.2, N  $=$  3

Table 9 Effects of the radiation parameter for different types of nanofluids on Nusselt number when t  $=$  0.5, Pr  $=$  6.2, $\phi = 0.04$

The behavior of the skin friction coefficient and Nusselt number using different nanofluids is demonstrated in Tables 3, 4, 5, 6, 7, 8 and 9. It is found in Tables that, by using different types of nanofluid the values of the skin friction coefficient and Nusselt number change. This means that the nanofluids type will be important in the cooling and heating processes. It is also seen in Tables 3, 4, 5, 6 and 7 that, for all values of nanoparticle volume fraction $\phi$, magnetic parameter M, radiation parameter N, thermal Grashof number Gr, and accelerating parameter a, choosing aluminium oxide as the nanoparticle leads to the minimum magnitude of the skin friction coefficient, while selecting silver leads to the maximum magnitude of it. The skin-friction coefficient at the surface is also observed to decrease for all nanofluids namely, aluminium oxide, copper, titanium oxide and silver with the increase in nanoparticle volume fraction, magnetic parameter, radiation parameter, and accelerating parameter. But the reverse effect of thermal Grashof number is observed on skin-friction coefficient for all nanofluids namely, aluminium oxide, copper, titanium oxide and silver. Further it is found in Tables 8 and 9 that, for all values of nanoparticle volume fraction $\phi$ and radiation parameter N, choosing copper as the nanoparticle leads to the maximum amount of Nusselt number, while selecting titanium oxide leads to the minimum amount of it. The Nusselt number at the surface is also found to increase for all nanofluids namely, aluminium oxide, copper, titanium oxide and silver with the increase in nanoparticle volume fraction or radiation parameter.

Conclusions

The problem of unsteady laminar boundary layer flow of a viscous incompressible electrically conducting nanofluid past an exponentially accelerated vertical plate with variable temperature and thermal radiation in the presence of an applied magnetic field has been investigated. The governing equations of the flow are solved by Laplace transform technique. The effects of important parameters such as nanoparticle volume fraction, nanofluids type, magnetic parameter, radiation parameter, accelerating parameter and thermal Grashof number on the velocity and temperature profiles, skin friction coefficient and Nusselt number are examined and discussed.

The conclusions of the study are as follows:

• 1. As the nanoparticle volume fraction and radiation parameter increased, the Nusselt number increased for all nanofluids namely, aluminium oxide, copper, titanium oxide and silver-water.

• 2. Choosing copper as the nanoparticle leads to the maximum amount of Nusselt number.

• 3. Selecting titanium oxide as the nanoparticle leads to the minimum amount of Nusselt number.

• 4. As the thermal Grashof number Gr increased, the Skin-friction coefficient increased for all nanofluids namely, aluminium oxide, copper, titanium oxide and silver-water.

• 5. As the nanoparticle volume fraction, magnetic parameter, radiation parameter and accelerating parameter increased, the Skin-friction coefficient decreased for all nanofluids namely, aluminium oxide, copper, titanium oxide and silver-water.

• 6. Choosing aluminium oxide as the nanoparticle leads to the minimum magnitude of the skin friction coefficient.

• 7. Selecting silver as the nanoparticle leads to the maximum magnitude of the skin friction coefficient.

• 8. As the magnetic parameter M increased, the velocity of Al$_2$O$_3$-water nanofluid decreased.

• 9. As the thermal radiation parameter N increased, the velocity and the temperature of Al$_2$O$_3$-water nanofluid decreased.

• 10. The velocity and the temperature of Al$_2$O$_3$-water nanofluid increased with the increase in dimensionless time.

• 11. As the thermal Grashof number Gr and the exponential accelerated parameter a increased, the velocity of Al$_2$O$_3$-water nanofluid increased.

• 12. As the nanoparticle volume fraction$\phi$ increased, the velocity and the temperature of Al$_2$O$_3$-water nanofluid increased.