1 Introduction

The concept of fuzzy sets (FSs) was presented by Zadeh [34] in 1965 which become useful tool to solve the problems containing uncertainties. In contrast to classical set theory, FS allocates membership degree to each member of a given set X. This allocated membership value relax the researchers to discuss the characteristics of elements in a data set with uncertainties. Due to this, many generalizations of FSs have been explored in the literature. Interval-valued fuzzy sets (IVFSs) was the very first generalization of FSs which was also introduced by Zadeh [35]. In IVFSs, the membership values were considered as subintervals of [0, 1] instead of numbers from this unit interval. IVFSs creates more space for membership values and so on. The idea of intuitionistic fuzzy set (IFSs) was given by Atanassov [3]. In IFSs, each member is characterized by membership and non-membership values. An extension of IFSs termed interval-valued intuitionistic fuzzy sets (IVIFSs) was also initiated in [4]. In IVIFSs, the membership and non-membership values were comprise of specific subintervals of [0, 1]. In the theory of IFSs, the term "neutrality degree" was ignored however the neutrality degree plays a key role in many real-life circumstances such as democratic election. Human beings normally give their opinions in the form: yes, no, abstain, and refusal. Hence, by using IFSs we are unable to handle such circumstances because we miss the the information of voting for non-candidates (refusal). To overcome such types of hurdles, Cuong [8] included neutral value in the IFS structure and created new structure named picture fuzzy sets(PFSs). Consequently, PFS contains three values: membership, neutral, and non-membership values which map the values varies within the interval [0, 1] implies that its sum is also contained in unit interval. Numerous researches have been conducted on PFSs and various extensions of PFSs have been explored like bipolar picture fuzzy sets (BPPFSs) [12] and interval-valued picture fuzzy sets(IVPFSs) [11]. Many applications of PFSs have been investigated in [6, 16, 36].

The concept of fuzzy graphs (FGs) was initiated by Rosenfield in [25]. Afterward, numerous generalizations of FGs were explored such as fuzzy tolerance graphs [27], bipolar fuzzy graphs [2], and fuzzy threshold graphs [28]. The notion of interval-valued fuzzy graphs (IVFG) was introduced by Akram et al. [1]. After this, various concepts in the setting of IVFGs were suggested such as IVF-planar graphs [19], highly irregular IVFGs [22, 23], isometry and IVFGs [24]. Then, the term intuitionistic fuzzy graphs (IFGs) was introduced in [18]. Some new operation on IFGs were described in [33]. Several new concepts in IFGs were explored in [29]. The concepts of covering and domination in IFGs were described by Sahoo et al. [26]. Extension of IFGs named picture fuzzy graphs (PFGs) was explored in [37]. A PFG is the extension of IFG which is more effective in modeling the real-world problems having uncertainties and where the IFGs fails to give the appropriate models. The term "main energies" of picture fuzzy graphs (PFGs) was discussed in [30]. Furthermore, several studies have been conducted on PFGS and various types of PFGs have been introduced in the literature such as Cayley picture fuzzy graphs(CPFGs) [14], bipolar picture fuzzy graphs(BPPFGs) [13], and picture fuzzy line graphs(PFLGs) [7].

Recently, Khan (with Shi and Kosari) [32] have introduced the notion of interval-valued picture fuzzy graphs (IVPFGs). The framework of IVPFGs allows the modeling of vague information in a robust manner. Moreover, IVPFGs with different attributes are highly applicable in decision making theory. For example, during purchasing a product while shopping, customers may act in many ways: they may decide to purchase a product, opt not to buy it, decide to wait, or reject the purchase completely. In comparison, IVPFGs offers an advanced framework for analyzing customer behavior. Consequently, IVPFGs assists businesses in making strategic decisions by comprehending the uncertainty surrounding purchase decisions within the defined intervals. A flow chart given in Fig. 8 and Table 1 further demonstrate the significance of the study of interval-valued picture fuzzy graph models.

Table 1 Generalization of fuzzy sets
Full size table

The concepts of covering, matching, and domination in FGs were introduced by Manjusha and Sunitha [17]. On the same pattern, the concepts of domination and some other relevant properties in vague graphs (VGs) were explored in [15, 20, 31]. However, we elaborate our contributions to the existing literature in Table 14, where we provide the analysis that how our presented model of domination in IVPFGs is more flexible compared to other generalization of FGs.

In our study, we first define SAs in IVPFGs and then apply it to describe the new concept of covering, SNC and SAC. After this, we initiate the concepts of matching, strong matching (SM), perfect strong matching (PSM), strong matching number (SMN) etc in IVPFGs. We also present some useful results related to some special IVPFGs related to these terms. These ideas are followed by appropriate examples and graphical interpretations. Finally, we provide the utilization of strong arcs (SAs) and SIS to arrange the meeting of the members of social network comprising players engaged in various games. We also develop some fascinating results results to these terms. Overall, matching and covering in IVPFGs are useful for our study due to its non-specific structure (Fig. 1).

Fig. 1
figure 1

A view to the generalizations of FSs

Full size image

1.1 Motivations and Novelty

The membership, neutral, and non-membership values in terms of subintervals of [0, 1] in an IVPFGs makes the structure more flexible and has an extensive domain as compared to the other extensions of FGs. On the other hands, FGs has only membership values, IFG have membership and non-membership values. Overall, IVPFGs are the best in comparison with the other existing generalizations of FGs. Moreover, the terms covering and matching in FGs and IFGs have been established in the literature which motivated us to shift these terms toward IVPFGs along with its application. We summarize the novelty of our work as follows.

  1. 1.

    In the beginning, we introduce the terms SNC, SAC, SAC number SIS based on SAs in IVPFGs.

  2. 2.

    We provide numerous useful results related to these terms and investigate some special IVPFGs like complete IVPFGs and bipartite IVPFGs.

  3. 3.

    We also initiate the concepts of matching, SM etc in IVPFGs.

  4. 4.

    We produce several important characterizations of some special IVPFGs based on the established terms in IVPFGs.

  5. 5.

    To demonstrate the usefulness of the terms which we have introduced, we offer their application in the context of selection criteria.

1.1.1 Contributions of Our Study

The contributions of our present article are given below.

  1. 1.

    The notions of covering, matching, SM, perfect matching etc of IVPFGs based on SAs are introduced. Furthermore, we explore some new results on covering and matching of some special graphs such as complete-IVPFGs and complete bipartite IVPFGs.

  2. 2.

    The upper and lower bounds of SACs of some special IVPFGs are investigated.

  3. 3.

    We provide discussions about different types of matching based on SACs.

  4. 4.

    We provide application of newly established concepts toward social network in order to validate the affectivity of our newly introduced model.

  5. 5.

    Comparative analysis of our proposed model with the existing models related to IVFGs and IVIFGs, is also conducted.

This article is organized as: Sect. 2 covers the important definitions and explanations related to FSs, FGs etc. In Sect. 3, SNC, various useul properties of SAs, SIS, SM using SAs are discussed. In Sect. 4, we provide the application of covering in IVPFGs toward special social network. In Sect. 5, we provide the comparative analysis of our proposed model with the other existing models in the literature. We provide the evidences superiority of our presented model. Finally, concluding remarks, limitations, and future directions are provided in Sect. 6.

2 Preliminaries

In this section, we add some useful concepts from the literature which are helpful in understanding the forthcoming sections.

Definition 1

[34] \((\eta , X)\) be a fuzzy set on X, where \(\eta{:} X\longrightarrow [0, 1]\) represents the membership function.

Definition 2

[3] A collection \(\{({\tilde{v}}, \varepsilon _{A}({\tilde{v}}), \eta _{A}({\tilde{v}}): {\tilde{v}} \in X)\}\) is an IFS, where \(\varepsilon _{A}({\tilde{v}}) \in [0, 1]\) represents the membership value of element \({\tilde{v}}\) in A, \(\eta _{A}({\tilde{v}}) \in [0, 1]\) is the non-membership value of \({\tilde{v}}\) in A, satisfying \(\varepsilon _{A}{\tilde{v}} + \eta _{A}({\tilde{v}}) \le 1,\) for all \({\tilde{v}} \in V.\)

Definition 3

[8] A picture fuzzy sets (PFSs) A on V is a collection \(\{(\grave{v}, \varepsilon _{A}(\grave{v}), \zeta _{A}(\grave{v}), \eta _{A}(\grave{v})): \grave{v} \in V\}\), where \(\varepsilon _{A}(\grave{v}) \in [0, 1]\) represents membership value of element \(\grave{v}\) in A, \(\zeta _{A}(\grave{v}) \in [0, 1]\) represents the neutral membership value of element \(\grave{v}\) in A, and \(\eta _{A}(\grave{v}) \in [0, 1]\) is a non-membership value of an element \(\grave{v}\) in A, satisfying \(\varepsilon _{A}(\grave{v}) + \zeta _{A}(\grave{v}) + \eta _{A}(\grave{v}) \le 1\), for all \(\grave{v} \in V\). We call \(1 - (\varepsilon _{A}(\grave{v}) + \zeta _{A}(\grave{v}) + \eta _{A}(\grave{v}))\) a degree of refusal membership of \(\grave{v}\) in A.

Definition 4

[11] An interval-valued picture fuzzy sets (IVPFSs) S on U is the object

$$\{(\grave{v}, \varepsilon _{A}(\grave{v}), \zeta _{A}(\grave{v}), \eta _{A}(\grave{v})): \grave{v} \in V\},$$

where \(\varepsilon _{A}{:} U \rightarrow \text{int}([0, 1]),\) \(\varepsilon _{A}(w) = [\varepsilon _{A}(w), \varepsilon _{A}(w)] \in \text{int}([0, 1])\)

\(\zeta _{A}{:} U \rightarrow \text{int}([0, 1]),\) \(\zeta_{A}(w) = [zeta_{A}(w), zeta_{A}(w)] \in \text{int}([0, 1])\)

\(\eta_{A}(w) = [\eta_{A}(w), \eta_{A}(w)] \in \text{int}([0, 1])\) and

for all \(w \in U, \varepsilon _{A}(w) + \zeta _{A}(w) + \eta _{A}(w) \le 1.\)

Definition 5

[32] An object H = (W, X) is an interval-valued picture fuzzy graph (IVPFG) defined on the graph \(G^{\ast}=(V,E),\) where \(W= ([\varepsilon^{L}_{W}, \varepsilon^{U}_{W}]\), \([\zeta^{L}_{W}, \zeta^{U}_{W}],\) \([\eta^{L}_{W}, \eta^{U}_{W}])\) be an IVPFS on V and X = \(([\varepsilon^{L}_{X}, \varepsilon^{U}_{X}]\), \([\zeta^{L}_{X}, \zeta^{U}_{X}],\) \([\eta^{L}_{X}, \eta^{U}_{X}])\) be an IVPFS on \(E \subseteq V \times V\), where \(\varepsilon^{L}_{X}(\grave{u}, \grave{v})\) and \(\varepsilon^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper membership values, \(\zeta^{L}_{X}(\grave{u}, \grave{v})\) and \(\zeta^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper neutral values, and \(\eta^{L}_{X}(\grave{u}, \grave{v})\) and \(\eta^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper non-membership values, such that for each edge \(\grave{u}\grave{v} \in E\)

$$\begin{aligned} \varepsilon^{L}_{X}(\grave{u}, \grave{v}) & \le \min (\varepsilon^{L}_{W}(\grave{u}), \varepsilon^{L}_{W}(\grave{v})), \varepsilon^{U}_{X}(\grave{u}, \grave{v})\le \min (\varepsilon^{U}_{W}(\grave{u}), \varepsilon^{U}_{W}(\grave{v}))\\ \zeta^{L}_{X}(\grave{u}, \ \grave{v}) & \le \min (\zeta^{L}_{W}(\grave{u}), \zeta _{WL}(\grave{v})), \zeta^{U}_{X}(\grave{u}, \ \grave{v}) \le \min (\zeta^{U}_{W}(\grave{u}), \zeta^{U}_{W}(\grave{v}))\\ \eta^{L}_{X}(\grave{u}, \ \grave{v}) & \ge \max (\eta^{L}_{W}(\grave{u}), \eta^{L}_{W}(\grave{v})), \eta^{U}_{X}(\grave{u}, \ \grave{v}) \ge \max (\eta^{U}_{W}(\grave{u}), \eta^{U}_{W}(\grave{v})) \end{aligned}$$

satisfying \(0\le \varepsilon^{U}_{X}(\grave{u}, \grave{v})+\zeta^{U}_{X}(\grave{u}, \grave{v})+\eta^{U}_{X}(\grave{u}, \ \grave{v})\le 1\), for all \(\grave{u} \grave{v}\in E.\)

3 Covering and Matching in IVPFGs

In this section, we comprehensively discuss the concepts of covering and matching in IVPFGs based on SAs. We provide many fascinating results and consequences related to them.

Definition 6

Strong arc (SA) of an IVPFG is an edge \((\grave{u}, \ \grave{v})\) satisfying

$$\begin{aligned} \varepsilon^{L}_{X}(\grave{u}, \grave{v})& = \min (\varepsilon^{L}_{W}(\grave{u}), \varepsilon^{L}_{W}(\grave{v})), \varepsilon^{U}_{X}(\grave{u}, \grave{v})= \min (\varepsilon^{U}_{W}(\grave{u}), \varepsilon^{U}_{W}(\grave{v}))\\ \zeta^{L}_{X}(\grave{u}, \ \grave{v})& = \min (\zeta^{L}_{W}(\grave{u}), \zeta _{WL}(\grave{v})), \zeta^{U}_{X}(\grave{u}, \ \grave{v}) = \min (\zeta^{U}_{W}(\grave{u}), \zeta^{U}_{W}(\grave{v}))\\ \eta^{L}_{X}(\grave{u}, \ \grave{v})& = \max (\eta^{L}_{W}(\grave{u}), \eta^{L}_{W}(\grave{v})), \eta^{U}_{X}(\grave{u}, \ \grave{v}) = \max (\eta^{U}_{W}(\grave{u}), \eta^{U}_{W}(\grave{v})). \end{aligned}$$

where \(\varepsilon^{L}_{X}\), \(\zeta^{L}_{X}\), and \(\eta^{L}_{X}\) are the lower membership, lower neutral membership, and lower nonmembership values, respectively.

Now we provide the concepts of strong node cover (SNC) in IVPFG based on SAs.

Definition 7

Let \(H=(W, X)\) be an IVPFG. Then the set of nodes E which covers all SAs of H is called SNC in an IVPFG H. The (interval-valued picture) fuzzy weight \(\grave{W}\) of SNC E is given by

$$\begin{aligned} \grave{W}_{nc}& = \langle [\grave{W}^{L_{\varepsilon }}_{nc}(E), \grave{W}^{U_{\varepsilon }}_{nc}(E)],[\grave{W}^{L_{\zeta }}_{nc}(E), \grave{W}^{U_{\zeta }}_{nc}(E)],\\ & \quad [\grave{W}^{L_{\eta }}_{nc}(E), \grave{W}^{U_{\eta }}_{nc}(E)]\rangle \\ \grave{W}_{nc}& = \left\langle \left[ \displaystyle \sum _{\grave{u} \in E}\varepsilon^{L}_{X}(\grave{u}, \grave{v}), \sum _{\grave{u} \in E}\varepsilon^{U}_{X}(\grave{u}, \grave{v})\right] ,\right. \\ & \quad \left[ \sum _{\grave{u} \in E}\zeta^{L}_{X}(\grave{u}, \grave{v}), \sum _{\grave{u} \in E}\zeta^{U}_{X}(\grave{u}, \grave{v})\right] ,\\ & \quad \left. \left[ \sum _{\grave{u} \in E}\eta^{L}_{X}(\grave{u}, \grave{v}), \sum _{\grave{u} \in E}\eta^{U}_{X}(\grave{u}, \grave{v})\right] \right\rangle \end{aligned}$$

where \(\varepsilon^{L}_{X}(\grave{u}, \grave{v})\) and \(\varepsilon^{U}_{X}(\grave{u}, \grave{v})\) represent the minimum of the lower and upper membership values of all SAs, \(\zeta^{L}_{X}(\grave{u}, \grave{v})\) and \(\zeta^{U}_{X}(\grave{u}, \grave{v})\) represent the minimum of the lower and upper neutral values of all SAs, and \(\eta^{L}_{X}(\grave{u}, \grave{v}),\) \(\eta^{U}_{X}(\grave{u}, \grave{v})\) are the maximum of the lower and upper non-membership values of all SAs of IVPFG H which are incident on \(\grave{u}\), respectively.

Definition 8

A collection \(\gamma _{0}(H)=\gamma _{0}=\langle [\gamma^{L_{\varepsilon }}_{10}, \gamma^{U_{\varepsilon }}_{10}], [\gamma^{L_{\zeta }}_{20}, \gamma^{U_{\zeta }}_{20}],[\gamma^{L_{\eta }}_{30}, \gamma^{U_{\eta }}_{30}]\rangle\) is a SNC number of IVPFG if it satisfies

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{10} & =\min \{\grave{W}^{L_{\varepsilon }}_{nc}(E)| E \text { is the fuzzy weight of SNCs of H}\}\\ \gamma^{U_{\varepsilon }}_{10} & =\min \{\grave{W}^{U_{\varepsilon }}_{nc}(E)| E\; \text{is\; the\; fuzzy\; weight\; of\; SNCs \;of\; H}\}\\ \gamma^{L_{\zeta }}_{20} & =\min \{\grave{W}^{L_{\zeta }}_{nc}(E)| E\; \text{is\; the\; fuzzy\; weight\; of\; SNCs\; of\; H}\}\\ \gamma^{U_{\zeta }}_{20} & =\min \{\grave{W}^{U_{\zeta }}_{nc}(E)| E\; \text{is \;the\; fuzzy\; weight\; of\; SNCs\; of\; H}\}\\ \gamma^{L_{\eta }}_{30} & =\max \{\grave{W}^{L_{\eta }}_{nc}(E)| E \text { is the fuzzy weight of SNCs of H}\}\\ \gamma^{U_{\eta }}_{30}&=\max \{\grave{W}^{U_{\eta }}_{nc}(E)| E\; \text{is\; the\; fuzzy\; weight\; of\; SNCs\; of\; H}\}. \end{aligned}$$

The minimum membership value, minimum neutral value, and maximum non-membership value of SNC is called a minimum SNC in IVPFG H.

Definition 9

An IVPFG is said to be complete IVPFG, if

$$\begin{aligned} \varepsilon^{L}_{X}(\grave{u}, \grave{v})& = \min (\varepsilon^{L}_{W}(\grave{u}), \varepsilon^{L}_{W}(\grave{v})), \varepsilon^{U}_{X}(\grave{u}, \grave{v}) = \min (\varepsilon^{U}_{W}(\grave{u}), \varepsilon^{U}_{W}(\grave{v})) \\ \zeta^{L}_{X}(\grave{u}, \ \grave{v})& = \min (\zeta^{L}_{W}(\grave{u}), \zeta _{WL}(\grave{v})), \zeta^{U}_{X}(\grave{u}, \ \grave{v}) =\min (\zeta^{U}_{W}(\grave{u}), \zeta^{U}_{W}(\grave{v}))\\ \eta^{L}_{X}(\grave{u}, \ \grave{v})& = \max (\eta^{L}_{W}(\grave{u}), \eta^{L}_{W}(\grave{v})), \eta^{U}_{X}(\grave{u}, \ \grave{v})=\max (\eta^{U}_{W}(\grave{u}), \eta^{U}_{W}(\grave{v})) \end{aligned}$$

for all \(\grave{u} \grave{v}\in E.\)

Definition 10

Any IVPFG that can be partitioned into two non-empty subsets \({\check{V}}_{1}\) and \({\check{V}}_{2}\) in such a way that for \(\grave{u} \grave{v}\in {\check{V}}_{1}\) or \(\grave{u} \grave{v}\in {\check{V}}_{2}\), \(\varepsilon^{L}_{X}(\grave{u}, \grave{v})=\varepsilon^{U}_{X}(\grave{u}, \grave{v})=0\), \(\zeta^{L}_{X}(\grave{u}, \grave{v})=\zeta^{U}_{X}(\grave{u}, \grave{v})=0\), and \(\eta^{L}_{X}(\grave{u}, \grave{v})=\eta^{U}_{X}(\grave{u}, \grave{v})=0\), is called bipartite IVPFG. If for all \(\grave{u} \in {\check{V}}_{1}\) and \(\grave{v} \in {\check{V}}_{2}\),

$$\begin{aligned} \varepsilon^{L}_{X}(\grave{u}, \grave{v})& = \min (\varepsilon^{L}_{W}(\grave{u}), \varepsilon^{L}_{W}(\grave{v})), \varepsilon^{U}_{X}(\grave{u}, \grave{v})= \min (\varepsilon^{U}_{W}(\grave{u}), \varepsilon^{U}_{W}(\grave{v}))\\ \zeta^{L}_{X}(\grave{u}, \ \grave{v})& = \min (\zeta^{L}_{W}(\grave{u}), \zeta _{WL}(\grave{v})), \zeta^{U}_{X}(\grave{u}, \ \grave{v})=\min (\zeta^{U}_{W}(\grave{u}), \zeta^{U}_{W}(\grave{v}))\\ \eta^{L}_{X}(\grave{u}, \ \grave{v})& = \max (\eta^{L}_{W}(\grave{u}), \eta^{L}_{W}(\grave{v})), \eta^{U}_{X}(\grave{u}, \ \grave{v})=\max (\eta^{U}_{W}(\grave{u}), \eta^{U}_{W}(\grave{v})) \end{aligned}$$

then H is said to be a complete IVPFG.

Theorem 1

Let \(H=(W, X)\) be a complete IVPFG. Then

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{10}&=(s-1)\varepsilon^{L}_{X}(\grave{u}, \grave{v})\\ \gamma^{L_{\zeta }}_{20}&=(s-1)\zeta^{L}_{X}(\grave{u}, \grave{v})\\ \gamma^{L_{\eta }}_{30}&=(s-1)\eta^{L}_{X}(\grave{u}, \grave{v})\\ \gamma^{U_{\varepsilon }}_{10}&=(s-1)\varepsilon^{U}_{X}(\grave{u}, \grave{v})\\ \gamma^{U_{\zeta }}_{20}&=(s-1)\zeta^{U}_{X}(\grave{u}, \grave{v})\\ \gamma^{U_{\eta }}_{30}&=(s-1)\eta^{U}_{X}(\grave{u}, \grave{v}) \end{aligned}$$

where \(\varepsilon^{L}_{X}(\grave{u}, \grave{v})\) and \(\varepsilon^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper membership values, \(\zeta^{L}_{X}(\grave{u}, \grave{v})\) and \(\zeta^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper neutral values, and \(\eta^{L}_{X}(\grave{u}, \grave{v})\), \(\eta^{U}_{X}(\grave{u}, \grave{v})\) are the lower and upper non-membership values of the weakest arc in H. Here s is the number of vertices in H.

Proof

Let H be a complete IVPFG. Then it is evident that every node related with H consists of the arcs which are all strong arcs. Thus either of the set of \((s-1)\) nodes is used to structure the SNC of H. Let us consider a node in H which has the minimum membership value, neutral value, and maximum non-membership value of H is \(\grave{u}\). Let \(\grave{u}\) is connected to the distinct nodes \(\grave{v}_{1}, \grave{v}_{2},..., \grave{v}_{s-1}\). Then among all the weakest arcs of H, \((\grave{u},\grave{v}_{1}), (\grave{u}, \grave{v}_{2}),..., (\grave{u}, \grave{v}_{s-1})\) is the arc having membership value \([\varepsilon^{L}_{X}(\grave{u}, \grave{v}),\varepsilon^{U}_{X}(\grave{u}, \grave{v})]\), neutral value \([\zeta^{L}{X}(\grave{u}, \grave{v}), \zeta^{U}_{X}(\grave{u}, \grave{v})]\), and non-membership value \([\eta^{L}_{X}(\grave{u}, \grave{v}),\eta^{U}_{X}(\grave{u}, \grave{v})]\), where \(\grave{v} \in {\grave{v}_{1}, \grave{v}_{2},..., \grave{v}_{s-1}}\). Hence the set E of nodes is the set \({\grave{v}_{1}, \grave{v}_{2},..., \grave{v}_{s-1}}\) forms SNC of H with

$$\begin{aligned} \grave{W}^{L_{\varepsilon }}_{nc}(E)& = \displaystyle \sum _{\tilde{v_{j}} \in E}\varepsilon^{L}_{X}(\grave{u}, \tilde{v_{j}})\\& = \varepsilon^{L}_{X}(\grave{u},\tilde{v_{1}})+\varepsilon^{L}_{X}(\grave{u}, \tilde{v_{2}})+...+\varepsilon^{L}_{X}(\grave{u}, \grave{v}_{s-1})\\ \grave{W}^{U_{\varepsilon }}_{nc}(E)& = \displaystyle \sum _{\tilde{v_{j}} \in E}\varepsilon^{U}_{X}(\grave{u}, \tilde{v_{j}})\\& = \varepsilon^{U}_{X}(\grave{u}, \tilde{v_{1}})+\varepsilon^{U}_{X}(\grave{u}, \tilde{v_{2}})+...+\varepsilon^{U}_{X}(\grave{u}, \grave{v}_{s-1}) \end{aligned}$$

where \(\varepsilon^{L}_{X}(\grave{u}, \tilde{v_{j}}), j=1,2,...,(s-1)\) and \(\varepsilon^{U}_{X}(\grave{u}, \tilde{v_{j}}),j=1,2,...,(s-1)\) represent the minimum of the lower and upper membership values of SAs incident on \(\tilde{v_{j}}\), respectively. Then

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{10}&=\varepsilon^{L}_{X}(\grave{u}, \grave{v})+\varepsilon^{L}_{X}(\grave{u}, \grave{v})+\varepsilon^{L}_{X}(\grave{u}, \grave{v})\\ \gamma^{U_{\varepsilon }}_{10}&=\varepsilon^{U}_{X}(\grave{u}, \grave{v})+\varepsilon^{U}_{X}(\grave{u}, \grave{v})+\varepsilon^{U}_{X}(\grave{u}, \grave{v})\\ \end{aligned}$$

where \(\varepsilon^{L}_{X}(\grave{u}, \grave{v})\) and \(\varepsilon^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper membership values of weakest arc in IVPFG H. Hence

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{10} & =(s-1)\varepsilon^{L}_{X}(\grave{u}, \grave{v})\\ \gamma^{U_{\varepsilon }}_{10} & = (s-1)\varepsilon^{U}_{X}(\grave{u}, \grave{v}) \end{aligned}$$

Similarly

$$\begin{aligned} \grave{W}^{L_{\zeta }}_{nc}(E)& = \displaystyle \sum _{\zeta {v_{j}} \in E}\zeta^{L}_{X}(\grave{u}, \tilde{v_{j}})\\& = \zeta^{L}_{X}(\grave{u},\tilde{v_{1}})+\zeta^{L}_{X}(\grave{u}, \tilde{v_{2}})+...+\zeta^{L}_{X}(\grave{u}, \grave{v}_{s-1})\\ \grave{W}^{U_{\zeta }}_{nc}(E)& = \displaystyle \sum _{\tilde{v_{j}} \in E}\zeta^{U}_{X}(\grave{u}, \tilde{v_{j}})\\& = \zeta^{U}_{X}(\grave{u}, \tilde{v_{1}})+\zeta^{U}_{X}(\grave{u}, \tilde{v_{2}})+...+\zeta^{U}_{X}(\grave{u}, \grave{v}_{s-1}) \end{aligned}$$

where \(\zeta^{L}_{X}(\grave{u}, \tilde{v_{j}}), j=1,2,...,(s-1)\) and \(\zeta^{U}_{X}(\grave{u}, \tilde{v_{j}}),j=1,2,...,(s-1)\) represent the minimum lower and upper neutral values of the SAs incident on \(\tilde{v_{j}}\), respectively. Then

$$\begin{aligned} \gamma^{L_{\zeta }}_{20}& = \zeta^{L}_{X}(\grave{u}, \grave{v})+\zeta^{L}_{X}(\grave{u}, \grave{v})+\zeta^{L}_{X}(\grave{u}, \grave{v})\\ \gamma^{U_{\zeta }}_{20}& = \zeta^{U}_{X}(\grave{u}, \grave{v})+\zeta^{U}_{X}(\grave{u}, \grave{v})+\zeta^{U}_{X}(\grave{u}, \grave{v})\\ \end{aligned}$$

where \(\zeta^{L}_{X}(\grave{u}, \grave{v})\) and \(\zeta^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper neutral values of weakest arc in IVPFG H. Consequently,

$$\begin{aligned} \gamma^{L_{\zeta }}_{20} & =(s-1)\zeta^{L}_{X}(\grave{u}, \grave{v})\\ \gamma^{U_{\zeta }}_{20} & =(s-1)\zeta^{U}_{X}(\grave{u}, \grave{v}) \end{aligned}$$

Similarly

$$\begin{aligned} \grave{W}^{L_{\eta }}_{nc}(E)& = \displaystyle \sum _{\eta {v_{j}} \in E}\eta^{L}_{X}(\grave{u}, \tilde{v_{j}})\\& = \eta^{L}_{X}(\grave{u},\tilde{v_{1}})+\eta^{L}_{X}(\grave{u}, \tilde{v_{2}})+...+\eta^{L}_{X}(\grave{u}, \grave{v}_{s-1})\\ \grave{W}^{U_{\eta }}_{nc}(E)& = \displaystyle \sum _{\tilde{v_{j}} \in E}\eta^{U}_{X}(\grave{u}, \tilde{v_{j}})\\& = \eta^{U}_{X}(\grave{u}, \tilde{v_{1}})+\eta^{U}_{X}(\grave{u}, \tilde{v_{2}})+...+\eta^{U}_{X}(\grave{u}, \grave{v}_{s-1}) \end{aligned}$$

where \(\eta^{L}_{X}(\grave{u}, \tilde{v_{j}}), j=1,2,...,(s-1)\) and \(\eta^{U}_{X}(\grave{u}, \tilde{v_{j}}),j=1,2,...,(s-1)\) represent the maximum lower and upper non-membership values of the SAs incident on \(\tilde{v_{j}}\), respectively. Then

$$\begin{aligned} \gamma^{L_{\eta }}_{30} & =\eta^{L}_{X}(\grave{u}, \grave{v})+\eta^{L}_{X}(\grave{u}, \grave{v})+\eta^{L}_{X}(\grave{u}, \grave{v})\\ \gamma^{U_{\eta }}_{30} & =\eta^{U}_{X}(\grave{u}, \grave{v})+\eta^{U}_{X}(\grave{u}, \grave{v})+\eta^{U}_{X}(\grave{u}, \grave{v}) \end{aligned}$$

where \(\eta^{L}_{X}(\grave{u}, \grave{v})\) and \(\eta^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper non-membership values of weakest arc in IVPFG H. Hence

$$\begin{aligned} \gamma^{L_{\eta }}_{30} & =(s-1)\eta^{L}_{X}(\grave{u}, \grave{v})\\ \gamma^{U_{\eta }}_{30}&=(s-1)\eta^{U}_{X}(\grave{u}, \grave{v}). \end{aligned}$$

\(\square\)

Theorem 2

Let \({\tilde{\kappa }}\) be a complete bipartite IVPFG which can be partitioned into two non-empty subsets \({\check{V}}_{1}\) and \({\check{V}}_{2}\). Then

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{10}({\tilde{\kappa }})&=\min \{\grave{W}^{L_{\varepsilon }}_{nc}({\check{V}}_{1}),\grave{W}^{L_{\varepsilon }}_{nc}({\check{V}}_{2})\}\\ \gamma^{U_{\varepsilon }}_{10}({\tilde{\kappa }})&=\min \{\grave{W}^{U_{\varepsilon }}_{nc}({\check{V}}_{1}),\grave{W}^{U_{\varepsilon }}_{nc}({\check{V}}_{2})\}\\ \gamma^{L_{\zeta }}_{20}({\tilde{\kappa }})&=\min \{\grave{W}^{L_{\zeta }}_{nc}({\check{V}}_{1}),\grave{W}^{L_{\zeta }}_{nc}({\check{V}}_{2})\}\\ \gamma^{U{\zeta }}_{20}({\tilde{\kappa }})&=\min \{\grave{W}^{U_{\zeta }}_{nc}({\check{V}}_{1}),\grave{W}^{U_{\zeta }}_{nc}({\check{V}}_{2})\}\\ \gamma^{L_{\zeta }}_{30}({\tilde{\kappa }})&=\max \{\grave{W}^{L_{\eta }}_{nc}({\check{V}}_{1}),\grave{W}^{L_{\eta }}_{nc}({\check{V}}_{2})\}\\ \gamma^{U{\zeta }}_{30}({\tilde{\kappa }})&=\max \{\grave{W}^{U_{\eta }}_{nc}({\check{V}}_{1}),\grave{W}^{U_{\eta }}_{nc}({\check{V}}_{2})\}\\ \end{aligned}$$

Proof

Let \({\tilde{\kappa }}\) is a complete bipartite IVPFG, then each of its arc is a SA. Let \({\check{V}}_{1}\) and \({\check{V}}_{2}\) are the two non-empty subsets of the nodes such that each node in \({\check{V}}_{1}\) is connected to each other node in \({\check{V}}_{2}\) and vice versa. Union of the collection of each arc which is incident on every vertex of \({\check{V}}_{1}\) and the collection of each arc which is incident on every node of \({\check{V}}_{2}\) is the set of all arcs of a complete bipartite graph \({\tilde{\kappa }}\). Moreover, \({\check{V}}_{1}\), \({\check{V}}_{2}\) and their union \({\check{V}}_{1}\cup {\check{V}}_{2}\) are IVPFG in \({\tilde{\kappa }}\). Clearly

$$\begin{aligned} \grave{W}^{L_{\varepsilon }}_{nc}({\check{V}}_{1}\cup {\check{V}}_{2}) &> \grave{W}^{L_{\varepsilon }}_{nc}({\check{V}}_{1})\\ \grave{W}^{L_{\varepsilon }}_{nc}({\check{V}}_{1}\cup {\check{V}}_{2}) & > \grave{W}^{L_{\varepsilon }}_{nc}({\check{V}}_{2}) \end{aligned}$$

Hence

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{10}({\tilde{\kappa }})=\min \{\grave{W}^{L_{\varepsilon }}_{nc}({\check{V}}_{1}),\grave{W}^{L_{\varepsilon }}_{nc}({\check{V}}_{2})\}. \end{aligned}$$

Similarly,

$$\begin{aligned} \gamma^{U_{\varepsilon }}_{10}({\tilde{\kappa }})=\min \{\grave{W}^{U_{\varepsilon }}_{nc}({\check{V}}_{1}),\grave{W}^{U_{\varepsilon }}_{nc}({\check{V}}_{2})\} \end{aligned}$$

Also, we have

$$\begin{aligned} \grave{W}^{L_{\zeta }}_{nc}({\check{V}}_{1}\cup {\check{V}}_{2}) & > \grave{W}^{L_{\zeta }}_{nc}({\check{V}}_{1})\\ \grave{W}^{L_{\zeta }}_{nc}({\check{V}}_{1}\cup {\check{V}}_{2})&> \grave{W}^{L_{\zeta }}_{nc}({\check{V}}_{2}) \end{aligned}$$

Consequently,

$$\begin{aligned} \gamma^{L_{\zeta }}_{20}({\tilde{\kappa }})=\min \{\grave{W}^{L_{\zeta }}_{nc}({\check{V}}_{1}),\grave{W}^{L_{\zeta }}_{nc}({\check{V}}_{2})\} \end{aligned}$$

Similarly

$$\begin{aligned} \gamma^{U_{\zeta }}_{20}({\tilde{\kappa }})=\min \{\grave{W}^{U_{\zeta }}_{nc}({\check{V}}_{1}),\grave{W}^{U_{\zeta }}_{nc}({\check{V}}_{2})\} \end{aligned}$$

Also, we have

$$\begin{aligned} \grave{W}^{L_{\eta }}_{nc}({\check{V}}_{1}\cup {\check{V}}_{2}) & < \grave{W}^{L_{\eta }}_{nc}({\check{V}}_{1})\\ \grave{W}^{L_{\eta }}_{nc}({\check{V}}_{1}\cup {\check{V}}_{2}) & < \grave{W}^{L_{\eta }}_{nc}({\check{V}}_{2}) \end{aligned}$$

Hence

$$\begin{aligned} \gamma^{L_{\eta }}_{30}({\tilde{\kappa }})=\max \{\grave{W}^{L_{\eta }}_{nc}({\check{V}}_{1}),\grave{W}^{L_{\eta }}_{nc}({\check{V}}_{2})\} \end{aligned}$$

Similarly, we have

$$\begin{aligned} \gamma^{U_{\eta }}_{30}({\tilde{\kappa }})=\max \{\grave{W}^{U_{\eta }}_{nc}({\check{V}}_{1}),\grave{W}^{U_{\eta }}_{nc}({\check{V}}_{2})\}. \end{aligned}$$

\(\square\)

Definition 11

Let H be an IVPFG. Then two nodes in H are known as strongly independent (SI), if there does not exist any SA between them. If the set of nodes containing any two nodes that are strongly independent, then we call it a SIS.

Definition 12

In an IVPFG H (interval-valued picture)fuzzy weight of SIS E is represented as

$$\begin{aligned} \grave{W}_{is}& = \langle [\grave{W}^{L_{\varepsilon }}_{is}(E), \grave{W}^{U_{\varepsilon }}_{is}(E)],[\grave{W}^{L_{\zeta }}_{is}(E), \grave{W}^{U_{\zeta }}_{is}(E)],\\ {[}\grave{W}^{L_{\eta }}_{is}(E), \grave{W}^{U_{\eta }}_{is}(E)]\rangle \\ \grave{W}_{is}& = \left\langle \left[ \displaystyle \sum _{\grave{u} \in E}\varepsilon^{L}_{X}(\grave{u}, \grave{v}), \sum _{\grave{u} \in E}\varepsilon^{U}_{X}(\grave{u}, \grave{v})\right] ,\right. \\ & \quad \left[ \sum _{\grave{u} \in E}\zeta^{L}_{X}(\grave{u}, \grave{v}), \sum _{\grave{u} \in E}\zeta^{U}_{X}(\grave{u}, \grave{v})\right] , \\ & \quad \left. \left[ \sum _{\grave{u} \in E}\eta^{L}_{X}(\grave{u}, \grave{v}), \sum _{\grave{u} \in E}\eta^{U}_{X}(\grave{u}, \grave{v})\right] \right\rangle \end{aligned}$$

where \(\varepsilon^{L}_{X}(\grave{u}, \grave{v})\) and \(\varepsilon^{U}_{X}(\grave{u}, \grave{v})\) represent the minimum of the lower and upper membership values of all SAs, \(\zeta^{L}_{X}(\grave{u}, \grave{v})\) and \(\zeta^{U}_{X}(\grave{u}, \grave{v})\) represent the minimum of the lower and upper neutral values of all SAs, and \(\eta^{L}_{X}(\grave{u}, \grave{v})\) and \(\eta^{U}_{X}(\grave{u}, \grave{v})\) represent the maximum of the lower and upper non-membership values of all SAs of IVPFG H which are incident on \(\grave{u}\), respectively.

SI number of IVPFG is denoted by \(\delta _{0}(H)=\delta _{0}=\langle [\delta^{L_{\varepsilon }}_{10}, \delta^{U_{\varepsilon }}_{10}], [\delta^{L_{\zeta }}_{20}, \delta^{U_{\zeta }}_{20}],[\delta^{L_{\eta }}_{30}, \delta^{U_{\eta }}_{30}]\rangle\) with

$$\begin{aligned} \delta^{L_{\varepsilon }}_{10}&=\max \{\grave{W}^{L_{\varepsilon }}_{is}(E)| E \text { is the SISs of nodes in H}\}\\ \delta^{U_{\varepsilon }}_{10}&=\max \{\grave{W}^{U_{\varepsilon }}_{is}(E)| E \text { is the SISs of nodes in H}\}\\ \delta^{L_{\zeta }}_{20}&=\max \{\grave{W}^{L_{\zeta }}_{is}(E)| E \text { is the SISs of nodes in H}\}\\ \delta^{U_{\zeta }}_{20}&=\max \{\grave{W}^{U_{\zeta }}_{is}(E)| E \text { is the SISs of nodes in H}\}\\ \delta^{L_{\eta }}_{30}&=\min \{\grave{W}^{L_{\eta }}_{is}(E)| E \text { is the SISs of nodes in H}\}\\ \delta^{U_{\eta }}_{30}&=\min \{\grave{W}^{U_{\eta }}_{is}(E)| E \text { is the SISs of nodes in H}\} \end{aligned}$$

SIS having maximum membership value, maximum neutral value, and minimum non-membership value is a maximum SIS in IVPFG H.

Theorem 3

Let \(H=(W, X)\) be a complete IVPFG. Then

$$\begin{aligned} \delta _{0}(H)& = \langle [\varepsilon^{L}_{X}(\grave{u}, \grave{v}), \varepsilon^{U}_{X}(\grave{u}, \grave{v})], [\zeta^{L}_{X}(\grave{u}, \grave{v}), \zeta^{U}_{X}(\grave{u}, \grave{v})], \\ & \quad [\eta^{L}_{X}(\grave{u}, \grave{v}), \eta^{U}_{X}(\grave{u}, \grave{v})]\rangle \end{aligned}$$

where \(\varepsilon^{L}_{X}(\grave{u}, \grave{v})\) and \(\varepsilon^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper membership values, \(\zeta^{L}_{X}(\grave{u}, \grave{v})\) and \(\zeta^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper neutral values, and \(\eta^{L}_{X}(\grave{u}, \grave{v})\) and \(\eta^{U}_{X}(\grave{u}, \grave{v})\) represent the lower and upper non-membership values of the weakest arc in H, respectively.

Proof

Let us consider that H is a complete IVPFG. Then all of its arcs are SAs and each node is connected to every other node in H. Therefore, \(E=\{\grave{v}\}\) is a single SIS for each \(\grave{v} \in {\check{V}}\). \(\square\)

Theorem 4

Let \({\tilde{\kappa }}\) be a complete bipartite IVPFG which can be partitioned into two non-empty subsets \({\check{V}}_{1}\) and \({\check{V}}_{2}\), then

$$\begin{aligned} \delta^{L_{\varepsilon }}_{10}({\tilde{\kappa }})&=\min \{\grave{W}^{L_{\varepsilon }}_{is}({\check{V}}_{1}),\grave{W}^{L_{\varepsilon }}_{is}({\check{V}}_{2})\}\\ \delta^{U_{\varepsilon }}_{10}({\tilde{\kappa }})&=\min \{\grave{W}^{U_{\varepsilon }}_{is}({\check{V}}_{1}),\grave{W}^{U_{\varepsilon }}_{is}({\check{V}}_{2})\}\\ \delta^{L_{\zeta }}_{20}({\tilde{\kappa }})&=\min \{\grave{W}^{L_{\zeta }}_{is}({\check{V}}_{1}),\grave{W}^{L_{\zeta }}_{is}({\check{V}}_{2})\}\\ \delta^{U{\zeta }}_{20}({\tilde{\kappa }})&=\min \{\grave{W}^{U_{\zeta }}_{is}({\check{V}}_{1}),\grave{W}^{U_{\zeta }}_{is}({\check{V}}_{2})\}\\ \delta^{L_{\eta }}_{30}({\tilde{\kappa }})&=\max \{\grave{W}^{L_{\eta }}_{is}({\check{V}}_{1}),\grave{W}^{L_{\eta }}_{is}({\check{V}}_{2})\}\\ \delta^{U{\eta }}_{30}({\tilde{\kappa }})&=\max \{\grave{W}^{U_{\eta }}_{is}({\check{V}}_{1}),\grave{W}^{U_{\eta }}_{is}({\check{V}}_{2})\} \end{aligned}$$

Proof

Let \({\tilde{\kappa }}\) is a complete bipartite IVPFG. Then each of its arc is a SA. Also, every node in \({\check{V}}_{1}\) is connected to every node in \({\check{V}}_{1}\), and every node in \({\check{V}}_{2}\) is connected to every node in \({\check{V}}_{1}\). Therefore, \({\check{V}}_{1}\) and \({\check{V}}_{2}\) are SISs in \({\tilde{\kappa }}\). Hence proved.

\(\square\)

Theorem 5

Let H be an IVPFG having no isolated nodes. Then

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{10}+\delta^{L_{\varepsilon }}_{10}&=\grave{W}^{L_{\varepsilon }}({\check{V}})\\ \gamma^{L_{\zeta }}_{20}+\delta^{L_{\zeta }}_{20}&=\grave{W}^{L_{\zeta }}({\check{V}})\\ \gamma^{L_{\eta }}_{30}+\delta^{L_{\eta }}_{30}&=\grave{W}^{L_{\eta }}({\check{V}})\\ \gamma^{U_{\varepsilon }}_{10}+\delta^{L_{\varepsilon }}_{10}&=\grave{W}^{U_{\varepsilon }}({\check{V}})\\ \gamma^{U_{\zeta }}_{20}+\delta^{L_{\zeta }}_{20}&=\grave{W}^{U_{\zeta }}({\check{V}})\\ \gamma^{U_{\eta }}_{30}+\delta^{L_{\eta }}_{30}&=\grave{W}^{U_{\eta }}({\check{V}})\\ \end{aligned}$$

Proof

Let us consider that the minimum SNC of H is \(N_{0}\). Then

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{10}&=\grave{W}^{L_{\varepsilon }}(N_{0})\\ \gamma^{L_{\zeta }}_{20}&=\grave{W}^{L_{\zeta }}(N_{0})\\ \gamma^{L_{\eta }}_{30}&=\grave{W}^{L_{\eta }}(N_{0})\\ \gamma^{U_{\varepsilon }}_{10}&=\grave{W}^{U_{\varepsilon }}(N_{0})\\ \gamma^{U_{\zeta }}_{20}&=\grave{W}^{U_{\zeta }}(N_{0})\\ \gamma^{U_{\eta }}_{30}&=\grave{W}^{U_{\eta }}(N_{0}) \end{aligned}$$

and \({\check{V}}-N_{0}\) forms SIS of nodes. Moreover, \({\check{V}}-N_{0}\) contains the nodes which are incident on SAs of H. Thus

$$\begin{aligned}\delta^{L_{\varepsilon }}_{10}&\ge \grave{W}^{L_{\varepsilon }}({\check{V}}-N_{0})=\grave{W}^{L_{\varepsilon }}({\check{V}})-\gamma^{L_{\varepsilon }}_{10}\Rightarrow \gamma^{L_{\varepsilon }}_{10}+\delta^{L_{\varepsilon }}_{10}&\ge \grave{W}^{L_{\varepsilon }}({\check{V}})\\ \delta^{U_{\varepsilon }}_{10}&\ge \grave{W}^{U_{\varepsilon }}({\check{V}}-N_{0})=\grave{W}^{U_{\varepsilon }}({\check{V}})-\gamma^{U_{\varepsilon }}_{10}\Rightarrow \gamma^{U_{\varepsilon }}_{10}+\delta^{U_{\varepsilon }}_{10}&\ge \grave{W}^{U_{\varepsilon }}({\check{V}})\\ \delta^{L_{\zeta }}_{20}&\ge \grave{W}^{L_{\zeta }}({\check{V}}-N_{0})=\grave{W}^{L_{\zeta }}({\check{V}})-\gamma^{L_{\zeta }}_{20}\Rightarrow \gamma^{L_{\zeta }}_{20}+\delta^{L_{\zeta }}_{20}&\ge \grave{W}^{L_{\zeta }}({\check{V}})\\ \delta^{U_{\zeta }}_{20}&\ge \grave{W}^{U_{\zeta }}({\check{V}}-N_{0})=\grave{W}^{U_{\zeta }}({\check{V}})-\gamma^{U_{\zeta }}_{20}\Rightarrow \gamma^{U_{\zeta }}_{20}+\delta^{U_{\zeta }}_{20}&\ge \grave{W}^{U_{\zeta }}({\check{V}})\\ \delta^{L_{\eta }}_{30}&\le \grave{W}^{L_{\eta }}({\check{V}}-N_{0})=\grave{W}^{L_{\eta }}({\check{V}})-\gamma^{L_{\eta }}_{30}\Rightarrow \gamma^{L_{\eta }}_{30}+\delta^{L_{\eta }}_{30}&\le \grave{W}^{L_{\eta }}({\check{V}})\\ \delta^{U_{\eta }}_{30}&\le \grave{W}^{L_{\eta }}({\check{V}}-N_{0})=\grave{W}^{U_{\eta }}({\check{V}})-\gamma^{U_{\eta }}_{30}\Rightarrow \gamma^{U_{\eta }}_{30}+\delta^{U_{\eta }}_{30}&\le \grave{W}^{U_{\eta }}({\check{V}}) \end{aligned}$$
(1)

Let the maximum SIS of H is \(P_{0}\), i.e., \(P_{0}\) contains the nodes which are not neighbor to each other by SAs. Thus \({\check{V}}-P_{0}\) contains the nodes which cover all SAs of H. Hence, \({\check{V}}-P_{0}\) forms SNC of H. Also, \(\gamma^{L_{\varepsilon }}_{10}\) and \(\gamma^{U_{\varepsilon }}_{10}\) are the minimum lower and upper membership values, \(\gamma^{L_{\zeta }}_{20}\) and \(\gamma^{U_{\zeta }}_{20}\) are the minimum lower and upper neutral values, \(\gamma^{L_{\eta }}_{30}\), \(\gamma^{U_{\eta }}_{30}\) are the maximum lower and upper non-membership values.

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{10}\le \grave{W}^{L_{\varepsilon }}({\check{V}}-P_{0})&=\grave{W}^{L_{\varepsilon }}({\check{V}})-\delta^{L_{\varepsilon }}_{10}\Rightarrow \gamma^{L_{\varepsilon }}_{10}+\delta^{L_{\varepsilon }}_{10}\le \grave{W}^{L_{\varepsilon }}({\check{V}})\\ \gamma^{U_{\varepsilon }}_{10}\le \grave{W}^{U_{\varepsilon }}({\check{V}}-P_{0})&=\grave{W}^{U_{\varepsilon }}({\check{V}})-\delta^{U_{\varepsilon }}_{10}\Rightarrow \gamma^{U_{\varepsilon }}_{10}+\delta^{U_{\varepsilon }}_{10}\le \grave{W}^{U_{\varepsilon }}({\check{V}})\\ \gamma^{L_{\zeta }}_{20}\le \grave{W}^{L_{\zeta }}({\check{V}}-P_{0})&=\grave{W}^{L_{\zeta }}({\check{V}})-\delta^{L_{\zeta }}_{20}\Rightarrow \gamma^{L_{\zeta }}_{20}+\delta^{L_{\zeta }}_{20}\le \grave{W}^{L_{\zeta }}({\check{V}})\\ \gamma^{U_{\zeta }}_{20}\le \grave{W}^{U_{\zeta }}({\check{V}}-P_{0})&=\grave{W}^{U_{\zeta }}({\check{V}})-\delta^{U_{\zeta }}_{20}\Rightarrow \gamma^{U_{\zeta }}_{20}+\delta^{U_{\zeta }}_{20}\le \grave{W}^{U_{\zeta }}({\check{V}})\\ \gamma^{L_{\eta }}_{30}\ge \grave{W}^{L_{\eta }}({\check{V}}-P_{0})&=\grave{W}^{L_{\eta }}({\check{V}})-\delta^{L_{\eta }}_{30}\Rightarrow \gamma^{L_{\eta }}_{30}+\delta^{L_{\eta }}_{30}\ge \grave{W}^{L_{\eta }}({\check{V}})\\ \gamma^{U_{\eta }}_{30}\ge \grave{W}^{L_{\eta }}({\check{V}}-P_{0})&=\grave{W}^{U_{\eta }}({\check{V}})-\delta^{U_{\eta }}_{30}\Rightarrow \gamma^{U_{\eta }}_{30}+\delta^{U_{\eta }}_{30}\ge \grave{W}^{U_{\eta }}({\check{V}})\end{aligned}$$
(2)

From (1) and (2), we have

$$\begin{aligned}\gamma^{L_{\varepsilon }}_{10}+\delta^{L_{\varepsilon }}_{10}&=\grave{W}^{L_{\varepsilon }}({\check{V}}), \gamma^{U_{\varepsilon }}_{10}+\delta^{U_{\varepsilon }}_{10}&=\grave{W}^{U_{\varepsilon }}({\check{V}})\\ \gamma^{L_{\zeta }}_{20}+\delta^{L_{\zeta }}_{20}&=\grave{W}^{L_{\zeta }}({\check{V}}), \gamma^{U_{\zeta }}_{20}+\delta^{U_{\zeta }}_{20}&=\grave{W}^{U_{\zeta }}({\check{V}})\\ \gamma^{L_{\eta }}_{30}+\delta^{L_{\eta }}_{30}&=\grave{W}^{L_{\eta }}({\check{V}}), \gamma^{U_{\eta }}_{30}+\delta^{U_{\eta }}_{30}&=\grave{W}^{U_{\eta }}({\check{V}}) \end{aligned}$$

which completes the proof. \(\square\)

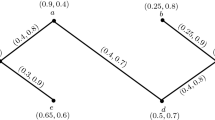
Example 1

Let us consider an IVPFG given in Fig. 2. Each of its arc is SA and each SNC of IVPFG H are: \(E_{1}=\{v, x\}\), \(E_{2}=\{u, v, w\}\), \(E_{3}=\{w, x, u\}\), \(E_{4}=\{v, x, w\}\), \(E_{5}=\{u, v, x\}\), \(E_{6}=\{u, v, w, x\}\). Calculations regarding (interval-valued picture) fuzzy weight of SNC number \(\grave{W}_{nc}(E)\) of an IVPFG H is shown in Table 2 and the Table 3 shows the (interval-valued picture) fuzzy weight \(\grave{W}_{nc}(E)\) of SNC number. Hence\(\gamma _{0}(H)=\langle [0.2,0.4],[0.2,0.6],[0.4,1.1]\rangle\)

Fig. 2
figure 2

An IVPFG H for a strong node cover (SNC)

Full size image

Example 2

Consider a strong IVPFG shown in Fig. 3. All SISs are: \(E_{1}=\{u, w\}\), \(E_{2}=\{v, x\}\) The method of calculating the fuzzy weight of SI number of IVPFG H is shown in Table 4. Thus \(\delta _{0}(H) =\langle [0.3, 0.4], [0.3, 06], [0.7, 0.7]\rangle.\)

Table 2 Calculating the weight of SNC number
Full size table
Table 3 Weight of SNC number
Full size table
Fig. 3
figure 3

A strong IVPFG H for a SIS

Full size image
Table 4 Weight of SI number
Full size table

Definition 13

Let H be the IVPFG without isolated node. The set \({\tilde{A}}\) of SAs that covers all nodes of IVPFG H is said to be a strong arc cover (SAC) in H. Fuzzy weight \(\grave{W}\) of SAC \({\tilde{A}}\) is as under

$$\begin{aligned} \grave{W}_{ac}& = \langle [\grave{W}^{L_{\varepsilon }}_{ac}({\tilde{A}}),\grave{W}^{U_{\varepsilon }}_{ac}({\tilde{A}})],[\grave{W}^{L_{\zeta }}_{ac}({\tilde{A}}), \grave{W}^{U_{\zeta }}_{ac}({\tilde{A}})],\\ & \quad [\grave{W}^{L_{\eta }}_{ac}({\tilde{A}}),\grave{W}^{U_{\eta }}_{ac}({\tilde{A}})]\rangle \\ \grave{W}_{ac}& = \left\langle \left[ \displaystyle \sum _{(\grave{u},\grave{v})\in {\tilde{A}}}\varepsilon^{L}_{X}(\grave{u},\grave{v}), \sum _{ (\grave{u},\grave{v})\in {\tilde{A}}}\varepsilon^{U}_{X}(\grave{u},\grave{v})\right] ,\right. \\ & \quad \left[ \sum _{(\grave{u},\grave{v})\in {\tilde{A}}}\zeta^{L}_{X}(\grave{u},\grave{v}), \sum _{(\grave{u},\grave{v})\in {\tilde{A}}}\zeta^{U}_{X}(\grave{u},\grave{v})\right] ,\\ & \quad \left. \left[ \sum _{(\grave{u},\grave{v})\in {\tilde{A}}}\eta^{L}_{X}(\grave{u},\grave{v}), \sum _{(\grave{u},\grave{v})\in {\tilde{A}}}\eta^{U}_{X}(\grave{u},\grave{v})\right] \right\rangle \end{aligned}$$

where \(\varepsilon^{L}_{X}(\grave{u}, \grave{v})\) and \(\varepsilon^{U}_{X}(\grave{u}, \grave{v})\) represent the minimum of the lower and upper membership values of all SAs, \(\zeta^{L}_{X}(\grave{u}, \grave{v})\) and \(\zeta^{U}_{X}(\grave{u}, \grave{v})\) represent the minimum of the lower and upper neutral values of all SAs, and \(\eta^{L}_{X}(\grave{u}, \grave{v})\) and \(\eta^{U}_{X}(\grave{u}, \grave{v})\) represent the maximum of the lower and upper non-membership values of SAs.

A set \(\gamma _{1}(H)=\gamma _{1}=\langle [\gamma^{L_{\varepsilon }}_{11}, \gamma^{U_{\varepsilon }}_{11}], [\gamma^{L_{\zeta }}_{21}, \gamma^{U_{\zeta }}_{21}],[\gamma^{L_{\eta }}_{31}, \gamma^{U_{\eta }}_{31}]\rangle\) is a SAC number of IVPFG, if

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{11} & =\min \{\grave{W}^{L_{\varepsilon }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of H}\}\\ \gamma^{U_{\varepsilon }}_{11} & =\min \{\grave{W}^{U_{\varepsilon }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of H}\}\\ \gamma^{L_{\zeta }}_{21} & =\min \{\grave{W}^{L_{\zeta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of H}\}\\ \gamma^{U_{\zeta }}_{21} & = \min \{\grave{W}^{U_{\zeta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of H}\}\\ \gamma^{L_{\eta }}_{31} & = \max \{\grave{W}^{L_{\eta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of H}\}\\ \gamma^{U_{\eta }}_{31}& =\max \{\grave{W}^{U_{\eta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of H}\} \end{aligned}$$

SAC having minimum membership value, minimum neutral value, and maximum non-membership value is a minimum SAC in IVPFG H.

Theorem 6

Let H be a complete IVPFG. Then

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{11}&=\min \left\{ \grave{W}^{L_{\varepsilon }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of } H \text { with } |{\tilde{A}}|\ge \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \\ \gamma^{U_{\varepsilon }}_{11}=\min \left\{ \grave{W}^{U_{\varepsilon }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of } H \text { with } |{\tilde{A}}|\ge \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \\ \gamma^{L_{\zeta }}_{21}=\min \left\{ \grave{W}^{L_{\zeta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of } H \text { with } |{\tilde{A}}|\ge \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \\ \gamma^{U_{\zeta }}_{21}=\min \left\{ \grave{W}^{U_{\zeta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of } H \text { with } |{\tilde{A}}|\ge \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \\ \gamma^{L_{\eta }}_{31}=\max \left\{ \grave{W}^{L_{\eta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of } H \text { with } |{\tilde{A}}|\ge \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \\ \gamma^{U_{\eta }}_{31}=\max \left\{ \grave{W}^{U_{\eta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC of } H \text { with } |{\tilde{A}}|\ge \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \end{aligned}$$

where \(\breve{n}\) denotes the number of vertices in H.

Proof

Let H be a complete IVPFG. Then all of its arcs are SAs and each vertex is connected to every other vertex. Since each arc is SAs in an IVPFG H and a crisp graph \(G^{\ast}\), the number of arcs in SAC in both the graphs are same. Now \(\lceil \frac{\breve{n}}{2}\rceil\) is the SAC number of a crisp graph \(G^{\ast}\). Hence \(\lceil \frac{\breve{n}}{2}\rceil\) is a minimum arc in SAC of H. \(\square\)

Theorem 7

Let \({\tilde{\kappa }}\) be a complete bipartite IVPFG which can be partitioned into two non-empty subsets \({\check{V}}_{1}\) and \({\check{V}}_{2}\). Then

$$\begin{aligned} \gamma^{L_{\varepsilon }}_{11}({\tilde{\kappa }}) & =\min \{\grave{W}^{L_{\varepsilon }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC in } {\tilde{\kappa }} \text { with } |{\tilde{A}}|\ge \max \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\}\\ \gamma^{U_{\varepsilon }}_{11}({\tilde{\kappa }}) & =\min \{\grave{W}^{U_{\varepsilon }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC in } {\tilde{\kappa }} \text { with } |{\tilde{A}}|\ge \max \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\}\\ \gamma^{L_{\zeta }}_{21}({\tilde{\kappa }}) & =\min \{\grave{W}^{L_{\zeta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC in } {\tilde{\kappa }} \text { with } |{\tilde{A}}|\ge \max \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\}\\ \gamma^{U_{\zeta }}_{21}({\tilde{\kappa }}) & =\min \{\grave{W}^{U_{\zeta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC in } {\tilde{\kappa }} \text { with } |{\tilde{A}}|\ge \max \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\}\\ \gamma^{L_{\eta }}_{31}({\tilde{\kappa }}) & =\max \{\grave{W}^{L_{\eta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC in } {\tilde{\kappa }} \text { with } |{\tilde{A}}|\ge \max \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\}\\ \gamma^{U_{\eta }}_{31}({\tilde{\kappa }}) & =\max \{\grave{W}^{U_{\eta }}_{ac}({\tilde{A}})| {\tilde{A}} \text { is SAC in } {\tilde{\kappa }} \text { with } |{\tilde{A}}|\ge \max \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\} \end{aligned}$$

Proof

Let H be a complete bipartite IVPFG. Then all of its arcs are SAs and also each node in \({\check{V}}_{1}\) is connected to every other node in \({\check{V}}_{2}\). Since each arc is SA in IVPFG H and crisp graph \(G^{\ast}\), therefore the number of arcs in SAC in both the graphs are same. Now the SAC number of \({\tilde{\kappa }}^{\ast}\) is \(\max \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\). Hence in the SAC of \({\tilde{\kappa }}\), the minimum number of arcs is \(\max \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\). \(\square\)

Definition 14

Let \(H = (W, X)\) be an IVPFG. The set R of SACs is said to be SIS, if none of its any two arcs shares a node. We also call such a set R, a SM in H.

Definition 15

Let R is a SM in IVPFG then, if \((\grave{u}, \grave{v})\in R\) then it is said that \(\grave{u}\) is strongly matched to \(\grave{v}\) by R. The (interval-valued picture) fuzzy weight \(\grave{W}\) of SM R can be described as

$$\begin{aligned} \grave{W}_{sm}(R)& = \langle [\grave{W}^{L_{\varepsilon }}_{sm}(R),\grave{W}^{U_{\varepsilon }}_{sm}(R)],[\grave{W}^{L_{\zeta }}_{sm}(R), \grave{W}^{U_{\zeta }}_{sm}(R)], \\ & \quad [\grave{W}^{L_{\eta }}_{sm}(R), \grave{W}^{U_{\eta }}_{sm}(R)]\rangle \\ \grave{W}_{sm}(R)& = \left\langle \left[ \displaystyle \sum _{(\grave{u},\grave{v})\in R}\varepsilon^{L}_{X}(\grave{u}, \grave{v}),\sum _{(\grave{u},\grave{v})\in R}\varepsilon^{U}_{X}(\grave{u}, \grave{v})\right] ,\right. \\ & \quad \left[ \sum _{(\grave{u},\grave{v})\in R}\zeta^{L}_{X}(\grave{u}, \grave{v}),\sum _{(\grave{u},\grave{v})\in R}\zeta^{U}_{X}(\grave{u}, \grave{v})\right] ,\\ & \quad \left. \left[ \sum _{(\grave{u},\grave{v})\in R}\eta^{L}_{X}(\grave{u}, \grave{v}),\sum _{(\grave{u},\grave{v})\in R}\eta^{U}_{X}(\grave{u}, \grave{v})\right] \right\rangle \end{aligned}$$

A collection \(\delta _{1}(H)=\delta _{1}=\langle [\delta^{L_{\varepsilon }}_{11}, \delta^{U_{\varepsilon }}_{11}], [\delta^{L_{\zeta }}_{21}, \delta^{U_{\zeta }}_{21}],[\delta^{L_{\eta }}_{31}, \delta^{U_{\eta }}_{31}]\rangle\) is a SM in IVPFG, if

$$\begin{aligned} \delta^{L_{\varepsilon }}_{11} & =\max \{\grave{W}^{L_{\varepsilon }}_{is}(R)| R \text { is the SM of H}\}\\ \delta^{U_{\varepsilon }}_{11} & = \max \{\grave{W}^{U_{\varepsilon }}_{is}(R)| R \text { is the SM of H}\}\\ \delta^{L_{\zeta }}_{21} & = \max \{\grave{W}^{L_{\zeta }}_{is}(R)| R \text { is the SM of H}\}\\ \delta^{U_{\zeta }}_{21} & = \max \{\grave{W}^{U_{\zeta }}_{is}(R)| R \text { is the SM of H}\}\\ \delta^{L_{\eta }}_{31} & = \min \{\grave{W}^{L_{\eta }}_{is}(R)|R\; \text{is\; the\; SM \;of\; H}\}\\ \delta^{U_{\eta }}_{31} & = \min \{\grave{W}^{U_{\eta }}_{is}(R)| R\; \text{is\; the\; SM \;of\; H}\} \end{aligned}$$

SM having maximum membership value, maximum neutral value, minimum non-membership value is a maximum SM in IVPFG H.

Theorem 8

Let H be a complete IVPFG. Then

$$\begin{aligned} \delta^{L_{\varepsilon }}_{11} & =\max \left\{ \grave{W}^{L_{\varepsilon }}_{sm}(R)| R \text { is SM with } |R|\le \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \\ \delta^{U_{\varepsilon }}_{11} & =\max \left\{ \grave{W}^{U_{\varepsilon }}_{sm}(R)| R \text { is SM with } |R|\le \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \\ \delta^{L_{\zeta }}_{21}&=\max \left\{ \grave{W}^{L_{\zeta }}_{sm}(R)| R \text { is SM with } |R|\le \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \\ \delta^{U_{\zeta }}_{21} & =\max \left\{ \grave{W}^{U_{\zeta }}_{sm}(R)| R \text { is SM with } |R|\le \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \\ \delta^{L_{\eta }}_{31} & =\min \left\{ \grave{W}^{L_{\eta }}_{sm}(R)| R \text { is SM with } |R|\le \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \\ \delta^{U_{\eta }}_{31} & =\min \left\{ \grave{W}^{U_{\eta }}_{sm}(R)| R \text { is SM with } |R|\le \bigg \lceil \frac{\breve{n}}{2}\bigg \rceil \right\} \end{aligned}$$

where \(\breve{n}\) denotes the number of vertices in H.

Proof

Let H be a complete IVPFG. Then all of its arcs are SAs and each vertex is connected to every other vertices. Since each arc is a strong arc in an IVPFG H and a crisp graph \(G^{\ast}\), therefore in both the graphs the number of arcs in the SM are same. Now the SM number of a crisp graph \(G^{\ast}\) is \(\lceil \frac{\breve{n}}{2}\rceil\). Hence in SM of H the maximum number of arcs is \(\lceil \frac{\breve{n}}{2}\rceil\). \(\square\)

Theorem 9

Let \({\tilde{\kappa }}\) be a complete bipartite IVPFG which can be partitioned into two non-empty subsets \({\check{V}}_{1}\) and \({\check{V}}_{2}\). Then

$$\begin{aligned} \delta^{L_{\varepsilon }}_{11}({\tilde{\kappa }})&=\max \{\grave{W}^{L_{\varepsilon }}_{sm}(R)| R \text { is SM in } {\tilde{\kappa }} \text { with } |R|\le \min \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\}\\ \delta^{U_{\varepsilon }}_{11}({\tilde{\kappa }})&=\max \{\grave{W}^{U_{\varepsilon }}_{sm}(R)| R \text { is SM in } {\tilde{\kappa }} \text { with } |R|\le \min \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\}\\ \delta^{L_{\zeta }}_{21}({\tilde{\kappa }})&=\max \{\grave{W}^{L_{\zeta }}_{sm}(R)| R \text { is SM in } {\tilde{\kappa }} \text { with } |R|\le \min \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\}\\ \delta^{U_{\zeta }}_{21}({\tilde{\kappa }})&=\max \{\grave{W}^{U_{\zeta }}_{sm}(R)| R \text { is SM in } {\tilde{\kappa }} \text { with } |R|\le \min \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\}\\ \delta^{L_{\eta }}_{31}({\tilde{\kappa }})&=\min \{\grave{W}^{L_{\eta }}_{sm}(R)| R \text { is SM in } {\tilde{\kappa }} \text { with } |R|\le \min \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\}\\ \delta^{U_{\eta }}_{31}({\tilde{\kappa }})&=\min \{\grave{W}^{U_{\eta }}_{sm}(R)| R \text { is SM in } {\tilde{\kappa }} \text { with } |R|\le \min \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\} \end{aligned}$$

Proof

Let H be a complete bipartite IVPFG. Then all of its arcs are SAs and each node in \({\check{V}}_{1}\) is connected to every other node in \({\check{V}}_{2}\). Since each arc is strong arc in IVPFG H and crisp graph \(G^{\ast}\), therefore the number of arcs in SM of both the graphs are same. Since the SM number of \({\tilde{\kappa }}^{\ast}\) is \(\max \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\). Thus in SM of \({\tilde{\kappa }}\) the maximum number of arcs is \(\min \{|{\check{V}}_{1}|, |{\check{V}}_{2}|\}\). \(\square\)

Example 3

Let us consider an IVPFG shown in Fig. 4. Here, each arc is a SA and all SACs of IVPFG H are: \({\tilde{A}}_{1}=\{uv, xw\}\), \({\tilde{A}}_{2}=\{ux, vw\}\), \({\tilde{A}}_{3}=\{uv, vx, xw\}\), \({\tilde{A}}_{4}=\{vx, xu, vw\}\), \({\tilde{A}}_{5}=\{vx, uv, vw\}\), \({\tilde{A}}_{6}=\{uv, ux, xw\}\), \({\tilde{A}}_{7}=\{ux, uv, vw\}\), \({\tilde{A}}_{8}=\{ux, xw, wv\}\). The method of calculating the fuzzy weight of SAC number \(\grave{W}_{ac}({\tilde{A}})\) of IVPFG H is shown in Table 5. Thus, \(\gamma _{1}(H)=\langle [0.2,0.5],[0.3,0.6],[0.3,08]\rangle\). Also, the only SAC and SM in H are the two sets \({\tilde{A}}_{1}\) and \({\tilde{A}}_{2}\). Hence \(\grave{W}_{sm}({\tilde{A}})=\langle [0.2,0.5],[0.3,0.6],[0.2,0.5]\rangle\), \(\grave{W}_{sm}({\tilde{A}})=\langle [0.2,0.6],[0.3,0.6],[0.2,0.5]\rangle.\) Thus, \(\delta _{1}=\langle [0.2,0.6],[0.3,0.6],[0.2,0.5]\rangle.\)

Table 5 Calculating the weight of SAC number
Full size table
Fig. 4
figure 4

An IVPFG H for a SAC

Full size image
Fig. 5
figure 5

An IVPFG H for a strong independent arc cover (SIAC)

Full size image

Example 4

Consider an IVPFG H shown in Fig. 5. ux, wx, and vw are its all SAs and all SACs of H are: \({\tilde{A}}_{1}=\{ux, vw\}\), \({\tilde{A}}_{2}=\{ux, wx, vw\}\) The method of calculating the (interval-valued picture)fuzzy weight of SAC number of IVPFG H is given in Table 6. Thus, \(\gamma _{1}(H)=\langle [0.3,0.4],[0.3,0.6],[0.9,0.9]\rangle\). The set \({\tilde{A}}_{1}=\{ux, vw\}\) is the only strong independent arc cover (SIAC). Therefore, \(\delta _{1}(H)=\langle [0.3,0.4],[0.3,0.6],[0.7,0.7]\rangle .\)

Table 6 Calculating the weight of SAC set
Full size table

Definition 16

Let N be the SM in IVPFG H. Then, N is called perfect strong matching (PSM), if each node of N in H is strongly matched to few nodes of H.

Example 5

Consider an IVPFG shown in Fig. 6. Each arc is SA and the sets \(N_{1}\) and \(N_{2}\) are PSM. All SMs of H are: \(N_{1}=\{ux, vw\}\), \(N_{2}=\{uw, vx\}\), \(N_{3}=\{ux, uw, vw\}\), \(N_{4}=\{ux, xv, vw\}\). The method of calculating the (interval-valued picture) fuzzy weight of SM is shown in Table 7. Therefore, \(\gamma _{1}(N)=\langle [0.2, 0.7],[0.3, 0.7],[0.9, 1.3]\rangle\), \(\delta _{1}(N)=\langle [0.4, 1.2],[0.5, 1.2],[0.5, 0.7]\rangle\)

Fig. 6
figure 6

An IVPFG H for SM

Full size image
Table 7 Calculating the weight of SM
Full size table

4 Application

Group of organizations or individuals having common interests that are connected to each other to attain specific goals are called social network. Every member of network is called actor. Interactions and complex relationship between the actors characterized the social networks. Individual relationship, gaming relations, shared taste, hobbies and interest, sociopolitical motives, and analysis of the virtual network are the main reasons for establishing social networks.

Fig. 7
figure 7

Community network of players

Full size image

Visual representation of a social network in terms of graph help to observe social networks. Vertices represent the actors in these graphs and the connection between the actors are represented by edges. Instinctively, the distribution between the edges in social networks are locally, i.e., in between the group of vertices, the distribution of number of edges is much greater than the distribution of the number of edges between this group of vertices and the remaining vertices of the graph. In this way when we represent real data in terms of graph, is said to be a community. We called community as a module or cluster, in some sense. Moreover, set of vertices that probably share common interests or features in comparison with the rest of the graph are communities. In social networks forum, information of the people which probably have common interest helps us to promote specific products. Many social networks which are online have overlapping communities. This means that one vertex can be connected to multiple communities. Figure 7 demonstrates the social networks of players in a country that are members of different gaming communities in accordance with the games being played. These communities include cricket, basketball, baseball, badminton, table tennis, hockey, volleyball, boxing. Each community containing the number of members, the average number of members present at the meeting and the number of members who were not present in the meeting are shown in Table 8. Since, the variables which are mentioned have uncertain values so for the total impact of the community on its member, it is more feasible to deal these through IVPFS. Since the members present in the community meeting is effective on the promotions of members, so we describe the ratio of the average number of members present in the meetings to the total numbers and ratio of the number of members which were not present in the meeting to the total number through IVPFG. For example, refer to the Table 9 cricket community is 82 to 92% effective in promoting the games of its members, 1 to 8% neutral who haven’t attended the meeting and 1 to 8% ineffective. These values are described in Table 9. In between the gaming communities, there is a strong relationship which is shown in Fig. 8 through IVPFG. In this IVPFG, effect of members of the two communities on their promotion is shown by the membership value of edges. For example, the relationship between two communities of basket ball and table tennis is 72 to 82% effective, 3 to 18% neutral, and 13 to 19% ineffective. These values are shown in Table 10.

Table 8 Data set
Full size table
Table 9 The IVPFG of gaming communities
Full size table
Fig. 8
figure 8

The gaming communities IVPFG

Full size image
Table 10 The IVPFG relation between gaming communities
Full size table

Generally, there is no polynomial algorithm to find the maximal IS for any arbitrary graph. It means that in a short time, it is impossible to access to the collection of maximal IS. By using less number of vertices, we can obtain maximal SIS of IVPFG by following the instructions. Since each arc is SA, so all the cardinalities and maximal SIS are shown in Table 11. By applying the steps mentioned in Algorithm 1, we can also find the maximal SIS by calculating the cardinals of SIS through these steps.

Algorithm 1
figure e

Finding maximal SIS S of IVPFG having an arbitrary vertex v

Full size image

The maximum SISs are \(E_{1}=\{s, w, y\}\), \(E_{2}=\{s, x, y\}\), and \(E_{3}=\{t, u, z\}\). (Interval-valued picture) Fuzzy weight of the sets given above are \(\grave{W}(E_{1})=\langle [2.22, 2.52], [0.33, 0.44], [0.30, 0.43]\rangle\), \(\grave{W}(E_{2})=\langle [2.28, 2.58], [0.46, 0.5], [0.23, 0.36]\rangle\), and \(\grave{W}(E_{3})=\langle [2.25, 2.55], [0.38, 0.5], [0.30, 0.48]\rangle\).

Therefore, \(E_{2}\) has maximum membership value, maximum neutral value, minimum non-membership value, so it can be selected as best option. Hence, \(E_{2}\) has number of members which are maximum in gaming communities, i.e., cricket, hockey, and volley ball are included in SI gaming communities.

Table 11 The IVPFG relation between gaming communities
Full size table

Further to the above, assume that an exhibition was organized by game development companies at the meeting place of players to make them familiar with their gaming products. Players at the game development companies can be a part of different gaming communities. The goal is to conduct as many exhibitions as able to be done at the same time provided that at the specific time period each game development company has maximum of one exhibition and to conduct other exhibition at different time interval. In this result, the maximum numbers of exhibition that can be conducted at one time in gaming communities is the maximum IS.

5 Comparative Study and Superiority of Our Presented Model

The concept of covering and matching in graphs is of great importance and has many applications. In the context of FGs, many problems in real world problems containing uncertainties are solved using the idea of covering and matching. The concept of FGs introduced by Rosenfeld has been further generalized in different ways. FGs uses membership degree for vertices and edges under certain conditions. Numerus problems were modeled using FGs and effective outcomes were obtained. FGs like FSs were generalized in different ways to model complex problems containing uncertainties. IVFGs was the generalization of FGs and it use IVFSs to express values for vertices and edges. Both FGs and IVFGs express data using membership values and received much attention of the researchers. However, with each day going on uncertainties in problems also getting complex. Therefore, there is a need of new big structures to achieve accurate outcomes. Consequently, the notion of IFGs was introduced using IFSs, i.e., membership and non-membership values were used for vertices and edges. The concept of covering and matching was also initiated for IFGs. To deal with uncertain problems with more accuracy, the idea of IVIFGs was presented. IVIFGs is a bigger structure than FGS, IVFGS, and IFGs. The membership and non-membership values of vertices and edges in case of IVIFGs were expressed using the sub-intervals of [0, 1] instead of using the fix values, it gives the range for values of vertices and edges. Afterward, the concepts covering and matching for IVIFGs were also added in the literature and it helped to model more complex uncertain problems, obtaining accurate results for them. Further extension of both FSs and IFSs named PFSs with three values membership, neutral membership, and non-membership was explored. Using PF-relation, the structure of PFGs was presented. The values of vertices and edges of PFGs are expressed using PFSs. The terms covering and matching for PFGs was also added in the literature and using these under PF-environment increased the accuracy level for uncertain problems. Further to this, the idea of IVPFGs was proposed which similar to IVFGs and IVIFGs use the sub-intervals of [0, 1] to express the values of vertices and edges. IVPFGs were more generalized than IVFGs and IVIFGs as depicted in Table. 12. Moreover, the notions of covering and matching were established in the literature as elaborated in Table. 13. However, we have observed the gap in the existing literature, i.e., the notions of covering and matching have not yet been introduced for IVPFGs. Therefore, the first aim of our study is to fill this gap by introducing the concepts of covering and matching in IVPFGs. Since, IVPFGs deal the uncertain problems with greater precision. In this regard, we present an application with illustrative example by utilizing these terms that proves the effectiveness of our proposed study. Table 13 also indicates that our presented model is comparatively better than the existing ones.

Table 12 Generalization of fuzzy graphs
Full size table
Table 13 Covering and matching in different structures
Full size table

Moreover, our presented concepts of covering and matching in IVPFGs are comparatively more useful than other generalizations of FGs existing in literature such as IVFGs, IVIFGs, and PFGs. As evidence, if we deal the above application in the context of IVFGs, then the cricket community is 82 to 92% effective in promoting the games of its members. Consequently, it has only lower and upper membership values which provide a limited representation of community engagement presented in the analysis. Thus, it becomes one sided when non-attendance and ineffectiveness are overlooked. As a result, the overall effectiveness of community promotion efforts may be inaccurately accessed. Similarly, if we address our application using IVIFGs, then for selecting the gaming communities having maximum number of members and by finding the maximal SISs solely for lower and upper membership values. Thus the chosen values for maximal SISs are according to the effectiveness. Hence, these values only represent the number of members who attended the meeting, potentially yielding better results. However, ignoring the impact of non-attendees and ineffective members on community dynamics and using solely membership values can result in an inaccurate approach. To overcome this situation, one should study such problems through IVIFGs, which utilize lower and upper membership and non-membership values to determine maximal SISs. In this way, one can express the percentage of the effectiveness as well as ineffectiveness of the gaming communities promoting the games. For example, the cricket community’s effectiveness ranges from 82 to 92% represents the lower and upper membership values and 1 to 8% ineffective represents the lower and upper non-membership values. In addition to membership values which represent effectiveness in promoting the games of its members due to number of members attended the meeting and non-membership values which represent ineffectiveness, there may required PFGs which includes "neutrality degree" that shows the number of members who haven’t attended the meeting. This inclusion may help in developing a specific interventions and strategies to enhance engagement and participation. For example, cricket community is 92% effective in promoting the games of its members, 8% neutral or ineffective. It is an additional consideration in the analysis and it also offers more comprehensive viewpoint on the effectiveness and engagement of the community. Thus, by including non-attendees one can gain insights regarding the causes of their absences, possible obstacles to participation and areas for improvement. However, PFGs lack precision, making it difficult to precisely measure the effectiveness, neutrality, and ineffectiveness of the community’s participation. Therefore, the larger structure is needed to represent the total impact of the community, accurately. Hence the introduced notion of covering and matching in IVPFGs is the best to represent the total impact of gaming communities in a best possible way. For example, table tennis is 72 to 82% effective, 17 to 18% neutral, and 13 to 18% ineffective, which represent the values within the defined interval providing greater precision. As we have demonstrated in the above application that the maximal SISs are helpful in selecting the gaming communities. Hence our model’s approach is more generalized and flexible, providing a vast space for modeling and analyzing uncertain information across different domains. A characteristic comparison of our proposed model with IVFGs, IVIFGs is also presented in Table 14.

Table 14 The characteristic comparison of IVPFG with IVFG and IVIFG
Full size table

6 Conclusion

The problems which cannot be handled through FGs and IFGs can be described through IVPFG. IVPFGs provides more flexibility and integrity to the system, so it is important for analysis and determination of the problems containing uncertainties. In this paper, we have discussed the concepts of covering and matching by using SAs in IVPFGs. In this regard, we have initiated many new terms and results related to IVPFGs. We have discussed the concepts of SI number, SNC, SAC, Matching, and SM in IVPFGs and explored different relationships among these. Moreover, we have specifically targeted some special IVPFGs like complete and bipartite. Finally, an application of IVPFG toward social network have been presented. One can shift the concepts presented in this article toward T-spherical fuzzy graphs.

7 Limitations and Future Directions

In our study, we have provided the model based on limited games communities. However, if we apply our model to large data, it could be refined by designing a specific algorithm to achieve the best solution. In this regard, we could explore some other advanced form of the FSs and FGs to obtain even more suitable results.