1 Introduction

Complex networks(CNs) which compose of multiple interacting nodes generalize complex systems as network systems. With the help of CNs such as neural networks, information networks, biological networks and social networks, complex systems are widely investigated. Note that many real systems and processes are nonlinear, many T-S fuzzy CNs are established because of their advantages in the analysis of nonlinear systems. T-S fuzzy model is described by a set of fuzzy IF-THEN rules [1]. By means of IF-THEN rules, the nonlinear system as well as the output space will acquire a linear representation [2]. As a result, nonlinear system are represented as a sum form of some linear subsystems, then T-S fuzzy models become an effective link between linear system and complex nonlinear systems.

The couplings of CNs can be grouped into linear coupling and nonlinear coupling. Although linear coupling is usually considered in large quantities of references, the coupling of real-world applications is always nonlinear coupling. The nonlinear coupling can be classified as two cases: nonlinear relative state coupling and nonlinear absolute state coupling, one can see it in [3, 4] and some the other references. Relative state coupling refers to the direct detection of relative states between subsystems, while absolute state coupling refers to the transmission of absolute information between adjacent subsystems. In practice, we may obtain different couplings in variable engineering scenarios. The switch of couplings is always random, which can be described by a random variable. Bernoulli random variable is considered in some papers to describe a random switch variable, for example, Bernoulli random variable denotes whether the nodes is attacked or not in [5], Bernoulli random variable is used to described random time delays in [6, 7].

As one of the significant dynamic behaviors, synchronization of CNs has received extensive attention from many scholars. When the synchronization of dynamic systems is mentioned, finite-time(FET) synchronization is always considered at present stage. There are two main reasons: FET synchronization has optimal convergence and it also has better robustness [8,9,10]. Accordingly, FET synchronization has aroused considerable interest in control science and engineering. Note that the evolution of systems will be influenced by lots of factors such as environment, time delay and stochastic perturbations. Those interference factors will bring some difficulties to the control of systems, which means that the error states may not approach to the origin accurately. Then the viewpoint of practical stability is proposed in [11, 12]. According, practical synchronization means that system errors can converge to a small region of origin [13, 14], which expands the practical application of synchronization and stability. Based on FET synchronization and practical synchronization, practical finite-time(PFET) stability and synchronization are considered actively, some results can be seen in references [15,16,17,18,19].

As we all know, the synchronization of dynamic systems will not be realized automatically, then additional controller is always necessary. The control schemes can be summarized as continuous control and discontinuous control. Especially, discontinuous control methods are considered commonly, such as sampled-data control, event-triggered control, impulsive control, intermittent control and so on. On one hand, discontinuous control does not need to control constantly and control technique can be implemented easily. On the other hand, control resources can be saved. For example, intermittent control which is one of discontinuous controls is flexible and economical. For class intermittent control, control is exerted in control interval while control is not implemented in rest interval which can be seen in references [6, 20,21,22] and so on. In order to adapt the applications, many improved intermittent control methods are also developed, such as intermittent pinning control, semi-intermittent control, adaptive intermittent control in [23,24,25,26] and some other references. Especially, semi-intermittent control is designed via the idea of intermittent control, but the control is also implemented in rest interval to realize control goal. It is worth noting that the control schemes are different in control interval and rest interval.

Inspired by the above analysis, we focus on the study of PFET synchronization of T-S fuzzy CNs with different couplings. The main contributions of the paper are as follows:

  1. (1)

    The system of this paper contains not only the linear coupling but also the nonlinear coupling, where the nonlinear dynamic behavior can be expressed as nonlinear relative state coupling and absolute state coupling;

  2. (2)

    We improve a stability lemma. This lemma can guarantee the systems synchronize to an interval, which is different from some previous results that the systems synchronize to the origin accurately;

  3. (3)

    Two new semi-intermittent controllers via tanh are designed to help to realize PFET synchronization.

The arrangement of this paper are as follows. In Sect. 2, the considered model of this paper as well as some assumptions and lemmas are presented. In Sect. 3, two different controllers are designed to deal with PFET synchronization of T-S fuzzy CNs. Then in Sect. 4, two numerical simulations are presented to prove the effectiveness of the results. In Sect. 5, the conclusions are drawn.

2 Model Description and Some Preliminaries

Notations: In this paper, the notations are standard. \(\mathbb {N}=\{0,1,2,\cdots \}\), \(\mathbb {R}_{+}\), \(\mathbb {R}\), \(\mathbb {R}^{n}\) and \(\mathbb {R}^{n\times m}\) denote the set of positive real numbers, the real numbers set, n-dimensional Euclidean space and the set of all \(n\times m\) real matrices, respectively. \(\Vert v\Vert =\sqrt{v^{T}v}\), \(|v|=(|v_{1}|, |v_{2}|, \cdots , |v_{n}|)^{T}\in \mathbb {R}^{n}\), \(\textrm{diag}(v)=\textrm{diag}(v_{1}, v_{2}, \cdots , v_{n})\) and \(|v|^{\ell }=(|v_{1}|^{\ell }, |v_{2}|^{\ell }, \cdots , |v_{n}|^{\ell })^{T}\in \mathbb {R}^{n}\) with \(\ell \in \mathbb {R}_{+}\) for \(v=(v_{1}, v_{2},\cdots , v_{n})^{T}\in \mathbb {R}^{n}\). Moreover, \(I_{n}\) denotes the identity matrix of n, \(\Vert \cdot \Vert\) is 2–norm of a vector or a matrix. \(\lambda _{\max }(A)\) denotes the the maximum eigenvalue of matrix A, \(\mathcal {P}\{a\}\) represents the probability of occurrence of a and \(\mathcal {E}[\cdot ]\) means the mathematical expectation.

The considered T-S fuzzy CNs can be presented as:

Rule s: IF \(z_{1}(t)\) is \(M_{s1}\), and \(z_{2}(t)\) is \(M_{s2}\), \(\cdots\), \(z_{q}(t)\) is \(M_{sq}\), THEN

$$\begin{aligned} \dot{x}_{i}(t)=&\sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\bigg [A_{s}x_{i}(t)+B_{s}f(x_{i}(t)) \nonumber \\&+\beta (t)\gamma (t)\sum \limits _{j=1,j\ne i}^{N}c_{ij}D(x_{j}(t)-x_{i}(t)) \nonumber \\&+(1-\beta (t))\gamma (t)\sum \limits _{j=1,j\ne i}^{N}c_{ij}Dg(x_{j}(t)-x_{i}(t)) \nonumber \\&+(1-\gamma (t))\sum \limits _{j=1,j\ne i}^{N}c_{ij}D({\wp }(x_{j}(t))\nonumber \\&-{\wp }(x_{i}(t)))+U_{i}^{s}(t)\bigg ]. \end{aligned}$$
(1)

where \(i\in \mathcal {N}=\{1, 2, \cdots , N\}\), \(x_{i}(t)=(x_{i1}(t), x_{i2}(t), \cdots , x_{in}(t))^{T}\in \mathbb {R}^{n}\) is the state vector, \(A_{s}\in \mathbb {R}^{n\times n}\) and \(B_{s}\in \mathbb {R}^{n\times n}\) are known constant matrices. \(f(x_{i}(t))=(f_{1}(x_{i1}(t)), f_{2}(x_{i2}(t)), \cdots , f_{n}(x_{in}(t)))^{T} \in \mathbb {R}^{n}\) is a continuous function. The continuous nonlinear coupling functions where \(g(x_{j}(t)-x_{i}(t))\in \mathbb {R}^{n}\) is nonlinear relative state coupling, which meets \(g(x_{i}(t)-x_{j}(t))=0\) if and only if \(x_{i}(t)=x_{j}(t)\) and \(\wp (x_{j}(t))-\wp (x_{i}(t))\in \mathbb {R}^{n}\) is nonlinear absolute state coupling. \(\beta (t)\) and \(\gamma (t)\) are Bernoulli random variables, and there are \(\mathcal {P}\{\beta (t)=1\}=\mathcal {E}[\beta (t)]=\beta\) and \(\mathcal {P}\{\beta (t)=0\}=1-\beta\), \(\mathcal {P}\{\gamma (t)=1\}=\mathcal {E}[\gamma (t)]=\gamma\) and \(\mathcal {P}\{\gamma (t)=0\}=1-\gamma\), where \(\beta\) and \(\gamma\) are constants and satisfy the inequalities: \(0\le \beta \le 1\) and \(0\le \gamma \le 1\). \(D=\text{ diag }\{d_{1}, d_{2}, \cdots , d_{n}\}\) with \(d_{l}>0(l=1, 2, \cdots , n)\), submits the inner coupling matrix; \(C=(c_{ij})_{N\times N}\) is the outer coupling matrix, which meets the conditions of \(c_{ij}\ge 0(i\ne j)\), \(c_{ii}=-\sum \nolimits _{j=1,j\ne i}^{N}c_{ij}\) and \(c_{ij}=c_{ji}\). \(U_{i}^{s}(t)\in \mathbb {R}^{n}\) is the controller. The initial value of system (1) \(x_{i}(0)\in \mathbb {R}^{n}\). \(z(t)=(z_{1}(t), z_{2}(t), \cdots , z_{q}(t))^{T}\) is the premise variable vector, \(M_{sj}(s=1, 2, \cdots , m, j=1, 2, \cdots , q)\) is the fuzzy set. Moreover,

$$\begin{aligned}&\vartheta _{s}(z(t))=\frac{w_{s}(z(t))}{\sum _{s=1}^{m}w_{s}(z(t))}, w_{s}(z(t))\\&\quad =\prod _{j=1}^{q}M_{sj}(z_{j}(t)), \end{aligned}$$

with \(w_{s}(z(t))\ge 0\) and \(\sum _{s=1}^{m}w_{s}(z(t))>0\), \(s=1, 2, \cdots , m\), it is clear that

$$\begin{aligned} \sum \limits _{s=1}^{m}\vartheta _{s}(z(t))=1,~~\vartheta _{s}(z(t))\ge 0,~~\text{ for }~~ t\in \mathbb {R}^{+}. \end{aligned}$$

Remark 1

The system (1) can be divided into the following circumstances:

$$\begin{aligned} (\beta (t), \gamma (t))= {\left\{ \begin{array}{ll} (1, 1),~\mathrm {linear~coupling},\\ (1, 0),~\mathrm {nonlinear~absolute~state~coupling},\\ (0, 1),~\mathrm {nonlinear~relative~state~coupling},\\ (0, 0),~\mathrm {nonlinear~absolute~state~coupling}. \end{array}\right. } \end{aligned}$$

It can be seen that different couplings can be obtained by different values of Bernoulli random variables.

The target nodes are presented as follows:

$$\begin{aligned} \dot{y}(t)=\sum \limits _{s=1}^{m}\vartheta _{s}(z(t)) \bigg [A_{s}y(t)+B_{s}f(y(t))\bigg ], \end{aligned}$$
(2)

and the initial value of system (2) \(y(0)\in \mathbb {R}^{n}\).

Let \(e_{i}(t)=x_{i}(t)-y(t)\), \(\bar{f}(e_{i}(t))=f(x_{i}(t))-f(y(t))\), \({\bar{\wp }}(e_{j}(t))={\wp }(x_{j}(t))-{\wp }(y(t))\). From system (1) and (2), then error system can be expressed as the following form:

$$\begin{aligned} \dot{e}_{i}(t)=&\sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\bigg [A_{s}e_{i}(t)+B_{s}\bar{f}(e_{i}(t)) \nonumber \\&+\beta (t)\gamma (t)\sum \limits _{j=1}^{N}c_{ij}De_{j}(t)\nonumber \\&+(1-\beta (t))\gamma (t) {\sum \limits _{j=1}^{N}}c_{ij}Dg(e_{j}(t)-e_{i}(t))\nonumber \\&+(1-\gamma (t))\sum \limits _{j=1}^{N} c_{ij}D{\bar{\wp }}(e_{j}(t))+U_{i}^{s}(t)\bigg ]. \end{aligned}$$
(3)

Based on references [15], this paper gives the following definition of PFET synchronization.

Definition 1

System (1) is said to be practical synchronized with system (2) in finite time if there exists a constant \(\Lambda >0\) and a settling time \(T_{1}>0\) such that \(\lim \limits _{t\rightarrow T_{1}}\mathcal {E}[\Vert e_{i}(t)\Vert ]\le \Lambda\) and \(\mathcal {E}[\Vert e_{i}(t)\Vert ]\le \Lambda\) for any \(t>T_{1}\).

So as to facilitate the derivation of the final results, the following assumptions and lemmas are utilized:

Assumption 1

There are positive constants \(L_{1}\) and \(L_{2}\) such that

$$\begin{aligned}&\Vert f(x)-f(y)\Vert \le L_{1} \Vert x-y\Vert ~~\textrm{and}~~ \Vert {\wp }(x)-{\wp }(y)\Vert \le L_{2}\\&\quad \Vert x-y\Vert ,~~\forall x,~y\in \mathbb {R}^{n}. \end{aligned}$$

The following Assumption 2 is a useful assumption to deal with nonlinear relative state coupling in some existing papers, such as [3, 4] and so on.

Assumption 2

[3] It is assumed that the nonlinear function \(g(x_{i}(t)-x_{j}(t))\), which satisfies the following natures:

\(\mathrm {(i)}\):

\(g(x_{i}(t)-x_{j}(t))=-g(x_{j}(t)-x_{i}(t))\);

\(\mathrm {(ii)}\):

\(\epsilon _{1}(x_{i}(t)-x_{j}(t))^{T}(x_{i}(t)-x_{j}(t))\le (x_{i}(t)-x_{j}(t))^{T}g(x_{i}(t)-x_{j}(t))\le \epsilon _{2}(x_{i}(t)-x_{j}(t))^{T}(x_{i}(t)-x_{j}(t))(0<\epsilon _{1}\le \epsilon _{2})\).

Lemma 1

[27] As for any \(\chi \in \mathbb {R}\), there exists \(0\le |\chi |-\chi \tanh (\varepsilon \chi )\le \frac{\iota }{\varepsilon }\), where \(\varepsilon \gg 1\) and \(\iota =0.2785\).

Lemma 2

[28] If \(\theta _{1}, \theta _{2}, \dots , \theta _{n}\ge 0\), \(0<\upsilon \le 1\), the inequality is tenable

$$\begin{aligned} \sum \limits _{i=1}^{n}\theta _{i}^{\upsilon }\ge \bigg (\sum \limits _{i=1}^{n}\theta _{i}\bigg )^{\upsilon }. \end{aligned}$$

Lemma 3

It is assumed that there is a time sequence \(\{t_{k}, k\in \mathbb {N}\}\), which meets \(0=t_{0}<t_{1}<\cdots<t_{k}<\cdots\), and \(\lim \limits _{k \rightarrow +\infty }t_{k}=+\infty\), \(\mathcal {V}(t): \mathbb {R}^{n}\rightarrow \mathbb {R}\) is C-regular and satisfies the following condition:

$$\begin{aligned} \dot{\mathcal {V}}(t)\le {\left\{ \begin{array}{ll} -\phi _{1}\mathcal {V}(t)-\phi _{2}\mathcal {V}^{\omega }(t)+\phi _{0}, &{}t\in [t_{2k}, t_{2k+1}), \\ \phi _{3}\mathcal {V}(t)+\phi _{0}, &{}t\in [t_{2k+1}, t_{2k+2}), \end{array}\right. } \end{aligned}$$
(4)

where \(t\in \big [0, +\infty )\), \(\omega \in (0, 1)\), \(\phi _{0}\), \(\phi _{1}\), \(\phi _{2}\) and \(\phi _{3}\) are positive constants. Moreover, if there exists a \(k\in \mathbb {N}\) such that

$$\begin{aligned} \Upsilon (k)=\big (\Theta (k-1)+\Delta o\big )\exp (-\sigma _{1}(t_{2k+1}-t_{2k})) -\Delta o\le 0, \end{aligned}$$

then there exists a positive constant \(T_{1}\) such that \(\mathcal {V}(t){\le \big (\frac{\phi _{0}}{\phi _{2}(1-\rho )}\big )^{\frac{1}{\omega }}}\) for \(t>T_{1}\), and

$$\begin{aligned} T_{1}=t_{2k_{*}}+\frac{1}{\sigma _{1}}\ln \big (\frac{1}{\Delta o} \Theta (k_{*}-1)+1\big ), \end{aligned}$$

where \(\sigma _{1}=(1-\omega )\phi _{1}\), \(\sigma _{2}=(1-\omega )\phi _{2}\rho\), \(\sigma _{3}=(1-\omega )\phi _{3}\), \(\sigma _{4}=(1-\omega )\phi _{2}\), \(\rho \in (0,1)\), \(o_{1}=\frac{\sigma _{2}}{\sigma _{1}}\), \(o_{2}=\frac{\sigma _{4}}{\sigma _{3}}\) and \(o_{1}>o_{2}\) with \(\Delta o=o_{1}-o_{2}\), \(\Theta (k-1)=(\mathcal {V}^{1-\omega }(0)+o_{1}) \exp \big (\sum _{i=0}^{k-1}(-\sigma _{1}(t_{2i+1}-t_{2i})+\sigma _{3} (t_{2i+2}-t_{2i+1}))\big )\) with \(t_{-2}=t_{-1}=t_{0}=0\), \(k_{*}=\min \{k \in \mathbb {N}: \Upsilon (k)\le 0\}\).

Proof

As for \(\rho \in (0,1)\), the inequality (4) can be rewritten as

$$\begin{aligned} \dot{\mathcal {V}}(t)\le {\left\{ \begin{array}{ll} -\phi _{1}\mathcal {V}(t)-\rho \phi _{2}\mathcal {V}^{\omega }(t)-(1-\rho )\phi _{2}\mathcal {V}^{\omega }(t)+\phi _{0}, &{}t\in [t_{2k}, t_{2k+1}), \\ \phi _{3}\mathcal {V}(t)+\phi _{2}\mathcal {V}^{\omega }(t)-(1-\rho )\phi _{2}\mathcal {V}^{\omega }(t)+\phi _{0}, &{}t\in [t_{2k+1}, t_{2k+2}). \end{array}\right. } \end{aligned}$$
(5)

Define two sets as \(\Omega _{1}=\{t|\mathcal {V}^{\omega }(t)\le \frac{\phi _{0}}{\phi _{2}(1-\rho )}\}\) and \(\Omega _{2}=\{t|\mathcal {V}^{\omega }(t)>\frac{\phi _{0}}{\phi _{2}(1-\rho )}\}\).

Case 1: If \(t\in \Omega _{2}\), overwrite inequality (5) yields,

$$\begin{aligned} \dot{\mathcal {V}}(t)\le {\left\{ \begin{array}{ll} -\phi _{1}\mathcal {V}(t)-\rho \phi _{2}\mathcal {V}^{\omega }(t), &{}t\in [t_{2k}, t_{2k+1}), \\ \phi _{3}\mathcal {V}(t)+\phi _{2}\mathcal {V}^{\omega }(t), &{}t\in [t_{2k+1}, t_{2k+2}), \end{array}\right. } \end{aligned}$$
(6)

thus, the proof of (4) converts to (6).

Consider the comparison system below:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{v}(t)= {\left\{ \begin{array}{ll} -\phi _{1}v(t)-\rho \phi _{2}v^{\omega }(t), &{}t\in [t_{2k}, t_{2k+1}), \\ \phi _{3}v(t)+\phi _{2}v^{\omega }(t), &{}t\in [t_{2k+1}, t_{2k+2}), \end{array}\right. }\\ v(0)=\mathcal {V}(0). \end{array}\right. } \end{aligned}$$
(7)

Due to \(0\le \mathcal {V}(t)\le v(t)\), then if there exists \(T_{1}>0\) such that \(v(T_{1})=0\) and \(v(t)\equiv 0\) for \(t\ge T_{1}\), it has \(\mathcal {V}(t)\equiv 0\) for \(t\ge T_{1}\). Therefore, it just remains to prove the zero solution stability of system (7).

Let \(W(t)=v^{1-\omega }(t)\), one has

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{W}(t)= {\left\{ \begin{array}{ll} -\sigma _{1}W(t)-\sigma _{2}, &{}t\in [t_{2k}, t_{2k+1}), \\ \sigma _{3}W(t)+\sigma _{4}, &{}t\in [t_{2k+1}, t_{2k+2}), \end{array}\right. }\\ W(0)=v^{1-\omega }(0), \end{array}\right. } \end{aligned}$$

then one obtains

$$\begin{aligned} W(t)= {\left\{ \begin{array}{ll} (W(t_{2k})+o_{1})\exp (-\sigma _{1}(t-t_{2k}))-o_{1}, t\in [t_{2k}, t_{2k+1}),\\ (W(t_{2k+1})+o_{2})\exp (\sigma _{3}(t-t_{2k+1}))-o_{2}, t\in [t_{2k+1}, t_{2k+2}). \end{array}\right. } \end{aligned}$$
(8)

When \(t\in [t_{2k}, t_{2k+1})\), it can be concluded from (8) that

$$\begin{aligned} W(t)=&(W(t_{2k})+o_{1})\exp (-\sigma _{1}(t-t_{2k}))-o_{1}\\ =&\big ((W(t_{2k-1})+o_{2})\exp (\sigma _{3}(t_{2k}-t_{2k-1}))+\Delta o\big ) \\&\exp (-\sigma _{1}(t-t_{2k}))-o_{1}\\ =&\big ((W(t_{2k-2})+o_{1})\exp (-\sigma _{1}(t_{2k-1}-t_{2k-2})+\sigma _{3}(t_{2k}-t_{2k-1})) -\Delta o\\&\exp (\sigma _{3}(t_{2k}-t_{2k-1}))\\&+\Delta o\big )\exp (-\sigma _{1}(t-t_{2k}))-o_{1}\\&\vdots \\ =&\bigg ((W(0)+o_{1})\exp \big (\sum _{i=0}^{k-1}(-\sigma _{1}(t_{2i+1}-t_{2i}) +\sigma _{3}(t_{2i+2}-t_{2i+1}))\big )\\&-\Delta o\sum _{j=1}^{k-1}\big [\big (\exp (\sigma _{3}(t_{2j}-t_{2j-1}))-1\big ) \\&\exp \big (\sum _{i=j}^{k-1}(-\sigma _{1}(t_{2i+1}\\&-t_{2i})+\sigma _{3}(t_{2i+2}-t_{2i+1}))\big )\big ]\\&-\Delta o\exp (\sigma _{3}(t_{2k}-t_{2k-1}))+\Delta o\bigg ) \\&\exp (-\sigma _{1}(t-t_{2k}))-o_{1}. \end{aligned}$$

Because of \(o_{1}>o_{2}\), so \(-\Delta o\exp (\sigma _{3}(t_{2k}-t_{2k-1}))<0\), and \(-\Delta o(\exp (\sigma _{3}(t_{2j}-t_{2j-1}))-1)<0\), \(j\in \{1, 2, \cdots , k-1\}\). Then, we can obtain the following result:

$$\begin{aligned} W(t)\le&\big ((W(0)+o_{1})\exp \big (\sum _{i=0}^{k-1}(-\sigma _{1}(t_{2i+1}-t_{2i})\nonumber \\&+\sigma _{3}(t_{2i+2}-t_{2i+1}))\big )+\Delta o\big )\exp (-\sigma _{1}(t-t_{2k}))-o_{1}\nonumber \\ <&(\Theta (k-1)+\Delta o)\exp (-\sigma _{1}(t-t_{2k}))-\Delta o. \end{aligned}$$
(9)

In the same way, when \(t\in [t_{2k+1}, t_{2k+2})\), one derives from (8) that

$$\begin{aligned} W(t)=&\,(W(t_{2k+1})+o_{2})\exp (\sigma _{3}(t-t_{2k+1}))-o_{2}\nonumber \\ =&\, \big ((W(t_{2k})+o_{1})\exp (-\sigma _{1}(t_{2k+1}-t_{2k}))\nonumber \\&-\Delta o\big ) \exp (\sigma _{3}(t-t_{2k+1}))-o_{2}\nonumber \\ =&\, \bigg [\bigg ((W(0)+o_{1})\exp \big (\sum _{i=0}^{k-1}(-\sigma _{1}(t_{2i+1}-t_{2i})\nonumber \\&+\sigma _{3}(t_{2i+2}-t_{2i+1}))\big )\nonumber \\&-\Delta o\sum _{j=1}^{k-1}\big [\big (\exp (\sigma _{3}(t_{2j}-t_{2j-1}))-1\big ) \nonumber \\&\exp \big (\sum _{i=j}^{k-1}(-\sigma _{1}(t_{2i+1}-t_{2i})+\sigma _{3}(t_{2i+2}-t_{2i+1}))\big )\big ]\nonumber \\&-\Delta o\exp (\sigma _{3}(t_{2k}-t_{2k-1}))+\Delta o\bigg ) \nonumber \\&\quad \exp (-\sigma _{1}(t_{2k+1}-t_{2k}))-\Delta o\bigg ] \exp (\sigma _{3}(t-t_{2k+1}))-o_{2}\nonumber \\ \le&\big ((\Theta (k-1)+\Delta o)\exp (-\sigma _{1}(t_{2k+1}-t_{2k}))\nonumber \\&-\Delta o\big ) \exp (\sigma _{3}(t-t_{2k+1}))-o_{2}\nonumber \\ <&\big ((\Theta (k-1)+\Delta o)\exp (-\sigma _{1}(t_{2k+1}-t_{2k}))\nonumber \\&-\Delta o\big ) \exp (\sigma _{3}(t-t_{2k+1})). \end{aligned}$$
(10)

As a result, from (9) and (10), it can be acquired that

$$\begin{aligned} W(t)< {\left\{ \begin{array}{ll} (\Theta (k-1)+\Delta o)\exp (-\sigma _{1}(t-t_{2k}))-\Delta o, &{}t\in [t_{2k}, t_{2k+1}), \\ \big ((\Theta (k-1)+\Delta o)\exp (-\sigma _{1}(t_{2k+1}-t_{2k}))-\Delta o\big ) \exp \,(\sigma _{3}(t-t_{2k+1})), &{}t\in [t_{2k+1}, t_{2k+2}). \end{array}\right. } \end{aligned}$$

Same analysis method as [22], one can obtain that there exists a unique \(k_{*}\in \mathbb {N}\) and \(T_{1}\in [t_{2k_{*}}, t_{2k_{*}+1})\) such that \(W(T_{1})=0\) with the help of the following comparison system

$$\begin{aligned} S(t)={\left\{ \begin{array}{ll} (\Theta (k-1)+\Delta o)\exp (-\sigma _{1}(t-t_{2k}))-\Delta o, &{}t\in [t_{2k}, t_{2k+1}), \\ \big ((\Theta (k-1)+\Delta o)\exp (-\sigma _{1}(t_{2k+1}-t_{2k}))-\Delta o\big ) \exp \,(\sigma _{3}(t-t_{2k+1})), &{}t\in [t_{2k+1}, t_{2k+2}). \end{array}\right. } \end{aligned}$$
(11)

Then, we estimate the settling time \(T_{1}\), which belongs \([t_{2k_{*}}, t_{2k_{*}+1})\). Let \(S(T_{1})=0\), one has from (11) that

$$\begin{aligned} (\Theta (k_{*}-1)+\Delta o)\exp (-\sigma _{1}(t-t_{2k_{*}}))=\Delta o, \end{aligned}$$

by solving the above equation, we can obtain

$$\begin{aligned} T_{1}&=t_{2k_{*}}+\frac{1}{\sigma _{1}}\ln \big (\frac{1}{\Delta o}\Theta (k_{*}-1)+1\big ). \end{aligned}$$

Case 2: If \(t\in \Omega _{1}\), according to Case 1, \(\mathcal {V} (t)\) is bounded. Here, \(T_{1}\) is still an effective estimation. The proof is completed. \(\square\)

Remark 2

Lemma 3 is employed to investigate the issues of PFET synchronization of intermittent control systems and has wide applicability. We identify the sets \(\Omega _{1}\) and \(\Omega _{2}\) by means of \(\phi _{0}\), \(\phi _{2}\), \(\omega\) and \(\rho\) to determine the range of convergence. In this case, it is required to satisfy \(\phi _{0}>0\). In case \(\phi _{0}=0\), which implies that Lemma 3 will transform into the form presented in [22], and it is capable of achieving FET synchronization. In addition, Lemma 3 indicates that if \(\Upsilon (k)\le 0\), \(\mathcal {V}(t)\) is able to converge to an interval \([0, \big (\frac{\phi _{0}}{\phi _{2}(1-\rho )}\big )^{\frac{1}{\omega }}]\) at the moment, and PFET stability is achievable.

3 PFET Synchronization via Semi-intermittent Control

This section we design two kinds of controllers. Based on those controllers, two PFET synchronization criteria are established. In order to present the advantages of our results, some comparisons are given.

One controller is designed as follows:

$$\begin{aligned} U_{i}^{s}(t)= {\left\{ \begin{array}{ll} -\zeta _{i}^{s}h(e_{i}(t))-\xi _{1}\textrm{diag}(\textrm{sign}(e_{i}(t)))|h(e_{i}(t))|^{\ell } -\xi _{2}\tanh (\varepsilon h(e_{i}(t))), &{}t\in [t_{2k}, t_{2k+1}),\\ -\zeta _{i}^{s}h(e_{i}(t))-\xi _{2}\tanh (\varepsilon h(e_{i}(t))), &{}t\in [t_{2k+1}, t_{2k+2}), \end{array}\right. } \end{aligned}$$
(12)

where \(\zeta _{i}^{s}>0, s=1, 2, \cdots , m\) are control gains, \(\xi _{1}>0\), \(\xi _{2}>0\), \(\varepsilon \gg 1\), and \(0<\ell <1\) are tunable constants. \(\mathfrak {h}(\cdot )\): \(\mathbb {R}\rightarrow \Pi\) is a quantizer, where \(\Pi =\{\pm \tau _{\kappa }=\pi ^{\kappa }\tau _{0}, 0<\pi <1, \kappa =0, \pm 1, \pm 2, \cdots \}\cup \{0\}\), \(\tau _{0}\) is a positive constant. For \(\forall \nu \in \mathbb {R}\), the quantizer \(\mathfrak {h}(\nu )\) is defined as follows:

$$\begin{aligned} \mathfrak {h}(\nu )= {\left\{ \begin{array}{ll} \tau _{\kappa },&{}\textrm{if}~~\frac{1}{1+\varrho }\tau _{\kappa }<\nu<\frac{1}{1-\varrho }\tau _{\kappa },\\ 0,&{}\textrm{if}~~ \nu =0,\\ -\mathfrak {h}(-\nu ),&{}\textrm{if}~~ \nu <0, \end{array}\right. } \end{aligned}$$

where \(\varrho =\frac{1-\pi }{1+\pi }\), it can be seen that there is a Filipov solution \(\delta \in [-\varrho , \varrho )\) such that \(\mathfrak {h}(\nu )=(1+\delta )\nu\). In this paper, \(h(e_{i}(t)) =(\mathfrak {h}(e_{i1}(t)), \mathfrak {h}(e_{i2}(t)), \cdots , \mathfrak {h}(e_{in}(t)))^{T}\), \(|h(e_{i}(t))|^{\ell } =(|\mathfrak {h}(e_{i1}(t))|^{\ell }, |\mathfrak {h}(e_{i2}(t))|^{\ell }, \cdots , |\mathfrak {h}(e_{in}(t))|^{\ell })^{T}\).

Via controller (12), we give the following Theorem 1.

Theorem 1

If Assumptions 1 and 2 hold, the control gains of (12) satisfy the following condition

$$\begin{aligned}&\zeta _{i}^{s}\ge \frac{1}{2(1-\varrho )}(2\Vert A_{s}\Vert +2\Vert B_{s}\Vert L_{1}+2\beta \gamma \lambda _{\max }(\bar{C}) \nonumber \\&\quad +2(1-\gamma )L_{2}{\lambda _{\max }(\tilde{C})}+1), \end{aligned}$$
(13)

and there exist constants \(\omega \in (0, 1)\), \(\rho \in (0,1)\), \(\phi _{0}>0\), \(\phi _{1}>0\), \(\phi _{2}>0\), \(\phi _{3}>0\) and a \(k\in \mathbb {N}\) such that

$$\begin{aligned} \Upsilon (k)=\big (\Theta (k-1)+\Delta o\big ) \exp (-\sigma _{1}(t_{2k+1}-t_{2k}))-\Delta o\le 0, \end{aligned}$$
(14)

where \(\hat{C}=({\hat{c}}_{ij})_{N\times N}\), \(\hat{c}_{ij}=d_{\max }c_{ij}\), \(\hat{c}_{ii}=d_{\min }c_{ii}\), \(\check{C}=({\check{c}}_{ij})_{N\times N}\), \(\check{c}_{ij}=\hat{c}_{ij}\), \(\check{c}_{ii}=d_{\min }|c_{ii}|\) with \(d_{\max }=\max \{d_{1},d_{2}, \cdots , d_{n}\}\) as well as \(d_{\min }=\min \{d_{1},d_{2}, \cdots , d_{n}\}\), \(\bar{C}=\frac{1}{2}(\hat{C}+\hat{C}^{T})\) and \(\tilde{C}=\frac{1}{2}(\check{C}+\check{C}^{T})\). Moreover, \(\sigma _{1}\), \(\sigma _{2}\), \(\sigma _{3}\), \(\sigma _{4}\), \(o_{1}\), \(o_{2}\), \(\Delta o\), \(\Theta (k-1)\), \(k_{*}\) are defined as those in Lemma 3 with \(\phi _{0}=\frac{nN\iota \xi _{2}}{\varepsilon (1-\varrho )}\), \(\phi _{1}=1\), \(\phi _{2}=2^{\frac{\ell +1}{2}}\xi _{1}(1-\varrho )^{\ell }\), \(\omega =\frac{\ell +1}{2}\). Then, under the controller (12), the systems (1) and (2) can achieve PFET synchronization within a finite time,

$$\begin{aligned} T_{1}=t_{2k_{*}}+\frac{1}{\sigma _{1}}\ln \big (\frac{1}{\Delta o} \Theta (k_{*}-1)+1\big ). \end{aligned}$$
(15)

Proof

Consider the following Lyapunov function:

$$\begin{aligned} \mathcal {V}(t)=\frac{1}{2}\sum \limits _{i=1}^{N}e_{i}^{T}(t)e_{i}(t). \end{aligned}$$
(16)

Next, via Lyapunov function (16), two cases will be given.

Case1: when \(t\in [t_{2k}, t_{2k+1})\), \(k\in \mathbb {N}\), considering error system (3) and controller (12), we obtain

$$\begin{aligned} \mathcal {L}{\mathcal {V}}(t)=&\sum \limits _{i=1}^{N}e_{i}^{T}(t)\nonumber \\&\quad \bigg [\sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\bigg ( A_{s}e_{i}(t)+B_{s}\bar{f}(e_{i}(t))\nonumber \\&+\beta (t)\gamma (t)\sum \limits _{j=1}^{N}c_{ij}De_{j}(t)\nonumber \\&+(1-\beta (t))\gamma (t){\sum \limits _{j=1}^{N}}c_{ij}Dg(e_{j}(t)-e_{i}(t)) \nonumber \\&+(1-\gamma (t))\sum \limits _{j=1}^{N}c_{ij}D{\bar{\wp }}(e_{j}(t)) \nonumber \\&-\zeta _{i}^{s}h(e_{i}(t)) -\xi _{1} \textrm{diag}(\textrm{sign}(e_{i}(t)))|h(e_{i}(t))|^{\ell }\nonumber \\&-\xi _{2}\tanh (\varepsilon h(e_{i}(t)))\bigg )\bigg ]. \end{aligned}$$
(17)

It is obvious that

$$\begin{aligned}&\sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\sum \limits _{i=1}^{N}e_{i}^{T}(t)A_{s}e_{i}(t)\nonumber \\&\quad \le \sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\Vert A_{s}\Vert \sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}. \end{aligned}$$
(18)

Using Assumptions 1, we know

$$\begin{aligned}&\sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\sum \limits _{i=1}^{N}e_{i}^{T}(t)(B_{s}\bar{f}(e_{i}(t)))\nonumber \\&\quad \le \sum \limits _{s=1}^{m}\vartheta _{s}(z(t))L_{1}\Vert B_{s}\Vert \sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}. \end{aligned}$$
(19)

The following inequality can be easily derived

$$\begin{aligned}&\sum \limits _{i=1}^{N}\sum \limits _{j=1}^{N}e_{i}^{T}(t)c_{ij}De_{j}(t)\nonumber \\&\quad \le \sum \limits _{i=1}^{N}c_{ii}d_{\min }e_{i}^{T}(t)e_{i}(t)+\sum \limits _{i=1}^{N}\sum \limits _{j=1,j\ne i}^{N}c_{ij}d_{\max }\Vert e_{i}(t)\Vert \Vert e_{j}(t)\Vert \nonumber \\&\quad = \sum \limits _{i=1}^{N}\hat{c}_{ii}e_{i}^{T}(t)e_{i}(t)+\sum \limits _{i=1}^{N}\sum \limits _{j=1,j\ne i}^{N}\hat{c}_{ij}\Vert e_{i}(t)\Vert \Vert e_{j}(t)\Vert \nonumber \\&\quad \le \sum \limits _{i=1}^{N}\lambda _{\max }(\bar{C})\Vert e_{i}(t)\Vert ^{2}. \end{aligned}$$
(20)

Similarly, according to Assumptions 1, it can be acquired that

$$\begin{aligned}&\sum \limits _{i=1}^{N}\sum \limits _{j=1}^{N}e_{i}^{T}(t)c_{ij}D{\bar{\wp }}(e_{j}(t))\nonumber \\&\quad \le \sum \limits _{i=1}^{N}{|c_{ii}|}d_{\min }L_{2}e_{i}^{T}(t)e_{i}(t)\nonumber \\&\qquad +\sum \limits _{i=1}^{N}\sum \limits _{j=1,j\ne i}^{N}c_{ij}d_{\max }L_{2}\Vert e_{i}(t)\Vert \Vert e_{j}(t)\Vert \nonumber \\&\quad = \sum \limits _{i=1}^{N}\check{c}_{ii}L_{2}e_{i}^{T}(t)e_{i}(t) \nonumber \\&\qquad +\sum \limits _{i=1}^{N}\sum \limits _{j=1,j\ne i}^{N}\check{c}_{ij}L_{2}\Vert e_{i}(t)\Vert \Vert e_{j}(t)\Vert \nonumber \\&\quad \le \sum \limits _{i=1}^{N}L_{2}{\lambda _{\max }(\tilde{C})}\Vert e_{i}(t)\Vert ^{2}. \end{aligned}$$
(21)

According to Assumptions 2, by using \(c_{ij}=c_{ji}\) and \(e_{j}(t)-e_{i}(t)=x_{j}(t)-x_{i}(t)\), we can obtain

$$\begin{aligned}&\sum \limits _{i=1}^{N}{\sum \limits _{j=1}^{N}}e_{i}^{T}(t)c_{ij}Dg(e_{j}(t)-e_{i}(t))\nonumber \\&\quad = \frac{1}{2}\sum \limits _{i=1}^{N}\sum \limits _{j=1}^{N}(e_{i}(t)-e_{j}(t))^{T}c_{ij}Dg(e_{j}(t)-e_{i}(t))\nonumber \\&\quad = -\frac{1}{2}\sum \limits _{i=1}^{N}\sum \limits _{j=1}^{N}(e_{i}(t)-e_{j}(t))^{T}c_{ij}Dg(e_{i}(t)-e_{j}(t))\nonumber \\&\quad \le -\frac{1}{2}\sum \limits _{i=1}^{N}\sum \limits _{j=1}^{N}\epsilon _{1}(e_{i}(t)-e_{j}(t))^{T}c_{ij}d_{\min } (e_{i}(t)-e_{j}(t))\nonumber \\&\quad \le 0. \end{aligned}$$
(22)

The following inequality can be easily gained

$$\begin{aligned}&-\sum \limits _{s=1}^{m}\vartheta _{s}(z(t)) \sum \limits _{i=1}^{N}e_{i}^{T}(t)\zeta _{i}^{s}h(e_{i}(t)) \nonumber \\&\quad \le -\sum \limits _{s=1}^{m}\vartheta _{s}(z(t)) \sum \limits _{i=1}^{N}(1-\varrho )\nonumber \\&\quad \zeta _{i}^{s}\Vert e_{i}(t)\Vert ^{2}. \end{aligned}$$
(23)

With the help of Lemma 1 and Lemma 2, one can derive that

$$\begin{aligned}&-\xi _{2}\sum \limits _{i=1}^{N}e_{i}^{T}(t)\tanh (\varepsilon h(e_{i}(t)))\nonumber \\&\quad \le -\xi _{2}\sum \limits _{i=1}^{N}\sum _{j=1}^{n}\big (e_{ij}(t) \tanh (\varepsilon (1-\varrho ) e_{ij}(t))\big )\nonumber \\&\quad \le \xi _{2}\big (\frac{nN\iota }{\varepsilon (1-\varrho )}-\sum _{i=1}^{N}\sum _{j=1}^{n}|e_{ij}(t)|\big )\nonumber \\&\quad \le -\sqrt{2}\xi _{2}\big (\frac{1}{2}\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}\big )^{\frac{1}{2}} \nonumber \\&\qquad +\frac{nN\iota \xi _{2}}{\varepsilon (1-\varrho )}. \end{aligned}$$
(24)

From \(0<\ell <1\), we know \(0<\frac{\ell +1}{2}<1\). From Lemma 2, it is obtained that

$$\begin{aligned}&-\xi _{1}\sum \limits _{i=1}^{N}e_{i}^{T}(t)\textrm{diag}(\textrm{sign}(e_{i}(t)))|h(e_{i}(t))|^{\ell }\nonumber \\&\quad \le -\xi _{1}(1-\varrho )^{\ell }\sum \limits _{i=1}^{N}|e_{i}(t)|^{\ell +1}\nonumber \\&\quad \le -\xi _{1}(1-\varrho )^{\ell }\big (\sum \limits _{i=1}^{N} \sum \limits _{j=1}^{n}e_{ij}^{2}(t)\big )^{\frac{\ell +1}{2}}\nonumber \\&\quad = -2^{\frac{\ell +1}{2}}\xi _{1}(1-\varrho )^{\ell }\big (\frac{1}{2}\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}\big ) ^{\frac{\ell +1}{2}}. \end{aligned}$$
(25)

Substituting inequalities (18)–(25) into (17), it is easy to derive that

$$\begin{aligned}&\mathcal {L}\mathcal {V}(t)\le \sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\nonumber \\&\quad \sum \limits _{i=1}^{N}\bigg [\Vert A_{s}\Vert +L_{1}\Vert B_{s}\Vert +\beta (t)\gamma (t)\lambda _{\max }(\bar{C})+(1-\gamma (t))L_{2}{\lambda _{\max }(\tilde{C})} \nonumber \\&\qquad -(1-\varrho )\zeta _{i}^{s}\bigg ]\Vert e_{i}(t)\Vert ^{2}\nonumber \\&\qquad -2^{\frac{\ell +1}{2}}\xi _{1}(1-\varrho )^{\ell } (\frac{1}{2}\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2})^{\frac{\ell +1}{2}} \nonumber \\&\qquad -\sqrt{2}\xi _{2}(\frac{1}{2}\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2})^{\frac{1}{2}} \nonumber \\&\qquad +\frac{nN\iota \xi _{2}}{\varepsilon (1-\varrho )}. \end{aligned}$$
(26)

Furthermore, taking mathematical expectations on both sides of (26) and considering the condition (13), it generates

$$\begin{aligned}&\mathcal {E}[\mathcal {L}\mathcal {V}(t)]\le \mathcal {E}\nonumber \\&\quad \bigg [\frac{1}{2}\sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\sum \limits _{i=1}^{N}\nonumber \\&\quad \bigg (\big ( 2\Vert A_{s}\Vert +2L_{1}\Vert B_{s}\Vert +2\beta \gamma \lambda _{\max }(\bar{C}) +2(1-\gamma )L_{2}{\lambda _{\max }(\tilde{C})}\nonumber \\&\quad -2(1-\varrho )\zeta _{i}^{s}+1\big )\nonumber \\&\quad \Vert e_{i}(t)\Vert ^{2}-\Vert e_{i}(t)\Vert ^{2}\bigg )-2^{\frac{\ell +1}{2}}\xi _{1}(1-\varrho )^{\ell } (\frac{1}{2}\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2})^{\frac{\ell +1}{2}} \nonumber \\&\quad -\sqrt{2}\xi _{2}(\frac{1}{2}\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2})^{\frac{1}{2}} +\frac{nN\iota \xi _{2}}{\varepsilon (1-\varrho )}\bigg ]\nonumber \\&\quad \le -\mathcal {E}[\mathcal {V}(t)]-\phi _{2}\mathcal {E}[\mathcal {V}(t)]^\frac{\ell +1}{2} +\phi _{0}. \end{aligned}$$
(27)

Case2: when \(t\in [t_{2k+1}, t_{2k+2})\), \(k\in \mathbb {N}\), we can obtain the following inequality

$$\begin{aligned}&\mathcal {E}{[\mathcal {L}\mathcal {V}(t)]}\le \mathcal {E}\bigg [\frac{1}{2}\sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\nonumber \\&\quad \sum \limits _{i=1}^{N}\bigg ( 2\Vert A_{s}\Vert +2L_{1}\Vert B_{s}\Vert +2\beta \gamma \lambda _{\max }(\bar{C}) \nonumber \\&\qquad +2(1-\gamma )L_{2}{\lambda _{\max }(\tilde{C})}-2(1-\varrho )\zeta _{i}^{s}\nonumber \\&\qquad -\phi _{3}\bigg )\Vert e_{i}(t)\Vert ^{2}+\phi _{3}(\frac{1}{2}\sum \limits _{s=1}^{m} \vartheta _{s}(z(t))\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2})\nonumber \\&\qquad -\sqrt{2}\xi _{2}(\frac{1}{2}\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2})^{\frac{1}{2}} +\frac{nN\iota \xi _{2}}{\varepsilon (1-\varrho )}\bigg ]\nonumber \\&\qquad \le \phi _{3}\mathcal {E}[\mathcal {V}(t)]+\phi _{0}. \end{aligned}$$
(28)

Based on the inequalities (27)–(28) and Lemma 3, it obtains that \(\mathcal {E}[\mathcal {V}(t)]\le \big (\frac{\phi _{0}}{\phi _{2}(1-\rho )}\big )^{\frac{2}{1+\ell }}\) within the settling time \(T_{1}\), which is described by equality (15). Furthermore, one can derive \(\mathcal {E}[\Vert e_{i}(t)\Vert ]\le \sqrt{2}\big (\frac{\phi _{0}}{\phi _{2}(1-\rho )}\big )^{\frac{1}{1+\ell }}\). According to Definition 1, PFET synchronization can be realized. The proof of Theorem 1 is completed. \(\square\)

Remark 3

By Assumptions 2, nonlinear relative state coupling is overcome by means of inequality (22). Note that there are very few results about PFET synchronization via semi-intermittent control. The results of Theorem 1 improve some existing results in the sense of application. Moreover, our model includes linear and nonlinear couplings which are more general than those results that only linear or nonlinear couplings are considered.

Note that some control parameters are always large in some applications. Some control parameters of adaptive control will adjust automatically according to the states of systems, then it can save control cost to a certain extent. Considering the advantages of adaptive control, the following controller is designed

$$\begin{aligned} U_{i}^{s}(t)= {\left\{ \begin{array}{ll} -\zeta _{i}^{s}(t)h(e_{i}(t))-\xi _{1}\textrm{diag}(\textrm{sign}(e_{i}(t)))|h(e_{i}(t))|^{\ell } -\xi _{2}\tanh (\varepsilon h(e_{i}(t))),&{}t\in [t_{2k},t_{2k+1}),\\ -\zeta _{i}^{s}(t)h(e_{i}(t))-\xi _{2}\tanh (\varepsilon h(e_{i}(t))),&{}t\in [t_{2k+1},t_{2k+2}), \end{array}\right. } \end{aligned}$$
(29)

with adaptive laws

$$\begin{aligned} \dot{\zeta }_{i}^{s}(t)= {\left\{ \begin{array}{ll} \frac{1-\varrho }{(1+\varrho )^{2}}\alpha _{i}\vartheta _{s}(z(t))(h(e _{i}(t)))^{T}h(e_{i}(t)) -\eta _{i}(\zeta _{i}^{s}(t)-\bar{\zeta }_{i}^{s})\\ -\varphi _{i}\textrm{sign}(\zeta _{i}^{s}(t)-\bar{\zeta }_{i}^{s})|\zeta _{i}^{s}(t) -\bar{\zeta }_{i}^{s}|^{\ell },&{}t\in [t_{2k},t_{2k+1}),\\ \frac{1-\varrho }{(1+\varrho )^{2}}\alpha _{i}\vartheta _{s}(z(t))(h(e_{i}(t)))^{T}h(e_{i}(t)) -\eta _{i}(\zeta _{i}^{s}(t)-\bar{\zeta }_{i}^{s}),&{}t\in [t_{2k+1},t_{2k+2}), \end{array}\right. } \end{aligned}$$

where \(\alpha _{i}\), \(\eta _{i}\) and \(\varphi _{i}\) are positive constants, other parameters are the same as those in controller (12).

Theorem 2

If Assumptions 1 and 2 hold, and under the adaptive controller (29), there exists constants \(\omega \in (0, 1)\), \(\rho \in (0,1)\), \(\phi _{0}>0\), \(\bar{\phi }_{1}>0\), \(\bar{\phi }_{2}>0\), \(\bar{\phi }_{3}>0\) and a \(k\in \mathbb {N}\) such that

$$\begin{aligned} \bar{\Upsilon }(k)=\big (\bar{\Theta }(k-1)+\Delta \bar{o}\big )\exp (-\bar{\sigma }_{1}(t_{2k+1}-t_{2k})) -\Delta \bar{o}\le 0, \end{aligned}$$
(30)

then there exists \(T_{1}\) such that the systems (1) and (2) achieve PFET synchronization, where \(\bar{\sigma }_{1}=(1-\omega )\bar{\phi }_{1}\), \(\bar{\sigma }_{3}=(1-\omega )\bar{\phi }_{3}\), \(\bar{\sigma }_{2}=(1-\omega )\bar{\phi }_{2}\rho\), \(\bar{\sigma }_{4}=(1-\omega )\bar{\phi }_{2}\), \(\bar{o}_{1}=\frac{\bar{\sigma }_{2}}{\bar{\sigma }_{1}}\), \(\bar{o}_{2}=\frac{\bar{\sigma }_{4}}{\bar{\sigma }_{3}}\) with \(\Delta \bar{o}=\bar{o}_{1}-\bar{o}_{2}>0\), \(\bar{\Theta }(k-1)=(\mathcal {V}^{1-\omega }(0)+\bar{o}_{1}) \exp \big (\sum _{i=0}^{k-1}(-\bar{\sigma }_{1}(t_{2i+1}-t_{2i})+\bar{\sigma }_{3}(t_{2i+2}-t_{2i+1}))\big )\), and \(\bar{\phi }_{1}=\min \{1, 2\eta _{m}\}\), \(\bar{\phi }_{2}=\min \{2^{\frac{\ell +1}{2}}\xi _{1}(1-\varrho )^{\ell }, \varsigma \}\), \(\eta _{m}=\min \limits _{i\in \mathcal {N}}\{\eta _{i}\}\), \(\varsigma =\min \limits _{i\in \mathcal {N}}\{2^{\frac{\ell +1}{2}}\varphi _{i}\alpha _{i}^{\frac{\ell -1}{2}}\}\), the values of \(\phi _{0}\) and \(\omega\) are the same as in Theorem 1.

Proof

Define the following Lyapunov function:

$$\begin{aligned} \mathcal {V}(t)=\mathcal {V}_{1}(t)+\mathcal {V}_{2}(t), \end{aligned}$$
(31)

where

$$\begin{aligned} \mathcal {V}_{1}(t)=\frac{1}{2}\sum \limits _{i=1}^{N}e_{i}^{T}(t)e_{i}(t),~\mathcal {V}_{2}(t) =\sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N}\frac{1}{2\alpha _{i}}(\zeta _{i}^{s}(t)-\bar{\zeta }_{i}^{s})^{2}. \end{aligned}$$

When \(t\in [t_{2k}, t_{2k+1})\), \(k\in \mathbb {N}\), considering error system (3) and controller (29), and according to (18)–(25), it is easy to derive that

$$\begin{aligned}&\mathcal {L}\mathcal {V}_{1}(t)\le \sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\sum \limits _{i=1}^{N}\nonumber \\&\quad \bigg [\Vert A_{s}\Vert +L_{1}\Vert B_{s}\Vert +\beta (t)\gamma (t)\lambda _{\max }(\bar{C})+(1-\gamma (t))L_{2}{\lambda _{\max }(\tilde{C})}\nonumber \\&\qquad -(1-\varrho )\zeta _{i}^{s}(t)\bigg ]\nonumber \\&\quad \Vert e_{i}(t)\Vert ^{2}-2^{\frac{\ell +1}{2}}\xi _{1}(1-\varrho )^{\ell } (\frac{1}{2}\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2})^{\frac{\ell +1}{2}} \nonumber \\&\qquad -\sqrt{2}\xi _{2}\big (\frac{1}{2}\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}\big )^{\frac{1}{2}} \nonumber \\&\qquad +\frac{nN\iota \xi _{2}}{\varepsilon (1-\varrho )}. \end{aligned}$$
(32)

By \(\mathcal {V}_{2}(t)\), it can be attained that

$$\begin{aligned}&\mathcal {L}\mathcal {V}_{2}(t)= \sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N}(\zeta _{i}^{s}(t)\nonumber \\&\quad -\bar{\zeta }_{i}^{s})\bigg (\vartheta _{s}(z(t)) \frac{1-\varrho }{(1+\varrho )^{2}}(h(e_{i}(t)))^{T}h(e_{i}(t))\nonumber \\&\quad -\frac{\eta _{i}}{\alpha _{i}}(\zeta _{i}^{s}(t)-\bar{\zeta }_{i}^{s}) -\frac{\varphi _{i}}{\alpha _{i}}\textrm{sign}(\zeta _{i}^{s}(t) \nonumber \\&\quad -\bar{\zeta }_{i}^{s})|\zeta _{i}^{s}(t)-\bar{\zeta }_{i}^{s}|^{\ell }\bigg )\nonumber \\&\quad \le \sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\sum \limits _{i=1}^{N}\bigg ((1-\varrho )\zeta _{i}^{s}(t)\nonumber \\&\quad -\frac{(1-\varrho )^{3}}{(1+\varrho )^{2}}\bar{\zeta }_{i}^{s}\bigg )\Vert e_{i}(t)\Vert ^{2}\nonumber \\&\quad +\sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N}\bigg (-\frac{\eta _{i}}{\alpha _{i}}(\zeta _{i}^{s}(t) \nonumber \\&\quad -\bar{\zeta }_{i}^{s})^{2}-\frac{\varphi _{i}}{\alpha _{i}}|\zeta _{i}^{s}(t) -\bar{\zeta }_{i}^{s}|^{\ell +1}\bigg ). \end{aligned}$$
(33)

The following inequalities can be easily got

$$\begin{aligned}&-\sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N}\frac{\eta _{i}}{\alpha _{i}}(\zeta _{i}^{s}(t) -\bar{\zeta }_{i}^{s})^{2} \nonumber \\&\quad = -2\sum \limits _{i=1}^{N}\eta _{i}\frac{1}{2\alpha _{i}}(\zeta _{i}^{s}(t) -\bar{\zeta }_{i}^{s})^{2}\nonumber \\&\quad \le -2\eta _{m}\sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N}\frac{1}{2\alpha _{i}}(\zeta _{i}^{s}(t) -\bar{\zeta }_{i}^{s})^{2}. \end{aligned}$$
(34)
$$\begin{aligned}&\quad -\sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N} \frac{\varphi _{i}}{\alpha _{i}}|\zeta _{i}^{s}(t)-\bar{\zeta }_{i}^{s}|^{\ell +1}\nonumber \\&\quad \le -\sum \limits _{s=1}^{m} \sum \limits _{i=1}^{N}2^{\frac{\ell +1}{2}}\varphi _{i}\alpha _{i}^{\frac{\ell -1}{2}} \bigg (\frac{1}{2\alpha _{i}}(\zeta _{i}^{s}(t)\nonumber \\&\qquad -\bar{\zeta }_{i}^{s})^{2}\bigg )^\frac{\ell +1}{2}\nonumber \\&\quad \le -\varsigma \bigg (\sum \limits _{s=1}^{m} \sum \limits _{i=1}^{N}\frac{1}{2\alpha _{i}}(\zeta _{i}^{s}(t) \nonumber \\&\quad -\bar{\zeta }_{i}^{s})^{2}\bigg )^\frac{\ell +1}{2}. \end{aligned}$$
(35)

Substituting (34) and (35) into (33), \(\mathcal {L}\mathcal {V}_{2}(t)\) can be rewritten as follows:

$$\begin{aligned}&\mathcal {L}\mathcal {V}_{2}(t)\le \sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\nonumber \\&\quad \sum \limits _{i=1}^{N}\bigg ((1-\varrho ) \zeta _{i}^{s}(t)-\frac{(1-\varrho )^{3}}{(1+\varrho )^{2}}\nonumber \\&\quad \bar{\zeta }_{i}^{s}\bigg )\Vert e_{i}(t)\Vert ^{2}\nonumber \\&\qquad -2\eta _{m}\sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N}\nonumber \\&\quad \frac{1}{2\alpha _{i}}(\zeta _{i}^{s}(t)-\bar{\zeta }_{i}^{s})^{2} \nonumber \\&\qquad -\varsigma \bigg (\sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N}\frac{1}{2\alpha _{i}}(\zeta _{i}^{s}(t) \nonumber \\&\qquad -\bar{\zeta }_{i}^{s})^{2}\bigg )^\frac{\ell +1}{2}. \end{aligned}$$
(36)

From (31)–(32) and (36), it derives

$$\begin{aligned}&\mathcal {E}[\mathcal {L}\mathcal {V}(t)]\le \mathcal {E}\\&\quad \bigg [\frac{1}{2}\sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\sum \limits _{i=1}^{N}\bigg ((2\Vert A_{s}\Vert \\&\qquad +2L_{1}\Vert B_{s}\Vert +2\beta (t)\gamma (t)\lambda _{\max }(\bar{C})+2(1-\gamma (t))L_{2}{\lambda _{\max }(\tilde{C})}\\&\qquad -2\frac{(1-\varrho )^{3}}{(1+\varrho )^{2}}\bar{\zeta }_{i}^{s})\Vert e_{i}(t)\Vert ^{2}\bigg ) \\&\qquad -2^{\frac{\ell +1}{2}}\xi _{1}(1-\varrho )^{\ell }(\frac{1}{2}\sum \limits _{i=1}^{N} \Vert e_{i}(t)\Vert ^{2})^{\frac{\ell +1}{2}}\\&\qquad -\sqrt{2}\xi _{2}\big (\frac{1}{2}\sum \limits _{i=1}^{N} \Vert e_{i}(t)\Vert ^{2}\big )^{\frac{1}{2}}\\&\qquad -2\eta _{m}\sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N}\frac{1}{2\alpha _{i}}(\zeta _{i}^{s}(t) \\&\qquad -\bar{\zeta }_{i}^{s})^{2}+\varsigma \bigg (\sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N} \frac{1}{2\alpha _{i}}(\zeta _{i}^{s}(t)\\&\qquad -\bar{\zeta }_{i}^{s})^{2}\bigg )^\frac{\ell +1}{2} +\frac{nN\iota \xi _{2}}{\varepsilon (1-\varrho )}\bigg ]. \end{aligned}$$

Let \(\bar{\zeta }_{i}^{s}=\frac{(1+\varrho )^{2}}{2(1-\varrho )^{3}}(2\Vert A_{s}\Vert +2L_{1}\Vert B_{s}\Vert +2\beta \gamma \lambda _{\max }(\bar{C})+2(1-\gamma )L_{2}{\lambda _{\max }(\tilde{C})}+1)\), then

$$\begin{aligned}&\mathcal {E}[\mathcal {L}\mathcal {V}(t)]\le -\mathcal {E}[\mathcal {V}_{1}(t)]\nonumber \\&\qquad -2^{\frac{\ell +1}{2}}\xi _{1}(1-\varrho )^{\ell }\mathcal {E} [\mathcal {V}_{1}(t)]^\frac{\ell +1}{2}-2\eta _{m}\mathcal {E}[\mathcal {V}_{2}(t)] \nonumber \\&\qquad +\varsigma \mathcal {E}[\mathcal {V}_{2}(t)]^\frac{\ell +1}{2} -\sqrt{2}\xi _{2}\mathcal {E}[\mathcal {V}_{1}(t)]^{\frac{1}{2}} +\phi _{0}\nonumber \\&\quad \le -\bar{\phi }_{1}\mathcal {E}[\mathcal {V}(t)]-\bar{\phi }_{2}\mathcal {E}[\mathcal {V}(t)]^\frac{\ell +1}{2} +\phi _{0}. \end{aligned}$$
(37)

Case2: when \(t\in [t_{2k+1}, t_{2k+2})\), \(k\in \mathbb {N}\), similarly calculation, we can obtain the inequality:

$$\begin{aligned}&\mathcal {E}{[\mathcal {L}\mathcal {V}(t)]}\le \mathcal {E}\nonumber \\&\quad \bigg [\frac{1}{2}\sum \limits _{s=1}^{m}\vartheta _{s}(z(t))\sum \limits _{i=1}^{N}\bigg ((2\Vert A_{s}\Vert \nonumber \\&\qquad +2L_{1}\Vert B_{s}\Vert +2\beta (t)\gamma (t)\lambda _{\max }(\bar{C})+2(1-\gamma (t))L_{2} {\lambda _{\max }(\tilde{C})}\nonumber \\&\qquad -2\frac{(1-\varrho )^{3}}{(1+\varrho )^{2}}\bar{\zeta }_{i}^{s})\Vert e_{i}(t)\Vert ^{2}\bigg ) \nonumber \\&\qquad -\sqrt{2}\xi _{2}\big (\frac{1}{2}\sum \limits _{i=1}^{N}\Vert e_{i}(t)\Vert ^{2}\big )^{\frac{1}{2}} \nonumber \\&\qquad -2\eta _{m}\sum \limits _{s=1}^{m}\sum \limits _{i=1}^{N}\frac{1}{2\alpha _{i}}(\zeta _{i}^{s}(t) \nonumber \\&\qquad -\bar{\zeta }_{i}^{s})^{2}+\frac{nN\iota \xi _{2}}{\varepsilon (1-\varrho )}\bigg ]\nonumber \\&\quad \le (-1-\bar{\phi }_{3})\mathcal {E}[\mathcal {V}_{1}(t)]+\bar{\phi }_{3}\mathcal {E}[\mathcal {V}_{1}(t)]-(2\eta _{m} \nonumber \\&\qquad +\bar{\phi }_{3})\mathcal {E}[\mathcal {V}_{2}(t)]+\bar{\phi }_{3}\mathcal {E}[\mathcal {V}_{2}(t)]\nonumber \\&\qquad -\sqrt{2}\xi _{2}\mathcal {E}[\mathcal {V}_{1}(t)]^{\frac{1}{2}}+\phi _{0}\nonumber \\&\quad \le \bar{\phi }_{3}\mathcal {E}[\mathcal {V}(t)]+\phi _{0}. \end{aligned}$$
(38)

Based on the inequalities (37)–(38), Lemma 3 and the identical analysis method with Theorem 1, it obtains that PFET synchronization can be realized. The proof of Theorem 2 is completed. \(\square\)

Remark 4

In controller (12) and (29), \(-\xi _{2}\tanh (\varepsilon h(e_{i}(t)))\) is introduced which plays an important role in PFET synchronization and can be seen in [27]. The roles of \(-\zeta _{i}^{s}(t)h(e_{i}(t))\) and \(-\xi _{1}\textrm{diag}(\textrm{sign}(e_{i}(t)))|h(e_{i}(t))|^{\ell }\) can be seen the reference [20]. Theorem 1 can be realized flexibly while Theorem 2 can improve the efficiency of control resources by using some adaptive parameters. In practical applications, one can choose Theorem 1 or Theorem 2 according to the requires.

4 Numerical Example

In this section, consider system (2), where \(m=2\), then \(s=1, 2\), \(\vartheta _{1}(z(t))=\cos ^{2}(z(t)), \vartheta _{2}(z(t))=\sin ^{2}(z(t))\) and

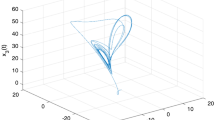
$$\begin{aligned} A_{1}=\left( \begin{array}{ccc} -0.42 &{}-0.29 &{}-0.06\\ -0.08 &{}0.13 &{}0.3\\ 0.13 &{}-0.31 &{}0.06 \end{array} \right) , B_{1}=\left( \begin{array}{ccc} 0.07 &{}0 &{}0\\ 0 &{}0 &{}0\\ 0 &{}0 &{}0 \end{array} \right) ,\\ A_{2}=\left( \begin{array}{ccc} -0.23 &{}-0.31 &{}0.07\\ 0.13 &{}-0.07 &{}0.21\\ 0.04 &{}-0.23 &{}-0.13 \end{array} \right) , B_{2}=\left( \begin{array}{ccc} 0.06 &{}0 &{}0\\ 0 &{}0 &{}0\\ 0 &{}0 &{}0 \end{array} \right) , \end{aligned}$$

and \(y(t)=(y_{1}(t), y_{2}(t), y_{3}(t))^{T}\), for \(p=1, 2, 3\), \(f_{p}(y_{p}(t))=\frac{1}{2}(|y_{p}(t)+1|-|y_{p}(t)-1|)\), \(z(t)=(y_{1}(t),y_{1}(t),y_{1}(t))^{T}\). Figure 1 shows the chaotic trajectory of T-S fuzzy system with \(y(0)=(0.64, 0.78, 0.85)^{T}\).

Fig. 1
figure 1

Chaotic trajectories of isolated nodes with \(y(0)=(0.64,0.78,0.85)^{T}\)

Full size image
Fig. 2
figure 2

The Bernoulli random variables \(\beta (t)\) with \(\beta =0.85\) and \(\gamma (t)\) with \(\gamma =0.8\)

Full size image

As for T-S fuzzy system (1), where \(N=6\), \(n=3\), \(D=\textrm{diag}([1,0.1,1])\), and the outer coupling matrix C is given as

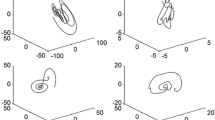
$$\begin{aligned} C=\left( \begin{array}{cccccc} -6.2 &{}3 &{}0 &{}0.1 &{}1 &{}2.1\\ 3 &{}-5.2 &{}1.2 &{}1 &{}0 &{}0\\ 0 &{}1.2 &{}-6.4 &{}3.2 &{}0 &{}{2}\\ 0.1 &{}1 &{}{3.2} &{}-6.3 &{}2 &{}0\\ 1 &{}0 &{}0 &{}2 &{}-5.5 &{}2.5\\ 2.1 &{}0 &{}2 &{}0 &{}2.5 &{}-6.6 \end{array} \right) . \end{aligned}$$

We take the Bernoulli random variables \(\beta (t)\) with \(\beta =0.85\) and \(\gamma (t)\) with \(\gamma =0.8\), then the Bernoulli sequences are plotted in Fig. 2. For nonlinear relative state coupling, we select \({\wp }_{p}(x_{jp}(t))=2x_{jp}(t)+\sin (x_{jp}(t))\). As for nonlinear absolute state coupling, we take \(g_{p}(x_{jp}(t)-x_{ip}(t))=(x_{jp}(t)-x_{ip}(t))(3-\cos (x_{jp}(t)-x_{ip}(t)))\). By simple calculation, Assumptions 1 holds with \(L_{1} = 1\), \(L_{2} = 3\) and Assumptions 2 is satisfied when \(\epsilon _{1}=2\) and \(\epsilon _{2}=4\). The quantizer parameter is given as \(\pi =0.9\), and then we obtain \(\varrho =\frac{1}{9}\), if the time sequence \(\{t_{k}, k\in \mathbb {N}\}\) meets \(t_{2k+1}-t_{2k}=0.08\) and \(t_{2k+2}-t_{2k+1}=0.02\). The time sequence is presented in Fig. 3.

Fig. 3
figure 3

The time sequence \(\{t_{k}, k\in \mathbb {N}\}\)

Full size image

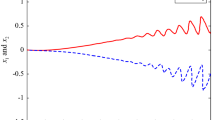
Now, we verify Theorem 1. By simply computing, we can attain \(\zeta _{i}^{1}=9.9129\) and \(\zeta _{i}^{2}=9.7935\), \(i=1, 2, 3, 4, 5, 6\). Take \(\ell =\frac{1}{5}\), \(\rho =0.9\), \(\xi _{1}=10\), \(\xi _{2}=1\), \(\varepsilon ={100}\), and \(\phi _{3}=2\). Then by calculating, we can obtain the following parameter values: \(\omega =0.6\), \(\sigma _{1}=0.4\), \(\sigma _{2}=5.3295\), \(\sigma _{3}=0.8\), \(\sigma _{4}=5.9217\), \(\phi _{0}={0.0564}\), \(\phi _{2}=14.8043\). Furthermore, one obtains \(\Upsilon (289)=-0.0014<0\), \(o_{1}=13.3239\), \(o_{2}=7.4021\), \(o_{1}>o_{2}\), \(\mathcal {V}(0)=93.9696\) and \(T_{1}=28.9794\). The trajectories \(\Vert e_{i}(t)\Vert\) and \(\Vert h(e_{i}(t))\Vert\) are presented in Fig. 4. Through calculation, we can derive \(\mathcal {V}(t)\le 0.0043\), along with \(\mathcal {E}[\Vert e_{i}(t)\Vert ]\le \Lambda =0.0929\). That is to say, the errors of systems (1) and (2) converge to a small interval as time goes by, and \(\mathcal {E}[\Vert e_{i}(t)\Vert ]\) progressively stabilizes to an exact range of [0, 0.0929]. Therefore, one can see that PFET synchronization based on controller (12) achieved within the settling time from Fig. 4.

Fig. 4
figure 4

Trajectories \(\Vert e_{i}(t)\Vert\) and \(\Vert h(e_{i}(t))\Vert\) under the PFET fuzzy controller (12)

Full size image
Fig. 5
figure 5

Trajectories \(\Vert e_{i}(t)\Vert\) and \(\Vert h(e_{i}(t))\Vert\) under the PFET fuzzy adaptive controller (29)

Full size image

Next, in the simulation of Theorem 2, the relevant parameters of the adaptive laws are selected as \(\alpha _{i}=0.4\), \(\eta _{i}=0.8\) and \(\varphi _{i}=0.8\) for \(i=1, 2, 3, 4, 5, 6\). Let \(\ell =\frac{1}{5}\), \(\rho =0.9\), \(\xi _{1}=10\), \(\xi _{2}=1\), \(\varepsilon ={100}\) and take \(\bar{\phi }_{3}=2\), it is calculated by known conditions that \(\omega =0.6\), \(\bar{\sigma }_{1}=0.4\), \(\bar{\sigma }_{2}=0.6298\), \(\bar{\sigma }_{3}=0.8\), \(\bar{\sigma }_{4}=0.6998\), \(\phi _{0}=0.0564\), \(\bar{\phi }_{1}=1\) and \(\bar{\phi }_{2}=1.7494\). Accordingly, \(\bar{o}_{1}=1.5744\) and \(\bar{o}_{2}=0.8747\) satisfy \(\bar{o}_{1}>\bar{o}_{2}\) and \(\bar{\Upsilon }(446)=-0.0003288<0\). In addition, we acquire \(\mathcal {V}(t)\le 0.1516\) by computing, and verify that \(\mathcal {E}[\Vert e_{i}(t)\Vert ]\le \Lambda =0.5506\) is valid within a finite time. Ultimately, the trajectories \(\Vert e_{i}(t)\Vert\) and \(\Vert h(e_{i}(t))\Vert\) are presented in Fig. 5, indicating that the system (1) and (2) are synchronized to an interval in a finite time.

5 Conclusions

Via semi-intermittent control, this paper establishes some sufficient conditions to realized the PFET synchronization of T-S fuzzy complex networks with different couplings. Firstly, Lemma 3 presents a improvement PFET stability result which is used to guarantee the PFET synchronization. Secondly, two kinds of semi-intermittent controllers are designed, then the proof of PFET synchronization is proposed via the designed control schemes. Moreover, some comparisons are given to present the advantages of our results. Finally, simulation examples are presented to confirm the validness of theoretical results. Note that the relationships of nodes are always assumed to be cooperative in many existing CNs. However, there also exists competition between the nodes of CNs. Then both competition and cooperation should be considered if the CNs are considered. The PFET synchronization of T-S fuzzy CNs with competition and cooperation will be our future research focus.