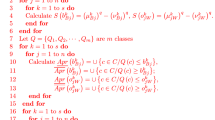Abstract
Owing to the limitations of existing fuzzy sets and fuzzy numbers, researchers have developed a new form of fuzzy numbers called R-numbers. For problems related to planning or forecasting future events, or where there is some uncertainty in the available data, R-number uses a certain percentage of risk and error as a confidence factor for such data, eliminating discrepancies between available data and determined values. Given its advantages and flexibility, this study aims to propose an R-number multi-attributive real–ideal comparative analysis (RN-MARICA) method suitable for using in multi-attribute group decision-making (MAGDM). In this regard, firstly, this study defines the Aczel–Alsina operation for R-numbers. Based on this, the R-number Aczel–Alsina operators were created, namely R-number Aczel–Alsina weighted geometric averaging (RNAAWGA) operator, R-number Aczel–Alsina ordered weighted geometric averaging (RNAAOWGA) operator, and R-number Aczel–Alsina hybrid weighted geometric averaging (RNAAHWGA) operator, and their related properties were studied. Secondly, based on the R-number Aczel–Alsina operators, the multi-attributive real–ideal comparative analysis (MARICA) method is extended to the R-number MAGDM environment, which is called the RN-MARICA method. Finally, this study applies the proposed RN-MARICA method to the risk analysis of 5G base station project construction, proving the feasibility and applicability of the proposed framework.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Uncertainty and incompleteness of data has always been a problem in multi-attribute decision-making. Many scholars have put forward a variety of fuzzy set theories, such as intuitionistic fuzzy sets [1], Pythagorean fuzzy sets [2], neutrosophic fuzzy sets [3], picture fuzzy sets [4], spherical fuzzy set [5], fermatean fuzzy set [6], cognitive fuzzy set [7], volumetric fuzzy set [8] and so on. However, these fuzzy sets have some flaws and do not take into account the risk factors in the data. To this end, Seiti et al. [9] proposed the R-number, which is modeled by considering information source risk and future event risk. The reliability of fuzzy points is no longer considered as the main factor affecting the assessment, and risk is considered as the main assessment factor. In R-number theory, fuzzy pessimistic and optimistic risks, fuzzy pessimistic and optimistic acceptable risks, and fuzzy risk perceptions are considered. In the study of R-numbers, pessimistic and optimistic risks are defined as the effects of risk that make ambiguous data worse or better. Furthermore, the pessimistic and optimistic acceptable risk factors are defined as the acceptable percentages of risk for pessimism and optimism. Finally, risk perception is incorporated into the R-number formula as the percentage of error in risk estimates. Seiti and Hafezalkotob [10] developed the R-TOPSIS methodology for risk-based preventive maintenance planning. Seiti et al. [11] developed the modified R-numbers for risk-based fuzzy information fusion and applied it to failure modes, effects, and system resilience analysis (FMESRA). Mousavi et al. [12] defined an R-VIKOR approach. Liu et al. [13] developed the risk -based decision framework based on R-numbers and best–worst method.
The aggregation of information is the basis for obtaining a comprehensive evaluation. So far, various aggregation operators have been developed. Filev and Yager [14] defined the OWA operators. Yager [15] proposed the generalized Bonferroni mean operators for multi-criteria aggregation. Wang and Liu [16] developed the Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. Huang [17] defined the Intuitionistic fuzzy Hamacher aggregation operators. Qin and Liu [18] proposed an approach to intuitionistic fuzzy MADM based on Maclaurin symmetric mean operators. Liu et al. [19] developed the intuitionistic fuzzy Dombi Bonferroni mean operators. Li et al. [20] extended the methods for multiple attribute group decision-making based on Intuitionistic fuzzy Dombi Hamy mean operators.
The study of t-norms and t-conorms is the key operation in fuzzy set theory. In 1982, Aczel and Alsina [21] proposed the new operations of Aczel–Alsina t-norms and Aczel–Alsina t-conorms. It has great priority because of the variability of the parameters. Based on new operations, Senapati et al. [22] defined the Aczel–Alsina aggregation operators and their application to intuitionistic fuzzy multiple attribute decision-making. Senapati et al. [23] developed the novel Aczel–Alsina operations-based interval-valued intuitionistic fuzzy aggregation operators. Subsequently, Senapati [24] proposed the picture fuzzy Aczel–Alsina average aggregation operators. And Naeem et al. [25] developed a novel picture fuzzy Aczel–Alsina geometric aggregation information and applied it to determine the factors affecting mango crops. Ye et al. [26] defined the Aczel–Alsina weighted aggregation operators of Neutrosophic Z-numbers. Hussain et al. [27] developed the Aczel–Alsina aggregation operators on T-Spherical fuzzy (TSF) information with application to TSF multi-attribute decision-making.
There are various MADM methods including analytic hierarchy process (AHP) [28], technique for order of preference by similarity to ideal solution (TOPSIS) [29], Vlsekriterijumska Optimizacija I Kompromisno Resenje (VIKOR) [30], complex proportional assessment (COPRAS) [31], multi-attributive border approximation area comparison (MABAC) [32], evaluation based on distance from average solution (EDAS) [33]. MARICA [34] is the MADM method proposed by Pamuar et al. in 2014. The core idea of MARICA is to apply the theoretical ponder matrix and the actual ponder matrix for modeling, and the optimal alternative has the smallest gap between the theoretical ponder matrix and the actual ponder matrix. Compared with the above MADM method, this method has many advantages in decision-making: (1) the concept of theoretical ponder matrix and the actual ponder matrix is introduced, taking into account the decision maker's preference for alternatives; (2) in calculating the gap between the theoretical ponder matrix and the actual ponder matrix, the distance measurement formula does not need to be defined; (3) the core idea is simple and easy to understand.
This study aims to propose Aczel–Alsina t-norm and t-conorm operations and new operation-based aggregation operators in the R-number environment. And using these operators to create a MAGDM method for RN-MARICA is also the focus of this study. The contribution of this paper lies in the following aspects:
-
1.
We create the Aczel–Alsina operation for R-numbers, which can overcome the shortcomings of algebraic, Einstein and Hamacher operations, and can capture the connections between different R-numbers.
-
2.
We extend the Aczel–Alsina operators to the R-number Aczel–Alsina operators: RNAAWGA operator, RNAAOWGA operator, and RNAAHWGA operator. Aggregating R-number data with these operators can overcome the disadvantages of existing operators.
-
3.
Based on the R-number Aczel–Alsina operators, we establish a MARICA algorithm to deal with the MAGDM problem with R-number data.
-
4.
To demonstrate the feasibility and reliability of the proposed R-number Aczel–Alsina aggregation operator and the proposed RN-MARICA method, we perform the proposed operators and method on the MAGDM problem.
The rest of this paper is organized as follows: Sect. 2 describes some basic information related to R-number, Aczel–Alsina t-norms, Aczel–Alsina t-conorms and R-number operation rules. Section 3 discusses the definition and related properties of R-number Aczel–Alsina. In Sect. 4, we define some R-number Aczel–Alsina aggregation operators, namely RNAAWGA operator, RNAAOWGA operator, and RNAAHWGA operator, and study some of their properties. In Sect. 5, we use the R-number Aczel–Alsina aggregation operators to establish the RN-MARICA algorithm to solve the MAGDM problem. In Sect. 6, we provide an illustrative example related to risk analysis of 5G base station construction projects to study the risk indicators that should be most concerned in 5G base station construction projects. In Sect. 7, we do a sensitivity analysis to investigate how parameters affect decision outcomes. In Sect. 8, a comparative evaluation of the proposed MARICA method with existing MAGDM methods is performed. Section 9 concludes the paper, illustrates the research gaps and addresses future research. The research structure of the whole paper is shown in Fig. 1.
2 Preliminaries
This section provides some basic concepts of R-number, Aczel–Alsina t-norms and t-conorms.
2.1 R-numbers
Definition 1
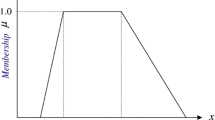
[35] A fuzzy number \(\tilde{A}\) on R can be a triangular fuzzy number (TFN) if its membership function \(\mu_{{\tilde{A}}} \left( x \right):R \to \left[ {0,1} \right]\) is defined as.
Here, \(a_{1}\) and \(a_{3}\) are the lower and upper bounds of the fuzzy number \(\tilde{A}\), respectively, and \(a_{2}\) is the modal value. The TFN can also be defied as \(\tilde{A} = \left( {a_{1} ,a_{2} ,a_{3} } \right)\).
Definition 2
[36] A Type-2 fuzzy set \(\tilde{A}\) can be defined by \(\mu_{{\tilde{A}}} :X \times U \to U\), in which \(x\) is the primary variable of \(\tilde{A}\) and \(X\) is the universe of discourse of \(x\). The three-dimensional membership function of \(\tilde{A}\left( {\mu_{{\tilde{A}}} \left( {x,u} \right)} \right)\) can be described by the following equation:
where \(u\) is the secondary variable and \(u \in \left[ {0,1} \right]\). Besides \(\mu_{{\tilde{A}}} \left( {x,u} \right)\) is recognized as secondary membership grade of \(x\) and the primary membership of \(x\) is defined as \(J_{x} = \left\{ {\left( {x,u} \right)|u \in \left[ {0,1} \right],\mu_{{\tilde{A}}} \left( {x,u} \right) > 0} \right\}\).
Definition 3
[37] The Type-2 triangular fuzzy number \(\tilde{\tilde{A}}\) can be defined using a triangular fuzzy number with fuzzy elements as follows:
where \(\tilde{A}_{l}\) and \(\tilde{A}_{u}\) are the fuzzy lower and upper bounds of \(\tilde{\tilde{A}}\), respectively, and \(\tilde{A}_{m}\) is the fuzzy modal value.
Definition 4
[9] The R-numbers for arbitrary fuzzy number \(\tilde{B}\) with lower limit \(l_{{\tilde{B}}}\) and upper limit \(u_{{\tilde{B}}}\) in beneficial and non-beneficial modes are denoted by \(R_{b} \left( {\tilde{B}} \right)\) and \(R_{c} \left( {\tilde{B}} \right)\), respectively, and can be described as follows:
where
where
in which \(\tau\) is a number infinitely close to one and \(\tilde{r}^{ - }\) and \(\tilde{r}^{ + }\) are fuzzy negative and positive risks and are defined as the fuzzy error and risk, which leads the fuzzy numbers becomes worse or better in the future. The fuzzy amount of positive and negative risks that can be tolerated by decision makers are denoted by \(\widetilde{AR}^{ - }\) and \(\widetilde{AR}^{ + }\), respectively, and \(\widetilde{RP}^{ - }\) and \(\widetilde{RP}^{ + }\) are decision makers’ fuzzy risk perceptions related to negative and positive risks. In these relations, \(\widetilde{AR}^{ - }\) and \(\widetilde{AR}^{ + }\) values are always between zero and one, but the possible range of \(\widetilde{RP}^{ - }\) and \(\widetilde{RP}^{ + }\) is defined as follows:
-
Optimistic experts \({0 < }\widetilde{RP}^{ - } ,\widetilde{RP}^{ + } < 1\);
-
Neutral experts \({0}\);
-
Pessimistic experts \({ - }\infty { < }\widetilde{RP}^{ - } ,\widetilde{RP}^{ + } < 0\).
In this article, we assume that \(\tilde{B}\) is a triangular fuzzy number, then \(R\left( {\tilde{B}} \right)\) is the Type-2 triangular fuzzy number. defined as
where \(R_{1} \left( {\tilde{B}} \right) = \left( {\mu_{11} ,\mu_{12} ,\mu_{13} } \right)\),\(R_{2} \left( {\tilde{B}} \right) = \left( {\mu_{21} ,\mu_{22} ,\mu_{23} } \right)\)\(R_{3} \left( {\tilde{B}} \right) = \left( {\mu_{31} ,\mu_{32} ,\mu_{33} } \right)\).
Definition 5
[9] Let us assume that two R-numbers \(R\left( {\tilde{B}} \right)\) and \(R\left( {\tilde{C}} \right)\) are Type-2 triangular fuzzy numbers, then the operations between them are defined as.
Definition 6
[9] The defuzzification operation of R-number \(R\left( {\tilde{B}} \right)\) is defined:
2.2 Aczel–Alsina t-norms and t-conorms
The definition of Aczel–Alsina t-norms \(T_{\delta } \left( {a,b} \right):\left[ {0,1} \right]^{2} \to \left[ {0,1} \right]\) and Aczel–Alsina t-conorms \(S_{\delta } \left( {a,b} \right):\left[ {0,1} \right]^{2} \to \left[ {0,1} \right]\) for all \(a,b \in \left[ {0,1} \right],\delta \ge 0\) are presented as follows.
Definition 7
[21] The Aczel–Alsina t-norms are defined as
And the Aczel–Alsina t-conorms are defined as
where \(T_{0} \left( {a,b} \right)\) and \(S_{0} \left( {a,b} \right)\) are the drastic t-norm and the drastic t-conorm, respectively, which are represented below:
3 Operations of R-Number Based on the Aczel–Alsina t-Norm and t-Conorm
In this section, we define some operations of R-number based on the Aczel–Alsina t-norms and t-conorms.
Definition 8
Let us assume that two R-numbers \(R\left( {\tilde{B}} \right)\) and \(R\left( {\tilde{C}} \right)\) are Type-2 triangular fuzzy numbers, and \(\delta \ge 1\), then the operations between them based on the Aczel–Alsina t-norms and t-conorms are defined as.
Example 1
Let \(R\left( {\tilde{B}} \right) = \left( {\left( {0.1,0.2,0.3} \right),\left( {0.2,0.3,0.4} \right),\left( {0.3,0.4,0.5} \right)} \right)\), \(R\left( {\tilde{C}} \right) = \left( {\left( {0.2,0.3,0.4} \right),\left( {0.3,0.4,0.5} \right),\left( {0.4,0.5,0.6} \right)} \right)\), be two R-numbers, and suppose \(\delta = 3\) and \(\lambda = 2\). Then using the operation rules in Definition 8, we can get.
\(R\left( {\tilde{B}} \right) \oplus R\left( {\tilde{C}} \right) = \left( \begin{gathered} \left( {e^{{ - \left( {\left( { - \ln \left( {0.1 + 0.2} \right)} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln \left( {0.2 + 0.3} \right)} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln \left( {0.3 + 0.4} \right)} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} } \right), \hfill \\ \left( {e^{{ - \left( {\left( { - \ln \left( {0.2 + 0.3} \right)} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln \left( {0.3 + 0.4} \right)} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln \left( {0.4 + 0.5} \right)} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} } \right), \hfill \\ \left( {e^{{ - \left( {\left( { - \ln \left( {0.3 + 0.4} \right)} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln \left( {0.4 + 0.5} \right)} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln \left( {0.5 + 0.6} \right)} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} } \right) \hfill \\ \end{gathered} \right) = \begin{array}{*{20}l} {\left( {\left( {0.3,0.5,0.7} \right),\left( {0.5,0.7,0.9} \right),\left( {0.7,0.9,1.1} \right)} \right)} \hfill \\ \end{array} ;\) \(\begin{gathered} R\left( {\tilde{B}} \right) \otimes R\left( {\tilde{C}} \right) \hfill \\ = \left( \begin{gathered} \left( \begin{gathered} e^{{ - \left( {\left( { - \ln 0.1} \right)^{3} + \left( { - \ln 0.2} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln 0.2} \right)^{3} + \left( { - \ln 0.3} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} , \hfill \\ e^{{ - \left( {\left( { - \ln 0.3} \right)^{3} + \left( { - \ln 0.4} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} \hfill \\ \end{gathered} \right), \hfill \\ \left( \begin{gathered} e^{{ - \left( {\left( { - \ln 0.2} \right)^{3} + \left( { - \ln 0.3} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln 0.3} \right)^{3} + \left( { - \ln 0.4} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} , \hfill \\ e^{{ - \left( {\left( { - \ln 0.4} \right)^{3} + \left( { - \ln 0.5} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} \hfill \\ \end{gathered} \right), \hfill \\ \left( \begin{gathered} e^{{ - \left( {\left( { - \ln 0.3} \right)^{3} + \left( { - \ln 0.4} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln 0.4} \right)^{3} + \left( { - \ln 0.5} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} , \hfill \\ e^{{ - \left( {\left( { - \ln 0.5} \right)^{3} + \left( { - \ln 0.6} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right) \hfill \\ = \begin{array}{*{20}l} {\left( \begin{gathered} \left( {0.0789,0.1639,0.2567} \right),\left( {0.1639,0.2567,0.3559} \right), \hfill \\ \left( {0.2567,0.3559,0.4605} \right) \hfill \\ \end{gathered} \right)} \hfill \\ \end{array} ; \hfill \\ \end{gathered}\) \(2R\left( {\tilde{B}} \right) = \left( \begin{gathered} \left( {e^{{ - \left( {\left( { - \ln 2 \times 0.1} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln 2 \times 0.2} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln 2 \times 0.3} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} } \right), \hfill \\ \left( {e^{{ - \left( {\left( { - \ln 2 \times 0.2} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln 2 \times 0.3} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln 2 \times 0.4} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} } \right), \hfill \\ \left( {e^{{ - \left( {\left( { - \ln 2 \times 0.3} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln 2 \times 0.4} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {\left( { - \ln 2 \times 0.5} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} } \right) \hfill \\ \end{gathered} \right) = \begin{array}{*{20}l} {\left( {\left( {0.2,0.4,0.6} \right),\left( {0.4,0.6,0.8} \right),\left( {0.6,0.8,1} \right)} \right)} \hfill \\ \end{array} ;\) \(\left( {R\left( {\tilde{B}} \right)} \right)^{2} = \left( \begin{gathered} \left( {e^{{ - \left( {2 \times \left( { - \ln 0.1} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {2 \times \left( { - \ln 0.2} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {2 \times \left( { - \ln 0.3} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} } \right), \hfill \\ \left( {e^{{ - \left( {2 \times \left( { - \ln 0.2} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {2 \times \left( { - \ln 0.3} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {2 \times \left( { - \ln 0.4} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} } \right), \hfill \\ \left( {e^{{ - \left( {2 \times \left( { - \ln 0.3} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {2 \times \left( { - \ln 0.4} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} ,e^{{ - \left( {2 \times \left( { - \ln 0.5} \right)^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }} } \right) \hfill \\ \end{gathered} \right) = \begin{array}{*{20}l} {\left( \begin{gathered} \left( {0.055,0.1316,0.2194} \right),\left( {0.1316,0.2194,0.3152} \right), \hfill \\ \left( {0.2194,0.3152,0.4176} \right) \hfill \\ \end{gathered} \right)} \hfill \\ \end{array} .\)
4 Aczel–Alsina Geometric Aggregation Operators of R-Number
This section will develop new aggregation operators based on the Aczel–Alsina norm in the R-number environment. The content of the study is shown in Fig. 2.
4.1 R-Number Aczel–Alsina Weighted Geometric Averaging Operator
This part proposes the R-number Aczel–Alsina weighted geometric averaging (RNAAWGA) operator based on the operations of Definition 8.
Definition 9
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be a collection of R-numbers, \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). Then the R-number Aczel–Alsina weighted geometric averaging (RNAAWGA) operator is defined as
Theorem 1
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be a collection of R-numbers, \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). Then the aggregated value by the RNAAWGA operator is still a R-number and.
where
Proof
We can prove Theorem 1 by the following mathematical induction technique.
-
(a)
Set \(n = 2\). Based on Definition 8 and Definition 9, we have
$$ \begin{gathered} RNAAWGA\left( {R\left( {\tilde{B}_{1} } \right),R\left( {\tilde{B}_{2} } \right)} \right) = R\left( {\tilde{B}_{1} } \right) \otimes R\left( {\tilde{B}_{2} } \right) \hfill \\ = \left( \begin{gathered} \left( \begin{gathered} e^{{ - \left( {\omega_{1} \left( { - \ln \mu_{111} } \right)^{\delta } + \omega_{2} \left( { - \ln \mu_{112} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\omega_{1} \left( { - \ln \mu_{121} } \right)^{\delta } + \omega_{2} \left( { - \ln \mu_{122} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} , \hfill \\ e^{{ - \left( {\omega_{1} \left( { - \ln \mu_{131} } \right)^{\delta } + \omega_{2} \left( { - \ln \mu_{132} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} \hfill \\ \end{gathered} \right), \hfill \\ \left( \begin{gathered} e^{{ - \left( {\omega_{1} \left( { - \ln \mu_{211} } \right)^{\delta } + \omega_{2} \left( { - \ln \mu_{212} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\omega_{1} \left( { - \ln \mu_{221} } \right)^{\delta } + \omega_{2} \left( { - \ln \mu_{222} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} , \hfill \\ e^{{ - \left( {\omega_{1} \left( { - \ln \mu_{231} } \right)^{\delta } + \omega_{2} \left( { - \ln \mu_{232} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} \hfill \\ \end{gathered} \right), \hfill \\ \left( \begin{gathered} e^{{ - \left( {\omega_{1} \left( { - \ln \mu_{311} } \right)^{\delta } + \omega_{2} \left( { - \ln \mu_{312} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\omega_{1} \left( { - \ln \mu_{321} } \right)^{\delta } + \omega_{2} \left( { - \ln \mu_{322} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} , \hfill \\ e^{{ - \left( {\omega_{1} \left( { - \ln \mu_{331} } \right)^{\delta } + \omega_{2} \left( { - \ln \mu_{332} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right) \hfill \\ = \left( \begin{gathered} \left( {e^{{ - \left( {\sum\limits_{i = 1}^{2} {w_{i} \left( { - \ln \mu_{11i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{2} {w_{i} \left( { - \ln \mu_{12i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{2} {w_{i} \left( { - \ln \mu_{13i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \left( {e^{{ - \left( {\sum\limits_{i = 1}^{2} {w_{i} \left( { - \ln \mu_{21i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{2} {w_{i} \left( { - \ln \mu_{22i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{2} {w_{i} \left( { - \ln \mu_{23i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \left( {e^{{ - \left( {\sum\limits_{i = 1}^{2} {w_{i} \left( { - \ln \mu_{31i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{2} {w_{i} \left( { - \ln \mu_{32i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{2} {w_{i} \left( { - \ln \mu_{33i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \end{gathered} \right). \hfill \\ \end{gathered} $$ -
(b)
Suppose \(n = m\), then we have
\(\begin{gathered} RNAAWGA\left( {R\left( {\tilde{B}_{1} } \right),R\left( {\tilde{B}_{2} } \right),...,R\left( {\tilde{B}_{m} } \right)} \right) \hfill \\ = \left( \begin{gathered} \left( {e^{{ - \left( {\sum\limits_{i = 1}^{m} {w_{i} \left( { - \ln \mu_{11i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{m} {w_{i} \left( { - \ln \mu_{12i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{m} {w_{i} \left( { - \ln \mu_{13i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \left( {e^{{ - \left( {\sum\limits_{i = 1}^{m} {w_{i} \left( { - \ln \mu_{21i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{m} {w_{i} \left( { - \ln \mu_{22i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{m} {w_{i} \left( { - \ln \mu_{23i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \left( {e^{{ - \left( {\sum\limits_{i = 1}^{m} {w_{i} \left( { - \ln \mu_{31i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{m} {w_{i} \left( { - \ln \mu_{32i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{i = 1}^{m} {w_{i} \left( { - \ln \mu_{33i} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered}\) .
-
(c)
Suppose \(n = m + 1\), then we have
$$ \begin{gathered} RNAAWGA\left( {R\left( {\tilde{B}_{1} } \right),R\left( {\tilde{B}_{2} } \right),...,R\left( {\tilde{B}_{{m + 1}} } \right)} \right) \hfill \\ = \left( \begin{gathered} \left( {e^{{ - \left( {\sum\limits_{{i = 1}}^{m} {w_{i} \left( { - \ln \mu _{{11i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{m} {w_{i} \left( { - \ln \mu _{{12i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{m} {w_{i} \left( { - \ln \mu _{{13i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \left( {e^{{ - \left( {\sum\limits_{{i = 1}}^{m} {w_{i} \left( { - \ln \mu _{{21i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{m} {w_{i} \left( { - \ln \mu _{{22i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{m} {w_{i} \left( { - \ln \mu _{{23i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \left( {e^{{ - \left( {\sum\limits_{{i = 1}}^{m} {w_{i} \left( { - \ln \mu _{{31i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{m} {w_{i} \left( { - \ln \mu _{{32i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{m} {w_{i} \left( { - \ln \mu _{{33i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \end{gathered} \right) \hfill \\ {\text{ }} \otimes \left( \begin{gathered} \left( {e^{{ - \left( {\left( { - \ln \mu _{{11m + 1}} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\left( { - \ln \mu _{{11m + 1}} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\left( { - \ln \mu _{{11m + 1}} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right), \hfill \\ \left( {e^{{ - \left( {\left( { - \ln \mu _{{21m + 1}} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\left( { - \ln \mu _{{22m + 1}} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\left( { - \ln \mu _{{11m + 1}} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right), \hfill \\ \left( {e^{{ - \left( {\left( { - \ln \mu _{{31m + 1}} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\left( { - \ln \mu _{{32m + 1}} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\left( { - \ln \mu _{{11m + 1}} } \right)^{\delta } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \end{gathered} \right) \hfill \\ = \left( \begin{gathered} \left( {e^{{ - \left( {\sum\limits_{{i = 1}}^{{m + 1}} {w_{i} \left( { - \ln \mu _{{11i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{{m + 1}} {w_{i} \left( { - \ln \mu _{{12i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{{m + 1}} {w_{i} \left( { - \ln \mu _{{13i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \left( {e^{{ - \left( {\sum\limits_{{i = 1}}^{{m + 1}} {w_{i} \left( { - \ln \mu _{{21i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{{m + 1}} {w_{i} \left( { - \ln \mu _{{22i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{{m + 1}} {w_{i} \left( { - \ln \mu _{{23i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \left( {e^{{ - \left( {\sum\limits_{{i = 1}}^{{m + 1}} {w_{i} \left( { - \ln \mu _{{31i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{{m + 1}} {w_{i} \left( { - \ln \mu _{{32i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} ,e^{{ - \left( {\sum\limits_{{i = 1}}^{{m + 1}} {w_{i} \left( { - \ln \mu _{{33i}} } \right)^{\delta } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} }} } \right) \hfill \\ \end{gathered} \right). \hfill \\ \end{gathered} $$
From the above (a), (b), and (c), we can get that Theorem 1 is holds for all \(n\).
Theorem 2
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be a collection of R-numbers. And \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right) = R\left( {\tilde{B}} \right) =\)
\(\left( {\left( {\mu_{11} ,\mu_{12} ,\mu_{13} } \right),\left( {\mu_{21} ,\mu_{22} ,\mu_{23} } \right),\left( {\mu_{31} ,\mu_{32} ,\mu_{33} } \right)} \right)\), then
This property is called Idempotency Property.
Proof
Since \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right) = R\left( {\tilde{B}} \right) =\)
\(\left( {\left( {\mu_{11} ,\mu_{12} ,\mu_{13} } \right),\left( {\mu_{21} ,\mu_{22} ,\mu_{23} } \right),\left( {\mu_{31} ,\mu_{32} ,\mu_{33} } \right)} \right)\), then we have
Therefore, \(RNAAWGA\left( {R\left( {\tilde{B}_{1} } \right),R\left( {\tilde{B}_{2} } \right),...,R\left( {\tilde{B}_{n} } \right)} \right) = R\left( {\tilde{B}} \right)\).
Theorem 3
For \(n\) R-numbers \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\), and.
\(R\left( {\tilde{B}_{i} } \right)^{ + } = \left( \begin{gathered} \left( {\mathop {\max }\limits_{i} \left\{ {\mu_{11i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{12i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{13i} } \right\}} \right), \hfill \\ \left( {\mathop {\max }\limits_{i} \left\{ {\mu_{21i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{22i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{23i} } \right\}} \right), \hfill \\ \left( {\mathop {\max }\limits_{i} \left\{ {\mu_{31i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{32i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{33i} } \right\}} \right) \hfill \\ \end{gathered} \right)\), we have
This property is called Boundedness Property.
Proof
Clearly, we can get \(R\left( {\tilde{B}_{i} } \right)^{ - } \le R\left( {\tilde{B}_{i} } \right) \le R\left( {\tilde{B}_{i} } \right)^{ + }\). Thus based on Theorems 1 and 2, we have.
Theorem 4:
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\).
\(\left( {i = 1,2,...,n} \right)\) be two collection of R-numbers and \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). If \(\mu_{11i} \le \mu^{\prime}_{11i} ,\)\(\mu_{12i} \le \mu^{\prime}_{12i} ,\)\(\mu_{13i} \le \mu^{\prime}_{13i} ,\)\(\mu_{21i} \le \mu^{\prime}_{21i} ,\)\(\mu_{22i} \le \mu^{\prime}_{22i} ,\)\(\mu_{23i} \le \mu^{\prime}_{23i} ,\) \(\mu_{31i} \le \mu^{\prime}_{31i} ,\) \(\mu_{32i} \le \mu^{\prime}_{32i} ,\)\(\mu_{33i} \le \mu^{\prime}_{33i}\), then
This property is called Monotonicity Property.
Proof
The above theorem obviously holds.
Theorem 5
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\).
\(\left( {i = 1,2,...,n} \right)\) be two collection of R-numbers and \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\), \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\), and \(R\left( {\tilde{B}^{\prime}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be any permutation of \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\). Then
This property is called Commutativity Property.
Proof
Based on the Definition 8, we have
4.2 R-Number Aczel–Alsina Ordered Weighted Geometric Averaging Operator
This part proposes the R-number Aczel–Alsina ordered weighted geometric averaging (RNAAOWGA) operator based on the operations of Definition 8.
Definition 10
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be a collection of R-numbers, \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). Then the R-number Aczel–Alsina ordered weighted geometric averaging (RNAAOWGA) operator is defined as.
where \(\left( {\tau \left( 1 \right),\tau \left( 2 \right),...,\tau \left( n \right)} \right)\) are the permutation in such a way as \(R\left( {\tilde{B}_{\tau \left( i \right)} } \right) \le R\left( {\tilde{B}_{{\tau \left( {i - 1} \right)}} } \right)\).
Theorem 6
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be a collection of R-numbers, \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). Then the aggregated value by the RNAAOWGA operator is still a R-number and.
where
and \(\left( {\tau \left( 1 \right),\tau \left( 2 \right),...,\tau \left( n \right)} \right)\) are the permutation in such a way as \(R\left( {\tilde{B}_{\tau \left( i \right)} } \right) \le R\left( {\tilde{B}_{{\tau \left( {i - 1} \right)}} } \right)\).
Based on a similar verification of Theorem 1, Theorem 6 can be easily proved and will not be repeated here.
Theorem 7
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be a collection of R-numbers. And \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right) = R\left( {\tilde{B}} \right) =\)
\(\left( {\left( {\mu_{11} ,\mu_{12} ,\mu_{13} } \right),\left( {\mu_{21} ,\mu_{22} ,\mu_{23} } \right),\left( {\mu_{31} ,\mu_{32} ,\mu_{33} } \right)} \right)\), then
This property is called Idempotency Property.
Theorem 8
For \(n\) R-numbers \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) and
\(R\left( {\tilde{B}_{i} } \right)^{ + } = \left( \begin{gathered} \left( {\mathop {\max }\limits_{i} \left\{ {\mu_{11i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{12i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{13i} } \right\}} \right), \hfill \\ \left( {\mathop {\max }\limits_{i} \left\{ {\mu_{21i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{22i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{23i} } \right\}} \right), \hfill \\ \left( {\mathop {\max }\limits_{i} \left\{ {\mu_{31i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{32i} } \right\},\mathop {\max }\limits_{i} \left\{ {\mu_{33i} } \right\}} \right) \hfill \\ \end{gathered} \right)\), we have
This property is called Boundedness Property.
Theorem 9:
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\).
\(\left( {i = 1,2,...,n} \right)\) be two collection of R-numbers and \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). If \(\mu_{11i} \le \mu^{\prime}_{11i} ,\)\(\mu_{12i} \le \mu^{\prime}_{12i} ,\)\(\mu_{13i} \le \mu^{\prime}_{13i} ,\)\(\mu_{21i} \le \mu^{\prime}_{21i} ,\)\(\mu_{22i} \le \mu^{\prime}_{22i} ,\)\(\mu_{23i} \le \mu^{\prime}_{23i} ,\) \(\mu_{31i} \le \mu^{\prime}_{31i} ,\) \(\mu_{32i} \le \mu^{\prime}_{32i} ,\)\(\mu_{33i} \le \mu^{\prime}_{33i}\), then
This property is called Monotonicity Property.
Theorem 10
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\).
\(\left( {i = 1,2,...,n} \right)\) be two collection of R-numbers and \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\), \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\), and \(R\left( {\tilde{B}^{\prime}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be any permutation of \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\). Then
This property is called Commutativity Property.
Theorems 7–10 can be proved easily according to a similar proof method of Theorems 2–5, which is not stated here.
4.3 R-Number Hybrid Aczel–Alsina Ordered Weighted Geometric Averaging Operator
This part proposes the R-number Aczel–Alsina hybrid weighted geometric averaging (RNAAHWGA) operator based on the operations of Definition 8.
Definition 11
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be a collection of R-numbers, \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). Then the R-number Aczel–Alsina hybrid weighted geometric averaging (RNAAHWGA) operator is defined as.
where \(\psi = \left( {\psi_{1} ,\psi_{2} ,...,\psi_{n} } \right)^{T}\) is the weight vector associated with the RNAAHWGA operator, with \(\psi_{i} \in \left[ {0,1} \right]\left( {i = 1,2,...,n} \right)\) and \(\sum\nolimits_{i = 1}^{n} {\psi_{i} } = 1\); \(R\left( {\tilde{B}_{i}^{*} } \right) = nw_{i} R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\), and \(\left( {R\left( {\tilde{B}_{\tau \left( 1 \right)}^{*} } \right),R\left( {\tilde{B}_{\tau \left( 2 \right)}^{*} } \right),...,R\left( {\tilde{B}_{\tau \left( n \right)}^{*} } \right)} \right)\) is any permutation of the weighted R-number \(\left( {R\left( {\tilde{B}_{1}^{*} } \right),R\left( {\tilde{B}_{2}^{*} } \right),...,R\left( {\tilde{B}_{n}^{*} } \right)} \right)\), such that \(R\left( {\tilde{B}_{\tau \left( i \right)}^{*} } \right) \le R\left( {\tilde{B}_{{\tau \left( {i - 1} \right)}}^{*} } \right)\).
Theorem 11
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be a collection of R-numbers, \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). Then the aggregated value by the RNAAHWGA operator is still a R-number and
where
and \(\psi = \left( {\psi_{1} ,\psi_{2} ,...,\psi_{n} } \right)^{T}\) is the weighting vector associated with the RNAAHWGA operator, with \(\psi_{i} \in \left[ {0,1} \right]\left( {i = 1,2,...,n} \right)\) and \(\sum\nolimits_{i = 1}^{n} {\psi_{i} } = 1\); \(R\left( {\tilde{B}_{i}^{*} } \right) = nw_{i} R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\), and \(\left( {R\left( {\tilde{B}_{\tau \left( 1 \right)}^{*} } \right),R\left( {\tilde{B}_{\tau \left( 2 \right)}^{*} } \right),...,R\left( {\tilde{B}_{\tau \left( n \right)}^{*} } \right)} \right)\) is any permutation of the weighted R-number \(\left( {R\left( {\tilde{B}_{1}^{*} } \right),R\left( {\tilde{B}_{2}^{*} } \right),...,R\left( {\tilde{B}_{n}^{*} } \right)} \right)\), such that \(R\left( {\tilde{B}_{\tau \left( i \right)}^{*} } \right) \le R\left( {\tilde{B}_{{\tau \left( {i - 1} \right)}}^{*} } \right)\).
Based on a similar verification of Theorem 1, Theorem 11 can be easily proved and will not be repeated here.
Theorem 12
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be a collection of R-numbers. And \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right) = R\left( {\tilde{B}} \right) =\)
\(\left( {\left( {\mu_{11} ,\mu_{12} ,\mu_{13} } \right),\left( {\mu_{21} ,\mu_{22} ,\mu_{23} } \right),\left( {\mu_{31} ,\mu_{32} ,\mu_{33} } \right)} \right)\), then
This property is called Idempotency Property.
Theorem 13
For \(n\) R-numbers \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) and
This property is called Boundedness Property.
Theorem 14:
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\).
\(\left( {i = 1,2,...,n} \right)\) be two collection of R-numbers and \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). If \(\mu_{11i} \le \mu^{\prime}_{11i} ,\)\(\mu_{12i} \le \mu^{\prime}_{12i} ,\)\(\mu_{13i} \le \mu^{\prime}_{13i} ,\)\(\mu_{21i} \le \mu^{\prime}_{21i} ,\)\(\mu_{22i} \le \mu^{\prime}_{22i} ,\)\(\mu_{23i} \le \mu^{\prime}_{23i} ,\) \(\mu_{31i} \le \mu^{\prime}_{31i} ,\) \(\mu_{32i} \le \mu^{\prime}_{32i} ,\)\(\mu_{33i} \le \mu^{\prime}_{33i}\), then
This property is called Monotonicity Property.
Theorem 15
Let \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\).
\(\left( {i = 1,2,...,n} \right)\) be two collection of R-numbers and \(w = \left( {w_{1} ,w_{2} ,...,w_{n} } \right)^{T}\) be the weight vector of \(R\left( {\tilde{B}_{i} } \right)\) and \(R\left( {\tilde{B}_{i}^{\prime } } \right)\), satisfying \(w_{i} \in \left[ {0,1} \right]\), \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\), and \(R\left( {\tilde{B}^{\prime}_{i} } \right)\left( {i = 1,2,...,n} \right)\) be any permutation of \(R\left( {\tilde{B}_{i} } \right)\left( {i = 1,2,...,n} \right)\). Then
This property is called Commutativity Property.
Theorems 12–15 can be proved easily according to a similar proof method of Theorems 2–5, which is not stated here.
5 Decision Support Algorithm
The core idea of MARICA is to choose the lowest gap between ideal and empirical ponder. The total gap for each alternative is determined by summing the gaps between the ideal and empirical ponder of the alternatives under each criteria. Then rank the total gap of alternatives. The optimal alternative is the one with the lowest total gap value. This section extends the MARICA method to the R-number MAGDM environment based on the R-number geometric aggregation operator in Sect. 4. The specific RN-MARICA method is implemented through the following steps, and the decision-making process is shown in Fig. 3.
Step 1. Construct initial decision matrix and weight matrix according to the following equation.

where \(m\) is the number of alternatives \(A_{1} ,A_{2} ,...,A_{m}\); \(n\) is the number of decision criteria \(C_{1} ,C_{2} ,...,C_{n}\); \(\tilde{s}_{mn}^{k}\) is the value of the \(n\) criteria in; \(\tilde{D}_{k}\) is in the form of triangular fuzzy number, corresponding to \(kth\) decision maker; \(\tilde{W}\) is the weight vector of criteria; \(\tilde{V}\) is the weight vector of decision makers.
Step 2. Convert the fuzzy number to R-number.
In the RN-MARICA method proposed in this paper, the values of risk parameters are given by decision makers, namely pessimistic risk \(\tilde{r}^{ - }\), optimistic risk \(\tilde{r}^{ + }\), pessimistic acceptable risk \(\widetilde{AR}^{ - }\), optimistic acceptable risk \(\widetilde{AR}^{ + }\), pessimistic risk perception \(\widetilde{RP}^{ - }\), optimistic risk perception \(\widetilde{RP}^{ + }\). According to the R-number definition, convert the initial decision matrix to the form of R-number.
where \(s_{ij}^{k} = R\left( {s_{ij}^{k} } \right) = \left( \begin{gathered} \left( {s_{ij11}^{k} ,s_{ij12}^{k} ,s_{ij13}^{k} } \right), \hfill \\ \left( {s_{ij21}^{k} ,s_{ij22}^{k} ,s_{ij23}^{k} } \right), \hfill \\ \left( {s_{ij31}^{k} ,s_{ij32}^{k} ,s_{ij33}^{k} } \right) \hfill \\ \end{gathered} \right),i = 1,2, \ldots ,m,j = 1,2, \ldots ,n.\)
The beneficial and non-beneficial modes are as follows, respectively:
\(R_{b} \left( {\tilde{s}_{ij}^{k} } \right) = \left( {R_{1b} \left( {\tilde{s}_{ij}^{k} } \right),R_{2b} \left( {\tilde{s}_{ij}^{k} } \right),R_{3b} \left( {\tilde{s}_{ij}^{k} } \right)} \right),\) where
and \(R_{c} \left( {\tilde{s}_{ij}^{k} } \right) = \left( {R_{1c} \left( {\tilde{s}_{ij}^{k} } \right),R_{2c} \left( {\tilde{s}_{ij}^{k} } \right),R_{3c} \left( {\tilde{s}_{ij}^{k} } \right)} \right),\) where
Step 3. Aggregate the R-number matrix \(R^{k} \left( {k = 1,2,...,K} \right)\) to get \(R_{{}}^{T}\).
Aggregate decision makers’ uncertain data \(R^{k} \left( {k = 1,2,...,K} \right)\) with the proposed R-number Aczel–Alsina geometric operators in Sect. 4.
Step 3(a). Use RNAAWGA operator to aggregate.
Step 3(b). Use RNAAOWGA operator to aggregate.
Step 3(c). Use RNAAHWGA operator to aggregate.
The aggregated matrix \(R_{{}}^{T}\) is as followed.
where
Step 4. Determine the preference based on the \(P_{{A_{i} }}\) choice of alternatives. If the decision makers are neutral, the decision makers have no choice preference based on alternatives. Then each alternative occurs with equal probability.
where \(m\) is the number of alternatives.
Step 5. Determine the theoretical ponder matrix \(T_{P}\).
where \(n\) is the number of criteria.
Step 6. Determine the actual ponder matrix \(T_{r}\).
For the criteria is beneficial type.
For the criteria is non-beneficial type.
Step 7. Calculate the total gap matrix \(G\).
where
Step 8. Calculate the final values of the criterion functions \(Q_{i}\).
Step 9. Defuzzify \(Q_{i}\) using the defuzzification operation of R-number of Eq. 9 to get \(COA\left( {Q_{i} } \right)\left( {i = 1,2,...m,j = 1,2,...,n} \right)\). Then rank the alternatives according to \(COA\left( {Q_{i} } \right)\). The optimal alternative is the minimum value of \(COA\left( {Q_{i} } \right)\).
6 Case Study
In this section, an example is used to illustrate the feasibility of the RN-MARICA method proposed in Sect. 5. The proposed algorithm can be used for risk assessment of the fifth generation mobile communication technology (5G) base station construction project.
Compared with 4G, 5G has the characteristics of higher speed, wider bandwidth, higher reliability, and lower latency, which can meet the needs of users and industries such as virtual reality, ultra-high-definition video, intelligent manufacturing, and autonomous driving in the future. application requirements. 5G base station is the core equipment of 5G network, which provides wireless coverage and realizes wireless signal transmission between wired communication network and wireless terminals. Since the commercialization of 5G in China in June 2019, China's basic telecom operators have adhered to the principle of overall planning and moderate advance, and promoted joint construction and sharing, so that 5G network construction can be faster and more efficient. According to the latest statistics from the Ministry of Industry and Information Technology, by the end of April 2022, China had built 1.615 million 5G base stations, becoming the first country in the world to build a 5G network on a scale based on an independent networking model.
The risk management of 5G base station construction projects has become a difficult problem to consider in project construction. There are many methods of risk management research, and the FMEA method is the most practical method. It calculates the risk priority number (\(RPN\)) of failure occurrence factors such as Severity (\(S\)), Occurrence (\(O\)), and Detection (\(D\)). Then according to the value of the RPN, it is judged whether improvement is needed or the priority of improvement is determined, so as to reduce the subsequent loss at a lower cost and improve the reliability of the system.
The R-number has a huge advantage in capturing risk and can improve the reliability of decision-making. Therefore, this paper uses the evaluation indicators Severity (\(S\)), Occurrence (\(O\)), and Detection (\(D\)) of FMEA, and uses the proposed RN-MARICA method to sort the risk indicators of 5G base station construction projects to evaluate the risks of 5G communication construction projects with pointing out the direction for project risk control. The risk assessment indicators of 5G base station project construction are shown in Table 1. Table ***shows the fuzzy assessments of the different risk indicators under each risk criterion by three experts, the assessments were performed using Table 2. Due to the uncertainty of the expert evaluation, Table 3 is used to evaluate the pessimistic risk \(\tilde{r}^{ - }\), optimistic risk \(\tilde{r}^{ + }\), pessimistic acceptable risk \(\widetilde{AR}^{ - }\), and optimistic acceptable risk \(\widetilde{AR}^{ + }\) in the expert evaluation. Due to the risk perception in expert assessment, suitable \(\widetilde{RP}\) were considered according to Table 4, where positive risk perception and negative risk perception were considered to be the same, i.e., \(\widetilde{RP}^{ + } = \widetilde{RP}^{ - }\).
Step 1. Table 5 presents the language assessment information of the three experts. The criteria weight vector is \(\tilde{W} = \left[ {{0}{\text{.4 }}0.2{ 0}{\text{.4}}} \right]\) The expert weight vector is \(\tilde{V} = \left[ {{0}{\text{.4 }}0.3{ 0}{\text{.3}}} \right]\).
Step 2. Table 5 also gives the three experts' language assessment information about pessimistic risk \(\tilde{r}^{ - }\), optimistic risk \(\tilde{r}^{ + }\), pessimistic acceptable risk \(\widetilde{AR}^{ - }\), optimistic acceptable risk \(\widetilde{AR}^{ + }\), pessimistic risk perception \(\widetilde{RP}^{ - }\), optimistic risk perception \(\widetilde{RP}^{ + }\). Since this case is an assessment of risk, the pessimistic acceptable risk and the optimistic acceptable risk are identified as 0. The given risk parameter linguistic terms is converted into the form of triangular fuzzy number using Tables 2, 3, and 4, and the conversion result is shown in Table 6.
According to the definition of R-number, convert the data in Table 6 into the form of R-number, as shown in Table 7.
Step 3. The R-number matrix is aggregated with three aggregated operators, respectively, namely RNAAWGA, RNAAOWGA, RNAAHWGA, and the results are shown in Table 8 (Noted that we assume \(\delta = 1\)).
Step 4. Determine the preference based on the \(P_{{A_{i} }}\) choice of alternatives.
Step 5. Determine the theoretical ponder matrix \(T_{P}\) in the form of R-number.
Step 6. Since the three criteria S, O, D are all non-beneficial criteria, determine the actual ponder matrix \(T_{r}\) as shown in Table 9.
Step 7. Calculate the total gap matrix \(G\) as shown in Table 10.
Step 8. Calculate the final values of the criterion functions \(Q_{i}\) as shown in Table 11.
Step 9. Defuzzify \(Q_{i}\) using the defuzzification operation of R-number of Eq. 9 to get \(COA\left( {Q_{i} } \right)\left( {i = 1,2,...m,j = 1,2,...,n} \right)\). Then rank the alternatives according to \(COA\left( {Q_{i} } \right)\). The optimal alternative is the minimum value of \(COA\left( {Q_{i} } \right)\), which is the alternative Q61 (Construction safety). The results are shown in Table 11.
To sum up, according to the RN-MARICA method proposed in Sect. 4 to analyze the risk indicators of 5G base station construction projects, it can be concluded that Q61 (Construction safety) is the key risk indicator and should be paid attention to.
7 Sensitivity Analysis
In this section, we apply the proposed method RN-MARICA to score and rank alternatives by varying different parameter values \(\delta\) to highlight the effect of the size of parameter \(\delta\). Table 12 shows the results obtained by changing different parameter values \(\delta\) using different RNAAWGA, RNAAOWGA, and RNAAHWGA operators. In addition, we can see in Table 12 that even if the value of parameter \(\delta\) is changed in the operation, the optimal alternatives obtained are the same, but for individual parameter values, the optimal solution is Q61, but Q23 is still in the second position. This proves the consistency of the proposed RNAAWGA, RNAAOWGA, and RNAAHWA operators.
Figures 4, 5, and 6 gives a graphical representation of the effect of parameter values using different aggregation operators, respectively. It can be clearly seen from the figure that as the parameter value increases, the calculated score value becomes smaller, but the ranking changes for different alternatives are basically unchanged.
8 Comparative Analysis
To illustrate the effectiveness of the RN-MAICA method mentioned in this paper. In this section, the existing methods R-TOPSIS [10], R-SAW [9], R-VIKOR [12] method and the proposed RN-MARICA method are compared and calculated for the cases in Sect. 5. The results of the comparative calculations are shown in Table 13.
As can be seen from Table 13, no matter which decision-making method is adopted, the ranking of Q61 (Construction safety) occupies the first place. Therefore, among the 17 risk indicators of 5G base station construction projects determined, Q61 (Construction safety) is a key risk indicator for 5G base station construction projects, which should be paid attention to. Figure 7 also gives a more intuitive description of the comparison results. Furthermore, it can also be concluded that the RN-MARICA method proposed in this paper is effective.
In order to verify the reliability of the final results, we calculate Spearman’s rank correlation coefficient on the ranking results obtained by applying different methods. Spearman’s rank correlation coefficient was used to illustrate the significance of the differences between the rankings produced by different methods in the case studies. According to Table 14, it is observed that all the correlation coefficients are higher than 0.70, and the average value is 0.7910, which means that there is a strong correlation between the existing MADM method and the proposed RN-MARICA method.
9 Conclusion
In the study of fuzzy numbers, the study of aggregation operators has always been the focus and difficulty of researchers. In this paper, we define three R-number geometric mean operators, namely RNAAWGA operator, RNAAOWGA operator, and RNAAHWGA operator. And their related properties were studied. Based on these aggregation operators, we propose the MARICA method in the context of R-number. Finally, a risk analysis of a 5G base station construction project is given to illustrate the feasibility of the proposed RN-MARICA method.
The RN-MARICA method proposed in this study has several advantages in modeling. First, the concepts of the theoretical ponder matrix and the actual ponder are defined, taking into account decision makers' preferences for alternatives. Secondly, this method omits many calculation formulas and simplifies the entire mathematical calculation process. Therefore, the method has greater scalability in practical applications. However, this study also has some shortcomings: (1) The gap between the theoretical ponder matrix and the actual ponder of the MARICA method is calculated by simple subtraction, and this calculation method is too ideal; (2) The preferences determined in the method proposed in this paper assume that decision makers are neutral, but in practical applications, decision makers may not be neutral due to personal experience preferences, and preferences no longer occur with equal probability. This situation requires a more nuanced solution; (3) This research only gives 5G base station construction projects FMEA analysis, more application cases need to be expanded.
Here are some areas worth exploring in the future: (1) Using other kinds of fuzzy numbers (such as picture fuzzy sets, Z-numbers, fermatean fuzzy sets, cognitive fuzzy sets, volume fuzzy sets) in the MARICA method to create theoretical ponder matrix and the actual ponder matrix; (2) Using other different aggregation operators (interactive ensemble operator, Dombi ensemble operator, Bonferroni ensemble operator, Hamacher ensemble operator) to aggregate the expert opinion matrix values in the RN-MARICA method; (3) Researching other MAGDM methods for R-number; (4) Looking for the extension of RN-MARICA method to more application fields.
References
Atanassov, K.T.: Intuitionistic fuzzy sets. Fuzzy Set Syst. 20(1), 87–96 (1986)
Yager, R.R.: Pythagorean membership grades in multi-criteria decision making. IEEE Trans. Fuzzy Syst. 22(4), 958–965 (2014)
Smărăndache, F.: Neutrosophic probability, set and logic. Bull. Transilv. Univ. Braov. Ser. B 41–48 (2016)
Cuong, B.C., Kreinovich, V.: Picture fuzzy sets—a new concept for computational intelligence problems. In: Information & Communication Technologies. IEEE (2015).
Mahmood, T., Ullah, K., Khan, Q., et al.: An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 31(11):7041–7053 (2019).
Senapti, T., Yager, R.R.: Fermatean fuzzy sets. J. Amb. Intel. Hum. Comput. 663–774 (2020).
Jiang, L.S., Liao, H.C.: Cognitive fuzzy sets for decision making. Appl. Soft Comput. 93 (2020). https://doi.org/10.1016/j.asoc.2020.106374.
Arman, H.: Volumetric fuzzy set and its application in optimization problems. Int. J. Intell. Syst. 36(7), 3613–3639 (2021)
Seiti, H., Hafezalkotob, A., Martinez, L.: R-numbers, a new risk modeling associated with fuzzy numbers and its application to decision making. Inform Sci. 483, 206–231 (2019)
Seiti, H., Hafezalkotob, A.: Developing the R-TOPSIS methodology for riskbased preventive maintenance planning: a case study in rolling mill company. Comput. Ind. Eng. 128, 622–636 (2019)
Seiti, H., Fathi, M., Hafezalkotob, A., et al.: Developing the modified R-numbers for risk-based fuzzy information fusion and its application to failure modes, effects, and system resilience analysis (FMESRA). ISA Trans. 113, 9–27 (2021)
Mousavi, S.A., Seiti, H., Hafezalkotob, A., et al.: Application of risk-based fuzzy decision support systems in new product development: an R-VIKOR approach. Appl. Soft Comput. 109 (2021).
Liu, P.D., Zhu, B.Y., Seiti, H., et al.: Risk-based decision framework based on R-numbers and best-worst method and its application to research and development project selection. Inform. Sci. 571, 303–322 (2021)
Filev, D., Yager, R.R.: Analytic properties of maximum entropy OWA operators. Comput. Int. Eng. 85(1–3), 11–27 (1995)
Yager, R.R.: On generalized Bonferroni mean operators for multi-criteria aggregation. Int. J. Approx. Reason. 50(8), 1279–1286 (2009)
Wang, W., Liu, X.: Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. Int. J. Intell. Syst. 26(11), 1049–1075 (2011)
Huang, J.Y.: Intuitionistic fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 27(1), 505–513 (2014)
Qin, J.D., Liu, X.W.: An approach to intuitionistic fuzzy multiple attribute decision making based on Maclaurin symmetric mean operators. J. Intell. Fuzzy Syst. 27(5), 2177–2190 (2014)
Liu, P.D., Liu, J.L., Chen, S.M.: Some intuitionistic fuzzy Dombi Bonferroni mean operators and their application to multi-attribute group decision making. J. Oper. Res. Soc. 69(1), 1–24 (2018)
Li, Z.X., Gao, H., Wei, G.W.: Methods for multiple attribute group decision making based on Intuitionistic fuzzy Dombi Hamy mean operators. Symmetry-Basel 10(11) (2018).
Aczél, J., Alsina, C.: Characterizations of some classes of quasilinear functions with applications to triangular norms and to synthesizing judgements. Aequ. Math. 25(1), 313–315 (1982)
Senapati, T., Chen, G.Y., Yager, R.R.: Aczel-Alsina aggregation operators and their application to intuitionistic fuzzy multiple attribute decision making. Int. J. Intell. Syst. 37(2), 1529–1551 (2022)
Senapati, T., Chen, G.Y., Mesiar, R., et al.: Novel Aczel-Alsina operations-based interval-valued intuitionistic fuzzy aggregation operators and their applications in multiple attribute decision-making process. Int. J. Intell. Syst. (2021). https://doi.org/10.1002/int.22751
Senapati, T.: Approaches to multi-attribute decision-making based on picture fuzzy Aczel–Alsina average aggregation operators. Comput. Appl. Math. 2022;41(1).
Naeem, M., Khan, Y., Ashraf, S., et al.: A novel picture fuzzy Aczel-Alsina geometric aggregation information: application to determining the factors affecting mango crops. AIMS Math. 7(7), 12264–12288 (2022)
Ye, J., Du, S.G., Yong, R.: Aczel-Alsina weighted aggregation operators of neutrosophic Z-numbers and their multiple attribute decision-making method. Int. J. Fuzzy Syst. (2022). https://doi.org/10.1007/s40815-022-01289-w
Hussain, A., Ullah, K., Yang, M.S., et al.: Aczel-Alsina aggregation operators on T-Spherical fuzzy (TSF) information with application to TSF multi-attribute decision making. IEEE Access. 10, 26011–26023 (2022)
Saaty, T.L.: Decision making with the analytic hierarchy process. Int. J. Ser. Sci. 1(1), 83–98 (2008)
Yoon, K.P., Hwang, C.L.: Multiple attribute decision making: an introduction. Eur. J. Oper. Res. 4(4), 287–288 (1995)
Opricovic, S.: Multicriteria optimization of civil engineering systems. Fac. Civil Eng. Belgrad. 2(1), 5–21 (1998)
Kaklauskas, A., Zavadskas, E.K., Raslanas, S., et al.: Selection of low-e windows in retrofit of public buildings by applying multiple criteria method COPRAS: a Lithuanian case. Energy Build 38(5), 454–462 (2006)
Pamucar, D., Cirovic, G.: The selection of transport and handling resources in logistics centers using Multi-Attributive Border Approximation area Comparison (MABAC). Expert Syst. Appl. 42(6), 3016–3028 (2015)
Keshavarz, G.M., Zavadskas, E.K., Olfat, L.: Multi-criteria inventory classifification using a new method of evaluation based on distance from average solution (EDAS). Informatica-Lithuan 26(3), 435–451 (2015)
Pamuar, D., Vasin, L., Lukovac, V.: Selection of railway level crossings for investing in security equipment using hybrid DEMATEL-MARIC model: application of a new method of multi-criteria decision-making. In: XVI International Scientific-expert Conference on Railways (2014).
Chang, D.Y.: Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 95(3), 649–655 (1996)
Mendel, J.M.: Type-2 fuzzy sets and systems: an overview. IEEE Comput. Intell. Mag. 2(2), 20–29 (2007)
Balezentis, T., Zeng, S.Z.: Group multi-criteria decision making based upon interval-valued fuzzy numbers: an extension of the MULTIMOORA method. Expert Syst. Appl. 40(2), 543–550 (2013)
Funding
Funding was provided by Shanxi “1331 Project” Key Innovative Research Team, and “The Discipline Group Construction Plan for Serving Industries Innovation”, Shanxi, China: The Discipline Group Program of Intelligent Logistics Management for Serving Industries Innovation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Cheng, R., Fan, J. & Wu, M. An Extended R-Number MARICA Fuzzy Method with Aczel–Alsina Operators and Its Application to Risk Analysis of 5G Base Station Construction Project. Int. J. Fuzzy Syst. 25, 684–714 (2023). https://doi.org/10.1007/s40815-022-01396-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40815-022-01396-8