1 Introduction

Location selection problem (LSP) is one of the branches of operations research that aims at reducing costs in industrial sectors. Center’s location selection problem (CLSP) involves selecting a location for one or more centers which needs to take into account the existing constraints and the location of other centers so that a specific goal is optimized. This goal can be transportation costs, covering a wider area of the market, and providing fair service to customers. As such, the facility location problem (FLP) is regarded as a critical issue for public and private companies which in turn, necessitate examining the cost and the distance of demand points in different fields [1].

Set covering problem (SCP) is one of the most common issues in FLP that requires further investigations, particularly in emergency and service facilities. In many coverage problems, customers receive services based on their distance from the service facility. Each customer is able to receive services from the provided facilities where the distance between them is less than a pre-determined value; the value which is called coverage distance [2]. Set covering problem has been applied to solve various problems including practical and non-practical applications such as airline staff scheduling, fire stations layout plan, radar layout plan, police stations layout plan, hospitals, libraries, post offices, delivery points, design and simplification of switch circuits, assembly line balance, vehicle routing, ship scheduling, defense and offensive networks, bus drivers scheduling, information retrieval, production, investment, project selection, traffic allocation in satellite communication systems, calculation of limits in integer programming, computer networks, transportation systems, bioinformatics, etc. [3,4,5,6,7]. Going through the literature indicates that SCP was first introduced by Jain et al. [8] to examine the minimum number of required police wearing the nodes of the highway network. They modeled the problem as a vertex coverage problem in a graph. Regarding studies of location problems, continuous location models, network location, mixed integer programming models and their applications are presented [9, 10]. This study was then proceeded to solve a discrete location problem when facilities are potentially prone to failure [10]. In another study, the location problem was defined regarding uncertainty. A multi-objective location problem solution was also developed based on a meta-heuristic algorithm constructed by tabu search [11]. Subsequently, a new model for locating hazardous waste [12] was proposed. The purpose of this model was to minimize the total cost and risk of transportation. Considering the problem of designing routes for hazardous materials transportation in a densely crowded area, the integer programming method with the function of minimizing transport risk was proposed [13]. Afterward, using a constructive heuristic algorithm, the solution to the tree design problem was developed. A probabilistic coverage location model for perishable and non-perishable items was also presented [14]. In this regard, the effect of goods’ spoilage cost on the issue of location has been also investigated.

From the above discussion, SCP is a NP-hard problem. Researchers have proposed various heuristic algorithms regarding this problem. Optimization models including combinational and multi-objective have been presented for this problem. Different algorithms of ant, tabu, pso, genetic and hybrid have been also applied to deal with the development of these models. Due to the nature of SCP, which is one of the NP-hard problems, this class of problems cannot be solved exactly in real dimensions. Hence, to overcome this issue, a new heuristic algorithm is proposed that can solve the real problem in polynomial time. Meanwhile, to evaluate the efficiency of the proposed algorithm, the simulated annealing (SA) algorithm has been applied to extend its application to the problems in larger dimensions, and the Taguchi method has been used to tune its parameters. Although there are very few polynomial time algorithms that can solve NP-hard problems in polynomial time; there is no polynomial time algorithm to deal with SCP. Hence, the presented algorithm's superiority to the other algorithms is its specified approach for SCP. In other words, the main contribution of this paper is to present a new heuristic algorithm that is not only capable of constructing an answer within polynomial time, but can solve complex SCPs without conventional restrictions that previous studies have applied.

To this end, in the following section, the research background is reviewed. In the third section, the mathematical model of the problem is stated. The fourth and fifth sections cover the SA algorithm and the new proposed heuristic algorithm, respectively. Computational results are accordingly discussed in the sixth section.

2 Literature

A considerable logistic problem appears when there is a set of demands which need to be satisfied with services to be located at many points to supply those demands. This is a renowned problem in operations research, entitled ‘set covering problem’ [15,16,17].

The set covering problem is a well-known optimization problem in the heuristics and mathematical programming literature [18, 19]. In this background, most studies in SCP considered the earlier SCP formulation presented by Lanza-Gutierrez et al. [20] and defined it as follows. If K is a set of n objects and L is a set of m subsets of k where subsets take non-negative cost, then the purpose of SCP is to minimize the cost group of subsets X ⊆ L, in a way that each agent of K belongs to at least one subset of the group X. In addition, early works proposed to solve it using exact methods, which typically count on the branch and bound [21, 22] and branch-and-cut algorithms [23, 24]. However, the main concern is the long time these algorithms take to deal with hard instances. To tackle this concern, recent studies have been mostly focused on the evolvement of new heuristics with the ability to find solutions in a logical time [25]. The greedy randomized adaptive search procedure (GRASP) is a technique that builds a solution through a specified number of steps applying a set of specific rules. Among recent studies pertaining to GRASP, the local search and rewarded procedures [25] has been proposed to improve the solutions discovered by GRASP. The approach had been tested by applying non-unicost SCP benchmark instances from the OR-library, indicating promising results. Traditional greedy algorithms are fast enough for implementation, despite their weakness in producing high-quality solutions due to their deterministic character. For instance, GRASP has been applied by [26] for the set covering problem. The objective of this study was to find a column subset from a zero–one matrix to cover all of the rows with the least possible cost.

Salehipour [27] developed an effective heuristic algorithm applying lower bounds to generate a feasible solution which was obtained through a local search. Nogueira et al. and Hashemi et al. [28, 29] also developed a heuristic local search algorithm for large SCP applying SA. This study used an improvement routine to generate near-optimal solutions within reasonable CPU time. In addition, Chiscop et al. [30] developed a hybrid algorithm for multi-service SCP. This algorithm applied a process that began from an initial seed solution to repetitively create sub-problems to be resolved more efficiently. A configuration checking-based algorithm for SCP [31] was developed to not only consider subset states but also take into account the element states, leading to cutting down the unnecessary search space. Sadeghi et al. [32] developed a simple Lagrangian heuristic algorithm for SCP. This algorithm had an application for low-density with the dimension of 1000 rows and 10,000 columns wherein the density is equal to the ratio of 1 s in the matrix of the coefficients of the model constraints. Later on, Mandal et al. [33] designed an algorithm to indicate the application of SCP in natural disaster management. This algorithm was proposed to find supply vertices for covering sets of fuzzy graphs. In a similar study, Alizadeh and Nishi [34] proposed an algorithm for dynamic modular SCP. In this study, the algorithm applied a fitness function to deal with locating first aid centers in logistic services in Japan. Lorena and de Souza Lopes, Aickelin and Idrees and Al-Yaseen [35,36,37] have applied a Genetic Algorithm (GA) to resolve SCP. Lorena and de Souza Lopes [35] presented a new GA for the SCP. This study applied GA to provide a decoder from which the actual solution was taken. Meanwhile, Aickelin [36] applied a GA-based heuristic for non-unicost SCP which led to a high-quality solution. This heuristic was built based on three developed operators which included a new fitness-based crossover, a variable mutation rate, and a feasibility operator. Idrees and Al-Yaseen [37] implemented a classical GA for computationally difficult SCP. The proposed algorithm tests finally showed an optimal solution for incidence matrices. Aourid and Kaminska and Yang and Rajgopal [38, 39] have developed meta-heuristic algorithms of neural networks to deal with SCP. Aourid and Kaminska [38] proposed a neural network for a large-scale SCP. The network applied connections between nonlinear and integer programming based on concavity and penalty functions. The simulation finally indicated that the system coverage ability was within a few neural times. Applying neural networks, the study of [39] developed a machine learning approach to deal with SCP. This study provided a condition to learn from recorded optimal solutions taken from Machine Learning Problem (MLP) formulation. Vasko and Wolf [40] applied a two-step meta-heuristic algorithm of heuristic concentration (HC). In the first step, various local optimal solutions are proposed, and in the second step, these solutions are used to determine the centralized problem so that this problem is small enough to be solved.

The first mathematical model on the coverage problem was developed by [5] in which the location of emergency service facilities was investigated aiming to minimize the number of laid out facilities [41]. Hwang [42] studied the issue of complementary connecting arcs, which is one of the issues of complementary edge covering problem. This paper presented a new linear integer programming model for the problem. They also suggested a number of reduction rules that increase the speed of achieving the optimal answer. Rajagopalan et al. [43] presented a model for the distribution of relief goods aiming to satisfy the demand in the shortest possible time. Finally, the proposed model in that research was solved with exact and heuristic methods. The results showed that the heuristic method is able to provide high-quality answers compared to exact methods.

Amoaning-Yankson [44] developed a multi-objective programming model in which it provided the possibility of locating temporary warehouse cycles and allocating them to affected areas for the distribution of relief goods. The two main goals of his model were to minimize set-up and relocation costs between supply centers, temporary warehouses, and affected areas; as well as, to maximize the sum of minimum demand ratios covered to ensure fair distribution of goods. In this research, two meta-heuristic algorithms of GA and SA were presented to solve the model which finally, the computational results showed the efficiency of the developed model for practical issues. Mandal et al. [45] presented an efficient algorithm for conditional covering problems. They also proposed the design of algorithms with polynomial time for more complex graphs of structures such as distance graphs and serial and parallel diagrams for future research.

Wang and Qin [46] proposed a new multi-objective imperialist competitive algorithm to solve the stochastic multi-state model. The problem model was the coverage of the hub network, which according to the location of the risk, minimizes the current investment costs and the transportation time between each pair of nodes in the hub network. Murray and Wei [47] also proposed a solution to ensure complete coverage of the area with a minimum number of facilities that eliminates the potential error. Also, to demonstrate the efficiency of the proposed solution, the method mentioned in this study has been developed for the application of emergency alarm sirens and fire station locations. Meanwhile, Hosseininezhad et al. [48] presented a location model of continuous coverage with the risk factor. In this model, the coverage radius and the degree of customer satisfaction with the coverage are defined using the fuzzy concept. This study introduced a method of risk analysis based on the level of response to deal with the model.

Bagherinejad et al. [49] presented a new method for solving the coverage problem. The proposed algorithm for solving the coverage problem was efficient using a reversal method to produce each partial coverage without any non-partial iteration. Meanwhile, Furini et al. [50] proposed several models of the knapsack problem, including the cover problem in which entities must be allocated and the multidimensional knapsack in which the constraint replacement strategy was also used. The proposed model was validated and verified as competitive with former ones. Regarding the issue of coverage aiming to develop the current state of hybrid intelligent technology and meta-heuristic combination with Lagrangian relaxation, Al-Shihabi [51] proposed Greedy Randomized Adaptive Search Procedures (GRASP) and adaptive Lagrangian relaxation heuristic based on sub-gradient optimization to escape local optimization to find better answers. The results indicated that the proposed algorithm on benchmark instances from the literature had the effectiveness of their approach in producing better quality solutions.

Dastmardi et al. [52] emphasized the time of the problem, the seller's coverage, and the positioning of the problem. Meanwhile, they developed an integer linear programming model as a method of improvement and tried to improve the quality of the solution. Bagheri et al. [53] developed a traditional coverage problem model that can disrupt service delivery facilities in disruption situations such as floods and earthquakes. Then, they used the Bee Colony Optimization (BCO) algorithm to solve the proposed problem and validated the algorithm by comparing the results with exact algorithms for small problems. Additionally, Shi et al. [54] proposed a new method for selecting a landmark point within the neighborhood for the weighted coverage problem. As a result of his research, it was shown that the set covering problem can be solved applying the heuristic method based on Lagrangian relaxation with sub-gradient optimization. Meanwhile, Khorsi et al. [55] presented a multi-objective mathematical model to minimize the total time to reach the affected areas. The model was to maximize the satisfaction of the affected areas with higher priority and minimize costs including set-up costs, relocation, and shortages. In this research, to solve this multi-objective model, the Weighted Comprehensive Criterion Method (WCCM) had been applied to the single-purpose model.

Mahrach et al. [56] presented a multi-objective mathematical model that was able to generate all Pareto solutions to multi-objective combination optimization problems including two well-known multi-objective vendor and coverage problems. In another study, Bogue et al. [57] proposed a hybrid algorithm based on the neighborhood search variable and integer programming to solve the vehicle routing problem with a time window. In the proposed algorithm, a combination of a meta-heuristic and exact method was applied. Moreover, among the studies applying integer programming for SCP, the study [58] developed a novel integer programming formulation for the first time wherein the demands and facility locations align with the edges. In order to build acceptable solutions in a logical time, a heuristic algorithm was constructed to add vertices along the edges iteratively and solve a non-complex problem that dismisses non-nodal facility locations. Finally, numerical results indicated that the meta-heuristic algorithm generates good quality solutions in a very short time.

These studies were the most significant research conducted so far on the major model of the SCP. A special case of the original model, considering the same layout cost for all facilities, is also widely applied. Some researchers like [59] who proposed a Surrogate Heuristic (SH) for SCP have focused only on this issue. The conducted investigations of SCP have taken into account the issues with different dimensions which either examined the major model of SCP or a specific mode of the model that considers the layout cost of all facilities. These two modes of the model have the ability to determine the optimal points for the facilities’ layout disregarding the points where the facility is located.

The set covering problem has an exponential complexity and is one of the NP-hard problems [60]. Hence, it is almost impossible to find an optimal solution in polynomial time [61]. Basically, since any formulation (mathematical modeling) of real-world problems is to control the behavior of occurring phenomena, it is necessary to formulate the problems in such a way that different aspects of the problem appear in the model. Therefore, modeling real-world problems and encountering their large dimensions or problems with several objective functions, in the form of behavioral simulation of phenomena, can increase problem solving time. The time required to solve large problems is one of the criteria for evaluating the problem solving technique.

The reviewed studies indicated that the research in this area can be classified into three divisions. The first division encompasses studies dealing with SCPs applying either meta-heuristic or new meta-heuristic-based algorithms. The proposed algorithms of this division lack the efficiency of polynomial time solutions for SCPs. Next, the second division of studies covers very little research that proposes heuristic algorithms for non-complex SCPs. These non-complex SCPs include those problems which add vertices along the edges dismissing non-nodal facility locations. Finally, the third division includes studies that do not propose a reasonable approach to tackle the infeasibility of large problems. Hence, the current study aims to propose a heuristic algorithm to tackle: (1) the issue of studies including algorithms inefficiency to deal with polynomial time solutions; and (2) the issue of studies pertaining to the restrictions of SCPs taken into account in constructing heuristic algorithms. Thus, the current study presents a heuristic algorithm that is not only capable of constructing an answer within polynomial time but also can solve complex SCPs without non-nodal restrictions and infeasibility of large problems. To this end, the most relevant articles have been systematically summarized in Table 1.

Table 1 The summary of the most relevant published studies
Full size table

3 Coverage Problem

The weighted set covering problem (WSCP) is to select a number of subsets to cover all the members in a total set at the lowest cost. It is a well-studied conventional problem with applications in fields like machine learning, planning, facility allocation, etc. If the cost of all facilities layout is equal, the objective function of the model is to minimize the number of those laid out facilities, which is called the minimum cardinality set covering problem (MCSCP) [1].

3.1 Assumptions, Parameters, and Decision Variables

The current study took discrete WSCP into account. This means that the demand points are considered discontinuous. In the discrete model, the problem is defined in the form of a network of customers as a node wherein it is possible at the same time to establish a facility on each, for which all facilities are considered the same. There are no restrictions on the provision of services by facilities to customers and each customer can be covered by several facilities at the same time. Hence, the parameters and decision variables of the study are as follow:

\(i\) the index of demand points.

\(j\) the index of layout points.

\(m\) number of demand points.

\(n\) number of layout points.

\(f_{j}\) layout cost at point j

\( a_{{ij}} = \left\{ {\begin{array}{ll} 1 & {{\text{If }}\,{\text{layout}}\,{\text{ point }}\,{\text{of }}\,j\,{\text{ can }}\,{\text{cover }}\,i} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right. \)

\( y_{j} = \left\{ {\begin{array}{ll} 1 & {{\text{If}}\,{\text{ any}}\,{\text{ layout}}\,{\text{ at }}\,{\text{point}}\,{\text{ }}j\,{\text{ happen}}} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right. \)

3.2 The Model of Study

Regarding mentioned explanation, the study goes to cover all points of demand with the least possible cost with a mathematical model as follows [2]:

$$ {\text{Min }}\sum\limits_{j = 1}^{n} {f_{j} } \, y_{j} $$
(1)
$$ {\text{s.t.}} $$
$$ \sum\limits_{j = 1}^{n} {a_{ij} } \, y_{j} \ge {\text{1 , for }}i = 1, 2, \ldots , m $$
(2)
$$ y_{j} \in \left\{ {0,1} \right\},{\text{ for }}j = 1, 2, \ldots , n $$
(3)

The objective function (1) minimizes the total cost of facilities layout and the constraint (2) ensures that all points of demand will be covered. It should be noted that the left side of the constraint (2) indicates the number of facilities that can cover demand i. In other words, constraint (2) states that for each point of demand i, we need to lay out a device in at least one of the places that can cover that point of demand.

According to the model, the goal is to calculate the values of \(y_{j}\) in such a way that constraint (2) is met and the value of the objective function is minimized. The current study, applies 20 problems with different sizes which 18 are reproduced by authors and 2 selected of OR-library to assess the performance of the proposed algorithm. Dealing with issues, the study solves these problems by the proposed algorithm along with a meta-heuristic algorithm of SA to highlight the efficiency of the proposed algorithm. Hence, the functionality of the algorithms is briefly described and then the calculations are presented subsequently.

4 Simulated Annealing (SA) Algorithm

Simulated Annealing is an approach based on the Monte Carlo model applied to study the relationship between atomic clusters, entropy, and temperature during the annealing of a material. This algorithm simulates the cooling process of materials by gradually decreasing the temperature to a point of temperature equilibrium. This method moves towards the optimal solution step by step through creating and evaluating consecutive answers. To do so, a new neighborhood is randomly created and evaluated. It examines the points close to the given point in the search space. If the new point is better (reduces the cost function), it would be selected as the new point in the search space, and if it is worse (increases the cost function), it would be selected based on a probabilistic function. In other words, to minimize the cost function, the search is always conducted to reduce the value of the cost function; however, it is possible that sometimes the move is to increase the cost function. Usually, a criterion called the metropolis criterion is used to accept the next point as following Eq. 4 [64]:

$$ P\,({\text{accept}}) = \left\{ {\begin{array}{ll} 1 & {\Delta f \le 0} \\ {e^{{\frac{{ - \Delta f}}{c}}} } & {\Delta f \ge 0} \\ \end{array} } \right. $$
(4)

\(P\) is the probability of accepting the next point, \(C\) is the A control parameter, \(\Delta f\) is the cost change.

The optimization algorithm of SA starts from a random initial solution for decision variables so that the new solution is randomly generated in the suitable neighborhood of the previous solution. Therefore, neighborhood production is one of the important issues in SA. To implement the thermal simulation algorithm, the basic factors including starting point, generator of motion, neighborhood generation, acceptance criterion and stop condition are needed [62, 63].

4.1 Representation of Answer Structure

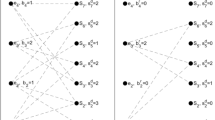
The answer structure expresses a point in the possible space of the problem, so the way it is represented in any heuristic approach is a matter of consideration. In SCP, an achievable answer should indicate whether the facility is laid out in any location. Therefore, the structure of the answer can be considered as a vector of zero and one, so that the presence of element one in the number i house indicates the layout of facility in place i. The notation i simply shows the number of nodes which based on fitness function value takes zero or one. This structure is shown in Fig. 1.

Fig. 1
figure 1

An instance of answer structure representation

Full size image

According to Fig. 1, the nodes with higher fitness will take value 1 and the rest take 0. For example, if at the 1st iteration, the node (4) takes value 1, then due to the number of nodes covered by it (a), there will be a vector with i-a nodes at the next iteration. At the 2nd iteration, node (5) plays the same role, but it covers b number nodes. The iterations go on so that all nodes are covered which means all demand points are met. In fact, at the last iteration, node 6 covers the rest of nodes (c) which is equal to the difference between i and the existing nodes (i-a-b).

4.2 Tune of Parameters Applying Taguchi

The method of Taguchi experiment designs was first introduced in 1960 by Professor Taguchi [64]. This method can determine the optimal conditions with the least number of tests and significantly reduces the time and cost of performing the required tests. In the Taguchi method, according to the number of selected parameters and related surfaces, different orthogonal arrays are used as test matrices. In this method, changes are introduced with a factor called signal-to-noise ratio (S/N), and the experimental conditions with the highest signal-to-noise ratio are selected as the optimal conditions [64, 65]. Taguchi method has been used to adjust the factors of temperature decrement coefficient, iteration at each temperature, final temperature, initial temperature, and maximum iteration of the main loop.

Accordingly, 3 levels are defined for each factor as presented in Table 2. As a result, there are 27 scenarios for evaluating these factors, known as Taguchi tables. Since the purpose of the problem is to minimize the cost of allocating facilities to demand points, loss function and signal-to-noise (S/N) are calculated from Eqs. 5 and 6, respectively, and the final results are also submitted in Table 3. The desired values for tuning the parameters were calculated on a problem sample with 1000 nodes. In this study, S/N ratio with a smaller-the-better methodology was used for wear rate as follow:

$$ SB = \frac{1}{n}\sum {o_{i}^{2} } $$
(5)
$$ \left( \frac{S}{N} \right)_{SB} = - 10\log_{10} \left( {\frac{{\sum {o_{i}^{2} } }}{n}} \right) $$
(6)
Table 2 Problem parameters and levels
Full size table
Table 3 The final results of values (S/N)
Full size table

where \(n\) and \(o_{i}\) are notating the number of experimental observation and experimental observations results, respectively.

Based on the general strategy for optimizing the levels of controlling parameters, the study evaluates the effects of controlling factors on the signal-to-noise (S/N) ratio and the mean (Fig. 2). It applies the appropriate factorial experimental design on the signal-to-noise ratio and the average of the desired feature. In this case, the experimental design method can be used.

Fig. 2
figure 2

The experimental design to compare levels of controlling parameters

Full size image

For factors that have a significant effect on the signal-to-noise ratio (S/N), the levels that can maximize S/N are selected. Factors that do not have a significant effect on the signal-to-noise ratio (S/N) and have a significant effect on the mean, are considered as an adjusting factor and the levels are selected in a way that the mean is closer to the target. Factors that have neither an effect on the signal-to-noise ratio nor on mean are considered as economic factors and the levels are selected to improve performance.

The levels are now compared to determine which level should be used for each parameter; the results of which are determined using the diagrams in Fig. 2. The results in these graphs are obtained from the implementation of the Taguchi method in Matlab software to calculate S/N ratio in the case where the smaller is optimal. Accordingly, Alfa (\(\alpha\)) level 1 (0.999 in Table2) maximizes the S/N. Similarly, \(Tek\_Temp\) in Fig. 2 as iteration parameter at each temperature maximizes the S/N in its Level 1 (100 in Table2). Hence, these two parameters are tuned assigning values of 0.999 and 100, respectively. To tune initial temperature parameter \(T_{0}\), the value of Level 3, which is equal to 10, is assigned. As well as, the value of Level 1 (0.001 in Table 2) is assigned to tune final temperature parameter \(T_{f}\). Meanwhile, the value of level 1 (20,000 in Table2) is determined to tune \(Max\_iter\) as maximum iteration of the main loop.

4.3 The Simulated Annealing (SA) Flowchart

The general overview of how the SA algorithm works with the tuned parameters, using Taguchi method, is indicated in Fig. 3 and explained in the following section.

Fig. 3
figure 3

The tuned SA algorithm flowchart for the study problem

Full size image

5 Proposed Algorithm

Unlike meta-heuristic algorithms that start from a random initial solution with a neighborhood construction mechanism in each step and calculate the value of the objective function for possible solutions and finally report the best answer, the current algorithm constructs directly an answer through the defined mechanism that logically tries to get the closest to the optimal state. In the existing meta-heuristic algorithms, during the defined iterations, the solution to the problem must be solved from \(2n\) possible modes by creating an initial solution and improving it during the solution process, while the proposed algorithm decides whether or not to establish a facility at one point (Node). In other words, the binary mode (one or zero) of each variable has a maximum of \(2n\) possibilities to check. This is the case in which the algorithm will encounter this number in the worst case. In other words, regarding that the number of steps to achieve the answer is equal to \(2n\), in some simultaneous steps, the certainty of determining the value of several variables is decided together, which in turn helps to improve the performance of this algorithm.

The above explanation refers to the polynomial growth of the proposed algorithm, which indicates desirability in this regard with respect to performance expectations. In cover problems where the coefficient of facility cost is equal for each variable in the objective function, it is obvious that the optimized answer is equal to the minimum number of possible facilities that meet all constraints requirements. By changing the coefficients in the objective function and assigning different values to them, it makes sense that the optimal answer of the minimum number of facilities will not be possible, and understanding the problem and finding the answer is no longer as simple as the previous circumstance.

In this case, there should be a balance between the two views of the objective function and the constraints. Hence, from the perspective of the objective function, it is more desirable to select variables whose coefficient value is lower in the objective function. On the other hand, from the point of view of constraints, it is more desirable to select variables that at the same time satisfy more constraints, which practically removes them from the analysis in the next steps, leading to sooner decision making. To make such a balance to select the best option for the layout, a mechanism is presented in the proposed algorithm in which a parameter attributed to the amount of improvement is calculated for each variable in each step; the steps for which the weight and importance of each variable in terms of desirability for the problem is calculated. Based on the above, the algorithm needs to be able to distinguish between two variables, one of which satisfies six constraints while the coefficient value in the objective function is 10 and the variable that satisfies five constraints while the coefficient in the objective function is 8. According to the applied logic, when the facility layout in location \(j\) can cover several other points at the same time, it practically exempts-from the layout of the new facility in those covered areas leading to exempting the equivalent of those in the objective function with coefficient value of \(f_{j}\); unless there are other points of demand which it is more cost-effective for us to cover, regarding the cost they have. Hence, there will be an exemption from the facilities layout in those places which will reduce the cost \(f_{j}\) subsequently. Thus, the fitness function \(b(y_{j} )\) can be defined as follow:

$$ b(y_{j} ) = (\sum\limits_{{K \in S_{j} }} {f_{k} } ) - f_{j} $$
(7)

In Eq. (7), \(S_{j}\) is the indices set of variables covered by \(y_{j}\). As mentioned earlier, previously covered areas are exempt from layout; however, they will remain candidates for layout, as long as they do not cover anything other than the points covered. The algorithm works in such a way that in the first step, for all layout candidate points, the improvement parameter \(b(y_{j} )\) is calculated as a fitness function. Then the variable that has the maximum improvement is selected as the location of the facilitation in this step and takes the value of 1. In the next step, the fitness function values are updated; however, the coefficients of the variables previously covered by the facility are not included in \(\sum {f_{j} }\) to calculate the improvement values. In this step, if after the update, the covered variables by facilities do not cover anything other than the variables that are covered by this step; they take the value of zero. This process will be repeated until the decision on the layout of all variables is ended. In other words, the parameter \(b(y)\) indicates the fitness value of variable \(y\) for layout. As we know, with the layout of facilities at the desired point, three other variables (nodes) are also covered. As a result, it would be better not to have another facility layout in these three since at the same time the coverage of these areas is satisfied and there will be cost reduction by the coefficients of these three variables in the objective function. This cost reduction in the calculation of improvement is given as \(\sum {f_{j} }\). Meanwhile, due to the layout of facilities at the desired point, there will incur cost as the same as the value of its coefficient in the objective function and this cost will be also deducted in the calculation of improvement.

5.1 Algorithm Pseudo Code

According to the explanation, a set of variables whose value has not been assigned is initially formed, which in the first stage will be equal to the indices set of all variables. In the second step, sets consisting of the indices of variables covered by each of the variables in the first step are calculated. In the third step, the amount of improvement is calculated for the variables of the first step applying the fitness function. In the next step, the index of the variable that has the most improvement is determined. In the fifth step, the variable with the most improvement is assigned value 1, and to the variables covered by that variable with improvement value less than or equal to zero, the value of zero is assigned. Steps one to five will be repeated so that a value of 1 or 0 is assigned to all variables. In summary, the run steps of the proposed algorithm in the form of pseudo-code are as follow:

figure h

5.2 A Case Study Problem

To present the performance of the proposed algorithm, a case study problem will be solved step by step. For this purpose, the study assumes a set of variables \(\{ y_{1} ,y_{2} ,...,y_{7} \}\) with a coverage radius of \(D_{c}\) as follow:

$$ \{ y_{2} ,y_{3} ,y_{4} \} = \{ \left. y \right|d(y,y_{1} ) \le D_{c} \} $$
(8)
$$ y_{1} ,y_{4} \} = \{ \left. y \right|d(y,y_{2} ) \le D_{c} \} $$
(9)
$$ y_{1} ,y_{4} \} = \{ \left. y \right|d(y,y_{3} ) \le D_{c} \} $$
(10)
$$ \{ y_{1} ,y_{2} ,y_{5} ,y_{6} \} = \{ \left. y \right|d(y,y_{4} ) \le D_{c} \} $$
(11)
$$ \{ y_{4} \} = \{ \left. y \right|d(y,y_{5} ) \le D_{c} \} $$
(12)
$$ \{ y_{4} \} = \{ \left. y \right|d(y,y_{6} ) \le D_{c} \} $$
(13)
$$ \{ \} = \{ \left. y \right|d(y,y_{7} ) \le D_{c} \} $$
(14)

Conceding in the first step, \(y_{1}\) assigns the value 1 to itself. In the second step, the improvement for the remaining variables is calculated based on the following order:

$$ (y_{2} ) = S_{2} - f_{2} = - f_{2} \, , \, S_{2} = (f_{4} + f_{1} ) $$
(15)
$$ b(y_{3} ) = S_{3} - f_{3} = - f_{3} \, , \, S_{3} = (f_{4} + f_{1} ) $$
(16)
$$ b(y_{5} ) = S_{5} - f_{5} = - f_{5} \, , \, S_{5} = (f_{4} ) $$
(17)
$$ b(y_{6} ) = S_{6} - f_{6} = - f_{6} \, , \, S_{6} = (f_{4} ) $$
(18)
$$ b(y_{7} ) = S_{7} - f_{7} = - f_{7} \, , \, S_{7} = () $$
(19)

The values \(S_{j}\) are equal to the sum of the coefficients in the objective function of the variables that are covered and are not calculated in the improvement. For variables \(y_{3}\) and \(y_{2}\), since they are already covered by \(y_{1}\), their value is zero, unless they have an improvement at this stage, which is not the case in this example, and the decision will be made to assign zero to them. Variable \(y_{4}\) is examined as \(y_{3}\) and \(y_{1}\). Variable \(y_{4}\) takes the value of 1 whether it has a less-equal cost or even more than \(y_{7}\), \(y_{6}\) and \(y_{5}\) if it has a positive improvement.

$$ b(y_{5} ) = S_{5} - f_{5} = - f_{5} \, , \, S_{5} = (f_{4} ) $$
(20)
$$ b(y_{6} ) = S_{6} - f_{6} = - f_{6} \, , \, S_{6} = (f_{4} ) $$
(21)
$$ b(y_{7} ) = S_{7} - f_{7} = - f_{7} \, , \, S_{7} = () $$
(22)

Applying the same reasoning, for variables \(y_{6}\) and \(y_{5}\), since they are already covered by \(y_{4}\), their value is considered zero. Meanwhile, the variable \(y_{7}\) takes the value of 1 without a competitor.

5.3 The Proposed Algorithm Flowchart

To clarify how the proposed algorithm works, a general overview is represented in the following flowchart in Fig. 4.

Fig. 4
figure 4

The flowchart of the proposed algorithm

Full size image

6 Computational Results

To evaluate the proposed algorithm performance, the report of MATLAB code of this algorithm is presented within 20 different sizes. Then, a comparison between this algorithm results and SA is conducted. In this comparison, the best results of the proposed algorithm are reported, as listed in Tables 4, 5, and 6.

Table 4 20 examples of proposed problems
Full size table
Table 5 Results solved by simulated annealing (SA)
Full size table
Table 6 Results solved by the proposed algorithm
Full size table

The main issue taken into account in this study is to deal with full coverage of 1000 variables (\(y_{j}\)) and 200 applicable constraints that assure the coverage of all 1000 demand points. The coefficients of this problem are available in an online and pre-determined form on the website of OR-library, which is a set of coefficients of layout cost and indices number of variables presented over the sub-categories of the SCP like SCP41 and SCP51 and so on. Other issues used in this study have been randomly designed and tested. First, a small-scale problem is solved to understand the solution process of the proposed algorithm and compare it with the exact answer obtained from the Gams software. In this regard, the small-scale problem is considered according to Fig. 5 where the coverage distance is equal to 6 and its cost function is as follows:

$$ {\text{Min }}Z \, = 2y_{1} + 2y_{2} + 6y_{3} + 3y_{4} + 4y_{5} + 3y_{6} + 4y_{7} + 4y_{8} $$
(23)
$$ {\text{Subject to:}} $$
$$ y_{1} + y_{2} + y_{4} + y_{6} \ge 1 $$
(24)
$$ y_{1} + y_{2} + y_{3} \ge 1 \, $$
(25)
$$ y_{2} + y_{3} + y_{4} + y_{5} + y_{6} + y_{7} \ge 1 $$
(26)
$$ y_{1} + y_{3} + y_{4} + y_{6} \ge 1 \, $$
(27)
$$ y_{3} + y_{5} + y_{6} + y_{7} + y_{8} \ge 1 $$
(28)
$$ y_{1} + y_{3} + y_{4} + y_{5} + y_{6} \ge 1 $$
(29)
$$ y_{3} + y_{5} + y_{7} + y_{8} \ge 1 \, $$
(30)
$$ y_{5} + y_{7} + y_{8} \ge 1 $$
(31)
Fig. 5
figure 5

A small-scale problem of set covering problem with 8 nodes and 11 connecting arcs

Full size image

To solve the problem applying the proposed algorithm, at the first step regarding the improvement value of fitness function for each variable there will be:

$$ b(y_{1} ) = 2 + 3 + 3 - 2 = 6 \, $$
(32)
$$ b(y_{2} ) = 2 + 6 - 2 = 6 $$
(33)
$$ b(y_{3} ) = 2 + 3 + 4 + 3 + 4 - 6 = 10 $$
(34)
$$ b(y_{4} ) = 2 + 6 + 3 - 3 = 8 $$
(35)
$$ b(y_{5} ) = 6 + 3 + 4 + 4 - 4 = 13 $$
(36)
$$ b(y_{6} ) = 2 + 6 + 3 + 4 - 3 = 12 $$
(37)
$$ b(y_{7} ) = 6 + 4 + 4 - 4 = 10 $$
(38)
$$ b(y_{8} ) = 4 + 4 - 4 = 4 $$
(39)

In this step, value 1 is assigned to variable \(y_{5}\) and the improvement values of the fitness function are updated. As a result, the improvement values for the second step will be as follow:

$$ b(y_{1} ) = 2 + 3 - 2 = 3 $$
(40)
$$ b(y_{2} ) = 2 - 2 = 0 $$
(41)
$$ b(y_{4} ) = 2 - 3 = - 1 $$
(42)

At this stage, a value of 1 is assigned to variable \({\text{y}}_{j}\) and the algorithm ends by covering all points of demand. Finally, the value of the objective function for this problem will be equal to Z = 2 + 4 = 6 according to the proposed algorithm. Following the verification of the algorithm, the answer values for this problem are obtained from the exact solution methods in the Gams software, equal to 6, which confirms the good and acceptable performance of the proposed algorithm.

The strength of the algorithm is determined in high-dimensional problems, which is emphasized in Table 4. Due to this issue, in small-scale problems, the importance of the algorithm in terms of time is not understood; rather, it is a problem on a large scale that this heuristic algorithm can be applied for a very convenient time with desired quality of the answer.

To better compare the performance of the solution methods used for different problems in Table 4, the cost reduction percentage of the objective function by the proposed algorithm to cost reduction of the objective function using the SA algorithm is calculated and plotted in Fig. 6 for different problems. As can be seen in Fig. 6, the proposed algorithm in most cases has a better answer than the SA algorithm.

Fig. 6
figure 6

Reduction percentage of the objective function value by the proposed algorithm relative to SA

Full size image

Thus, it can be said that according to Tables 4, 5 and 6 and Fig. 6, the proposed algorithm has a better answer quality compared to algorithm SA, wherein parameters are tuned by the Taguchi method. Meanwhile, the strength of the proposed algorithm is in high-dimensional problems with a number of polynomial iterations (NP-hard problems). Since the best answer obtained from algorithm SA is given after 10 times due to its random nature, the solution time of the algorithm will be 10 times the current value, which has been ignored for the pessimistic review of the algorithm. In other words, the best answer of the algorithm is given after running 10 times, while the time of algorithm’s first run is reported. Therefore, it can be concluded that in terms of quality, the proposed heuristic algorithm clearly performs better than algorithm SA and is competitive in terms of time.

7 Conclusion

In this study, a new heuristic algorithm for the set covering problems based on coefficient and fitness values was presented due to the complexity of the problems. However, heuristic algorithms are more likely to succeed in such cases where they start from a certain point. There is a characteristic of the presented algorithm which contributes to its superior performance. The proposed algorithm applies a mechanism that improves the set covering solution through a particular fitness function. In other words, it evaluates the qualification of subsets by directly applying a fitness function. This fitness function is formulated based on sets and subsets coefficients in a way that the subsets of selected sets have the lowest probability to be selected in the next iteration.

In addition, due to the exponential complexity of the coverage problem, the optimal solution cannot be achieved in a logical time. To solve the problems presented in this study via applying the exact method, the resource limitation error was observed. Hence, the study suffices to present a comparison of the results obtained from meta-heuristic methods for large problems. The experimental results indicated that the proposed algorithm has a relative improvement compared to other methods including SA algorithm wherein parameters were tuned using the Taguchi method. In other words, the proposed algorithm submits better results in terms of quality than the SA algorithm and in terms of time, the algorithm is quite competitive.

For future studies, it is suggested to develop the proposed algorithm for other problems, including stochastic problems. It is also recommended to use this method and its generalization for other NP-hard problems to examine whether this algorithm can be combined with other algorithms leading to a more efficient way to deal with SCP.