1 Introduction

In an interconnected power system, the load frequency control (LFC) problem is responsible for maintaining the frequency of each area near its nominal value and regulating tie-line power flows within some pre-determined tolerances [1]. In LFC, the tie-lines are used by utilities to exchange contractual energy under normal conditions, and they mutually help each other in atypical situations. Changes in area loads or generations result in errors in frequency and tie-line power. LFC, which is defined as the regulation of the power output of the generators within a prescribed area, corrects these types of perturbations [2]. In the LFC designing problem, the lag related to actuator operation, failure in the communication links, and distance between control centers and power stations give rise to new challenges like input time-delay, which is an inevitable phenomenon [3]. Also, the governor dead band (GDB) and generation rate constraint (GRC) are the main sources of nonlinearities and uncertainties [4]. Disregarding these issues can deteriorate the dynamic performance of LFC and, also it may cause power system instability and oscillation. Therefore, designing an efficient controller for LFC is necessary significant research.

1.1 Literature Review

The controllers introduced for the LFC problem can be classified into two main groups: classical and intelligent approaches. Adaptive [5, 6] and robust controllers [7, 8] are some examples of the classical approach. Fuzzy logic system (FLS) [9, 10] and artificial neural network (ANN) [11] based controllers are some examples of the intelligent techniques that have been designed for the LFC problem in the power systems. To improve both transient and steady-state performances, some authors have considered time-delays, uncertainties, and nonlinearities in designing the LFC problem [12,13,14,15,16,17]. Although PI/PID controllers are considerably applied in the LFC topics, it is evident that delays and uncertainties can degrade the performance of these fixed and linear structure controllers. To solve this problem, many researchers have applied robust control design methods to adjust PI/PID parameters to surmount the mentioned problems and enhance the control operation. The robust PI-based controllers in [18] and [14, 17], the H∞ controller in a linear matrix inequality (LMI) framework in [13], and the robust PID-type LFC scheme in [16] are some examples of the mentioned robust PI/PID controllers. In most applications of the robust control methods, the linear model of the plants is required. Moreover, these methods lead to high-order controllers which result in some difficulties in their implementation. Considering the mentioned nonlinearities and time-delay in the power system, a hybrid gravitational searching algorithm was utilized for optimal tuning of the PID parameters [19]. In these offline modern heuristic optimization techniques, the stability of the controlled systems was demonstrated only by simulations [3]. Moreover, precise information about the system parameters and nonlinearities is required for implementing the aforesaid controllers in LFC. On the other hand, intelligent approaches such as the FLS and ANN controllers do not necessitate an exact model of the controlled system, and the sensors can provide their required information from the plant to construct the controller. Moreover, these intelligent approaches can incorporate the PI/PID controllers and fine-tune them to a specific plant suffering from nonlinearities, uncertainties, and delays. In this way, a self-tuning fuzzy PID controller based on the peak observer idea [20] has been utilized to tune the scaling factors of a delay-free power system for solving LFC. A fractional order fuzzy PID controller was designed for LFC of a linear and delay-free power system in [21]. In [22] and [23], the fuzzy PID controllers were adjusted in the offline fashion using the hybrid evolutionary optimization algorithms for a delay-free power system. In these methods, any change in the power system operating points and measurement noise by sensors can deteriorate the LFC performances. Because of the capability of type-2 fuzzy controllers in dealing with the measurement noise and parametric ambiguities, these controllers were introduced by authors for some uncertain plants [24,25,26]. In this case, as mentioned before, the robust classical controllers are not a good solution, because, in most cases, all of the state variables of the system are required for designing the controller. Like most industrial systems, the power system LFC suffers from parametric uncertainties and measurement noise. A convenient intelligent approach to tackle these problems is using type-2 fuzzy controllers. In type-1 fuzzy sets, membership functions (MF)s are certain, whereas in type-2 fuzzy sets MFs are themselves fuzzy [27]. As the type-2 fuzzy MFs provide us with more parameters, they can handle uncertainties and measurement noise in a better way [28]. Regarding this matter, the Big Bang–Big Crunch optimized type-2 fuzzy PID (T2FPID) controller was introduced for a four-area LFC in [29]. In that work, the scaling factors and the footprint of uncertainty of MFs were tuned to minimize frequency deviations of the power system against load demand. In [30], a type-2 fuzzy neural network (T2FNN) controller was designed in parallel with the PD controller for a nonlinear power system with time-delay. Since both the antecedent and consequent parameters of the T2FNN controller are essential to be adjusted, this issue increased the computational time in the on-line applications. Using the fuzzy logic system approximation capabilities, direct–indirect adaptive controllers were developed for unknown interconnected LFC areas in [31, 32]. According to the estimation of nonlinear functions for controller realization, these methods cannot be suitable methods for the online application. The researchers in [33] designed a multi–input–multi–output (MIMO) type-2 fuzzy controller to tune the PID parameters in LFC, where the particle swarm optimization (PSO) was included to facilitate designing the controller. However, the effect of the delay was considered neither in the analysis nor in the synthesis of the controllers.

1.2 Contributions

Since the studied controllers were suffering from the stability issue, and most of them have a fixed structure and by considering the capability of the FPID controllers, in this paper, an adaptive stable T2FPID controller has been designed for LFC in an interconnected nonlinear power system with input time-delays. The proposed controller is simple, Lyapunov–Krasovskii (L–K) stable, and some of its parameters are tuned online to meet the requirements under different operating conditions and various load demands. The most significant contributions of this paper can be listed as follows:

(a) an adaptive T2FPID controller has been designed for LFC to deal with uncertainties, nonlinearities, and input time-delay in the power system. The type-2 fuzzy controller has been exploited for minimizing the effects of uncertainties in the system parameters and the measured signals by the sensors.

(b) A Lyapunov–Krasovskii (L–K) theorem joint with a gradient-descent (GD) algorithm is applied to assess the stability of the designed T2FPID controller, and the adaptation rules for the output scaling factors of this controller have been obtained using this theorem. In the reviewed works related to fuzzy PID controllers, the capability of the controllers was shown just by simulations. While in this paper, the stability problem is shown mathematically.

(c) Since the obtained adaptation laws for the T2FPID controller required a little knowledge about the plant and its parameters, it can be easily implemented in the LFC for the power system. For this, the measurable area control errors (ACE)s are utilized to construct the L-K functional, and the controller outputs and ACEs are required to get the adaptation laws. It is worth pointing out that, to construct the proposed controller, there is no need to estimate the nonlinear functions of the power system model.

In the designed controller, the structural type-2 fuzzy logic system (T2FLS) parameters are settled during the off-line design, and just the output scaling factors are tuned during the on-line one based on the L-K stable algorithm. A two-area nonlinear power system is used to show the efficiency of the suggested controller. The rest of this paper is organized as follows: Sect. 2 provides the mathematical model of the two-area nonlinear time-delay power system. In Sect. 3, the designed adaptive controller and its stability are explained. Section 4 presents the simulation results for a two-area power system. Finally, the conclusions are provided in Sect. 5.

2 Two-Area Power System Model

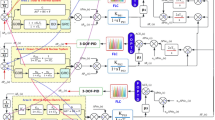
The block diagram of a two-area interconnected power system with input delays is shown in Fig. 1 [16]. Each control area has its own turbine, governor, and generator which can supply the loads in its own area and all contracted power with its neighbour. Although the electric power can flow between the areas through the tie-line to enhance the reliability of the power system, every load demand in each area influences the output frequencies of both areas and also the power flow on the tie-line. In the LFC problem, it is desirable to adjust the frequency and tie-line power deviations with a satisfactory dynamic performance in the presence of delays and nonlinearities. To do this, the tie-line power and frequency deviations are measured using sensors, fed back into both areas, and combined into a single signal as the controller inputs. This signal is named ACE, which must be regulated. It is defined by:

$${{ACE}}_{i} = \Delta P_{{{\text{tie}}}} + B_{i} \Delta f_{i}$$
(1)
Fig. 1
figure 1

Two- area input- delayed power system

Full size image

where ∆Ptie is the deviation of power exchange from the nominal value between areas, \({\Delta f}_{i}\) the frequency deviation of area i, and \({B}_{i}\) is the bias coefficient. Moreover, in Fig. 1, \({R}_{i}\) is the regulation constant, \({K}_{pi}\) is power system gains, and \({T}_{pi}\) is the power time constant.

Slow operation of actuators, control commands processing, and any failure in the communication links can cause delays. Also, the distance between control centers and power plants are another issue that leads to communication delays. To make the analysis less complicated, the mentioned delays are mixed as a single delay and showed in the input of the controlled system by an exponential block, where τ is the amount of delay [16, 33]. This delay can be a fixed value or a time-varying signal, which must be considered in the LFC control design. Naturally, the delay can make the control problem much more difficult, and, in most cases, it may lead to instabilities [34, 35]. Nonlinearity is another important characteristic that should be considered in the analysis and design of the controller. Almost all components of a power system have nonlinear characteristics, and in most cases, their exact modeling is difficult. Turbines with GRC and GDB are of the most typical types of these nonlinearities. These nonlinearities can be modeled in several ways, among which the block diagram represented in Fig. 2 has been used in this study [12].

Fig. 2
figure 2

A nonlinear model of governor and turbine [36]

Full size image

The following assumption is made about the time-delay in the control areas:

Assumption (a):

Delay and its derivative are bounded in each control area:

$$\tau \left( t \right) \le \tau_{{{\text{max}}}} ,\,\,\,\,\,\,\left| {\dot{\tau }\left( t \right)} \right| < 1$$
(2)

where \(\tau_{{{\text{max}}}}\) is the time-delay upper bound. The proposed adaptive fuzzy PID controller is developed in the following section.

3 Developing Adaptive Fuzzy PID Controller for LFC

Due to the simplicity and efficiency of the PID controllers, these controllers are widely used in industrial systems such as LFC. However, these fixed structure controllers exhibit poor dynamic performance when they encounter uncertainties and time-varying delays. To improve the performance of these controllers, some population-based methods such as genetic algorithm (GA) and particle swarm optimization (PSO) have been exploited to tune their parameters [37, 38]. In these offline methods, the PID gains are investigated in the feasible area of the response until a pre-specified cost function is minimized. To improve the performance of the PID controllers, a combination of them with fuzzy logic systems is an important issue, and it can be done in two ways: (i) The parameters of the PID controller are adjusted (in an on-line manner) using a fuzzy logic inference system. In this structure, the fuzzy rule bases can be defined by an expert, and the PID controller produces the final control signal. (ii) The PID controller is established using the fuzzy rules, and the control signal is derived directly from the fuzzy inference system; this structure is named fuzzy PID controller. The structure of a fuzzy PID controller is shown in Fig. 3 [20].

Fig. 3
figure 3

The structure of a fuzzy PID controller

Full size image

The fuzzy PID controller output \(u\left(t\right)\) can be written as follows

$$u\left( t \right) = u_{1} + u_{2} = \alpha u_{f} \left( t \right) + \beta \mathop \int \limits_{0}^{t} u_{f} \left( t \right){\text{d}}t$$
(3)

where \({u}_{f}\) is the output of the fuzzy controller and \(\alpha\) and \(\beta\) are the output scaling factors.

It is shown that the input–output relation of this controller is similar to that of a PID controller, except that the fuzzy PID controller can be considered as a nonlinear controller.

To improve the performance of the fuzzy PID controller, in [20] and [39, 40], the input/output (I/O) scaling factors were tuned during the on-line manner based on the overshoot observer idea, while the other structural parameters of the fuzzy controller were settled during the off-line design. In those works which benefit from the type-1 fuzzy (T1F) controllers, it was shown that the proposed adaptive controllers enhanced the process performance. But some important problems such as the stability analysis and dealing with measurement noise and time-delays were not discussed. Considering the mentioned problems and in order to enhance the performance of the fuzzy PID controller in applying to the LFC of power system, the following steps are done in this study:

(a) Since the power system LFC suffers from parametric uncertainties and measurement noise, and, the type-1 fuzzy controllers cannot directly handle such uncertainties, the interval T2FLS is utilized in the fuzzy controller to construct the T2FPID controller. In this case, the type-2 fuzzy controllers have the potential to overcome these limitations, and they are a convenient model-free approach to produce better performance for many applications that require handling high levels of uncertainties.

(b) A L-K functional has been used to assess the stability of the designed T2FPID controller, and the adaptation rules for the output scaling factors of this controller parameters have been extracted using this functional. To decrease the computational time in the proposed adaptive method, the antecedent/consequent MFs of the type-2 fuzzy controllers are tuned during the offline procedure. This enables the T2FPID controller to produce a better real-time response.

The structure of the proposed adaptive T2FPID controller for the ith area of the power system (controller parts in Fig. 1) is provided in Fig. 4. As can be seen, the designed controller includes adaptive mechanism part, which tunes the output scaling factors of the T2FPID parameters in an online manner (βi and αi are the output scaling factors of the ith control area). This adaptive part is designed to enhance the performance of LFC in dealing with time-delay and time-varying parameters. Moreover, the interval type-2 fuzzy set [41], whose mathematics is much simpler than that of the general type-2 fuzzy set [42, 43], has been utilized to construct the T2FLS controller for the ith control area in the power system. The adoption of interval type-2 fuzzy allows reducing the computational complexity in the real-time applications [44, 45].

Fig. 4
figure 4

The structure of the proposed adaptive T2FPID controller for the ith control area

Full size image

In this controller, \({r}_{1i}\) and \({r}_{2i}\) are regarded as the inputs of the T2FLS controller, where \({r}_{1i }={K}_{1}{ACE}_{i}\) and \({r}_{2i }={K}_{1}{\dot{ACE}}_{i}\). This type-2 fuzzy controller has three triangular MFs and five singleton MFs in the antecedent and consequence parts, respectively. The input and output MFs are presented in Fig. 5.

Fig. 5
figure 5

MFs of the T2FLS controller

Full size image

The fuzzy if–then \({R}^{j}\) rule is described as follows:

$$R^{j} :\,IF\;\;r_{1i } \;\;is\;\; \tilde{A}_{j1} \;\;{\text{and}}\;\; r_{2i } \;\;is\;\; \tilde{A}_{j2}\;\; {\text{THEN}} \;\;u_{fi} = c_{j}\;\;\;\;\; j = 1,2, \ldots ,M$$
(4)

where \({\stackrel{\sim }{A}}_{jk}\) are type-2 MFs for the jth rule and the kth input and \({c}_{j}\) is a singleton for the consequence parameters. According to the considered MFs for the inputs and output, Table 1 shows the complete rule base of the T2FPID controller for the ith area of the power system with nine rules. These rules cover all the necessary control actions to enforce the system error to zero, and the adaptive mechanism compensates for the possible inaccuracies in the MFs’ universe of discourses to improve the performance of the designed controller.

Table 1 Rule base of the T2FLS controller
Full size table

The structure of the designed T2FLS controller, which involves inputs, fuzzifier, inference, and rule base, type reduction, and defuzzifier and output is shown in Fig. 6 [46].

Fig. 6
figure 6

The structure of the designed T2FLS controller

Full size image

3.1 Stability Analysis and Adaptation Rules

Applying the proposed controller in Fig. 4 for the power system presented in Fig. 1, it is desirable to regulate \({ACE}_{i}\) to meet the LFC objectives. In this nonlinear and uncertain system, time-delay exists in the input of the plant and ignoring that not only can reduce the performance of the power system but also it can cause instability. Since time-delay and some parameters of the power system such as load demand can be time-varying, in the proposed T2FPID structure, the adaptive mechanism is designed to deal with these problems and enhance the dynamic performance. In the proposed scheme, a L-K functional combined with the gradient descent (GD) learning algorithm has been utilized to examine the stability issue as well as to get the adaptation rules for the output scaling factors of the T2FPID controller. Since it is necessary for GD to compute the derivative of the squared error function regarding the controller parameters, this algorithm may get stuck in the local minima and become unstable. Therefore, the L-K theorem guarantees the stability of the proposed GD algorithm. To implement the stable adaptive mechanism for the proposed T2FPID controller, the considered L-K functional is as follows:

$${V}_{i}\left(t\right)=\frac{1}{2}{e}_{i}{(t)}^{2}+\frac{1}{2}{\int }_{t-\tau (t)}^{t}{e}_{i}{(s)}^{2}ds+{\int }_{-{\tau }_{max}}^{0}{\int }_{t+\theta }^{t}{e}_{i}{(\theta )}^{2}d\theta ds$$
(5)

where

$${e}_{i}(\mathrm{t})={y}_{i}(t)-{y}_{d}\left(t\right),$$
(6)

and \({y}_{i}\) is \({ACE}_{i}\) and \({y}_{d}\) is the reference signal (in this study \({y}_{d}=0\)). The index i indicates the ith control area of the power system. It is notable that by enforcing \({ACE}_{i}\) to zero, the LFC objectives such as maintaining the area frequency and tie-line power for their scheduled values are achieved.

Theorem 1

If the adaptation rules for the output scaling factors (\({\alpha }_{i}\) and \({\beta }_{i}\) ) of the designed T2FPID controller are considered as:

$$\dot{\beta }_{i} = - 0.5\left( {1 + \tau_{{{\text{max}}}} } \right)e_{i} \left( {J_{i} \mathop \int \limits_{0}^{t} u_{fi} } \right)^{ - 1}$$
(7)
$$\dot{\alpha }_{i} = - 0.5\left( {1 + \tau_{{{\text{max}}}} } \right)e_{i} \left( {J_{i} u_{fi} } \right)^{ - 1}$$
(8)

then \({\dot{V}}_{i}\left(t\right)\le 0\) is satisfied and \({ACE}_{i}\) reaches zero in the presence of time-varying delay, uncertainties, and nonlinearities of the power system. In the adaptation laws in Eqs. (7) and (8), \({J}_{i}\) is known as the Jacobean of the plant (or the sensitivity of the plant).

Remark 1

To obtain the sensitivity of plant \({J}_{i}\), some approaches were introduced in [47, 48]. In this study, \({J}_{i}=\frac{\partial {y}_{i}}{\partial {u}_{i}}\approx \frac{\Delta {y}_{i}}{\Delta {u}_{i}}\) approximation has been exploited to obtain the sensitivity of the controlled system in the adaptation laws in Eqs. (7) and (8).

Remark 2

To avoid division to zero in the adaptive laws in Eq. Equations (7) and (8), in the inverse calculations, an algorithm is provided always to make them equal to 0.001 when their computed values are less than this threshold.

Proof

The time-derivative of the L-K functional in (5) can be calculated as follows:

$${\dot{\mathrm{V}}}_{\mathrm{i}}\left(\mathrm{t}\right)={\mathrm{e}}_{\mathrm{i}}{\dot{\mathrm{e}}}_{\mathrm{i}}+{{\mathrm{e}}_{\mathrm{i}}}^{2}-(1-\dot{\tau }){{\mathrm{e}}_{\mathrm{i}}}^{2}(\mathrm{t}-\uptau )+{\uptau }_{\mathrm{max}}{{\mathrm{e}}_{\mathrm{i}}}^{2}-{\int }_{\mathrm{t}+\uptheta }^{\mathrm{t}}{{\mathrm{e}}_{\mathrm{i}}}^{2}(\mathrm{s})\mathrm{ds}$$
(9)

Using assumption (a), the following inequality can be obtained:

$${\dot{V}}_{i}\left(t\right)\le {e}_{i}{\dot{e}}_{i}+(1+{\tau }_{max}){{e}_{i}}^{2}$$
(10)

Taking the time derivative of the regulation error in (6) and applying the chain rule (regarding the controller parameters) recursively yields:

$$\begin{aligned} \dot{e}_{i} \left( t \right) & = \frac{{\partial e_{i} }}{\partial t} = \frac{{\partial e_{i} }}{{\partial y_{i} }}\frac{{\partial y_{i} }}{{\partial u_{i} }}\left( {\frac{{\partial u_{i} }}{{\partial u_{1i} }}\frac{{\partial u_{1i} }}{{\partial \alpha_{i} }}\frac{{\partial \alpha_{i} }}{\partial t} + \frac{{\partial u_{i} }}{{\partial u_{2i} }}\frac{{\partial u_{2i} }}{{\partial \beta_{i} }}\frac{{\partial \beta_{i} }}{\partial t}} \right) \\ & = \left( 1 \right)\left( {J_{i} } \right)\left( {\dot{\alpha }_{i} u_{fi} + \dot{\beta }_{i} \mathop \int \limits_{0}^{t} (u_{fi} ){\text{d}}t} \right) \\ \end{aligned}$$
(11)

Substituting (11) into (10) gives:

$$\begin{aligned} \dot{V}_{i} \left( t \right) & \le e_{i} \left( {J_{i} } \right)\left( {\dot{\alpha }_{i} u_{fi} + \dot{\beta }_{i} \mathop \smallint \limits_{0}^{t} (u_{fi} ){\text{d}}t} \right) + \left( {1 + \tau_{{{\text{max}}}} } \right)e_{i}^{2} \\ & \le e_{i} \left( {J_{i} \dot{\beta }_{i} \mathop \smallint \limits_{0}^{t} (u_{fi} ){\text{d}}t + J_{i} \dot{\alpha }_{i} u_{fi} + \left( {1 + \tau_{{{\text{max}}}} } \right)e_{i} } \right) \\ \end{aligned}$$
(12)

Finally, substituting adaptation laws in (7) and (8) into (12) gives:

$${\dot{V}}_{i}\left(t\right)\le 0$$
(13)

Therefore, the designed control system is L-K stable. To better understand the procedure of the proposed controller, the flowchart of the proposed control algorithm is given in Fig. 7.

Fig. 7
figure 7

Flowchart of implementation of the proposed T2FPID controller

Full size image

4 Simulation results

In the present study, the nominal parameters and dynamical equation of the two-area power system are given in Table 2 and appendix [20, 29], respectively.

Table 2 Parameters of the power system under study
Full size table

The considered system is controlled by using (1) the proposed T2FPID controller, (2) the non-adaptive T2FPID controller designed in [29], and (3) the non-adaptive T1FPID controller designed in [22]. The stability of both non-adaptive T2FPID and T1FPID controllers was not studied, and also, they were tuned in an offline manner using the evolutionary optimization methods. In the proposed T2FPID controller, the initial values for the adaptive parameters are set as \({\beta }_{1}(0)=2\), \({\beta }_{2}(0)=1.5\), \({\alpha }_{1}(0)=1.5\), and \({\alpha }_{2}(0)=1\). In this controller, we set \({K}_{1}=1.2\) and \({K}_{2}=0.5\). Moreover, for considering uncertainty, it is assumed that a random noise with the normal distribution distorted the measured ACEi So, the following measurement of \({ACE}_{i}\) is considered for the ith area:

$$y_{i} = {ACE}_{i} + 0.1randn$$
(14)

where function randn is random numbers with Gaussian distribution (with SNR = 30 dB). By applying different amounts of input delay and load demands, the superiority and efficiency of the proposed T2FPID controller are demonstrated by comparing to the mentioned fixed structure controllers.

Case 1: In this case, we assume that the first and second area load demands are \({\Delta P}_{d1}=0.2\) p.u and \({\Delta P}_{d2}=0.1\) p.u, respectively. In this case, the delays in each control area are small in value but time-varying as \(\tau (t)=1.5+0.5sin(t)\) (sec). The results of the frequency deviations \({\Delta f}_{1}\) and \({\Delta f}_{2}\) and also tie-line power deviation \(\Delta {P}_{tie}\) are presented in Fig. 8, Fig. 9, and Fig. 10, respectively.

Fig. 8
figure 8

The frequency deviations for the 1st control area (case 1, SNR = 30 dB)

Full size image
Fig. 9
figure 9

The frequency deviations for the 2nd control area (case 1, SNR = 30 dB)

Full size image
Fig. 10
figure 10

The tie-line power deviation (case 1, SNR = 30 dB)

Full size image

In the proposed T2FPID controller, since the output scaling factors which are very significant in the controller performance are tuned in the on-line design (using the L-K theorem), this controller outperforms the other controller with the fixed structure. In other words, with a small amount of delay, due to the fixed structure of the non-adaptive T2FPID and T1FPID controllers, they cannot deal with this issue and, therefore, they start to oscillate around zero. It can be seen that, as the T1FPID controller benefits from the type-1 fuzzy system and because of its drawback in handling nonlinearities and uncertainties, the performance of this controller is the worst compared to the other type-2 fuzzy based controllers. Also, the adaptation process for the output scaling factors (\({\alpha }_{i}\) and \({\beta }_{i}\)) is shown in Fig. 11. From this figure, it can be concluded that these parameters in both areas adaptively change (according to Eq. (7) and (8)) and, they finally converge to an appropriate value to deal with the time-varying delays and load changes. Figure 12 and Fig. 13 illustrate the generated power in the first and second areas to supply the load demands of \({\Delta P}_{d1}=0.2\) p.u and \({\Delta P}_{d2}=0.1\) p.u, respectively. It is concluded that the designed T2FPID controller is capable of supplying the demanded loads with fast response speed compared to other controllers. As mentioned, having the adaptive properties and the use of T2FLS are the main reasons for the better performance of the proposed controller.

Fig. 11
figure 11

The adaptation process of \({\alpha }_{i}\) and \({\beta }_{i}\) (case 1)

Full size image
Fig. 12
figure 12

The generated power of the 1st control area (case 1, SNR = 30 dB)

Full size image
Fig. 13
figure 13

The generated power of the 2nd control area (case 1, SNR = 30 dB)

Full size image

The time history of the L-K functional and its time derivative is shown in Fig. 14. As can be seen, at the beginning the applied load demands (disturbances) make the system deviate from its equilibrium point (zero) and after a second, the proposed controller takes control of the power system and enforces the closed-loop error to zero. This matter can be visualized from V and it’s derivate that they become decreasing and negative, respectively. After \(t=4\) sec, the L-K functional and its derivative are zero and, the system error is stabilized at the zero equilibrium point.

Fig. 14
figure 14

Time history of L-K functional and its derivative

Full size image

To clarify the effectiveness of the proposed T2FPID controller in dealing with high level of uncertainties, the simulation in case1 is repeated for the measurement noise with SNR = 20 dB. The responses of the three controllers are illustrated in Figs. 15 and 16.

Fig. 15
figure 15

The frequency deviations for the 1st control area (case 1, SNR = 20 dB)

Full size image
Fig. 16
figure 16

The frequency deviations for the 2nd control area (case 1, SNR = 20 dB)

Full size image

It can be seen that the proposed adaptive controller handles the high level of sensor noise in a better way. As previously mentioned, this result is compatible with the mentioned aspects of type-2 fuzzy sets in their handling of uncertainty and the ability of the proposed adaptive T2FPID controller. On the other hand, the T1FPID controller cannot handle such uncertainties and starts to oscillate around zero and, therefore, it fails to meet the LFC objectives.

Case 2: It is considered that the area load demands are \({\Delta P}_{d1}=0.1\) p.u and \({\Delta P}_{d2}=0.2\) p.u and a long delay with the amount of \(\tau (t)=4.5+0.5sin(t)\) (sec) is affecting the communication channels in each control area of the power system. Moreover, it is supposed that some power system parameters changed from their nominal values, i.e. \({K}_{pi}=140\) and \({T}_{12}=0.345\). By applying the designed controllers, the results of \({\Delta f}_{1}\), \({\Delta f}_{2}\), and \(\Delta {P}_{tie}\) are illustrated in Figs. 17, 18, and 19, respectively.

Fig. 17
figure 17

The frequency deviations for the 1st control area (case 2)

Full size image
Fig. 18
figure 18

The frequency deviations for the 2nd control area (case 2)

Full size image
Fig. 19
figure 19

The tie-line power deviation (case 2)

Full size image

Because the proposed strategy has been designed using the L-K theorem and considering the effect of delay on this procedure, this controller can deal with the long time-delay and change in the power system operations and effectively acts to keep the area frequency and tie-line power near to the scheduled values. On the other hand, from these figures and by increasing the amount of delay and changes in the power system operating points, the fixed structure controllers begin to yield an oscillatory output. Among the fixed structure controllers, the non-adaptive T2FPID controller has better performance because of its nonlinear functioning and better dealing with uncertainty characteristics. It is worth pointing out that for \({\tau }_{max}>5\) and by doing a simulation, the T1FPID controller is not able to keep the stability, and as a result, this delay leads to instability in the power system. Also, the non-adaptive T2FPID controller yields a response with high oscillation. Also, the adaptation process for the adaptive parameters of the proposed controller is illustrated in Fig. 20. From this figure, it can be observed that these parameters are trained using the obtained stable learning algorithm and then, converged to the appropriate values. As said before, these output scaling factors have a crucial role in the performance of the designed T2FPID controller and their adaptive changes are to satisfy this issue.

Fig. 20
figure 20

The adaptation process of \({\boldsymbol{\alpha }}_{{\varvec{i}}}\) and \({{\varvec{\beta}}}_{{\varvec{i}}}\) for case 2

Full size image

The values of the integral of the time multiplied squared of the error (ITSE) and the integral of the time multiplied by the absolute value of the error (ITAE) indices related to the controller types (the proposed adaptive T2FPID controller, the non-adaptive T2FPID controller in [29], and the T1FPID controller in [22]) for case 1 (with SNR = 30 dB and SNR = 20 dB) and case 2 are given in Table 3. It is worth pointing out that these criteria are calculated for each area and their sum is given in this table. Among these criteria, a small amount of ITAE indicates that the system has small overshoots/undershoots and well-damped oscillations. Also, ITSE is a measure of the number of steady-state errors occurring late in the system response. From this table, it can be observed that the proposed T2FPID controller outperforms the other controllers in both of the two mentioned criteria. For example, in the case 1, the value of ITSE in the non-adaptive T2FPID controller in [29] is almost two times higher than that of the proposed controller. In the non-adaptive T1FPID controller in [22], this value is nearly nine times more than the ones with the proposed controller. Moreover, a comparison of the ITSE and ITAE values for case 1 with SNR = 30 dB and SNR = 20 dB shows that T1FPID controller did not tackle the applied uncertainty in a better way. On the other hand, the better performance of the proposed adaptive T2FPID controller can be seen from the values in this table. As mentioned earlier, the better ability of the T2FPID controller in handling uncertainties and its adaptive characteristic is the most important reason for its better performance.

Table 3 Performance index values related to the different controller types
Full size table

5 Conclusion

An adaptive L-K stable T2FPID controller has been designed for LFC in an interconnected and nonlinear power system with the input time-varying delay. In this paper, the stability of the designed T2FPID has been assessed using the L-K theorem, and the adaptation laws to adjust the output scaling factors of this controller have been derived based on this theorem. It is worth pointing out that, in the previous works, these controller parameters were settled in offline fashion, and their stability was not studied. As the obtained adaptation laws for the output scaling need a little knowledge about the power system parameters, the advantage of the proposed T2FPID controller is its simplicity in terms of tuning and implementation. For different amounts of input delay, uncertainty, and changes in the power system operating points, some simulation has been carried out to demonstrate the superiority of the proposed adaptive T2FPID controller compared to the other exiting FPID controllers. Using these simulations, it can be observed the proposed adaptive controller can successfully force the frequency deviations and ACEs to zero in the presence of the high level of sensor noise, long time-delay, and nonlinearities.

Future work could investigate the mathematical analysis of the sensitivity of the proposed T2FPID controller to the input delay. Using this analysis, the permissible upper bound limit can be introduced for the closed-loop system. Moreover, the penetration of wind farms and plug-in electric vehicles in the power system can be considered as a new form of generation units for the design of the LFC problem.