1 Introduction

Recently, the research on switched systems has been developed because of many physical or man-made systems possessing switching features [1]. A typical switched system is composed of a finite number of continuous-time or discrete-time subsystems and a switching signal which orchestrates the switching among these subsystems. So far, two stability issues have been well addressed, i.e., the stability under arbitrary switching and the stability under constrained switching. As one typical example of constrained switching, the average dwell time (ADT) logic is proposed in [2]. By combining the ADT switching with the MLFs approach [3], stability analysis and controller synthesis problems are addressed for switched systems [4,5,6]. As we know, the nonlinearity is very common in real world. Therefore, it is theoretical significance and practical importance for us to study the nonlinear switched systems. However, it is difficult to analyze the nonlinear switched systems directly because of the nonlinearity. The T–S fuzzy model is proven to be an effective tool in approximating most complex nonlinear systems [7,8,9,10,11,12,13,14,15,16], which utilizes local linear system description for each rule. Using the T–S fuzzy model to describe each nonlinear subsystem of nonlinear switched systems, the nonlinear switched systems can be modeled as the switched T–S fuzzy systems. Many significant results have been obtained for switched T–S fuzzy systems [17,18,19,20].

During the past decades, the state estimation and filtering problems for dynamic systems have also received considerable attention because of their practical applications in the signal processing and control. Among the various methods of state estimation, the \(H_\infty\) filtering keeps attracting more and more attention [21,22,23,24]. The advantage of \(H_\infty\) filtering is that there is no restriction on the statistical properties of disturbances, which is more general than the classical Kalman filtering [25]. So far, the \(H_\infty\) filtering problem of switched systems has been extensively investigated [26,27,28,29,30]. On the other hand, the passivity theory was an effective tool to analyze and synthesize the dynamical systems [31, 32]. Furthermore, the passivity concept was extended to switched systems [33]. Then, a natural problem arises: Can the \(H_\infty\) filtering problem and the passive filtering problem of nonlinear switched systems be solved in a unified framework? This motivates the study of this paper.

Very recently, some works have studied the mixed \(H_\infty\) and passive filtering problem for singular systems with time delays [34], networked Markov jump systems with impulses [35] and discrete fuzzy neural networks with stochastic jumps and time delays [36]. However, different from these works, the mixed \(H_\infty\) and passive filtering problem of switched systems will be another case. On the one hand, it has been pointed out that the switched systems can only achieve a weighted \(H_\infty\) performance [37]; On the other hand, the existence of switching among the subsystems makes the mixed \(H_\infty\) and passive filtering problem of switched systems much more complicated. Therefore, it is important and necessary for us to study the mixed \(H_\infty\) and passive filtering problem of switched systems.

In most of the work about the \(H_\infty\) filter design for switched systems, all the subsystems of switched systems are assumed to be stable. However, switched systems with unstable subsystems are inevitably encountered in many real plants, e.g., controller failures or sensor faults [38,39,40]. Some efforts have been made to study the stability analysis problem of switched systems with unstable subsystems [41, 42]. To design more general filters for switched systems, this work studies the mixed \(H_\infty\) and passive filtering problem of switched systems with unstable subsystems. It should be pointed out that if the switched systems contain unstable subsystems, the filtering error systems obtained by using the augmentation technique will contain unstable filtering error subsystems. When the switched systems switch to the unstable subsystem, the states of filtering error systems will become divergent. To overcome this problem, a set of mode-dependent filters of a Luenberger-like observer type are constructed in this paper. Through designing appropriate filter gains, the filter error systems will not contain any unstable filtering error subsystems even if the existence of unstable subsystem in the switched systems.

The main contributions of this paper are listed as follows: (1) A new performance index is proposed for switched systems. Based on this new performance index, the weighted \(H_\infty\) filtering problem and the passive filtering problem for nonlinear switched systems with unstable subsystems are solved in a unified framework. (2) The states of the filtering error systems constructed by the augmentation technique will be divergent when unstable subsystems are activated. This problem is addressed in this paper. (3) New sufficient conditions for the existence of mixed \(H_\infty\) and passive filters of nonlinear switched systems with unstable subsystems are obtained. (4) The obtained conditions are more general because of using this new performance index. (5) The obtained results can be used to study the filtering problem for other systems. (6) Compared with some existing work [30], the filters designed by our approach can guarantee a better \(H_\infty\) performance and have a less computational burden.

The rest of this paper is organized as follows. Section 2 gives preliminaries and problem formulation. The main results are given in Sect. 3. Numerical examples are provided in Sect. 4. Finally, some conclusions are given in Sect. 5.

Notations The notations used in this paper are fairly standard. N denotes the set of the natural numbers. I and 0 represent the identity matrix and zero matrix, respectively, in the block matrix with appropriate dimensions. The symbol “\(*\)” in a matrix stands for the transposed elements in the symmetric positions. The subscript “T” is the matrix transposition. The n-dimensional Euclidean space is denoted by \({R^n}\). The notation \(\left\| {\;}\cdot {\;} \right\|\) refers to the Euclidean vector norm. \({L_2}[0,\infty )\) is the space of square-integrable functions and for \(v(t) \in {L_2}[0,\infty )\), and its norm is given by \({\left\| {v(t)} \right\| _2} = \sqrt{\int _0^\infty v(t)^T v(t)\hbox {d}t}\). \({\mathcal {C}}^1\) denotes the space of continuously differentiable functions. A continuous function \(\alpha\) : \([0, \infty )\) \(\rightarrow\) \([0,\infty )\) is said to be of class \({\mathcal {K}}\) if it is strictly increasing and \(\alpha (0)=0\). If \(\alpha\) is also unbounded, then it is said to be of class \({\mathcal {K}}_{\infty }\). A function \(\beta :[0,\infty ) \times [0,\infty ) \rightarrow [0,\infty )\) is said to be of class \({\mathcal {KL}}\) if \(\beta (\cdot ,t)\) is of class \({\mathcal {K}}\) for each fixed \(t \ge 0\) and \(\beta (s,t)\) decreases to 0 as \(t \rightarrow \infty\) for each fixed \(s \ge 0\). We use \(P > 0 ( \ge , < , \le )\) to denote a positive definite (semi-positive definite, negative definite, semi-negative definite) matrix P. If not explicitly stated, matrices are assumed to have compatible dimensions.

2 Preliminaries and Problem Formulation

Let us consider the following continuous-time nonlinear switched systems

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = {f_{\sigma (t)}}(x(t),w(t)), \\ y(t) = {s_{\sigma (t)}}(x(t),w(t)), \\ z(t) = {u_{\sigma (t)}}(x(t)), \\ \end{array} \right. \end{aligned}$$
(1)

where \(x(t) \in R^{n_x}\) is the state vector, \(y(t) \in R^{n_y}\) is the measurement vector, \(z(t) \in R^{n_z}\) is the output signal to be estimated, and \(w(t) \in R^{n_w}\) is the disturbance input that belongs to \(L_2[0,\infty )\). A piecewise constant function of time \(\sigma (t) : [0, +\infty ) \rightarrow {\mathcal {S}} = \{ 1, 2, \ldots , N\}\) is the switching signal, where N is the number of subsystems. For a switching sequence \(0 = t_0< t_1< \cdots< t_k< t_{k + 1} < \cdots\), \(\sigma (t)\) is continuous from right everywhere. When \(t \in [{t_k},{t_{k + 1}})\), the \(\sigma (t_k) = p\) (\(p \in {\mathcal {S}}\)) subsystem is activated. In this paper, the p subsystem can be either stable or unstable. It is supposed that there are \(g (1\le g < N)\) stable subsystems and \(N - g\) unstable subsystems. For brevity, we denote \({\mathcal {S}}_s \triangleq \{1, 2, \ldots , g\}\), \({\mathcal {S}}_u \triangleq \{g+1, g+2, \ldots , N\}\). \({\mathcal {S}}_s\) and \({\mathcal {S}}_u\) are the sets of stable subsystems and unstable subsystems, respectively, and \({\mathcal {S}}_s \bigcup {\mathcal {S}}_u = {\mathcal {S}}\).

The rule m for the subsystem p: IF \({\nu _{p1}}(t)\) is \({M_{p1m}}\) and \(\cdots\) and \({\nu _{pv}}(t)\) is \({M_{pvm}}\), THEN

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = A_{pm} x(t) + B_{pm} w(t), \\ y(t) = C_{pm} x(t) + D_{pm} w(t), \\ z(t) = E_{pm} x(t), \\ \end{array} \right. \end{aligned}$$
(2)

where \({\nu _p}(t) = (\nu _{p1}(t),\nu _{p2}(t), \ldots , \nu _{pv}(t))\) are some measurable premise variables, and \({M_{pjm}}(j = 1,2, \ldots ,v)\) are fuzzy sets. For the m local model of the p subsystem, \(A_{pm}\), \(B_{pm}\), \(C_{pm}\), \(D_{pm}\) and \(E_{pm}\) are constant real matrices with appropriate dimensions. The matrices \(C_{pm}\) are assumed to have full row rank.

Using “fuzzy blending,” the final output of the p subsystem is inferred as follows

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = \sum \limits _{m = 1}^{r} h_{pm}(t)\left[ A_{pm}x(t) + B_{pm}w(t) \right] , \\ y(t) = \sum \limits _{m = 1}^{r} h_{pm}(t)\left[ C_{pm}x(t) + D_{pm}w(t) \right] , \\ z(t) = \sum \limits _{m = 1}^{r} h_{pm}(t)E_{pm}x(t), \\ \end{array} \right. \end{aligned}$$
(3)

where \(h_{pm}(t) = w_{pm}(t)/\sum \nolimits _{m = 1}^{r} w_{pm}(t)\), \(w_{pm}(t) = \prod \nolimits _{j = 1}^v M_{pjm}(\nu _{pj}(t))\), r is the number of IF–THEN rules, and \(M_{pjm}(\nu _{pj}(t))\) is the grade of the membership function of \(\nu _{pj}\) in \({M_{pjm}}\). It is assumed that \({w_{pm}}(t) \ge 0\) for all t, \(m = 1,2, \ldots , r\). It is obvious that the normalized membership function \(h_{pm}(t)\) satisfies

$$\begin{aligned} h_{pm}(t)\ge 0, \quad \sum \limits _{m = 1}^{r} h_{pm}(t) = 1. \end{aligned}$$
(4)

In this paper, we consider to design the following mode-dependent filter of a Luenberger-like observer type for switched T–S fuzzy system (3).

Rule m: IF \({\nu _{p1}}(t)\) is \({M_{p1m}}\) and \(\cdots\) and \({\nu _{pv}}(t)\) is \({M_{pvm}}\), THEN

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_f(t) = A_{pm} x_f(t) + L_{pm} (y(t) - y_f(t)), \\ y_f(t) = C_{pm} x_f(t), \\ z_f(t) = E_{pm} x_f(t), \\ \end{array} \right. \end{aligned}$$
(5)

where \(L_{pm}\) are the filter parameters to be designed. The final output of the filter is inferred as follows

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_f(t) = \sum \limits _{m = 1}^{r} h_{pm}(t)\left[ A_{pm} x_f(t) + L_{pm} (y(t) - y_f(t)) \right] , \\ y_f(t) = \sum \limits _{m = 1}^{r} h_{pm}(t) C_{pm} x_f(t), \\ z_f(t) = \sum \limits _{m = 1}^{r} h_{pm}(t) E_{pm} x_f(t). \\ \end{array} \right. \end{aligned}$$
(6)

By combing (3) with (6) and defining \(x_e(t) = x(t) - x_f(t)\), \(z_e(t) = z(t) - z_f(t)\), the following filtering error subsystem can be obtained

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_e(t) = \bar{A}_p(t) x_e(t) + \bar{B}_p(t) w(t), \\ z_e(t) = E_p(t) x_e(t), \\ \end{array} \right. \end{aligned}$$
(7)

where \(\bar{A}_p(t)\), \(\bar{B}_p(t)\) and \(E_p(t)\) are defined as follows

$$\begin{aligned} \bar{A}_p(t)= & {} \sum \limits _{m = 1}^{r} \sum \limits _{n = 1}^{r} h_{pm}(t)h_{pn}(t) \left[ A_{pm} - L_{pm} C_{pn}\right] , \\ \bar{B}_p(t)= & {} \sum \limits _{m = 1}^{r} \sum \limits _{n = 1}^{r} h_{pm}(t)h_{pn}(t) \left[ B_{pm} - L_{pm} D_{pn} \right] , \\ E_p(t)= & {} \sum \limits _{m = 1}^{r} h_{pm}(t) E_{pm}. \end{aligned}$$

Some definitions are presented in the end of this section, which will be used to obtain the main results of this paper.

Definition 1

[1] Filtering error system (7) with \(w(t) \equiv 0\) is globally uniformly asymptotically stable (GUAS) if there exists a class \({\mathcal {KL}}\) function \(\beta\) such that for all initial conditions \(x_e(t_0)\) and all switching signals \(\sigma (t)\), the solutions of (7) satisfy the following inequality

$$\begin{aligned} \left\| x_e(t) \right\| \le \beta (\left\| x_e(t_0) \right\| ,t), \quad \forall t \ge {t_0}. \end{aligned}$$
(8)

Definition 2

[2] For a switching signal \(\sigma (t)\) and any \(T_2 \ge T_1 \ge 0\), let \(N_{\sigma (t)}(T_1,T_2)\) denote the number of switching of \(\sigma (t)\) over \((T_1, T_2)\). We say that \(\sigma (t)\) has an average dwell time \(\tau _{a}\) if there exist two constants \(N_0 \ge 0\) (Here we call \(N_0\) the chatter bound) and \(\tau _{a}>0\) such that the following inequality holds:

$$\begin{aligned} N_{\sigma (t)}(T_1, T_2) \le N_0 + \frac{T_2 - T_1}{\tau _a}. \end{aligned}$$
(9)

Definition 3

For \(\gamma > 0\), \(\lambda > 0\), \(0 \le \psi \le 1\), all \(t > 0\) and any nonzero \(w(t) \in L_2[0,\infty )\), if under zero initial condition (i.e., \(x_e(t_0)=0\)), the following inequality holds

$$\begin{aligned} \int _0^{t} \left[ -\gamma ^{-1} \psi e^{-\lambda s} e^T(s)e(s) + 2(1 - \psi ) e^T(s) w(s) \right] \hbox {d}s \ge -\gamma \int _0^{t} w^T(s)w(s)\hbox {d}s, \end{aligned}$$
(10)

filtering error system (7) is said to have a mixed weighted \(H_\infty\) and passivity performance \(\gamma\). \(\psi\) denotes a weighting parameter that represents the trade-off between the weighted \(H_\infty\) performance and the passivity performance.

Remark 1

As shown in Definition 3 that by setting \(\psi = 1\), inequality (10) reduces to the weighted \(H_\infty\) performance index [29, 30, 37]. Letting \(\psi = 0\), inequality (10) becomes the passivity performance index [33].

The mixed \(H_\infty\) and passive filtering problem considered in our work can be described as follows: For a given scalar \(\gamma > 0\), determine filters (6) such that:

  1. (1)

    Filtering error system (7) is GUAS when \(w(t) = 0\).

  2. (2)

    Filtering error system (7) can achieve the mixed weighted \(H_\infty\) and passivity performance index described by (10) under zero initial conditions for any nonzero \(w(t) \in L_2[0, \infty )\).

3 Main Results

In order to obtain the main results of our work, the following lemmas are needed.

Lemma 1

Consider the continuous-time nonlinear switched systems (1) with \(w(t) \equiv 0\), and let \(\eta _s < 0\), \(\eta _u > 0\) and \(\lambda \ge 1\) be given constants. \(\forall \left( \sigma (t_k) = p, \sigma (t_k^-) = q \right) \in {\mathcal {S}} \times {\mathcal {S}}, p \ne q\), if there exist positive definite \({\mathbb {C}}^{1}\) functions \(\bar{V}_p(x(t)):{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}\), with \(\bar{V}_{\sigma (t_0)}(x(t_0)) \equiv 0\) satisfying the following inequalities

$$\begin{aligned} \dot{\bar{V}}_{p}(x(t))\le & {} \eta _s \bar{V}_p(x(t)), \quad p \in {\mathcal {S}}_s, \end{aligned}$$
(11)
$$\begin{aligned} \dot{\bar{V}}_{p}(x(t))\le & {} \eta _u \bar{V}_p(x(t)), \quad p \in {\mathcal {S}}_u, \end{aligned}$$
(12)

and

$$\begin{aligned} \bar{V}_p(x(t_k))\le \lambda \bar{V}_q(x(t_k^-)), \end{aligned}$$
(13)

the nonlinear switched systems (1) with \(w(t) \equiv 0\) are GUAS for any switching signal satisfying

$$\begin{aligned} \left\{ \begin{array}{ll} \tau _{s} \ge -\frac{\ln {\lambda }}{\eta _s}, &{}(\eta _s< 0,\, p \in {\mathcal {S}}_s), \\ \tau _{u} \ge \tau _{u}^*, &{}(\eta _u> 0,\,\forall \tau _{u}^*>0, p \in {\mathcal {S}}_u), \\ \frac{T^-}{T^+}>\frac{\gamma ^+ + \gamma ^*}{\gamma ^- - \gamma ^*}, &{}(0<\gamma ^*<\gamma ^-), \end{array} \right. \end{aligned}$$
(14)

where \(T^- = \sum _{p = 1}^g T_p(t,0)\) and \(T^+ = \sum _{p = g+1}^N T_p(t,0)\) correspond to the total running time of stable and unstable subsystems, respectively, \(-\gamma ^- = \eta _s + \frac{\ln \lambda }{\tau _{s}}\), and \(\gamma ^+ = \eta _u + \frac{\ln \lambda }{\tau _{u}}\).

Proof

The proof of Lemma 1 is similar to that of Lemma 2 in [42]. It is omitted here. \(\square\)

Remark 2

In Lemma 1, \(\eta _s\) denotes the decline rate of the Lyapunov function of stable subsystems. \(\eta _u\) represents the increasing rate of the Lyapunov function of unstable subsystems. Lemma 1 shows if the ratio of running time of stable subsystems and unstable subsystems is no less than a certain constant, the nonlinear switched systems with unstable subsystems can still be stable.

Lemma 2

Consider filtering error system (7) and let \(\alpha> 0, \gamma > 0\) and \(\mu \ge 1\) be given constants. \(\forall (\sigma (t_k) = p, \sigma (t_k^-) = q) \in {\mathcal {S}} \times {\mathcal {S}}, p \ne q\), if there exist positive definite \({\mathcal {C}}^1\) functions \(V_{p}(x(t))\): \(R^n \rightarrow R\), with \(V_{\sigma (t_0)}(x_e(t_0)) \equiv 0\) satisfying

$$\begin{aligned} V_p(x_e(t_k)) \le \mu V_q(x_e(t_k^-)), \end{aligned}$$
(15)

and

$$\begin{aligned} \dot{V}_p(x_e(t)) \le -\alpha V_p(x_e(t)) - J(t), \end{aligned}$$
(16)

where \(J(t) = \gamma ^{-1} \psi e^T(t)e(t) - 2(1 - \psi ) e^T(t) w(t) - \gamma w^T(t)w(t)\), filtering error system (7) is GUAS for any switching signal satisfying

$$\begin{aligned} \tau _{a} \ge \tau _{a}^* = \displaystyle \frac{\ln \mu }{\alpha }, \end{aligned}$$
(17)

and has a mixed weighted \(H_\infty\) and passivity performance index.

Proof

Together (15) with (16) and by induction, one can obtain

$$\begin{aligned} {V}_{\sigma (t)}(x_e(t))&\le e^{-\alpha (t-t_k)} {V}_{\sigma (t_k)}(x_e(t_k)) - \int _{t_k}^t e^{-\alpha (t-s)}J(s)\hbox {d}s \nonumber \\&\le \mu e^{-\alpha (t-t_k)} {V}_{\sigma (t_{k-1})}(x_e(t_k^-)) - \int _{t_k}^t e^{-\alpha (t-s)}J(s)\hbox {d}s \nonumber \\&\le \mu e^{-\alpha (t-t_k)}\left[ e^{-\alpha (t_k - t_{k-1}))}{V}_{\sigma (t_{k-1})}(x_e(t_{k-1})) - \int _{t_{k-1}}^{t_k} e^{-\alpha (t_k - s)}J(s)\hbox {d}s \right] \nonumber \\&\quad - \int _{t_k}^t e^{-\alpha (t-s)}J(s)\hbox {d}s \nonumber \\&\le \cdots \nonumber \\&\le \mu ^{N_{\sigma }(0,t)} e^{-\alpha t} {V}_{\sigma (t_0)}(x_e(t_0)) - \int _{0}^{t} \mu ^{N_{\sigma }(s,t)} e^{-\alpha (t - s)} J(s)\hbox {d}s \nonumber \\&= \Lambda (t) - \int _{0}^{t} \mu ^{N_{\sigma }(s,t)} e^{-\alpha (t - s)} J(s)\hbox {d}s, \end{aligned}$$
(18)

where

$$\begin{aligned} \Lambda (t) = \mu ^{N_{\sigma }(0,t)} e^{-\alpha t} V_{\sigma (t_0)}(x_e(t_0)). \end{aligned}$$
(19)

From Definitions 2 and (19), one can get the following inequality

$$\begin{aligned} \Lambda (t) \le \exp \left\{ \left( \frac{\ln \mu }{\tau _a} -\alpha \right) t \right\} V_{\sigma (t_0)}(x_e(t_0)). \end{aligned}$$
(20)

If supposing

$$\begin{aligned} \frac{\ln \mu }{\tau _a} -\alpha \le 0, \end{aligned}$$
(21)

one can from inequality (20) get a sufficient condition that guarantees the GUAS of filtering error system (7). Inequality (21) can be rewritten as follows

$$\begin{aligned} \tau _{a} \ge \tau _{a}^* = \frac{\ln \mu }{\alpha }. \end{aligned}$$

Then it can be concluded if (17) is satisfied, \({V}_{\sigma (t)}(x_e(t)) \rightarrow 0\) as \(t \rightarrow \infty\).

Next, it will be shown that filtering error system (7) can achieve a mixed weighted \(H_\infty\) and passivity performance. From (18) and under zero initial conditions, it can be obtained

$$\begin{aligned} \int _{0}^{t} e^{-\alpha (t - s) + N_{\sigma }(s,t)\ln \mu } J(s)\hbox {d}s \le 0. \end{aligned}$$
(22)

Since \(J(s) = \gamma ^{-1} \psi e^T(s)e(s) - 2(1 - \psi ) e^T(s) w(s) -\gamma w^T(s)w(s)\), it can be obtained

$$\begin{aligned}&\int _{0}^{t} e^{-\alpha (t - s) + N_{\sigma }(s,t)\ln \mu } \gamma ^{-1} \psi e^T(s)e(s)\hbox {d}s \nonumber \\&\quad \le \int _{0}^{t} e^{-\alpha (t - s) + N_{\sigma }(s,t)\ln \mu } [2(1 - \psi ) e^T(s) w(s) + \gamma w^T(s)w(s)]\hbox {d}s. \end{aligned}$$
(23)

Multiplying both sides of (23) by \(e^{- N_{\sigma }(0,t)\ln \mu }\), one can obtain the following inequality

$$\begin{aligned}&\int _{0}^{t} e^{-\alpha (t - s) - N_{\sigma }(0,s)\ln \mu } \gamma ^{-1} \psi e^T(s)e(s)\hbox {d}s \nonumber \\&\quad \le \int _{0}^{t} e^{-\alpha (t - s) - N_{\sigma }(0,s)\ln \mu } [2(1 - \psi ) e^T(s) w(s) + \gamma w^T(s)w(s)]\hbox {d}s. \end{aligned}$$
(24)

From Definition 2, one can obtain

$$\begin{aligned} -N_{\sigma }(0, s) \ge -\frac{s}{\tau _a}. \end{aligned}$$
(25)

Combining (24) with (25), it can be obtained

$$\begin{aligned} \int _{0}^{t} e^{-\alpha (t - s) - \frac{s\ln \mu }{\tau _a}} \gamma ^{-1} \psi e^T(s)e(s)\hbox {d}s \le \int _{0}^{t} e^{-\alpha (t - s)} [2(1 - \psi ) e^T(s) w(s) + \gamma w^T(s)w(s)]\hbox {d}s. \end{aligned}$$
(26)

Inequality (26) is equivalent to the following inequality

$$\begin{aligned} \int _{0}^{t} e^{-\alpha t + s(\alpha - \frac{\ln \mu }{\tau _a})} \gamma ^{-1} \psi e^T(s)e(s)\hbox {d}s \le \int _{0}^{t} e^{-\alpha (t - s)} [2(1 - \psi ) e^T(s) w(s) + \gamma w^T(s)w(s)]\hbox {d}s. \end{aligned}$$
(27)

The following inequality can be obtained from (17)

$$\begin{aligned} \alpha - \frac{\ln \mu }{\tau _a} \ge 0. \end{aligned}$$
(28)

Together (27) with (28), one can get

$$\begin{aligned} \int _{0}^{t} e^{-\alpha t} \gamma ^{-1} \psi e^T(s)e(s)\hbox {d}s \le \int _{0}^{t} e^{-\alpha (t - s)} [2(1 - \psi ) e^T(s) w(s) + \gamma w^T(s)w(s)]\hbox {d}s. \end{aligned}$$
(29)

Following (29), the following inequality holds

$$\begin{aligned} \int _{0}^{t} e^{-\alpha s} \gamma ^{-1} \psi e^T(s)e(s)\hbox {d}s \le \int _{0}^{t} [2(1 - \psi ) e^T(s) w(s) + \gamma w^T(s)w(s)]\hbox {d}s. \end{aligned}$$
(30)

For all \(t > 0\), the following inequality can be obtained from inequality (30)

$$\begin{aligned} \int _0^{t} \left[ -\gamma ^{-1} \psi e^{-\alpha s} e^T(s)e(s) + 2(1 - \psi ) e^T(s) w(s) \right] \hbox {d}s \ge -\gamma \int _0^{t} w^T(s)w(s)\hbox {d}s. \end{aligned}$$
(31)

From Definition 3, it can be concluded that filtering error system (7) achieves a mixed weighted \(H_\infty\) and passivity performance index. The proof is completed. \(\square\)

Based on Lemmas 1 and 2, the following lemma presents new stability conditions which guarantee switched T–S fuzzy system (3) and filtering error system (7) to be GUAS simultaneously.

Lemma 3

Consider switched T–S fuzzy system (3) and filtering error system (7). Let \(\eta _s < 0\), \(\eta _u > 0\), \(\lambda \ge 1\), \(\alpha > 0\), \(\mu \ge 1\) and \(\gamma > 0\) be given constants. \(\forall (p,q) \in ({\mathcal {S}} \times {\mathcal {S}})\), \(p \ne q\), if there exist matrices \(P_p > 0\) and \(Q_p > 0\) satisfying

$$\begin{aligned}&A_p^T(t) P_p + P_p A_p(t) -\eta _s P_p \le 0, \quad p \in {\mathcal {S}}_s, \end{aligned}$$
(32)
$$\begin{aligned}&A_p^T(t) P_p + P_p A_p(t) -\eta _u P_p \le 0, \quad p \in {\mathcal {S}}_u, \end{aligned}$$
(33)
$$ \left[ {\begin{array}{ccc} \bar{A}_p^T(t) Q_p + Q_p \bar{A}_p(t) + \alpha Q_p &{} * &{} * \\ \bar{B}_p^T(t) Q_p - (1- \psi) E_{p}(t)&{} -\gamma I &{} * \\ \sqrt{\psi}E_p(t) &{} 0 &{} -{\gamma} I \\ \end{array}} \right] \le 0, $$
(34)
$$\begin{aligned}&P_p \le \lambda P_q, \end{aligned}$$
(35)
$$\begin{aligned}&Q_p \le \mu Q_q, \end{aligned}$$
(36)

switched T–S fuzzy system (3) with \(w(t) \equiv 0\) is GUAS, and filtering error system (7) is GUAS and has a mixed weighted \(H_\infty\) and passivity performance for any switching signal satisfying:

  1. (1)

    if \(\frac{\ln \mu }{\alpha } \ge -\frac{\ln \lambda }{\eta _s}\),

    $$\begin{aligned} \left\{ \begin{array}{l} \tau _{s} \ge \frac{\ln \mu }{\alpha }, \quad p \in {\mathcal {S}}_s, \\ \tau _{u} \ge \frac{\ln \mu }{\alpha }, \quad p \in {\mathcal {S}}_u, \\ \frac{T^-}{T^+}>\frac{\gamma ^+ + \gamma ^*}{\gamma ^- - \gamma ^*}, \quad (0<\gamma ^*<\gamma ^-), \end{array} \right. \end{aligned}$$
    (37)
  2. (2)

    if \(\frac{\ln \mu }{\alpha } < -\frac{\ln {\lambda }}{\eta _s}\),

    $$\begin{aligned} \left\{ \begin{array}{l} \tau _{s} \ge -\frac{\ln {\lambda }}{\eta _s}, \quad p \in {\mathcal {S}}_s, \\ \tau _{u} \ge \frac{\ln \mu }{\alpha }, \quad p \in {\mathcal {S}}_u, \\ \frac{T^-}{T^+}>\frac{\gamma ^+ + \gamma ^*}{\gamma ^- - \gamma ^*}, \quad (0<\gamma ^*<\gamma ^-). \end{array} \right. \end{aligned}$$
    (38)

Proof

Choose the following Lyapunov function for switched T–S fuzzy system (3)

$$\begin{aligned} \bar{V}_p(t) = x^T(t) P_p x(t). \end{aligned}$$
(39)

And choose the following Lyapunov function for filtering error system (7)

$$\begin{aligned} V_p(t) = x_e^T(t) Q_p x_e(t). \end{aligned}$$
(40)

Assuming the subsystem is switching from the q subsystem to the p subsystem. From system (3) with \(w(t) \equiv 0\), one can obtain

$$\begin{aligned} \dot{\bar{V}}_{p}(x(t)) - \eta _s \bar{V}_p(x(t))= x^T(t)(A_p^T(t) P_p + P_p A_p(t) -\eta _s P_p)x(t), \end{aligned}$$
(41)
$$\begin{aligned} \dot{\bar{V}}_{p}(x(t)) - \eta _u \bar{V}_p(x(t))= x^T(t)(A_p^T(t) P_p + P_p A_p(t) -\eta _u P_p)x(t). \end{aligned}$$
(42)

From inequalities (32) and (33), the following inequalities can be obtained

$$\begin{aligned} \dot{\bar{V}}_{p}(x(t))\le & {} \eta _s \bar{V}_p(x(t)),\\ \dot{\bar{V}}_{p}(x(t))\le & {} \eta _u \bar{V}_p(x(t)). \end{aligned}$$

From filtering error system (7), one can obtain

$$\begin{aligned} \dot{V}_p(t) + \alpha V_p(t) + z_e^T(t) z_e(t) - \gamma ^2 w^T(t)w(t) = \eta ^T(t)\mathop \Pi \eta (t), \end{aligned}$$

where

$$\begin{aligned} \eta ^T(t)= & {} \left[ x_e^T(t), w^T(t) \right] ,\\ \mathop \Pi= & {} \left[ {\begin{array}{cc} Q_p \bar{A}_p(t) + \bar{A}_p^T(t) Q_p + \alpha Q_p + \gamma^{-1}\psi E_p^T(t) E_p(t) &{} * \\ \bar{B}_p^T(t) Q_p - (1-\psi) E_{p} (t)&{} -\gamma I \\ \end{array}} \right] . \end{aligned}$$

By Schur complement, it can be concluded that inequality (34) implies \(\mathop \Pi <0\). Then the following inequality can be obtained

$$\begin{aligned} \dot{V}_p(t) \le -\alpha V_p(t) - J(t). \end{aligned}$$

Since \(P_p \le \lambda P_q\), the following inequality can be obtained

$$\begin{aligned} \bar{V}_p(x(t_k))\le \lambda \bar{V}_q(x(t_k^-)). \end{aligned}$$

Due to \(Q_p \le \mu Q_q\), the following inequality can be obtained

$$\begin{aligned} V_p(x(t_k)) \le \mu V_q(x(t_k^-)). \end{aligned}$$

In this paper, the synchronous switching is considered, which means that the p filtering error subsystem is activated simultaneously if the p subsystem is activated. Therefore, to guarantee the switched T–S fuzzy system and the filtering error system to be GUAS simultaneously, the switching signal designed in this paper should be satisfied (8) and (11) simultaneously. If \(\frac{\ln \mu }{\alpha } \ge -\frac{\ln \lambda }{\eta _s}\), (37) can guarantee the switching signal to be designed satisfies (14) and (17) simultaneously. For the case \(\frac{\ln \mu }{\alpha } < -\frac{\ln {\lambda }}{\eta _s}\), (38) can guarantee the switching signal satisfies (14) and (17) simultaneously.

By Lemmas 1 and 2, one can conclude that for any switching signal satisfying (37) or (38), switched T–S fuzzy system (3) with \(w(t) \equiv 0\) is GUAS, and filtering error system (7) is GUAS and has a mixed weighted \(H_\infty\) and passivity performance index. The proof is completed. \(\square\)

Remark 3

As shown in Lemma 3, for any switching signal satisfying (37) or (38), the stability of switched T–S fuzzy system (3) is guaranteed by inequalities (32), (33) and (35). The filtering error system is said to be GUAS and has a mixed weighted \(H_\infty\) and passivity performance index if inequalities (34) and (36) hold. Therefore, the conditions shown in Lemma 3 can guarantee the switched T–S fuzzy system and the filtering error system to be GUAS simultaneously.

Lemma 3 provides a new method for the filter design of nonlinear switched systems with unstable subsystems. However, in Lemma 3, the matrix variables \(Q_p\) are coupled with filter parameter matrices \(L_p(t)\) in (34), which makes the filter design difficult. To deal with this problem, a decoupling technique is introduced, which is shown in the following lemma.

Lemma 4

Consider switched T–S fuzzy system (3) and filtering error system (7). Let \(\eta _s < 0\), \(\eta _u > 0\), \(\lambda \ge 1\), \(\alpha > 0\), \(\mu \ge 1\) and \(\gamma > 0\) be given constants. \(\forall (p,q) \in ({\mathcal {S}} \times {\mathcal {S}})\), \(p \ne q\), if there exist matrices \(P_p > 0\), \(Q_p > 0\) and \(U_p(t)\) satisfying

$$\begin{aligned}&A_p^T(t) P_p + P_p A_p(t) -\eta _s P_p \le 0, \quad p \in {\mathcal {S}}_s, \end{aligned}$$
(43)
$$\begin{aligned}&A_p^T(t) P_p + P_p A_p(t) -\eta _u P_p \le 0, \quad p \in {\mathcal {S}}_u, \end{aligned}$$
(44)
$$\left[ {\begin{array}{ccc} Q_p A_p(t) - U_p(t) C_p(t) + A_p^T(t) Q_p -C_p^T(t) U_p^T(t) + \alpha Q_p &{} * &{} * \\ B_p^T(t) Q_p - D_p^T(t) U_p^T(t) - (1-\psi )E_p(t) &{} -\gamma I &{} * \\ \sqrt{\psi } E_p(t) &{} 0 &{} -\gamma I \\ \end{array}} \right] \le 0,$$
(45)
$$\begin{aligned}&P_p \le \lambda P_q, \end{aligned}$$
(46)
$$\begin{aligned}&Q_p \le \mu Q_q, \end{aligned}$$
(47)

switched T–S fuzzy system (3) with \(w(t) \equiv 0\) is GUAS, and filtering error system (7) is GUAS and has a mixed weighted \(H_\infty\) and passivity performance index for any switching signal satisfying (37) or (38). Moreover, the filter gains \(L_p(t)\) are given as follows

$$\begin{aligned} L_p(t) = Q_p^{-1} U_p(t). \end{aligned}$$
(48)

Proof

From (48), one can obtain

$$\begin{aligned} U_p(t) = Q_p L_p(t). \end{aligned}$$
(49)

Substituting (49) into (45), one can get inequality (34). Together with (43), (44), (46), (47) and by Lemma 3, it can be concluded that for any switching signal satisfying (37) or (38), switched T–S fuzzy system (3) with \(w(t) \equiv 0\) is GUAS, and filtering error system (7) is GUAS and has a mixed weighted \(H_\infty\) and passivity performance index. The proof is completed.\(\square\)

Based on the above Lemmas, we will design a set of mode-dependent filters and find a set of admissible switching signals such that switched T–S fuzzy system (3) with \(w(t) \equiv 0\) is GUAS, and filtering error system (7) is GUAS and has a mixed weighted \(H_\infty\) and passivity performance index.

Theorem 1

Consider switched T–S fuzzy system (3) and filtering error system (7). Let \(\eta _s < 0\), \(\eta _u > 0\), \(\lambda \ge 1\), \(\alpha > 0\), \(\mu \ge 1\) and \(\gamma > 0\) be given constants. \(\forall (p,q) \in ({\mathcal {S}} \times {\mathcal {S}})\), \(p \ne q\), if there exist matrices \(P_p > 0\), \(Q_p > 0\) and \(U_{pm}\) satisfying

$$\begin{aligned}&A_{pm}^T P_p + P_p A_{pm} -\eta _s P_p \le 0, \quad p \in {\mathcal {S}}_s, \end{aligned}$$
(50)
$$\begin{aligned}&A_{pm}^T P_p + P_p A_{pm} -\eta _u P_p \le 0, \quad p \in {\mathcal {S}}_u, \end{aligned}$$
(51)
$$\begin{aligned}&\Lambda _{pmn} + \Lambda _{pnm} \le 0, \quad m \le n, \end{aligned}$$
(52)
$$\begin{aligned}&P_p \le \lambda P_q, \end{aligned}$$
(53)
$$\begin{aligned}&Q_p \le \mu Q_q, \end{aligned}$$
(54)

where

$$\begin{aligned} \Lambda _{pmn} = \left[ {\begin{array}{ccc} Q_p A_{pm} - U_{pm} C_{pn} + A_{pm}^T Q_p -C_{pn}^T U_{pm}^T + \alpha Q_p &{} * &{} * \\ B_{pm}^T Q_p - D_{pn}^T U_{pm}^T - (1-\psi )E_{pm} &{} -\gamma I &{} * \\ \sqrt{\psi } E_{pm} &{} 0 &{} -\gamma I \\ \end{array}} \right] , \end{aligned}$$

switched T–S fuzzy system (3) with \(w(t) \equiv 0\) is GUAS, and filtering error system (7) is GUAS and has a mixed weighted \(H_\infty\) and passivity performance index for any switching signal satisfying (37) or (38). Moreover, the filter gains \(L_{pm}\) are given as

$$\begin{aligned} L_{pm} = Q_p^{-1} U_{pm}. \end{aligned}$$
(55)

Proof

Denote the left side of (43–(45) as \(\bar{\Theta }_p(t)\), \(\hat{\Theta }_p(t)\) and \(\Lambda _p(t)\), respectively. If the conditions in Theorem 1 are satisfied, it can be obtained

$$\begin{aligned} \bar{\Theta }_p(t)= & {} \sum \limits _{m = 1}^{r} h_{pm}(t) (A_{pm}^T P_p + P_p A_{pm} -\eta _s P_p)\nonumber \\\le & {} 0, \end{aligned}$$
(56)
$$\begin{aligned} \hat{\Theta }_p(t)= & {} \sum \limits _{m = 1}^{r} h_{pm}(t) (A_{pm}^T P_p + P_p A_{pm} -\eta _p P_p)\nonumber \\\le & {} 0, \end{aligned}$$
(57)

and

$$\begin{aligned} \Lambda _p(t)= & {} \sum \limits _{m = 1}^{r} \sum \limits _{n = 1}^{r} h_{pm}(t) h_{pn}(t) \Lambda _{pmn}\nonumber \\= & {} \sum \limits _{m = 1}^{r} h_{pm}^2(t) \Lambda _{pmm} + \sum \limits _{m = 1}^{r} \sum \limits _{n > m}^{r} h_{pm}(t) h_{pn}(t)(\Lambda _{pmn} + \Lambda _{pnm})\nonumber \\\le & {} 0. \end{aligned}$$
(58)

Together (56)–(58), (53) with (54), and by Lemma 4, it can be concluded that the mixed \(H_\infty\) and passive filtering problem for switched T–S fuzzy systems (3) is solved. Finally, it can be concluded from (48) that the filter gains in (6) can be constructed by (55). The proof is completed. \(\square\)

Remark 4

It should be pointed out that the results of Theorem 1 can also be applied to design the weighted \(H_\infty\) filters (\(\psi = 1\)) and the passive filters (\(\psi = 0\)) for continuous-time switched T–S fuzzy systems with unstable subsystems. Furthermore, the results of Theorem 1 can also be used to study the corresponding filtering problem for general T–S fuzzy systems if we do not consider the switching behavior. It is worth mentioning that the results of Theorem 1 can be reduced to study the corresponding filtering problem of linear switched systems or general linear systems without considering the switching behavior.

Remark 5

In our method, in order to reduce the fuzzy approximation error, much more fuzzy rules should be used, which will cause to greater computational complexity.

Remark 6

All of the parameters \(\eta _s < 0\), \(\eta _u > 0\), \(\lambda \ge 1\), \(\alpha > 0\) and \(\mu \ge 1\) of Theorem 1 have their physical meaning. The parameter \(\eta _s\) denotes the decline rate of the Lyapunov function of stable subsystems. The parameter \(\eta _u\) represents the increasing rate of the Lyapunov function of unstable subsystems. The parameter \(\alpha\) denotes the decline rate of the Lyapunov function of the filtering error systems. The parameters \(\lambda\) and \(\mu\) denote the increasing rate bound from the q subsystem to the p subsystem. In practice, we can adjust the values of these parameters to make the systems reach the desired performance.

Theorem 1 provides new sufficient conditions for the filter design of nonlinear switched systems with unstable subsystems. Under these conditions, a mixed weighted \(H_\infty\) and passivity performance \(\gamma\) can be achieved. It should be noted that, for given parameters (\(\eta _s\), \(\eta _u\), \(\lambda\), \(\alpha\), \(\mu\) and \(\psi\)), these conditions are LMIs which are not only over the matrix variables but also over the scalar \(\gamma\). Therefore, for given parameters (\(\eta _s\), \(\eta _u\), \(\lambda\), \(\alpha\), \(\mu\) and \(\psi\)), when \(\gamma\) is given, Theorem 1 provides the methods to design the filters for nonlinear switched systems with unstable subsystems. On the other hand, when \(\gamma\) is unknown, the optimal (minimum) mixed weighted \(H_\infty\) and passivity performance \(\gamma\) can be obtained and solved as the following LMIs optimization problem

$$\begin{aligned} \begin{array}{ll} &{} \min \quad \gamma , \\ &{} \text{ s.t. } \quad (48)-(52). \end{array} \end{aligned}$$
(59)

Remark 7

For fixed constant parameters \(\eta _s\), \(\eta _u\), \(\lambda\), \(\alpha\), \(\mu\) and \(\psi\), an optimal \(\gamma\) can be obtained by (59). However, how to determine suitable values of \(\eta _s\), \(\eta _u\), \(\lambda\), \(\alpha\), \(\mu\) and \(\psi\) which lead to the smallest \(\gamma\) is an open problem. In practice, based on specific system parameters, an acceptable mixed weighted \(H_\infty\) and passivity performance \(\gamma\) as well as a reasonable average dwell time \(\tau _a\) should be tried to obtain.

It is shown in Remark 4 that Theorem 1 can be applied to study the mixed \(H_\infty\) and passive filtering problem for switched T–S fuzzy systems with all stable subsystems. For this case, the following corollary can be obtained.

Corollary 1

Consider filtering error system (7), and let \(\alpha > 0\), \(\mu \ge 1\) and \(\gamma > 0\) be given constants. \(\forall (p,q) \in ({\mathcal {S}} \times {\mathcal {S}})\), \(p \ne q\), if there exist matrices \(Q_p > 0\) and \(U_{pm}\) satisfying

$$\begin{aligned}&\left[ {\begin{array}{ccc} Q_p A_{pm} - U_{pm} C_{pn} + A_{pm}^T Q_p -C_{pn}^T U_{pm}^T + \alpha Q_p &{} * &{} * \\ B_{pm}^T Q_p - D_{pn}^T U_{pm}^T - (1-\psi )E_{pm} &{} -\gamma I &{} * \\ \sqrt{\psi } E_{pm} &{} 0 &{} -\gamma I \\ \end{array}} \right] \le 0, \end{aligned}$$
(60)
$$\begin{aligned}&Q_p \le \mu Q_q, \end{aligned}$$
(61)

filtering error system (7) is GUAS and has a mixed weighted \(H_\infty\) and passivity performance index for any switching signal satisfying

$$\begin{aligned} \tau _{a} \ge \frac{\ln \mu }{\alpha }. \end{aligned}$$
(62)

Moreover, the filter gains \(L_{pm}\) are given as

$$\begin{aligned} L_{pm} = Q_p^{-1} U_{pm}. \end{aligned}$$
(63)

Recently, the \(H_\infty\) filtering problem for continuous-time linear switched systems with all stable subsystems was solved in [30]. As shown in Remark 4, our results can also be reduced to study the \(H_\infty\) filtering problem for linear switched systems with all stable subsystems. To make a comparison between our method and the approach in [30], Corollary 2 is introduced. Here, let us consider the following linear switched system with all stable subsystems

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = A_{p} x(t) + B_{p} w(t), \\ y(t) = C_{p} x(t) + D_{p} w(t), \\ z(t) = E_{p} x(t). \\ \end{array} \right. \end{aligned}$$
(64)

Using our method, the following filtering error system can be obtained for linear switched system (64)

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_e(t) = (A_{p} - L_{p} C_{p}) x_e(t) + (B_{p} - L_{p} D_{p}) w(t), \\ z_e(t) = E_p x_e(t), \\ \end{array} \right. \end{aligned}$$
(65)

where \(L_{p}\) are the filter parameters to be designed.

For filtering error system (65), the following corollary is given, which ensures filtering error system (65) is GUAS and has a weighted \(H_\infty\) performance index.

Corollary 2

Consider filtering error system (65) and let \(\alpha > 0\), \(\mu \ge 1\) and \(\gamma > 0\) be given constants. \(\forall (p,q) \in ({\mathcal {S}} \times {\mathcal {S}})\), \(p \ne q\), if there exist matrices \(Q_p > 0\) and \(U_{p}\) satisfying

$$\begin{aligned}&Q_p \le \mu Q_q, \end{aligned}$$
(66)
$$\begin{aligned}&\left[ {\begin{array}{ccc} Q_p A_{p} - U_{p} C_{p} + A_{p}^T Q_p -C_{p}^T U_{p}^T + \alpha Q_p &{} * &{} * \\ B_{p}^T Q_p - D_{p}^T U_{p}^T &{} -\gamma ^2 I &{} * \\ E_{p} &{} 0 &{} -I \\ \end{array}} \right] < 0, \end{aligned}$$
(67)

filtering error system (65) is GUAS and has a weighted \(H_\infty\) performance for any switching signal satisfying

$$\begin{aligned} \tau = \frac{\ln \mu }{\alpha }. \end{aligned}$$
(68)

Moreover, the filter gains \(L_{p}\) are given as follows

$$\begin{aligned} L_{p} = Q_p^{-1} U_{p}. \end{aligned}$$
(69)

Proof

The proof of Corollary 2 is similar to that of Theorem 1, so it is omitted here. \(\square\)

Remark 8

Comparing Corollary 2 with Theorem 3.3 of [30], we find that under the same conditions the number of LMIs in Corollary 2 is less than that of Theorem 3.3 of [30]. Therefore, we can conclude that under the same conditions the filters designed by our approach can guarantee a better \(H_\infty\) performance and have a less computational burden than the filters obtained in [30].

4 Numerical Example

In this section, two numerical examples are provided to illustrate the effectiveness and advantage of the obtained results.

Example 1

Consider switched T–S fuzzy system (3) consisting of two subsystems, and each subsystem has two fuzzy rules, where

$$\begin{aligned} A_{11}= & {} \left[ {\begin{array}{cc} -4 &{} -1 \\ -15 &{} -5 \\ \end{array}} \right] , A_{12} = \left[ {\begin{array}{cc} -4 &{} -0.8 \\ -10 &{} -6 \\ \end{array}} \right] , A_{21} = \left[ {\begin{array}{cc} -5 &{} -2.45 \\ -84 &{} -40 \\ \end{array}} \right] , A_{22} = \left[ {\begin{array}{cc} -4.5 &{} -2.2 \\ -78 &{} -38 \\ \end{array}} \right] , \\ B_{11}= & {} \left[ {\begin{array}{c} 0.3 \\ 0.4 \\ \end{array}} \right] , B_{12} = \left[ {\begin{array}{c} -0.3 \\ 0.5 \\ \end{array}} \right] , B_{21} = \left[ {\begin{array}{c} -2 \\ -1 \\ \end{array}} \right] , B_{22} = \left[ {\begin{array}{c} 2 \\ -1.5 \\ \end{array}} \right] ,\\ C_{11}= & {} \left[ {\begin{array}{cc} 1 &{} -0.5 \\ -1 &{} 1 \\ \end{array}} \right] , C_{12} = \left[ {\begin{array}{cc} 1 &{} 1 \\ -1 &{} 1.2 \\ \end{array}} \right] , C_{21} = \left[ {\begin{array}{cc} 1 &{} 1.5 \\ 0.9 &{} 0.5 \\ \end{array}} \right] , C_{22} = \left[ {\begin{array}{cc} 1 &{} 1.5 \\ 1 &{} 0.5 \\ \end{array}} \right] ,\\ D_{11}= & {} \left[ {\begin{array}{c} 0.15 \\ 0.1 \\ \end{array}} \right] , D_{12} = \left[ {\begin{array}{c} 0.1 \\ 0.1 \\ \end{array}} \right] , D_{21} = \left[ {\begin{array}{c} 0.12 \\ 0.1 \\ \end{array}} \right] , D_{22} = \left[ {\begin{array}{c} -0.12 \\ 0.1 \\ \end{array}} \right] ,\\ E_{11}= & {} \left[ {\begin{array}{cc} -0.5 &{} 0.5 \\ \end{array}} \right] , E_{12} = \left[ {\begin{array}{cc} -0.2 &{} 0.2 \\ \end{array}} \right] , E_{21} = \left[ {\begin{array}{cc} -0.5 &{} 0.2 \\ \end{array}} \right] , E_{22} = \left[ {\begin{array}{cc} -1 &{} 1 \\ \end{array}} \right] . \end{aligned}$$

The fuzzy membership functions are taken as

$$\begin{aligned} \left\{ \begin{array}{l} h_{11} = {\sin ^2}(x_1 + 0.5),\quad h_{12} = 1 - h_{11}, \\ h_{21} = 1 - \displaystyle \frac{1}{{1 + \exp ( - 3{x_2}/(0.5 - \pi /2))}} \times \frac{1}{{1 + \exp ( - 3{x_2}/(0.5 + \pi /2))}}, \quad h_{22} = 1 - h_{21}. \end{array}\right. \end{aligned}$$

The state responses of subsystem 1 and subsystem 2 with initial conditions \(x(t_0) = [1,2]^T\) are shown in Fig. 1. It is shown in Fig. 1 that subsystem 1 is stable and subsystem 2 is unstable.

Fig. 1
figure 1

State responses of subsystem 1 and subsystem 2

Full size image

The parameters used in Theorem 1 are given as: \(\eta _s = -0.5\), \(\eta _u = 0.3\), \(\lambda = 1.1\), \(\alpha = 0.15\), \(\mu = 1.1\), and \(\gamma = 1\). Then, one can obtain \(-\ln \lambda /\eta _s = 0.1906\) and \(\ln \mu /\alpha = 0.6354\). Since \(\ln \mu /\alpha > -\ln \lambda /\eta _s\), by Theorem 1, the ADT for the stable subsystem 1 should be \(\tau _{s} \ge \ln \mu /\alpha\), and the ADT for the unstable subsystem 2 should be \(\tau _{u} \ge \ln \mu /\alpha\). Moreover, the ratio of running time of the stable subsystem 1 and the unstable subsystem 2 should be more than a constant.

To illustrate the effectiveness of the obtained results, the ADT for subsystem 1 and subsystem 2 are chosen as \(\tau _{s} = 2\), \(\tau _{u} = 1\) and \(\gamma ^* = 0.1\). By Theorem 1, the ratio of running time of the stable subsystem 1 and the unstable subsystem 2 should satisfy \(T^-/T^+ \ge 1.6529\). Through assuming the initial condition to be \(x(t_0)=[1, 2]^T\), the state response of the nonlinear switched system is shown in Fig. 2. In this case, the ADT for subsystem 1 and subsystem 2 is \(\tau _{s} = 2\), \(\tau _{u} = 1\), and \(T^-/T^+ = 2.333\), which satisfy the conditions specified by Theorem 1. It is shown in Fig. 2 that the nonlinear switched system with unstable subsystem can still be GUAS if the switching signals satisfy certain conditions.

Fig. 2
figure 2

State response of the nonlinear switched system with \(\tau _{s} = 2\), \(\tau _{u} = 1\) and \(T^-/T^+ = 2.333\)

Full size image

Based on the obtained results, a set of mode-dependent mixed \(H_\infty\) and passive filters will be designed to estimate the output of switched T–S fuzzy system (3). The parameter \(\psi\) is set to be \(\psi = 0.5\). Using the LMI toolbox to solve the LMIs (50)–(54) and by (55), the filter parameters of filters (6) can be obtained as follows:

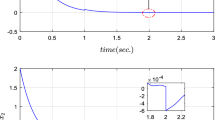
$$\begin{aligned} L_{11}= & {} \left[ {\begin{array}{cc} 0.8957 &{} -0.2620 \\ -15.9366 &{} 11.8548 \\ \end{array}} \right] , L_{12} = \left[ {\begin{array}{cc} -1.0422 &{} -1.0607 \\ -1.7380 &{} 14.0076 \\ \end{array}} \right] ,\\ L_{21}= & {} \left[ {\begin{array}{cc} -9.4326 &{} 1.3622 \\ -2.8314 &{} -24.6014 \\ \end{array}} \right] , L_{22} = \left[ {\begin{array}{cc} -9.6611 &{} 3.7921 \\ -1.4653 &{} -24.7346 \\ \end{array}} \right] . \end{aligned}$$

Furthermore, the disturbance input is set as \(w(t) = \cos (0.2t)\exp (-0.5t)\). The output signal z(t), the filter output signal \(z_f(t)\) and the filtering error e(t) are shown in Fig. 3. As shown in Fig. 3, the designed filters under the switching signals can effectively estimate the output of the nonlinear switched systems with unstable subsystems. Especially, when the nonlinear switched system switches to the unstable subsystem, the filter can still well estimate the output of the nonlinear switched system. From Figs. 2 and 3, it can be concluded that if the switching signals satisfy the conditions of Theorem 1, the nonlinear switched systems and the filtering error systems can be GUAS simultaneously even if the existence of unstable subsystems.

Fig. 3
figure 3

The output signal z(t), the filter output signal \(z_f(t)\) and the filtering error e(t)

Full size image

Example 2

Taking the \(H_\infty\) performance index as an example, a comparison between our work and a related peer work [30] is given to show the advantage of our results. Let us consider linear switched system (64). The system parameters are borrowed from [30], which are given as follows

$$\begin{aligned} A_{1}= & {} \left[ {\begin{array}{cc} -10 &{} 0 \\ -91.19 &{} -40 \\ \end{array}} \right] , A_{2} = \left[ {\begin{array}{cc} -1.2 &{} 1 \\ -75 &{} -25 \\ \end{array}} \right] , B_{1} = \left[ {\begin{array}{c} 0.3 \\ 0.5 \\ \end{array}} \right] , B_{2} = \left[ {\begin{array}{c} 1.95 \\ 1.4 \\ \end{array}} \right] ,\\ C_{1}= & {} [{\begin{array}{cc} 1 &{} 1 \\ \end{array}}], C_{2} = [{\begin{array}{cc} 1.4 &{} 1.2 \\ \end{array}}], D_{1} = 0.2, D_{2} = 0.05,\\ E_{1}= & {} [{\begin{array}{cc} 0.2 &{} 0.3 \\ \end{array}} ], E_{2} = [{\begin{array}{cc} 1 &{} 0.8 \\ \end{array}} ].\\ \end{aligned}$$

To complete the comparison, some parameters used in [30] are set as \(\beta = 0\) and \(T_M = 0\), which means that the asynchronous switching is not considered. For different \(\alpha\) and \(\mu\) sets, setting the same parameters for Corollary 2 and Theorem 3.3 of [30], the minimum values \(\gamma _{\min }^2\) for these two approaches are computed. The computation results are shown in Table 1. All the results of Table 1 reveal that under the same conditions Corollary 2 of our work has a better performance than Theorem 3.3 of [30].

Table 1 The minimum value \(\gamma _{\min }^2\) by different work for different \(\alpha\) and \(\mu\)
Full size table

5 Conclusion

The mixed \(H_\infty\) and passive filtering problem for continuous-time nonlinear switched systems with unstable subsystems is investigated in this paper. The T–S fuzzy model is used to represent each nonlinear subsystem. A set of mode-dependent filters of a Luenberger-like observer type are constructed in this paper, which can guarantee the filtering error system to be GUAS even if the existence of unstable subsystems. Using the MLFs approach and the ADT technique, new sufficient conditions for the existence of mixed weighted \(H_\infty\) and passive filters are obtained. All these conditions can be expressed as a set of LMIs. The desired filters can be constructed by solving these LMIs. It is remarked that the obtained results can also be applied to study the corresponding filtering problem for other systems. Finally, two numerical examples are given to demonstrate the effectiveness and advantage of the obtained results.

It has been shown that the T–S fuzzy affine dynamic model has much improved function approximation capabilities [8, 9]. Therefore, it would be our future work to investigate the filtering problem for the switched T–S fuzzy affine systems.