A coupled approach to investigate the entropy parameter dynamics in open-channel flow with submerged flexible vegetation

Abstract

Submerged flexible vegetation modifies the open-channel dynamics by altering the hydrological and ecological characteristics. The velocity profiles at the top and bottom of the vegetation layer indicate the stochastic nature of the flow and hydraulic parameters. The randomness in the velocity profile at different degrees of submergence and vegetation density is explicitly represented by the channel entropy parameter. This study proposes a novel entropy-based vertical velocity distribution model by linking the 2D shallow-water model (SWM) with Shanon’s entropy theory. The convergence of the coupled model at different $\frac{\text{flow depth}}{\text{vegetation height}}$ is investigated by comparing the computed model results with the mixing length model and the published experimental data. Results indicate that the predicted velocity profiles from the entropy model agree with the experimental results than the mixing length model. Although the channel entropy parameter (M) is invariant with the flood dynamics, the submerged vegetation influences the drag force and modifies the flow-entropy nexus. The relationship between the vegetation densities and the channel entropy parameter at different $\frac{\text{flow depth}}{\text{vegetation height}}$ is derived, and a power-law profile is observed.

Introduction

Velocity distribution in vegetated channels influences the channel roughness, turbulence intensity, shear stress characteristics, water quality parameters, etc., and consequently reduces the flow velocity, solute, and sediment transport processes. The submerged and emergent flexible vegetation is abundant on the streams modifying the channel flow dynamics and the aquatic ecology, which turns out to be a prime concern for hydrologists and environmentalists (Armanini et al. 2005; Chakraborty and Sarkar 2020). The precise estimation of the velocity profile under the vegetated environment helps in understanding the river hydraulics at different flow regimes (Wang et al. 2021; Albayrak et al. 2012). Depending on the flexural rigidity, the instream vegetation is classified as flexible and rigid (Koftis and Prinos 2018). The bending profile of the flexible vegetation varies with the variation of the imposed load, increasing the degree of complexity in the vertical velocity profile estimation, especially in submerged conditions. Chen (2010) proposed an integrated approach to solve the large-deflection cantilever beam problems. He suggested that the same hypothesis can model the deflected shape of flexible plants under various flow events.

Under submerged conditions, the multilayered models are quite widespread for vertical velocity distribution in open-channel flow. Particularly, two-layer models divide the water column into the top-free water layer and the bottom vegetation layer and distribute the velocity from the channel bed to the free surface. For instance, Klopstra et al. (1996) proposed an analytical model to estimate the velocity profile in open channels having submerged flexible stems. The turbulent stresses in the bottom layers are calculated from the Boussinesq eddy viscosity theory. The mixing length model is adopted in the free water layer for the velocity distribution in their model. The velocity profile within the vegetation zone is uniformly distributed, and above the vegetation zone, logarithmic distribution is adopted (Yang and Choi 2010; Huai et al. 2021). Huai et al. (2013) divided the flow regime into a top-free surface layer and a bottom vegetated layer. Using a constant drag approach, they distributed the velocity profile in the outer zone with the wake law (Coles 1956). They considered the modified wake law separately in the vegetated and non-vegetated regions because of the complexity in secondary current and free surface effects. Erduran and Kutija (2003) stated that the velocity profile in a flow area with flexible stems having a high rigidity factor could be approximated from the rigid vegetation velocity profile. However, for high degree deformation, the behavior is not the same. He proposed a quasi-three-dimensional model to study the vegetated flow characteristics, and the model findings are validated with the experimental results.

According to Chen and Kao (2011), the mixing length models induce some errors in the vertical velocity profile near the free water surface in vegetated channel flows. This discrepancy in the flow profile is primarily due to the resistance from the submerged stems. However, mixing length models also fails to capture the flow anomaly due to the secondary current effect between the low and high momentum fluids, causing the maximum flow velocity below the free surface through the flux exchange from rigid sidewalls to the channel center (Moramarco et al. 2004; Baruah and Sarma 2020). Another shortcoming of the mixing length model is the requirement of multiple hydraulic and geometric parameters for velocity profile estimation, viz., shear velocity, energy slope, hydraulic radius, etc. Assessing these parameters under a complex flow environment is challenging and tedious (Moramarco and Singh 2010). However, the entropy theory proposed by Chiu (1989) is another alternative method for vertical profile estimation in open channels. It is a single-layer theorem derived from Shannon’s entropy using the principle of maximum entropy. The requirement of fewer input parameters and the capability of capturing the velocity dip make the entropy model advantageous over the logarithmic distribution models in open-channel flow (Chiu and Said 1995). Various researchers used this model in open-channel hydraulics from the advent of the study on velocity distribution by entropy theory (Vyas et al. 2020). The entire structure of the entropy formulation is based on a single parameter termed entropy parameter ($M$). The entropy parameter $(M)$ is a function of the average and maximum velocity in a cross-section (Kundu 2017a, b; Kundu and Ghoshal 2019).

Submerged vegetation often acts as a cover and habitat for the marine species and maintains an intact aquatic ecosystem. In natural flow domains with submerged vegetation, the fluctuations in $\frac{\text{flow depth}}{\text{vegetation height}}\left(\frac{H}{{h}_{v}}\right)$ inevitably influence the vertical velocity structure. The changes in the flow parameters at different $H/{h}_{v}$ and vegetation density eventually alter the velocity distribution and modifies the energy gradients in open-channel flow. For instance, during a high flood event, the increase in the flow depth leads to a higher degree of $H/{h}_{v}$ than that in low-flow events, and under those circumstances, it is necessary to evaluate the accuracy and performance of the velocity distribution models under the vegetated environment. Previous studies indicated the development of several analytical and experimental models for vertical velocity estimation in vegetated sections. However, the inadequacy of those models to compute the vertical velocity profiles under adverse flow and morphological conditions restricts their application in natural terrain. The analytical models are valid for steady-state flow and cannot incorporate the bed profile anomaly in velocity distribution. Moreover, no such literature has been found that relates the channel entropy parameter with the vegetation characteristics and flow parameter.

With this understanding, a novel entropy-based two-layer vertical velocity distribution model is proposed in this study to investigate the flow-entropy nexus in the vegetated environment with submerged flexible stem. The two-dimensional full shallow-water equation is solved using the explicit McCormack predictor–corrector finite-difference method in MATLAB. The model stability at each time step is checked using the Courant Criteria. The flow depth and velocity from the SWM are integrated into the entropy model to compute the vertical velocity profiles. In the second phase of the study, the relationship between the channel entropy parameter, vegetation density, and the degree of submergence is evaluated. So far, the author's knowledge, none of such attempts have been made to establish the dependency of the channel entropy parameter with the flexible vegetation characteristics in an open channel. The computed results are compared with the conventional mixing length model and also with the published experimental datasets reported by Jarvela (2005) and Kubrak (2008).

Methodology

Governing equation and numerical scheme

Full 2D Saint Venant equations (continuity and momentum equation) are solved using an explicit Mc-Cormack predictor–corrector scheme in MATLAB. The vegetation effect on the flow dynamics is incorporated by adding the drag force in the source term of the momentum equation,

$$ \frac{\partial }{\partial t}\left[ \eta \right] + \frac{\partial }{\partial x}\left[ {hu} \right] + \frac{\partial }{\partial y}\left[ {hv} \right] = 0, $$

(1)

$$ \frac{\partial }{\partial t}\left[ {hu} \right] + \frac{\partial }{\partial x}\left[ {\left\{ {hu^{2} } \right\}} \right] + \frac{\partial }{\partial y}\left[ {\left\{ {huv} \right\}} \right] = - gh\left( {\frac{d\eta }{{dx}} - s_{fx} } \right) - \frac{{F_{Dx} }}{\rho }, $$

(2)

$$ \frac{\partial }{\partial t}\left[ {hv} \right] + \frac{\partial }{\partial x}\left[ {\left\{ {huv} \right\}} \right] + \frac{\partial }{\partial y}\left[ {\left\{ {hVv} \right\}} \right] = - gh\left( {\frac{d\eta }{{dy}} - s_{fy} } \right)\, - \frac{{F_{Dy} }}{\rho }, $$

(3)

where $\eta \mathrm{ is}$ the water surface elevation (m), $hu$ and $hv$ are the unit discharges in x- and y-direction, $\frac{d\eta }{\partial x}$ and $\frac{d\eta }{\partial y}$ water surface gradients, h is the flow depth (m) measured from the bed up to the free surface, ${s}_{fx}$ and ${s}_{fy}$ are the bed friction components in the longitudinal and transverse direction, ρ is the density of water, and ${F}_{Dx}$ and ${F}_{Dy}$ are the drag force due to the vegetation. The drag force per unit area from the vegetation in the x- and y-direction is expressed as,

$$ F_{Dx} = \,\frac{1}{2} \times C_{D} \times \rho \times A_{v} \times u_{v} \times \sqrt {u_{v}^{2} + v_{v}^{2} } , $$

(4a)

$$ F_{Dy} = \,\frac{1}{2} \times C_{D} \times \rho \times A_{v} \times v_{v} \times \sqrt {u_{v}^{2} + v_{v}^{2} .} $$

(4b)

In the above expression, ${A}_{v}$= projected or frontal area of vegetation, ${C}_{D}$= drag coefficient,m = vegetation density, and ${u}_{v}$ and ${v}_{v}$ are the apparent velocities in x and y-direction. The expression for ${u}_{v}$ and ${v}_{v}$ is proposed by Stone and Shen (2002) as,

$$ u_{v} = {\text{u}}\left( {\frac{{h_{v} }}{h}} \right)^{\frac{1}{2}} ;v_{v} = {\text{ v}}\left( {\frac{{h_{v} }}{h}} \right)^{\frac{1}{2}} , $$

(5a, b)

${h}_{v}$ is the projected height of the flexible vegetation.

An Explicit Mc-Cormack predictor–corrector scheme with second-order accuracy is used in the solution of the unsteady flow equations. A splitting algorithm is employed in the solution by dividing the two-dimensional equations into four one-dimensional equations. The computed flow variables are substituted and solved successively. The x-direction momentum equations and the mass conservation equation are solved in the first cycle, and y-direction equations are solved in the next cycle. Variables determined during the predictor part used in the corrector part. The TVD scheme used in the model suppressed the non-physical oscillations near the steep regions.

Boundary condition and stability

The initial and boundary conditions are essential for the smooth functioning of the numerical model. In the hydrodynamic simulation, a discharge value is provided as the initial condition. The solid walls are simulated as a no-slip boundary(Anderson and Wendt 1995), i.e., both the streamwise and transverse velocity components are assigned with a zero value. At the upstream boundary, the flow discharge and the water depth corresponding to that discharge are set as the downstream boundary.

The CFL condition best assures the stability of the Mc-Cormack scheme used in the formulation. The following expression specifies Courant number:

$$ C_{r} = {\text{ delt}} \times \left( {(\sqrt {\left( {u^{2} + v^{2} } \right)) + (g \times h} )} \right)/{\text{min }}\left( {{\text{delx}},{\text{ dely}}} \right); $$

(5c)

delx and dely represents grid size in longitudinal and lateral direction, g is the acceleration due to gravity, and delt is the time step. Model is found to be stable and convergent when the courant number is less than 1.

Computation of deflected height of the flexible vegetation

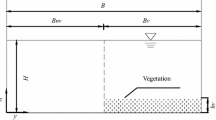
The bending profile of the flexible stem is estimated using the large-deflection cantilever beam approach with an assumption that the effects of vegetation gravity and buoyant force due to the water column are negligible. In Fig. 1, z coordinates represent the distance from the bed to the top of the vegetation; L is the flexible vegetation height before bending and ${h}_{v}$ is the projected deflection height.

Fig. 1

Deflection of flexible vegetation

Imposed load P, on a single flexible stem due to the upstream water column is expressed as (Huai et al. 2013),

$$ P = \frac{{\rho gS_{f} H}}{m}, $$

(6)

where m is the vegetation density per unit area, ${s}_{\mathrm{f}}$ is the energy slope, $\rho$ is the density of water (KN/${m}^{3})$, H is the computed flow depth from the shallow-water model(m), $\theta$ is the angle of rotation after bending, $EI$ is the flexural rigidity (N${\mathrm{m}}^{2})$, and g is the acceleration due to gravity. Load on the stem tends to bend the flexible structure, and curve length (S) of the element can be obtained from (Huai et al. 2013),

$$ S = \mathop \smallint \limits_{0}^{{h_{v} }} \sqrt {\frac{dz}{{1 - \left[ {\left( \frac{P}{2EI} \right)\left( {\frac{{z^{3} }}{{3h_{v} }} - z^{2} + zh_{v} } \right)} \right]^{2} }}} . $$

(7)

The imposed load (P) on the vegetation stems under various flow events is calculated from Eq. 1. The variation of load P depends upon the magnitude of the flood wave and the vegetation density. The computed water depth and the velocity from the shallow-water model are used in Eq. 6 to calculate the load on the stem. Depending upon the load P, the degree of curvature of the flexible stem varies, and the same is calculated by employing the large deflection beam theory (Eq. 7). An iterative technique is used in the calculation of the bending height (${h}_{v}$) of the vegetation after the application of load. Initially, a default value of ${h}_{v}$ is assumed and substituted in Eq. 7. The iteration continues till abs (s-L) <  = € where € = 0.00001 and ${h}_{v}$ is computed.

Velocity distribution in the vegetated layer

The velocity profile is estimated from the momentum equation in the vegetation layer by applying the force balancing between the Reynolds shear stress, vegetation roughness, and vegetation roughness,

$$ \frac{d\tau }{{dz}} + \rho gS_{f} - \frac{{dF_{x} }}{dz} = 0. $$

(8)

Net Resultant force (${F}_{x})$ on the bending vegetation is evaluated from the drag force and friction force component (Bootle 1971) and, finally, the velocity profile in the vegetation layer is expressed as (Huai et al. 2013),

$$ \alpha = \sqrt {\frac{{C_{d} mD}}{{0.3\left( {H - h_{v} } \right)}}} $$

(9)

$$ U = \frac{{2gS_{f} \left\{ {\alpha hexp\left( {\alpha \left( {z - h_{v} } \right)} \right) + 1} \right\}}}{{\sqrt {mD\left\{ {C_{d} \left[ {1 - \left( \frac{P}{2EI} \right)^{2} \left( {\frac{{z^{3} }}{{3h_{v} }} - z^{2} + zh_{v} } \right)^{2} } \right] + C_{f} C_{p} \left( {\left( \frac{P}{2EI} \right)\left( {\frac{{z^{3} }}{{3h_{v} }} - z^{2} + zh_{v} } \right)^{3} } \right)/\sqrt {1 - \left[ {\left( \frac{P}{2EI} \right)\left( {\frac{{z^{3} }}{{3h_{v} }} - z^{2} + zh_{v} } \right)^{2} } \right]} } \right\}} }}. $$

(10a)

At $z={h}_{v}$

$$ u_{v} = \frac{{2gS_{f} \left( {\alpha h + 1} \right)}}{{\sqrt {mD\left\{ {C_{d} \left[ {1 - \left( {\frac{{Ph_{v} }}{6EI}} \right)^{2} } \right] + C_{f} C_{p} \left( {\left( {\frac{{Ph_{v}^{2} }}{6EI}} \right)^{3} } \right)/\sqrt {1 - \left[ {\left( {\frac{{Ph_{v}^{2} }}{6EI}} \right)^{2} } \right]} } \right\}} }}; $$

(10b)

${C}_{d}=$ drag coefficient, ${C}_{p}$=perimeter of the stem cross-section and ${C}_{f}=$ friction coefficient, and $\alpha =$ constant relating the hydraulic and vegetation characteristic

By substituting the deflected vegetation height (${h}_{v}$), imposed load (P), and the friction slope (${s}_{f}$) in Eqs. 5(a) and 5(b), the velocity profile in the vegetated region and at the tip of the stem is calculated.

Mixing length model for velocity distribution

Based on the force balancing, the momentum equation in the non-vegetated layer is written as (Huai et al. 2009),

$$ \frac{d\tau }{{dz}} + \rho gS_{f} = 0. $$

(11)

Integral of the Eq. 14 from free water layer to upward (z-axis) yields the Reynolds stress distribution as,

$$ - \rho u^{\prime}w^{\prime} = \rho gl\left( {h - z} \right). $$

(12)

From Prandtl mixing length hypothesis, LHS of Eq. 15 can be expressed as

$$ u^{\prime}w^{\prime} = l^{2} \left( {\frac{dy}{{dz}}} \right)^{2} . $$

(13)

Combining these equations, (Huai et al. 2009) proposed the following expression for velocity distribution in the non-vegetated portion:

$$ \frac{u}{{u_{*} }} = \left( {\frac{H}{{H - h_{v} }}} \right)\frac{1}{k}ln\left( {\frac{z}{{h_{v} }}} \right) + u_{av} , $$

(14)

where u = streamwise velocity, ${u}_{*}=\mathrm{shear velocity }\left(\sqrt{g{S}_{f}(H-{h}_{v})}\right)$, H = total flow depth, ${h}_{v}=\mathrm{vegetation height}$, $k=$ von-karman constant (0.41), $\mathrm{and }{u}_{av}$= velocity at the tip of the vegetation element.

Entropy model for velocity distribution

The expression of vertical velocity distribution from the entropy concept was primarily derived by Chiu (1989) using the maximum entropy principle (POME) to the Shannon entropy (Shannon 1948). A unique coordinate system was defined for representing the flow, such that the velocities are a function of $\xi$. The Velocity is assumed to increase from zero (at $\xi ={\xi }_{o}$) to a maximum value ${u}_{max}$ (at ${\xi =\xi }_{max}$),

$$ \frac{u}{{u_{max} }} = \frac{1}{M}\ln \left[ {1 + \left( {e^{M} - 1} \right)\frac{{\xi - \xi_{o} }}{{\xi_{max} - \xi_{o} }}} \right]. $$

(15)

The term $\frac{\xi -{\xi }_{o}}{{\xi }_{max}-{\xi }_{o}}$ is analogous to the cumulative distribution function, which can be represented as

$$ \frac{{\xi - \xi_{o} }}{{\xi_{max} - \xi_{o} }} = \mathop \smallint \limits_{0}^{u} k\left( u \right)du, $$

(16)

where $k\left(u\right)$, $0\le u\le {u}_{max}$ represents the probability density function, which can be obtained by maximizing Shannon’s entropy(Shannon 1948; Chiu 1989)

$$ k\left( u \right) = e^{{a_{1} + a_{2} u}} . $$

(17)

Here the parameters ${a}_{1}$ and ${a}_{2}$ are related to $M$ and ${u}_{max}$ by the following equations (Chiu and Tung 2002):

$$ a_{2} = \frac{M}{{u_{max} }}, $$

(18)

$$ e^{{a_{1} }} = \frac{M}{{u_{max} \left( {e^{M} - 1} \right)}}, $$

(19)

If the velocity $u$ increases with respect to the vertical distance $y$ from zero at the channel bed ($y$= 0) to the ${u}_{max}$ at the surface ($y=D$), then $\xi$ can be formulated as,

$$ \xi = \frac{y}{D} , \,\,\,\,\,\,\,0 \le \xi \le 1, $$

(20)

The entropy parameter, $M$ which is a characteristic of a channel domain that remains constant (Moramarco et al. 2004), can be related with the average, and maximum velocity in a channel cross-section as (Chiu and Tung 2002)

$$ \phi \left( M \right) = \left( {\frac{{e^{M} }}{{e^{M} - 1}} - \frac{1}{M}} \right) = \frac{{u_{avg} }}{{u_{max} }}, $$

(21)

where, ${u}_{avg}=$ depth-averaged velocity in the vegetated section, ${u}_{max}=$ maximum velocity in the vegetated section, ${y}_{max}=$ location of maximum velocity in the vertical sample, ${y}_{0}$= water depth near the channel bed, $g=$ acceleration due to gravity and $\phi \left(M\right)$ is a function of entropy parameter. The vertical velocity profile is then distributed in the free water layer from the following equation (Ammari et al. 2017):

$$ \frac{u}{{u_{max} }} = \frac{1}{M}ln\left[ {1 + \left( {e^{M} - 1} \right)\left( {\frac{{z - y_{o} }}{{y_{max} - y_{o} }}} \right)} \right]; $$

(22)

$u=$ Velocity at different depths $(z)$.

The classical velocity profile in a vegetated channel in a two-layer region with flexible elements is presented in Fig. 2.

Fig. 2

Velocity profile in an open channel with submerged flexible vegetation

Development of the coupled model

The imposed load (P) on the vegetation stems under various flow events is calculated from Eq. 6. The variation of load P is a function of the magnitude of the flood wave and the vegetation density. Depending upon the load on the stem, the degree of curvature of the flexible stem varies, and the same is calculated by employing the large-deflection beam theory (Eq. 7). An iterative technique is used in the calculation of the bending height (${h}_{v}$) of the vegetation after the application of load. Initially, a default value of ${h}_{v}$ is assumed and substituted in Eq. 7. The iteration continues till abs(s-L) <  = € where € = 0.00001. Substituting the deflected vegetation height (${h}_{v}$), imposed load (P), and the friction slope (${s}_{f}$) in Eq. 10(a) and 10(b), the velocity profile in the vegetated region and at the tip of the stem is calculated.

Entropy theory distributes the vertical velocity profile from the maximum and the mean velocity information in the channel. The basic assumption associated with the entropy theory is the channel entropy parameter (M) is invariant with the flood dynamics (Moramarco and Singh 2010). However, in the vegetated channel, this assumption contradicts the physical understandings. Irrespective of the type of vegetation, the roughness offer by the plants retards the flow velocity and alters the flow characteristic. Depending upon the vegetation characteristics such as the plant density, flexural rigidity, and stem diameter, the mean and average velocity profile varies and thus the entropy parameter. The shallow-water model runs for different flow events at different vegetation characteristics and computes the depth-averaged velocities in the domain. At high vegetation density, the drag force will be more and retards the velocity profile and vice versa. The computed depth average velocities and the observed maximum velocities are substituted in the Eq. 21 and estimate the $\phi \left(M\right)$ and entropy parameter $\left(M\right)$. The entropy parameter is then substituted in Eq. 22 to compute the velocity profile (u) at different depths (z). The programming language used in this study is MATLAB. The details of the coupled model are presented in Fig. 3.

Fig. 3

Flowchart of the proposed model

Experimental datasets used in the simulation

Two experimental datasets have been used during the study to validate the proposed numerical model. In the first case, the performance of the present model is assessed by setting up the model with series of experimental test cases carried out by Kubrak et al. (2008). The model computed output is then compared with the experimental outputs reported in their laboratory flume experiment. Kubrak et al. (2008) conducted the experiments in the hydraulic laboratory containing vegetation without foliage at the department of Hydraulic structure, Warsaw Agricultural University. The experiment was performed in a glass-walled flume of 16 m length, 0.58 m wide, and 0.6 m depth. In their experiment, the cylindrical stems of elliptical cross sections having diameter d1 = 0.00095 m and d2 = 0.0007 m were placed in a removal plate of 3 m length, 0.58 m wide made of PVC. The longitudinal and transverse velocity profiles were measured using a programmable electromagnetic liquid velocity meter. The schematic diagram of the experimental channel is available in (Amreeva and Kubrak 2007). The details of the different test runs of the experimental flume are enlisted in Table 1.

Table 1 Experimental data from Kubrak et al. (2007)

In the second case, the experimental study conducted by Jarvela (2005) is used in the simulation. The experiments were conducted in a 50 m long and 1.1 m-wide recirculating glass-walled flume, where vegetation was rooted in a thin-walled metal box. The average length and width of the stems are 280 mm and 2.8 mm, respectively. The vegetation covered the test area with an average density of 12,000 stems/m² Flow was released from an overhead tank to the flume through a silting basin and a flow straighter. Velocities were measured using a 3D acoustic Doppler velocimeter manufactured by Nortek. Water surface along the test section was measured using a differential pressure transducer in 3–7 longitudinal sections averaging over a period of 30–60 s. Deflected vegetation heights are determined visually using a ruler or a measuring tape fixed to the flume wall. The experimental datasets used in the simulation are presented in Table 2.

Table 2 Experimental data from Järvelä (2005)

Results and discussion

In the first case, the experimental datasets from Kubrak et al. (2008) are used in the simulation. The imposed load is computed for different flow events. The hydrodynamic simulation provides the flow depth and velocity information at different discharges and locations in the channel. The computed velocity profiles from the shallow-water model for experiment numbers 1.2.1 and 4.1.1 is are shown in Fig. 3. In experiment no 1.2.1, a very high vegetation density (m = 10,000) is used with a moderate flow rate of 0.0422 ${\mathrm{m}}^{3}$/s. However, in experiment 4.1.1, vegetation density is significantly lower. The x-axis and y-axis represent the length and width of the channel. The resistance offered by the vegetation retards the flow momentum and reducing the velocity in the channel. The vegetation covers a region of 3×.58 m in the channel, and the computed velocity contour maps indicate that the velocity profile is significantly decreased, as shown in Fig. 4(a, b). The velocity profile from the above figures indicates that in the non-vegetated regions, the maximum velocity lies between 0.09 and 0.14 m/s for the given discharges. However, from the velocity contour maps, it is observed that with the vegetation, the computed depth-averaged velocity is 0.01 m/s to 0.03 m/s. It is observed that the velocity progressively reduces at a higher vegetation density (m = 10,000) region compared to the lower vegetation density (m = 2500).

Fig. 4

Computed depth-averaged velocity profile for experiment: (a) 1.2.1 and (b) 4.1.1

For illustrating the entropy-based model, the present study considered experiment no 4.1.1. After reaching the steady state, the computed water level is substituted in Reynold's stress model to calculate the vertical velocity profile within the vegetation zone and at the crown of the stem. The maximum velocity at the crown is found as 0.67 m/s. The entropy model is used in the free water layer is obtained by subtracting the vegetation depth from the total water depth. The depth-averaged velocities from the hydrodynamic simulation lie between 0.01 and 0.015 m/s, and the maximum velocity is 0.92 m/s. From these two values, Ø (M) and the entropy parameter (M) are calculated and substituted in Eq. 17 to calculate the velocity profile. The computed vertical velocity profiles for different experiments are presented in Fig. 5. The figure indicates that the present model predicts the velocity profiles under different flow events with high accuracy. In the second case, the experimental results reported by Jarvela (2005) are used in the computations. The simulations are performed with nine different degrees of submergence (H/${h}_{v}$=1.49–2.54) at different energy gradients. A similar procedure is adopted for the estimation of vertical velocity profiles.

Fig. 5

Comparison of computed and measured velocity profiles at various experiment numbers (Kubrak et al. 2008)

Both the entropy model and mixing length models are simulated under the same vegetation and flow conditions. Figure 5(a) shows the computed and measured velocity profiles for experiment number 1.1.3. The vegetation density is 10000/${\mathrm{m}}^{2}$ and H/${h}_{v}$ is 1.51, having an energy slope of 0.0087. Both the model output is found satisfactory with the experimental results. However, a small discrepancy (7.10%) is noticed near the free surface in the calculated and measured velocity profile from the mixing length model. The same vegetation density is used in the second case, having an energy slope of 0.0174 and $H/{h}_{v}$ is1.38. Figure 5(b) shows the computed and measured profiles and found that both the model outputs agree with the measured data. The subsequent simulations are carried out at sparse vegetation density having friction slope 0.0087 at $H/{h}_{v}$=1.57and 1.61. Figure 5(c) indicates that at $H/{h}_{v}$=1.57, a satisfactory result is obtained from the entropy model, but a significant anomaly is noticed in the velocity profile computed from the mixing length model. Again, in the next case keeping the same physical flow properties at $H/{h}_{v}$=1.61, the computed profiles show a maximum 10–12% divergence from the experimental results. From Fig. 5(a–d), the results indicate a satisfactory agreement with the experimental results.

In the second case, the experimental results reported by Jarvela (2005) are used in the computations. The simulations are performed with seven different degrees of submergence ($H/{h}_{v}$=1.49–2.54) at different energy gradients. Figure 6(a–g) shows the computed and measured vertical velocity profiles. Although both the model behavior is consistent, the simulations show that irrespective of the vegetation density and friction slope, and the performance of the entropy model in velocity computation is preferable to the mixing length model. The capacity of the entropy model to mimic the near-bed finite velocity gradients helps in converging the solution with the experimental results. With both the experimental datasets, the computed profiles from the entropy model at different degrees of submergence ($\frac{H}{{h}_{v}}$) indicate a good correlation with the measured results than the mixing length model.

Fig. 6

Comparison of computed and measured velocity profiles at various experiment numbers (Järvelä 2005)

The mean velocity in channel cross sections changes as the vegetation density varies from sparse to dense. The velocity profile near the densely distributed submerged flexible vegetation is lower than the sparse vegetation for a given discharge. These velocity variations due to the vegetation also influence the channel entropy parameter (M), a function of $\frac{{U}_{avg}}{{u}_{max}}$. For instance, at a cross-section with high vegetation density, the imposed load on the vegetated region reduces and modifies the current speed compared to the sparse vegetated zone. This anomaly in the flow structure certainly influences the velocity distribution process in the channel section. Different hypothetical vegetation densities are added to the entropy model, and a series of simulations are carried out to establish a relationship between the vegetation characteristics (m,$H/{h}_{v}$) and entropy parameter. The entropy model is applied in seven different flow scenarios having $\frac{H}{{h}_{v}}$ varies from 1.27 to 2.54. Eight different vegetation density is incorporated (2000–10,000/m²) in the entropy model. The interrelation between the entropy parameter and the vegetation density is presented in Fig. 5. It is observed that a power-law relation ($y=a{x}^{b})$ is best suited between the entropy parameter and the vegetation density at different $H/{h}_{v}$(Table 3). As mentioned earlier, from Fig. 7, it is observed that the entropy parameter progressively decreases as the vegetation density changes from sparse to dense.

Table 3 Coefficient of correlation at different H/h_v

Fig. 7

Relation between the vegetation density and entropy parameter

In natural vegetated sections having submerged flexible stems, the measurement of depth-averaged velocity is complex, tedious, and even during monsoon, it is associated with high-risk factors. However, in the present study, the relationship derived between the channel entropy parameter, vegetation density, and degree of submergence can be used to estimate depth-averaged velocity in the open channel. For instance, gathering the vegetation characteristics such as the plant height and the vegetation density, the entropy parameter (M) in any section can be calculated from the derived relationship as presented in Fig. 5. Thus, by knowing the M and the maximum velocity information, the depth-averaged velocity at different sections can be calculated using Eq. 12. Again, from the known M, the vertical velocity profiles to varying degrees of vegetation density and submergence ratio can be derived along the vertical water column (from bed to the free surface).

Conclusion

Vegetation plays a pivotal role in ecosystem dynamics and biodiversity restoration. This work applies a novel entropy-based vertical velocity distribution model in a vegetated channel with submerged flexible stems. The model is run with different vegetation densities, degrees of submergence, and flexural rigidity. A two-dimensional shallow-water model is employed in the study to compute the depth-averaged velocities and flow depth in the channel. The computed velocities are integrated with the entropy model to estimate the vertical profiles in the vegetated region. The performance of the model is evaluated by comparing the computed outputs with the outputs from the mixing length model and the experimental data. However, the results from the mixing length model show some anomaly in the results at a high $H/{h}_{v}$ ratio. Apparently, the entropy model shows a good correlation with the experimental results during each simulation. In the second phase of the study, a relationship between the channel entropy parameter (M) and the vegetation characteristics was derived. Typically, the channel entropy parameter is primarily an indicator of channel geometry and morphological characteristics and invariant with the flow characteristics. However, the varying vegetation density alters the flow patterns leading to the modification of the entropy parameter. The relationship between the entropy parameter and vegetation density is calculated from the model, and a power-law relation is observed between these two parameters. The derived relationship between the entropy parameter and the vegetation characteristics provides a relatively easier approach to estimate the mean velocity in a vegetated channel. The study can be further extended to evaluate the variation of the entropy parameter with the vegetation density by incorporating the sediment characteristics in the channel flow under the vegetated environment.