Introduction

In daily operation of high-speed railway transportations, train services are operated according to a preplanned timetable so that the performance, efficiency and feasibility of the services can be ensured in most scenarios. However, disruption in a railway network may occur due to various unexpected events, which results in train delays and renders the original timetable infeasible [1]. Train delays can be categorized into two types, namely, the primary delays and the secondary delays. Primary delays are the delays caused by external environment factors (e.g., severe weather, flooding or earthquake), maintenance and infrastructures failures (e.g., the breakdown of track circuits, vehicles, communication or signaling systems) and human factors (e.g., longer dwell time, driver’s behaviors). A delayed train could interfere the operations of other trains in turn delaying them (secondary delays). Since the railway timetables are planned with appropriate time margins (referred to as supplement time), minor delays usually do not lead to conflicts and the affected train(s) may be able to recover from the effects of the minor disturbance provided the supplement time in the original timetable. However, in case of a disturbance that causes significant delays to one or more trains, conflicts arise and the original timetable becomes operationally infeasible. The procedure of resolving these conflicts during train operations in a real-time manner by adjusting the train’s operation time, such as arrival/departure/dwell/run time, to obtain a revised and feasible timetable is referred to as Timetable Rescheduling Problem (TRP).

Timetable rescheduling has been a critical and tactic task in daily train operations and works together with long-term dispatching strategies, such as rolling stock and crew rescheduling [2]. In practice, the TRP is usually processed manually by train dispatchers and they make the decision based on their experiences [3]. Two tactics are often employed to reduce train delays and restore the original timetable: (1) reordering, i.e., prioritizing a train over another, (2) retiming, i.e., allocating new arrival and departures times to one or more trains. There are several benchmark strategies for TRP, such as the First-Scheduled-First-Served (FSFS) and the First-Come-First-Serve (FCFS) rescheduling [4], although these strategies may not always lead to the optimal solution because of the complexity of (re)scheduling problem [5]. Furthermore, the time allowance is very limited for a dispatcher to select the tactics, analyze and evaluate alternative decisions to make the appropriate timetable. As a result, it is expected that the computer-aided decision support system for supporting dispatchers work with an appropriate solution should be fast and make the near-optimal decision on reordering and retiming in near real time.

In the literatures, various models and solutions have been proposed [5, 6]. The commonly used models for TRPs are integer programming (IP) models, mixed integer linear programming (MILP) models, alternative graph (AG) models [7] and job-shop models. Similar to the job shop scheduling, the railway TRP is an NP-complete problem [7]. It is very difficult to obtain an optimal rescheduling solution by mathematical optimization approaches, even for state-of-the-art solvers, in reasonable computational time, especially for a large-scale problem. For example, solving the TRP was solved by a branch and bound algorithm, but some instances were unsolved within 2 h [8]. Over 25 min is needed for a typical Lagrangian relaxation decomposition algorithm [9] to reschedule 20 trains with a planning horizon of 120 min. An IP formulations was proposed for timetable rescheduling and demonstrated that all scenarios can be solved about 30 min by CPLEX [10]. However, this is still not applicable in practice, as the expected response time is usually in a few minutes.

It is noteworthy that the TRP can be converted first in many literatures. After converted, there are more expandable operations to reduce computational time. After formulating basic model based on an event-activity network, S. Zhan et al. [11] ignored some additional constraints to improve the efficiency of the computation without losing much quality of the solutions. S. P. Josyula et al. [12] developed a search tree to solve the TRP, where the nodes represent the conflicts and the edges represent rescheduling decisions. A parallel algorithm is designed to solve the real-time railway rescheduling problem by decomposing the sequential depth-first search (DFS). P. Wang et al. [13] developed a modified \({A}^{*}\) algorithm by reducing the scope of the selection and limiting the backtracking capability to save computational time after the railway system is converted into Timed Colored Petri Nets (TCPNs). However, the complex converting and modeling process is not easy to solve, and computational time does not achieve the reasonable requirement.

It is possible to obtain an near-optimal solution within an acceptable computation time by the (meta-)heuristic approaches [14][15]. Z. Feng et al. [16] developed a Tabu search algorithm to solve a multi-objective optimization problem about train routing in a high-speed railway station. S. Dündar et al. [17] used artificial neural networks and genetic algorithms to solve train rescheduling for single-track railways. M. Wang et al. [18] developed a genetic algorithm based on the particle swarm optimization (PSO) to solve the TRP under primary delays. Y. Zhang et al. [19] studied the problem of re-optimization of train platform in case of train delays, where the station is modeled using the discretization of the platform track time–space resources. In addition, for solving the MILP model, an efficient heuristic algorithm is designed to speed up the re-optimization process with good solution precision. However, the (meta-)heuristic approaches have some drawbacks (e.g., easily trapped in local optima) and, especially, have to balance the solution quality and computation time [5]. It is necessary to explore a large number of parameters and their feasibility for the improvement of (meta-) heuristic approaches.

This paper addresses the TRP in high-speed railways in a different way by proposing a dynamic programming (DP) with adaptive state generation, since DP has been proved being a powerful tool for solving many optimal scheduling problems, such as vehicle routing problem with pickup [20], optimal coordination of public transit vehicles [21], and shortest path problem (SPP) of traffic scheduling [22][23]. Nevertheless, the state space for many real-world applications can be immense, making the tradition DP algorithm very computational intensive [24]. However, one of the main challenges in TRP is the large search space and constraints and few researches use DP to solve TRP of high-speed railway. A. A. Lazarev et al. [25] were concerned with scheduling trains moving in both directions between two stations connected by a single-track railway with a siding. In addition, they presented DP-based algorithms which minimizes two objective functions. X. Tian et al. [26] designed a DP approach to synchronize the timetables of train services at a single rail transfer station. Y. Zinder et al. [27] developed a DP to schedule the two-way traffic between two stations connected by a single-track railway with a siding, but it considered only the simple scenario of two stations. C. Schön et al. [28] presented a multi-stage stochastic dynamic programming model to make wait-depart decisions in the presence of uncertain future delays for a single line railway and they proposed a DP to minimize the total passengers’ delay at destination. T. Ghasempour et al. [29] presented an adaptive railway traffic controller for real-time operations based on approximate dynamic programming (ADP) to limit consecutive delays resulting from trains by sequencing them at critical locations and their case study only included five stations.

There are disadvantages about computational efficiency and solution quality in existing researches, especially for TRP about high-speed railway. However, in this paper, the timetable rescheduling for a high-speed railway corridor is converted into a multi-stage decision-making process, and a multi-stage timetable-rescheduling approach is proposed. In the proposed multi-stage timetable rescheduling, a railway network is modeled as a set of sequentially connected sections. A section is modeled as a stage, and all trains’ arrival and departure times at a section are converted as the state of a stage. Furthermore, the state transfer equation is built and Bellman equation is developed to derive the solution to minimize the total delay time (TT). To apply the DP to solve the TRP in high-speed railways, the procedure of high-speed railway rescheduling is first converted into a multi-stage decision-making process with the definition of states, actions, nodes and edges. Then a network of nodes connected by edges is developed to model the railway operation and the space of all the possible rescheduling solutions. An improved DP is proposed to solve the rescheduling problem by finding the shortest route in the network.

For the TRP of a high-speed railway corridor, the challenge lies in the large scale of the problem and a lot of safety constraints that makes a lot of “holes” in the feasible regions. The main contribution of this paper is: (1) combination of adaptive search space generation together with the DP to have a fast and reliable solution to the high-speed railway timetable rescheduling. There have been some reports about the importance of ordering in train scheduling, however, their focuses are mainly in the optimization techniques, with less attention on the construction of the search space in a better way. To address the challenges of rapid solving which is the main obstacle in applying the advanced and complicated theory to real-world TRP in practice, this paper pays more attention on the combination of problem reconstruction and how it is solved (optimized). Due to the high speed, the optimization problem of high-speed railway timetable rescheduling changes quickly and it is better to generate the search space dynamically and adaptively, which means the proposed method has better applicability. The challenge lies in how to transform the high-speed railway problem into a multi-stage decision-making problem and construct the state space that can be solved quickly. (2) To the best knowledge of authors, this is the first time that a DP is used to solve the reorder problem in high-speed railway timetable rescheduling. DP is widely used in job-shop problems, but it is rarely used in high-speed railway. As a mathematical programming method, DP usually has relatively better solution quality than other intelligent or heuristic methods (e.g., ant colony and partial optimization).

The structure of this paper is as follows. In the second section, the TRP of high-speed railways and the scope of this study are presented. In the third section, the multi-stage timetable rescheduling is formulated by reordering and retiming. In the fourth section, the TRP is converted into an optimization problem to find the shortest route in the route network and the DP approach is proposed to find the optimal solution to the TRP. The fifth section reports on the empirical evaluation of our method on a series of simulation high-speed railway rescheduling experiments and a real-world railway rescheduling case of high-speed railway in China. The simulation experiments are carried out to evaluate the performance of our method for high-speed railway rescheduling, while the real-world case study is to demonstrate utility of the solution in a real-world scenario. The final section concludes the paper.

Problem formulation

Given a high-speed railway line of a group of stations, a set of track segments that connect the stations, a set of operational constraints and a planned timetable, when some trains are delayed (referred to as primary delays) due to unexpected events, the TRP is to find a feasible rescheduled timetable satisfying the constraints while reducing the secondary delays caused by the primary delays as much as possible, so that the disrupted timetable can be recovered to the original planned one as soon as possible. The counter measures against the delay disruption depend on the situations of delays and railway facilities, as well as the dispatchers. Train dispatchers in China high-speed railway usually perform [5]: changing arrival and/or departure times of trains (termed retiming), changing the order of trains (termed reordering), changing tracks and/or platforms, changing the unplanned stops, cancelling and/or adding trains or changing the route (termed rerouting). On a daily basis, large disruptions are rare and so are the changes of train stops, routes and train cancelation, which usually require high-level authorization and a series of approval processes in high-speed railway, because it will significantly disrupt both railway operation and passenger’s travel plan. Except the changes of tracks/platforms, other rerouting tactics are not recommended in daily operation of high-speed railways. Instead, the most common rescheduling tactics in daily operation is retiming and reordering to reduce primary delays propagation, so that train cancellation, stop and route changes can be avoided. Therefore, this paper focuses on timetable rescheduling by retiming and reordering with less change to the passengers’ traveling plans. The goal is to guarantee service quality and ensure that passengers can arrive at their destinations with less delays and less changes to passenger’s travel plan.

As shown in Fig. 1, this paper considers N trains running on a railway line of M + 1 stations connected through M station-to-station railway sections. The stations are regarded as nodes with given capacities (i.e., the number of siding tracks) in the railway network. High-speed railways are of double-track and trains run along one track line and reverse direction, namely up-bound line and down-bound line, independently. In daily operation, there are neither interactions nor conflicts among trains in the opposite direction and no trains are allowed to run in the opposite direction. Except in extremely rare event (e.g., one track is blocked and reverse running is allowed) high-speed trains in both directions do not share the same track. Since the operations of trains in up-bound and down-bound lines are two independent systems, the railway network can be separated by two sub-networks without interactions between them. For a simplified notation, this paper makes use the down-bound line to facilitate the theory analysis and model development. In practice, the proposed approach can be applied to up-bound line or both with simple extension.

Fig. 1
figure 1

Modeling of timetable rescheduling for N trains running at a high-speed railway line of M + 1 stations and M sections

Full size image

In Fig. 1, these M + 1 stations are connected by M station-to-station sections. A train’s departure time from \(i\)-th station is the same as its arrival time at the following section (\(i\)-th section) because the train enters into the \(i\)-th section once it departs from \(i\)-th station. Similarly, a train’s arrival time at next station (i.e., \((i+1)\)-th station) is its departure time from \(i\)-th section. For the sack of compact notation, this paper takes a section-oriented model to represent the train timetable. Let \({a}_{i,j}^{*}\) and \({d}_{i,j}^{*}\) are the desired arrival and departure time of train \(j\) at \(i\)-th section according to the predetermined operation plan (referred to as the original timetable), \({a}_{i,j}\) and \({d}_{i,j}\) are the arrival and departure time to be determined by the dispatcher after the occurrence of a primary delay. Let \(\Delta {a}_{i,j}\) be the arrival delay for train \(j\) at \(i\)-th section:

$$\Delta {a}_{i,j}={a}_{i,j}-{a}_{i,j}^{*}.$$
(1)

Let \({\tau }_{i}\) be the arrival delay of all trains at i-th section:

$${\tau }_{i}=\sum_{j=1}^{N}\Delta {a}_{i,j},i=\mathrm{1,2},\dots ,M$$
(2)

For N trains, their arrival and departure time of a section can be represented in a vector form. Let vector \({{\varvec{a}}}_{i}\) and \({{\varvec{d}}}_{i}\) represent arrival time and departure time of N trains at i-th section, respectively:

$${{\varvec{a}}}_{i}=[{a}_{i,1},{a}_{i,2},\dots ,{a}_{i,N}]$$
(3)
$${{\varvec{d}}}_{i}=[{d}_{i,1},{d}_{i,2},\dots ,{d}_{i,N}]$$
(4)

The TRP can be represented as follows: given a railway line of N trains, M sections, the original timetable X and an operation constraints set \(C=\{{C}_{1},{C}_{2},\dots ,{C}_{k}\}\) consisting of \(k\) constraint rules, the TRP is to determine a sequence of departure time \(\{{{\varvec{d}}}_{1}, {{\varvec{d}}}_{2},\cdots {{\varvec{d}}}_{M}\}\) and arrival time \(\left\{{{\varvec{a}}}_{2}, {{\varvec{a}}}_{3},\cdots {{\varvec{a}}}_{M}\right\}\) of N trains at the following M sections under constraints \(C\) with the target of minimizing some railway’s key performance index (KPI) when some trains are delayed at some stations. A typical KPI is the TT that is the sum of all trains’ delays at all stations. Here, of the N trains, the primary train arriving late at \(i\)-th section is defined as primary delay train, and the other trains, which are delayed due to delay of the primary train, are defined as associated delay trains. The timetable that will be adjusted can be determined through the primary delay, which involves a primary delay train and many associated delay trains. In this paper, the timetable is adjusted after a primary delay is detected.

Please note that, the problem definition above implies that retiming and reordering are the two rescheduling actions to be considered in the proposed approach. The purpose of retiming is to adjust the departure and arrival times according to the running time supplements, dwell buffer time and operation constraints. The procedure of reordering is to determine the trains’ departure sequence at a station (equivalent to the arrival sequence at the station’s following section) when train movements would come into conflicts. Since overtaking is only allowed at stations, once the departure sequence is determined, the arrival sequence in the following section is the same as the departure sequence at the preceding station.

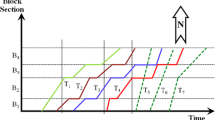
The nature of train timetable scheduling indeed is a sequential multi-stage decision-making process. Once the arrival time of section i is determined, the departure time of the same section \(i\) can be determined, followed by the determination of the arrival time at next section (\(i+1\)) and so on. An example of 4 stations, 3 sections and 4 trains in a down-bound high-speed railway line is illustrated in Fig. 2, where train 1 suffers a primary delay of \(\Delta {a}_{\mathrm{1,1}}\)= 20. The time–distance graph shown in Fig. 2 contains four down-bound trains and each line represents a train running from station 1 to station 4, in which the dotted lines are the original train lines and the solid lines are the rescheduled train line. In the original planned timetable, train 1 should have departed from station 1 before train 2 (see the dotted red and blue lines). However, due to some disruptions (e.g., longer dwell time caused by too many transit passengers), train 1 has to depart from station 1 with a primary delay of 20 min, resulting in train 1 is overtaken by train 2 at station 1. The trains run at an order of [2, 1, 3]. Figure 2a shows a timetable rescheduling without reordering. To reduce the delays, train 1 runs faster in section 1 and stops at station 2 with the expected dwell time. However, train 1 conflicts with train 2 at station 2 since their departure time does not meet the departure interval constraint of 3 min. According to FCFS strategy, train 2 arrives earlier and departs earlier, therefore, train 1 stops at station 2 with a longer dwell time until the constraints of departure interval are met. For this strategy without reordering, the order will never be recovered, because in all the flowing stations, all the trains run at the disrupted order when the primary delay occurs at the first station. This is a very common phenomenon in practice [12] and the dispatchers always give the priority to the on-time trains to avoid the propagation of delays from delayed train to on-time trains and \({\tau }_{4}\) at station 4 is 29 min. As shown in Fig. 2a, the side effect of retiming only is that the delayed train will suffer more and more delays.

Fig. 2
figure 2

Examples of rescheduling under a primary delay of a train

Full size image

Figure 2b shows a timetable rescheduling with reordering. Similar with the rescheduling without reordering in Fig. 2a, delayed train 1 conflicts with train 2, due to the departure interval constraints. The difference is that, by adopting reordering techniques, the departure order of train 1 and train 2 is updated and train 1 is scheduled to depart from station 2 before train 2. Although this reordering causes an associated delay to on-time train 2 at stations 2, the trains’ operation order is recovered from the disrupted [2, 1, 3] to the originally planned [1, 2, 3]. With the assistance of retiming by reducing the buffer time at following sections, \({\tau }_{4}\) at station 4 is only 9 min. Then, change of train sequence (reordering) and determination of arrival and departure time (retiming) will be solved in the paper. Meantime there are two key problems that are solved in the process of timetable rescheduling: (1) for mixed adjustment with overtaking, in which stations will the overtaking take place; (2) which is the best of FSFS, FCFS and mixed adjustment with overtaking.

To convert TRP into a multi-stage decision-making process, a section in the high-speed railway corridor is abstracted as a stage indexed with integer \(i, i=1, \mathrm{2,3},\dots , M\). For the sack of notation, M sections are numbered from 1 to M along the trains’ traveling direction from the left to the right as shown in Fig. 3. A section of the corridor is converted into a decision-making stage. And each stage needs to find the corresponding states, multi-stage timetable rescheduling describes how to establish a connection between the timetable and the state, mainly from two aspects, reordering that means changing the sequence of all trains arriving at the current section, and retiming that changing planned times at reference points. By constantly reordering and retiming, the whole multi-stage decision-making process is formed by continuous iteration. As shown in Fig. 3. Here, \({\mathbb{S}}_{i}\) is set of state variables of i-th stage, \({s}_{i}\) is a state variable of i-th stage, \({{\varvec{s}}}_{i}\in {\mathbb{S}}_{i}\). \({x}_{i}\) is a decision variable of i-th stage. In addition, \(v({{\varvec{s}}}_{i},{x}_{i})\) is cost function of i-th stage. In addition, Fig. 3 describes the process from state to decision. In this way, we can recursively decompose a multistage problem into simpler sub-problems. Once these sub-problems are solved, they will be combined into an overall solution.

Fig. 3
figure 3

Multi-stage decision-making process for railway timetable rescheduling

Full size image

Table 1 summaries the parameter and constraint variables will be used in the proposed optimization process. In addition, the problem of the TRP studied in this paper is formulated as follows:

Table 1 The parameter and constraint variables of the optimization process
Full size table

The TRP is to get a new timetable such that the KPI of TT of all trains at all stations is minimized:

$$\begin{array}{c}\mathrm{Z}=\underset{\{{a}_{i,j},{d}_{i,j}\}}{\mathrm{min}}\sum_{i=1}^{M}\sum_{j=1}^{N}(|{a}_{i,j}-{a}_{i,j}^{*}|+|{d}_{i,j}-{d}_{i,j}^{*}|)\\ {s.t. \{C}_{1},{C}_{2},\dots {C}_{5}\}\end{array}$$
(5)

After giving the primary delay of a certain train at a certain station, the train and associated trains should be adjusted to obtain a rescheduled arrival and departure time. To guarantee service quality and safety of the trains, it is necessary to satisfy certain constraints to ensure the rescheduled timetable is feasible. During the process of multi-stage model, the following constrains should be satisfied.

(1) Headway of arrival and departure trains: The headway of arrival at each section and departure from each section should be satisfied.

$${C}_{1}: \left\{\begin{array}{c}\left|{a}_{i,{j}_{1}}-{a}_{i,{j}_{2}}\right|\ge Tz\\ |{d}_{i,{j}_{1}}-{d}_{i,{j}_{2}}|\ge Tz\end{array} \forall {j}_{1}\ne {j}_{2},{j}_{1}=1,\dots ,N,{j}_{2}=1,\dots ,N,i=1,\dots ,M\right.$$
(6)

(2) No overtaking in station-to-station sections: this is a constraint of sequential arrival. As overtaking being not allowed in a section, the follower train: for a section, the requirements of first-in first-out and last-in last-out should be met for adjacent trains.

$${C}_{2}: if {a}_{i,j}\ge {a}_{i,j+1} then {d}_{i,j}\ge {d}_{i,j+1} \forall i=1,\dots ,M,j=1,\dots ,N-1$$
(7)

(3) Minimum running time: the running time of each section need to be greater than the one which is equal to the minimum running time.

$${C}_{3}: {a}_{i,j}-{d}_{i,j}\ge {Q}_{i,j} \forall i=1,\dots ,M,j=1,\dots ,N$$
(8)

(4) Because of rescheduling based on the original timetable strictly, rescheduled time need to be earlier than the original time.

$${C}_{4}: {a}_{i,j}\ge {\widehat{a}}_{i,j} \forall i=1,\dots ,M,j=1,\dots ,N$$
(9)

(5) Minimum dwell time: to guarantee adequate time for passengers alight and board, the minimum dwell time of train service at a station should be satisfied.

$${C}_{5}: {a}_{i+1,j}-{d}_{i,j}\ge {\delta }_{i+1}Ts \forall i=1,\dots ,M-1,j=1,\dots ,N$$
(10)

Multi-stage timetable rescheduling

In this section, TRP is converted into a multi-stage decision-making process. As shown in Fig. 4, M sections are represented by M stages, labeled as i = 1,2,…,M. The box of dotted green line represents the state space \({\mathbb{S}}_{i}\) of stage i, \({\mathbb{S}}_{i}=\{{{\varvec{s}}}_{i}\}\) and each circle represents a state \({{\varvec{s}}}_{i}\):

Fig. 4
figure 4

State transition between stages and state generation procedure

Full size image
$${{\varvec{s}}}_{i}=\left[{{\varvec{a}}}_{i},{{\varvec{d}}}_{i}\right]$$
(11)

Here, \(\left[{{\varvec{a}}}_{i},{{\varvec{d}}}_{i}\right]\) is the decision variable to be determined by reordering and retiming, \({{\varvec{a}}}_{i}\) is all \(N\) trains’ arrival time at \(i\)-th section (formula 3) and \({{\varvec{d}}}_{i}\) is all \(N\) trains’ departure time from \(i\)-th section (formula (4)). A section of a high-speed railway corridor is converted into a decision-making stage.

It is worth noting that the size of the state space, i.e., the number of possible states, at a stage, is varying and different stages may have different size. To identify each possible states of i-th stage, a bracketed superscript is introduced. For example, for a i-th stage with three states (as shown in Fig. 4), its state space is \({\mathbb{S}}_{i}=\{{{\varvec{s}}}_{i}^{\left(1\right)},{{\varvec{s}}}_{i}^{(2)},{{\varvec{s}}}_{i}^{(3)}\}\). More specifically,

$${\mathbb{S}}_{i}=\left\{{{\varvec{s}}}_{i}|{{\varvec{s}}}_{i}=\left[{{\varvec{a}}}_{i},{{\varvec{d}}}_{i}\right],i=\mathrm{1,2},\dots ,M\right\}$$
(12)

Let \({x}_{i}\) represent the decision variable to be determined at i-th stage, since the decision variable is made from the observation of the state \({{\varvec{s}}}_{{\varvec{i}}}\) of the stage, this can be written explicitly as:

$${x}_{i}={u}_{i}({{\varvec{s}}}_{i})$$
(13)

Let \({D}_{i}({{\varvec{s}}}_{i})\) be the set of admissible decisions, \({u}_{i}({{\varvec{s}}}_{i})\in {D}_{i}({{\varvec{s}}}_{i})\).

The arrow linking two circles in adjacent stage represents the possible transition from a state at present stage to the next state at next stage. For example, at starting from state \({{\varvec{s}}}_{i}^{(1)}\) at i-th stage, as shown in Fig. 4, the decision variable \({x}_{i}\) may take any value from two different decisions, and the decision set \({D}_{i}\left({{\varvec{s}}}_{i}^{(1)}\right)=\left\{{{\varvec{s}}}_{i+1}^{\left(3\right)},{{\varvec{s}}}_{i+1}^{\left(4\right)}\right\}\). If the next state is decided to be \({{\varvec{s}}}_{i+1}^{\left(3\right)}\), then \({{\varvec{s}}}_{i+1}^{\left(3\right)}\) is the new state driven the decision \({{x}_{i}=u}_{i}({{\varvec{s}}}_{i}^{\left(1\right)})\). This can be denoted as:

$${u}_{i}\left({{\varvec{s}}}_{i}^{\left(1\right)}\right)={{\varvec{s}}}_{i+1}^{\left(3\right)}$$
(14)

As shown in Fig. 4, for \({{\varvec{s}}}_{i}^{\left(1\right)}\), \({{\varvec{s}}}_{i}^{(2)}\) and \({{\varvec{s}}}_{i}^{(3)}\), different decision sets are given and consolidation of the different decision sets forms the next state space \({\mathbb{S}}_{i+1}\):

$${D}_{i}\left({{\varvec{s}}}_{i}^{\left(1\right)}\right)=\left\{{{\varvec{s}}}_{i+1}^{\left(3\right)},{{\varvec{s}}}_{i+1}^{\left(4\right)}\right\}$$
(15)
$${D}_{i}\left({{\varvec{s}}}_{i}^{(2)}\right)=\left\{{{\varvec{s}}}_{i+1}^{\left(1\right)},{{\varvec{s}}}_{i+1}^{\left(2\right)},{{\varvec{s}}}_{i+1}^{\left(3\right)}\right\}$$
(16)
$${D}_{i}\left({{\varvec{s}}}_{i}^{(3)}\right)=\left\{{{\varvec{s}}}_{i+1}^{\left(3\right)},{{\varvec{s}}}_{i+1}^{\left(4\right)}\right\}$$
(17)
$${{\mathbb{S}}_{i+1}=D}_{i}\left({{\varvec{s}}}_{i}^{\left(1\right)}\right)\cup {D}_{i}\left({{\varvec{s}}}_{i}^{\left(1\right)}\right)\cup {D}_{i}\left({{\varvec{s}}}_{i}^{\left(2\right)}\right)=\left\{{{\varvec{s}}}_{i+1}^{\left(1\right)},{{\varvec{s}}}_{i+1}^{\left(2\right)},{{\varvec{s}}}_{i+1}^{\left(3\right)},{{\varvec{s}}}_{i+1}^{\left(4\right)}\right\}$$
(18)

It can be seen that that state transition from one stage to next stage is a multiple-to-multiple mapping. Furthermore, the state space at a stage is not fixed and it depends on the possible states of preceding stage and cannot be determined in advance before the stage space of its preceding stage is known. In another word, \({\mathbb{S}}_{i+1}\) is determined by \({\mathbb{S}}_{i}\) at running time and \({{\varvec{s}}}_{i+1}\) changes when \({{\varvec{s}}}_{i}\) changes in proceeding states. The state transition of the proposed method can be described as:

$${{\varvec{s}}}_{i+1}={T}_{i}({{\varvec{s}}}_{i},{x}_{i})$$
(19)

With the multi-stage decision-making model of the TRP in high-speed railways, the whole complex problem of timetable rescheduling can be recursively decomposed into a sequence of simpler sub-problems. Once these sub-problems are solved, they can be combined into an overall solution to the TRP.

It is possible to determine in advance the maximum state space that contains all the possible states of a stage before starting solving the TRP, but it is not efficient or feasible due to the exponential increase of the number of stages. In theory, given a single initial state at the first stage, the maximum number of possible states at (i + 1)-th stage should be

$${{\mathrm{\rm P}}_{i+1}=\mathrm{\rm P}}_{i}\bullet ({\lambda }_{i+1}\bullet N!),i=\mathrm{0,1},\mathrm{2,3},\dots ,M$$
(20)

Here, \({\lambda }_{i+1}\) represents the maximum number of possible state in an order at (i + 1)-th stage and \({\mathrm{\rm P}}_{0}\) represents the number of states under the initial condition. This is too large to be solved in reasonable time. This paper proposes a state space dynamic generation method, in which the stage space of each stage is determined dynamically in the running time according to the feasible stage in preceding stage. Furthermore, it is noteworthy that while retiming in the context of utilizing the time supplements, we do not delay a train unless it is violating the departure time constraint (\({C}_{1}\)) at a station section [12]. In other words, when a train is delayed, we should choose the time closest to the original time and the sequences of associated delay trains are unchanged. In running time, the state space is determined by reordering, and the specific state is determined by retiming, e.g., \({S}_{i+1}\) is determined by \({S}_{i}\), and at the same time, the connection between states is also determined, i.e., the connection of \({s}_{i}^{\left(1\right)}\) in \({S}_{i}\) and \({s}_{i+1}^{\left(3\right)}\) in \({S}_{i+1}\). The proposed procedure is presented below in two steps of recording and retiming.

Reordering and adaptive state space generation

Changing the order of trains is seen as a critical action to restore the original timetable in the restricted infrastructure capacity of trains [30]. How to reorder the arrival orders for all trains at the current section affects the subsequent retiming and KPI, e.g., TT. According to state set of the previous stage, the trains are sorted in a way, and the sequence of associated delay trains remains unchanged to reduce the size of state space reasonably.

In theory, a rule of thumb is that for a TRP of \(\mathrm{M}\) stations, \(\mathrm{N}\) trains, the maximum number of possible arrival or departure sequences is \(\mathrm{N}!\), the number of sequences at final station is \({\left(\mathrm{N}!\right)}^{2\mathrm{M}}\), as a result, when the number of trains is large, the state space of a stage is too large to be searched by the DP in an acceptable duration. Fortunately, since trains are mainly operated as much as possible according to the planned timetable and, even in the disruption, trains will still arrive at or depart from a station at some order, rather than a totally random sequence. For example, given an arrival order of trains at a station, their departure order from the station should not be in random order. Instead, the possible departure order is closely related to these trains’ arrival order.

This is illustrated by an example shown in Fig. 5, where at the i-th stage that represents the i-th section between station i and station i + 1, four trains should depart from the i-th station at an order of [1 2 3 4] as specified by the original timetable. Due to train 1 suffering a primary delay, 4 trains’ departure sequence from i-th section (stage) is [2, 3, 4,1]. The green order [2, 3] in Order represents the original sequence of train 2 and train 3 at i-th stage (section), and the green order [2, 3] in Order1, Order2, Order3 and Order4 represents the original sequence of train 2 and train 3 at (i + 1)-th stage (section). It can be seen that the original sequence between stages may be changed, but the sequence of associated delay trains at current stage remains unchanged. The arrival sequences of all trains at (i + 1)-th stage (section) will be determined. Before the primary delay train is restored to the scheduling time, the train will restore scheduling time as soon as possible, so other trains (associated delay trains) may be required to give way to the train. Since the sequences of the associated delay trains are unchanged, as shown in Fig. 4, Order1, Order2, Order3 and Order4 four sequences are obtained, respectively. The Order1 is [3, 2, 4, 1] that means 4 trains’ arrival sequence at i-th section is unchanged. The Order2 is [3, 2, 1, 4], it means that train 1 overtakes train 4 and other trains start before train 1. The Order3 is [3, 1, 2, 4], it means that train 1 overtakes train 4 and train 3 and other trains start before train 1. The Order4 is [1, 3, 2, 4], it means that train 1 arrives at i-th section before train 2, train 3 and train 4 starts, respectively, and train 2, train 3, train 4 maybe be put off, respectively, or all.

Fig. 5
figure 5

The process of reordering

Full size image

Taking this into account, the state space at a stage is not necessary \(N!\) and many arrival/departure orders are invalid. Therefore, it is possible to reduce the searching space so that the computation time for a solution to the TRP can be shortened.

The sequence of associated delay trains remains unchanged, so the trains’ four arrival sequences at i-th section are obtained. According to process of reordering, the number of arrival sequences at (i + 1)-th section (stage) could be calculated by a state of i-th stage (section), and the formula is as follows:

$${C}_{i+1}=\mathrm{max}\left(\left\{j|{d}_{i,1}>{d}_{i,j},j=\mathrm{1,2},3,\dots ,N\right\}\right),i=\mathrm{0,1},2,\dots ,M$$
(21)

Here, \({d}_{i,1}\) is the departure time of primary delay train from i-th section (stage). When \(i=0\), \({d}_{0,j}\) represents departure time of train \(j\) from previous section (i.e., arrival time train \(j\) at the first station). Due to the sequences of associated delay trains being unchanged, \({C}_{i+1}\ll N!\), and by this way, the size of state space is reduced.

One arrival sequence corresponds to a series of \({{\varvec{s}}}_{i}={\left[{{\varvec{a}}}_{i},{{\varvec{d}}}_{i}\right]}^{\mathrm{T}}\) at i-th section (stage). By determining the specific arrival time and departure time of all trains from i-th section under one arrival sequence from i-th section, different states (\({{\varvec{s}}}_{i}\)) are obtained. From the formula 20, \({\mathrm{\rm P}}_{i}\) is the maximum number of possible state in an order at i-th stage (section). In addition, some states may be infeasible in the state set of i-th stage (section), so conflicts are resolved by retiming when the arrival and/or departure times of trains are determined.

Retiming and conflicts resolution

Once the possible sequences of all trains are decided in the reordering procedure, the conflict-free departure time of each train now should be decided, and the best combination of trains’ order and arrival/departure time can be optimized, After reordering, arrival sequences for all trains at the current section can be decided, and all these sequences result in times associated to train operations. Retiming involves normally adjusting the speed profile of trains, making them go slower or faster than planned [30]. Retiming a train means adjusting the departure and/or arrival times of the train (by shifting the originally allocated time slots, delaying or speeding up the train). Based on previous work [12], this paper uses the following tactics to resolve conflicts in the process of retiming: (1) Increasing the dwell time or running time on a chosen station or section, respectively; (2) decreasing the dwell and run times on all other line and station, respectively, while satisfying the respective constraints; (3) by appropriately increasing the dwell times at stations, to satisfy constraint (\({C}_{5}\)).

Combined with the above tactics and based on the principle of utilizing the time supplements, the arrival and departure time \({\left[{a}_{i},{d}_{i}\right]}^{T}={\left[{a}_{i,1},{a}_{i,2},\dots ,{a}_{i,N},{d}_{i,1},{d}_{i,2},\dots ,{d}_{i,N}\right]}^{T}\in {R}^{2N}\) of all trains [1,2,…j,…N] at i-th section (stage), will be obtained.

Arrival time of all trains

After arrival sequences for all trains at current section are given, it is easy to determine the specific arrival times of all trains by the headway of arrival and departure trains (\({C}_{1}\)), original schedule (\({C}_{4}\)) and minimum dwell time (\({C}_{5}\)). The calculation is as follows:

$${a}_{i,j}=\mathrm{max}\left({{a}_{i,j}^{*}, a}_{i,1}+Tz,{ d}_{i-1,j}+P{M}_{i,j}\times Ts\right)$$
(22)

Departure time of all trains

The departure times of all trains at current section are determined by the arrival times. In case of a primary delay train, the primary delay train is in conflict with other associated delay trains, and for solving the conflicts, new departure times for the primary delay train and the associated trains have to be determined. In Fig. 6, the black solid lines are in conflict with the red dotted train lines, and the red dotted lines are adjusted to red solid line for elimination of conflicts. In Fig. 6a, the headway of arrival and departure trains (\({C}_{1}\)) is violated. In addition, in Fig. 6b, the red dotted line crosses the black solid line that cannot satisfy \({C}_{2}\) and meantime, \({q}_{1}\) represents the time of the primary delay train passing through i-th section, \({q}_{1}<{Q}_{i}\) that cannot satisfy \({C}_{3}\). In Fig. 6c, the train has to run according to the requirements of planned departure time and cannot depart from i-th section in advance (i.e., it is not allowed to arrive at the station in advance). Therefore (Fig. 7),

Fig. 6
figure 6

Conflicts resolution of departing from a section

Full size image
Fig. 7
figure 7

Framework of the proposed method

Full size image
$${d}_{i,j}=\mathrm{max}({a}_{i,j}+{Q}_{i},{d}_{i,j-1}+Tz,{d}_{i,j}^{*})$$
(23)

Due to rescheduled time closer to the original time as far as possible, the maximum number of possible state in an order at (i + 1)-th stage, \({\lambda }_{i+1}==1\), \({\mathrm{\rm P}}_{i+1}={\mathrm{\rm P}}_{i}\bullet N!,i=\mathrm{2,3},\dots ,M\). Combined with the sequences of associated delay trains being unchanged (reordering above), the size of the state space of (i + 1)-th stage is \({{\mathrm{\rm P}}_{i}\bullet C}_{i+1}\ll {{\mathrm{\rm P}}_{i}\bullet \left({\lambda }_{i+1}\bullet N!\right)=\mathrm{\rm P}}_{i+1},i=\mathrm{0,1},\mathrm{2,3},\dots ,M\). Therefore, the size of state space can be reduced by dynamic state space generation and conflicts resolution.

Remark: after generating dynamic state space by reordering and resolving conflicts by retiming, specific states of (i + 1)-th stage are obtained. And the states of (i + 1)-th stage may be coincident, i.e., different states of i-th stage may generate the same state of (i + 1)-th stage, \({{\varvec{s}}}_{i}^{(1)}\) and \({{\varvec{s}}}_{i}^{(2)}\) of \({\mathbb{S}}_{i}\) all generate the state \({{\varvec{s}}}_{i+1}^{(3)}\) of \({\mathbb{S}}_{i+1}\) as shown in Fig. 4. The state between stages is actually a many-to-many relationship.

Dynamic programming approach

Based on the multi-stage model of the TRP in high-speed railways and the proposed tactics of reordering and retiming, the solution to the TRP is converted into an optimization problem to find the shortest route in the route network. By generating conflict-free states, the nodes are determined, and by consolidating states, the many-to-many connection between nodes is established in the route network. In addition, DP is proposed to find the optimal solution to the TRP.

Conflict-free state generation

The method to get the states of all stages will be explored to form specific nodes in the route network after converting the TRP into a multi-stage decision-making process. It mainly includes two steps: (1) initialization, including interception of original timetable and generation of initial condition (Algorithm 1) and (2) obtaining states of all stages (Algorithm 2).

(1) Initialization. The primary delay of a certain train cannot affect all trains of a high-speed railway corridor generally, so by intercepting original timetable, the intercepted timetable for rescheduling is necessary. It will reduce the dimension of state and the number of stages, and improve the computational efficiency ((1–5)-th lines of Algorithm 1). A multi-stage process has an initial condition. By the initial condition, all states of all stages can be obtained by continuous iteration. The initial condition is generated by (7–14)-th lines of Algorithm 1. Function getSequence0() (11-th line) obtains an initial sequence, i.e., reordering, and function getTime0() (12-th line) represents the initial time obtained closed to scheduled time. Here, the \({s}_{0}^{{(c}_{0})}={{\varvec{d}}}_{0}=\left[{d}_{\mathrm{0,1}},{d}_{\mathrm{0,2}},..,{d}_{0,N}\right]\)

figure a

(2) Obtaining states of all stages. After initialization of Algorithm 1, the intercepted timetable and initial condition S0 are obtained. Here, Sset (states of all stages) and Valueset (the relationship between states and function value) by the timetable will be obtained. M represents the stage number, Si represents state set of i-th stage, Valuei represents function value of i-th stage and (i-1)-th stage and stores the relationship between states. Si and Valuei of each stage are obtained by (5–20)-th lines of Algorithm 2. S represents state set of previous stage, and each state of the previous stage is the condition of the current stage. Function sequence() obtains a sequence, i.e., reordering. Function time() obtains the specific arrival time obtained by the sequence, and function resolveConflicts() obtains the specific departure time obtained by the arrival time after resolving some conflicts, i.e., retiming. So specific state by time() and resolveConflicts() will be determined. Function cumputeValue() obtains the relationship between states and function value of i-th stage and (i-1)-th stage by the specific state, the state of previous stage and intercepted original timetable. Sset and Valueset can be obtained by continuous iteration.

figure b

In the process of obtaining all the states, after generating all states of a certain stage, it is necessary to further clarify the relationship between the states. For specific method, see consolidation of states (Algorithm 3).

State consolidation

State consolidation is to combine the same state from different states of previous stage together as one. As mentioned above, the states between stages are actually many-to-many connection, the same states of each stage are consolidated to complete the many-to-many connection as shown in Fig. 4, so many-to-many connection between nodes is established in the route network. The consolidation of the same states can reduce the number of states of current stage; further, it can be more efficient to generate states in the next stage, so as to compress the state space.

In Algorithm 2, Valuei is obtained by the function cumputeValue() and the relationship of states between two stages is one-to-one. By consolidating the same states, the relationship between states is obtained and it further clarifies the relationship of states between two stages as shown in Fig. 4. By updating Si and Valuei, the number of states in each stage can be reduced. See Algorithm 3 for specific method.

figure c

Single-stage cost function and Bellman equation

In this subsection, the Bellman equation is presented for obtaining the solution of the TRP inversely. For i-th stage, following single-stage cost function can characterize the immediate penalty:

$$ v({\varvec{s}}_{i} ,u_{i} ({\varvec{s}}_{i} )) = \sum\limits_{j = 1}^{N} {|{\varvec{s}}_{i} (j) - a_{i,j}^{*} |} + |{\varvec{s}}_{i} (N + j) - d_{i,j}^{*} |. $$
(24)

After giving the single-stage cost functions (24), because of minimizing the TT, the Bellman equation of the TRP can be formulated as:

$$ \left\{ {\begin{array}{*{20}c} {f_{i} ({\varvec{s}}_{i} ) = \mathop {min}\limits_{{x_{i} = u_{i} ({\varvec{s}}_{i} ) \in D_{i} ({\varvec{s}}_{i} )}} \left\{ {v({\varvec{s}}_{i} ,u_{i} ({\varvec{s}}_{i} )) + f_{i + 1} (u_{i} ({\varvec{s}}_{i} ))} \right\} \, i = M,M - 1,M - 2,...,1} \\ {f_{M + 1} ({\varvec{s}}_{M + 1} ) = C, \, C{\text{ is a constant}}} \\ \end{array} } \right. $$
(25)

In which, the boundary condition is \({f}_{M+1}\left({{\varvec{s}}}_{M+1}\right)=C\). This setting has no effect on the inverse solution of M stages. After state space, state transition equation, the single-stage cost function and Bellman equation are all obtained, the TRP is solved by inverse solution.

In “Reordering and adaptive state space generation”, reordering can form the condition of mixed adjustment with overtaking and we obtain the state that contains overtaking strategy. Through the reverse solution of DP, the optimal solution may include the situation of overtaking strategy at the appropriate station. For different delay time or different train density, DP can find the timetable rescheduling that may include the situation of overtaking strategy, which is also a big advantage of our method. The overall process of train operation adjustment is given below:

Simulation experiment and case study

A series of simulation experiments are to evaluate the performance of our method for high-speed railway rescheduling and the results are compared against FSFS, FCFS and ant colony optimization (ACO). Furthermore, a real-world case study is to demonstrate utility of the solution by comparing with ACO, PSO and actual timetable rescheduling in practice by train dispatchers.

Simulation experiment

In this section, our method is presented with a virtual high-speed railway rescheduling experiment. This experiment mainly solves two key problems: (1) for mixed adjustment with overtaking, find the station in which will the overtaking take place; (2) which is the best of FSFS, FCFS and mixed adjustment with overtaking. There are 8 trains, 11 railway stations and 10 sections in the original timetable as shown in Table 2, the minimum dwell is 2 min and the minimum headway is 4 min. Minimum running time of each section is shown in Table 3. Here, the first train departed from first station BJN 50 min late caused by disturbance (e.g., unscheduled stop, prolonged process, or route conflict).

Table 2 Original timetable
Full size table
Table 3 Minimum running time of each section
Full size table

Result analysis

In this section, the result will be analyzed, and during rescheduling, in which stations will the overtaking take place. As shown in Fig. 8, each circle represents a state of the current stage (i.e., the time for all trains of arriving and departing the current section). The connection between each stage indicates the relationship between the states of two adjacent stages. We choose a circle at each stage to form a connected route. In this way, a rescheduled timetable can be obtained. The red path shown in Fig. 8 is the optimal rescheduled timetable of the problem obtained by our method.

Fig. 8
figure 8

Relationship between the states of each stage of this experiment (the red line represents optimal path)

Full size image

As shown in Fig. 9, the optimal timetable is obtained by our method, the black line labeled with Train1* is the original train line for Train1, the black line labeled with Train2* is the original train line for Train2 and so on. In addition, the red line labeled with Train1 is the rescheduled line by our method. Two overtakes are scheduled at BJN and TJN separately (involving Train3, Train2 red with secondary delay, the red line labeled with Train3 is the rescheduled line and the red line labeled with Train2 is the rescheduled line by the proposed method). After giving a primary delay (i.e., the primary train depart from BJN with delay), Train2 and Train3 start ahead of time at the first station. With the trains running, our method is to make Train1 close to the scheduled time as much as possible and reduce the TT in the following ways. The first overtaking occurs and Train1 crosses Train3 when it arrives at LF station. In addition, the second overtaking occurs when Train1 arrives at JNX station. Finally, Train1 recovers the scheduled time at TZD station. It should be noted that when Train1 overtakes at a station, the involved trains need to wait for a short time. However, these involved trains can be adjusted to the original time back in the next section quickly.

Fig. 9
figure 9

Timetable after rescheduling by our method

Full size image

On this basis, the goal of timetable rescheduling is realized, the optimal solution is obtained, and the stations in which will the overtaking take place are found.

Comparisons of strategies

Here, we will illustrate that the mixed adjustment with overtaking is best for FSFS and FCFS which are commonly adopted in railway practice. FSFS corresponds to deciding the order of the trains by keeping the trains’ order as the same as the one planned in the original timetable [31]. In another words, the train that is planned to depart earlier in the original timetable will be scheduled to depart earlier, without considering their actual arrival time. In FCFS, the trains’ order is determined by trains’ actual arrival time. The train that actually arrives first will depart earlier, even it is scheduled later than other train in the original timetable [1][33]. The FSFS and FCFS are widely used by the human dispatcher in daily operation and we compare the proposed method with the FSFS and FCFS to evaluate the performance (e.g., TT) to demonstrate that the optimization method may give a much better solution when applied to the real-world TRP. It is worth noting that FSFS and FCFS are all rule-based strategies without consideration of “optimization” at almost negligible computation cost.

For a primary delay, the timetable can be intercepted as a new timetable, in which the first train is late at first station. For the convenience of statistical explanation, 13 cases of different primary delay are set, in these cases, the first trains all are late at first station, as shown in Table 4. The cases are solved by our method, FSFS and FCFS, respectively. The other indicators are related to the TT such as first station of all trains running by original schedule (FS), affected trains (AT), delay frequency of all trains after passing the whole corridor (DF), overtaking stations (OS), the maximum adjusted number of trains in each station and the number of affected stations. The change of the TT will reflect these indicators, and the indicators can also reflect the TT. Through the analysis of the above indicators, we can directly reflect the effect of our method for TRP in high-speed railway.

Table 4 Delay cases
Full size table

(1) Results of rescheduling with different primary delay are shown in Table 5. It can be noted that with the increase of the primary delay time, FS is delayed, AT and DF increase, respectively, by our method and FSFS. It is not hard to find out that our method is better than FSFS.

Table 5 Rescheduling of trains with different delay time
Full size table

For FCFS, with the increase of primary delay time, few other trains are involved in the whole rescheduling process except for the first train and DF is 11 or 12 which is almost a fixed value. This phenomenon can be explained by the rescheduling strategy of FCFS. Since the primary delay train always consumes redundant time or buffer time, and there is no overtaking in the middle of the corridor, the train always follows the previous train safely. The primary delay train always delays. In Table 5, with cases 6, 11, 12 and 13 (i.e., the primary delay is 35, 60, 65 and 70 min, respectively), because the minimum safe headway should be maintained, there is one added delayed train, respectively. The added delayed trains are delayed, but in the next section, they will be adjusted to the scheduled time back. For AT, FCFS has achieved a good result, but for DF, FCFS has never been able to adjust all trains to the original schedules. The primary delay train is always late and has not been adjusted to original schedule in the whole corridor. In addition, if the corridor is very long, the primary delay train will be delayed continuously, which will seriously affect the passengers’ travel experience. From this point, our method and FSFS are superior to FCFS.

Figure 10 shows affected trains and stations under different delay time. In Fig. 10a, the maximum adjusted number of trains in each station by FCFS is 1 or 2 and it is the least by FSFS, our method and FSFS. However, in Fig. 10b, all stations of the whole corridor are affected by FCFS and the number of adjusted trains is 11. In addition, the number of affected stations by FSFS is minimal, and the number of affected stations by our method is almost the same. Above all, from two perspectives of adjusted trains and stations, our method can get better results.

Fig. 10
figure 10

Affected trains and stations under different delay time

Full size image

(2) The tendencies of the TT under different primary delay time are shown as Fig. 11 by different methods. On the whole, with increase of primary delay, the TT is the smallest and its increasing is slowest by our method.

Fig. 11
figure 11

Total delay time (TT) of different methods under different delay time

Full size image

When the primary delay time is less than 20 min, the TT by our method and FSFS is almost the same. However, with the increase of primary delay, the TT adjusted by FSFS increases rapidly. When the primary delay time is less than 35 min, the TT by FCFS increases slowly, but it is larger than our method and FSFS. That is because the primary delay train always follows Train2 by FCFS. According to FCFS, the primary delay train cannot cross Train2 in the whole rescheduling process and cannot drive towards its own schedule. When the primary delay is more than 35 min and less than 65 min, the first train always follows Train3. The primary delay train cannot cross Train3 in the whole rescheduling process and cannot drive towards its own schedule and so on. In short, the jump of TT by FCFS depends on which train the first train follows. From the perspective of TT, with the increase of primary delay, FCFS is better than FSFS. In addition, it is because other trains pass ahead of time if the delay time of primary delay train is too long by FCFS. From the perspective of TT, because of the mixed adjustment with overtaking, our method can get better results than FCFS and FSFS with the increase of primary delay. In addition, our method reduces the TT by averagely 62.7% and 41.5% with respect to FCFS and FSFS.

Comparisons with ACO

Our method (DP with adaptive state space generation) and intelligent algorithm ACO are used for the problem, respectively. The characteristics of every method are analyzed, and the advantages of our method are illustrated from the perspective of TT and computational time.

Figure 12 shows change of \({\tau }_{i}\) at i-th section (stage) of the simulation experiment (the first train leaves first station BJN 50 min late) after the timetable rescheduling by ACO (the blue lines) and our method (the red lines). The horizontal axis indicates that all trains arrive at the section. The longitudinal axis represents \({\tau }_{i}\) at i-th section (stage). It can be seen that from first section to final section, the \({\tau }_{i}\) is gradually reduced by ACO and our method. With ACO, there are strategies of overtaking. Train1 overtakes Train3 at TJN and overtakes Train2 at QFD. Point C represents the first overtaking occurs and point D represents the second overtaking occurs. But in our method, overtaking occurs differently with rescheduling by ACO. Train1 overtakes Train3 at LF and overtakes Train2 at JNX. The first overtaking leads to a slow decline of \({\tau }_{i}\) from section 1 to section 2 at Point A, but from section 2 to section 3, there is a rapid decline. The second overtaking leads to the increase of delay time at point D. Although rescheduling with overtaking all by two methods, DP with adaptive state space generation can optimize the TT by the appropriate overtaking station, and from the perspective of the whole, by our method, the delay gradually recovers and TT decreases even more, so as not to affect associated delay trains as far as possible, so that the primary delay train is as close as possible to the original time.

Fig. 12
figure 12

Change of \({\tau }_{i}\) after rescheduling by ACO and our method

Full size image

Figure 13 shows the results obtained by ACO and our method. The black line labeled with Train1* is the original train line for Train1, the black line labeled with Train2* is the original train line for Train2 and so on. In addition, the red line labeled with Train1 is the rescheduled line by our method. Two overtakes are scheduled at LF and JNX separately (involving Train3, Train2 with secondary delay, the red line labeled with Train3 is the rescheduled line and the red line labeled with Train2 is the rescheduled line by our method) and the resulting total delays of the schedule is 398 min. The blue line labeled with G399 is the rescheduled line by ACO. Two overtakes are scheduled at TJN and QFD separately (involving Train3, Train2 with secondary delay, the blue line labeled with Train3 is the rescheduled line and the blue line labeled with Train2 is the rescheduled line by ACO) and the resulting TT of the schedule is 635 min. The green box indicates the situation of overtaking in the station according to the two methods from LF to CZX. It can be seen that ACO make the Train1 pass through the TJN ahead, while our method make Train1 pass through the LF ahead. And the station where the second overtaking occurs is also different. Combined with Fig. 12, Train overtaking at the appropriate station plays a key role in the TT of TRP in high-speed railway and our method chooses the appropriate stations for overtaking to reduce TT.

Fig. 13
figure 13

Timetable after rescheduling by ACO and our method

Full size image

Our method converts timetable rescheduling into a multi-stage decision-making process. By timetable mapping model, the stages and the states, which are indispensable elements, are limited and rescheduled timetable is obtained by DP, which greatly increases the computational speed. In Table 6, from this experiment, the computational time of our method is only 0.35 s, while ACO needs 30 s. With obtaining timetable rescheduling quickly, the TT by our method is 398 min, which is better than ACO (635 min).

Table 6 Minimum running time of each section
Full size table

A real-world case study

In this section, we evaluate the performance of our method on a real-world high-speed railway rescheduling scenario in Northeast of China. In this case study, the original timetable consists of 8 railway stations, 7 sections from station 1 to station 8 and 8 trains which are G1211, G399, D27, D23, G8023, G239, G1233 and G731. The minimum headway and minimum dwell are 2 min and 1 min, respectively. Minimum running time of each section is shown in Table 7. G399 arrives at the first station 26 min late caused by disturbance (e.g., unscheduled stop, prolonged process, and route conflict).

Table 7 Minimum running time of each section
Full size table

Figure 14 shows that change of \({\tau }_{i}\) of the actual timetable rescheduling in practice by train dispatchers (the red line), of the timetable rescheduling by our method (the blue line). The horizontal axis indicates that all trains arrive at the section. The longitudinal axis represents \({\tau }_{i}\) at i-th section (stage). It can be seen that from first section to final section, the \({\tau }_{i}, i=\mathrm{1,2},\dots ,7\) gradually increases in practice by train dispatchers, while \({\tau }_{i}\) is gradually reduced by our method. In the actual, point C represents that \({\tau }_{4}\) at section 3 increases suddenly, and G8023 avoids the through train G239, which leads to the increase of delay time. The delay time increases continuously from section 5 to section 7, which represents that the front train D23 is at low speed, and G399 follows the train, which leads to continuous delay. In our method, G8023 avoids G399 at section 4, which leads to the increase of delay time at point A. G399 overtakes D23 at CTX which leads to the increase of delay time at point B.

Fig. 14
figure 14

Change of \({\tau }_{i}\) after rescheduling by the actual and our method

Full size image

Figure 15 shows the results that are obtained by our method and the dispatcher. The black line labeled with G399* is the original train line of G399, and the blue line labeled with G399 is the rescheduled line by our method. One overtaking is scheduled at station CCX and the resulting TT of the schedule is 220 min (involving G8023, D23 with secondary delay, the blue line labeled with G8023 is the rescheduled line and the blue line labeled with D23 is the rescheduled line by the proposed method). The red line labeled with G399 is the rescheduled line by the actual. One overtaking is scheduled at station TLX, but the one is original. G399 is late continuously on the real-world high-speed railway scenario and the resulting TT of the schedule is 480 min. It can be seen that the blue line adjusted according to the planned train diagram by our method, and the blue line is close to the original train line. Although G8023 and D23 have short secondary delays, it can be adjusted quickly in next sections, which will not affect the passengers of the trains. In CCX (the terminal station of the studied corridor), G399 are almost adjusted to the original time, while the red line continues to deviate from the original line. Our method makes rescheduled time closer to the original time as far as possible, and achieves timetable rescheduling according to original time.

Fig. 15
figure 15

Rescheduled timetable by our method and the actual timetable by the dispatcher

Full size image

Our method can increase the computational speed. In Table 8, from this experiment, the computational time of our method is only 0.32 s, while ACO needs 43 s, and PSO needs 43 s and TT is too long by PSO (467 min). The actual is a method by train dispatcher and rescheduling time will take seconds or minutes according to the complexity of different cases. With obtaining timetable rescheduling quickly, the TT by our method is 220 min, which is better than ACO (250 min), PSO (467 min) and the actual (480 min). Other typical algorithms, such as IP, MILP and alternative graph (AG), need to consume more computational time. We also compare our method with more intelligent methods in the literatures which have the similar problem scale and our method can consume less time to get the results.

Table 8 Computational time and TT of different method
Full size table

Conclusions

In this paper, the TRP is solved by a DP approach with adaptive state generation and conflicts resolution. On the basis of some reasonable assumptions, train rescheduling model is formed to satisfy the basic requirements of traffic safety and passenger service. A multi-stage decision-making model is developed for the TRP of high-speed railways, adaptive state space generates by reordering when the orders of trains at a station are determined, and conflicts are resolved by retiming when the arrival and/or departure times of trains. Further, the state transfer equation is obtained and Bellman equation is constructed to derive the solution to minimize the TT. A series of simulation experiments are designed to find stations in which will the overtaking take place, and illustrate that the mixed adjustment is best for FSFS and FCFS. In addition, TT and computational time of our method have obvious advantages compared with ACO. A real-world case study illustrates the TRP is effectively solved by comparing with the actual. In addition, the case also shows that the multi-stage decision-making model for timetable rescheduling has practical value.

For future research, first, the psychological factors of the decision-making of dispatchers should be considered. Second, from the perspective of the problem’s construction, the multi-stage decision-making model can be developed for more complex railway network.