A Two-Phase Multi-criteria Fuzzy Group Decision Making Approach for Supplier Evaluation and Order Allocation Considering Multi-objective, Multi-product and Multi-period

Abstract

Due to severe competition among business organizations, the selection of supplier becomes more important for business success. However, supplier selection problems are complex and unstructured since it involves a large number of criteria and some of the criteria cannot be assessed accurately. Also, supplier’s performance fluctuations and unknown information always exist in the real-world decisions. Moreover, the criteria may be qualitative or quantitative in nature as well as supplier evaluation involves a group of experts with diverse opinions. To handle such uncertain and vague information of suppliers, use of fuzzy sets is an appropriate option. Hence, for making a realistic decision, this research proposes a two-phase method to select the suitable suppliers and allocate appropriate orders to them. In first phase of the study, the ranking of supplier is performed by using fuzzy MULTIMOORA method with regard to the important criteria. Then, multi-objective linear programming (MOLP) method in fuzzy environment is proposed to allocate orders to the preferred suppliers in the second phase. The model is developed in multi-product environment by satisfying demand, lead time and capacity constraints. We used expected value method to transform the fuzzy multi objective problem into a crisp single objective problem. Appropriate orders are assigned to the preferred suppliers by considering the closeness coefficient to the fuzzy MOLP model. At last, a case study is performed in an Indian manufacturing organization to illustrate the proposed model.

1 Introduction

Presently, manufacturing organizations rely heavily on suppliers for procurement of raw materials and semi finished components used in the final products. Lee and Drake [22], Ghodsypour and O’Brien [12] estimated that around 50–70% of the production costs are spent on the purchased materials and components. The process of selecting the right supplier who is capable of providing the requisite products or services to the buyer at the competitive price and at the appropriate time is the main purpose of supplier selection. Mohammadshahi [28] suggested that a suitable supplier could reduce production interruption, quality improvement and better customer satisfaction. Krajewsld and Ritzman [21] found that every manufacturer invests almost 60% of the total sales on the purchased items. In this situation, the purchasing department plays a significant role in cost reduction, and hence, suppliers evaluation and performance measurement have become one of the most critical activity of supply chain management [30, 31]. Liu and Hai [24] pointed out that selecting an appropriate supplier can contribute substantial savings to the organization in conflicting and competitive environment. Thus, the goal of supplier evaluation for an organization is to maximize overall profit, decrease purchase risk and build the long-term relations with suppliers [11]. Dickson [9], Ellram [10] identified various factors that affect the performance of supplier. The study on supplier evaluation made by Dickson [9] identified 23 important criteria to be judged before a final decision. Weber et al. [37] classified 74 articles related to the supplier evaluation. They concluded that all the criteria are not always necessary to judge before a final decision making because every product requires different criteria to select.

Several influencing factors namely incomplete information, qualitative criteria, and vagueness etc. are often not considered while making the decisions [41]. Under these circumstances the best method for handling uncertainty is fuzzy set theory. Li et al. [23] discussed various applications of this tool in supplier selection problem. Chen et al. [7] used fuzzy decision making tool to handle uncertainty in the supplier evaluation process. They used type-1 fuzzy numbers to determine the ratings of alternatives and the weights for different criteria involved in the decision making process. Amid et al. [1] developed fuzzy multi-objective models to include uncertainty of the information in the decision process. They used fuzzy set theory in supplier evaluation process to assist the decision makers to allocate weights to different criteria. Wang et al. [36] presented a hierarchical TOPSIS method for supplier selection. The usefulness of their work is shown by a numerical example. Zeydan et al. [40] proposed a two stage model for supplier evaluation considering quantitative and non-quantitative criteria. At first they used MCDM techniques to assign the weight to the various criteria and then they performed DEA to rank the suppliers. Recently, a bi-fuzzy multi-objective inventory model found in Bera and Jana [5] to consider uncertainty in the decision-making process.

Various methods are found in the literature for solution of MCDM problems including AHP, TOPSIS, ELECTRE, VIKOR, MULTIMOORA, ANP, DEA, GA and many others. Obviously, there are fuzzy extensions of each method we quoted here. Thus, a vast literature on this area has been developed over several years. However, we will concentrate on MCDM problems for supplier assessment. A broader perspective of supplier assessment methods using MCDM can be found in Chen and Hwang [8] and Mendel et al. [27]. Tahriri et al. [34] solved the supplier evaluation problem in a steel producing industry. They solved the problem using AHP and six most important criteria were considered for supplier evaluation. Setiawan et al. [32] developed the ANP method for determining the performance of supplier in Unilever Company, Indonesia. The different criteria they considered were price, quality, availability of supply, and reputation of supplier. Elanchezhian et al. [11] proposed an ANP-TOPSIS hybrid model for supplier’s evaluation considering eight dimensions such as delivery, quality, price, technology, customer satisfaction, quality of sales team, relationship with suppliers. Recently, Bera et al. [6] proposed a supplier selection model using IT2 fuzzy TOPSIS and IT2 fuzzy MOORA method for effective supplier selection considering subjective and objective factors.

Currently, the researchers are addressing hybrid methods for effective solution of supplier selection problem. Pal et al. [29] reviewed and analyzed the literature thoroughly and addressed the problems associated with supplier selection methods and criteria. They concluded that additional considerations are required for integration of objective and subjective factors. Tam and Tummala [33] solved a case study by using AHP to observe the feasibility of the model in a vendor selection method in telecommunications system. Handfield et al. [16] integrated environment factors in their supplier selection problem using AHP. An ANP and TOPSIS hybrid method developed by Elanchezhian et al. [11] to determine the best vendor. Haldar et al. [15] developed an integrated MCDM model using AHP-QFD for resilient supplier evaluation problem. Kilincci and Onal [20] used fuzzy AHP based methodology in a manufacturing company to assess supplier selection located in Turkey. Asadabadi [3] proposed a hybrid QFD method to solve supplier evaluation problem. Kassaee et al. [18] developed a hybrid fuzzy MCDM model using ANP and TOPSIS to find out the weights of criteria used for vendor rating.

Purchasing is a primary activity of any organization and related to the overall achievement of the supply chain. Selection of right suppliers and allocation of appropriate orders to them can improve the overall performance of the organization. It is a complex MCDM process involves many alternatives, huge number of criteria and a group of experts. Although previous studies developed numerous methods for supplier selection but further studies are essential to consider the imprecise information concerning the product features, supplier assessment criteria, multi product environment, consideration of objective and subjective factors and allocation of appropriate orders to selected suppliers. Thus, this research proposes an integrated fuzzy MULTIMOORA method and multi-objective method for selection of the suitable suppliers and allocation of appropriate orders to them.

The objectives of the paper are listed in the following paragraph:

• 1. This study suggests a combined group decision making approach with fuzzy multi-objective linear programming model for effective supplier selection.

• 2. Fuzzy MULTIMOORA method is used to evaluate the suppliers and rank them with regard to the important criteria.

• 3. Orders are allocated to the preferred suppliers by using fuzzy MOLP model.

• 4. A case study in a manufacturing industry from eastern India is provided to show the applicability of the proposed integrated model.

• 5. This study is helpful to the researchers in better understanding the problem theoretically and helpful to the organizations in designing the supplier’s evaluation systems in an uncertain and vague environment.

The rest of the paper is organized as follows. The concepts of fuzzy set and fuzzy MULTIMOORA method is described briefly in Sect. 2. Section 3 deals mainly with the concept of fuzzy MOLP methodology. In Sect. 4, a case study from an Indian manufacturing company is presented. Results of analysis followed by a sensitivity analysis is presented in Sect. 5. Finally, Sect. 6 presents the managerial implications; conclusions and future research directions are presented in Sect. 7.

2 Preliminaries

There exist numerous methods in addressing supplier evaluation/selection and order allocation problem. The most important methods highlights that the right suppliers are selected depending on the strategies and policies of the organization and to improve and maintain the long-term relationship with the suppliers in today’s highly turbulent markets. Majority of the studies in the literature have suggested quality, price, on-time delivery, lead time, flexibility, and relationship between buyer and supplier as the main criteria in supplier selection process [13]. In this paper, integrated fuzzy MULTIMOORA and fuzzy multi-objective liner programming method is used to select the suppliers and allocate appropriate orders to them. In 1st phase, fuzzy MULTIMOORA method is used to evaluate and rank the suppliers in an Indian manufacturing organization. Then, in the 2nd phase, appropriate orders are allocated to various suppliers by using fuzzy multi-objective liner programming model. The flowchart of the proposed model is shown in Fig. 1.

Fig. 1

Proposed approach for supplier selection and order allocation

2.1 The Fuzzy Set Theory and Triangular Fuzzy Numbers

The fuzzy set theory was introduced by Zadeh [39] in the year 1965. It is an extension of the crisp set. These are powerful tools for modeling uncertain systems. A crisp set allows either full or no-membership, while a fuzzy set allows partial membership. The basics of fuzzy set are illustrated by Chen [7]. In a universe of discourse X, a fuzzy subset ${\tilde{A}}$ of X is defined with a membership function $\mu _{{\tilde{A}}}(x)$ which maps each element $x \in X$ to a real number in the interval [0, 1]. The function value of $\mu _{{\tilde{A}}}(x)$ resembles the degree of membership of $x \in {\tilde{A}}$. The higher the value of $\mu _{{\tilde{A}}}(x)$, the higher the membership of x in ${\tilde{A}}$ [19].

A fuzzy number ${\tilde{A}}$ is described as a subset of real number whose membership function is a continuous mapping from the real line R to a closed interval [0, 1], which has the following characteristics: (1) $\mu _{{\tilde{A}}}(x){\tilde{z}} = 0$, for all $x \in ( -\infty , a] \text{ and } [ c, \infty )$ (2) $\mu _{{\tilde{A}}}(x)$ is strictly increasing in [a, b] and strictly decreasing in [b, c]; (3) $\mu _{{\tilde{A}}}(x){\tilde{z}} = 1$, for $x = b$, where $a, b, \text{ and } c$ are real numbers, and $-\infty< a \le b \le c <\infty$. A triangular fuzzy number is represented by a triplet (a, b, c) shown in Fig. 2. Triangular fuzzy numbers will therefore be used in this study to characterize the alternatives. The membership function $\mu _{{\tilde{A}}}(x)$ is thus defined as:

$$\begin{aligned} \mu _{{\tilde{A}}}(x) = \left\{ \begin{array}{lll} \displaystyle 0, &{} {\hbox {for}}\, x < a \\ \displaystyle \frac{x - a}{b - a}, &{} {\hbox {for}}\,a \le x \le b\\ \displaystyle \frac{x - c}{b - c}, &{} {\hbox {for}}\,b \le x \le c\\ \displaystyle 0 , &{} {\hbox {for}}\, x > c \end{array} \right. \end{aligned}$$

(1)

In addition, the parameters a, b, and c in Eq. (1) can be considered as indicating respectively the smallest possible value, the most promising promising value, and the largest possible value that describe a fuzzy event [35].

Fig. 2

Triangular fuzzy number

Let ${\tilde{A}}$ and ${\tilde{B}}$ be two positive fuzzy numbers . The main algebraic operations of any two positive fuzzy numbers ${\tilde{A}} = (a, b, c)$ and ${\tilde{B}}= (d, e, f )$ can be defined in the following way [26]:

• 1. Addition:

  $$\begin{aligned} {\tilde{A}}\oplus {\tilde{B}}= (a, b, c)\oplus (d, e, f)= (a + d, b + e, c + f) \end{aligned}$$

  (2)

• 2. Subtraction:

  $$\begin{aligned} {\tilde{A}}\ominus \tilde{ B }= (a, b, c)\ominus (d, e, f)= (a - d, b - e, c - f) \end{aligned}$$

  (3)

• 3. Multiplication:

  $$\begin{aligned} {\tilde{A}}\otimes {\tilde{B}}= (a, b, c)\otimes (d, e, f)= (ad, be, cf) \end{aligned}$$

  (4)

• 4. Division:

  $$\begin{aligned} {\tilde{A}}\oslash {\tilde{B}}= (a, b, c)\oslash (d, e, f)= (a/f, b/e, c/d) \end{aligned}$$

  (5)

• 5. Expected value of Triangular fuzzy variables:

There are many ways of defining an expected value operator for fuzzy variables. Kassaee et al. [18] described the most general form of expected value operator. This definition is appropriate for both discrete and continuous variables Let $\xi$ be a fuzzy variable. Then the expected value of $\xi$ is defined by $E [\xi ] = \int \nolimits _{0}^{+ \infty } Cr\{ \xi \ge r\}dr - \int \nolimits _{- \infty }^{+0} Cr\{ \xi \ge r\}dr$ such that at least one of the integrals out of two is finite. The expected value of triangular fuzzy variable $\xi = (a, b, c)$ is given by [25].

$$\begin{aligned} E(\xi )=(a+2b+c)/4. \end{aligned}$$

(6)

2.2 The Fuzzy MULTIMOORA

The fuzzy MULTIMOORA is a group decision making method was developed by Brauers et al. [4]. This method of group decision making starts with decision matrices represents ${\tilde{X}}^k = {\tilde{x}}_{ij}^k = ({\tilde{x}}_{ij1}^k, {\tilde{x}}_{ij2}^k, {\tilde{x}}_{ij3}^k)$, where ${\tilde{x}}_{ij}^k$ denotes $i^{th}$ alternative of the $j^{th}$ objective assessed by the $k^{th}$ decision maker. where, $(i = 1, 2, \cdots , m;$ $j = 1, 2, \cdots , n;$ and $k = 1, 2, \cdots , K)$. The variables for decision making can represent both objective and subjective assessment of alternatives with respect to various criteria. Then, fuzzy weighted averaging (FWA) method is used to aggregate the responses of the experts [38].

$$\begin{aligned} {\tilde{x}}_{ij}= \sum \limits _{k = 1}^K {\tilde{w}}_k {\tilde{x}}_{ij}^k/\sum \limits _{k = 1}^K {\tilde{w}}_k \end{aligned}$$

(7)

where ${\tilde{w}}_k$ is the fuzzy weight for the $k^{th}$ decision maker. The equal coefficients of importance may be applied when the decision making team is homogenous, namely ${\tilde{w}}_k = (1/K, 1/K, 1/K)$. Hence, the fuzzy decision matrix X with $x_{ij} = (x_{ij1}, x_{ij2}, x_{ij3})$ is the combined responses of decision makers regarding alternatives on various criteria.

2.2.1 The Fuzzy Ratio System

The fuzzy numbers ${\tilde{x}}_{ij}$ in the Ratio System are normalized to make the decision matrix dimensionless. It is calculated by appropriate values of fuzzy numbers as obtained by [24].

$$\begin{aligned}&{\tilde{x}}_{ij}^* = ({\tilde{x}}_{ij1}^*, {\tilde{x}}_{ij2}^*, {\tilde{x}}_{ij3}^*)= \left\{ \begin{array}{ll} x_{ij1}^* = x_{ij1}\Big/ \sqrt{\sum \limits _{i=1}^m[(x_{ij1}^2)+(x_{ij2}^2)+(x_{ij3}^2)],}\\ x_{ij2}^* = x_{ij2}\Big/\sqrt{\sum \limits _{i=1}^m[(x_{ij1}^2)+(x_{ij2}^2)+(x_{ij3}^2)],} \forall {ij}\\ x_{ij3}^* = x_{ij3}\Big/\sqrt{\sum \limits _{i=1}^m[(x_{ij1}^2)+(x_{ij2}^2)+(x_{ij3}^2)].}\\ \end{array} \right. \end{aligned}$$

(8)

Calculation of ${\tilde{y}}_i^*$ ratios for each alternatives is done by Eq. (8).

$$\begin{aligned} {\tilde{y}}_i^* = \sum _{j = 1}^q {\tilde{x}}_{ij}^* \end{aligned}$$

(9)

Then each ratio ${\tilde{y}}_i^* = ( {\tilde{y}}_{i1}^*, {\tilde{y}}_{i2}^*, {\tilde{y}}_{i3}^*)$ is de-fuzzified by applying Eq. (9).

$$\begin{aligned} BNP_i = \frac{(y_{i3}^* - y_{i1}^*) - (y_{i2}^* - y_{i1}^*)}{3} + y_{i1}^* \end{aligned}$$

(10)

where best non-fuzzy performance value of $i^{th}$ alternative is denoted by $BNP_i$. Then the ranking of alternatives are obtained by decreasing values of BNP.

2.2.2 The Fuzzy Reference Point

This approach is developed considering the fuzzy Ratios obtained by Eq. (8). The Reference point r, in the proposed application is set as (1, 1, 1). Every element of the ratio matrix is then calculated and final rank is obtained according to vertex method and the Min-Max method of Tchebycheff.

$$\begin{aligned} min_i ( max_j d( {\tilde{r}}_j, {\tilde{x}}_{ij}^*)) \end{aligned}$$

(11)

Finally the alternatives are ranked in an ascending order.

2.2.3 The Fuzzy Full Multiplicative Form

The Overall utility of the alternatives are expressed as dimensionless number by:

$$\begin{aligned} {\tilde{U}}_i^{'} = {\tilde{A}}_i = (A_{i1}, A_{i2}, A_{i3})=\prod _{j = 1}^q {\tilde{x}}_{ij} \end{aligned}$$

(12)

Since overall utility ${\tilde{U}}_i^{'}$ is a fuzzy number, BNP values of alternatives are calculated to rank them in descending order. The fuzzy MULTIMOORA is an effective method for evaluating various parameters resulting in unbiased ranking of alternatives.

3 Proposed Fuzzy Multi-objective Linear Programming Model

Notations and Assumptions:

Following notations and assumptions are used for developing the mathematical model.

Notations

• i: index for product, $i = 1, 2, \cdots , I$

• j: index for periods, $j = 1, 2, \cdots , J$

• k: index for suppliers, $k = 1, 2, \cdots , K$

Variables

$Q_{ijk}$ : Amount of product i purchased from supplier k in period j.

$$\begin{aligned} \begin{array}{l} y_{xijk} = \left\{ \begin{array}{l} 1; \text{ if } \text{ supplier } k \text{ is } \text{ selected } ; (x_{ijk} > 0)\\ 0, \text{ otherwise. } \end{array}\right. \end{array} \end{aligned}$$

Parameters

• ${\tilde{D}}_{ij}$: fuzzy demand of product i in planning period j.

• $f_k$: fixed cost of demand from supplier i if demand is made.

• ${\tilde{C}}_{ijk}$: unit price of product i offered by supplier k in period j.

• ${\tilde{l}}_k$: late delivery ratio of supplier k.

• $d_k$: defective item ratio of supplier k.

• $w_k$: overall score of supplier k calculated by fuzzy MULTIMOORA method.

• ${\tilde{C}}_{ik}$ : capacity of supplier i for product k.

3.1 Assumptions

Following assumptions are made for the proposed mathematical model.

• 1. First three objectives are fuzzy in nature.

• 2. Demand and capacity constraints are fuzzy.

3.2 Proposed Model

Based on the literature review we have identified four different objectives: cost, delivery performance, quality and utility. We measure the cost objective as a function of procurement cost. It represents overall cost of procurement process, from placing an order to receiving the items. The delivery performance of the suppliers is calculated by late delivery ratio. It is the ratio of total number of products which is delivered after due date to the number of products delivered. Commonly the quality of product is measured by the percentage of defectives (or the acceptance rate of the products). The defective item ratio is obtained by dividing total number of poor quality products to total number of delivered products. Finally, we use utility objective in the mathematical model. This measure provides organizations to maximize the aggregated value of procurement activities considering multiple criteria.

Total procurement cost

The first objective of the model is to minimize total procurement cost of the products. This includes purchasing and procurement cost.

$$\begin{aligned} \min {\tilde{Z}}_1 = \sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K {\tilde{C}}_{ijk}.Q_{ijk}+ f_k . y_{xijk} \end{aligned}$$

(13)

where

$$\begin{aligned} \begin{array}{l} y_{xijk} = \left\{ \begin{array}{l} 1; \text{ if } Q_{ijk}\ne 0 \\ 0, \text{ if } Q_{ijk}=0. \end{array}\right. \end{array} \end{aligned}$$

Total late deliveries

The second objective of the model is to minimize total late deliveries. It is computed by multiplying late delivery ratio by the amount of delivered products.

$$\begin{aligned} \min {\tilde{Z}}_2 = \sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K {\tilde{l}}_{k}. Q_{ijk} \end{aligned}$$

(14)

Total quality of products

The third objective of the model is to maximize total quality of products. It is computed by multiplying ratio of quality of product by the amount of total item delivered.

$$\begin{aligned} \max {\tilde{Z}}_3 = \sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K (1 - {\tilde{d}}_{k}) . Q_{ijk} \end{aligned}$$

(15)

Total utility

The fourth objective of the model is to maximize total utility of the purchasing activity. It is computed as given in the following equation.

$$\begin{aligned}&\max Z_4 = \sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K w_{k}. Q_{ijk} \end{aligned}$$

(16)

where $w_i$ is the weights of the suppliers obtained by the fuzzy MULTIMOORA method and ${\tilde{s}}_{ijk}, {\tilde{C}}_{ijk} \text{ and } {\tilde{M}}_{ijk}$ are the selling price, cost price and maintenance cost of product i in period j by supplier k.

Constraints

Demand constraint

The total demand of product i from supplier k in period j should be greater than or equal to its demand over the planning period.

$$\begin{aligned} \sum _{k=1}^K Q_{ijk} \ge {\tilde{D}}_{ij}; i = 1, 2, \cdots , I; j= 1,2, \cdots , J. \end{aligned}$$

(17)

Capacity constraint

The total order quantity of product i in period j to be placed to the supplier k cannot exceed supplier capacity.

$$\begin{aligned} \sum _{j =1}^J Q_{ijk} \le {\tilde{C}}_{ik}; i = 1, 2, \cdots , I; k = 1, 2, \cdots , K \end{aligned}$$

(18)

Non-negativity constraints

$$\begin{aligned}&Q_{ijk}\ge 0; y_{ijk}: 0, 1; i = 1, 2, \cdots ,I;\nonumber \\&j = 1, 2, \cdots , J; k = 1, 2, \cdots , K \end{aligned}$$

(19)

The first objective function Eq. (13) reduces the total purchasing cost which includes unit cost, ordering, and inventory costs. The second objective function Eq. (14) minimizes total late deliveries. The third objective Eq. (15) maximizes the total quality of product delivered by the suppliers. The fourth objective function Eq. (16) is related to the total utility of the purchasing activity. The importance of the suppliers obtained from fuzzy MULTIMOORA analysis is included in Eq. (16) to determine the total utility. Constraint (17) considers the demands of the products. Constraint (18) takes into account the available capacity of suppliers. Eq. (19) takes into account the non-negativity and binary nature of variables. The model is stochastic in nature and multi-objective. The proposed model is solved by weighted sum method by converting the fuzzy objectives and constraints to crisp value by expected value method.

3.3 Conversion of the Model by Using Expected Value Method

Now, the expected value method mentioned in Sect. 2 [25] is used to convert both the objective functions and the constraints of the above mentioned model and given as follows:

$$\begin{aligned}&\min E[\tilde{Z_1}] = \sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K E[{\tilde{C}}_{ijk}]Q_{ijk} + E[f_i] \cdot y_{xijk}\le E(\tilde{z_1^0})\nonumber \\&\min E(\tilde{Z_2}) = \sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K E({\tilde{l}}_{k})\cdot Q_{ijk}\le E(\tilde{Z_2^0})\nonumber \\&\max E(\tilde{Z_3 })= \sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K (1 - E({\tilde{d}}_{k})) \cdot Q_{ijk}\le E(\tilde{Z_3^0})\nonumber \\&\max {Z_4} = \sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K w_{k}\cdot Q_{ijk}\nonumber \\&s.t.\nonumber \\&\sum _{k=1}^K Q_{ijk} \ge E({\tilde{D}}_{ij})\nonumber \\&\sum _{j =1}^J Q_{ijk} \le E({\tilde{C}}_{ik})\nonumber \\&\text{ and } \text{ Eq. } \text{(19) } \end{aligned}$$

(20)

3.4 Weighted Sum Method

Weighted-sums method is the most straightforward technique for solving multi-objective problems. It has been applied in various fields [2, 17]. In this section, the objective function $Z_5$ is defined as given below which is to be minimized. $W_1 , W_2 , W_3 , \text{ and } W_4$ are the weights of the objective functions. $'a'$ in the formulation is defined as the index of the objectives, where $a = 1, 2, 3, 4$. Thus, the problem is written as (21).

$$\begin{aligned}&Z_5= W_1Z_1 + W_2Z_2 + W_3Z_3 + W_4Z_4 \nonumber \\&s.t.\nonumber \\&\sum _{a} W_a = 1\nonumber \\&W _a \ge 0\nonumber \\&\text{ and } \text{ Eq. } 20. \end{aligned}$$

(21)

4 A Case Study

Fig. 3

Hierarchy model for supplier selection

In this section, we implement the proposed methodology to solve the suppliers selection and order allocation problem for an Indian manufacturing company. The case covers two types of products that are determined by the company management. The company procures the finished materials from multiple sources to fulfil their needs. The suppliers are capable of supplying these two types of items in different time periods with regard to the magnitude of the purchases for each product. The management of the company wants to maximize benefits of purchasing. In this pursuit, we determine appropriate suppliers to be employed for the next period and the order quantities to be allocated.

4.1 Phase 1: Supplier Evaluation Using Fuzzy MULTIMOORA

At the beginning of the group evaluation process, we analyze various factors of the supplier selection by face to face meetings with experts in the purchasing department and by comprehensive literature review. The hierarchical structure of the proposed supplier selection model is shown in Fig. 3.

As seen from the Fig. 3, the model has three levels. We have determined 10 major criteria for the study in an Indian manufacturing organization for selection of suitable suppliers and order allocation. The various criteria considered for the supplier evaluation process are: quantity discount $(C_1)$, Quality control $(C_2)$, compatibility $(C_3)$, rejection rate $(C_4)$, lead time $(C_5)$, flexibility $(C_6)$, warranty $(C_7)$, response to change $(C_8)$, unit price $(C_9)$ and transportation cost $(C_{10})$. The model is analyzed carefully by using various steps of fuzzy MULTIMOORA as described below for final evaluation.

• 1. In this study all the criteria are considered as subjective in nature and assessed by decision makers in linguistic terms using seven-point scale shown in Table 1.

  Table 1 Linguistic terms for qualitative evaluation

• 2. First of all, each of decision makers assessed every supplier with respect to various criteria according to the ten attributes shown in Table 2. The ratings assessed by the experts in linguistic terms are transformed into corresponding fuzzy numbers using the seven point scale shown in Table 1 and given in Table 3.

• 3. Then FWA operator [Eq. (7)] with equal coefficients of importance, namely ${\tilde{w}}_k = (1/4, 1/4, 1/4)$ for all k, is applied. The expert committee is homogenous. The results of aggregation are depicted in Table 4.

• 4. The aggregated matrix is then normalized by using Eq. (8). The result of calculations are depicted in Table 5.

• 5. The suppliers are ranked by fuzzy Ratio System using Eqs. (9) and (10). The fourth supplier $(S_4)$ is considered the best one with a score of 0.790, whereas the third supplier $(S_3)$—the worst one with a score of 0.305.

  Table 2 Linguistic assessments given by three decision makers

  Table 3 The ratings of three decision-makers expressed in triangular fuzzy numbers

  Table 4 Aggregated ratings for each alternative (supplier)

  Table 5 Normalized aggregated ratings for each alternative (supplier)

• 6. Calculation of the fuzzy Reference point approach for each supplier is done by using Eq. (11) and shown in Table 6. According to this approach Supplier 3 $(S_3)$ is considered the best alternative with a score of 0.187 and fourth supplier $(S_4)$ is the worst supplier with a score of 0.057 (Table 7).

• 7. A result of analysis of the Full Multiplicative Form using Eq. (12) is shown in Table 8. The rank for the suppliers obtained by this method is shown in Table 8. This method suggested that the fourth supplier $(S_4)$ is the best supplier with a score of 2.87 and third supplier $(S_3)$ is the worst supplier with a score of 0.17.

Table 6 Ranking of the suppliers according to the fuzzy Reference Point approach

Table 7 Ranking of the suppliers with fuzzy Ratio System

Table 8 Ranking of the suppliers with fuzzy Full Multiplicative Form

The theory of dominance [4] was applied when summarizing the ranks provided by three approach of fuzzy MULTIMOORA group decision making. The final ranking of the suppliers is obtained by assigning scores of 100, 80 and 60 to the 4th, 1st, and 5th suppliers sequentially. Thus, $S_4$ with a total score of $300(100 \times 3)$ is ranked as the most appropriate supplier, then it is followed by $S_1$ with a total score of $240(80\times 3)$ and $S_5$ with $180(60 \times 3)$. The percentage of importance of Supplier $4 (S_4)$ can be calculated as $w_4 = 42.86\%(300/(300+240+160))$. Similarly, the percentages of importance for Supplier $1 (S_1)$ and Supplier $5 (S_5)$ are $34.86\%$ and $25.71\%$, respectively. The results are shown in Table 9. The study exhibited the possibilities for improvement of supplier selection method by using MULTIMOORA group decision making. The comparison of ranks obtained by different MULTIMOORA method is also shown in Fig. 4.

Table 9 Ranking of the suppliers with MULTIMOORA—FG

Fig. 4

Comparative ranking of suppliers obtained by various MULTIMOORA methods

4.2 Phase 2: Order Allocation Using Fuzzy MOLP model

The mathematical model developed in Sect. 3.3 is used to solve the company’s problem for determining orders allocated to selected suppliers. Three best suppliers evaluated by MCDM method (Rank 1, 2 and 3) are selected for order allocation. The parameter values for all the objectives are gathered from the company’s records, the importance of suppliers $w_i$ are calculated by fuzzy MULTIMOORA analysis. All the constraints in the model are fuzzy in nature. Demand of products and capacity of suppliers to supply two kinds of products in different periods are summarized in Table 10.

Table 10 Input data for the selected suppliers

Each objective function is solved independently over the same set of constraints using Eqs. (13)–(17) and Lingo 14 software package. The results are shown in Table 11. The fuzzy model is converted to the crisp model by means of expected value method (6). Then, multi objective model is converted to single objective problem by weighted sums method. The optimum solution of the model is given in Table 12.

Table 11 Data set for membership functions

Table 12 Optimum results of weighted sum method

5 Results and Sensitivity Analysis

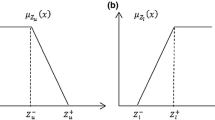
In this study a multi sourcing, multi product, multi period supplier selection problem is considered as a multi objective linear programming problem. In the first phase of the study we have used fuzzy MULTIMOORA approach to find out the ranking of prospective suppliers. The results are shown in Table 9. Then the dominance theory is used to find out the total score of three best suppliers for the company. According to the result the importance of suppliers are: $S_4 = 42.86\%, S_1 = 34.86\%, S_5 = 25.71\%.$ The importance of supplier is then used in the MOLP model along with the data set obtained from three best suppliers i.e. $S_4; S_1$ and $S_5$ are depicted in Table 12. In the second phase, each objective function is solved independently over the same set of constraints by using Lingo 14 software. The results of analysis by considering individual objectives are shown in Table 11. Finally, by using weighted sums method the optimum allocation of orders to the selected suppliers is obtained and the results are shown in Table 12. Sensitivity analysis of the result is carried out and the variation of $Z_1, Z_2, Z_3$ and $Z_4$ values with respect to different weights of objective values are shown in Figs. 5a, b, 6a, b respectively.

Fig. 5

a Sensitivity analysis of $Z_1$ b Sensitivity analysis of $Z_2$

Fig. 6

a Sensitivity analysis of $Z_3$ , b Sensitivity analysis of $Z_4$

6 Managerial Implication

This case study provides additional insights for research and practical applications. The results of this study help the firms to set up a standardized approach for evaluating and selecting the suppliers in an imprecise environment. The results of this study can enhance the quality and product development capability of the organization; reduce the cost for the organization, and finally increasing the market share. Also the developed method helps to reduce purchase risk through evaluating each supplier against a set of imprecise and vague criteria. The suppliers’ evaluation results also guide the suppliers to benchmark their activity against criteria used in the supplier selection process and finally helps to improve their performances.

7 Conclusions and Future Research Directions

Supplier’s assessment and order allocation are the most important and complex decisions for organizations. This study suggests a two phase methodology to address supplier evaluation and order allocation problem considering multi objective, multi period and multi product under demand and quantity constraints. Although, there are numerous studies in the subject area, still there are gaps in the literature for supplier evaluation and order allocation under multiple product and imprecise environment. Fuzzy MCDM is a group decision making method that provides an effective solution for ranking the potential suppliers with respect to their overall performance when the criteria are imprecise and conflicting and subjectivity in human judgments. Here, we propose a fuzzy MULTIMOORA method combined with fuzzy MOLP model that considers both objective and subjective information in real-life decision making. In the presented method, the performance of suppliers related to the selected criteria as well as the importance of the criteria were expressed in linguistic terms and then converted into fuzzy variables. Then the suppliers are assessed with respect to various related criteria and then in the second phase MOLP method is used to allocate appropriate orders to the preferred suppliers.

The outcome of the analysis shows that the developed approach may be helpful for judging the appropriate suppliers according to operational strategy and expectations of the company management. Furthermore, the proposed MOLP model is useful for estimating the trade-offs among different objectives by assigning different weights. Finally, to check the validity and suitability of our model, one illustrative example is presented for the supplier selection of a company in the manufacturing sector.

In summary, this study helps the organizations to analyze the multi-objective supplier selection problem and allocate appropriate orders effectively, and contributes a new tool to the supply chain literature. Although, the presented fuzzy MULTIMOORA with MOLP method was applied for selection of the supplier, it can be utilized for making a best decision in any other fields of management and engineering problem.