Fuzzy Inference Systems: Selection of the most Appropriate Fuzzy Implication from Available Lake Water Quality Statistical Data

Abstract

To this day, models such as empirical and dynamic, along with the multi-criteria analysis methods, have helped us towards the very understanding and estimation of all the functions (physical, chemical, biological) existing in freshwater ecosystems. The rich and variable system of the Greek lake Karla is a perfect candidate for our study and its purpose, which is to investigate the factors responsible for eutrophication (water temperature, nitrates, total phosphorus, secchi depth, chlorophyll-a) using fuzzy logic. In fuzzy logic, where the proposition can take any value in the close interval [0,1], there are infinite numbers of fuzzy implications which can be used; hence, a method of selecting the most appropriate implication is required. In this paper, we propose a method of evaluating fuzzy implications using available statistical data. The choice of the appropriate implication is based on the deviation of the true value of the fuzzy implication from the real values, as described by the statistical data.

1 Introduction

Last decades, the primary production rate and eutrophication level in lakes rose rapidly due to nutrient enrichment (mainly nitrates and phosphorus) empowered by humans. In contrast with traditional eutrophic condition development methods that are dependent on concentrations of phosphorus and nitrate, shallow Mediterranean lakes, being complicated systems, present a profile that is more complex (Scheffer et al. 1993). This way, the estimation of the trophic state becomes a topic that is challenging and should be based on multi-criteria analysis.

Systems, such as PCLake, provide us with information that is rich in details about quality parameter spatial and temporal variation. However, we cannot ignore drawbacks such as the great possibility of an error due to complex calculations as far as dynamic models are concerned. On the other hand, the multi-criteria analysis might be less reliable should the factors’ impacts change.

Water quality evaluation entails both randomness and fuzziness. Considering that water eutrophication evaluation involves many indices, and different classifications and interval values, fuzzy variable sets theory is an alternative way to approach complex ecosystems (Abbasi and Abbasi 2012). The fuzzy logic can be helpful in the classification of many environmental issues or in coping with missing data, and can also be used to manage uncertainty when applied to complex systems, difficult to illustrate with ordinary mathematics (Silvert 2000; Kotti et al. 2016).

We know that the implication in classic logic depends only on whether the premise is true or false. Every proposition in classic logic has two values 0 or 1, which is true or false, holds or does not hold. In fuzzy logic, the true or false of a fuzzy proposition is a matter of the degree, in contrast to classical logic, where the true or false take values in the set {0,1}. Similarly, fuzzy implications generalize those of classical logic (Botzoris et al. 2015).

The main aim of this study is to use fuzzy implication in order to search eutrophication parameters in the extremely changeable system of Lake Karla. The key to the uniqueness of this method is the ability to select the most appropriate implication among others for each study case, after a detailed analysis. In this way, the opportunity of understanding the mechanisms which affect the proper function of the ecosystem is offered. Generally, the goal of the paper is to gain further knowledge, so the new ecosystem can be managed and preserved with great efficiency. In previous work (Ellina and Kagalou 2016), we considered this ecosystem as a linear model using fuzzy linear regression (Papadopoulos and Sirpi 1999, 2004). In the fuzzy linear regression modeling, we somehow assume linearity. In this paper, we avoid making this assumption, so the approach is more realistic. Using this type of mathematical modeling, we try to build an inference system using the most appropriate implication.

2 Methodology

2.1 Study Area

The need for flood protection in the area and the acquisition of agricultural land were the cause of lake drainage projects in 1962 and the creation of smaller reservoir in part (Sidiropoulos et al. 2012). Such is the case of Lake Karla in south-eastern Thessaly, central Greece. The reflooding for restoration of Lake Karla, and its accompanying works, began in 2000. The research area is the new Lake Karla (39^ο29’02″Ν, 22^ο51’41″Ε).

The restoration of Lake Karla is the largest environmental project in the Balkans, implemented by the Region of Thessaly. Furthermore, this newly re-established water body is considered a vital aquatic ecosystem as it is listed in the network of Natura 2000 and has been characterized as a Permanent Wildlife Refuge by Greek Law. Karla’s Lake restoration project faces entangled challenges in the hydro-ecological management (Beklioglu et al. 2007). It is a project of local development and national importance with multiple positive impacts on the Lake area, in Thessaly and the wider environmental development. The general characteristics of this artificial lake and its drainage area are given by Fig. 1.

Fig. 1

Study area location, DEM, geomorphology and general characteristics

2.2 Database and Model Application in Lake Karla

Lake Karla water quality statistical data (water temperature, nitrates, total phosphorus, secchi depth, chl-a) have been collected in three stations (S1, S2, S3) (Chamoglou et al. 2014; Ellina and Kagalou 2016). In this paper we will process the average of the stations’ data as presented in Fig. 2 (for details see the Appendix).

Fig. 2

Average of the measured water quality data in lake Karla from the period 2012–2013

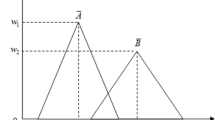
We have classified the studied parameters based on experience, bibliography and legislation, in three linguistic variables (LOW, MEDIUM, HIGH) in order to form trapezoidal fuzzy numbers (Fig. 3) (Lu et al. 1999; Ellina and Kagalou 2016). In this study, the independent parameters are: Water temperature, Nitrates, Total Phosphorus and Secchi Depth. The dependent parameter is chlorophyll-a. We examined pairs consisting of each of the independent parameters with the dependent one. At this point, it should be mentioned that generally the high levels of chlorophyll-a in aquatic systems are related to increased nutrients, low to moderate temperature and low SD; but, in our case, having few datasets, we could not ignore some of them. Furthermore, in Karla’s changeable ecosystem everything depends on everything. For this reason, we categorized all the independent parameters to three classes and we investigated separately one by one. The dependent variable chl-a was not meant to be categorized, since this ecosystem is already a eutrophic system, with apparent signals of hypertrophication during the warm period (OECD 1982). Also, it should be specified that, using the studied pairs above in every produced class is considered credible because in fuzzy logic everything is valid with a measure of fuzziness. Besides, such pairs can be seen in the experimental data (Figs. 2 and 3; Table 5 in Appendix).

Fig. 3

Data classification in trapezoidal fuzzy numbers: (a) Temperature; (b) Nitrates; (c) Total phosphorus; (d) Secchi depth; (e) Chlorophyll-a

2.3 Description of the Fuzzy Implications

We applied the following symmetric and asymmetric fuzzy implications to the datasets above, with the aim of evaluating the quality of fuzzy implications. The existence of observations allows us to assume that in the ideal fuzzy inference system, the true value of the implication x⇒y has to be equal to 1, since the values of x and also of y are related to observations, that is, they have to do with verified relations of assumed cause and implied effect. Starting from this finding, the evaluation of the fuzzy implications was based on the deviation of the true values of each implication from 1. The fuzzy implication (Klir and Yuan 1995; Botzoris et al. 2015) assigns a true value J(x,y) to the fuzzy proposition “If p then q” for every true value (x,y) of the fuzzy propositions p, q. It is a function of the form J:[0,1] × [0,1] → [0,1] which satisfies the following symmetric and asymmetric implications (Klir and Yuan 1995; Botzoris et al. 2015) that are used in this paper:

$$ {\displaystyle \begin{array}{c}\kern1.00em {\mathrm{J}}_{\mathrm{Mandami}}\left(\mathrm{x},\mathrm{y}\right)=\min \left\{\mathrm{x},\mathrm{y}\right\}\kern1.00em \\ {}\kern1.00em {\mathrm{J}}_{\mathrm{Larsen}}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}\cdot \mathrm{y}\kern1.00em \\ {}\kern1.00em {\mathrm{J}}_{\mathrm{Zadeh}}\left(\mathrm{x},\mathrm{y}\right)=\max \left(\min \left\{\mathrm{x},\mathrm{y}\right\},1-\mathrm{x}\right)\kern1.00em \\ {}\kern1.00em {\mathrm{J}}_{\mathrm{Reichenbach}}\left(\mathrm{x},\mathrm{y}\right)=1-\mathrm{x}+\mathrm{x}\cdot \mathrm{y}\kern1.00em \\ {}\kern1.00em {\mathrm{J}}_{\mathrm{Lukasiewicz}}\left(\mathrm{x},\mathrm{y}\right)=\min \left(1-\mathrm{x}+\mathrm{y},1\right)\kern1.00em \end{array}} $$

To illustrate the last implication, we use the t-norm (probor) x∇y = x + y − xy, and the class of fuzzy complements ${n}_{\lambda }(x)=\frac{1-x}{1+\lambda x},\kern0.36em \lambda >-1$. So, we deduce the implication (see Klir and Yuan 1995):

$$ {\displaystyle \begin{array}{c}\hfill J\left(x,y\right)={n}_{\lambda }(x)\nabla y={n}_{\lambda }(x)+y-{n}_{\lambda }(x)y=\hfill \\ {}\hfill =\frac{1-x+y\left(1+\lambda x\right)-y\left(1-x\right)}{1+\lambda x},\lambda >-1.\hfill \end{array}} $$

We will investigate each and every independent variable with chlorophyll-a in the following combinations: x ⇒ y as low ⇒ high, x ⇒ y as medium ⇒ high and x ⇒ y as high ⇒ high. As a result, for every variable, we will have three possible implications. From those three, the smallest is the proper implication for the examined parameter with chl-a.

3 Results and Discussion

3.1 Fuzzy Model

We calculate the deviations of every implication mentioned above from unit:

$$ {\sigma}_{p,r,i}=\sqrt{{\left(1-{{\mu_p}_{,r,i}}^{(1)}\right)}^2+{\left(1-{{\mu_p}_{,r,i}}^{(2)}\right)}^2+\dots +{\left(1-{{\mu_p}_{,r,i}}^{\left({j}_{{{}_p}_{,r}}\right)}\right)}^2} $$

(1)

where p=1,2,3,4 the examined independent parameters (water temperature, NO₃, TP, Secchi Depth), r=l (low), m (medium), h (high), i=1,2,3,4,5,6 the implications (Mandami, Larsen, Zadeh, Lukasiewicz, Reichenbach, Probor), j_p,r is the number of true values.

It should be mentioned that in the last implication, we computed λ so as Eq. (1) is minimized for every studied parameter, and we took λ =  − 0.99 (for details see Appendix) (Tables 1, 2 and 3).

Table 1 Deviations of the fuzzy implication LOW ⇒ HIGH per parameter (σ _{p , l , i} )

Table 2 Deviations of the fuzzy implication MEDIUM ⇒ HIGH per parameter (σ _{p , m , i} )

Table 3 Deviations of the fuzzy implication HIGH ⇒ HIGH per parameter (σ _{p , h , i} )

For a better explanation of this application, a numerical example follows (for the pair of water temperature-chl-a, low class, and the implication of Mandami): First of all, from the statistical data and the trapezoidal fuzzy numbers of Fig. 3 all the true values of the two studied parameters are computed. In this way, are calculated the true values of every dataset of temperature and chl-a. As mentioned above, the implication of Mandami estimates the minimum of the two true values. Hence, the minimum of the two is the implication ${{\mu_1}_{,l,1}}^{\left({j}_{1,l}\right)}$, where i is the number of datasets that composes the class of low. The first deviation of Table 1 (1.29) is derived from Eq. (1). From the above, the best implications for each parameter are separately presented in the Table 4.

Table 4 Most suitable implication per examined couple

In fuzzy inference systems, there is the possibility to choose the most appropriate implication. More precisely, we check the deviation of each implication and we choose the implication with the smallest deviation. For instance, as we see in Table 4, in the combination of low temperature and high chlorophyll-a, we observe that the implication with the smallest deviation is the implication deduced by Probor.

4 Conclusions

Running a water system through a modelling process comes with important problems. One of them is the combination of the lacking data of the time series with the risky water quality parameters. Fuzzy logic can be used as a powerful tool in categorizing environmental status and describing multifaceted changes. This alternative method gives the opportunity to combine many approaches such as traditional indices derived from crisp sets to constant parameters. The main advantage of this tool is the ability to unite many kinds of perceptions by offering stability between social, economic and biological impacts. This paper proposed a method for the selection of the appropriate fuzzy implication in a specific application using real water quality observations in the restored Lake Karla (Thessaly, Greece). This approach presents progress when compared to the arbitrary choice of fuzzy implications. The selection of the most appropriate fuzzy implication has an utter purpose, the application in the inference mechanism, existing in every fuzzy controller of a fuzzy inference system (i.e., Matlab software). In this paper, we observe that generally the most suitable implication for the description in this case study is the implication deduced by probor.

Appendix

For the sixth implication (probor) we take the general function:

$$ f\left(\lambda \right)=\sum_{i=1}^s{\left(1-J\left({x}_i,{y}_i\right)\right)}^2=\sum_{i=1}^s{\left(1-\frac{1-{x}_i+{x}_i{y}_i+\left.\lambda {x}_i{y}_i\right)}{1+\lambda {x}_i}\right)}^2,\lambda >-1,s\in \left\{1,2,\dots \right\}. $$

where x,y are the values of implications for each and every studied combination. We show that f is an increasing function with respect to λ. For this, for every i ∈ {1, 2,  … , s} we take the term:

$$ {h}_i\left(\lambda \right)={\left(1-\frac{1-{x}_i+{x}_i{y}_i+\left.\lambda {x}_i{y}_i\right)}{1+\lambda {x}_i}\right)}^2. $$

We can prove that the derivative of h _i is given by:

$$ {h}_i^{\prime}\left(\lambda \right)=\frac{2{\left(1-{y}_i\right)}^2\left(1-{x}_i\right){x}_i^2\left(1+\lambda \right)}{{\left(1+\lambda {x}_i\right)}^3}. $$

Then, since λ >  − 1 and 0 < x _i  < 1 , i = 1 , 2 ,  …  , s, we have that h _i ^′(λ) > 0 and so, h _i , i ∈ {1, 2,  … , s} is an increasing function for λ >  − 1, and therefore, f is an increasing function for λ >  − 1. So, for λ >  − 0.99, we get f(λ) > f(−0.99) which implies that$\sqrt{f\left(\lambda \right)}>\sqrt{f\left(-0.99\right)}$.

In what follows, for reader’s convenience, we state the data (Ellina and Kagalou 2016) concerning the studied parameters in Table 5.

Table 5 Experimental data from the Lake Karla

First, we calculate the deviation concerning the probor for water temperature and chl-a.

• A. LOW = > HIGH

Arguing as above and the function [1] we take

$$ {f}_{1,l,6}\left(\lambda \right)={\left(1-\frac{0.9122+0.2322\lambda }{1+0.32\lambda}\right)}^2+{\left(1-\frac{0.3648+0.3248\lambda }{1+0.96\lambda}\right)}^2+{\left(1-0.2675\right)}^2+{\left(1-0.6529\right)}^2+{\left(1-0.6907\right)}^2 $$

and so

$$ {\sigma}_{1,l,6}=\sqrt{f\left[-0.99\right]}=0.88. $$

• B. MEDIUM = > HIGH

$$ {f}_{1,m,6}\left(\lambda \right)={\left(1-\frac{0.9669+0.0169\lambda }{1+0.05\lambda}\right)}^2+{\left(1-\frac{0.97097+0.29597\lambda }{1+0.325\lambda}\right)}^2+{\left(1-\frac{0.7673+0.5673\lambda }{1+0.8\lambda}\right)}^2+{\left(1-\frac{0.7667+0.6167\lambda }{1+0.85\lambda}\right)}^2+{\left(1-0.4872\right)}^2+{\left(1-0.8631\right)}^2 $$

and so

$$ {\sigma}_{1,m,6}=\sqrt{f\left[-0.99\right]}=0.53. $$

• C. HIGH = > HIGH

$$ {f}_{1,h,6}\left(\lambda \right)={\left(1-\frac{0.97097+0.29597\lambda }{1+0.325\lambda}\right)}^2+{\left(1-\frac{0.8473+0.3723\lambda }{1+0.525\lambda}\right)}^2+{\left(1-0.3748\right)}^2 $$

and so

$$ {\sigma}_{1,h,6}=\sqrt{f\left[-0.99\right]}=0.63. $$

We calculate the deviation concerning the probor for Nitrates and chl-a.

• A. Α. LOW = > HIGH

$$ {f}_{2,l,6}\left(\lambda \right)={\left(1-\frac{0.8992+0.2250\lambda }{1+0.3258\lambda}\right)}^2+{\left(1-\frac{0.5986+0.1466\lambda }{1+0.548\lambda}\right)}^2+{\left(1-\frac{0.8496+0.3976\lambda }{1+0.548\lambda}\right)}^2+{\left(1-\frac{0.9401+0.6103\lambda }{1+0.67\lambda}\right)}^2+{\left(1-0.3383\right)}^2+{\left(1-0.4872\right)}^2+{\left(1-0.65292\right)}^2+{\left(1-0.7091\right)}^2 $$

and so

$$ {\sigma}_{2,l,6}=\sqrt{f\left[-0.99\right]}=0.96. $$

• B. MEDIUM = > HIGH

$$ {f}_{2,m,6}\left(\lambda \right)={\left(1-\frac{0.9712+0.2934\lambda }{1+0.32\lambda}\right)}^2+{\left(1-\frac{0.9452+0.3452\lambda }{1+0.4\lambda}\right)}^2+{\left(1-\frac{0.7249+0.1649\lambda }{1+0.44\lambda}\right)}^2+{\left(1-\frac{0.6745+0.1189\lambda }{1+0.44\lambda}\right)}^2+{\left(1-\frac{0.8780+0.3225\lambda }{1+0.44\lambda}\right)}^2+{\left(1-\frac{0.7938+0.4605\lambda }{1+0.67\lambda}\right)}^2 $$

and so

$$ {\sigma}_{2,m,6}=\sqrt{f\left[-0.99\right]}=0.011. $$

• C. HIGH = > HIGH

$$ {f}_{2,h,6}\left(\lambda \right)={\left(1-\frac{0.6499+0.2099\lambda }{1+0.56\lambda}\right)}^2+{\left(1-\frac{0.9178+0.5178\lambda }{1+0.599\lambda}\right)}^2 $$

and so

$$ {\sigma}_{2,h,6}=\sqrt{f\left[-0.99\right]}=0.008. $$

We calculate the deviation concerning the probor for Total Phosphorus and chl-a.

• A. Α. LOW = > HIGH

$$ {f}_{3,l,6}\left(\lambda \right)={\left(1-\frac{0.63368+0.1338\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.7436+0.2436\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.8265+0.3265\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.8454+0.3454\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.8545+0.3545\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.8628+0.3628\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.9315+0.4315\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.9315+0.6982\lambda }{1+0.77\lambda}\right)}^2+{\left(1-0.3383\right)}^2+{\left(1-0.3748\right)}^2 $$

and so

$$ {\sigma}_{3,l,6}=\sqrt{f\left[-0.99\right]}=0.91. $$

• B. MEDIUM = > HIGH

$$ {f}_{3,m,6}\left(\lambda \right)={\left(1-\frac{0.97912+0.2125\lambda }{1+0.23\lambda}\right)}^2+{\left(1-\frac{0.6338+0.1338\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.7436+0.2436\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.8265+0.3265\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.8454+0.3454\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.8545+0.3545\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.8628+0.3628\lambda }{1+0.5\lambda}\right)}^2+{\left(1-\frac{0.9315+0.4315\lambda }{1+0.5\lambda}\right)}^2 $$

and so

$$ {\sigma}_{3,m,6}=\sqrt{f\left[-0.99\right]}=0.0108232. $$

We calculate the deviation concerning the probor for Secchi depth and chl-a.

• A. LOW = > HIGH

$$ {f}_{4,l,6}\left(\lambda \right)={\left(1-0.2675\right)}^2+{\left(1-0.3748\right)}^2+{\left(1-0.7256\right)}^2 $$

and so

$$ {\sigma}_{4,l,6}=\sqrt{f\left[-0.99\right]}=1.004 $$

• B. MEDIUM = > HIGH

$$ {f}_{4,m,6}\left(\lambda \right)={\left(1-\frac{0.9851+0.1518\lambda }{1+0.17\lambda}\right)}^2+{\left(1-\frac{0.9498+0.3164\lambda }{1+0.37\lambda}\right)}^2+{\left(1-\frac{0.6753+0.3086\lambda }{1+0.63\lambda}\right)}^2+{\left(1-\frac{0.8158+0.4491\lambda }{1+0.63\lambda}\right)}^2+{\left(1-\frac{0.4927+0.2594\lambda }{1+0.77\lambda}\right)}^2+{\left(1-\frac{0.7423+0.5756\lambda }{1+0.83\lambda}\right)}^2 $$

and so

$$ {\sigma}_{4,m,6}=\sqrt{f\left[-0.99\right]}=0.02. $$

• C. HIGH = > HIGH

$$ {f}_{4,h,6}\left(-0.99\right)={\left(1-\frac{0.9485+0.1151\lambda }{1+0.17\lambda}\right)}^2+{\left(1-\frac{0.8456+0.07894\lambda }{1+0.23\lambda}\right)}^2+{\left(1-\frac{0.81199+0.1787\lambda }{1+0.37\lambda}\right)}^2+{\left(1-\frac{0.8933+0.2599\lambda }{1+0.37\lambda}\right)}^2+{\left(1-\frac{0.9133+0.5466\lambda }{1+0.63\lambda}\right)}^2+{\left(1-\frac{0.9256+0.7589\lambda }{1+0.83\lambda}\right)}^2+{\left(1-0.6529\right)}^2 $$

and so

$$ {\sigma}_{4,h,6}=\sqrt{f\left[-0.99\right]}=0.35. $$