Grinding Wheel Parametric Design for Machining Arbitrary Grooves on the Helical Rake Face of the Tool

Abstract

In the present study, a novel grinding wheel design method is proposed to design a wheel for grinding different small helical grooves on the existing helical rake faces of the tool. The proposed method can be applied to manufacture tools with uneven helical rake face like zigzag-edge twist drills. In the proposed method, the processing of the non-wedge groove is initially converted into a superposition of processing steps of several wedge grooves. Then, based on the simplified non-thickness grinding wheel parametric design and envelop graphic design, the grinding wheel capable of processing small wedge grooves with various specified shapes can be obtained. Moreover, through establishing quantitative evaluation criteria, the determination of design parameters concerning the non-thickness grinding wheel is transmitted into an optimization problem. Finally, helical grooves with trapezoid truncation and wedge truncations are simulated on a virtual five-axis machine tool to verify the effectiveness of the grinding wheel design method.

1 Introduction

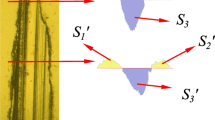
During the cutting process of long-edge tools, chip-ejection interference often occurs, which causes the chip curling and increases the cutting force [1, 2]. Experiments show that the discontinuous design of the cutting edge is an effective way to reduce the influence of chip-ejection interference, thereby reducing the corresponding cutting force and cutting width [3]. A twist drill is a typical tool, which is affected by chip-ejection interference [4]. In this regard, Xiong proposed a zigzag edge twist drill [5]. Further investigations revealed that this innovative tool not only has a lower cutting force than standard drills but also does not require expensive regrinding equipment compared to group drills. Accordingly, this scheme has been widely accepted by small businesses.

Although various methods have been proposed for machining the helical body of the cutting tool [6,7,8,9,10], there is no appropriate method for processing millimeter-level depth helical grooves on the rake face. For example, micro-texturing processing technology is a widely adopted scheme for the surface treatment of the tool rather than the forming process of the tool body [11,12,13,14]. Moreover, the grindability of the non-smooth helical flute needs further investigation [15]. Ehmann and DeVries [16] and Friedman et al. [17] proposed the conjunction line method and CAD method, respectively. However, further investigations revealed that these widely adopted methods for designing the forming grinding wheel could not get the desired structure. The conjunction line method [18] relies on the rotating conjunction line between the grinding wheel and given helical surfaces around the wheel axis to obtain the wheel profile. Accordingly, this method is not an appropriate choice for cases where the truncated line of the spiral body is not continuous. Because the calculated conjunction line through the engagement principle is discontinuous [19] so that incomplete or overlapped wheel profile may be obtained. In this regard, Fig. 1 illustrates a sample design for the grinding wheel obtained from the conjunction line method. On the other hand, the CAD method solves the positive problem between the grinding wheel and the helix [20,21,22,23]. Although the CAD method can be applied to solve some wheel designs in inverse problems with trial and error, there are too many related parameters and coupling effects, thereby increasing the computational expenses. Moreover, uncertainties in the solution interval of parameters and insufficient reference for designing the grinding wheel adversely affect the performance of the CAD method. Based on the foregoing discussions, it is inferred that exploring a simple and efficient method to design the grinding wheel is of significant importance to the dissemination of new cutters with small grooves on the helical rake face. Meanwhile, the required time and labor of the new design may reduce remarkably.

Fig. 1

 A sample non-acceptable profile of the grinding wheel obtained from the conjunction lines method

2 Design Method for the Grinding Wheel

Although there are different axial truncations of small grooves on the helical surface, their profiles can be often regarded as the superimposed combination of several wedge grooves. Typically, the helical surface is not applied for precision transmission. Therefore, a slight divergence between the ideal groove shape and the actual groove shape is acceptable. Consequently, if wedge grooves with different parameters could be ground by grinding wheels, several ideal groove shapes ranging from the triangle to the trapezoid may be produced. In order to avoid serious interference and over-cut, and verify that the processing accuracy of arbitrary grooves, a novel method for designing a grinding wheel is discussed in the next section.

2.1 Modelling of the Blank and Simplified Grinding Wheel

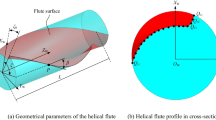
The first step to design the grinding wheel is to establish the coordinate systems and mathematical models of the blank and the grinding wheel [24]. Figure 2 shows an arbitrary position and orientation correlation between the grinding wheel and the blank coordinate systems. Moreover, the simplified grinding wheel in the Cartesian and cylindrical coordinate systems is presented in Fig. 2b, where the Z-axis coincides with the axis of the blank. It should be indicated that O^*X^*Y^*Z^* is the translation transformation of OXYZ and O^* in OXYZ is O^*(m_x, m_y, m_z). Moreover, O¹X¹Y¹Z¹ is the Cartesian coordinate system where the Z-axis coincides with the axis of the grinding wheel. O¹X¹Y¹Z¹ can overlap with O^*X^*Y^*Z^* by counter-clockwise rotation of φ₁ around X^* and then counter-clockwise rotation of φ₂ around Y^*.

Fig. 2

Drill blank and the grinding wheel coordinate systems. a Drill blank in the Cartesian coordinate system (OXYZ), and cylindrical coordinate system (O_ρθ_CZ), and the grinding wheel in the Cartesian coordinate system (O¹ × ¹Y¹Z¹); b translation transformation coordinate system of OXYZ (O^*X^*Y^*Z^*)

It is worth noting that the helical surface is obtained by the helical scanning of the generating line around the Z-axis. Moreover, the function of the line in the space can be expressed as:

$$\left\{ \begin{gathered} X={f_1}\left( t \right) \hfill \\ {\kern 1pt} Y{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ={f_2}\left( t \right) \hfill \\ {\kern 1pt} Z{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ={f_3}\left( t \right) \hfill \\ \end{gathered} \right.,$$

(1)

where t is a variable. The helical surface swept by the generating line can be expressed as:

$$\left\{ \begin{gathered} X={f_1}\left( t \right)\cos \left( \theta \right) - {f_2}\left( t \right)\sin \left( \theta \right) \hfill \\ {\kern 1pt} Y{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ={f_1}\left( t \right)\sin \left( \theta \right)+{f_2}\left( t \right)\cos \left( \theta \right) \hfill \\ {\kern 1pt} Z{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ={f_3}\left( t \right)+\frac{{{T_0}\theta }}{{2\pi }} \hfill \\ \end{gathered} \right.,$$

(2)

where T₀ and θ denote the lead and variable whose range is related to the height of the helix, respectively.

In order to avoid considering many parameters simultaneously, the grinding wheel is simplified as a round piece without thickness and its diameter is equal to the maximum diameter of the grinding wheel. In that case, the grinding wheel is represented by a characteristic circle in Fig. 2b. Then, the characteristic circle is transformed into a blank Cartesian coordinate system by translation and rotation. The corresponding equation is expressed as the following:

$$\left[ \begin{gathered} {x^1} \\ {y^1} \\ {z^1} \\ 1 \\ \end{gathered} \right]={{\text{T}}_{\text{1}}}{{\text{T}}_{\text{2}}}{{\text{T}}_{\text{3}}}\left[ \begin{gathered} {R_C}\cos \left( \varepsilon \right) \\ {R_C}\sin \left( \varepsilon \right) \\ 0 \\ 1 \\ \end{gathered} \right],$$

(3)

where (x¹ y¹ z¹) and R_C denote the coordinates of the points on the characteristic circle and the maximum radius of the grinding wheel, respectively. Moreover, ε is a variable from 0 to 2π.

The transform operators T₁, T₂, T₃ in Eq. (3) can be expressed as:

$${{\text{T}}_{\text{1}}}{\text{=}}\left[ {\begin{array}{*{20}{c}} 1&0&0&{{m_x}} \\ 0&1&0&{{m_y}} \\ 0&0&1&{{m_z}} \\ 0&0&0&1 \end{array}} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\text{T}}_{\text{2}}}{\text{=}}\left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&{\cos \left( {{\varphi _1}} \right)}&{ - \sin \left( {{\varphi _1}} \right)}&0 \\ 0&{\sin \left( {{\varphi _1}} \right)}&{\cos \left( {{\varphi _1}} \right)}&0 \\ 0&0&0&1 \end{array}} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\text{T}}_{\text{3}}}{\text{=}}\left[ {\begin{array}{*{20}{c}} {\cos \left( {{\varphi _2}} \right)}&0&{ - \sin \left( {{\varphi _2}} \right)}&0 \\ 0&1&0&0 \\ {\sin \left( {{\varphi _2}} \right)}&0&{\cos \left( {{\varphi _2}} \right)}&0 \\ 0&0&0&1 \end{array}} \right].$$

(4)

The generating line is helically projected to the Z = 0 plane by moving each point on it helically to obtain the rake face section line in the Z = 0 plane. Where the function in the OXYZ coordinate system can be expressed as:

$$\left[ \begin{gathered} {X^G} \\ {Y^G} \\ {Z^G} \\ \end{gathered} \right]=\left[ \begin{gathered} \left( {{f_1}\left( t \right)\cos \left( \theta \right) - {f_2}\left( t \right)\sin \left( \theta \right)} \right)\cos \left( {{\varepsilon _G}} \right)+\left( {{f_1}\left( t \right)\sin \left( \theta \right)+{f_2}\left( t \right)\cos \left( \theta \right)} \right)\sin \left( {{\varepsilon _G}} \right) \\ - \left( {{f_1}\left( t \right)\cos \left( \theta \right) - {f_2}\left( t \right)\sin \left( \theta \right)} \right)\sin \left( {{\varepsilon _G}} \right)+\left( {{f_1}\left( t \right)\sin \left( \theta \right)+{f_2}\left( t \right)\cos \left( \theta \right)} \right)\cos \left( {{\varepsilon _G}} \right) \\ 0 \\ \end{gathered} \right],$$

(5)

where:

$${\varepsilon _G}=2\pi \frac{{{f_3}\left( t \right)}}{{{T_0}}}+\theta.$$

(6)

Similarly, the characteristic circle is projected to the Z = 0 plane by moving each point on it helically and the projection line in OXYZ coordinate system can be expressed as:

$$\left[ \begin{gathered} {X^H} \\ {Y^H} \\ {Z^H} \\ \end{gathered} \right]=\left[ \begin{gathered} \left( {{R_C}\cos \left( \varepsilon \right)\cos \left( {{\varphi _2}} \right)+{m_x}} \right)\cos \left( {{\varepsilon _H}} \right)+ \\ \left( {{R_C}\sin \left( \varepsilon \right)\cos \left( {{\varphi _1}} \right) - {R_C}\cos \left( \varepsilon \right)\sin \left( {{\varphi _2}} \right)\sin \left( {{\varphi _1}} \right)+{m_y}} \right)\sin \left( {{\varepsilon _H}} \right) \\ \\ - \left( {{R_C}\cos \left( \varepsilon \right)\cos \left( {{\varphi _2}} \right)+{m_x}} \right)\sin \left( {{\varepsilon _H}} \right)+ \\ \left( {{R_C}\sin \left( \varepsilon \right)\cos \left( {{\varphi _1}} \right) - {R_C}\cos \left( \varepsilon \right)\sin \left( {{\varphi _2}} \right)\sin \left( {{\varphi _1}} \right)+{m_y}} \right)\cos \left( {{\varepsilon _H}} \right) \\ \\ 0 \\ \end{gathered} \right],$$

(7)

where:

$${\varepsilon _H}=2\pi \frac{{{R_C}\sin \left( \varepsilon \right)+{R_C}\cos \left( \varepsilon \right)\sin \left( {{\varphi _2}} \right)\cos \left( {{\varphi _1}} \right)+{m_z}}}{{{T_0}}}.$$

(8)

According to the transformation correlation between the Cartesian coordinate system and the Cylindrical coordinate system, m_x and m_y in Eqs. (7) and (8) can be replaced by ρ and θ_c as follows:

$$\left\{ \begin{gathered} {m_x}=\rho \sin \left( {{\theta _c}} \right) \hfill \\ {m_y}=\rho \cos \left( {{\theta _c}} \right) \hfill \\ \end{gathered} \right..$$

(9)

Since the helical surface has a constant cross-sectional truncation perpendicular to the Z-axis, θ_c and m_z can be unified into one parameter ω, which represents the rotation angle of the helical projection line around the Z-axis. In conclusion, there are five parameters (ρ, φ₁, φ₂, R_C, ω), which can determine the shape and position of the projection line of the characteristic circle in Z = 0 plane.

2.2 Evaluation Criteria for Parameters of the Simplified Grinding Wheel

Before selecting ρ, φ₁, φ₂, R_C, ω that can determine the characteristic circle of the simplified wheels and its helical projection line, evaluation criteria to judge whether these parameters are appropriate should be established.

Figure 3 shows that P and r_S are the points with the smallest curvature radius on the projection line and the curvature radius of point P, respectively. Moreover, R_n and L denote the rotation trajectory of the wedge groove bottom apex and the distance between R_n and P, respectively. L₁ and L₂ are two side lengths of the wedge groove corresponding to R_n. A₁ and A₂ are two points on the projection line and the distance between them and P is L₁. Similarly, B₁ and B₂ are two points on the projection line and the distance between them and P is L₂. Moreover, A₁ is the point where the distance between A₁, A₂ and original point O is farther and that B₂ is the point where the distance between B₁, B₂ and O is closer. A₁, B₂, O and P are connected with rays to obtain the angles of Kr₁ and Kr₂. Moreover, O, two side apexes and the bottom apex of the groove with rays are connected to obtain the angles of Kr₁^* and Kr₂^*.

Fig. 3

Parameters correlated to the evaluation criteria and the projection line of characteristic circle (R_C = 8 mm, ρ = 10 mm, φ₁ = 1.88 rad, φ₂ = 0.47 rad)

Figure 4 shows that if ρ, φ₁, φ₂ and R_C are selected correctly, the projection line of the characteristic circle has an appropriate drop shape. After rotating the drop shape at an appropriate angle ω, its cusp fits into the desired material removal area.

Fig. 4

Drop-shaped projection line of the characteristic circle with suitable parameters (R_C = 8 mm, ρ = 10 mm, φ₁ = 1.82 rad, φ₂ = 0.96 rad)

In other words, when r_S is too large, overcut at the bottom of the wedge groove is undeniable. Moreover, when Kr₁^* > Kr₁ or Kr₂^* > Kr₂, overcut occurs at the side of the wedge groove. Meanwhile, uncertainties in the wedge groove position appear for too large L values. However, when r_S and L are small enough, and Kr₁^* < Kr₁ and Kr₂^* < Kr₂, it can be said that parameters of the characteristic circle are properly selected. In order to avoid serious overcut caused by the final design of the grinding wheel structure and quantify the droplet shape, the following evaluation criteria for parameters selection with size level of small grooves are proposed:

$${r_S}<{\psi _1}\hbox{max} \left( {{L_1},{\kern 1pt} {L_{\text{2}}}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L<{\psi _2}\hbox{max} \left( {{L_1},{\kern 1pt} {\kern 1pt} {L_{\text{2}}}} \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K{r_1}^{*}<K{r_1},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K{r_2}^{*}<K{r_2},$$

(10)

where ψ₁ and ψ₂ are constants whose value ranges from 0.05 to 0.30 according to the acceptable accuracy.

2.3 Solving the Simplified Grinding Wheel Parameters with the Optimization Algorithm

According to the abovementioned section, ω is the rotation angle of the projection line and it is independent of the drop shape. Therefore, in order to simplify the problem, ω is ignored and only the remaining parameters, including ρ, φ₁, φ₂ and R_C are considered. However, since the correlation between these four parameters remains unknown, it is labor-intensive and time-consuming to select ρ, φ₁, φ₂ and R_C by trial and error based on the graphic method. Therefore, in order to save time and workforce, this problem is converted into an optimization problem with quantified function P_f incorporating ρ, φ₁, φ₂, R_C, which is described as the following:

$${P_f}=\left\{ \begin{gathered} {N_0}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {P{\text{ is not the first quadrant}}} \right) \hfill \\ \left( {{w_1}+{w_2}} \right){w_3}{w_4}{R_C}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {P{\text{ is in the first quadrant}}} \right) \hfill \\ \end{gathered} \right.,$$

(11)

where N₀ is a constant that is high enough to ensure that the cusp of the projection line is in the first quadrant. Therefore, it allows that the wedge groove can fit into the tip of the projection line by the clockwise rotation. Moreover, R_C is incorporated in Eq. (11) to increase the diameter of the grinding wheel as large as possible. It is worth noting that w₁, w₂, w₃, w₄ are four convergence correlated to Kr₁, Kr₁, r_S and L, respectively. Moreover, the adjustment of parameters shows that the optimization function converges easily if the abovementioned four factors fulfill the following requirements:

• (i) w₁, w₂, w₃ and w₄ are positive.

• (ii) w₁ and w₂ monotonically decrease with Kr₁and Kr₂, while w₃ and w₄ monotonically increase with r_S and L.

• (iii) When Kr₁, Kr₂, r_S and L are within a reasonable interval, the functions converge slowly. Once Kr₁, Kr₂, r_S and L exceed the reasonable interval, the function values will obtain a step-wise raise and the convergence rate will rise significantly.

However, piecewise functions w₁(Kr₁), w₂(Kr₂), w₃(r_S) and w₄(L) that are capable of meeting the abovementioned requirements are listed as the following:

$${w_1}=\left\{ \begin{gathered} K{r_1}^{*} - K{r_1}+{M_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K{r_1}^{*} \geq K{r_1} \hfill \\ {N_1}\left( {K{r_1}^{*} - K{r_1}} \right)+{M_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K{r_1}^{*}<K{r_1} \hfill \\ \end{gathered} \right.,$$

(12)

$${w_2}=\left\{ \begin{gathered} K{r_2}^{*} - K{r_2}+{M_3}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K{r_2}^{*} \geq K{r_2} \hfill \\ {N_2}\left( {K{r_2}^{*} - K{r_2}} \right)+{M_4}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K{r_2}^{*}<K{r_2} \hfill \\ \end{gathered} \right.,$$

(13)

$${w_3}=\left\{ \begin{gathered} {M_5}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {r_S} \leq {P_1} \hfill \\ {N_3}{r_S}+{M_6}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {P_1}<{r_S} \leq {P_2} \hfill \\ {N_4}{r_S}+{M_7}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {r_S}>{P_3} \hfill \\ \end{gathered} \right.,$$

(14)

$${w_4}=\left\{ \begin{gathered} L+{M_8}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L \leq {P_4} \hfill \\ {N_5}L+{M_9}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L>{P_4} \hfill \\ \end{gathered} \right.,$$

(15)

where, M₁ ~ M₉, P₁ ~ P₄ and N₁ ~ N₅ are constants whose values are correlated to specific issues. Moreover, by selecting them according to different situations, potential functions for optimization can be constructed.

Then, since the problem is converted into a minimum optimization problem, the genetic algorithm [25,26,27,28,29,30], which is a general and effective method for optimization, can be employed to solve the problem. After determination of ρ, φ₁, φ₂ and R_C, the graphic method is utilized to verify the rationality of the parameters and to solve the appropriate ω. According to the abovementioned ideas, an optimization program is written to solve ρ, φ₁, φ₂ and R_C.

2.4 Design of the Actual Grinding Wheel Based on the Simplified Grinding Wheel

Since the grinding wheel has a certain thickness as the simplified grinding wheel, it is necessary to consider the influence of the radial profile of the grinding wheel after determining the five parameters of the simplified grinding wheel. Figure 5a shows that in the wheel, not only the part with the maximum radius is involved in the grinding, but also other nearby parts are involved in the grinding process. Therefore, the parameters of the axial truncation of the grinding wheel also affect the grinding process.

Fig. 5

Radial profile of the grinding wheel. a Continuous representation; b discretized representation

The non-V-shaped grinding wheel design [31] will significantly increase the difficulty of the design process. Therefore, in this study, only the V shape grinding wheel with 5 profile parameters, including λ₁, λ₂, R_S, H₁, H₂ is designed and the influence of R_S is ignored. Therefore, set R_S = 0. Moreover, during the grinding of small grooves, not all working faces of the grinding wheel are involved in the cutting process. Therefore, as long as H₁ and H₂ are large enough (H₁ > 1.5L₁, H₂ > 1.5L₁), the actual grinding effect of the grinding wheel is not affected by H₁ and H₂. It should be indicated that the appropriate values of λ₁ and λ₂ are selected by the envelope method. Figure 5b shows that the grinding wheel with thickness is separated into several pieces and these pieces can be represented by several characteristic circles whose equations in the blank coordinate system is mathematically expressed as:

$$\left[ \begin{gathered} {X^i} \\ {Y^i} \\ {Z^i} \\ 1 \\ \end{gathered} \right]={T_1}{T_2}{T_3}\left[ \begin{gathered} \left( {{R_C}+H\cot \left( {{\lambda _1}} \right)} \right)\cos \left( \varepsilon \right) \\ \left( {{R_C}+H\cot \left( {{\lambda _1}} \right)} \right)\sin \left( \varepsilon \right) \\ H \\ 1 \\ \end{gathered} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( { - {H_1} \leq H<0} \right),$$

(16)

$$\left[ \begin{gathered} {X^i} \\ {Y^i} \\ {Z^i} \\ 1 \\ \end{gathered} \right]={T_1}{T_2}{T_3}\left[ \begin{gathered} \left( {{R_C} - H\cot \left( {{\lambda _2}} \right)} \right)\cos \left( \varepsilon \right) \\ \left( {{R_C} - H\cot \left( {{\lambda _2}} \right)} \right)\sin \left( \varepsilon \right) \\ H \\ 1 \\ \end{gathered} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {0 \leq H \leq {H_2}} \right),$$

(17)

where i is the number of the grinding wheel pieces.

All of the characteristic circles are helically projected to the Z = 0 plane. Moreover, Fig. 6 shows the obtained projection line bundles. It is observed that the blank entity within the envelope of the red line bundle is removed. Then, λ₁ and λ₂ are gradually increased to identify appropriate values according to envelopes obtained by the graphic method.

Fig. 6

Envelope of projection line bundles of grinding wheel discretized characteristic circles (R_C = 12.28 mm, ρ = 15.78 mm, φ₁ = 4.63 rad, φ₂ = 0.72 rad, ω = 0.50 rad, λ₁ = 0.41 rad, λ₂ = 1.23 rad)

3 Practice Examples

As mentioned above, the flow of the grinding wheel design is categorized into four steps as the following:

• (i) Extract several points on the truncation to construct several wedge grooves and determine H₁, H₂ based on the precision requirement and the size of the wedge.

• (ii) Import coordinates of three vertices of the wedge and T₀ into the optimization program to calculate the simplified grinding wheel parameters ρ, φ₁, φ₂, R_C.

• (iii) Determine profile parameters λ₁, λ₂ of the grinding wheel and rotation angle ω by the graphic method.

• (iv) Superimpose the processing effect of multiple wedge grooves to check whether the final groove shape meets the requirements.

Figure 7 shows that the trapezoidal groove (groove 1) is taken as an example. According to the shape and size of the groove, set H₁ = H₂ = 2 mm. Then, the trapezoidal groove is separated into three wedge grooves with different bottom points, which is presented as the thin line in Fig. 7b. Number these points and 1, 5 are the common points of three triangular grooves, while points 2, 3, 4 are the bottom points. It should be indicated that Table 1 lists the initial XY coordinates in OXYZ. Then, to determine appropriate values of ρ, φ₁, φ₂, R_C, the coordinates of points 1, 4, 5 are applied into the optimization program mentioned in Sect. 2.3. It is worth noting that M₁–M₉, P₁–P₄ and N₁–N₅ for this specific fitness function can be obtained by debugging parameters and are listed as the following:

Fig. 7

Multiple grinding wheel design of the helical groove with trapezoidal truncation

Table 1 Parameters of the grinding wheel with trapezoid groove type

$${P_f}=\left\{ \begin{gathered} {10^7}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {P{\text{ is not the first quadrant}}} \right) \hfill \\ \left( {{w_1}+{w_2}} \right){w_3}{w_4}{R_C}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {P{\text{ is in the first quadrant}}} \right) \hfill \\ \end{gathered} \right.,$$

(18)

where:

$${w_1}=\left\{ \begin{gathered} K{r_1}^{*} - K{r_1}+\frac{\pi }{2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K{r_1}^{*} \geq K{r_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ 10\left( {K{r_1}^{*} - K{r_1}} \right)+10\pi {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K{r_1}^{*}<K{r_1}{\kern 1pt} \hfill \\ \end{gathered} \right.,$$

(19)

$${w_{\text{2}}}=\left\{ \begin{gathered} K{r_{\text{2}}}^{*} - K{r_{\text{2}}}+\frac{\pi }{2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K{r_{\text{2}}}^{*} \geq K{r_{\text{2}}}{\kern 1pt} {\kern 1pt} \hfill \\ 10\left( {K{r_{\text{2}}}^{*} - K{r_{\text{2}}}} \right)+10\pi {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K{r_{\text{2}}}^{*}<K{r_{\text{2}}}{\kern 1pt} \hfill \\ \end{gathered} \right.,$$

(20)

$${w_3}=\left\{ \begin{gathered} 10{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {r_S} \leq 0.1 \hfill \\ 100{r_S}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.1<{r_S} \leq 0.3 \hfill \\ 20{r_S}+44{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {r_S}>0.3 \hfill \\ \end{gathered} \right.,$$

(21)

$${w_4}=\left\{ \begin{gathered} L+0.2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L \leq 0.2 \hfill \\ 20 L+10{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} L>0.2 \hfill \\ \end{gathered} \right..$$

(22)

It should be indicated that the solution intervals of ρ, R_C, φ₁, φ₂, are [6–18], [8–20], [0–2π]and [0–2π], respectively. Moreover, Table 1 presents the evaluation parameters related to the projection line of the characteristic circle. Table 2 illustrates the results of the optimization of the grinding wheel. It is observed that the optimized ρ, φ₁, φ₂, R_C can meet the evaluation criteria as in Eq. (10) (set ψ₁ = ψ₂ = 0.1 in this case). Then, through rotating the rake face section line to match the characteristic circle and increasing λ₁, λ₂ gradually to fit the envelope boundary with the trapezoidal groove, appropriate ω, λ₁, λ₂ can be determined. It is worth noting that all parameters correlated to the grinding wheel for machining wedge 1–2–5 in Fig. 7 are obtained and the other two grinding wheels for grinding wedge 1–3–5 and wedge 1–4–5 are designed similarly. Finally, three grinding effects are superimposed to check whether the final truncation can meet the requirement of the machining accuracy. Figure 7b shows that the actual ground area is very similar to the desired profile, which verifies the effectiveness of this method. Moreover, to verify the versatility of the method, a series of grinding wheels for machining grooves with different shapes, positions, and leads are designed according to the aforementioned flow. Figure 8 exhibits the truncation of these grooves and grinding wheel parameters are shown in Table 2.

Table 2 Grinding wheel parameter designed for grinding different grooves

Fig. 8

Multiple grinding wheel design of the helical groove with several truncations

Finally, in the present study, the effect of machining small helical grooves on a five-axis virtual machine tool with the designed grinding wheel is observed. Figure 9 illustrates the virtual five-axis machine tool used for the simulation. Moreover, Fig. 10 shows two types of grooves processing effects. It is observed that the helical groove obtained by the simulation processing has a reasonable similarity with the expected helical groove. The simulation results not only verify the validity and correctness of the grinding wheel design method proposed in this study but also prove the feasibility of producing a prototype of the zigzag edge twist drills by the grinding process.

Fig. 9

Grinding single-wedge groove on the twist drill by 5-axis machine tool

Fig. 10

Grinding simulation results. a Trapezoid groove processing; b zigzag edge twist drill with wedge grooves processing

It is worth noting that the calculation of the initial installation position and angle adjustment of the machine tool refers to the literature and methods proposed by other scholars [32, 33]. Therefore, due to space limitations and the scope of discussion, the calculations are not repeated in this study.

4 Conclusions

The following conclusions are drawn from the present study:

• 1. A small spiral groove with a specified shape can be machined on the spiral rake face of the tool by a grinding wheel. Moreover, it is observed that this method facilitates the manufacture and industrialization of tools with small grooves on the helical surface. Therefore, it can solve the technical problems in the process of a special helical surface.

• 2. A small spiral groove with a wedge-shaped section can be processed by one grinding wheel at a time. However, a small spiral groove with a non-wedge-shaped section requires multiple processes with multiple grinding wheels.

• 3. The key parameters of the grinding wheel for grinding the wedge groove are automatically designed by combining optimization algorithms, which provides a direction for reducing the difficulty and the cost of the grinding wheel design.