Abstract
We discuss the notion of properness of a polynomial map \(\varvec{f}:\mathbb {K}^m\rightarrow \mathbb {K}^n\), \(\mathbb {K}=\mathbb {C}\) or \(\mathbb {R}\), at a point of the target. We present a method to describe the set of non-proper points of \(\varvec{f}\) with respect to Newton polyhedra of \(\varvec{f}\). We obtain an explicit precise description of such a set of \(\varvec{f}\) when \(\varvec{f}\) satisfies certain condition (1.5). A relative version is also given in Sect. 3. Several tricks to describe the set of non-proper points of \(\varvec{f}\) without the condition (1.5) is also given in Sect. 5.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
We consider a polynomial map \(\varvec{f}=(f^1,\dots ,f^n):\mathbb {K}^m\rightarrow \mathbb {K}^n\), defined by
where \(\mathbb {K}=\mathbb {C}\) or \(\mathbb {R}\). We say that a point \(\varvec{y}_0\in \mathbb {K}^n\) is proper for \(\varvec{f}\) (or a proper point of \(\varvec{f}\)) if, for any (algebraic) arc \(\varvec{x}(t):\mathbb {K}^*,0\rightarrow \mathbb {K}^m\), \(\mathbb {K}^*=\mathbb {K}{\setminus }\{0\}\), the following condition holds:
Let \(S_{\varvec{f}}\) denote the set of points \(\varvec{y}_0\) in \(\mathbb {K}^n\) which are not proper points of \(\varvec{f}\). We say that \(\varvec{f}:\mathbb {K}^m\rightarrow \mathbb {K}^n\) is proper if \(S_{\varvec{f}}=\emptyset \).
In this paper, we are looking for a method to determine whether a point \(\varvec{y}_0\) in \(\mathbb {K}^n\) is proper or not. The first statement is Theorem 1.3, which gives a complete description of \(S_{\varvec{f}}\) when \(\varvec{f}\) satisfies certain non-degeneracy condition with respect to the Newton polyhedron of \(\varvec{f}\) (see (1.5) in Theorem 1.3). Our approach is based on simple and careful analysis of \(\varvec{f}\) along arcs \(\varvec{x}(t)\), which suggests us usefulness of using arcs to describe the set \(S_{\varvec{f}}\), even though \(\varvec{f}\) is degenerate (Remark 2.6). In Sect. 3, we describe a relative version of our discussion. We present several examples to show how our method works in Sect. 4.
The set \(S_{\varvec{f}}\) was introduced by Jelonek [4, 5] and showed that it is empty or a uniruled hypersurface of \(\mathbb {K}^n\) when \(\mathbb {K}=\mathbb {C}\) and \(m=n\). It is thus an interesting problem to seek a method to describe \(S_{\varvec{f}}\) in several concrete examples. Chen et al. [2] have investigated the bifurcation locus of a polynomial map \(\mathbb {K}^m\rightarrow \mathbb {K}^n\), \(m\ge n\), with respect to Newton polyhedron. The bifurcation locus is the minimal locus in the target where the map is not locally trivial, and they show a supset of the bifurcation locus under their non-degeneracy condition. Jelonek and Lasoń [6] called \(S_{\varvec{f}}\) as the non-properness set of \(\varvec{f}\) and showed that it is covered by parametric curves of degree at most \(d-1\) where d is the algebraic degree of \(\varvec{f}\) for \(\mathbb {K}=\mathbb {C}\). Their words “covered by parametric curves” mean that the set \(S_{\varvec{f}}\) has a “\(\mathbb {C}\)-ruling”. They also discuss real counterpart of their results. Recently, El Hilany [3] has investigated to describe the set \(S_{\varvec{f}}\) via the Newton polyhedra of \(\varvec{f}\). He calls \(S_{\varvec{f}}\) as Jelonek set. He has introduced the notion of T- maps and claimed that \(S_{\varvec{f}}\) is described using only the data of \(\varvec{f}\) at several faces of its Newton polyhedra. Comparing with these results, our method provides much precise information on the set \(S_{\varvec{f}}\) with simple description. For example, Theorem 1.3 shows an explicit decomposition of \(S_{\varvec{f}}\) providing an explicit ruling of each component in many cases. In Sect. 3, we present a relative version of our theorem. Namely, we consider the non-properness set \(S_{\varvec{f}|_X}\) for \(\varvec{f}|_X:X\rightarrow \mathbb {K}^n\) where \(\varvec{f}=(f^1,\dots ,f^n):\mathbb {K}^m\rightarrow \mathbb {K}^n\) is a certain polynomial map and \(X=(f^{n-k+1},\dots ,f^n)^{-1}(c)\), \(c\in \mathbb {K}^k\). In Sect. 5, we present tricks to describe \(S_{\varvec{f}}\) for certain degenerate \(\varvec{f}\).
We say some words for the definition of \(S_{\varvec{f}}\) here. We compactify \(\varvec{f}\) as \(\bar{\varvec{f}}:X\rightarrow Y\) where X and Y are suitable projective manifolds. We set \(X_\infty =X{\setminus }\mathbb {K}^m\), \(Y_\infty =Y{\setminus }\mathbb {K}^n\) and we can assume that \(X_\infty \) and \(Y_\infty \) are simple normal crossing divisors. Then, the condition \(\varvec{y}_0\in S_{\varvec{f}}\) is equivalent to one of the following conditions.
-
There exists an algebraic arc \(\varvec{x}(t):\mathbb {K},0\rightarrow X\), such that
$$\begin{aligned} \displaystyle {\lim _{t\rightarrow 0}\varvec{x}(t)\in X_\infty },\quad \text { and }\quad \displaystyle {\lim _{t\rightarrow 0}\varvec{f}(\varvec{x}(t))=\varvec{y}_0}. \end{aligned}$$(0.2) -
There exists an analytic arc \(\varvec{x}(t):\mathbb {K},0\rightarrow X\) defined near 0 with (0.2).
-
There exists a sequence \(\{\varvec{x}_k\}\) in X, such that \(\displaystyle {\lim _{k\rightarrow \infty }\varvec{x}_k}\in X_\infty \) and \(\displaystyle {\lim _{k\rightarrow \infty }\varvec{f}(\varvec{x}_k)=\varvec{y}_0}\).
The last condition is equivalent to the condition that \(\varvec{y}_0\) is not a proper point of f as a continuous map between metric spaces. We also have
Since \(\bar{\varvec{f}}\) is proper, the set \(\bar{\varvec{f}}(X_\infty )\) is closed in Y and we obtain that \(S_{\varvec{f}}\) is closed.
When \(\mathbb {K}=\mathbb {C}\) and \(m>n\), Noether’s normalization asserts that, for any \(\varvec{y}\in \mathbb {C}^n\), there is a linear surjection \(p:\varvec{f}^{-1}(\varvec{y})\rightarrow \mathbb {C}^d\), \(0\le d\le m\), where \(d=\dim _{\mathbb {C}}\varvec{f}^{-1}(\varvec{y})\). If \(\varvec{f}^{-1}(\varvec{y})\) is compact, then \(p(\varvec{f}^{-1}(\varvec{y}))=\mathbb {C}^d\) is compact and we obtain \(d=0\). Since \(d\ge m-n\), we conclude that \(m\le n\). This implies that \(S_{\varvec{f}}\) is the closure of the image of \(\varvec{f}\) whenever \(m>n\). Therefore, we assume \(m\le n\) when \(\mathbb {K}=\mathbb {C}\).
When \(\mathbb {K}=\mathbb {C}\), Jelonek’s result asserts that \(S_{\varvec{f}}\) is Zariski closed. However, if \(\mathbb {K}=\mathbb {R}\), \(S_{\varvec{f}}\) may not be Zariski closed (for example, \(S_{\varvec{f}}=\{(0,y_2)\in \mathbb {R}^{2}: y_2\ge 0\}\) for \(\varvec{f}:\mathbb {R}^2\rightarrow \mathbb {R}^2\), \((x_1,x_2)\mapsto (x_1,x_1^2x_2^2)\)).
Throughout the paper, we use the following notational convention:
for a subset J of \(\{1,\dots ,n\}\). We set \(\mathbb {Z}^J_{\ge 0}=\{(\nu _1,\dots ,\nu _n)\in \mathbb {Z}^J:\nu _i\ge 0, i\in J\}\). We also set \((\mathbb {Z}_{\ge 0})^n=\{(\nu _1,\dots ,\nu _n)\in \mathbb {Z}^n:\nu _i\ge 0, i=1,\dots ,n\}\). We often abbreviate \(\mathbb {Z}_{\ge 0}\) as \(\mathbb {Z}_\ge \) following custom. We identify \(\mathbb {K}^n\) with \(\mathbb {K}^J\times \mathbb {K}^{J^c}\) where \(J^c=\{1,\dots ,n\}{\setminus } J\) without notice.
1 Newton Polyhedra
Let \(\Delta (f^j)\) denote Newton polyhedron of \(f^j\), the convex hull of the set \(\{\varvec{\nu }:c^j_{\varvec{\nu }}\ne 0\}\), under the notation in (0.1). For \(\varvec{p}=(p_1,\dots ,p_m)\in \mathbb {Z}^m\), we define
We call \(\gamma _j(\varvec{p})\) the face of \(\Delta (f^j)\) supported by \(\varvec{p}\).
We say  which is a face of \(\varvec{\Delta }(\varvec{f})=(\Delta (f^1),\dots ,\Delta (f^n))\) if there exist \(\varvec{p}\in \mathbb {Z}^m\), so that \(\gamma _j\) is a face of \(\Delta (f^j)\) supported by \(\varvec{p}\). We denote
which is a face of \(\varvec{\Delta }(\varvec{f})=(\Delta (f^1),\dots ,\Delta (f^n))\) if there exist \(\varvec{p}\in \mathbb {Z}^m\), so that \(\gamma _j\) is a face of \(\Delta (f^j)\) supported by \(\varvec{p}\). We denote

When we need to mention \(\varvec{f}\) explicitly, we denote them by  , \(\gamma _j(\varvec{f};\varvec{p})\), and so on. We consider Minkowski sum \(\Delta (\varvec{f})=\Delta (f^1)+\cdots +\Delta (f^n)\) and its dual fan \(\Delta ^*\), which we identify with the set of polyhedral cones. Note that \(\gamma (\varvec{p})=\gamma _1(\varvec{p})+\cdots +\gamma _n(\varvec{p})\) is a face of \(\Delta (\varvec{f})\). We denote
, \(\gamma _j(\varvec{f};\varvec{p})\), and so on. We consider Minkowski sum \(\Delta (\varvec{f})=\Delta (f^1)+\cdots +\Delta (f^n)\) and its dual fan \(\Delta ^*\), which we identify with the set of polyhedral cones. Note that \(\gamma (\varvec{p})=\gamma _1(\varvec{p})+\cdots +\gamma _n(\varvec{p})\) is a face of \(\Delta (\varvec{f})\). We denote

Lemma 1.1
 \(\iff \) \(\gamma (\varvec{p})=\gamma (\varvec{q})\).
\(\iff \) \(\gamma (\varvec{p})=\gamma (\varvec{q})\).
Proof
“\(\Longrightarrow \)” part is clear, since “ \(\iff \) \(\gamma _j(\varvec{p})\!=\!\gamma _j(\varvec{q})\) (\(j\!=\!1,\dots ,n\))”.
\(\iff \) \(\gamma _j(\varvec{p})\!=\!\gamma _j(\varvec{q})\) (\(j\!=\!1,\dots ,n\))”.
Take \(\varvec{\nu }\in \gamma (\varvec{q})\), so that \(\varvec{\nu }=\varvec{\nu }_1+\cdots +\varvec{\nu }_n\) for \(\varvec{\nu }_j\in \gamma _j(\varvec{q})\). Since \(\gamma _j(\varvec{q})\subset \Delta (f^j)\), we have \(-d_j(\varvec{p})\le \langle \varvec{p},\varvec{\nu }_j\rangle \). If we assume \(\gamma (\varvec{q})\subset \gamma (\varvec{p})\), we then have
and \(\langle \varvec{p},\varvec{\nu }_j\rangle =-d_j(\varvec{p})\), that is, \(\varvec{\nu }_j\in \gamma _j(\varvec{p})\). We conclude \(\gamma _j(\varvec{q})\subset \gamma _j(\varvec{p})\). By symmetry, we complete the proof of “\(\Longleftarrow \)”. \(\square \)
Compositing \(\varvec{f}\) with a translation of the target, the set \(S_{\varvec{f}}\) is changed by its translation. Without loss of generality, we thus can assume the following condition:
Throughout the paper, we assume the condition (1.3) unless otherwise stated.
The condition (1.3) implies that \(d_j(\varvec{p})\ge 0\) and equality holds if \(\varvec{p}\in (\mathbb {Z}_{\ge 0})^n\). For a face  of \(\varvec{\Delta }(\varvec{f})\), we set
of \(\varvec{\Delta }(\varvec{f})\), we set  . We remark that
. We remark that

Definition 1.2
We say a face  of \(\varvec{\Delta }(\varvec{f})\) is non-coordinate if there is \(\varvec{p}\in \mathbb {Z}^m{\setminus }(\mathbb {Z}_{\ge 0})^m\), so that
of \(\varvec{\Delta }(\varvec{f})\) is non-coordinate if there is \(\varvec{p}\in \mathbb {Z}^m{\setminus }(\mathbb {Z}_{\ge 0})^m\), so that  . Let \(\varvec{\Delta }_{\mathrm {nc}}(\varvec{f})\) denote the set of non-coordinate faces of \(\varvec{\Delta (f)}\).
. Let \(\varvec{\Delta }_{\mathrm {nc}}(\varvec{f})\) denote the set of non-coordinate faces of \(\varvec{\Delta (f)}\).
For a polynomial map \(\varvec{g}=(g^1,\dots ,g^r):\mathbb {K}^m\rightarrow \mathbb {K}^r\), we set
where \(\mathop {\mathrm {Jac}}{(}\varvec{g})=(\partial _{x_i}g^j)_{i=1,\dots , m; j=1, \dots , r}\). Remark that the codimension of \(Z(\varvec{g}){\setminus }\Sigma (\varvec{g})\) is r.
Theorem 1.3
Assume that \(\varvec{f}\) is a polynomial map with (1.3) and

for any  where
where  . We have
. We have

where  ,
,  , and
, and  is the map defined by \(\varvec{x}\mapsto (f^j_{\gamma _j}(\varvec{x}))_{j\not \in J}\).
is the map defined by \(\varvec{x}\mapsto (f^j_{\gamma _j}(\varvec{x}))_{j\not \in J}\).
We often say that  has the dense nonsingular locus if the condition (1.5) holds.
has the dense nonsingular locus if the condition (1.5) holds.
When \(J=\{1,\dots ,n\}\), we have  is a constant map, since \(\mathbb {K}^\emptyset \) is a one-point set.
is a constant map, since \(\mathbb {K}^\emptyset \) is a one-point set.
Remark 1.4
Chen et al. [2] said that \(\varvec{f}\) is non-degenerate if  for all
for all  . This implies (1.5) for all
. This implies (1.5) for all  . However, our condition (1.5) is weaker than their non-degeneracy condition.
. However, our condition (1.5) is weaker than their non-degeneracy condition.
Remark 1.5
If  , the condition (1.5) implies that
, the condition (1.5) implies that  is empty. In fact, if we take a nonsingular point
is empty. In fact, if we take a nonsingular point  , then the condition (1.5) implies that
, then the condition (1.5) implies that  is of codimension n at \(\varvec{x}\). This implies that \(\varvec{x}\) is isolated in
is of codimension n at \(\varvec{x}\). This implies that \(\varvec{x}\) is isolated in  . However, this is impossible, since \(f^j_{\gamma _j}\) is weighted homogeneous with respect to the weight \(\varvec{p}\).
. However, this is impossible, since \(f^j_{\gamma _j}\) is weighted homogeneous with respect to the weight \(\varvec{p}\).
We also remark that  when
when  .
.
Corollary 1.6
A polynomial map \(\varvec{f}\) with (1.3) is proper, if for any  none of \(\gamma _j\), \(j=1,\dots ,n\), contains the origin and
none of \(\gamma _j\), \(j=1,\dots ,n\), contains the origin and  has a dense nonsingular locus for any
has a dense nonsingular locus for any  .
.
Remark 1.7
When \(k=\dim \gamma _J=\sum _{j\in J}\dim \gamma _j\),  ,
,  is a system of polynomials of k Laurent monomials of \(\varvec{x}\) and
is a system of polynomials of k Laurent monomials of \(\varvec{x}\) and  is isomorphic to \(X\times (\mathbb {K}^*)^{n-k}\) for some algebraic variety X in \((\mathbb {K}^*)^k\). If
is isomorphic to \(X\times (\mathbb {K}^*)^{n-k}\) for some algebraic variety X in \((\mathbb {K}^*)^k\). If  , \(d_j=0\) and \(f^j(x)\) (\(j\in J\)) is invariant under the natural \(\mathbb {K}^*\)-action(s). Thus,
, \(d_j=0\) and \(f^j(x)\) (\(j\in J\)) is invariant under the natural \(\mathbb {K}^*\)-action(s). Thus,  . When
. When  is complete intersection, we have that
is complete intersection, we have that

where F is a suitable fiber of  . We thus have
. We thus have  . When \(\mathbb {K}=\mathbb {C}\), \(S_{\varvec{f}}\) is a hypersurface and
. When \(\mathbb {K}=\mathbb {C}\), \(S_{\varvec{f}}\) is a hypersurface and  should be the union of the closures of
should be the union of the closures of  with
with  (and \(\dim F=0\)).
(and \(\dim F=0\)).
To prove Theorem 1.3, we actually show the following.
Theorem 1.8
If a polynomial map \(\varvec{f}:\mathbb {K}^m\rightarrow \mathbb {K}^n\) satisfies (1.3), then

where  . Here, \({\overline{Z}}\) denotes the closure of a set Z.
. Here, \({\overline{Z}}\) denotes the closure of a set Z.
Remark 1.9
Assume that \(m=n=2\). Take  for a non-degenerate map \(\varvec{f}:\mathbb {K}^2\rightarrow \mathbb {K}^2\). We assume that
for a non-degenerate map \(\varvec{f}:\mathbb {K}^2\rightarrow \mathbb {K}^2\). We assume that  , \(\varvec{p}=(p_1,p_2)\) with \(p_1<0\) and \(p_2>0\).
, \(\varvec{p}=(p_1,p_2)\) with \(p_1<0\) and \(p_2>0\).
-
If \(0\in \gamma _1\) and \(0\in \gamma _2\), then \(f^1_{\gamma _1}\) and \(f^2_{\gamma _2}\) are polynomial of a monomial \(u=x_1^{q_1}x_2^{q_2}\). We denote them as \(g_1(u)\) and \(g_2(u)\). The defining equation of
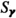 is the resultant of \(g_1-y_1\) and \(g_2-y_2\) where \((y_1,y_2)\) is a coordinate system of the target.
is the resultant of \(g_1-y_1\) and \(g_2-y_2\) where \((y_1,y_2)\) is a coordinate system of the target. -
If \(0\not \in \gamma _1\) and \(0\in \gamma _2\), then we can write \(f^1_{\gamma _1}=x_1^pg_1(u)\) and \(f^2_{\gamma _2}=g_2(u)\) with \(u=x_1^{q_1}x_2^{q_2}\) similarly. The defining equation of
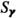 is the resultant of \(g_1\) and \(g_2-y_2\).
is the resultant of \(g_1\) and \(g_2-y_2\).
2 Proof of Theorem 1.8
We are going to evaluate \(\varvec{f}(x)=(f^1(x),\dots ,f^n(x))\) along a curve \(\varvec{x}(t)\) defined by
We denote \({\mathcal {A}}(\varvec{p})\) the set of such arcs. It is clear that
We have an obvious decomposition \(S_{\varvec{f}}=\bigcup _{\varvec{p}}S_{\varvec{f}}(\varvec{p})\), where
We have \(S_{\varvec{f}}(\varvec{p})=\emptyset \) if \(\varvec{p}\in (\mathbb {Z}_{\ge 0})^m\) by (2.3).
Remark 2.1
Observe that the arcs having several components being identically zero are not in \({\mathcal {A}}(\varvec{p})\). However, this does not affect to detect \(S_{\varvec{f}}\). Adding the terms \(t^l\), \(l\gg 1\), to such components does not affect the conditions for \(S_{\varvec{f}}\) and we can restrict our attention to \({\mathcal {A}}(\varvec{p})\).
Lemma 2.2
For \(\varvec{p}\not \in (\mathbb {Z}_{\ge 0})^m\), we have  .
.
Proof
We express \(f^j(\varvec{x}(t))\) as
where \(d_j=d_j(\varvec{p})\ge 0\). We have \({\hat{f}}^j_0=f^j_{\gamma _j}(\varvec{v}_0)\) where \(\gamma _j=\gamma _j(\varvec{p})\). Setting \(f^j(x)=\sum _{\varvec{\nu }}c^j_{\varvec{\nu }} \varvec{x}^{\varvec{\nu }}\), more precisely, we have
If \(\varvec{y}\in S_{\varvec{f}}(\varvec{p})\), then there exists an arc \(\varvec{x}(t)\in {\mathcal {A}}(\varvec{p})\), so that
Using the notation in (2.5) and  , we have
, we have
and \(f^j_{\gamma _j(\varvec{p})}(\varvec{v}_0)=0\) (\(j\in J\)). This implies that \(J^c\) component of \(\varvec{y}\) is given by  , and we complete the proof. \(\square \)
, and we complete the proof. \(\square \)
Remark 2.3
If \(\dim \gamma _j(\varvec{p})=0\) for some \(j\in J\), then \({\hat{f}}^j_0\ne 0\), and  is empty.
is empty.
Lemma 2.4
If  , then
, then

Proof
Take \(\varvec{p}\in \mathbb {Z}^n{\setminus }(\mathbb {Z}_{\ge })^n\) and consider a curve defined by (2.1). We compare (2.5) with (2.6) substituting by (2.2) and taking modulo \(t^{i+1}\). Remarking that the terms concerning \(\varvec{v}_i\) in \({\hat{f}}^j_i\) depend on the terms in \(f^j_{\gamma _j}\) only, we obtain that
where \(r^j_l(\varvec{v}_0,\dots ,\varvec{v}_{l-1})\) is a suitable polynomial of \(\varvec{v}_0,\dots ,\varvec{v}_{l-1}\).
Take a point  where
where  . Let \((a^j_k)_{j\in J; k\ge 1}\) be any sequence. Suppose we have already taken \(\varvec{v}_0\), \(\varvec{v}_1\), ..., \(\varvec{v}_{l-1}\), so that
. Let \((a^j_k)_{j\in J; k\ge 1}\) be any sequence. Suppose we have already taken \(\varvec{v}_0\), \(\varvec{v}_1\), ..., \(\varvec{v}_{l-1}\), so that
By (2.7), there exists \(\varvec{v}_l\), so that \({\hat{f}}^j_l=a^j_l\) for \(j\in J\), whenever \(\mathop {\mathrm {Jac}}{(}(f^j_{\gamma _j})_{j\in J})\) is of full rank at \(\varvec{v}_0\). Choose \((a^j_l)_{j\in J;l\ge 0}\), so that \(a^j_i=0\) (\(0\le i< d_j\)). Then, the corresponding curve \(\varvec{x}(t)\) has the following property:
Since one can choose \(a^j_{d_j}\) arbitrary, we conclude that  . \(\square \)
. \(\square \)
In the situation above, we have
Corollary 2.5
 for
for  .
.
Proof
We obtain

since \(S_{\varvec{f}}\) is closed. \(\square \)
Remark 2.6
In the case that \(\varvec{f}\) does not satisfy (1.5), we would proceed further analysis using higher order differentials of composite maps. Actually, in the expression (2.5), we have
where
Here, we use the notation in (2.1), (2.2), and \(d^kg\) denotes the symmetric multilinear form defined by kth-order differential of g. The first few of \({\hat{f}}^j_l\) are as follows:
The set \(S_{\varvec{f}}(\varvec{p})\) is described by eliminating \(\varvec{v}_0\), \(\varvec{v}_1\), \(\varvec{v}_2\), ... from the following system:
where \((y_1,\dots ,y_n)\) denotes the coordinate system of the target.
3 Relative Version
The definition of non-properness set has an obvious generalization for a polynomial map \(\varvec{f}:X\rightarrow Y\) between algebraic varieties X and Y defined over \(\mathbb {K}\). We say \(\varvec{f}\) is not proper at \(\varvec{y}_0\in Y\) if there exist an arc \(\varvec{x}(t):\mathbb {K}^*,0\rightarrow X\), so that
We denote by \(S_{\varvec{f}}\) the set of non-proper points of \(\varvec{f}:X\rightarrow Y\).
Let \(\varvec{f}=(f^1,\dots ,f^n):\mathbb {K}^m\rightarrow \mathbb {K}^n\) be a polynomial map with (1.3). Set \(\varvec{f}'=(f^1,\dots ,f^{n-k})\) and \(\varvec{f}''=(f^{n-k+1},\dots ,f^n)\). Set \(\varvec{y}=(\varvec{y}',\varvec{y}'')\) and \(\varvec{y}_0=(\varvec{y}'_0,\varvec{y}''_0)\). In this section, we describe a generalization of the discussion above to the map
Since \(\varvec{f}|_X=(\varvec{f}'|_X,\varvec{y}''_0)\), we identify \(\varvec{f}|_X\) with the map \(\varvec{f}'|_X\) via the embedding \(\mathbb {K}^{n-k}\times \{\varvec{y}''_0\}\subset \mathbb {K}^n\). This means that we identify \(\mathbb {K}^{n-k}\) with \(\mathbb {K}^{n-k}\times \{\varvec{y}''_0\}\), and we can identify \(\varvec{f}^{\{1,\dots ,n-k\}{\setminus } J}\) with \(\varvec{f}^{\{1,\dots ,n\}{\setminus } J}\). We call this map by \(\varvec{f}^{J^c}\). For a face  of \(\varvec{\Delta }(\varvec{f})\), we define
of \(\varvec{\Delta }(\varvec{f})\), we define  and
and  . In the same way, we can identify
. In the same way, we can identify  with
with  on the set
on the set  . So denote its image by
. So denote its image by  as
as  . Set
. Set

and  .
.
Under the notation and assumption above, we have the following:
Theorem 3.1
We assume that the nonsingular locus of X is dense in X and X has no component in \(\{x_1\cdots x_n=0\}\). Then

If  has dense nonsingular loci for
has dense nonsingular loci for  , we have equalities in (3.1).
, we have equalities in (3.1).
The assumption that X has no component in \(\{x_1\cdots x_n=0\}\) comes from Remark 2.1. If there is an arc \(\varvec{x}(t)\) in \(X\cap \mathbb {K}^I\), \(I\subsetneq \{1,\dots ,n\}\), with \(\varvec{x}(t)\rightarrow \infty \), and \(\varvec{f}(\varvec{x}(t))\rightarrow \varvec{y}_0\) (\(t\rightarrow 0\)), one can choose \(\hat{\varvec{x}}(t)\in {\mathcal {A}}(\varvec{p})\) for some \(\varvec{p}\) with \(\hat{\varvec{x}}(t)\rightarrow \infty \), and \(\varvec{f}(\hat{\varvec{x}}(t))\rightarrow \varvec{y}_0\) \((t\rightarrow 0)\). However, we do not know that \(\hat{\varvec{x}}(t)\) can be chosen in X in such a case.
Proof of Theorem 3.1
First, for \(\varvec{x}(t)\in {\mathcal {A}}(\varvec{p})\), we can write
where \(d_j=d_j(\varvec{p})\). We remark that \(\varvec{y}\in S_{\varvec{f}|_X}\) if and only if there is an arc \(\varvec{x}(t):\mathbb {K}^*,0\rightarrow X\), so that \(\displaystyle {\lim \nolimits _{t\rightarrow 0}\varvec{x}(t)}=\infty \), and that \(\displaystyle {\lim \nolimits _{t\rightarrow 0}\varvec{f}(\varvec{x}(t))}=\varvec{y}\). In a similar way to the proof of Lemma 2.2, we have

This implies that \(f^j_{\gamma _j(\varvec{p})}(\varvec{v}_0)=0\) for  , and \((f^j-y^j_0)_{\gamma _j(\varvec{p})}(\varvec{v}_0)=0\) for \(j=n-k+1,\dots ,n\), which show the second inclusion.
, and \((f^j-y^j_0)_{\gamma _j(\varvec{p})}(\varvec{v}_0)=0\) for \(j=n-k+1,\dots ,n\), which show the second inclusion.
By the discussion similar to the proof of Lemma 2.4, for any \(a^j\) (\(j\in J\)), we can construct a formal power series \(\varvec{v}(t)=(v^1(t),\dots ,v^n(t))\), such that
where \(\varvec{y}_0=(y_0^1,\dots ,y_0^n)\). Remark that we can reduce this system to polynomials by multiplying some power \(t^l\). By the approximation theorem of Artin ( [1]), we can take a convergent power series \(\varvec{v}(t)=(v^1(t),\dots ,v^n(t))\) which satisfies (3.2) and (3.3). This completes the proof of the first inclusion. \(\square \)
If X has a component \(X_1\) in \(\{x_1\cdots x_n=0\}\), we could proceed a similar computation for \(\varvec{f}|_{X_1}\) which is a polynomial map with less number of variables and obtain that \(S_{\varvec{f}|_{X_1}}\subset S_{\varvec{f}|_X}\).
4 Examples
Example 4.1
Let us start with the simplest example \(\mathbb {K}^2\rightarrow \mathbb {K}^2\), \(f(x,y)=(x,xy)\). For the assumption (1.3) we consider \(\varvec{f}(x,y)=(c_1+x,c_2+xy)\) where \(c_1\), \(c_2\) are non-zero constants. It suffices to consider only 3 faces below thanks to Remark 2.3. Since

we have \(S_{\varvec{f}}=\{(c_1,c_2+xy):(x,y)\in (\mathbb {K}^*)^2\}=\{c_1\}\times \mathbb {K}\).
Example 4.2
Consider the map \(\varvec{f}(x,y)=(x^2y^2+xy+y+1,x^2y+y+x+1)\). Since

we have
Example 4.3
Consider the map \(\varvec{f}(x,y)=(xy+y+1,x^2y^2+y^2+xy+1)\), we have

Therefore, we have
Example 4.4
Consider the map \(\varvec{f}:\mathbb {K}^3\rightarrow \mathbb {K}^3\) defined by
\(a\ne 0\), \(b\ne 0\). The Newton polyhedra look like

and we obtain the following data.
\(\varvec{p}\) |
| \((d_1,d_2,d_3)\) |
|
|
|---|---|---|---|---|
\((1,-1,-1)\) | \((1+xy+xz,1+axz,1+bxy)\) | (0, 0, 0) | \(\emptyset \) | \((\mathbb {K}^*)^3\) |
\((1,-1,-2)\) | \((xz,axz,1+bxy+x^2z)\) | (1, 1, 0) | \(\{1,2\}\) | \(\emptyset \) |
\((1,-2,-1)\) | \((xy,1-x^2y+axz,bxy)\) | (1, 0, 1) | \(\{1,3\}\) | \(\emptyset \) |
\((0,-1,-1)\) | \((x(y+z),x(xz-xy+az),x(xz+xy+by))\) | (1, 1, 1) | \(\{1,2,3\}\) | \(\emptyset \) |
\((-1,1,1)\) | \((1+xy+xz,x(1-xy+xz),x(1+xy+xz))\) | (0, 1, 1) | \(\{2,3\}\) |
We have

We conclude that  .
.
5 Degenerate Case
We present several tricks to handle the case when (1.5) does not hold for some  .
.
5.1 The First Trick
Let \(\varvec{h}:\mathbb {K}^{m+k}\rightarrow \mathbb {K}^{n+k}\) be a polynomial map with (1.5). We assume that \(h^{n+i}(x)=\varphi _1(x_1,\dots ,x_m)-x_{m+i}\) for \(i=1,\dots ,k\). Let X be a subset of \(\mathbb {K}^{m+k}\) defined by
The set X is isomorphic to \(\mathbb {K}^{m}\) by the map defined by
If \(\varvec{f}(x_1,\dots ,x_m)=\varvec{h}(x_1,\dots ,x_m,\varphi _1(x_1,\dots ,x_m),\dots ,\varphi _k(x_1,\dots ,x_m))\), then we have
via the identification of \(\mathbb {K}^n\) with \(\mathbb {K}^n\times \{0\}\). When \(\varvec{h}\) satisfies the required assumptions, one can use Theorem 3.1 to describe \(S_{\varvec{f}}\), even though \(\varvec{f}\) does not satisfy (1.5) for some  .
.
Example 5.1
Let \(\varvec{h}:\mathbb {K}^3\rightarrow \mathbb {K}^3\) be the map defined by
Let X be the subset of \(\mathbb {K}^3\) defined by \(z=y^2-x^3\). Setting \(\varvec{f}(x,y)=\varvec{h}(x,y,y^2-x^3)\), we have
Applying Theorem 3.1, we conclude that \(\varvec{h}\) is proper, and thus so is \(\varvec{f}\).
5.2 The Second Trick
We show another trick, which we do not use higher dimension. If  ,
,  , is not empty for some
, is not empty for some  , we may have a chance to change
, we may have a chance to change  (resp.
(resp.  ) in (1.6) by a smaller subset of
) in (1.6) by a smaller subset of  (resp. by a supset of
(resp. by a supset of  ).
).
Let \(\varvec{f}:\mathbb {K}^m\rightarrow \mathbb {K}^n\) be a polynomial map with (1.3). Set \(\varvec{f}^J_l=(f^j_l)_{j\in J}\) for \(J\subset \{1,\dots ,n\}\) where \(f^j_k\) is defined in (2.8). Remark that \(f^j_0(x)=f^j_{\gamma _j}(x)\). We set

where  , \(\varvec{y}^{J'}=(y^{j'})_{j'\in J'}\),
, \(\varvec{y}^{J'}=(y^{j'})_{j'\in J'}\),
Remark that \(J=J'\cup J''\) because of (1.4). Under the notations and the assumptions above, we have
Theorem 5.2
If  , \(\varvec{p}\in \mathbb {Z}^n{\setminus }(\mathbb {Z}_\ge )^n\), is not empty for
, \(\varvec{p}\in \mathbb {Z}^n{\setminus }(\mathbb {Z}_\ge )^n\), is not empty for  , then
, then

Moreover, we conclude that \(W'(\varvec{p})\subset S_{\varvec{f}}(\varvec{p})\), where

Proof
If \(\varvec{y}\in S_{\varvec{f}}(\varvec{p})\), \(\varvec{p}\in \mathbb {Z}^n{\setminus }(\mathbb {Z}_\ge )^n\), there exists \(\varvec{x}(t)\in {\mathcal {A}}(\varvec{p})\) with \(\varvec{f}(\varvec{x}(t))\rightarrow \varvec{y}\) (\(t\rightarrow 0\)). By (2.9) and (2.10), we have
Here, we use the expression in (2.1) and (2.2). This implies that
and we conclude  .
.
Now, we assume \(\varvec{y}\in W'(\varvec{p})\). There exists  , such that
, such that
By the discussion in the second paragraph of the proof of Lemma 2.4, we can choose \(\varvec{x}(t)\) to attain arbitrary \({\hat{f}}^{j''}_l\) (\(j''\in J''\), \(l\ge 1\)) whenever \(\varvec{x}\not \in \Sigma (\varvec{f}^{J''})\). This implies that \(W'(\varvec{p})\subset S_{\varvec{f}}(\varvec{p})\). \(\square \)
We present a trick to describe  where \(S_{\varvec{f}}(\varvec{p})\) is the set defined by (2.4).
where \(S_{\varvec{f}}(\varvec{p})\) is the set defined by (2.4).
Assume that \(\varvec{f}\) does not satisfy (1.5) for some face  . We take a primitive \(\varvec{p}\in \mathbb {Z}^n{\setminus }(\mathbb {Z}_\ge )^n\), so that
. We take a primitive \(\varvec{p}\in \mathbb {Z}^n{\setminus }(\mathbb {Z}_\ge )^n\), so that  . Here, \(\varvec{p}\) is primitive means that the greatest common divisor of all components of \(\varvec{p}\) is 1. Assume that there exists a rational map \(\mathbb {K}^m\times \mathbb {K}^n\rightarrow \mathbb {K}^n\), \((\varvec{x},\varvec{z})\mapsto \Psi (\varvec{x},\varvec{z})\) with the following properties.
. Here, \(\varvec{p}\) is primitive means that the greatest common divisor of all components of \(\varvec{p}\) is 1. Assume that there exists a rational map \(\mathbb {K}^m\times \mathbb {K}^n\rightarrow \mathbb {K}^n\), \((\varvec{x},\varvec{z})\mapsto \Psi (\varvec{x},\varvec{z})\) with the following properties.
-
There exist a certain rational map \(\varvec{g}:\mathbb {K}^{m}\rightarrow \mathbb {K}^n\), possibly with points of indeterminacy, so that \(\varvec{f}(\varvec{x})=\Psi (\varvec{x},\varvec{g}(\varvec{x}))\), and \(\varvec{g}\) satisfies (1.5) for the face supported by \(\varvec{p}\).
-
The limit \(\displaystyle {\lim _{t\rightarrow 0}\Psi (\varvec{x}(t),\varvec{z})}\) exists for \(\varvec{x}(t)\in {\mathcal {A}}(\varvec{p})\). We assume that this limit depends on \(\varvec{v}_0\), and denote the limit by \(\Psi _{\varvec{v}_0}(\varvec{z})\), under the notation in (2.1) and(2.2),
-
The limit \(\displaystyle {\lim _{t\rightarrow 0}\varvec{g}(\varvec{x}(t))}\) for \(\varvec{x}(t)\in {\mathcal {A}}(\varvec{p})\) exists.
Theorem 5.3
Under the notations and assumptions above, the set \(S_{\varvec{f}}(\varvec{p})\),  , is in the image of the following map:
, is in the image of the following map:

Proof
For \(\varvec{p}\in \mathbb {Z}^n{\setminus }(\mathbb {Z}_\ge )^n\)

\(\square \)
Since  , this may describe
, this may describe  , as we see in the following example.
, as we see in the following example.
Example 5.4
Consider the map \(\varvec{f}:\mathbb {K}^3\rightarrow \mathbb {K}^3\) defined by
The map \(\varvec{f}\) satisfies the condition (1.5) except the face  , as we see in the following data.
, as we see in the following data.
\(\varvec{p}\) |
| \((d_1,d_2,d_3)\) |
|
|---|---|---|---|
\((1,1,-1)\) | \((1+x_1x_3+x_2x_3,1,1)\) | (0, 0, 0) | \(\emptyset \) |
\((1,1,-2)\) | \((x_3(x_1+x_2),1+x_1x_3(x_2-x_1),1+x_2x_3(x_2-x_1))\) | (1, 0, 0) | \(\{1\}\) |
\((-1,0,1)\) | \((1+x_1x_3,x_1(1-x_1x_3),1+x_2-x_1x_2x_3)\) | (0, 1, 0) | \(\{2\}\) |
\((0,-1,1)\) | \((1+x_2x_3,1+x_1+x_1x_2x_3,x_2(1+x_2x_3))\) | (0, 0, 1) | \(\{3\}\) |
\((-1,-1,1)\) | \((1+x_1x_3+x_2x_3,x_1(1-x_1x_3+x_2x_3),x_2(1-x_1x_3+x_2x_3))\) | (0, 1, 1) | \(\{2,3\}\) |
We easily see that

We also have that
We will show that this coincides with  , considering the rational map
, considering the rational map
Remark that \(\varvec{g}(\varvec{x})=\Phi (\varvec{x},\varvec{f}(\varvec{x}))\) defines the map
and obtain the following data:
\(\varvec{p}\) |
| \((d_1,d_2,d_3)\) |
|
|---|---|---|---|
\((-1,-1,1)\) | \((1+x_1x_2+x_1x_3,x_1(1-x_1x_2+x_2x_3),1-\frac{x_2}{x_1})\) | (0, 1, 0) | \(\{2\}\) |
The Newton polyhedra look like

As in the proof of Theorem 1.8, we conclude that

For \((x_1,x_2,x_3)\) in (5.2), we have
Setting
we have \(\varvec{y}=\Psi (\varvec{x},\Phi (\varvec{x},\varvec{y}))\), and thus, \(\varvec{f}(\varvec{x})=\Psi (\varvec{x},\varvec{g}(\varvec{x}))\). The set

and we obtain  .
.
We thus obtain that \(S_{\varvec{f}}=\{y_1+y_3=2\}\cup \{y_1y_2-y_1y_3-2y_2+2=0\}\).
Example 5.5
Let us use the first trick to handle Example 5.4. We consider the map \(\varvec{h}:\mathbb {K}^4\rightarrow \mathbb {K}^4\) defined by
since \(\varvec{f}(x_1,x_2,x_3)=\varvec{h}(x_1,x_2,x_3,1-x_1x_3+x_2x_3)\). We analyze \(\varvec{h}(\varvec{x}(t))\) for \(\varvec{x}(t)\in {\mathcal {A}}(-1,-1,1,1)\), because \(\varvec{p}=(-1,-1,1,k)\), \(k\ge 1\), supports a three-dimensional face of \(\varvec{\Delta }(\varvec{g})\) if and only if \(k=1\). Setting
we have
Assuming \(\varvec{x}(t)\) is in \(X=\{\varvec{x}\in \mathbb {K}^4:1-x_1x_3+x_2x_3=x_4\}\), we obtain that \(1-x^1_0x^3_0-x^2_0x^3_0=x_0^4\). Under this condition, we eliminate \(x^1_0\), \(x^2_0\), \(x^3_0\) from the system
we conclude that  . We thus obtain that \(S_{\varvec{f}}=\{y_1+y_3=2\}\cup \{y_1y_2-y_1y_3-2y_2+2=0\}\).
. We thus obtain that \(S_{\varvec{f}}=\{y_1+y_3=2\}\cup \{y_1y_2-y_1y_3-2y_2+2=0\}\).
References
Artin, M.: On the solutions of analytic equations. Invent. Math. 5, 277–291 (1968)
Chen, Y., Dias, L.R.G., Takeuchi, K., Tibăr, M.: Invertible polynomial mappings via Newton non-degeneracy. Ann. Inst. Fourier Grenoble 64(5), 1807–1822 (2014)
El Hilany, B.: Describing the Jelonek set of polynomial maps via Newton polytopes. https://arxiv.org/abs/1909.07016v1
Jelonek, Z.: The set of points at which a polynomial map is not proper. Ann. Polon. Math. 58, 259–266 (1993)
Jelonek, Z.: Testing sets for properness of polynomial mappings. Math. Ann. 315(1), 1–35 (1999)
Jelonek, Z., Lasoń, M.: Quantitative properties of the non-properness set of a polynomial map. Manuscr. Math. 156, 383–397 (2018)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author is supported by Japan Society for the Promotion of Science Grant-in-Aid for Scientific Research (C) Grant Number 19K03486.
All data generated or analyzed during this study are included in this published article.
Rights and permissions
About this article
Cite this article
Fukui, T., Tsuchiya, T. Properness of Polynomial Maps with Newton Polyhedra. Arnold Math J. 9, 205–221 (2023). https://doi.org/10.1007/s40598-022-00205-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40598-022-00205-2




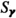 is the resultant of
is the resultant of  is the resultant of
is the resultant of 





