An ordinary state-based peridynamic computational investigation of fiber-reinforced composites

Abstract

An improved ordinary state-based peridynamic model for fiber-reinforced composite laminate was proposed and applied to fracture analysis in laminated plates with different configurations. The mechanical properties of composite materials are realized by bonds whose orientations lie along the principal axes. The new model works for general fiber orientations with respect to a uniform discretization grid, which is an extension of the state-based peridynamic laminate theory proposed by Madenci and Oterkus. Using the revised model, quantitative quasi-static simulations of laminates under uniaxial tensile loading and compact tensile tests are conducted to validate the elasticity and fracture behavior of laminated materials. The displacement fields and crack propagation are calculated and compared with existing numerical data. The enhanced model is able to represent the fracture characteristics and displacement fields of composite laminates with general fiber orientations, according to the results.

1 Introduction

Fiber-reinforced composite materials are extensively used in loading-bearing components in current aircraft and automotive systems due to their excellent mechanical properties [1]. Clearly, the advantages of fiber-reinforced polymers (FRP) materials surpass those of isotropic materials in many engineering and experimental designs, but the failure analysis process of FRP materials is much more difficult than that of non-anisotropy materials due to the complexity of the material structures [2, 3]. .Composite damage and fractures have been investigated experimentally and theoretically using the finite element method (FEM) [4,5,6]. However, since the basic equation of motion is based on a partial differential form of the displacement fields, FEM has limits when dealing with discontinuity issues. As a result, different fracture mechanics strategies have been developed to address this constraint, such as external crack growth criteria and re-meshing [7].

Peridynamics (PD) is a potent nonlocal formulation of continuum mechanics proposed by Sandia National Laboratory’s Silling [8, 9]. PD theory adopts integral-differential formulas as its main equations, which is applicable to issues involving the spontaneous production of discontinuities such as fractures and interfaces [10]. As a new nonlocal theory, PD inherits the properties of classical continuum theories (CCTS) and molecular dynamics (MD) approaches [11]. Damage analysis based on PD theory in isotropic materials [12,13,14,15] and composites [16,17,18,19,20,21] has recently gained popularity. These studies include corrosion damage [15], dynamic fracture [16, 17], quasi-static failure [18,19,20] and fatigue damage [21].

In fact, the initially suggested bond-based peridynamic (BB-PD)model is a central force model that assumes a paired axial force between material points inside one horizon, and BB-PD has its limitations because of the simplicity of the loading conditions between two particles. The limitation of the Poisson’s ratio, which is fixed to $v=1/4$ for 3D issues and $v=1/3$ for 2D problems [22], is a well-known drawback of the BB-PD model. Subsequently, Silling introduced the ordinary state-based peridynamic (OSB-PD)theory utilizing infinite-dimensional arrays [23]. Unlike BB-PD, OSB-PD method describes the internal forces acting on a particle in terms of the deformations of all the particles within its neighborhood [23, 24]. Thanks to this improvement, the Poisson’s ratio in linearized OSB-PD formulation can range from 0.1 to 0.45 [25]. The OSB-PD may not be suited for nonlinear anisotropic materials owing to the idea of collinear interaction forces along a bond, despite the fact that it removes the limitation of Poisson’s ratio [26, 27]. Considering this, Warren et al. [26] employed second-order strain tensor to represent the loading in the bonds, and a non-ordinary state-based peridynamic (NOSB-PD) theory was first proposed, which makes modeling a continuum considerably more realistic.

In recent years, the theory of PD has been used to the investigation of mechanical characteristics and damage propagation in composite constructions. Based on the inhomogeneous unique features of fiber and matrix, Kilic and Madenci [3] built a microscale PD model with fiber and matrix in discrete material locations and predicted matrix cracking in laminated composites. However, such models need a uniform grid of particles in addition to a highly precise discretization of the sites of interest. References [17,18,19] divide the bonds in composites into fiber bonds and matrix bonds, and these models use a homogenization strategy, which matches the parallel bond stiffness to the elastic modulus. However, in the macro-mechanics of a unidirectional lamina, the stiffness changes continuously from the fiber direction to the transverse direction. With this in mind, in order to get a close enough approximation of the bond stiffness function for orthotropic media, Ghajari et al. [28] created the first continuous model with spherical harmonic expansion. Zhou [7] and Hu et al. [29] also proposed a similar PD formulation, but this model is based on BB-PD theory, so that the model also has a severe limitation in the material modulus. Hu et al. [30] introduced a new state-based PD model of a composite laminate that can capture all kinds of material couplings in transverse shear deformation. The simulation findings match the test results quite well, but in solving the model, large sparse matrices need to be computed in each analysis step, which can lead to high computational costs without powerful additional hardware such as GPUs. Hattori et al. [22] first proposed a general anisotropic model for NOSB-PD, and the Tsai-Hill criterion for composites was used in this formulation. The failure criterion in CCTS is creatively integrated into this NOSB-PD approach in the study [22], but this PD model does not provide an effective way to control the zero-energy modes. Another orthotropic NOSB-PD model was introduced by Fang et al. [31], and in their work the zero-energy modes were efficiently suppressed by using the linearized BB-PD method. Although some other new models [32,33,34] for orthotropic materials have been proposed in recent years, there is still no general and perfect PD model for laminated composites under arbitrary operating conditions.

In addition to the PD formulation mentioned above, the OSB-PD laminated theory (OSB-PDLT) proposed by Oterkus and Madenci [11] is a relatively mature model. Different from the BB-PD and NOSB-PD models, OSB-PDLT model has no limitation in Poisson’s ratio and zero-energy mode, respectively. Nevertheless, there are also some limitations in this model, such as the restriction of the fiber direction due to the uniform grid of particles. Since the fiber bonds between material points can only be uniquely defined when the orientation of the bonds are parallel to the fiber direction, the fiber angle can only take specific values, such as $0^{\circ }, {\pm }45^{\circ }$ and $90^{\circ }$. Therefore, simulating composite laminates with various orientations is problematic. In addition, the damage of laminated composite panels under blast loading [35] and compression after impact (CAI) loading [36] has been studied, but there are few quantitative quasi-static analyses in the existing studies in detail based on the OSB-PDLT model.

In this study, an improved OSB-PDLT modeling is proposed, which is an extension of the study by Madenci and Oterkus [11]. In Reference [11], only the paired particles along the exact orientation of $\theta$ can be classified as fiber bonds, which may cause the discretization grid failing to align with the expected 1- and 2-principle orientations [37]. In this work, the angle tolerance is employed to locate the particles for extra bonds along the 1-principle and 2-principle axes [17, 38], which can avoid the invalid definition of fiber bond or matrix bond. Based on this, several numerical examples, including the displacement fields of laminated specimens and the fracture propagation of laminated plates, are utilized to verify the proposed model. The remainder of the paper is organized as this: Sect. 2 introduces the new OSB-PDLT model. Section 3 details the deformations of lamina with various fiber angles and the damage analysis of lamina with different initial conditions under quasi-static loadings. Section 4 summarizes the main conclusions.

2 Peridynamic laminate theory

2.1 OSB-PD model

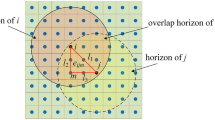
The peridynamic theory employs integral-differential equations, which exclude the partial derivatives of the geometry deformation [8,9,10]. And a material point interacts with other material points within a certain range, called horizon, $\delta$, as illustrated in Fig. 1. The locality of mutual effect relies on the value of horizon, and as the horizon shrinks, mutual effects of particles become more local. As particle interactions end, fractures may originate and spread along surfaces that create cracks, but the equations in PD theory still hold.

The equilibrium equation in the OSB-PD model can be expressed as [11]:

$$\begin{aligned} \rho \left( {\textbf{x}} \right) \ddot{{\textbf{u}} } \left( {\textbf{x}},t \right)= & {} \int \limits _{H_{{\textbf{x}} } }^{}\left\{ {\mathbf {{\underline{T}}}} \left[ {\textbf{x}},t \right] \left\langle \mathbf {x'-x} \right\rangle \right. \nonumber \\{} & {} \left. -{\mathbf {\underline{T}}} \left[ \mathbf {x'},t \right] \left\langle \mathbf {x-x'} \right\rangle \right\} dV_{{\textbf{x}} '} +{\textbf{b}}\left( {\textbf{x}},t \right) , \end{aligned}$$

(1)

where $\rho$ is the mass density and $\ddot{{\textbf{u}}}$ is the acceleration of point ${\textbf{x}}$ at time $\textit{t}$. $\mathbf {x'}$ is another material point in the neighborhood $H_{{\textbf{x}}}$ of ${\textbf{x}}$, and ${\textbf{b}} ({\textbf{x}},t)$ is the body force density of point ${\textbf{x}}$. As illustrated in Fig. 1, ${\varvec{\xi }} ={\textbf{x}} '-{\textbf{x}}$ is the bond vector. $\mathbf {\underline{T}} [{\textbf{x}},t]$ and $\mathbf {\underline{T}} [{\textbf{x}}',t]$ are the force vector states of points ${\textbf{x}}$ and ${\textbf{x}}'$, respectively.

Fig. 1

OSB-PD model

2.2 OSB-PD laminate composite model

According to the laminated plate’s structural characteristics, each FRP lamina of laminated material can be considered as a two-dimensional structure. The elevation of each ply in a laminate is illustrated in Fig. 2, and the subscript n denotes the ply number. $h_{\textrm{n}}$ denotes the thickness of $n$th ply and $h$ represents the total thickness of the laminate.

Fig. 2

Elevation of a laminate

In the present PD model for a lamina, after the grid is discretized, the particles along the principal material axes need to be defined as shown in Fig. 3. And based on this, the “bonds” between material points are divided into three types: fiber bond, matrix bond, and arbitrary bond. As mentioned above, the angle tolerance $\gamma$ is utilized to locate the particles for extra bonds along the 1-principle and 2-principle axes. Excessive angular tolerance may introduce particles of extra orientations, which may distort the material properties of the fiber longitudinal and transverse orientation. Too small angle tolerance may lead to insufficient number of particle pairs, resulting in invalid definition of the relevant bonds. And the values of $\gamma$ for fiber bond and matrix bond are both set as ${\pm }5^{\circ }$ in this paper referring to Zhang [38]. Accordingly, the material point ${\textbf{x}} _{(q)}$ represents particles along the 1-principle axis that interact with target particle ${\textbf{x}} _{(k)}$, corresponding to the origin of coordinate in Fig. 3. Similarly, particle ${\textbf{x}} _{(p)}$ represents particles that interact with particle ${\textbf{x}} _{(k)}$ along the 2-principle axis. And the particle ${\textbf{x}} _{(r)}$ represents particles that interact with any particles ${\textbf{x}}_{(k)}$ in intralayer plane, including the fiber and transverse directions [36].

Fig. 3

The discrete peridynamic model for a single layer

Fig. 4

Diagram of interlayer bonds

The domain of integration of a material point with a perfect in-plane horizon is a disk with radius $\delta$ and thickness $h_{\textrm{n}}$. As seen in Fig. 4, the particles of a lamina interact with the particles of its immediate adjacent lamina through interlayer bonds. The subscript or superscript, n or m, represents the sequence number of layer where the material point is located.

According to Madenci and Oterkus’s derivation [11], the equation of motion for particle ${\textbf{x}}_{(k)}^{n}$ in a laminate with N layers can be expressed as

$$\begin{aligned} \begin{aligned} \rho _{(k)}^{n} \ddot{{\textbf{u}}}_{(k)}^{n}&= \sum _{j=1}\left[ {\textbf{t}}_{(k)(j)}^{n}\left( {\textbf{u}}_{(j)}^{n}-{\textbf{u}}_{(k)}^{n}, {\textbf{x}}_{(j)}^{n}-{\textbf{x}}_{(k)}^{n}, t\right) \right. \\&\left. \quad -{\textbf{t}}_{(j)(k)}^{n}\left( {\textbf{u}}_{(k)}^{n}-{\textbf{u}}_{(j)}^{n}, {\textbf{x}}_{(k)}^{n}-{\textbf{x}}_{(j)}^{n}, t\right) \right] V_{(j)}^{n}\\&\quad + \sum _{m=n+1, n-1} {\textbf{p}}_{(k)}^{(n)(m)} V_{(k)}^{m}\\&\quad +2 \sum _{m=n+1, n-1} \sum _{j=1} {\textbf{q}}_{(k)(j)}^{(n)(m)} V_{(j)}^{m}+{\textbf{b}}_{(k)}^{n}, \end{aligned} \end{aligned}$$

(2)

where ${\textbf{x}}_{(k)}^{n}$ represents material point on the $n$th layer. $V_{(k)}^{n}$ is its incremental volume. $\rho _{(k)}^{n}$ is its mass density. $t$ is time [36]. In this equation of motion of Cartesian coordinate system, ${\textbf{u}}_{(k)}^{n}$ represents the displacement of the material point ${\textbf{x}}_{(k)}^{n}$, ${\textbf{t}}_{(k)(j)}^{n}$ is the PD force density vector that point $j$ exerts on the point $k$. ${\textbf{p}}_{(k)}^{(n)(m)}$ is the transverse normal bond force density vector, and ${\textbf{q}}_{(k)}^{(n)(m)}$ presents the transverse shear bond force density vector, respectively. ${\textbf{y}}_{(k)}^{n}$ represents the relative position of the two particles in the deformed configuration. The three types of force density vector are explicitly presented as [11]

$$\begin{aligned} {\textbf{t}}_{(k)(j)}^{(n)}= & {} 2\delta \left( ad\frac{\varLambda _{(k)(j)}^{(n)} }{|{\textbf{x}}_{(j)}^{n}- {\textbf{x}}_{(k)}^{n}|}\theta _{(k)}^{n}\right. \nonumber \\{} & {} \left. +(\mu _{F}b_{F}+b_{FT}+\mu _{T}b_{T})s_{(k)(j)}^{(n)}\right) \frac{{\textbf{y}}_{(j)}^{n}-{\textbf{y}}_{(k)}^{n}}{|{\textbf{y}}_{(j)}^{n}-{\textbf{y}}_{(k)}^{n}|}, \nonumber \\ \end{aligned}$$

(3)

$$\begin{aligned} {\textbf{p}}_{(k)}^{(n)(m)}= & {} 4~b_{N}(|{\textbf{y}}_{(k)}^{m}-{\textbf{y}}_{(k)}^{n}|\nonumber \\{} & {} -|{\textbf{x}}_{(k)}^{m}-{\textbf{x}}_{(k)}^{n}|)\frac{{\textbf{y}}_{(k)}^{m}-{\textbf{y}}_{(k)}^{n}}{{\textbf{y}}_{(k)}^{m}-{\textbf{y}}_{(k)}^{n}}, \end{aligned}$$

(4)

and

$$\begin{aligned} {\textbf{q}}_{(k)(\textrm{j})}^{(n)(m)}= & {} 4 b_{S}\left[ \frac{\left| {\textbf{y}}_{(j)}^{m}-{\textbf{y}}_{(k)}^{n}\right| -\left| {\textbf{x}}_{(j)}^{m}- {\textbf{x}}_{(k)}^{n}\right| }{\left| {\textbf{x}}_{(j)}^{m}-{\textbf{x}}_{(k)}^{n}\right| }\right. \nonumber \\{} & {} \left. -\frac{\left| {\textbf{y}}_{(k)}^{m}-{\textbf{y}}_{(j)}^{n}\right| -\left| {\textbf{x}}_{(k)}^{m}-{\textbf{x}}_{(j)}^{n}\right| }{\left| {\textbf{x}}_{(k)}^{m}-{\textbf{x}}_{(j)}^{n}\right| }\right] \frac{{\textbf{y}}_{(j)}^{m}-{\textbf{y}}_{(k)}^{n}}{\left| {\textbf{y}}_{(j)}^{m}-{\textbf{y}}_{(k)}^{n}\right| }, \nonumber \\ \end{aligned}$$

(5)

with

$$\begin{aligned} s_{(k)(j)}^{(n)}= & {} \frac{\left| {\textbf{y}}_{(j)}^{n}-{\textbf{y}}_{(k)}^{n}\right| -\left| {\textbf{x}}_{(j)}^{n}-{\textbf{x}}_{(k)}^{n}\right| }{\left| {\textbf{x}}_{(j)}^{n}-{\textbf{x}}_{(k)}^{n}\right| }, \end{aligned}$$

(6)

$$\begin{aligned} \mu _{F}= & {} \left\{ \begin{array}{ll} 1, &{} \varphi \in [(\phi -\gamma , \phi +\gamma ) \cup \\ {} &{}(\phi -\pi -\gamma , \phi -\pi +\gamma )] \\ 0, &{} \textrm{otherwise } \end{array}\right. , \end{aligned}$$

(7)

and

$$\begin{aligned} \mu _{T}=\left\{ \begin{array}{ll} 1, &{} \varphi \in [(\phi +\pi / 2-\gamma , \phi +\pi / 2+\gamma ) \cup \\ {} &{}(\phi -\pi / 2-\gamma , \phi -\pi / 2+\gamma )] \\ 0, &{} \textrm{otherwise} \end{array}\right. , \end{aligned}$$

(8)

where $\varphi$ is the angle of ${\textbf{x}}_{(j)}^{n}-{\textbf{x}}_{(k)}^{n}$ to x-axis.

The parameter $\theta _{(k)}^{n}$ is is defined as [11]

$$\begin{aligned} \theta _{(k)}^{n}= & {} d \sum _{j=1} \frac{\delta }{\left| {\textbf{x}}_{(j)}^{n}-{\textbf{x}}_{(k)}^{n}\right| }\left( \left| {\textbf{y}}_{(j)}^{n} -{\textbf{y}}_{(k)}^{n}\right| \right. \nonumber \\{} & {} \left. -\left| {\textbf{x}}_{(j)}^{n}-{\textbf{x}}_{(k)}^{n}\right| \right) \varLambda _{(k)(j)}^{(n)} V_{(j)}^{n}. \end{aligned}$$

(9)

The PD auxiliary parameter $\varLambda _{(k)(j)}^{(n)}$ is defined as [11]

$$\begin{aligned} \varLambda _{(k)(j)}^{(n)}=\frac{{\textbf{y}}_{(j)}^{n}-{\textbf{y}}_{(k)}^{n}}{\left| {\textbf{y}}_{(j)}^{n}-{\textbf{y}}_{(k)}^{n}\right| } \cdot \frac{{\textbf{x}}_{(j)}^{n}-{\textbf{x}}_{(k)}^{n}}{\left| {\textbf{x}}_{(j)}^{n}-{\textbf{x}}_{(k)}^{n}\right| }. \end{aligned}$$

(10)

The parameters in Eq. 3 are defined as [11]:

$$\begin{aligned} \textrm{a}= & {} \frac{1}{2}\left( Q_{12}-Q_{66}\right) , \end{aligned}$$

(11)

$$\begin{aligned} d= & {} \frac{2}{\pi h \delta ^{3}}, \end{aligned}$$

(12)

$$\begin{aligned} b_{F}= & {} \frac{\left( \textrm{Q}_{11}-Q_{12}-2 Q_{66}\right) }{2 \delta \left( \sum _{j=1}^{J_{F}}\left| {\textbf{x}}_{(j)}^{n}-{\textbf{x}}_{(\textrm{k})}^{\textrm{n}}\right| V_{(\textrm{j})}\right) }, \end{aligned}$$

(13)

$$\begin{aligned} b_{T}= & {} \frac{\left( \textrm{Q}_{22}-Q_{12}-2 Q_{66}\right) }{2 \delta \left( \sum _{j=1}^{J_{T}}\left| {\textbf{x}}_{(j)}^{n}-{\textbf{x}}_{(\textrm{k})}^{\textrm{n}}\right| V_{(\textrm{j})}\right) }, \end{aligned}$$

(14)

$$\begin{aligned} b_{F T}= & {} \frac{6 Q_{66}}{\pi h \delta ^{4}}, \end{aligned}$$

(15)

$$\begin{aligned} b_{N}= & {} \frac{E_{m}}{{\hat{\delta }}\left[ \left( h_{n+1}+h_{n}\right) V_{(k)}^{n+1}+\left( h_{n-1}+h_{n}\right) V_{(k)}^{n-1}\right] }, \end{aligned}$$

(16)

$$\begin{aligned} b_{S}= & {} \frac{G_{m}}{8 \pi {\tilde{\delta }}\left( H\left( h_{n+1}, h_{n}\right) +H\left( h_{n-1}, h_{n}\right) \right) }, \end{aligned}$$

(17)

with

$$\begin{aligned} \textrm{H} (x, y)=\left( \frac{x+y}{2}\right) \left( \frac{\delta ^{2}+2\left( \frac{x+y}{2}\right) ^{2}}{\sqrt{\delta ^{2}+2\left( \frac{x+y}{2}\right) ^{2}}}-(x+y)\right) , \end{aligned}$$

(18)

where

$$\begin{aligned} Q_{11}= & {} \frac{\textrm{E}_{11}}{1-\nu _{12} \nu _{21}}, Q_{12}=\frac{\nu _{12} \textrm{E}_{22}}{1-\nu _{12} \nu _{21}},\nonumber \\ Q_{22}= & {} \frac{\textrm{E}_{22}}{1-\nu _{12} \nu _{21}}, Q_{66}=G_{12}. \end{aligned}$$

(19)

The parameter $\delta$ represents the in-plane horizon, the parameter ${\hat{\delta }}$ in Eq.  16 denotes the thickness-direction horizon, and ${\tilde{\delta }}$ in Eq. 17 is defined as ${\tilde{\delta }}=\sqrt{\delta ^{2}+{\hat{\delta }}^{2}}$. The PD intralayer material parameters along the fiber direction, the transverse direction, and the remaining arbitrary directions are defined as $b_{F}$, $b_{T}$ and $b_{FT}$, respectively. $J_{F}$ and $J_{T}$ represent the number of particles along the fiber direction and the transverse direction, respectively, within the neighborhood of material point ${\textbf{x}}_{(k)}^{n}$.The PD interlayer material parameters related to the transverse normal and shear deformations are defined as $b_{N}$ and $b_{S}$. In Eq. 19, $E_{11}$ and $E_{22}$ represent the elastic modulus in fiber direction and transverse direction. $G_{12}$ is the major shear modulus. $\nu _{12}$ and $\nu _{21}$ are the major and minor Poisson’s ratio, respectively. And $E_{m}$ and $G_{m}$ represent the Young’s modulus and shear modulus, and the subscript denotes the matrix.

2.3 Failure criteria

Failure in peridynamic theory is imitated by irrevocably destroying PD bonds. If the stretch of the PD bond exceeds the critical value, the bond fails. Hence, the damage is directly integrated into the material reaction. However, determining the critical stretch value for laminated composite materials is difficult. In the recent investigations, there are three kinds of methods majorly used for in-plane failure criteria, except the combination of failure criteria in FEM and PD used in NOSB-PD [22, 32]. Bond critical values are determined using experimental techniques and inverse calibration in the first approach [11, 39]. The second means employed in the research is that the critical stretch is defined by the tension and compression strength of a lamina [29, 40, 41]. The critical stretch of the third method is determined by the critical strain energy release rate. Based on the third method, the critical stretches can not only be constant values [7, 38], but also change with the angular separation between the bond and the fiber direction [31]. In the present study, the PD prediction for in-plane damage is based on the second method, and the interlayer damage is based on the third method. The values of the critical stretch for intralayer bonds [41] and interlayer bonds [35] can be calculated by

$$\begin{aligned} \left\{ \begin{array}{ll} s_{0}^{\textrm{ft}} = \frac{X^{\textrm{T}}}{E_{11}}, &{} s \ge 0 \text{(fiber } \text{ bonds } )\\ \\ s_{0}^{\text{ fc } } = \frac{X^{\textrm{C}}}{E_{11}}, &{} s<0 \text{(fiber } \text{ bonds } ) \\ \\ s_{0}^{\textrm{mt}} = \frac{Y^{\textrm{T}}}{E_{22}}, &{} s \ge 0 \text{(matrix } \text{ bonds } \text{ and } \text{ abitrary } \text{ bonds } ) \\ \\ s_{0}^{\textrm{mc}} = \frac{Y^{\textrm{C}}}{E_{22}}, &{} s<0 \text{(matrix } \text{ bonds } \text{ and } \text{ abitrary } \text{ bonds } ) \\ \\ s_{0}^{\textrm{normal}} = \sqrt{\frac{2 G_{\textrm{IC}}}{h E_{m}}}, &{} s>0 \text{(interlayer } \text{ bormal } \text{ bonds } ) \\ \\ \phi _{0}^{\text{ shear } } = \sqrt{\frac{2 G_{\textrm{IIC}}}{h G_{m}}}, &{} \phi ^{\text {shear}}>0 \text { (interlayer shear bonds }) \end{array}\right. \nonumber \\ \end{aligned}$$

(20)

Fig. 5

Diagram of the lamina under uniaxial tensile load

Fig. 6

Deformation of the $\theta =0^{\circ }$ lamina

Fig. 7

Deformation of the $\theta =15^{\circ }$ lamina

Fig. 8

Deformation of the $\theta =30^{\circ }$ lamina

Fig. 9

Deformation of the $\theta =45^{\circ }$ lamina

Fig. 10

Deformation of the $\theta =60^{\circ }$ lamina

Fig. 11

Deformation of the $\theta =75^{\circ }$ lamina

Fig. 12

Deformation of the $\theta =90^{\circ }$ lamina

where $G_{\textrm{IC}}$ and $G_{\textrm{IIC}}$ are critical energy release for I and II mode for failure in CCTS, respectively. And $X^{\textrm{T}}$, $X^{\textrm{C}}$, $Y^{\textrm{T}}$,$Y^{\textrm{C}}$ are represented by local damage parameter as [9, 11]

$$\begin{aligned} \varphi ({\textbf{x}}, \textrm{t})=1-\frac{\int _{H_{{\textbf{x}}}} \mu \left( {\textbf{x}}^{\prime }-{\textbf{x}}, t\right) d V_{{\textbf{x}}^{\prime }}}{\int _{H_{x}} d V^{\prime }}. \end{aligned}$$

(21)

2.4 Numerical implementation

Similar to Silling and Askari [9], the continuum system is discretized into the finite material points uniformly. In all the examples followed, the grid size $\triangle x$ is used, and $\delta$ is the horizon size. In many PD researches, m-convergence of the model has been investigated time after time. For orthotropic materials, m usually takes the values of four, five, and six and so on [34,35,36,37,38]. And in Reference [34], it has been found that m = 5 is a good choice considering the accuracy and computational efficiency at the same time. Therefore, we set the horizon radius $\delta$ to be $5\triangle x$ in this research. Fictitious material layers are introduced along the upper and lower displacement constraint boundary. Especially for locations near the boundary, mistakes may result from the absence of interactions caused by free surfaces. Hence, the PD surface effect correction methods based on the strain energy density are utilized in this study [11]. In order to solve the quasistatic problems in following section, the adaptive dynamic relaxation (ADR) approach [13] is used to the present analysis.

Figure 6 –  12 present the deformations of the lamina with seven distinct fiber orientations generated from the FEM model and OSB-PDLT model. We can conclude that the displacement fields calculated by the improved OSB-PDLT model correlate well with the FEM results.

Table 1 Elastic properties of IM-7/977-3 [42]

Table 2 Strength properties of IM-7/977-3 [42]

3 Numerical results

3.1 Elastic deformation of the lamina under tensile test

To validate the improved OSB-PDLT model with general fiber angle in this study, the elastic deformations of the lamina are calculated. As illustrated in Fig. 5, the dimensions of the specimen are 40 mm in length, 70 mm in width, and 1 mm in thickness. The displacement loads and boundary conditions are imposed on the top and lower boundaries of the lamina. The in-plane grid of 81$\times$151 is utilized in the discretization process. The material parameters [42] of the lamina are illustrated in Table 1 and Table 2.

Fig. 13

Lamina displacements in the vertical-direction center line

Fig. 14

The compact tension (CT) specimen

Fig. 15

Crack paths of specimens with different fiber angles under CT test

Additionally, the displacements of particles in longitudinal central line of the lamina are provided as well. As illustrated in Fig. 13, the displacements of the particles in the central line of vertical direction calculated by PD agree well with the results of FEM solution. In Fig. 13, it can be seen that the displacements $u_{x}$ and $u_{y}$ show anti-symmetry shapes in the curves. Typically, when $\theta =45^{\circ }$, there is a certain difference between the displacements in x-direction calculated by FEM and PD method. However, the error is acceptable with respect to the length of the lamina. In other words, the vertical strain is much less than the horizontal strain components in the present study, and it has little effect on the whole strain response.

Fig. 16

Rectangular orthotropic lamina with a central fracture

Fig. 17

Damage paths of specimens of different fiber angles with a center crack

3.2 Lamina under compact tensile (CT) test

In an experimental study, the CT test is designed to determine the I-mode fracture toughness of metallic materials [43]. Additionally, it may be utilized to explore the fracture characteristics of anisotropic materials [31, 34, 38]. The dimension characteristics of the lamina are illustrated in Fig. 14, and the thickness is 1 mm, respectively. In this CT test, w is taken to be 40 mm, and the ratio of a to w is set as 0.5. A uniform grid 200$\times$192 is utilized in the discretization process. The grid interval $\bigtriangleup x$ is 0.00025 mm. The specimen is loaded at a constant velocity of 1 mm/s. The material used in this test is also IM-7/977-3.

Fig. 18

Schematics of the rectangular orthotropic lamina with a circle hole

Figure 15 depicts the fracture patterns of a series of CT test specimens with orientations varying from $0^{\circ }$ to $90^{\circ }$. The fracture always propagates in the direction that requires the least amount of energy. Due to this, the anticipated fracture path follows an orientation parallel to the fiber angle, independent of the pre-crack orientation in each instance, which is in excellent accord with experimental results from Reference [44] and simulation results from References [31, 38].

Table 3 Elastic properties of T300/7901 carbon fiber composite [6]

Table 4 Strength properties of T300/7901 carbon fiber composite [6]

Fig. 19

PD predictions of matrix cracking and displacements

3.3 Lamina with a center crack under uniaxial tensile loading

In this part, the OSB-PDLT model for a 2D orthotropic lamina with general fiber orientation is validated by capturing the crack propagation of several rectangular specimens with a central fracture subjected to uniform stretch. To analyze the damage propagation of the lamina, we assume the following setup: a lamina with dimensions $L = 127$mm, $W = 317.5$mm, and $h=1.27$mm including a center pre-crack with dimensions $a = 25.4$mm, as shown in Fig. 16. A uniform grid $100\times 260$ is utilized in the discretization process. Table 1 and Table 2 illustrate the material parameters of the lamina.

For the laminas of seven different fiber orientations, the damage path predictions at representative moment are extracted to illustrate the effect of fiber angles, as shown in Figure  17. The results of $0^{\circ }$, $45^{\circ }$ and $90^{\circ }$ correlate well with the experimental observations reported in [45], as well as the numerical results in Reference [3, 31, 34]. Similar to the laminas with the angles valued by $0^{\circ }$, $45^{\circ }$ and $90^{\circ }$, the numerical results of the other four fiber directions are satisfactory fairly. As expected, the damage originates from the pre-crack and grows along the fiber direction accordingly. For the laminas of $60^{\circ }$ and $75^{\circ }$ fiber directions as shown in Fig. 17, it can also be found that the damage not only originates from the pre-crack tip, but also the edge of the plate. It can be thought that the tensile strength of fiber is much larger than the matrix. Hence, the damage of the edge is caused by the matrix splitting and debonding between the fiber and matrix pattern.

Fig. 20

Comparison of the elastic deformation of the laminated specimen $[0/30/90/-30]_{\textrm{s}}$

Fig. 21

Displacement in y-direction and matrix damage of the composite laminated plate $[0/30/90/-30]_{\textrm{s}}$ at peak load

Fig. 22

Damage patterns of the composite laminated plate $[0/30/90/-30]_{\textrm{s}}$

3.4 Laminate with a circle hole under uniaxial tensile loading

The PD model shown in Fig. 18 describes a lamina with a circle hole, and the boundary and loading conditions of the computation model. The length, width and thickness of the lamina are defined by $L=138.43$mm, $W=38.1$mm, and $h=1$mm, respectively. In the center of the lamina is a round hole with a diameter of $d=6.35mm$. The lamina material is T300/7901, whose properties [6] are listed in Table 3 and Table 4. In the simulation, fiber orientations of $0^{\circ }$, $30^{\circ }$, $45^{\circ }$, $60^{\circ }$ and $90^{\circ }$ are investigated. The discretization is achieved by 60$\times$218$\times$1 grid points, and velocity ${\dot{u}}=0.0005$mm/s are specified.

The OSB-PDLT predictions of the matrix damage pattern and displacement field for five different fiber orientations are shown in Fig. 19. The displacement field displays obvious discontinuities along the fibers, which is in excellent accord with Reference [42].

To show that OSB-PDLT is valid for laminated plate, a simulation model with layup $[0/30/90/-30]_{\textrm{s}}$ is established. The length of the plate is 12.5 mms, and its width is 6.25 mms. The plate has a total thickness of 1 mm, with each individual ply having a thickness of 0.125 mm. The plate has a central hole with diameter $d = 1$mm and the material is still T300/7901. Both the current PD model and the FEM are used to simulate the behavior of the laminates when subjected to tensile loading. And the mesh of the PD model is $40\times 90\times 8$. After trying, it is found that the unity time step has better convergence results. In the tensile loading test, displacement loads $\textrm{u}_{y}$ = 0.02 mm are imposed at the upper and lower end. The displacement fields of the laminate are illustrated in Fig. 20. The numerical results of the displacement fields in three directions $\textrm{u}_{x}$, $\textrm{u}_{y}$ and $\textrm{u}_{z}$, between PD and FEM are compared. The calculated results of deformation field of FEM and PD model are highly consistent. It indicates that this PD model can accurately anticipate laminates with multidirectional layups.

Figure 21 shows the displacement component in the direction of the tension loading and the matrix damage of the entire laminate $[0/30/90/-30]_{\textrm{s}}$ at the peak load. Predictions show significant matrix damage near the hole boundary, and obvious discontinuity of displacement field along the x-axis can also be observed. Figure 22 presents the matrix damage and the interlayer damage of the composite laminated plate $[0/30/90/-30]_{\textrm{s}}$ at peak load. It can be seen from Fig. 22 that the matrix and interlayer patterns fail around the circle hole with along the $\pm 30^{\circ }$ fracture surfaces. It is interestingly worth mentioning that the $\theta =0^{\circ }$ ply shows obvious damage profile along the fiber orientation. The prediction results in this study are highly similar to those in Reference [41, 42].

In addition, when comparing the results of FEM and PD calculations in Section 3, the displacement components have some differences. The main factors causing these errors are as follows: (1) the surface effect of OSB-PD itself exists, and there is still no way to completely eliminate the surface effect [46]; (2) the OSB-PDLT method is based on the macroscopic homogenization method, which ignores the continuous change of stiffness from the 1-principle to 2-principle direction [33]; (3) the OSB-PDLT theory does not consider the role of Poisson’s ratio $v_{13}$ [41]. However, from the perspective of strain, these errors are negligible and do not affect the prediction of crack nucleation and propagation, which has been fully verified by the simulation results of this paper.

4 Conclusions

In this work, the classical OSB-PDLT model has been extended to composite laminates with general fiber orientations, which is achieved by considering any grid orientation relative to the principal material axes. The validation of the revised model is demonstrated by quasi-static simulations of the compact tensile test and the uniaxial tensile test. The deformation of a FRP plate with or without a circular hole is calculated by PD and FEM methods, and the displacement fields of the present PD model fit well with the FEM results. By comparing the results of existing research, the damage profiles obtained from the peridynamic model are consistent with the recent numerical and experimental observations in laminated composites. Hence, we can conclude that the improved OSB-PDLT model is capable of precisely capturing the damage patterns and mechanical properties.