1 Introduction

Agglomerates or granules of fine solid particles are omnipresent in industrial processes such as the iron-ores making [1,2,3,4,5,6], the manufacture of pharmaceuticals, the fertilizers, and food industry [7,8,9], and in nature such as powders and soils due to the addition of a small amount of liquid volume accounts for the capillary bridges between particles [10, 11]. The capillary bonds induce the capillary cohesion forces and lubrication forces that affect wet agglomerates [12,13,14]. The agglomerates may become strong aggregates depending on the liquid–vapor surface tension and the viscosity of the binding liquid [15,16,17]. When the granular material flows, the wet agglomerates interact with surrounding particles on their surface [12,13,14, 18,19,20,21,22,23,24]. These interactions may detach the primary wet particles on the surface of agglomerates by irreversibly breaking its capillary bonds [14]. Compared with the external stress on the surface of agglomerates caused by the flow of surrounding particles, the wet agglomerates may not be eroded due to sufficiently strong cohesive stress \(\sigma _{\mathrm{c}}\) and viscous stress \(\sigma _{\mathrm{v}}\).

The origins of these interactions either come from the external confining pressure \(\sigma _{\mathrm{p}}\) or the particle inertia of the free surface flows [25]. The particle flow is generated due to the collective movement of the particles. When the materials flow, they generate the inertial stress \(\sigma _{\mathrm{i}}\), which depends on the shear rate \(\dot{\gamma }\) of such flows and the particle properties (\(\sigma _{\mathrm{i}} \sim \rho \langle d \rangle ^2 \dot{\gamma }\)), where \(\rho \) is the particle density and \(\langle d \rangle \) is the mean particle diameter [26, 27]. In the case of wet agglomerates embedded in simple shear flow of noncohesive granular materials [14, 28, 29], we expect that the erosion dynamics of agglomerates depend on the external confining stress \(\sigma _{\mathrm{p}}\), the flow properties characterized by the inertial stress \(\sigma _{\mathrm{i}}\), and the agglomerate properties characterized by the cohesion stress \(\sigma _{\mathrm{c}}\) and the viscous stress \(\sigma _{\mathrm{v}}\). The erosion of agglomerates is also expected to control by the three dimensionless parameters including \(I^2 = \sigma _{\mathrm{i}}/\sigma _{\mathrm{p}}\) [27, 30,31,32,33,34,35,36], the cohesion index \(\xi = \sigma _{\mathrm{c}}/\sigma _{\mathrm{p}}\) [14, 33, 34, 37], and the Stokes number \(\text{ St } = \sigma _{\mathrm{i}}/\sigma _{\mathrm{v}}\) [20, 38,39,40,41]. The inertial number I of dry granular flows is defined as a ratio of the relaxation time (\(\langle d \rangle \sqrt{\rho /\sigma _{\mathrm{p}}}\)) and the shear time \(\dot{\gamma }^{-1}\) [27, 31, 33]. The inertial number I could control the flow properties in different flow regimes in both experiments and numerical simulations [30, 31, 42, 43].

The combinations of these dimensionless numbers have been shown in previous studies on wet granular flows and particle dense suspensions [33, 38,39,40,41]. Berger et al. [33] combine the inertial number I and the cohesion index \(\xi \) due to the additivity of the cohesive stress into the inertial stress to scale the rheological properties of the cohesive granular flow in two dimensions. In the same way, in the dense suspension of particles, where the lubrication stress \(\sigma _{\mathrm{v}}\) is presented instead of the cohesive stress \(\sigma _{\mathrm{c}}\), the flow properties of submerged granular materials are controlled by the modified inertial number by incorporating the inertial number I with the Stokes number St or the viscous number \(\eta \dot{\gamma }/\sigma _{\mathrm{p}}\) [38,39,40, 44]. More recently, when the inertial, cohesive, and viscous forces come into play together in the flows of unsaturated granular materials, the rheology and microstructure of such flows are well-described by a viscocohesive inertial number, which combines I, \(\xi \) and \(\text{ St }\) [41].

The simulated model of wet agglomerates embedded in simple shear flow of cohesionless granular materials is very different as compared to the above examples. In this case, all surrounding particles of agglomerates are dry, and this means that the capillary attraction force and viscous force only considered inside wet agglomerates. As in the agglomeration process, the agglomerates nucleated, and their diameters change as a consequence of the coalescence, erosion, and accretion phenomena [7, 13, 18, 45, 46]. In which, the erosion of agglomerates is a paramount importance that allows granules to survive or disintegrate in the agglomeration process. In recent studies, Lefebvre et al. [12] studied the erosion dynamics of a single wet agglomerate which fixed in the center of the half-fill flow of dry granular materials in a rotating drum. They showed the erosion rate decreases as a function of the liquid–vapor surface tension and the liquid viscosity. More recently, in our investigation, Vo et al. [14] studied the behavior of a single wet agglomerate inside an inertial shear flow of dry granular materials by only varying the cohesion index \(\xi \) of the agglomerate and the shear rate \(\dot{\gamma }\) of dry granular flow. We showed the erosion of a single agglomerate could be well-described by a scaling parameter, which combines I and \(\xi \). However, the erosion dynamics of wet particle agglomerates immersed in a cohesionless granular flow are still poorly understood with different parameters relating to the flow properties and the natural properties of the liquid as well as the relative dry–wet density and the position of agglomerates. In particular, whether the erosion rate of wet agglomerates can be well described by a definitely new scaling parameter that combines the inertial number I, the cohesion index \(\xi \), and the Stokes number \(\text{ St }\) when the liquid viscosity comes into play? This will be addressed in this work.

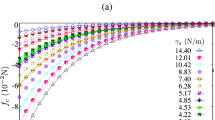
In this paper, we solve the above-mentioned interesting issue by considering wet agglomerates consisting of wet spherical particles embedded in simple shear flow of noncohesive particles by means of extensive particle dynamics simulations. The numerical method with the capillary attraction law enhanced by the theoretical expressions of the cohesive forces and viscous forces in addition to the elastic and frictional forces between particles at their contacts. The simulated model is prepared under pressure-controlled and periodic boundary conditions and sheared by applying a constant velocity. By varying a broad range of values of the shear rate, the amount of liquid accounted for by a debonding distance [47], the surface tension of the binding liquid, the liquid viscosity, the relative dry–wet density, and the initial position of wet agglomerates, we study the erosion dynamics of wet agglomerates. As we shall see, the erosion rate of wet particle agglomerates could be well-described by an erosion scaling parameter that represents the nontrivial combination of the key parameters.

In the following, we introduce the numerical method and the simulated model in Sect. 2. We present the simple shear flow and erosion phenomenon of wet agglomerates in Sect. 3. In Sect. 4, we introduce the erosion rate of agglomerates due to the effects of different system parameters. The scaling behavior of such agglomerates with an erosion scaling parameter is introduced in Sect. 5. Finally, we conclude in Sect. 6 with a salient summary of remarkable results and further research directions.

2 Numerical method and model description

2.1 Methodology

The simulations are modeled by using the cFGd-3D++code that originally developed by P. Mutabaruka, a collaborator of the author. Then, the code is developed by the author in order to perform this current work. This code has been extensively employed in research on the simulations of granular materials in three dimensions on the framework of the discrete element method (DEM), with the availability of the solid–liquid interaction. In DEM [48,49,50,51,52], the particles are assumed to be perfectly rigid with a large repulsive stiffness, and a high time resolution is required for the computation of the particle interactions. The particles interact with their neighbors via the local contact force laws [51, 53]. The forces are expressed as a function of the relative displacements of the particles. The particle displacements are calculated by step-wise resolution of Newton’s second law. The equation of motion of a particle i with its radius \(R_i\) is expressed under the action of the normal contact forces \(f_{\mathrm{n}}\), tangential contact forces \(f_{\mathrm{t}}\), capillary attraction forces \(f_{\mathrm{c}}\), and the lubrication forces \(f_{\mathrm{v}}\) [54]:

$$\begin{aligned} m_i \frac{\text{ d}^2 \mathbf {r}_i}{\text{ d }t^2}= & {} \sum _j [(f_{\mathrm{n}}^{ij} + f_{\mathrm{c}}^{ij} + f_{\mathrm{v}}^{ij})\mathbf {n}^{ij} + f_{\mathrm{t}}^{ij} \mathbf {t}^{ij}] \nonumber , \\ \mathbf {I}_i \frac{\text{ d } {\varvec{\omega }}_i}{\text{ d } t}= & {} \sum _j f_{\mathrm{t}}^{ij} \mathbf {c}^{ij} \times \mathbf {t}^{ij}, \end{aligned}$$
(1)

where particle i is assumed to interact with its neighboring particle j. \({\varvec{\omega }}_i\) is the rotation vector of the particle, and \(m_i\), \(\mathbf {I}_i\), and \(\mathbf {r}_i\) are the mass, inertia matrix, and position of particle i, respectively. \(\mathbf {n}^{ij}\) is the unit vector perpendicular to the contact plane between the particles i and j and pointing from j to i. \(\mathbf {t}^{ij}\) denotes the unit vector in the contact plane pointing in the direction opposite to the relative tangential displacement of the two particles. \(\mathbf {c}^{ij}\) is the vector joining the center of particle i to the contact point with particle j. We used a velocity-verlet time-stepping scheme for the integration of the equations of motion [51, 54, 55], in which the tangential viscous dissipation is neglected as compared to the normal viscous force.

The normal contact force \(f_{\mathrm{n}}\) is given by following expression:

$$\begin{aligned} f_{\mathrm{n}} = \left\{ \begin{array}{@{}ll@{}} 0, &{} \text{ for }\,\, \delta _{\mathrm{n}} \ge 0, \\ -k_{\mathrm{n}} \delta _{\mathrm{n}} - \gamma _{\mathrm{n}} \dot{\delta }_{\mathrm{n}}, &{} \text{ for }\,\, \delta _{\mathrm{n}} < 0, \end{array}\right. \end{aligned}$$
(2)

where \(k_{\mathrm{n}} \delta _{\mathrm{n}}\) is the normal elastic component, and \(k_{\mathrm{n}}\) and \(\delta _{\mathrm{n}}\) are the normal stiffness and the normal elastic deflection at the contact point, respectively. \(\gamma _{\mathrm{n}} \dot{\delta }_{\mathrm{n}}\) is the normal damping component, with \(\gamma _{\mathrm{n}}\) is the normal viscous damping parameter, and \(\dot{\delta }_{\mathrm{n}}\) denotes the relative normal velocity. \(\delta _{\mathrm{n}}\) is the gap between two particles. The expression in Eq. (2) has the undesirable property that it is possible to obtain \(f_{\mathrm{n}}\) as an attractive force, and this situation arises just before two particles separate. In order to avoid this case of the contact force, only the positive value of \(f_{\mathrm{n}}\) is considered in this work.

The tangential force \(f_{\mathrm{t}}\) is the sum of an elastic force \(f_{\mathrm{t}}^{\mathrm{e}} = k_{\mathrm{t}} \delta _t\) and a damping force \(f_{\mathrm{t}}^{\mathrm{d}} = \gamma _{\mathrm{t}} \dot{\delta }_t \), where \(k_{\mathrm{t}}\) is the tangential stiffness, \(\gamma _{\mathrm{t}}\) denotes the tangential damping parameter, and \(\delta _t\) and \(\dot{\delta }_t\) are the tangential displacement and velocity, respectively. According to the Coulomb friction law, the tangential force is below or equal to the force threshold \(\mu f_{\mathrm{n}}\), where \(\mu \) is the coefficient of friction of particles [51, 53, 56, 57]:

$$\begin{aligned} f_{\mathrm{t}} = -\!\min \left\{ (k_{\mathrm{t}}\delta _t + \gamma _{\mathrm{t}} \dot{\delta }_t), \mu f_{\mathrm{n}} \right\} . \end{aligned}$$
(3)

In “pendular” regime, we assume that the binding liquid is homogeneous distribution between particles as capillary bridges [52, 58,59,60,61,62]. The liquid distribution may be a consequence of the mixing of particles with the binding liquid, drainage of the liquid in granular packing, or the condensation of the liquid vapor in nature [7]. The liquid volume is not enough to fill all the roughness surface of particles besides their capillary bonds. Thus, the dry particles assumed to be not being trapped by wet particles including a weak collision between them. Furthermore, the model is also simulated by a weak size polydispersity of granular materials, and this system prevents the case that the small dry particles could collide with wet particles at its liquid bridges. The capillary bridges induce the capillary attraction forces and the viscous forces [13]. During the flow of granular materials in the agglomeration process, the primary wet particles may be eroded from agglomerates, and the liquid volume of a broken capillary bond is shared proportionally to the particle size and migrated outside agglomerates by eroded particles. We also assume that these wet particles definitely lose their liquid as a result of the evaporation, diffusion, or drainage. This means that these capillary bonds are broken irreversibly during the process.

The capillary attraction force \(f_{\mathrm{c}}\) between two spherical particles depends on the liquid volume \(V_{\mathrm{b}}\) of the capillary bond, liquid–vapor surface tension \(\gamma _{\mathrm{s}}\), and particle–liquid–gas contact angle \(\theta \) which always equals zero independently of the liquid viscosity due to the assumption that the binding liquid covers the particles. This cohesion force is given by the Laplace–Young equation. In the “pendular” regime, an approximate solution is given by the following expression [47, 63], as shown in Fig. 1a:

$$\begin{aligned} f_{\mathrm{c}} = \left\{ \begin{array}{@{}ll@{}} -\kappa \ R, &{} \text{ for }\,\, \delta _{\mathrm{n}} < 0, \\ -\kappa \ R\, {\hbox {e}}^{-\delta _{\mathrm{n}} /\lambda }, &{} \text{ for }\,\, 0 \le \delta _{\mathrm{n}} \le d_{\mathrm{rupt}}, \\ 0, &{} \text{ for }\,\, \delta _{\mathrm{n}} > d_{\mathrm{rupt}}, \end{array}\right. \end{aligned}$$
(4)

where \(R = \sqrt{R_i R_j}\) is the geometrical mean radius of two particles radii \(R_i\) and \(R_j\) and the capillary force prefactor \(\kappa \) is

$$\begin{aligned} \kappa = 2\pi \gamma _{\mathrm{s}} \cos \theta . \end{aligned}$$
(5)

The debonding distance \(d_{\mathrm{rupt}}\) is given by [58]

$$\begin{aligned} \displaystyle {d_{\mathrm{rupt}} = \left( 1+\frac{\theta }{2}\right) V_{\mathrm{b}}^{1/3} } \ . \end{aligned}$$
(6)

The capillary cohesion force was found to provide an excellent agreement with experimental data on the cohesion of wet granular materials [47] by considering the characteristic length \(\lambda \) in Eq. (4). \(\lambda \) is the factor that controls the exponential falloff of this cohesion force, as given by

$$\begin{aligned} \lambda = c\ h(r)\ \left( \frac{V_{\mathrm{b}}}{R'}\right) ^{1/2}, \end{aligned}$$
(7)

where \(R'= 2R_iR_j/(R_i+R_j)\) denotes the harmonic mean radius and \(r\!=\!\max \{ R_i/R_j ; R_j/R_i\}\) is the size ratio between two spherical particles, \(h(r) = r^{-1/2}\), and \(c \simeq 0.9\) [16, 47, 60]. Figure 1b displays the capillary attraction force as a function of the separation distance up to the rupture distance between two particles for different values of the cohesion index \(\xi \) by varying broad range of values of the liquid–vapor surface tension \(\gamma _{\mathrm{s}}\). The cohesion index \(\xi \) is defined as a ratio of the cohesive stress \(\sigma _{\mathrm{c}} \approx f_{\mathrm{c}}/\langle d \rangle ^2\) and the confining stress \(\sigma _{\mathrm{p}}\), as given by

$$\begin{aligned} \xi = \frac{\sigma _{\mathrm{c}}}{\sigma _{\mathrm{p}}} \approx \frac{\pi \gamma _{\mathrm{s}} \cos \theta }{\sigma _{\mathrm{p}} \langle d \rangle }. \end{aligned}$$
(8)

where \(\langle d \rangle \) is the mean particle diameter.

Fig. 1
figure 1

a A schematic drawing of a capillary bridge represents the forces acting between two spherical particles i and j, b capillary cohesion force \(f_{\mathrm{c}}\) as a function of the separation distance \(\delta _{\mathrm{n}}\) up to the rupture distance \(d_{\mathrm{rupt}}\) between two wet particles for different values of the cohesion index \(\xi \), clearly defined [Eq. (8)] as a ratio of the cohesive stress \(\sigma _{\mathrm{c}}\) (obtained by varying the liquid–vapor surface tension \(\gamma _s\)) and the confining stress \(\sigma _{\mathrm{p}}\)

Full size image
Fig. 2
figure 2

Viscous force \(f_{\mathrm{v}}\) as a function of the separation distance \(\delta _{\mathrm{n}}\) up to the rupture distance between \(d_{\mathrm{rupt}}\) between two wet particles for different values of the liquid viscosity \(\eta \) and a given value of the relative normal velocity \(v_{\mathrm{n}} = 5 \times 10^{-3}\) m/s and the characteristic length \(\delta _{\mathrm{n}0}=4 \times 10^{-7}\) m

Full size image

The normal viscous force \(f_{\mathrm{v}}\) due to the lubrication effect of the liquid bridges between two smooth spherical particles is given by [12,13,14, 41, 64]

$$\begin{aligned} f_{\mathrm{v}} = \frac{3}{2} \pi R^2 \eta \frac{{v_{\mathrm{n}}}}{\delta _{\mathrm{n}}}, \end{aligned}$$
(9)

where \(\eta \) is the liquid viscosity and \(v_{\mathrm{n}}\) is the relative normal velocity, assumed to be positive when the gap \(\delta _{\mathrm{n}}\) is decreasing. This expression implies that the viscous force diverges when the gap \(\delta _{\mathrm{n}}\) tends to zero. The characteristic size of the asperities of rough particles allows for collision in finite time. Hence, we introduce a characteristic length \(\delta _{\mathrm{n}0}\) reflecting the size of asperities. The viscous force is given by

$$\begin{aligned} f_{\mathrm{v}} = \frac{3}{2} \pi R^2 \eta \frac{{v_{\mathrm{n}}}}{\delta _{\mathrm{n}}+\delta _{\mathrm{n}0}} \; \; \; \; \text{ for } \; \; \delta _{\mathrm{n}} > 0 \end{aligned}$$
(10)

for the positive gap between particles. For the negative gap (\(\delta _{\mathrm{n}} <0\) or occurring contact between two spherical particles), we assume that the viscous force represents its largest value given by:

$$\begin{aligned} f_{\mathrm{v}} = \frac{3}{2} \pi R^2 \eta \frac{{v_{\mathrm{n}}}}{\delta _{\mathrm{n}0}} \; \; \; \; \text{ for } \; \; \delta _{\mathrm{n}} \le 0. \end{aligned}$$
(11)

Figure 2 shows the lubrication force \(f_{\mathrm{v}}\) as a function of the gap \(\delta _{\mathrm{n}}\) up to the debonding distance \(d_{\mathrm{rupt}}\) between two particles for a given value of the relative normal velocity for different values of the liquid viscosity. In our simulations, we set \(\delta _{\mathrm{n}0} = 5.10^{-4} d_{\mathrm{min}}\), where \(d_{\mathrm{min}}\) is the smallest particle diameter. This value is small enough to allow the viscous force to be effective without leading to its divergence at the contact point.

2.2 Model setting

The simulated model is first prepared by introducing an assembly of nearly 20,000 spherical particles inside a rectangular box by means of isotropic compaction under the presence of the confining stress \(\sigma _{\mathrm{p}}\). The particle diameter is varied in a range [\(d_{\mathrm{min}}, d_{\mathrm{max}}\)] with a given weak size polydispersity \(d_{\mathrm{max}}/d_{\mathrm{min}} = 2\). The particle size distribution is uniform by particle volume fraction. The particle size is divided into three different size classes, and all the size classes have the same volume of particles. The top and bottom rough walls are introduced by gluing monospheres, and their diameters equal 2.23 times of the smallest particle diameter in the rectangular box. After reaching an equilibrium state of dense granular packing, we removed the lateral walls and replaced them by the periodic boundary conditions along the x and y directions. Afterward, we defined two wet agglomerates in two different positions from the granular bed by applying two spherical probes, and these probe diameters increase until reaching exactly 300 primary particles inside each probe. Then, we introduced the theoretical expression of capillary attraction force and viscous force which induced from the capillary bridges homogeneous distribution inside agglomerates. The size of agglomerates is chosen based on the size of the granular bed, and the number of primary wet particles inside each agglomerate should be high enough in order to allow for quantifying the erosion of wet agglomerates.

Table 1 Simulation parameters
Full size table

The sample is sheared by applying a constant velocity v to the top rough wall along the x-direction. The bottom wall is fixed and keeping the constant value of the pressure-controlled condition \(\sigma _{\mathrm{p}}\). We ran totally 197 computations for different values of the amount of the liquid volume \((d_{\mathrm{rupt}} / d_{\mathrm{min}} = [0.075, 0.175])\), the liquid viscosity \(\eta \) in the range [1.0,3000.0] mPa s, the liquid–vapor surface tension \(\gamma _{\mathrm{s}}\) in the range [0.057, 0.458] N/m, the shear rate \(\dot{\gamma }\) in the range [0.21, 39.68] \({\hbox {s}}^{-1}\), the relative dry–wet density \(\alpha _{\mathrm{r}}\) [0.5, 1.5], and two initial positions of wet agglomerates along with the height of the simulation box. These two agglomerates do not meet in homogeneous shear flow of dry particles. All the system parameters are given in Table 1. The choice of values of crucial parameters is based on the numerical efficiency and the reference of the agglomeration process. The normal and tangential stiffnesses are chosen such that the elastic deflection of particles at the contact points under the action of the capillary cohesion forces and viscous forces is below 0.01. This means that the particles are nearly rigid. The samples were sheared for about 3 s in the steady flow of granular materials. The steady-state flow is presented from quasi-static regime to the inertial regime depending on the shear rate \(\dot{\gamma }\). These flow regimes are controlled by the dimensionless inertial number I, defined as a ratio of the relaxation time under load and the shear time

$$\begin{aligned} I = \dot{\gamma } \langle d \rangle \left( \frac{\rho }{\sigma _{\mathrm{p}}}\right) ^{1/2}, \end{aligned}$$
(12)

where \(\langle d \rangle \) denotes the mean particle diameter and \(\rho \) is the particle density.

Fig. 3
figure 3

a Average normal stress \(\langle f_{\mathrm{n}} \rangle / \langle d \rangle ^2\) and b average tangential stress \(\langle f_{\mathrm{t}} \rangle / \langle d \rangle ^2\) of cohesionless granular flow normalized by the confining stress \(\sigma _{\mathrm{p}}\) as a function of the inertial number I for different values of the cohesion index \(\xi \) of wet particle agglomerates

Full size image

Due to the presence of the capillary bridges of the binding liquid inside wet agglomerates, we considered the cohesion stress \(\sigma _{\mathrm{c}}\) and the viscous stress \(\sigma _{\mathrm{v}}\) in addition to the inertial, elastic, and frictional stresses. As in dense suspension, the fluid affects the flow of granular materials by its viscosity, which may be expressed as the viscous number \(I_v\) or the Stokes number St. The Stokes number is defined as a ratio of the inertial stress and the viscous stress

$$\begin{aligned} \text{ St } \equiv \frac{\sigma _{\mathrm{i}}}{\sigma _{\mathrm{v}}} \approx \frac{\rho \dot{\gamma } \langle d \rangle ^2}{\eta }. \end{aligned}$$
(13)

Figure 3a, b shows the normalized mean normal stress and mean tangential stress of the cohesionless granular flows by the confining stress \(\sigma _{\mathrm{p}}\), expressed as a function of the inertial number I for different values of the cohesion index \(\xi \) of wet particle agglomerates. We see that the stress distributions are uniform, and all the data points collapse on a master curve due to the choice of the roughness of the bottom and top walls. This also means that the strong or weak cohesion stress of wet agglomerates presented inside the flow of cohesionless granular materials does not affect its flowability. In this current work, thus, we only consider the effects of the flow regimes of cohesionless granular materials and agglomerate parameters such as liquid and particle properties on the erosion dynamics of agglomerates.

3 Erosion of agglomerates

Figure 4a, b shows the simulated model of wet agglomerates A and B embedded in simple shear flow of cohesionless granular flows generated by the confining stress \(\sigma _{\mathrm{p}}\) and the shearing velocity v and the erosion of these agglomerates inside such flows, respectively. The agglomerates have no or less eroded particles due to high values of the cohesion index, low values of the Stokes number, and low values of the inertial number I as well as large values of the liquid content in the pendular regime. The erosion occurs due to loss of wet primary particles as a consequence of irreversibly broken of capillary bonds during the interactions between agglomerates and their surrounding particles.

Fig. 4
figure 4

a Simulated model of wet agglomerates imbedded in a granular bed of cohesionless-spherical particles under pressure-controlled and periodic boundary conditions subjected to a simple shear flow by applying a constant shearing velocity v; b erosion of wet agglomerates during the flow of granular materials

Full size image

Figure 5 displays the force chains distributions of cohesive and noncohesive granular materials including wet–wet forces (in dark-green) between wet primary particles in each agglomerate, dry–dry forces (in gray) between dry particles, and the wet–dry forces (in red) between wet primary particles at the surface of wet agglomerates and their surrounding cohesionless particles. Due to having several capillary bonds of wet particles inside agglomerates as compared to wet primary particles at the surface of agglomerates, the wet agglomerates are not broken into several small agglomerates or lumps. In other words, wet particles are only detached from the surface of agglomerates. Thus, the erosion of agglomerates can easily measure by considering the cumulative number of wet primary particles eroded from initial agglomerates. The erosion of wet agglomerates over the time is defined by the cumulative erosion \(C_{\mathrm{e}}\), as a ratio of the number of wet particles \(N_\ell \) detaching from the agglomerates to the total number \(N_i\) of primary wet particles in the initial state:

$$\begin{aligned} C_{\mathrm{e}} = \frac{N_\ell }{N_i}. \end{aligned}$$
(14)
Fig. 5
figure 5

Snapshot represents the force chains distribution of wet and dry granular materials, wet–wet forces (in dark green) between wet primary particles inside agglomerates, dry–dry forces (in gray) of cohesionless granular particles, and dry–wet forces (in red) between dry particles of the flow and the wet particles on the surface of wet agglomerates

Full size image
Fig. 6
figure 6

Evolution of the cumulative erosion of wet agglomerates inside a simple shear flow of cohesionless granular materials as a function of the cumulative shear strain \(\varepsilon \) for two different initial positions of agglomerate for a given value of the cohesion index \(\xi =5\) and for \(I \simeq 10^{-1}\)

Full size image

Figure 6 shows the evolution of cumulative erosion \(C_{\mathrm{e}}\) of wet agglomerates as a function of the cumulative shear strain \(\varepsilon \) for two different wet agglomerates A and B for a given value of \(\xi \) and I. It is easy to see that this ratio increases proportionally to the time. However, it is not a continuous smooth function, this may be due to the difference of interactions between wet particles at the surface of agglomerates and the dry surrounding particles during the flow, and a wet particle only detaches from the surface of agglomerates after breaking all of its capillary bridges with other wet particles. We also see that the agglomerate A has more eroded particles than agglomerate B although the shear rate (\(\dot{\gamma }= v/h\)) of the flow is almost the same along with the height of the sample, where h is the height of the flow. This means that the agglomerate position also needs to be considered besides the quite clear effects of other parameters such as the shear rate, liquid properties, and the relative dry–wet density.

4 Effects of system parameters

The erosion of wet agglomerates is characterized by the erosion rate \(K_{\mathrm{e}}\), defined as the average slope of the evolution of the cumulative erosion, as given by

$$\begin{aligned} K_{\mathrm{e}} = \frac{\Delta C_{\mathrm{e}}}{\Delta t} \ (s^{-1}). \end{aligned}$$
(15)

We now consider the effects of various parameters on the erosion rate of agglomerates.

Fig. 7
figure 7

Evolution of the erosion rate \(K_{\mathrm{e}}\) of the wet agglomerate A as a function of the debonding distance \(d_{\mathrm{rupt}}\) for a given value of the cohesion index \(\xi =2\), the liquid viscosity \(\eta =1.0\) mPa s, and the inertial number \(I \simeq 10^{-2}\)

Full size image

Figure 7 shows the erosion rate \(K_{\mathrm{e}}\) as a decreasing nearly linear function of the liquid content accounted for by the rupture distance \(d_{\mathrm{rupt}}\) for a given value of the cohesion index, the liquid viscosity, and the inertial number. The mixing of particles with the liquid as agglomerates could be characterized by their connectivity with the particles or the number of particles in liquid clusters. In the “pendular” regime, the binding liquid is in the form of the capillary bridges. As the amount of the binding liquid increases, the liquid clusters have more and more particles in contact. This means that the number of the capillary cohesion forces and viscous forces exerted on each particle increases. As a result, the agglomerates clearly become more stable with higher values of the liquid content in the pendular regime under collision with the cohesionless granular flows.

The capillary bridges induce the capillary attraction forces and viscous forces. The cohesion forces come from the surface tension of the liquid bridges and the other one from the viscosity of the liquid. We assumed that only normal component is considered for the capillary and viscous forces. Due to the physical properties of the nature of the liquid, we expect that both the liquid–vapor surface tension and viscosity of the binding liquid increase the resistance of erosion of wet agglomerates, and this means observe lower values of the erosion rate as increasing these liquid properties. Figure 8 displays the evolution of the erosion rate \(K_{\mathrm{e}}\) of agglomerate A as a function of the liquid viscosity \(\eta \) for a given value of the liquid–vapor surface tension, the amount of liquid, and the inertial number. \(K_{\mathrm{e}}\) decreases as a nearly linear function of \(\eta \) due to the lubrication forces acting between particles. This means that the viscous forces tend to reduce the shear strength of cohesionless granular flow on the agglomerates, leading to smaller erosion. It is also noticeable that this observation is in good agreement with previous experiment [12] and numerical simulation [13].

By varying the liquid–vapor surface tension corresponding to the cohesion index \(\xi \) in the range [1, 8], we investigate the erosion dynamics of wet agglomerates for a broad range of values of the shear rate. Figure 9 illustrates the evolution of the erosion rate \(K_{\mathrm{e}}\) as a function of the cohesion index \(\xi \) for different values of the inertial number changing from quasi-static regime to inertial regime. It is really interesting to see that \(K_{\mathrm{e}}\) expressed as a nonlinear function of \(\xi \) for each value of I. We clearly observed a quick increase of the cumulative erosion for low values of the cohesion index and high values of the shear rate. The erosion rate declines with increasing the cohesion index \(\xi \) and decreasing the inertial number I. Remarkably, this nonlinear decrease of the erosion rate was also clearly observed in recent experiment although in different flow geometry and cohesive agglomerate [12].

Fig. 8
figure 8

Evolution of the erosion rate \(K_{\mathrm{e}}\) of the wet agglomerate A as a function of the liquid viscosity \(\eta \) with the cohesion index \(\xi =2\), the rupture distance \({\hbox {d}}_{\mathrm{rupt}}/{\hbox {d}}_{\mathrm{min}}=0.125\), and the inertial number \(I \simeq 10^{-2}\)

Full size image
Fig. 9
figure 9

Erosion rate \(K_{\mathrm{e}}\) of the wet agglomerate A as a function of the cohesion index \(\xi \) for different values of the inertial number I with the liquid viscosity \(\eta =1.0\) mPa s and the rupture distance \({\hbox {d}}_{\mathrm{rupt}}/{\hbox {d}}_{\mathrm{min}}=0.125\)

Full size image

Similarly, Fig. 10 shows the erosion rate \(K_{\mathrm{e}}\) of wet agglomerate A as a function of the inertial number I for different values of the cohesion index \(\xi \) for a given value of the liquid viscosity and the liquid content. The erosion rate increases with decreasing \(\xi \) and increasing I. \(K_{\mathrm{e}}\) is also a nonlinear function of the inertial number. It is also interesting to see that there is a lower threshold of the inertial number I below which no erosion occurs for each value of the cohesion index. We also seem to see that for each value of \(\xi \) there is a high threshold of I which wet agglomerates fully disintegrated. In which, the inertial stresses prevail as compared to the confining stress. This means that for high values of I, the collision forces are much larger than the force exerted by the confining pressure \(\sigma _{\mathrm{p}}\).

Fig. 10
figure 10

Erosion rate \(K_{\mathrm{e}}\) of the wet agglomerate A as a function of the inertial number I for different values of the cohesion index \(\xi \) with the liquid viscosity \(\eta =1.0\) mPa s and the rupture distance \({\hbox {d}}_{\mathrm{rupt}}/{\hbox {d}}_{\mathrm{min}}=0.125\)

Full size image

Besides investigation of the effects of flow regimes of dry granular materials and liquid properties of wet agglomerates, we also study the effects of particle properties characterized by its relative dry–wet density. The relative density \(\alpha _{\mathrm{r}}\) is defined as a ratio of the cohesionless particle density and the wet particle density (\(\alpha _{\mathrm{r}} = d_{\mathrm{d}}/d_{\mathrm{w}}\)), where \(d_{\mathrm{d}}\) and \(d_{\mathrm{r}}\) are the density of dry and wet particles, respectively. In order to keep the same properties of wet agglomerates, their cohesion forces are unchanged as compared to the above values. We only independently varied the density of cohesionless particles.

Fig. 11
figure 11

Evolution of the erosion rate \(K_{\mathrm{e}}\) of the agglomerate A as a function of the inertial number I for different values of the relative wet–dry density \(\alpha _{\mathrm{r}}\) with the rupture distance \({{d}}_{\mathrm{rupt}}/{{d}}_{\mathrm{min}}=0.125\) and the cohesion index \(\xi = 3.0\)

Full size image

Figure 11 represents the evolution of the erosion rate \(K_{\mathrm{e}}\) as a function of the inertial number I for different values of the relative dry–wet density \(\alpha _{\mathrm{r}}\) for a given value of the liquid content, the cohesion index, and the liquid viscosity. \(K_{\mathrm{e}}\) is as a nonlinear increasing function of I for each value of \(\alpha _{\mathrm{r}}\). As we can see, however, the data points of the erosion rate nearly collapse on a master curve as a function of I. This means that \(K_{\mathrm{e}}\) is nearly independent to the relative dry–wet density for each value of the inertial number. These results are different as compared to that observed in previous experiment when considered a fixed agglomerate in the center of a half-filled flow of granular materials in a rotating drum [12], where the collision forces between dry grains and fixed granule mainly come from the particle gravity and the kinetic energy of complex flow. Thus, this difference may be explained due to the differences of the simulated model and the flow geometry as well as without considering the gravity in a plane shear flow in our work, where the movement of agglomerates is due to the relative displacement between wet and dry particles.

The initial position of wet agglomerates is also studied in this work in order to fully get a general view of the erosion dynamics of such agglomerates inside a shear flow of cohesionless particles. We only considered two agglomerates A and B located at two different positions inside granular bed. Figure 12 displays the erosion rate \(K_{\mathrm{e}}\) as a function of I for agglomerates A and B for a given value of the liquid content, the liquid–vapor surface tension, and the cohesion index. The curves clearly show a significant difference of erosion of these two agglomerates especially for high values of the inertial number. This may be explained due to relative displacements between wet agglomerates and dry particles and the collective collisions between them as a consequence of imposed pressure-controlled conditions in inertial flow.

Fig. 12
figure 12

Erosion rate \(K_{\mathrm{e}}\) as a function of the inertial number I for two different initial positions of wet agglomerates with the cohesion index \(\xi = 3.0\) and the rupture distance \({{d}}_{\mathrm{rupt}}/{{d}}_{\mathrm{min}}=0.125\)

Full size image

5 Scaling behavior of wet agglomerates

We see that all variations of the erosion rate of wet agglomerates as shown above mainly come from the changes of the inertial number I, the cohesion index \(\xi \), and the liquid viscosity or Stokes number St. These presentations suggest that all these data points may collapse on a master curve as a function of the new scaling parameter when the viscous stress comes into play in addition to the inertial stress and cohesion stress, which may be extended from the scaling behavior of a single wet agglomerate proposed in our previous publication [14]. Before going to consider this issue, we should define a dimensionless erosion rate independently to other parameters. We know that \(K_{\mathrm{e}}\) defined above has the dimension of inverse of time. Although we varied a broad range of values of the viscosity of the binding liquid, the shear time (\(t_i = \dot{\gamma }^{-1}\)) is still much higher than other characteristic time such as the relaxation time and viscous time. Thus, we normalized the erosion rate \(K_{\mathrm{e}}\) by the shear rate \(\dot{\gamma }\) in order to get the dimensionless erosion rate \(K_{\mathrm{e}} t_i\).

In comparison with the previous scaling parameters which scale the rheology and granular texture of cohesive granular flows [33], the viscoinertial shear flows [40, 44], the viscocohesive inertial flows [41], and the properties of a single wet agglomerate [14], we assumed an erosion scaling parameter \(I^{\alpha _a} \{ (1+\beta /\text{St})\xi \}^{\alpha _b}\) of wet particle agglomerates. By searching different values of \(\alpha _a\) and \(\alpha _b\), we find that for \(\alpha _a = 1/4\) and \(\alpha _b = -1\), all the data points nearly collapse for small values of \(\beta \). Hence, the erosion scaling parameter of wet agglomerates is given by:

$$\begin{aligned} I_{\mathrm{m}} = \frac{I^{1/4}}{\big (1+\frac{\beta }{\text{ St }} \big )\xi } \ , \end{aligned}$$
(16)

where \(\beta \) is the prefactor. As we can see, if \({\hbox {St}} \rightarrow 0\) (as \(\eta \rightarrow \infty \)) or \(\xi \rightarrow \infty \), we get \(I_{\mathrm{m}} \rightarrow 0\). Inversely, \(I_{\mathrm{m}} \rightarrow \infty \) when \({\hbox {St}} \rightarrow \infty \) (as \(\eta \rightarrow 0\)) or \(\xi \rightarrow 0\).

Fig. 13
figure 13

The erosion rate \(K_{\mathrm{e}}\) of the wet agglomerate A normalized by the shear rate \(\dot{\gamma }\) as a function of the scaling parameter \(I_{\mathrm{m}} = I^{1/4}/\{(1 + \beta / {\text{ St }}) \xi \} \) with \(\beta = 0.0026\). Each symbol and its color refer to a group of the simulations in which the inertial number I or the liquid viscosity \(\eta \) was varied in a broad range of values by keeping each constant value of the cohesion index \(\xi \). The black-solid line represents a cutoff power-law fitting form Eq. (17)

Full size image

Figure 13 shows all data points of the normalized erosion rate \(K_{\mathrm{e}} t_i\) nicely collapse on a master curve as a function of the modified scaling parameter \(I_{\mathrm{m}}\) by setting \(\beta \simeq 0.0026\). Although this value is small but compared to a broad range of values of the Stokes number \(\text{ St } = [3.2 \times 10^{-4}, 119,5]\), we cannot neglect the effects of the liquid viscosity on the erosion rate of wet particle agglomerates. The erosion rate increases proportionally to the power 1/4 of the inertial number I, but inversely proportional to the cohesion index \(\xi \) and the liquid viscosity \(\eta \) (or \(1/\text{St }\)). All the data points plotted in Fig. 13 can be fitted by a cutoff power-law function form, as given following:

$$\begin{aligned} K_{\mathrm{e}} t_i = A (I_{\mathrm{m}}^{\alpha _e} - I_0^{\alpha _e}) \ , \end{aligned}$$
(17)

with \(A \simeq 0.045\), \(I_0 \simeq 0.05\), and \(\alpha _e \simeq 1.450\). The values of \(I_0\) and \(\alpha _e\) slightly change compared to the previous scaling due to considering the viscous effects of the liquid bridges inside wet agglomerates. The erosion threshold \(I_0\) is the value of the erosion scaling parameter \(I_{\mathrm{m}}\) below without erosion occurs. Hence, it is interesting to see that the erosion rate of wet agglomerates could describe as a cutoff function due to the additivity of cohesion and viscous stresses in addition to the inertial stress.

6 Conclusion

In this paper, we used 3D molecular dynamics DEM simulations to measure the evolution of erosion rate and propose the scaling behavior of wet particle agglomerates inside a simple shear flow of cohesionless particles. The wet agglomerates were introduced by the inclusion of the capillary attraction forces and viscous forces due to the presence of the capillary bridges between particles. The erosion occurs as a consequence of irreversibly breaking of the capillary bonds between eroded particle and its neighbors. we analyze the erosion dynamics, the erosion rate of wet agglomerates by systematically varying various parameters including the shear rate, the amount of the binding liquid, the liquid–vapor surface tension, the liquid viscosity, and the relative dry–wet density as well as the initial position of agglomerates.

We showed that the erosion rate of wet agglomerates increases with increasing the shear rate (or the inertial number), decreasing the amount of the binding liquid, the liquid viscosity, the cohesion index, and the height of agglomerates, whereas nearly independent to the relative dry–wet density of particles. In more detail, meanwhile, this rate decreases as a linear function of the liquid content and the liquid viscosity, the erosion rate decreases as a nonlinear function of the cohesion index, but it increases as a nonlinear function of the inertial number. We also showed that the erosion rate can be well-described as a function of the erosion scaling parameter which combines the inertial number, the cohesion index, and the Stokes number. The scaling of erosion rate of agglomerates can be expressed as a cutoff power-law function with an erosion threshold below without erosion occurs.

Although we considered a simple shear flow of granular materials under investigating the erosion dynamics of wet agglomerates, the results presented in this paper may provide a better understanding of the agglomeration process of solid particles in a rotating drum. Since the agglomeration process is a complex process which represents a complex granular flow as well as containing various physical phenomena such as nucleation, coalescence, accretion, and erosion. Thus, these above investigations could be extended for analyzing the accretion phenomenon and coalescence, which may also depend on the inertial number of complex granular flow and the cohesion index and Stokes number of the liquid that covers the particles.

The erosion rate presented in this paper was obtained by assuming the irreversible breaking of capillary bonds. This erosion rate may decrease by considering the re-formation of the capillary bonds after being broken. Since a part of the liquid volume may re-cover the eroded particles, meanwhile another one may be lost as a consequence of evaporation and drainage. This rate may also decrease by additionally considering the tangential cohesive force and the tangential viscous force in each capillary bridge since the tensile shear strength of the liquid bridge has the opposite direction to the direction of the particle being detachment. However, this is a complex phenomenon that needs more experiments in order to take into account the tangential cohesive and viscous forces as well as being validation the numerical results.