1 Introduction

The cracking phenomenon in reinforced concrete (RC) structures has a critical role not only under the serviceability conditions but also in the structural behavior leading to collapse, which is directly influenced by the steel–concrete interface (or bond). The tensile behavior and strength of reinforcement are essential to calculate the ultimate strength of RC members subjected to bending since the tensile strength of concrete is quite limited compared to its compression capacity. On the other hand, the tensile resistance and stiffness of concrete can change the load–deflection characteristics, member stiffness, and deformation of reinforced concrete members. For instance, the intact concrete part of the RC beam carries significant forces under typical in-service loads, which directly contributes to the stiffness of the member. Moreover, a direct tension test of a reinforced concrete tie exhibits gradual stiffness degradation at the macro-level with successive primary cracks in concrete when it is subjected to incremental tensile forces. Once a stabilized crack pattern appears in concrete, the stiffness of the cross section is much lower and stresses transfer to steel reinforcement through the steel–concrete interface. This phenomenon is called tension stiffening, and it should be taken into account in computational models to assess reinforced concrete members behavior accurately [1].

As a matter of fact, the tension stiffening in reinforced concrete structures is a complex problem, mostly affected by the local behavior (cracking of concrete and bond quality). Different numerical approaches have been developed in the literature to analyze this problem using both continuum- and discontinuum-based finite element modeling (or finite element analysis, FEA), where continuous or discrete zero-thickness interface elements are utilized, respectively [2,3,4,5,6]. Reinforcements are usually modeled as truss or beam elements associated with solid elements in FEA. In general, a perfect bond condition is assumed by using embedded reinforcement elements in concrete elements [7, 8]. In the case of weak (or deteriorated) bond conditions, more sophisticated models can be considered using interface elements to simulate the bond-slip interaction between steel and concrete surfaces [9,10,11,12].

Discontinuum-based modeling techniques have been also employed to explore the structural behavior of reinforced concrete members under service and extreme loading conditions since the mid-1970s. Pioneer work in DEM was published by Lorig and Cundall [13] to explore the behavior of reinforced concrete beams under static and dynamic loading conditions. The concrete texture was represented via 2D Voronoi polygons, discretized into elastic finite-difference zones, whereas truss (or link) elements were used to replicate steel rebars, assuming fully bonded (or perfect bond) condition. Hence, failure in reinforced concrete beams under bending was analyzed within the framework discrete element formulation, considering brittle contact displacement behavior among the adjacent Voronoi polygons. Note that progressive contact openings, slippage, and eventual diagonal tension cracks were obtained successfully. Similarly, in the finite–discrete element method (FDEM), fracture, and fragmentation processes of deformable bodies are simulated via contact elements that are implemented within the finite element mesh. The applications of FDEM on RC members can be found in [14, 15]. Furthermore, rigid-body-spring model, proposed by Kawai [16], was applied to analyze the crack propagation in reinforced concrete structures, where the concrete was represented via rigid bodies based on Voronoi diagrams, interconnected by springs [17]. Recently, a lattice-based approach was presented where the steel, concrete, and bond behaviors are explicitly modeled using overlapping truss elements to explore the structural response of reinforced concrete members [18, 19]. In this research, an alternative computational modeling strategy is proposed by further extending the pioneering work of Lorig and Cundall [13], in which the tension stiffening phenomenon is numerically investigated via discontinuum models composed of large polyhedral blocks in 3D. The fracture mechanism of the RC members is studied by dissecting the interaction between polyhedral blocks based on the appropriate softening contact constitutive laws.

The present study focuses on two essential points: (1) the influence of model parameters on the macro behavior and (2) the fracture mechanisms of reinforced concrete members. Also, the research further extends the application of recently implemented user-defined contact constitutive models executed in a commercial discrete element modeling software, 3DEC, by adopting the one-dimensional truss elements to simulate reinforced concrete behavior. It is worth to mention that there are very few applications of discontinuum models to simulate RC members using DEM. In this context, this study presents a novel approach to explore the composite action of reinforced concrete structures. The goals of this research are, thus, as follows:

  • To provide a discontinuum-based approach for the analysis of reinforced concrete members consisting of randomly generated polyhedral blocks interacting with cohesive contact models and one-dimensional truss elements for the reinforcement.

  • To simulate the fracture mechanism of tension stiffening by explicitly considering the concrete, the steel reinforcement, and the bond between the two materials.

Two experimental studies that have been previously analyzed by other researchers [20,21,22,23] are taken into consideration as benchmark studies. The obtained numerical results are compared with the experimental findings, and relevant inferences are made. In the first part, the tensile test of an RC prism, (also called RC tie, indicating a square cross section with a rebar at the center), tested by [24], is simulated, and parametric research is performed on the validated model. Then, a four-point bending test of a singly reinforced concrete beam, presented in [25], is investigated utilizing the outcomes and suggestions derived from the tension test.

Next, the mathematical formulation of DEM and the proposed discrete models are presented. Note that in the present research, cyclic response (e.g., bar slip history), time-dependent material, and bond degradations (i.e., creep and shrinkage) are not considered.

2 Theoretical background

In the present research, the discrete element method (DEM), proposed by Cundall [26], is applied to explore the cracking and fracture mechanism of reinforced concrete members using the commercial software 3DEC developed by ITASCA [27]. DEM falls into the category of discontinuum type of analysis, used to analyze the structural behavior of blocky systems. The discontinuous formulation of DEM provides a great advantage for the simulation of crack localization and propagation phenomena in quasi-brittle materials computationally since it does not require special crack tracking algorithms, remeshing, and material property updates.

In this study, the mechanical interaction between the distinct polyhedral blocks is used to represent the heterogeneous structure of plain concrete. The internal structure of concrete is represented by a tessellation into polyhedral blocks generated via the Neper software package. There is no attempt made to model the actual shape or number of aggregates in the examined concrete models. Recently, quasi-brittle construction materials (e.g., concrete and masonry) were analyzed with the same strategy, where the Laguerre tessellation was generated by the weighted points optimized to obtain specified morphological properties of the polyhedral bocks [28,29,30]. The objective was, therefore, to obtain a phenomenological approach in which the observed mechanisms are represented in such a fashion that simulations are in reasonable agreement with experiments. In a similar fashion to continuum mechanics, no attempt is made to formulate constitutive models that fully incorporate all the interacting mechanisms of concrete. But an important difference is that failure is discontinuous, and the discrete element method is used, thus avoiding the problems related to mesh sensitivity and convergence of the solution procedure. Further information about the software and the mathematical background of the tessellation algorithm can be found in [31,32,33,34]. The mechanical interaction between the blocks occurs through their contact points via linear/nonlinear spring and cohesive frictional elements. Furthermore, the deformability of each block is considered by internally subdividing them into constant strain tetrahedral elements (denoted as finite-difference zones), as shown in Fig. 1. Approximately, 20 tetrahedral elements are used for each polyhedral block. The interpenetration of the blocks is allowed assuming a soft contact approach based on the spring stiffness of the assigned contact in three orthogonal directions.

Fig. 1
figure 1

Polyhedral blocks generated via Neper software and representation of point contact

Full size image

The core part of the numerical procedure of DEM relies on the integration of the equations of motion via a central difference formulation to calculate the nodal velocities for each block in the discrete system. Quasi-static calculations are performed by means of a dynamic relaxation algorithm adopting artificial damping. The compact form of the equations of motion written for a deformable block is given in Eq. 1. Note that, in the given expression, nodal velocities are evaluated at the mid-intervals of the time step (\( \Delta t \)) considering as \( t - \Delta t/2 \) and \( t + \Delta t/2 \), which are denoted by \( t^{ - } \) and \( t^{ + } \), respectively.

$$ \begin{aligned} \dot{\varvec{u}}_{i}^{t + } & = \dot{\varvec{u}}_{i}^{t - } + \left[ {\Sigma \varvec{F}_{i}^{t} - \left( {\varvec{F}_{d} } \right)_{i} } \right]{{{\Delta t}} {\left/ {\vphantom {{\Delta t} {m_{n} }}}\right.} {m_{n} }} \\ \left( {\varvec{F}_{d} } \right)_{i} & = \gamma \left| {\Sigma \varvec{F}_{i}^{t} } \right|{\text{sgn}}\left( {\dot{u}_{i}^{t - } } \right) \\ \end{aligned} $$
(1)

where \( \dot{\varvec{u}}, \varvec{F}^{t} , \) and \( m_{n} \) are the velocity vector, net nodal force vector, and lumped nodal mass, respectively, calculated for each node (or so called gridpoint). The force vector \( F \) includes external loads, contact forces (only for gridpoint along the surface of the block), gravity forces, and the contribution to the internal stress in the zones adjacent to the gridpoint that can be obtained as

$$ \varvec{F} = \mathop \smallint \limits_{S} \sigma_{ij} n_{j} {\text{d}}s $$
(2)

where \( n_{j} \) is the outward normal to the surface \( S \) (closed polygonal surface) and \( \sigma_{ij} \) indicates the zone stress tensor. Here, a local form of damping is used by defining the force (\( F_{d} \)) with damping constant, \( \gamma \) (default value is 0.8). The damping force is proportional to the magnitude of unbalanced force which opposes the motion considering the velocity vector where \( \text{sgn} \left( \zeta \right) \) = 1, if \( \zeta \geqslant 0 \); \( \text{sgn} \left( \zeta \right) \) = − 1, if y \( \zeta < 0 \) [35]. The damping constant remains unchanged during the analysis. A detailed explanation of the implemented local damping algorithm can be found in [36]. Moreover, scaled masses are used to speed up the calculations, since, in quasi-static analysis, inertial forces have minimal effect as long as they are small compared to the other forces in the system.

Once the nodal velocities are calculated, the block positions are updated, and relative contact displacements are found. It is important to note that through the dynamic solution scheme of DEM, contact conditions are updated at each time step using a contact detection algorithm based on the common plane concept [37]. The contact detection algorithm requires a unit normal vector to define a plane that changes its direction during the analysis as blocks move relative to each other. In 3DEC, the contact detection algorithm provides uniquely defined “common-plane” bisecting the space between the two convex polyhedral blocks based on the geometrical configuration that maximizes the gap or minimizes the overlap between the blocks [38]. It is worth noting that the conditionally stable solution scheme of DEM necessitates sufficiently small time steps to capture inter-block displacement. To obtain a stable solution, the required critical time step (\( \Delta t_{\text{cr}} \)) can be estimated as

$$ \Delta t_{\text{cr}} = 2 \sqrt {m_{n} /k_{\text{gp}} } $$
(3)

where \( k_{\text{gp}} \) denotes nodal stiffness obtained by adding zone and contact (only the gridpoint on the faces) stiffness [39]. The employed numerical model has the ability to capture large deformations and rotations of the blocks as well as to take into account the interaction forces between the blocks by tracing relative geometrical configuration during the analysis in an updated Lagrangian approach.

2.1 Contact constitutive law

Through this research, relatively high elastic stiffness (i.e., ten times the value of the macro elastic stiffness) is assigned for continuum blocks, denoted as semi-rigid, to determine the governing deformation and nonlinear behavior of the material predominantly via discontinuities, as shown in [29]. Contact stress increments (normal \( \Delta \sigma \) and tangential \( \Delta \tau \)) are calculated based on the relative deformation increments between the blocks both in the normal, \( \Delta u_{n} \), and shear, \( \Delta u_{s} \), directions, as

$$ \Delta \sigma = k_{n} \Delta u_{n} $$
$$ \Delta \tau = k_{s} \Delta u_{s} $$
(4)

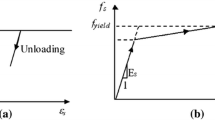
where \( k_{n} \) and \( k_{s} \) denote, respectively, the contact normal and shear stiffness. Once the contact stress increments are calculated, stresses are updated and corrected based on the stress–displacement law assigned to the contact trough the explicit solution scheme of DEM. Here, the mechanical response of plain concrete is simulated using softening functions (linear or polynomial) in tension, whereas elastic perfectly plastic behavior is assumed in compression. The Coulomb-slip joint model is employed in shear direction, which requires cohesion and friction angle parameters. The mathematical formulations of the contact models are given in Eq. 5. Furthermore, the graphical representation of the contact behaviors both in normal and shear directions is given in Fig. 2.

Fig. 2
figure 2

Contact behavior in the normal (elasto-plastic in compression and linear or power-law softening in tension as a function of the polynomial power α, left) and shear (brittle behavior with residual friction, right) directions

Full size image
$$ \begin{aligned} & {\text{if}}\;\sigma_{\text{tension}} \ge f_{T} \;{\text{then}} \left\{ {\begin{array}{*{20}l} {f_{t} = f_{T} \left( {1 - \frac{{u_{n} - \eta }}{\zeta - \eta }} \right)} \\ {\text{or}} \\ {f_{t} = f_{T} \left( {\frac{\zeta }{{\zeta - \eta + u_{n} }}} \right)^{\alpha } ;\zeta = \frac{{2G_{f}^{I} }}{{f_{T} }},\eta = \frac{{f_{T} }}{{k_{n} }}} \\ \end{array} } \right. \\ & \left| {\sigma_{\text{compression}} } \right| \le f_{c} \\ & {\text{if}}\;\tau \ge c_{0} + \sigma_{n} \tan \phi_{0} ;\;{\text{then}}\;\tau = c_{\text{res}} + \sigma_{n} \tan \phi_{\text{res}} \\ \end{aligned} $$
(5)

where \( c_{0} \), \( \phi_{0} \), and \( \alpha \) are the initial cohesion, friction angle, and the user-defined power for the polynomial softening function. Also, the residual cohesion and frictional angles are shown as \( c_{\text{res}} \), and \( \phi_{\text{res}} \), respectively. Note that tension and shear forces utilized in the proposed contact failure criterion are implemented in a decoupled manner, similarly to [40]. The adopted contact models are written in C++ and compiled as DLL (dynamic link library) into 3DEC via the user-defined constitutive model option. Furthermore, contact stiffnesses are defined in Eq. 6 [41], where \( t \) indicates the average thickness of the fracture zone.

$$ k_{n} = E/t $$
$$ k_{s} = G/t $$
(6)

2.2 Reinforcement elements in DEM

The reinforcement embedded in concrete provides remarkable tensile capacity to the material; however, the quality and contribution to the tensile strength mainly depend on the type of the rebar and performance of the bond between the two materials. To replicate the action of reinforcement, truss elements are utilized that may pass through the existing discontinuities. Truss elements use a force–displacement relationship to simulate axial and bond behavior of the reinforcement implemented into the finite-difference algorithm in 3DEC. The axial (\( \Delta F_{\text{axial}} \)) and bond (\( \Delta F_{\text{bond}} \)) force increments are calculated using relative normal (\( \Delta u_{\text{axial}} \)) and shear (\( \Delta u_{\text{bond}} \)) nodal displacements of a truss element as

$$ \Delta F_{\text{axial}} = K_{\text{axial}} \Delta u_{\text{axial}} $$
$$ \Delta F_{\text{bond}} = K_{\text{bond}} \Delta u_{\text{bond}} $$
(7)

where \( K_{\text{axial}} \) and \( K_{\text{bond}} \) denote axial and bond stiffness, respectively. The axial stiffness is determined in terms of the reinforcement cross-sectional area (\( A \)), the elastic modulus (\( E \)), and the length of the truss element (\( L_{\text{el}} \)), given in Eq. 8. Elasto-plastic behavior with a certain yield force is adopted both in tension and compression. There is no rupture limit assigned to truss elements meaning that the yielding deformation continues with no restriction.

$$ K_{\text{axial}} = \frac{{\left( {AE} \right)_{\text{steel}} }}{{L_{\text{el}} }} $$
(8)

The bond stiffness, \( K_{\text{bond}} \) (or shear resistance) is considered using a shear spring that is parallel to the reinforcement. The ratio between the bond stiffness and the axial stiffness of reinforcement is denoted by \( \xi \) and referred to as bond stiffness ratio throughout the article, which directly influences the bond performance and overall behavior of the structural member (Eq. 9). The adopted bond-slip constitutive law is similar to the Coulomb-slip joint model with an elastic–fully plastic response, which is readily available in 3DEC. Hence, only the cohesion (\( c_{\text{bond}} \)) and friction coefficient (\( \phi_{\text{bond}} \)) are required to define the shear failure criteria for the bond.

$$ \xi = \frac{{K_{\text{bond}} }}{{K_{\text{axial}} }} $$
(9)

Additionally, each reinforcement node passing through a constant strain tetrahedral element is linked with a particular tetrahedron (denoted as host zone) to calculate the axial displacement of the reinforcement node considering an interpolation scheme using moment equilibrium. Initially, the host zone is subdivided into tetrahedron based on the geometrical configuration of the reinforcement nodal point to calculate the weighting factors, which is the ratio of an individual tetrahedron to the total volume of the host zone, \( V_{i} /V_{T} \), as presented in Fig. 3. Then, the displacement increments for reinforcement node \( \Delta u_{rn} \) are obtained as,

$$ \Delta u_{rn} = \frac{{V_{1} }}{{V_{T} }}\Delta u_{1} + \frac{{V_{2} }}{{V_{T} }}\Delta u_{2} + \frac{{V_{3} }}{{V_{T} }}\Delta u_{3} + \frac{{V_{4} }}{{V_{T} }}\Delta u_{4} $$
(10)

where \( \Delta u_{i} \) denotes the incremental gridpoint displacements, including x, y, and z components that are utilized to find out the new local position of the rebar node and the axial deformation. In the end, forces calculated for the steel–concrete interface are distributed back to gridpoints applying the weighting factors mentioned earlier. Note that confining stress, acting in the plane perpendicular to the reinforcement axis is computed along the reinforcement for each reinforcement node (see Fig. 3), depending on the stress developing in the zone to which the nodal point is associated. Then, the confining stresses are utilized in the bond strength calculation.

Fig. 3
figure 3

Left Representation of a truss (reinforcement) element embedded into polyhedral blocks. Right Illustration of reinforcement nodal point passing through a tetrahedron element

Full size image

Different applications of reinforcement elements (truss or beam) in discrete and combined finite–discrete element methods were made in the literature to simulate reinforced concrete and masonry structures [15, 42,43,44].

3 Validation of discontinuum modeling of an RC tie

The direct tension test of a concrete prism is analyzed to ensure the replication of experimental data. Quasi-brittle materials, such as concrete, masonry, and rock, have a heterogeneous material structure, exhibiting micro- and macro-cracks that cause failure of the material. Specifically, the disordered structure of plain concrete includes various defects such as inclusions, flaws, stiffness, and geometrical differences of its constituents, leading to a highly nonlinear response and crack localization. Furthermore, concrete reveals a softening post-peak response (tension softening), implying a gradual decrease in the mechanical resistance together with an increasing crack opening after reaching its strength [45]. It is important to note that to capture this response, including the transition from micro- to macro-crack, a displacement-controlled test setup is required such that it eliminates any unnecessary snap-back behavior [46]. Moreover, boundary conditions in the test setup (fixed or rotating) should be defined carefully since they directly influence the fracture mechanism and energy obtained from the experiments [47].

First, the direct tension behavior of plain concrete prism without a notch is analyzed to demonstrate the unreinforced response of concrete obtained via discontinuum models using the same geometrical and material properties of the benchmark experimental study [24]. The contact properties used in the analyses are given in Table 1. The macro-elastic properties of the concrete specimens (\( E \), \( G \), and \( v \)) are taken from the experiment as \( E = 28\,{\text{GPa}} \) and \( v = 0.2 \), given in [24].

Table 1 Contact properties for concrete (contact stiffnesses are given for 100, 250, 500, and 750 blocks, respectively)
Full size table

Note that when the number of blocks is increased, the average thickness of the fracture zone gets smaller due to the decrease in the block sizes. For instance, in coarse and fine discrete models, the average thicknesses are taken as 24 and 14 mm, corresponding to 100 and 500 blocks, respectively. Thus, the contact stiffnesses (elastic contact parameters) are updated for the different number of blocks using Eq. 6, as depicted in Fig. 4. It can be seen that higher contact stiffnesses are utilized for higher number blocks. The average block edges are 12, 18, 14, and 12 mm for 100, 250, 500, and 750 blocks, respectively. However, identical cohesion, tensile strength, and fracture energy values are used for all concrete prism models. Therefore, the same energy dissipation at the contact point is achieved for different numbers of blocks during the analysis. Moreover, the bottom gridpoints are fixed, whereas roller supports are used at the top gridpoints to eliminate any excessive rotation in the specimen. Polynomial softening functions satisfying the appropriate mode-I fracture energy are used, whereas there is no compression limit assigned to the contact, given the nature of the problem. The cohesion strength is assumed two times of the tensile strength, which does not have drastic influence when it is larger than \( f_{T} \) as previously presented by Pulatsu et al. [29].

Fig. 4
figure 4

Contact stiffness variation based on the number block in the model

Full size image

The results of the analyses are presented in Fig. 5, revealing the stress–displacement curves of discrete element models with different numbers of blocks. Although similar pre- and post-peak trends are obtained in each analysis, the results vary slightly due to the irregular and random generation of the blocks, which is also observed in the experiments. In order to better represent this variation, the results are expressed in the form of a computational model envelope (CME), as shown in Fig. 5. Once the first crack occurs in concrete, it causes redistribution of the stresses in the material, yielding a rough surface of fracture pattern. Similar behavior can be observed in the computational model, in which the crack occurs at the contact point that has reached the capacity and presents an irregular cracking pattern under incremental tensile forces (see Fig. 5). For further details on the discontinuum analysis of plain concrete subjected to direct tension, the readers are referred to [29].

Fig. 5
figure 5

Stress–displacement curves obtained for different number of polyhedral blocks representing the plain concrete (CME computational model envelope)

Full size image

Hence, the results show that the tension softening response of concrete can be captured through semi-rigid discrete polyhedral blocks with tensile softening contact models based on the dynamic stress update scheme of DEM. It is worth noting that the number of blocks has a negligible role in the capacity (± 5%) and causes rational variation at the post-peak behavior regarding the morphology of the discontinuum representation. Also, it should be noted that the present research aims to simulate the fracture mechanism of concrete in a relatively cost-effective way with larger polyhedral blocks to capture progressive crack localization and gradual strength degradation. Next, the proposed modeling approach is further extended to explore the tension stiffening behavior of a reinforced concrete tie.

3.1 Tension stiffening

A typical tension stiffening curve obtained from the experiment [24], as well as the bare steel rebar behavior, is given in Fig. 6, where the stress drops and stiffness degradation of the section can be observed due to primary cracks in concrete. In the benchmark study, a 0.6-m-long RC prism with a cross section of 68 ×68 mm and a single 8-mm-diameter rebar embedded at the center is tested under direct tension.

Fig. 6
figure 6

Macro behavior of RC prism [24] and bare still rebar subjected to uniaxial tension

Full size image

To replicate the test setup, the first nodal point of the reinforcement is restricted in all directions, and roller supports are assigned to the right and left gridpoints in the numerical model. Then, the right reinforcement node is subjected to a fixed velocity boundary condition by setting a displacement rate (\( v_{n} \)) of 5 mm/s to elongate the steel reinforcement. During the analysis, the reaction forces are recorded from the left node of the rebar, extracted at each time step by the implemented subroutine in the software based on FISH functions (an executable programming language in 3DEC).

In Fig. 7, the numerical solution is compared with the experimental result for the perfect bond (no-slip) condition considering a relatively high cohesive strength (\( c_{\text{bond}} = 10^{9} \,{\text{N/m}} \)) to make sure that no sliding can occur at the bond. Furthermore, the number of truss elements and the bond stiffness ratio are assumed as 96 and 4, respectively. Therefore, approximately four truss elements can be located for each polyhedral block along the steel reinforcement, which yields \( K_{\text{Axial}} = 1.55\,{\text{GPa}} \). Accordingly, from the bond stiffness ratio of four, \( K_{\text{Bond}} \) can be calculated as \( 6.19\,{\text{GPa}} \). The contact and material properties are mentioned earlier (Table 1). The steel elastic modulus and yield stress are defined as \( 192.3\,{\text{GPa}} \) and \( 400\,{\text{MPa}} \), respectively. Overall, there is a good agreement found between the results from the proposed discontinuum model consisting of 100 blocks and the experiment. The computational model captures the stress drops and the convergence to yielding the force of rebar in a similar fashion with the experiment. Thus, the presented numerical model and its input parameters are considered as the validated baseline in the following section, where a parametric study is conducted.

Fig. 7
figure 7

Comparison between the experiment and discrete element model (100 Blocks)

Full size image

Furthermore, the velocity boundary condition, considered at the reinforcement node to extend the rebar, is varied to validate the influence of loading rate on the force–displacement response of the numerical model. As shown in Fig. 8, the results reveal a convergence trend when the applied displacement rate gets smaller (e.g., \( v_{n} \le 5\,{\text{mm/s}} \)).

Fig. 8
figure 8

Influence of the displacement rate applied to pull the rebar (m/s) on the macro-response of the RC specimen

Full size image

It is worth noting that three local peak points are obtained, representing the crack localization in the specimen that occurs sequentially under incremental forces. Each stress drop exhibits the loss of tensile strength in concrete as a local phenomenon, where the stresses gradually transfer to reinforcing rebar through the bond. The progressive cracking mechanism is presented in Fig. 9, in which the cracking in concrete and the tensile damage at the contact surfaces can be observed with the corresponding location on the force–displacement curve, denoted by a red circle. At the end of the analysis, three fully opened cracks are observed in the specimen, each one corresponding to a load drop in the response.

Fig. 9
figure 9

Numerical simulation revealing the fracture mechanism of an RC prism

Full size image

3.2 Sensitivity analyses

In this section, a comprehensive parametric study is presented, including contact models (tensile softening type), bond stiffness ratio, number of truss elements, number of polyhedral blocks, and bond cohesion strength. It is aimed at providing practical information compromising the computational cost and the accuracy obtained via the proposed modeling strategy with respect to each parameter.

First, two different tensile softening regimes, namely linear softening (LS) and polynomial softening (PS) at the contact points between the discrete polyhedral blocks, are investigated to demonstrate their influence on the macro-response of the RC specimen. It is also important to note the identical contact parameters (\( f_{T} , c \) and \( G_{f}^{I} \)) are employed in both computational models, and the polynomial function power (\( \alpha \)) is taken as 3. As shown in Fig. 10, both contact constitutive laws provide the close results to each other with small differences at the local peak points. However, since the linear softening contact model requires fewer input parameters, it may be a favorable solution in cases where experimental data are lacking.

Fig. 10
figure 10

Applications of different softening models (PS polynomial softening, LS linear softening) in reinforced discontinuum model of concrete

Full size image

Another critical aspect of the proposed modeling strategy is to estimate the appropriate bond stiffness ratio (\( \xi \)). In the present research, the bond stiffness (\( K_{\text{bond}} \)) is taken to be proportional to the stiffness of the truss elements (\( K_{\text{axial}} \)), as previously presented in [48], using the rigid circular particles in the framework of DEM. The bond stiffness ratio is varied as 2, 4, and 6, and the sensitivity of the numerical model to the bond stiffness ratio is shown in Fig. 11. According to the parametric study, lower values of the bond stiffness ratio (e.g., \( \xi = 2 \)) decrease the initial macro-stiffness by reducing force transfer between the concrete and rebar. On the other hand, a higher bond stiffness ratio (e.g., \( \xi = 6 \)) may yield unnecessary limitations in the numerical model by reducing the bond-slip displacement excessively. Thus, the best numerical estimation is obtained considering a bond stiffness ratio of four (\( \xi = 4 \)), which provided the perfect bond as well as the required force–displacement response from the system when compared to experimental behavior (see Fig. 11).

Fig. 11
figure 11

Influence of the bond stiffness ratio (\( \xi \)) on the macro behavior of the specimen

Full size image

Furthermore, the number of truss elements representing the steel reinforcement is analyzed considering the same contact parameters and bond stiffness ratio, as shown in Fig. 12. The total truss element number of 48, 96, and 120 is taken into consideration along the rebar that corresponds roughly to 2, 4, and 6 truss elements passing through a single polyhedral block, respectively. The results demonstrate that a lower number of truss elements (e.g., 48) cause poor force transfer between the concrete and rebar yielding higher deformation and a decrease in stiffness (see Fig. 12). According to the results of analyses, it is recommended to employ approximately four truss elements though each polyhedral block to make sure that there is a perfect bonding and proper force transfer between the two materials. However, in the case of finer mesh, more truss elements would be advisable. Also, it is observed that an increase in the number of truss elements (e.g., 126) converges to a particular initial stiffness at the macro-level; however, it may cause more brittle response as noticed from the stress drop at the second peak and small contact losses just before reaching to yielding force of steel (Fig. 12).

Fig. 12
figure 12

Influence of the number of truss elements on the macro behavior of the RC tie (\( \xi = 4 \))

Full size image

In order to increase the resolution in the cracking pattern in the computational model, a higher number of blocks are employed considering the same nonlinear contact parameters but different elastic stiffnesses that are predicted based on the average thickness of the fracture zone, as mentioned earlier. The results indicate that the proposed discontinuum models do not exhibit severe block size dependency on the macro behavior of the composite material, as shown in Fig. 13. However, due to the random generation of the blocks and orientation differences at the fracture surfaces, some small variation is noted for different block numbers. Furthermore, it is worth noting that the crack distribution along the RC prism convergences to a particular stabilization trend appearing at the four distinctive locations along the RC tie for higher number blocks (e.g., 250 and 500) that can be noticed from Fig. 14.

Fig. 13
figure 13

Influence of the number of polyhedral blocks on the macro behavior of the RC tie

Full size image
Fig. 14
figure 14

Crack pattern of the discrete model at the time of steel yielding for the different numbers of blocks

Full size image

Finally, the bond cohesive strength (\( c_{\text{bond}} \)) is gradually reduced from 1E9 to 1E4 N/m to explore the weak bond effect on the macro-response of the numerical model, as shown in Fig. 15. It is important to note that the adopted bond-slip contact law only depends on the constant value of cohesion. Thus, it should be considered as the most straightforward representation of the interaction between concrete and rebar. The results reveal that perfect and weak bond conditions are successfully captured via applied discontinuum models composed of large blocks. Moreover, it can be noticed that once the cohesive strength gets smaller than 1E5 N/m, bond-slip failure becomes dominant, and the response gets close to the bare steel behavior.

Fig. 15
figure 15

Influence of the bond cohesive strength, \( c_{\text{bond}} \) (N/m) on the macro behavior (100 Blocks)

Full size image

Through this research, the models are calculated using a computer system with Intel(R) Xeon(R) CPU @ 2.1 GHz processor and 128 GB memory RAM. As shown in Table 4, a significant increase in the computational cost occurs related to the number of blocks and the number of contact points used in the discontinuum system (Table 2).

Table 2 Computational time required to perform the direct tension test of RC prisms
Full size table

4 Discrete element modeling of bending test of an RC beam

To extend the application of the proposed modeling strategy from direct tension to flexural behavior, a four-point bending test of a singly reinforced concrete beam is analyzed, tested by Walraven [25]. Detailed information about geometrical properties, boundary, and loading conditions in the original testing can be found in [25], which are adopted in the numerical work here as appropriate. The same discontinuum modeling technique made up of semirigid polyhedral blocks is used, and the outcomes of the comprehensive sensitivity analysis provided in the previous section are utilized. Two discontinuum models consisting of 250 and 500 blocks are generated, where approximately four truss elements are employed for every single polyhedral block along the rebar in both models. Furthermore, to obtain an accurate stress distribution along the beam cross section, a minimum of ten contact points are considered between the bottom and top surface of the model, as discussed in [49, 50]. A perfect bond condition is assumed during the analysis using a relatively high bond cohesion strength (e.g., 1E9 N/m). Also, to reduce the computational cost, only the half-symmetric geometry of the RC beam is modeled considering roller supports, as shown in Fig. 16, together with its dimensions. It is noted that this forces cracks to be symmetric, thus slightly overestimating post-peak shear controlled inelastic failures. Similarly, nodes are subjected to a fixed velocity boundary condition by setting a displacement rate of 5 mm/s to apply flexural forces, represented in Fig. 16. During the analysis, the reaction forces are recorded from upper nodes, extracted at each time step by the implemented subroutine in the software based on FISH functions.

Fig. 16
figure 16

Left Dimension of the RC beam (all in mm) and boundary conditions; Right Cross section including reinforcements

Full size image

Additionally, elasto-plastic contact behavior for compression with linear tensile softening is assumed in the normal direction, whereas the Coulomb-slip joint model is defined in the shear direction to simulate the interaction between the blocks replicating concrete. The beam thickness is taken as 200 mm, and the elastic modulus of concrete is defined as 25 GPa. The linear contact stiffness (\( k_{n} \)) is predicted as 500 GPa/m and 625 GPa/m for 250 and 500 blocks, respectively. The additional nonlinear contact parameters can be found in Table 3. Note that the bond stiffness ratio is assumed as 4. The modulus of elasticity and yield stress of the longitudinal rebars are defined based on the reference study as 210 GPa and 440 MPa, respectively.

Table 3 Nonlinear contact parameters used for blocks representing concrete at the RC beam
Full size table

The results indicate that there is a good agreement between the numerical analyses and experiment, where the macro behavior of the tested RC beam is captured successfully, given in Fig. 17a. It is important to note that the results do not depend on the number of blocks. Initially, flexural tensile cracks are observed, which are developed along the constant moment region of the beam. Extensive yielding of reinforcement is found with wide cracks. Since there is a perfect bond assumed during analysis, the tensile forces are carried by the steel reinforcement, which yields new cracks closer to the support predominantly in the constant moment zone. Finally, the failure of the RC beam is obtained due to diagonal tension crack in the discontinuum model similar to the experiment, as shown in Fig. 17b. Note that the obtained failure mechanism is typical for reinforced concrete beams without stirrups, as discussed in [8, 13]. The average spacing of cracks in the pure bending zone of the beam is 90 mm, which agrees well with the experimental value. The number of cracks in both models (250 and 500 blocks) is the same. In Table 4, the computational times for the analyses are given.

Fig. 17
figure 17

Load–deflection response of the RC beam and failure mechanism

Full size image
Table 4 Computational time required to perform flexural analysis
Full size table

Finally, linear elastic contact constitutive behavior is assumed instead of the elasto-plastic model in compression as a simple alternative solution. Although the results do not exhibit a considerable difference in the macro behavior in this case (concrete crushing is not relevant for the global beam behavior), neglecting the plasticity in concrete results in slightly higher stiffness on the macro behavior, as shown in Fig. 18.

Fig. 18
figure 18

Influence of different contact constitutive models in the compression regime on the macro-response of the RC beam

Full size image

5 Conclusions

The primary contribution of this paper lies in combining randomly generated three-dimensional polyhedral blocks with one-dimensional truss elements to simulate the fracture mechanism of RC members within a discrete element modeling framework. The results clearly show the great potential of the applied modeling strategy to simulate the composite action of reinforced concrete members, including tension stiffening phenomenon. From the numerical results, the following conclusions are derived.

  • The proposed phenomenological discontinuum approach captures the fundamental fracture mechanism of RC members based on the inter-block interaction and defined elasto-plastic contact constitutive laws. Moreover, the applied contact models, including the mode-I fracture energy, provide an accurate estimation of the macro behavior, and numerical solutions do not exhibit a severe block size dependency.

  • It is shown that discrete element models have a clear advantage compared to the smeared crack approach since the discrete representation of concrete provides physical crack localizations and realistic fracture patterns that are in line with the experimental observations.

  • From the many numerical simulations carried out, practical inferences are made about the essential parameters in the discontinuum model (e.g., number of truss elements and bond stiffness ratio) to obtain a perfect bond action between concrete and reinforcement in the applied modeling strategy.

  • It is possible to estimate the capacity and corresponding failure patterns efficiently with a rather small number of discrete blocks. Hence, proposed models can be used as a robust research tool to better understand the brittle failure mechanisms of plain concrete subjected to tension and composite behavior of reinforced concrete members under tension and bending.

  • The proposed discontinuum approach can be used for various types of RC members to understand their cracking mechanism and predict their capacity.

In future studies, more elaborate bond-slip constitutive laws may be developed and implemented. Furthermore, the time-dependent material degradation effects, such as creep and shrinkage, may be considered to better estimate the current performance of structural RC members.